2010-2011线性代数试题 A
线性代数考试试卷及参考答案(A卷)

,,t α是AX t t c α++仍t c ++= .满足条件3.m n ⨯矩阵A ()12,,,n ααα=,方程组=AX B 有解的充要条件是( ).()A 12,,,n ααα线性无关; ()B 12,,,,n B ααα线性相关; ()C 12,,,,n B ααα线性无关; ()D 12,,,n ααα与12,,,,n αααB 等价.4. 设A 是n n ⨯矩阵,则下列结论错误的是( ).()A AX =B 无解时,0=A ; ()B AX =B 有无穷多个解时,0=A ;()C 若0=A ,则AX =B 无解; ()D AX =B 有惟一解时,0≠A .5.二次型2122213212x x x x )x ,x ,x (f -+=的矩阵是( ).(A )⎥⎦⎤⎢⎣⎡-1021; (B )⎥⎦⎤⎢⎣⎡--1111;(C )⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-000010021;(D )⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--000011011.三.计算下列各题(本题满分为55分)1. 已知行列式512345222113124527,1112243150D == 求414243A A A ++和4445A A +. 其中4(1,2,3,4,5)j A j =为5D 中第4行第j 列元素的代数余子式.(本题满分为10分);2.(本题满分为15分)已知矩阵1111222233334444⎛⎫⎪⎪= ⎪⎪⎝⎭A ,求100A ...3.(本题满分为15分)问a b 、取何值时123423423412340221(3)223231x x x x x x x x a x x b x x x ax +++=⎧⎪++=⎪⎨-+--=⎪⎪+++=-⎩无解?有唯一解?有无穷多解?并在有无穷多解时求出通解..4.(本题满分为15分)已知20000101A x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与20000001B y ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦相似, (1)求x 与y ;(2)求一个满足1P AP B -=的可逆阵P .四.证明(本题满分为10分)设A 是n 阶矩阵,证明:对于任意的B ,=AX B 都有解的充分必要条件是0≠A .线性代数试题答案与评分标准一、填空题1、62、-1283、(),i j E4、15、0k > 二、选择题1、B2、B3、D4、C5、D 三、计算题1、由已知条件得 41424344454142434445(111)(22)27,(222)(11)0.A A A A A A A A A A ⋅+⋅+⋅+⋅+⋅=⎧⎨⋅+⋅+⋅+⋅+⋅=⎩ ………………(5分)解方程得41424344459;18.A A A A A ++=-+= ………………(10分)2.将A 写成两个矩阵的乘积,即()11111222221111,3333344444⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A ……(5分) 故 ()()()100111222111111111111.333444⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A ………………(10分) 由于()12111110,34⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭则 ()10099999911111222221011111010.3333344444⎛⎫⎛⎫⎪ ⎪⎪ ⎪=== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭A A ……(15分)………………(15分)3、11110111100122101221(/)012(3)2002(2)01323100210B A b a b a b a a ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==→⎢⎥⎢⎥----+⎢⎥⎢⎥--⎣⎦⎣⎦111101111001221012210021000210002(2)01000(1)(2)1a a a b a a b ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥→→⎢⎥⎢⎥--⎢⎥⎢⎥-+---+⎣⎦⎣⎦(5分) 2,1a b =≠-且无解;2a ≠有唯一解;2,1a b ==-且有无穷多解。
线性代数试题A及答案
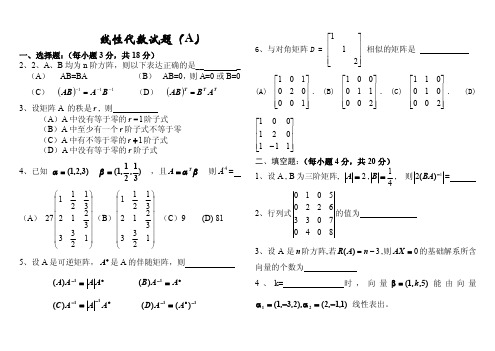
线性代数试题(A )一、选择题:(每小题3分,共18分)2、2、A 、B 均为n 阶方阵,则以下表达正确的是__ _ (A ) AB=BA (B ) AB=0,则A=0或B=0 (C ) ()111---=B A AB (D ) ()T T TA B AB =3、设矩阵A 的秩是r , 则(A )A 中没有等于零的1-r 阶子式 (B )A 中至少有一个r 阶子式不等于零 (C )A 中有不等于零的1+r 阶子式 (D )A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ,且b a T A = 则4A =(A ) 27÷÷÷÷÷÷øöççççççèæ1233321231211(B )÷÷÷÷÷÷øöççççççèæ1233321231211 (C )9 (D) 81 5、设A 是可逆矩阵,*A 是A 的伴随矩阵,则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题:(每小题4分,共20分)1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时,向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。
10-11(1)高数A(三)试卷

《高等数学 A(三)》(B 卷) 第 6 页 共 6 页
三、计算题(本大题 10 分)
11.计算 n 阶行列式
a1 − m a2 "
Dn =
a1 "
a2 − m " ""
a1
a2 "
an an 的值. " an − m
得分
《高等数学 A(三)》(B 卷) 第 2 页 共 6 页
答 题勿超装 订 线
------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------
通过正交变换 X = QY 化成标准形 f ( y1, y2 , y3 ) = 3y12 + 3y22 + by32 . (1)求参数 a, b 的值; (2)求正交矩阵 Q .
《高等数学 A(三)》(B 卷) 第 3 页 共 6 页
14.(本小题 10 分)甲、乙二人之间经常用 e-mail 联系,他们约定在收到对方邮件的当天即 给回复(即回一个 e-mail),由于线路问题,每 n 份 e-mail 中会有1份不能在当天送达收件人. 甲在某日发了1份 e-mail 给乙, (1)试求甲在当天收到乙的回复的概率; (2)如果已知甲在当天未收到乙的回复,试求乙在当天收到甲发出的 e-mail 的概率.
(完整版)线性代数试卷及答案详解

《线性代数A 》试题(A 卷)试卷类别:闭卷考试时间:120分钟考试科目:线性代数考试时间:学号:姓名:3的一组标准正交基,=___________《线性代数A》参考答案(A卷)一、单项选择题(每小题3分,共30分)二、填空题(每小题3分,共18分)1、 256;2、 132465798⎛⎫ ⎪--- ⎪ ⎪⎝⎭; 3、112211221122000⎛⎫⎪- ⎪ ⎪-⎝⎭; 4、; 5、 4; 6、 2 。
三. 解:因为矩阵A 的行列式不为零,则A 可逆,因此1X A B -=.为了求1A B -,可利用下列初等行变换的方法:231211201012010*******121011411033110331023211027210027810027801141010144010144001103001103001103---⎛⎫⎛⎫⎛⎫⎪⎪⎪-−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎪⎪⎪−−→--−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭―――――(6分)所以1278144103X A B -⎛⎫ ⎪==-- ⎪ ⎪⎝⎭.―――――(8分)四.解:对向量组12345,,,,ααααα作如下的初等行变换可得:1234511143111431132102262(,,,,)21355011313156702262ααααα--⎛⎫⎛⎫⎪ ⎪----- ⎪ ⎪=→ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭111431212011310113100000000000000000000--⎛⎫⎛⎫⎪⎪---- ⎪ ⎪→→⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭――――(5分)从而12345,,,,ααααα的一个极大线性无关组为12,αα,故秩12345{,,,,}ααααα=2(8分)且3122ααα=-,4123ααα=+,5122ααα=--――――(10分) 五.解:对方程组的增广矩阵进行如下初等行变换:221121121121110113011311101112002421120113400(2)(1)42p p p p p p p p p p p p p p p p p p p p p ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪−−→--−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--+--+⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪−−→------- ⎪ ⎪-+-+⎝⎭(分)(1) 当10,(2)(1)0,p p p -≠-+-≠且时即1,2,p p ≠≠-且时系数矩阵与增广矩阵的秩均为3,此时方程组有唯一解.――――(5分) (2) 当1,p =时系数矩阵的秩为1,增广矩阵的秩为2,此时方程组无解.――――(6分)(3) 当2,p =-时此时方程组有无穷多组解. 方程组的增广矩阵进行初等行变换可化为1122112211221211033301112111033300001011011180000------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-−−→-−−→-- ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭--⎛⎫⎪−−→------ ⎪ ⎪⎝⎭(分)故原方程组与下列方程组同解:132311x x x x -=-⎧⎨-=-⎩ 令30,x =可得上述非齐次线性方程组的一个特解0(1,1,0)Tξ=--;它对应的齐次线性方程组13230x x x x -=⎧⎨-=⎩的基础解系含有一个元素,令31,x =可得1(1,1,1)T ξ=为该齐次线性方程组的一个解,它构成该齐次线性方程组的基础解系.此时原方程组的通解为001101,,.k k k k ξξ+这里为任意常数――――(12分)六.解:(1)由于A的特征多项式2124||222(3)(6)421I A λλλλλλ----=-+-=+----故A 的特征值为13λ=-(二重特征值),36λ=。
线性代数A_复习题2011-1

4.0000000004321a a a a =( )(A) 4321a a a a (B ) -4321a a a a (C) 24321a a a a (D)-24321a a a a 6.设A 为n 阶行列式,则kA =( ) (A)A k (B)Ak⋅ (C ) A kn(D) A kn⋅7.设A ,B 均为n (n>2) 阶行列式,则( )(A)B A B A +=+ (B) B A B A -=-(C ) B A AB ⋅= (D)B A OBA O ⋅=9.已知333231232221131211a a a a a a a a a =3,则232333132222321221123111352352352a a a a a a a a a a a a ---=( ) (A) 18 (B ) -18 (C) -9 (D)2710.41332211000000a b a b b a b a =( )(A) 4321a a a a -4321b b b b (B) 4321a a a a +4321b b b b (C) (21a a -21b b )(43a a -43b b ) (D ) (41a a -41b b )(32a a -32b b )11.记行列式347534453542333322212223212---------------x x x xx x x x x x x x x x x x 为f(x),则方程f(x)=0根的个数为(A) 1 (B ) 2 (C) 3 (D)4 12.设A 为n 阶方阵,则A =0的必要条件是 (A) A 的两行元素对应成比例(B ) A 中必有一行为其余行的线性组合 (C) A 中有一行元素全为零(D) A 中任一行为其余行的线性组合13.是A 三阶矩阵,A =2,A 的伴随矩阵为*A ,则*A 2=( )(A) 4 (B) 8 (C) 16 (D ) 3215.如果D=333231232221131211a a a a a a a a a =M ≠0, 2322213332311312111222222222a a a a a a a a a D =,那么1D =( ) (A) 2M (B)-2M (C) 8M (D ) -8M16. 如果D=333231232221131211a a a a a a a a a =1,1D = 333231312322212113121111324324324a a a a a a a a a a a a ---,那么1D =( ) (A) 8 (B )-12 (C) 24 (D) -2417.已知11111321--x 是关于x 的一次多项式,该式中x 的系数为( ) (A) -1 (B) 2 (C) 3 (D ) 119.已知a ,b 为整数,且满足081100000=-a bb a,则( ) (A) a=1,b=0 (B )a=0,b=0 (C)a=0,b=1 (D) a=1,b=1 20.设A 为三阶矩阵,A =a, 则其伴随矩阵*A 的行列式*A=( )(A) a (B ) 2a (C) 3a (D) 4a 21.设A ,B ,C 为n 阶方阵,且ABC=I ,则( )(A) ACB=I (B)CBA=I (C) BAC=I (D ) BCA=I 22.设A 为n 阶可逆矩阵,*A 是A 的伴随矩阵,则( ) (A )A A =* (B )1-*=n AA (C )nA A=*(D )1-*=AA23.设A ,B 均为n ×n 阶矩阵,则必有( )(A )B A B A +=+ (B )AB=BA(C )BA AB = (D )111)(---+=+B A B A24.设A ,B 为n 阶方阵,且AB= O ,则必有( )(A )若r(A)=n, 则B=O (B )若A ≠O, 则B=O(C )或者A= O , 或者B=O (D )O B A =+25.设A 是n ×m 阶矩阵,C 是n 阶可逆矩阵,r(A)=r ,B=AC ,r(B)= 1r ,则( ) (A ) r >1r (B ) r<1r(C ) r =1r (D )1r 和r 的关系依而定 26.若A 为n 阶可逆矩阵,则下列各式正确的是( ) (A )112)2(--=A A (B )O AA ≠*(C )AAA 11)(--*=(D )T T T A A ])[(])[(111---=27.设A ,B 均为n 阶非零矩阵,且AB =O,则A 和B 的秩( ) (A) 必有一个等于零 (B)一个等于n ,一个小于n (C) 都等于n (D ) 都小于n28.设n 阶方阵A 经初等变化后所得方阵记为B ,则( ) (A) B A = (B) B A ≠(C) B A ⋅>0 (D ) ,若0=A 则0=B 29.A ,B 均为n 阶矩阵,下列各式中成立的为( ) (A) 2222)(B AB A B A ++=+ (B) T T T B A AB =)((C) O B O A O AB ===或则, (D ) ,若0=+AB A 则00=+=B I A ,或30.设A ,B ,B A +,11--+B A 均为n 阶可逆矩阵,则111)(---+BA等于(A )11--+B A (B )B A + (C )B B A A 1)(-+ (D )1)(-+B A31.设n 元齐次线性方程组AX=0的系数矩阵A 的秩为r ,则AX=0有非零解的充分必要条件是( )(A) r=n (B ) r<n (C) r ≥n (D) r>n 32.设A 是n 阶可逆矩阵,*A 是A 伴随矩阵,则( )(A ) 1-*=n AA (B) A A =* (C) nA A =* (D) 1-*=A A33.设n 阶矩阵A 非奇异(n ≥2),*A 是A 伴随矩阵,则( ) (A ) ()A A A n 2-**= (B) ()A A A n 1+**= (C) ()A AAn 1-**= (D) ()A AAn 2+**=34.设n 维向量⎪⎭⎫⎝⎛=21,0,0,21 α, 矩阵A=I -αα',B=I+2αα',其中I 为n 阶单位矩阵,则(A )0 (B )-I (C )I (D )I+αα'35.设A ,B 为同阶可逆矩阵,则 (A) AB=BA(B) 存在可逆矩阵P 使得B AP P =-1 (C) 存在可逆矩阵C 使得B AC C =' (D) 存在可逆矩阵P 和Q 使得B PAQ = 36.下列命题中不正确的是( ) (A) 初等矩阵的逆也是初等矩阵 (B ) 初等矩阵的和也是初等矩阵 (C) 初等矩阵都是可逆的 (D) 初等矩阵的转置仍初等矩阵38.设A 是任一阶方阵,*A 是A 伴随矩阵,又k 为常数,且k ≠0,±1,则必有()*kA =(A) *A k (B ) *-A kn 1(C) *A k n (D) *-A k139.设A ,B ,C 为n 阶方阵,若AB=BA ,AC=CA ,则ABC 等于(A ) BAC (B )CBA (C )BCA (D )CAB40.622211211=a a a a 若,则12020221221112--a a a a 的值为( ) (A) -12 (B )12 (C) 18 (D) 0 41.设A ,B 都是n 阶矩阵,且AB =O,则下列一定成立的为( ) (A )A= O , 或者B=O (B )A ,B 都不可逆 (C )A ,B 中至少有一个不可逆 (D )A+B=O42.设A ,B 均为n 阶矩阵,且满足等式AB =O,则必有( ) (A ),0=A 或0=B (B )A= O , 或B=O(C )A+B=O (D )O B A =+ 44.设A ,B 均为n 阶可逆矩阵,则AB 的伴随矩阵*)(AB = (A) **B A (B) 11--B A AB(C) 11--A B (D ) **A B46.设A ,B 均为n 阶矩阵,且22))((B A B A B A -=-+,则必有( ) (A )A= B (B )A=I (C )AB=BA (D )B=I 47.设A 为n 阶矩阵,且0≠=a A ,*A 是A 的伴随矩阵,则*A=( )(A )1-n a (B )1+n a (C )n a (D )a48.已知向量组⎪⎪⎪⎭⎫ ⎝⎛-=2111α,⎪⎪⎪⎭⎫ ⎝⎛=1302α,⎪⎪⎪⎭⎫ ⎝⎛=7033α与向量⎪⎪⎪⎭⎫ ⎝⎛-=2211β,⎪⎪⎪⎭⎫ ⎝⎛=5122β,⎪⎪⎪⎭⎫ ⎝⎛=333x β等秩,则x=( )(A) -1 (B) -2 (C) 3 (D ) 1 49.设有向量组()4,2,1,11-=α,()2,1,3,02=α,()14,7,0,33=α,()0,2,2,14-=α,()10,5,1,25=α,则该向量组的极大线性无关组是( )(A) ;321,,ααα (B ) ;421,,ααα (C) ;521,,ααα (D) ;5421,,,αααα 50.已知向量组4321,,,αααα线性无关,则向量组4312ααα++,42αα-,43αα+,2αα+,3212ααα++的秩是(A )1 (B )2 (C )3 (D )4 51.设A ,B 为n 阶方阵,A ≠0,AB=0则( )(A) B=0 (B ) 00==A B 或 (C) BA=0 (D) ()222B A B A +=-52.A ,B 为n 阶方阵,则( ) (A) A 或B 可逆,必有AB 可逆 (B ) A 或B 不可逆,必有AB 不可逆 (C) A 且B 可逆,必有A+B 可逆(D) A 且B 不可逆,必有A+B 不可逆53.A 为n 阶方阵,则下列矩阵中是对称矩阵的有( ) (A)A A '- (B)()阶矩阵为任意n C C CA ' (C )A A ' (D)A A '+254.设A 为三阶方阵,且2=A ,则*-+A A 14=( )(A) 214(B) 12 (C)6 (D ) 10855.设A ,B 为n 阶方阵,且()E AB =2,则下列各式中可能不成立的是( ) (A )1-=B A (B)1-=B ABA (C)1-=A BAB (D)E BA =2)( 56.若由AB=AC 必能推出B=C (A ,B ,C 均为n 阶矩阵)则A 必须满足( ) (A)A ≠O (B)A=O (C )0≠A (D) 0≠AB 57.A 为n 阶方阵,若存在n 阶方阵B ,使AB=BA=A ,则( ) (A) B 为单位矩阵 (B) B 为零方阵 (C) A B =-1 (D ) 不一定 58.设A 为n ×n 阶矩阵,如果r(A)<n , 则(A) A 的任意一个行(列)向量都是其余行(列)向量的线性组合(B) A 的各行向量中至少有一个为零向量(C )A 的行(列)向量组中必有一个行(列)向量是其余各行(列)向量的线性组合 (D)A 的行(列)向量组中必有两个行(列)向量对应元素成比例 59.设向量组s ααα,,2,1 线性无关的充分必要条件是(A) s ααα,,2,1 均不为零向量(B) s ααα,,2,1 任意两个向量的对应分量不成比例 (C) s ααα,,2,1 中有一个部分向量组线性无关(D ) s ααα,,2,1 中任意一个向量都不能由其余S-1个向量线性表示60.向量组的秩就是向量组的 (A) 极大无关组中的向量 (B) 线性无关组中的向量 (C ) 极大无关组中的向量的个数 (D) 线性无关组中的向量的个数 61.下列说法不正确的是( ) (A ) 如果r 个向量r ααα,,2,1 线性无关,则加入k 个向量k βββ,,2,1 后,仍然线性无关 (B) 如果r 个向量r ααα,,2,1 线性无关,则在每个向量中增加k 个分量后所得向量组仍然线性无关 (C)如果r 个向量r ααα,,2,1 线性相关,则加入k 个向量后,仍然线性相关 (D)如果r 个向量r ααα,,2,1 线性相关,则在每个向量中去掉k 个分量后所得向量组仍然线性相关62.设n 阶方阵A 的秩r<n ,则在A 的n 个行向量中 (A ) 必有r 个行向量线性无关(B) 任意r 个行向量均可构成极大无关组 (C) 任意r 个行向量均线性无关(D) 任一行向量均可由其他r 个行向量线性表示 63.设方阵A 的行列式0=A ,则A 中 (A) 必有一行(列)元素为零 (B) 必有两行(列)成比例(C ) 必有一行向量是其余行(列)向量的线性组合 (D) 任一行向量是其余行(列)向量的线性组合 64.设矩阵A=),,,,(54321ααααα经过初等行变换后变为⎪⎪⎪⎭⎫⎝⎛-=311012110231111A ,则A 的秩为3,i α为A 的第i 列向量, 且( )成立 (A ) s αααα++=214 (B) s αααα++=21423 (C) s αααα++-=2142 (D)列向量组线性无关 65.设n 元齐次线性方程组的一个基础解系为η1 ,η2 ,η3 ,η4则()也是该齐次线性方程组的基础解系 (A )1443,3221,,ηηηηηηηη----(B )1443,3221,,ηηηηηηηη++++(C )4321321,211,,ηηηηηηηηηη++++++(D )1443,3221,,ηηηηηηηη--++66.设A 是m ×n 矩阵,齐次线性方程组AX=0仅有零解的充分必要条件是( ) (A )A 的列向量线性无关 (B)A 的列向量线性相关 (C)A 的行向量线性无关 (D)A 的行向量线性相关67.n 元线性方程组AX=b ,r (A ,b )<n ,那么方程AX=b(A)无穷多组解 (B)有唯一解 (C)无解 (D )不确定 68.设向量组321,,ααα线性无关,则下列向量组中,线性无关的是(A) 133221,,αααααα-++(B) 3213221,,ααααααα++++(C ) 1332213,32,2αααααα+++(D) 321321321553,222,ααααααααα-++-++69.向量组s ααα,,,21 线性无关的充分条件是 (A)s ααα,,,21 均不为零向量(B)s ααα,,,21 中任意两个向量的分量均不成比例(C )s ααα,,,21 中任意一向量均不能由其余s-1个向量线性表示 (D)s ααα,,,21 中有一部分向量线性无关70.设m ααα,,,21 均为n 维向量, 那么下列结论正确的是( ) (A) 若02211=+++m m k k k ααα , 则m ααα,,,21 线性相关(B )若对任一组不全为零的数m k k k ,,,21 都有02211≠+++m m k k k ααα ,则m ααα,,,21 线性无关(C)若m ααα,,,21 线性相关则对任一组不全为零的数m k k k ,,,21 都有02211=+++m m k k k ααα(D) 若000021=+++m ααα , 则m ααα,,,21 线性无关 71.已知向量组4321,,,αααα线性无关则向量组 (A) 14433221,,,αααααααα++++线性无关 (B) 14433221,,,αααααααα----线性无关 (C) 14433221,,,αααααααα-+++线性无关 (D) 14433221,,,αααααααα--++线性无关72.当向量组m ααα,,,21 线性相关时, 使等式02211=+++m m k k k ααα 成立的常数m k k k ,,,21 为( )(A)任意一组常数(B)任意一组不全为零的常数(C )某些特定的不全为零的常数(D)唯一一组不全为零的常数 73.下列命题正确的是( )(A) 若向量组线性相关, 则其任意一部分向量也线性相关 (B) 线性相关的向量组中必有零向量(C) 向量组中部分向量线性无关, 则整个向量组必线性无关 (D ) 向量组中部分向量线性相关, 则整个向量组必线性相关74.如果向量b 可由向量组s ααα,,,21 线性表示, 则下列结论中哪个正确 (A )存在一组数s k k k ,,,21 , 使等式s s k k k b ααα+++= 2211成立(B)存在一组不全为零的数使s k k k ,,,21 , 使等式s s k k k b ααα+++= 2211成立 (C)存在一组全为零的数s k k k ,,,21 , 使等式s s k k k b ααα+++= 2211成立 (D)对b 的线性表达式唯一75.设向量组s ααα,,,21 的秩为r ,则 (A) 必定r<s(B) 向量组中任意小于r 个向量部分组无关 (C) 向量组中任意r 个向量线性无关 (D ) 向量组任意r+1个向量线性相关 76.设向量组Ⅰ: ⎪⎪⎪⎭⎫⎝⎛=3121111a a a α,⎪⎪⎪⎭⎫ ⎝⎛=3222122a a a α,⎪⎪⎪⎭⎫⎝⎛=3323133a a a α 向量组Ⅱ: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=413121111a a a a β,⎪⎪⎪⎪⎪⎭⎫⎝⎛=423222122a a a a β,⎪⎪⎪⎪⎪⎭⎫⎝⎛=433323133a aa a β, 则( ) (A) 向量组Ⅰ相关⇒Ⅱ相关 (B )Ⅰ无关⇒Ⅱ无关 (C)Ⅱ无关⇒Ⅰ无关 (D)Ⅰ相关⇒Ⅱ相关77.设向量组Ⅰ: ()1111,,c b a =α,()2222,,c b a =α,()3333,,c b a =α向量组Ⅱ:()11111,,,d c b a =β,()22222,,,d c b a =β,()33333,,,d c b a =β, 则( )(A) 向量组Ⅰ相关⇒Ⅱ相关 (B )Ⅰ无关⇒Ⅱ无关 (C)Ⅱ无关⇒Ⅰ无关 (D)Ⅰ相关⇒Ⅱ相关 78.若s ααα,,,21 为n 维向量组,且秩(s ααα,,,21 )=r, 则 (A) 任意r 个向量线性无关 (B ) 任意r+1个向量线性相关(C) 该向量组存在唯一极大无关组(D) 该向量组在s>r 时, 由若干个极大无关组79.设t ααα,,,21 和s βββ,,,21 为两个n 维向量组, 且秩(t ααα,,,21 )=秩(s βββ,,,21 )=r, 则 (A)两向量组等价, 也即可相互线性表出 (B)秩(t ααα,,,21 ,s βββ,,,21 )=r(C )当t ααα,,,21 被s βββ,,,21 线性表出时,两向量组等价 (D)当s=t 时,两向量组等价80.设向量s αααα+++= 21(s>1), 而s s ααβααβααβ-=-=-=,,,221 则( )(A )秩(s ααα,,,21 )=秩(s βββ,,,21 ) (B)秩(s ααα,,,21 )>秩(s βββ,,,21 ) (C)秩(s ααα,,,21 )<秩(s βββ,,,21 )(D)不能确定秩(s ααα,,,21 )与秩(s βββ,,,21 )间的关系 81.向量组s ααα,,,21 线性无关的充分条件是 (A) s ααα,,,21 均为非零向量(B) s ααα,,,21 中任意两个向量的分量不成比例(C ) s ααα,,,21 中任意一个向量不能被其余向量线性表示 (D) s ααα,,,21 中有一个部分组线性无关 82.设A 为n 阶方阵, 且r(A)=r<n, 则中 (A )必有r 个行向量线性无关 (B)任意r 个行向量线性无关 (C)任意r 个行向量构成极大无关组(D)任意一个行向量都能被其他r 个行向量线性表示 83.A 是m ×n 矩阵, r(A)=r 则A 中必( )(A)没有等于零的r-1阶子式至少有一个r 阶子式不为零 (B )有不等于零的r 阶子式所有r+1阶子式全为零 (C)有等于零的r 阶子式没有不等于零的r+1阶子式 (D)任何r 阶子式都不等于零任何r+1阶子式都等于零 84.设s ααα,,,21 和t βββ,,,21 均为nR 中向量,且秩(s ααα,,,21 )=秩(t βββ,,,21 )=r ,则( ) (A)两个向量组相等价(B)秩(s ααα,,,21 ,t βββ,,,21 )=r(C )当s ααα,,,21 能被t βββ,,,21 线性表示时两向量组等价 (D)当s=t 时两向量组等价 85.能表成向量()1,0,0,01=α,()1,1,1,02=α,()1,1,1,13=α的线性组合的向量是( ) (A) ()1,1,0,0 (B )()0,1,1,2 (C)()1,0,1,3,2- (D)()0,0,0,0,86.已知()3,2,11=α, ()2,1,32-=α,()x ,3,23=α 则x=( )时321,,ααα线性相关。
高数必不挂-高等数学A(一)2010-2011(A)解答

第 1 页 共 6 页上 海 海 事 大 学 试 卷2010 — 2011 学年第一学期期末考试 《 高等数学A (一)》(A 卷)解答一、单项选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中) (本大题分3小题, 每小题4分, 共12分).)( ;)(;2)( ; 0)(2coslim 120不存在,但不是无穷大为无穷大 等于 等于)(的值为、D C ••B A •••A••••••••••••••••xx x +→个不同的实根 有 有三个不同的实根 有唯一实根 无实根 )(则方程适合、设5)()()()(0432,,53,,2352D C •••B A ••••B•••••c bx ax x b a b a =+++< 为正常数 恒为零 为负常数 不为常数 )(则、设)()()()()(,)(32sin D C •••B A •••D•••••••••••x F dt e x F •x •xt ⎰+=π二、填空题(将正确答案填在横线上)(本大题分2小题, 每小题4分, 共8分)1、的值为201lim x x e x x --→ 212、设a b c ,,均为非零向量,满足c b a a c b b a c ⨯=⨯=⨯=,,,b ++三 计算题(必须有解题过程,否则不给分) (本大题分10小题,每题6分,共 60分)1、极限xx xx 2)4(lim +∞→ 884)41(lim e xxx =+=⋅∞→原式 6分2、)0(,)cos()(y y xy e x y y xy '=+=求确定由方程设--------------------------------------------------------------------------------------装 订线第 2 页 共 6 页解:y xy y x y y x y e xy '='+-'+)sin()()(, 4分2)0(,2.,0='==y y x 时当 6分3、.求dx xx••⎰--1145 解:令 ,541452-==-x t x t () 1分 原式=-⎰185213()t dt4分 =166分 4、.d )1(arctan x x x x⎰+求解:x x x xd )1(arctan ⎰+)d(arctan arctan 2x x ⎰= 3分C x +=2)(arctan 6分(遗留C 扣1分)5、.点处的连续性和可导性在试讨论,,已知 0)( , 00cos )(20=⎪⎩⎪⎨⎧≤>=⎰x x f x •••x x tdt t x f •x •解:0)0(0lim )(lim )0(0cos lim )0(200====-==+--+→→→⎰f x x f f tdt t f x x xx 又 2分∴= 在点处连续f x x ()0 3分lim )0()(lim )0(0)cos (lim cos lim )0()(lim )0(200000==-='===-='--+++→→-→→→+⎰x x xf x f f x x xtdt t xf x f f x x x xx x 5分第 3 页 共 6 页'==f f x x ()()000,在点处可导. 6分.,试求: 斜率等于处的切线,且它在原点通过原点具有连续导数,又曲线、设函数xx dtt f •••x f y x f •x•x sin )(lim100)()(60⎰→=解:,,由题意知,1)0(0)0(='=f f 2分lim()sin lim ()sin cos x xx f t dt x x f x x x x→→⎰=+000 4分='-→lim()cos sin x f x x x x 02 5分='=12012f () 6分7、)为驻点,,使得点(中的试确定442,,,,23-+++=d c b a d cx bx ax y(1,—10)为拐点。
线性代数本A卷及答案
昆明理工大学高等教育试卷( 2009 /2010 学年 上 学期)线性代数(A )专业年级: 学号: 姓名:试卷说明:A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 是单位矩阵,A 表示方阵A 的行列式。
一、单项选择题(本大题共8小题,每小题4分,共32分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.行列式543432321的值为( )A .2B .1C .0D .-12.设n 阶方阵A ,B ,C 满足ABC=E ,则必有( ) A .ACB=E B .CBA=E C .BAC=ED .BCA=E3.设n 阶方阵A 中有n 2-n 个以上元素为零,则A 的值( ) A .大于零 B .等于零 C .小于零D .不能确定4.线性方程组⎪⎩⎪⎨⎧=-α=-α=-1x x 2x x x x 133221 有解的充分必要条件是α=( )A .-1B .-31C .31 D .15.设A 为m×n 矩阵,则非齐次线性方程组Ax=b 有惟一解的充分必要条件是( ) A .m=nB .Ax=0只有零解C .向量b 可由A 的列向量组线性表出D .A 的列向量组线性无关,而增广矩阵A 的列向量组线性相关6.设A 为3阶矩阵,A 的特征值为0,1,2,那么齐次线性方程组Ax=0的基础解系所含解向量的个数为( ) A .0 B .1 C .2D .37.下列二次型中为规范形的是( )A .-2221y y - B .-2221y y + C .-2321y y -D .232221y 5y 3y ++8.已知A 是n 阶实对称矩阵,A 2=A ,秩(A )=n ,则x T Ax 是( ) A .正定二次型 B .负定二次型 C .半正定二次型D .不定二次型二、填空题(本大题共7小题,每小题4分,共28分)请在每小题的空格中填上正确答案.错填、不填均无分。
线性代数 考试试题(A)
2009 ~2010学年秋季学期 线性代数(B )课程考试试题(2010.1)一、填空题(本题满分15分,共有5道小题,每道小题3分,请将合适的答案填在每题的空中)1.已知为阶方阵,且A 32A =−,则2A −= ;2.已知矩阵,则的秩A =101021000⎛⎞⎜⎟⎜⎜⎟⎝⎠⎟A R A =() ; 3.设为阶方阵,满足,则A n 2A A E −=1A −= ;4.设12,ξξ是元非齐次线性方程组n Ax b =的两个解,且的秩,则 A ()R A 1=−n 的通解Ax b =x = ;5.设是阶方阵,A n 0A ≠,*A 是的伴随矩阵.若有特征值A A λ,则必有一个特()12*A −征值是 .二、选择题(本题共5小题,每小题3分,满分15分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内)1.阶方阵3A =33()ij a ×,的行列式A A =3−,ij A 是A 中元素的代数余子式,则ij a 2111112121313()++a A a A a A 2112112221323()+++a A a A a A 2113112321333()+++a A a A a A =【 】 ; (A) -3; (B) 2; (C) 9; (D) 0.2. 已知线性方程组0,2352.+=⎧⎪−+=⎨⎪+=⎩x y x y ,x y a有解,则【 】;=a (A) ; (B) ; (C) ; (D) 0. 21−33.设是4阶方阵,且的行列式A A 0A =,则中【 】; A (A) 必有一列元素全为0; (B) 必有两列元素成比例;(C) 必有一列向量是其余列向量的线性组合; (D) 任意列向量是其余列向量的线性组合.⎟⎟⎟⎜⎟⎝⎠4. 设相似于对角阵⎜122212221⎛⎞⎜=⎜⎜⎟⎝⎠A 15−⎛⎞⎜⎟=λ【 】; λ,则(A) ; (B) 2; (C) 3; (D) 0.1−5. 若二次型()2221231231223,,22f x x x x x x x x ax x =++++是正定二次型,则的取值范围是【 】..a(A) 2−<<a (B)<<a 22; (C) 2−<<a ; (D) 22<<−a .三、(本题满分14分)1.已知4阶行列式1111201212112101−−−=D ,求1121314122A A A A +++;2. 计算阶行列式1n +12112111231231111n n n nb a a a a b a a D a a a b a a a a −−+=""#####"".四、 (本题满分14分)设阶方阵和n A B 满足条件:A B AB +=.(1) 证明:是可逆矩阵,其中A E −E 是阶单位矩阵;n (2) 已知矩阵,求矩阵. 130210002B −⎛⎞⎜=⎜⎜⎟⎝⎠⎟⎟,.A 五、(本题满分14分) 当a 、b 为何值时,线性方程组()123423423412340,221,32321x x x x x x x x a x x b x x x ax +++=⎧⎪++=⎪⎨−+−−=⎪⎪+++=−⎩ 有唯一解,无解,有无穷多组解,并求出有无穷多组解时的通解.六、(本题满分10分) 设0η是非齐次线性方程组Ax b =的一个解,123,,ξξξ是对应的齐次线性方程组的一个基础解系,证明:Ax =0(1) 0123,,,ηξξξ线性无关;(2) 0102030,,,ηξηξηξη+++线性无关.七、(本题满分12分) 二次型22212312312(,,)2f x x x x x x x x =+++经正交变换x Py =变为标准形,求出该正交变换. 23222y y +八、(本题满分6分) 设,ξξ12是元非齐次线性方程组n Ax b =的两个解,为阶方阵,证明:A n (1) 存在一个非零向量与的每一个行向量都正交; A (2) 0A =.。
全国2010年1月自学考试线性代数试题答案(附详细解题过程)
全国2010年1月自学考试线性代数试题答案说明:本卷中,A T 表示矩阵A 的转置,αT 表示向量α的转置,E 表示单位矩阵,|A |表示方阵A 的行列式,A -1表示方阵A 的逆矩阵,R (A )表示矩阵A 的秩. 一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设行列式==1111034222,1111304z y x zy x 则行列式( A )A.32B.1C.2D.38 2.设A ,B ,C 为同阶可逆方阵,则(ABC )-1=( B ) A. A -1B -1C -1 B. C -1B -1A -1 C. C -1A -1B -1D. A -1C -1B -13.设α1,α2,α3,α4是4维列向量,矩阵A =(α1,α2,α3,α4),如果|A |=2,则|-2A |=(D ) A.-32 B.-4 C.4D.324.设方阵A 满足A 5=E ,则必有(C ) A.A=E B.A=-E C.|A|=1D.|A|=-1 5.设α1,α2,α3,α4 是三维实向量,则( C ) A. α1,α2,α3,α4一定线性无关 B. α1一定可由α2,α3,α4线性表出 C. α1,α2,α3,α4一定线性相关D. α1,α2,α3一定线性无关6.设A 是4×6矩阵,R (A )=2,则齐次线性方程组Ax =0的基础解系中所含向量的个数是( D )A.1B.2C.3D.47.设A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---496375254,则以下向量中是A 的特征向量的是( A)A.(1,1,1)TB.(1,1,3)TC.(1,1,0)TD.(1,0,-3)T8.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--111131111的三个特征值分别为λ1,λ2,λ3,则λ1+λ2+λ3 = (B )A.4B.5C.6D.79.三元二次型f (x 1,x 2,x 3)=233222312121912464x x x x x x x x x +++++的矩阵为(A ) A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963642321B.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963640341C.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡960642621D.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡912304232110.设矩阵A =⎥⎦⎤⎢⎣⎡a 321是正定矩阵,则a 满足( A ) A.a <2 B.a =2 C.a =6D.a >6二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
2011.4线性代数试题及答案
全国2011年4月高等教育自学考试线性代数试题课程代码:04184说明:A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 是单位矩阵,|A |表示方阵A 的行列式。
一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列等式中,正确的是( ) A.2001002001021⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭B. 1233693456456⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭C.1051002⎛⎫= ⎪⎝⎭D.120120035035--⎛⎫⎛⎫-= ⎪ ⎪--⎝⎭⎝⎭2.下列矩阵中,是初等矩阵的为( ) A.111010001⎛⎫ ⎪ ⎪ ⎪⎝⎭B.200020002⎛⎫⎪ ⎪ ⎪⎝⎭C.108010001⎛⎫⎪ ⎪ ⎪⎝⎭ D.108018001⎛⎫⎪ ⎪ ⎪⎝⎭3.设A 、B 均为n 阶可逆矩阵,且C =⎛⎫ ⎪⎝⎭0B A 0,则C -1是( )A.11B 00A --⎛⎫ ⎪⎝⎭B.110B A 0--⎛⎫⎪⎝⎭ C.110A B0--⎛⎫⎪⎝⎭D.11A 00B --⎛⎫ ⎪⎝⎭4.设A 为3阶矩阵,A 的秩r(A )=3,则矩阵A *的秩r(A *)=( ) A.0 B.1 C.2 D.35.设向量1α=(-1,4),2α=(1,-2),3α=(3,-8),若有常数a,b 使a 1α-b 2α-3α=0,则( )A.a=-1,b=-2B.a=-1,b=2C.a=1,b=-2D.a=1,b=26.向量组1α=(1,2,0),2α=(2,4,0),3α=(3,6,0),4α=(4,9,0)的极大线性无关组为( ) A.1α,4α B.1α,3α C.1α,2αD.2α,3α7.设矩阵A =100220340⎛⎫⎪⎪ ⎪⎝⎭,那么矩阵A 的列向量组的秩为( )A.3B.2C.1D.08.设λ=3是可逆矩阵A 的一个特征值,则矩阵114-⎛⎫⎪⎝⎭A 有一个特征值等于( )A.43-B.34-C.34 D.439.设矩阵A =100212312-⎛⎫ ⎪⎪ ⎪⎝⎭,则A 的对应于特征值λ=0的特征向量为( )A.(0,0,0)TB.(0,2,-1)TC.(1,0,-1)TD.(0,1,1)T 10.二次型f(x 1,x 2,x 3)=2x 1²-x 1x 2 +x 2²的矩阵为( ) A.⎪⎪⎭⎫⎝⎛--1112 B. ⎪⎪⎪⎪⎭⎫⎝⎛--121212C.⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--00001210212 D. ⎪⎪⎪⎭⎫ ⎝⎛--000011012二、填空题(本大题共10小题,每题2分,共20分)请在每小题的空格中填上正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 / 共2页
山东科技大学2010—2011学年第一学期
《线性代数》考试试卷(A卷)
班级 姓名 学号
一、填空题(每小题5分,共15分)
1、设4阶矩阵的A秩为2,则其伴随矩阵*A的秩是 。
2、设2是方阵A的一个特征值,4A,则EA2)(3*必有特征值 。
3、二次型321,,xxxf=23222111xxx在满足_________条件时是正定二
次型。
二、选择题(每小题5分,共15分)
1、设A为n阶可逆矩阵,则下列不正确...的是( )
(A) 0A; (B) 存在n阶矩阵B,使EAB;
(C) ()RArn; (D) A必是非奇异矩阵.
2、设A为n阶矩阵,1)(nAR,12, 是非齐次线性方程组Axb的两个不同的
解,则0xA的通解为( )
(A) 1k; (B) 12()k; (C) 2k; (D) 12()k.
3、设向量组 r,,,21 可由向量组 s,,,21 线性表示,则( ).
(A)sr; (B) ),,,(),,,(2121srRR;
(C) sr; (D) ),,,(),,,(2121srRR.
题号 一 二 三 四 总得分 评卷人 审核人
得分
第2页 / 共2页
三、解答题(共64分)
1、(12分)计算下列行列式的值:
(1)6416412793184211111D; (2)333naaaaDaa 3n.
2、(8分)求矩阵X,使BXAX2,其中410110003A,322154B.
3、(16分)当取何值时,非齐次线性方程组1231231230,3,1,xxxxxxxxx有唯一解、无解或
有无穷多解?并在有无穷多解时求出通解.
4、(10分)求向量组11234,22341,32583,4526912,
5
3
412
的秩及其一个最大无关组,并把其余向量用最大无关组线性表示.
5、(18分)已知二次型222123121323255448fxxxxxxxxx.
(1) 写出二次型f的矩阵表达式;
(2) 求一个正交变换 Pxy,把f化为标准形, 并写出标准形.
四、证明题(6分)
若A为n阶方阵,E为n阶单位阵,且OA3,证明:EA为可逆矩阵
.
