2013届河南中考数学复习方案课件专题二 探究性几何证明题
河南中考数学学科讲座PPT课件

(1)操作发现
如图2,固定三角形ABC,使三角形DEC绕点C旋转。当点D
恰好落在AB边上时,填空:
(1)、线段DE与AC的位置关系是
;
(2)、设三角形ABC的面积为S 1 , 三角形DEC的面积为S 2 。 则 S 1 与 S 2 的数量关系是 。
(2)猜想论证 当三角形DEC绕点C旋转到图3所示的位置时,小明
x1 2 3 4
x1 2 3 4
y6 8 9 7
y8 5 4 3
(A)
(B)
x1 2 3 4
x1 2 3 4
y5 8 7 6
y 1 1/2 1/3 1/4
(C)
(D)
反比例函数的本质:两个变量的
乘积是常数
知识点: 面积性质(一)
(2)过 P分别 x轴 作 ,y轴的,垂 垂线 足分 A,B 别 , 为
是y轴右侧的抛物线上一动点,过点P作 PE x轴于点E,交 CD于点F.
(1)求抛物线的解析式; (2)若点P的横坐标为m,当m为何值时,以O,C,P,F为 顶点的四边形是平行四边形?请说明理由。 (3)若存在点P,使 PCF45,请直接写出相应的点P 的坐标.
(二)、与往年相比河南中考的变化:
(2)、知识的应用拓展:
19、(9分)我国南水北调中线工程的起点是丹江 口水库,按照工程计划,需对原水库大坝进行混凝土 培厚加高,使坝高由原来的162米增加到176.6米,以 抬高蓄水位,如图是某一段坝体加高工程的截面示意 图,其中原坝体的高为,背水坡坡角,新坝体的高为, 背水坡坡角。求工程完工后背水坡底端水平方向增加 的宽度.
1、-2的相反数是【】 (A)2 (B) (C) (D)
2、下列图形中,既是轴对称图形又是中心对称图形的是【】
中考数学复习专项二解答题专项五简单的几何证明课件

我们还要注意课后的及时思考。利用课间休息时间,在心中快速把刚才上课时刚讲过的一些关键思路理一遍,把老师讲解的题目从题意到解答整个过 程详细审视一遍,这样,不仅可以加深知识的理解和记忆,还可以轻而易举地掌握一些关键的解题技巧。所以,2分钟的课后静思等于同一学科知识的课 后复习30分钟。
专项二 解答题专项
五、 简单的几何证明 (针对陕西中考第18题或第19
题)
解答题专项
中考解读:简单的几何证明为陕西近8年中考解答题的必考题,分值为5分或7 分。图形背景为三角形、四边形(一般为特殊平行四边形),设问类型有(1) 证明线段相等;(2)证明线段平行;(3)证明三角形全等。
一、证明三角形全等的思路
A D, 在△ABH和△DCG中, A H B D G C ,
A B D C ,
∴△ABH≌△DCG(AAS),∴AH=DG。 ∵AH=AG+GH,DG=DH+GH, ∴AG=DH。
编后语
常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
一、释疑难
对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已 经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。
二、补笔记
上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一 遍自己写的笔记,既可以起到复习的作用,又可以检查笔记中的遗漏和错误。遗漏之处要补全,错别字要纠正,过于潦草的字要写清楚。同时,将自己 对讲课内容的理解、自己的收获和感想,用自己的话写在笔记本的空白处。这样,可以使笔记变的更加完整、充实。
2013年河南中考数学试卷及答案
2013年河南省初中学业水平暨高级中等学校招生考试试卷数 学注意事项:1. 本试卷共8页,三个大题,满分120分,考试时间100分钟,请用蓝、黑色水笔或圆珠笔直接答在试卷上。
参考公式:二次函数图像2(0)y ax bx c a =++≠的顶点坐标为24(,)24b ac b a a--一、 选择题(每小题3分,共24分)下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填在题后括号内。
1、-2的相反数是【】(A )2 (B)2-- (C)12 (D)12-【解析】根据相反数的定义可知:-2的相反数为2【答案】A2、下列图形中,既是轴对称图形又是中心对称图形的是【】【解析】轴对称是指在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。
中心对称图形是指平面内,如果把一个图形绕某个点旋转180°后,能与自身重合,那么就说这两个图形关于这个点成中心对称。
结合定义可知,答案是D【答案】D3、方程(2)(3)0x x -+=的解是【】(A )2x = (B )3x =- (C )122,3x x =-= (D )122,3x x ==-【解析】由题可知:20x -=或者30x +=,可以得到:122,3x x ==-【答案】D4、在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是【】(A ) 47 (B )48 (C )48.5 (D )49【解析】中位数是将数据按照从小到大的顺序排列,其中间的一个数或中间两个数的平均数就是这组数的中位数。
本题的8个数据已经按照从小到大的顺序排列了,其中间的两个数是48和49,它们的平均数是48.5。
因此中位数是48.5【答案】C5、如图是正方形的一种张开图,其中每个面上都标有一个数字。
那么在原正方形中,与数字“2”相对的面上的数字是【】(A )1 (B )4 (C )5 (D )6【解析】将正方形重新还原后可知:“2”与“4”对应,“3”与“5”对应,“1”与“6”对应。
中考数学二轮复习 专题七 几何图形的探究猜想与证明数学课件

∵四边形ABCD是矩形,点E在AB的延长线上,∴∠CBE=∠ABC=∠N=90°. ∴∠1+∠3=90°. ∵四边形CEFG为正方形,
12/10/2021
∴EC=EF,∠CEF=90°.
∴∠1+∠2=90°,∴∠2=∠3.
∴△ENF≌△CBE.∴NF=BE,NE=BC.
∵四边形ABCD是矩形,∴AD=BC.
12/10/2021
证明; 探索发现: (3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C、 点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG 的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上?请写出一个你 发现的结论,并加以证明.
12/10/2021
PB PM 3
当点P在O的右侧时,如图所示,
过点B作BD⊥OA于点D, ∵MO=2PO,∴点P是OM的中点,
12/10/2021
设PM=x,则BD=2x, ∵∠AOM=∠ABP=90°,∴A、O、P、B四点共圆, ∴四边形AOPB是圆内接四边形, ∴∠BPM=∠A,∴△ABD∽△PBM,∴ AD= PM,
12/10/2021
开放解答 解析 (1)∵2BM=AO,2CO=AO, ∴BM=CO, ∵AO∥BM,∴四边形OCBM是平行四边形, ∵∠BMO=90°,∴▱OCBM是矩形, ∵∠ABP=90°,C是AO的中点, ∴OC=BC, ∴矩形OCBM是正方形.
12/10/2021
(2)如图,连接AP、OB, ∵∠ABP=∠AOP=90°,∴A、B、O、P四点共圆, 由圆周角定理可知∠APB=∠AOB, ∵AO∥BM,∴∠AOB=∠OBM, ∴∠APB=∠OBM,
河南中考数学18题几何证明与计算专练(含手写版答案)几何证明与推理——四边形存在性
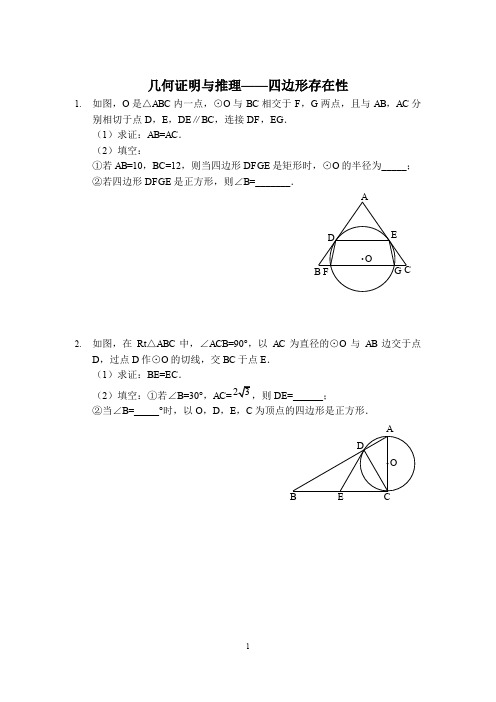
几何证明与推理——四边形存在性1.如图,O是△ABC内一点,⊙O与BC相交于F,G两点,且与AB,AC分别相切于点D,E,DE∥BC,连接DF,EG.(1)求证:AB=AC.(2)填空:①若AB=10,BC=12,则当四边形DFGE是矩形时,⊙O的半径为_____;②若四边形DFGE是正方形,则∠B=_______.2.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:BE=EC.(2)填空:①若∠B=30°,AC=DE=______;②当∠B=_____°时,以O,D,E,C为顶点的四边形是正方形.3.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD (AE<BD)的长是一元二次方程x2-5x+6=0的两个实数根.(1)求证:P A·BD=PB·AE.(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.4.如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.(1)求证:BC是⊙O的切线;(2)若AC=3,则⊙O的半径r为____________;(3)判断以A,O,E,F为顶点的四边形为哪种特殊四边形,并说明理由.5.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(1)求证:MD=ME.(2)填空:①若AB=6,当AD=2DM时,DE=___________;②连接OD,OE,当∠A的度数为__________时,四边形ODME是菱形.6.如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.(1)求证:GC是⊙F的切线.(2)填空:①若∠BAD=45°,AB=CDG的面积为_______;②当∠GCD的度数为_______时,四边形EFCD是菱形.7.如图所示,半圆O的直径AB=4,=,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.(1)求证:△CDF≌△BDE.(2)填空:①当AD=_______时,四边形AODC是菱形;②当AD=_______时,四边形AEDF是正方形.8.如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC,交⊙O于另一点D,连接P A,PB.(1)求证:AP平分∠CAB;(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则:①当弦AP的长是________时,以A,O,P,C为顶点的四边形是正方形;②当的长度是___________时,以A,D,O,P为顶点的四边形是菱形.CB9.如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC.(1)求证:AC是⊙O的切线;(2)连接EF,当∠D=______°时,四边形FOBE是菱形.CF EADO B10.如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D,连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.(1)求证:CD∥AB;(2)填空:①若DF=AP,当∠DAE=__________时,四边形ADFP是菱形;②若BF⊥DF,当∠DAE=__________时,四边形BFDP是正方形.A11.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.(1)求证:CE=EF;(2)连接AF并延长,交⊙O于点G.填空:①当∠D的度数为_________时,四边形ECFG为菱形;②当∠D的度数为_________时,四边形ECOG为正方形.B AB。
中考数学专题复习专题3几何证明省公开课一等奖百校联赛赛课微课获奖PPT课件

3.[·河南]如图,AB是⊙O直径,DO⊥AB于点O,连接DA交⊙O于点 C,过点C作⊙O切线交DO于点E,连接BC交DO于点F. (1)求证:CE=EF; (2)连接AF并延长,交⊙O于点G.填空: ①当∠D度数为______时,四边形ECFG为菱形; ②当∠D度数为______时,四边形ECOG为正方形.
②∠ACD=∠BAE;
③AF∶BE=2∶3;
④S四边形AFOE∶S△COD=2∶3.
其中正确结论有
.(填写全部正确结论序号)
①② ④
第4页
2.[·临安模拟]已知:如图,E,F是平行四边形ABCD对角线AC上 两点,AE=CF. 求证:(1)△ADF≌△CBE; (2)EB∥DF.
证实:(1)∵AE=CF,∴AE+EF=CF+FE,即AF=CE. 又∵ABCD是平行四边形,∴AD=CB,AD∥BC.∴∠DAF=∠BCE. 在△ADF与△CBE中,∵AF=CE,∠DAF=∠BCE,AD=CB, ∴△ADF≌△CBE(SAS). (2)∵△ADF≌△CBE, ∴∠DFA=∠BEC. ∴EB∥DF.
专题3 几何证实
类型 与四边形相关证实
满分技法►四边形问题要转化成三角形问题来处理,经过证实三角形全等或 相同得到相等角、相等边或成百分比边.要熟练掌握特殊四边形判定定理, 灵活选择解题方法,注意区分各种四边形之间关系.正确认识特殊与普通 关系,注意方程思想、对称思想以及转化思想相互渗透.
例1►[·贺州]如图,在△ABC中,∠ACB=90°,O,D分别是边AC, AB中点,过点C作CE∥AB交DO延长线于点E,连接AE.
分析:(1)利用直角三角形斜边中线性质定理即可证实;(2)利用
四边形内角和定理求出∠CME即可处理问题;(3)首先证实△ADE是
第2013届河南中考数学复习方案课件五单元 四边形
第26课时┃ 课堂热身
课堂热身
►
热身考点1 矩形的性质及判定的应用
1.[2011· 滨州] 如图 26-1,在△ABC 中,点 O 是 AC 边上(端点除外)的一个动点, 过点 O 作直线 MN∥BC.设 MN 交∠BCA 的平分线于点 E,交∠BCA 的外角平分线于点 F, 连接 AE、AF.那么当点 O 运动到何处时,四边形 AECF 是 矩形?并证明你的结论.
考点聚焦
考点1 矩形
矩形定义 有一个角是________的平行四边形叫做矩形 直角 矩形是一个轴对称图形,它有两条对称轴 矩形是中心对称图形,它的对称中心就是对角线的交点 (1)矩形的四个角都是______角; 直 相等 (2)矩形的对角线互相平分并且______
矩形 的性 质
对称性
定理 推论
斜边 在直角三角形中,斜边上的中线等于________的一半
第25课时┃ 考点聚焦 考点3 平行四边形的定义与性质
定义 两组对边分别平行的四边形是平行四边形 平行 (1)平行四边形的两组对边分别________;
相等 (2)平行四边形的两组对边分别________; 相等 (3)平行四边形的两组对角分别________; 平分 (4)平行四边形的对角线互相________ ;
正方形 (1)有一组邻边相等的矩形是正方形 的判定 (2)有一个角是直角的菱形是正方形
第26课时┃ 考点聚焦
判定正方形的思路图:
第26课时┃ 考点聚焦
考点4 中点四边形
定义 顺次连接四边形各边中点所得的四边形,我们称之为中点四 边形 顺次连接四边形各边中点所得到的四边形是___________ 平行四边形 菱形 顺次连接矩形各边中点所得到的四边形是______ 顺次连接菱形各边中点所得到的四边形是______ 矩形 常见 结论 顺次连接正方形各边中点所得到的四边形是______ 正方形 顺次连接等腰梯形各边中点所得的四边形是______ 菱形 顺次连接对角线相等的四边形各边中点所得到的四边形是 ______ 菱形 顺次连接对角线互相垂直的四边形各边中点所得到的四边 形是______ 矩形
中考数学专题复习课件:题型3 几何证明(共15张PPT)
5.[2017·重庆中考]在△ABM中,∠ABM=45°,AM⊥BM, 垂足为M,点C是BM延长线上一点,连接AC. (1)如图1,若AB=3 ,BC=5,求AC的长; (2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一 点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中 点,求证:∠BDF=∠CEF.
2.如图,已知BD是△ABC的角平分线,DE∥AB交BC于点E, EF∥AC交AB于点F. (1)求证:BE=AF; (2)连接DF,试探究当△ABC满足什么条件时,使得四边形 BEDF是菱形,并说明理由.
解:(1)证明:∵BD是△ABC的角平分线,∴∠ABD=∠DBC. ∵DE∥AB,∴∠ABD=∠BDE. ∴∠BDE=∠DBC.∴BE=DE. ∵EF∥AC,∴四边形ADEF是平行四边形. ∴AF=DE.∴AF=BE. (2)当AB=BC时,四边形BEDF是菱形.理由如下: ∵AB=BC,∴∠A=∠C. ∵EF∥AC,∴∠A=∠BFE,∠C=∠BEF. ∴∠BFE=∠BEF.∴BF=BE. ∵DE=BE,∴BF=DE. 又∵DE∥AB,∴四边形BEDF是平行四边形. 又∵BF=BE,∴平行四边形BEDF是菱形.
【解】证明:(1)∵四边形ABCD 是正方形, ∴AD=AB,∠BAD=90°. ∵MN⊥AF,∴∠AHM=90°. ∴∠BAF+∠MAH=∠MAH+∠AMH=90°. ∴∠BAF=∠AMH. 在△AMN和△BAF中,
∠AMN=∠BAF, AM=BA, ∠MAN=∠ABF
∴△AMN≌△BAF(ASA).∴AF=MN.
∵MD⊥DE,MN为⊙O的直径, ∴∠MDE=∠MEN=90°. ∵∠NME=∠DME,∴△MDE∽△MEN.
满分技法►与三角形有关的证明,通常是通过三角形相似进行相 关运算.看到证线段之间成比例,想到三角形相似,是在此问题 当中的一个定性思维.相似三角形有以下6种基本图形(如下图所 示).
中考数学复习 第二部分 题型研究 题型五 几何探究题 类型四 旋转变换问题课件
∴△PMN为等腰直角三角形;
第七页,共十一页。
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接 写出△PMN面积的最大值. 【思维教练】由(2)得到,当△ADE旋转时,△PMN无论怎么变化都 是等腰直角三角形,其面积可表示为 PM2,要使其面1 积最大,则 PM要最大.故问题转化(zhuǎnhuà)为在旋转过程中寻找2 PM的最大 值.
第九页,共十一页。
故△PMN为最大面积(miàn jī)为S△PMN=12
×7×7= 4 9 .
2
例4题解(tíjiě)图
第十页,共十一页。
内容(nèiróng)总结
No 第二(dìèr)部分 题型研究。解:(1)PM=PN,PM⊥PN。∴△BAD≌△CAE(SAS),。把△ADE绕
点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.。【思维教练】 由(2)得到,当△ADE旋转时,△PMN无论怎么变化都是等腰直角三角形,其面积可表示为 PM2, 要使其面积最大,则PM要最大.故问题转化为在旋转过程中寻找PM的最大值.
第八页,共十一页。
(3)△PMN面积的最大值为. 【解法提示】由(2)可知(kě zhī),当△ADE旋转时,△PMN为等腰直角 三角形, ∴S△PMN= P1M2,
2
要使△PMN的面积最大,即PM最大, 由(2)得,PM= C1 E,即当CE最大时,MP最大. 如解图所示,当点C2 、E在点A异侧,且在同一条直线上时,CE最大, 此时CE=AE+AC=14,
2
BD1 , 2
第三页,共十一页。
∴PM=PN,∠DPM=∠DCE,∠CNP=∠B, ∴∠DPN=∠PNC+∠PCN=∠B+∠PCN. ∵∠A=90°, ∴∠B+∠ACB=90°, ∴∠MPN=∠MPD+∠DPN=∠ACD+∠PCN+∠B=∠ACB+∠B=
中考数学专题复习课件专题三简单的几何证明与计算(共35张PPT(完整版)5
6.(导学号65244233)(2017·青岛)如图,在菱形ABCD中,点E,O,F分别为 AB,AC,AD的中点,连接CE,CF,OE,OF. (1)求证:△BCE≌△DCF; (2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
解:(1)证明:∵四边形 ABCD 是菱形,∴∠B=∠D, AB=BC=DC=AD.∵点 E,O,F 分别为 AB,AC,AD 的中点,
【思路引导】(1)先计算AM,CM的长,再由勾股定理可得AC的长.(2)延长 EF到点G,使得FG=EF,先证明△BMD≌△AMC,得AC=BD,再证明 △BFG≌△CFE,可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得 ∠BDG=∠G=∠E.
解:(1)∵∠ABM=45°,AM⊥BM, ∴AM=BM=ABcos45°=3 2× 22=3. 则 CM=BC-BM=5-3=2,∴AC= AM2+CM2= 22+32= 13.
【例2】 如图,正方形ABCD中,M为BC上一点,F是AM的中点, EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N. (1)求证:△ABM∽△EFA; (2)若AB=12,BM=5,求DE的长.
【思路引导】(1)由两角相等即可证明;(2)由勾股定理求出AM,得出AF, 由△ABM∽△EFA得出比例式,求出AE,即可求解.
5.(导学号65244232)(2017·包头)如图,在△ABC中,∠C=90°, ∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于 点F,已知CD=3. (1)求AD的长; (2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
解:(1)∵∠C=90°,∠B=30°,∴∠CAB=60°. ∵AD 平分∠CAB,∴∠CAD=12∠CAB=30°. 在 Rt△ACD 中,∵∠ACD=90°,∠CAD=30°,∴AD=2CD=6.
