结构力学 动力计算例题
结构力学计算题及结构力学练习题含答案

结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学,以下是一篇结构力学计算题及练习题,包括答案的示例。
结构力学计算题题目:一简支梁AB,跨度为4米,受到均布荷载q=2 kN/m,梁的截面惯性矩I=1.2×10^6 mm^4,弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤:1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式:\[ M_{max} = \frac{ql^2}{8} \]代入已知数据:\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式:\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据:\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案:梁的最大弯矩Mmax为4 kN·m,最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD,长度为3米,受到集中力F=5 kN作用在自由端,梁的截面惯性矩I=1.5×10^6 mm^4,弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax为5 kN·m,最大挠度y_max为0.013 mm。
2. 一连续梁EF,跨度为6米,分为两段,每段长度为3米,中间有一支点G。
梁上受到均布荷载q=1.5kN/m,梁的截面惯性矩I=2×10^6 mm^4,弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案:支点G的反力为4.5 kN,中间梁段的最大弯矩为2.25 kN·m。
结构力学专题七(单自由度体系的动力计算)

设: 2
k11 m
1
m11
运动方程: y(t) 2 y(t) 0
1、运动方程的解
y(t) c1sin t c2 cos t
(a)
或 y(t) csin( t )(ຫໍສະໝຸດ )当 y0、y0 为已知时
y(t)
y 0
sin
t
y
0
cos
t
(c)
方程(a)、(b)、(c)称为位移方程。
2、位移方程的几何意义
A1 5cm2
W 0.1kN
3m
(1)求竖向振动时的频率和周期,
(2)设: y0 10cm(向下),y0 0;
求: t
4
90
时质体的绝对位移。
A2 10cm2
4m
补2(选作):求图示体系的自振频率:
m
EI
m
k
l
l
l EI
FP (t)
EI
l/2 l/2
三、举例与讨论
例1: 建立图示体系运动微分方程 FP (t)
m EI
l/2 l/2
方程:
L3 48EI
(my(t)
cy(t))
y(t)
L3 48EI
FP (t)
my(t) cy(t)
48EI L3
y(t)
FP (t)
例2: 建立图示体系运动微分方程
FP (t)
EI0
m
h EI
EI
方程:
my(t) cy(t)
m
EI FP (t)
l/2 l/2
例3: 求图示体系的自振频率。
FP (t)
EI0
m
h EI
EI
结构力学——结构的动力计算

11
11[ P(t ) m(t )] y
P (t )
y(t ) 11[ P(t ) m(t )] y
l
l3 柔度系数 m(t ) 11 y 3EI 3EI (t ) 3 y (t ) P(t ) my l
二、刚度法
P (t )
l
EI
m m(t ) y y (t )
简谐荷载 周期 非简谐荷载 确定 冲击荷载 非周期 突加荷载 动荷载 其他确定规律的动荷载 风荷载 地震荷载 不确定 其他无法确定变化规律的荷载
§1.2
结构动力学的研究内容和任务
结构动力学是研究动荷作用下结构动力反应规律的学科。 一.结构动力学的研究内容 当前结构动力学的研究内容为: 第一类问题:结构动力荷载的确定
结构力学
傅向荣
第十章 结构的动力 计算
§1. 绪论
§1.1 动荷载及其分类
一.动荷载的定义 大小、方向和作用点随时间变化;在其作用下,结构上的惯性力 与外荷比不可忽视的荷载。
自重、缓慢变化的荷载,其惯性力与外荷比很小,分析时仍视作 静荷载。 静荷只与作用位置有关,而动荷是坐标和时间的函数。
二.动荷载的分类
P (t )
EI
m
EI1
EI
l
1
24 EI k 3 l
11
1
k
EI1
1 11 k
12 EI / l 3 12 EI / l 3
l l
EI EI
k2
EI1
EI EI
k1 ?
k1
k2 ?
24 EI k1 k 2 3 l
层间侧移刚度 对于带刚性横梁的刚架(剪切型刚架), 当两层之间发生相对单位水平位移时,两 层之间的所有柱子中的剪力之和称作该 层的层间侧移刚度. l l
结构力学计算题经典(有答案)
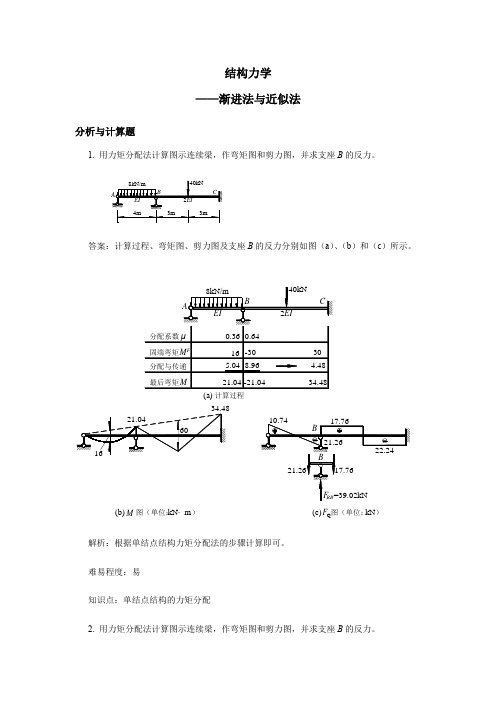
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
《结构力学习题集》(下)-结构的动力计算习题及答案

第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
结构力学专题十三(多自由度体系的动力计算)

FP1
m1
l
EI
l
FP 2
m2
l
二、任意荷载作用*
运动方程: M y(t) Ky(t) FP (t) (a)
1、主振型矩阵
1 2 n
2、广义质量、广义刚度
} M * T M 对角阵
K* T K
3、正则坐标
y(t) (t)
(b)
M y(t) Ky(t) FP(t) (a)
4、振型迭加法分析强迫振动
例1:求图示结构的动位移幅值和动内力幅值。
k1 k,k2 2k,
m1
m1 m,m2 2m;
P0 sin t
EI1
k1 m2
h
已知:
2
k m
EI1
k2
h
A
P0 k
1 0
1
1
I
F
0P0
P0
P0
P0 k
动位移幅值图
动荷载图(虚拟)
例2:求图示结构的动位移幅值和动内力幅值。
已知:
i
(t
)
i
(0)
cos
it
i (0) i
sin
it
(i 1, 2)
l
0E.I041
P0 L3 EI
sinP0 stin
m
t
EI
从以上例题的计算中可看出,一般情况下 1l 〉2 〉l〉n
故在振型迭加法中,一般是前几阶振型起主要作用。
思考:用振型叠加法求例1所示结构的位移幅值。
2
k m
2
1 3
k m
2 5 k 3m
2
k m
P0 sin t
P0 sin t
结构力学动力计算

M1
m
EI EI
L
图乘法得 柔度系数
自振频率
M1M1 2l3
EI 3EI
1
2m
3EI 4ml 3
L
L
L
自振周期
T 2 2 4m l3
3EI
M1图
m
EI
L
1
结构力学(2)
浙大宁波理工学院土建学院
算例.求图示体系的自振频率和周期,C端最大位移
A
∞
B
C
k
10个自由度 9个自由度
结构力学(2)
浙大宁波理工学院土建学院
10.2 单自由度体系的自由振动
1.自由振动运动微分方程
• 自由振动-由初位移或初速度引起的,在运动中无动荷载作 用的振动。
• 分析自由振动的目的 确定结构的动力特性,自振频率,自振周期。
结构力学(2)
浙大宁波理工学院土建学院m
静平衡方程
代入初始条件得
y(t 0) y0 Asin y(t 0) v0 Acos
解得
振幅: A
y02
v02
2
初始相位角:
tan1 y0
v0
结构力学(2)
浙大宁波理工学院土建学院
算例 求图示体系的自振频率和自振周期。(P359)
自振频率和自振周期是体系固有的, 只与内在因素有关,与外在因素无关。 算法:柔度法
动荷载: F(t) 刚度系数: k
柔度系数: =1/k
位移:y(t)
质量: m
时间:t
速度: y(t) dy
加速度:
dt y(t)
d
2y
dt 2
结构力学(2)
《结构力学习题集》9-结构动力计算

第九章 结构的动力计算一、是非题1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形,图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ,W =98.kN ,欲 使 顶 端 产 生 水 平位 移 ∆=001.m ,需 加 水 平 力 P =16kN ,则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ,杆 重 不 计 ,EA 为 常 数 ,在 C 点 的 竖 向 初 位 移 干 扰 下 ,W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ,图 示 体 系 的 运 动 方 程 为 :m m XX h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ,质 点 的 运 动 方 程 为 : A .()()()y l Ps i n m y EI =-77683θ t /; B .()()m y EIy l Ps i n /+=19273θ t ; C .()()m y EIy l Ps i n /+=38473θ t ; D .()()()y l Ps i n m yEI =-7963θ t / 。
ll0.50.5 2、在 图 示 结 构 中 ,若 要 使 其 自 振 频 率 ω增 大 ,可 以A .增 大 P ;B .增 大 m ;C .增 大 E I ; D .增 大 l 。
结构力学 结构的动力计算

§13-2 单自由度体系的运动方程
实际上,工程中很多问题可化成 单自由度体系进行动力分析或进行初 步估算。要掌握其动力反应的规律, 必须首先建立其运动方程。下面介绍 建立在达朗伯原理基础上的“动静 法”。
一.按平衡条件建立运动方程-刚度法
FP(t) m y(t)
FP(t) m
-my(t) -k y(t)
输出 (动力反应)
第二类问题:参数(或系统)的识别 结构 (系统)
输入 (动荷载)
输出 (动力反应)
第三类问题:荷载识别 输入 (动荷载) 结构 (系统)
输出 (动力反应)
第四类问题:控制问题
输入 (动荷载)
结构 (系统)
控制系统 (装置、能量)
输出 (动力反应)
2.结构动力计算的目的 研究结构在动荷载作用下的反应规 律,找出动荷载作用下结构的最大动内 力和最大动位移,为结构的动力可靠性 设计提供依据。
§13-3
单自由度体系的自由振动 (不计阻尼)
自由振动-由初位移或初速度引起的, 在运动中无动荷载作用的振动。 分析自由振动的目的-确定结构的动力 特性,自振频率,自振周期。
一.自由振动运动方程
y(t)
单自由度体系的自由 振动及相应的弹簧- 质量模型如图示。以 静平衡位置为坐标原 点,在 t 时刻,质量 m 的位移为 y(t)。
m
-my(t)
LLeabharlann EI刚度法建立平衡方程: 取质量 m 为隔离体,作用在隔离体上的力: 弹性力 -ky(t)与位移方向相反; 惯性力
y y - m(t ) 与加速度 方向相反。
y(t) k m
动平衡方程:
m(t ) ky(t ) 0 y
结构力学动力计算习题
m
m l l l
练习题 .按先处理法求图示连续梁的刚度方程 8 .按先处理法求图示连续梁的刚度方程 (不
考虑梁的轴向变形)。 考虑梁的轴向变形)。
2kN 5 k N .m
1 2EI 2 EI
4kN 1 2 k N /m
3 EI 4
4m
4m
4m
练习题
9. 求图示结构各元的杆端力,并画出内力图。 求图示结构各元的杆端力,并画出内力图。
E = 10 kN m , θ = 20s , 5 3 k = 3 × 10 N/m, P = 5 × 10 N, W = 9.8kN
5 2 -1
Psinθ t
W 2m 2m
k
练习题 图示刚架杆自重不计,各杆EI=常数。 EI=常数 7. 图示刚架杆自重不计,各杆EI=常数。求自 振频率及振型,并画出振型图。 振频率及振型,并画出振型图。
练习题 10. 按后处理法求图示结构的结点荷载列阵 。 按后处理法求图示结构的结点荷载列阵{P}。 各杆EI=常数。 常数。 各杆 常数
4 kN 5 kN 2 6 kN /m 1
2 0 kN. m 3
4 3 kN
6
5
4m
4m
4m
m1
EI
l
m2
2EI 2EI l
练习题
5. 图示三铰刚架各杆 图示三铰刚架各杆EI=常数,杆自重不计。 常数, 常数 杆自重不计。
求自振频率与主振型。 求自振频率法。 用柔度法。
练习题
3
f11 = 1 × ( 1 × l × l × 2 × l ) × 4 = l EI 2 2 3 2 3EI l3 f 22 = f11 = f12 = f 21 = 0 3EI
结构力学典型例题武汉理工大学
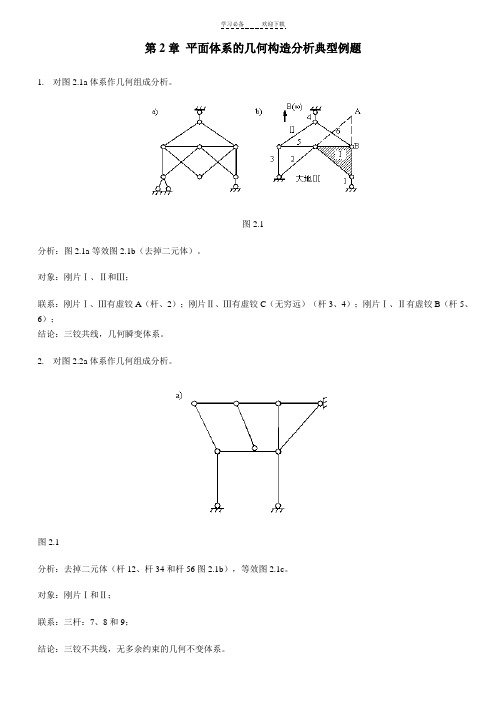
第2章平面体系的几何构造分析典型例题1. 对图2.1a体系作几何组成分析。
图2.1分析:图2.1a等效图2.1b(去掉二元体)。
对象:刚片Ⅰ、Ⅱ和Ⅲ;联系:刚片Ⅰ、Ⅲ有虚铰A(杆、2);刚片Ⅱ、Ⅲ有虚铰C(无穷远)(杆3、4);刚片Ⅰ、Ⅱ有虚铰B(杆5、6);结论:三铰共线,几何瞬变体系。
2. 对图2.2a体系作几何组成分析。
图2.1分析:去掉二元体(杆12、杆34和杆56图2.1b),等效图2.1c。
对象:刚片Ⅰ和Ⅱ;联系:三杆:7、8和9;结论:三铰不共线,无多余约束的几何不变体系。
3. 对图2.3a体系作几何组成分析。
图2.3 分析:图2.3a对象:刚片Ⅰ(三角形原则)和大地Ⅱ;联系:铰A和杆1;结论:无多余约束的几何不变体系。
对象:刚片Ⅲ(三角形原则)和大地Ⅱ;联系:杆2、3和4;结论:无多余约束的几何不变体系。
第3章静定结构的受力分析典型题1. 求图3.1结构的内力图。
图3.1解(1)支座反力(单位:kN)由整体平衡,得=100.= 66.67,=-66.67.(2)内力(单位:kN.m制)取AD为脱离体:,,;,,。
取结点D为脱离体:,,取BE为脱离体:,,。
取结点E为脱离体:,,(3)内力图见图3.1b~d。
2. 判断图3.2a和b桁架中的零杆。
图3.2分析:判断桁架零杆的常用方法是找出桁架中的L型结点和T型结点。
如果这两种结点上无荷载作用.那么L型纪点的两杆及T型结点的非共线杆均为零杆。
解:图3.2a:考察结点C、D、E、I、K、L,这些结点均为T型结点,且没有荷载作用,故杆件CG、DJ、EH、IJ、KH、LF 均为零杆。
考察结点G和H,这两个结点上的两竖向链杆均已判断为零杆,故这两个结点的受力也已成为T型结点的情形.由于没有荷载作用,故杆件AG、BH也为零杆。
整个结构共有8根零杆.如图3.2c虚线所示。
图3.2b:考察结点D,为“K”型结点且无荷载作用,故;对称结构对称荷载(A支座处的水平反力为零),有,故杆件DE和DF必为零杆。
龙驭球《结构力学Ⅱ》配套题库-课后习题(结构动力计算续论)【圣才出品】
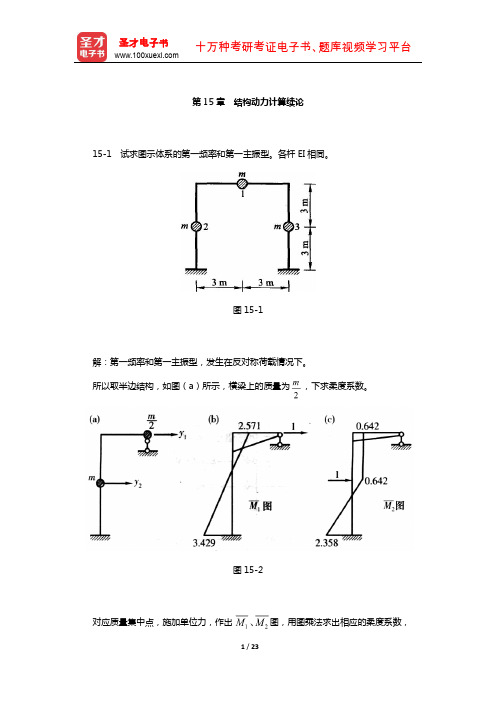
第15章结构动力计算续论15-1 试求图示体系的第一频率和第一主振型。
各杆EI相同。
图15-1解:第一频率和第一主振型,发生在反对称荷载情况下。
所以取半边结构,如图(a)所示,横梁上的质量为,下求柔度系数。
图15-2对应质量集中点,施加单位力,作出图,用图乘法求出相应的柔度系数,第一频率为,振型为15-2 试求图示三层刚架的自振频率和主振型,设楼面质量分别为m1=270 t,m2=270 t,m3=180 t;各层的侧移刚度分别为k1=245 MN/m,k2=196 MN/m,k3=98 MN/m;横梁刚度为无限大。
图15-3解:采用刚度法求解由振动控制方程,由可得,,,三层刚架的自振频率为即三层刚架的主振型为(2)(0.667,0.667,1.000)TY=--15-3 设在题15-2的三层刚架的第二层作用一水平干扰力F P(t):20 kN.sinθr,每分钟振动200次。
试求图示各楼层的振幅值。
图15-4 解:由题意可知,计算,荷载幅值向量为所以解方程,得到振幅向量为:15-4 试用振型叠加法重做题l0-23。
解:(1)由题10-23得到:,,设频率方程为解得,。
从而(2)求主振型由上述的计算结果,(3)建立广义坐标体系(4)计算广义质量和广义荷载(5)求正则坐标(6)求楼层振幅15-5 设在题10—22的两层刚架二层楼面处沿水平方向作用一突加荷载F P,试用振型叠加法求第一、二层楼面处的振幅值和柱端弯矩的幅值。
解:由题10-22可知,且在突加荷载作用下的广义荷载为求正则坐标求质点位移。
结构力学习题含答案解析

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p7、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移∆DV 。
EI = 常数,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数。
l l l /3/3q13、图示结构,EI=常数,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数。
16、求图示刚架中D点的竖向位移。
EI=常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI =常数。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l/219、求图示结构A、B两截面的相对转角,EI =常数。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
l l21、求图示结构B 点的竖向位移,EI =常数。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
结构力学力法习题及答案

结构力学力法习题及答案结构力学力法习题及答案结构力学是一门研究物体在外力作用下产生的应力和变形的学科。
在工程学中,结构力学是非常重要的一门学科,它为我们设计和分析各种建筑和机械结构提供了基础。
在学习结构力学的过程中,习题是必不可少的一部分。
下面将给出一些结构力学的力法习题及其答案,希望对读者有所帮助。
1. 一个悬臂梁上有一个集中力作用在梁的自由端,求该梁的弯矩分布图。
解答:根据悬臂梁的特点,自由端处的弯矩最大。
假设集中力为F,梁的长度为L,弹性模量为E,梁的截面惯性矩为I。
根据悬臂梁的弯矩公式M = F * L,可以得到弯矩分布图为一个从自由端开始逐渐减小的直线。
2. 一个等截面的梁上有一个均布载荷作用,求该梁的剪力分布图。
解答:假设均布载荷为q,梁的长度为L,根据梁的受力平衡条件,可以得到梁上任意一点的剪力大小为V = q * x,其中x为距离梁的一端的距离。
因此,该梁的剪力分布图为一个线性增长的直线。
3. 一个梁上有多个集中力作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
4. 一个悬臂梁上有一个集中力和一个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:首先,根据集中力的大小和悬臂梁的长度,可以求出集中力在悬臂梁上的弯矩分布图。
然后,根据均布载荷的大小和悬臂梁的长度,可以求出均布载荷在悬臂梁上的剪力分布图。
最后,将两者叠加在一起,即可得到梁的总弯矩和总剪力分布图。
5. 一个梁上有多个集中力和多个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力和均布载荷,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
通过以上习题的解答,我们可以看到结构力学中力法的应用。
在实际工程中,我们需要根据具体的结构形式和受力情况,运用结构力学的理论知识,求解结构的受力分布,从而保证结构的安全可靠。
结构力学例题

结构力学例题
题目:加载斜拉桥的结构力学分析
问题描述:
一座斜拉桥长L,其中铺装部分重量为W1,桥墩的重力荷载为W2。
斜拉桥的主梁采用直线模型,两侧各有m个斜拉索,每个斜拉索的倾角为α,斜拉索与水平方向的夹角为β。
主梁上负载作用的形状近似为三角形,其均布荷载为q。
问题要求:
1. 利用结构力学的原理,绘制该斜拉桥的受力示意图。
2. 计算斜拉桥的主梁在A点(主梁中央)的受力情况:弯矩、剪力、轴力。
3. 根据受力情况,确定主梁在A点的最大正向弯矩及其位置。
4. 根据受力情况,确定主梁的最大剪力及其位置。
5. 根据受力情况,确定主梁上的合力图。
解决方案:
1. 绘制斜拉桥的受力示意图:
a. 主梁受到均布荷载q,产生弯矩和剪力;
b. 主梁两侧斜拉索上的受力:水平拉力TH,竖直拉力TV,合力TF;
c. 桥墩受到重力荷载W2和部分主梁重力荷载W1。
2. 主梁在A点的受力情况:
a. 弯矩M = q * L * L / 8;
b. 剪力V = q * L / 2;
c. 轴力N = 0。
3. 主梁在A点的最大正向弯矩及其位置:
a. 最大正向弯矩为Mmax = q * L * L / 8;
b. 最大正向弯矩位置为主梁距离A点为L / 2。
4. 主梁的最大剪力及其位置:
a. 最大剪力为Vmax = q * L / 2;
b. 最大剪力位置为A点。
5. 主梁上的合力图:
a. 合力图为一负弯矩图,表明主梁在A点为凸向下弯曲;
b. 弯矩随距离A点的增加而减小;
c. 剪力图为一等值线型,剪力大小为Vmax。
结构力学应用-结构动力学

(小阻尼) 令
有阻尼的自振频率
1
2
y(t ) e
t
y0 y0 ( y0 cos t sin t )
*写成
y(t ) b e
2 0
t
sin(t )
(14-12)
y0 y0 2 其中 b y ( )
柔度法(力法)
MY KY 0 MY Y 0
10、按柔度法求解
振型方程: ([ ][ 2 [ 1 M ]){Y } 00} ([ I ] M ] ][ [ I ]){Y } { 2 频率(特征)方程
D [ ][ M ] [ I ] 0
y0 tg y0 y0
位移-时间曲线如图示:
阻尼比——阻尼的基本参数: a.阻尼对频率(周期)的影响
k
2m
1 2
T T 1 2 T
0.2
T T
b、阻尼对振幅的影响
be
t
——振幅随时间逐渐衰减
11m1
1
12 m2
(k )
0 0
(14 63)
{Y }
(k )
Y1 Y2
(k )
11m1 k 12 m2
12 m2
k2
(k=1、2)
结构的刚度和质量分布 ——对称 其主振型 ——对称、反对称 计算自振频率: ——分别就正、反对称情况 ——取半跨结构计算 ——两个单自由度问题计算 显然,振型分别为: [1 1]T、[1 -1]T
1
0.2,
yn ln 2 j yn j 相隔j个周期: 1
结构力学 动力计算例题

例题
K 2 M Y 0
第一主振型
K 12 M
YY1211 Y31
k 15
17.414
5
0
5 6.707
3
0 3 1.707
YY1211 Y31
0
5Y11 6.707Y21 3Y31 0 3Y21 1.707Y31 0
规定 Y31 1
Y 1
YY1211
0.163 0.569
Y31 1
例题8
(2)求主振型
例题
K 2 M Y 0
第二主振型
K 22 M
YY1222 Y32
k 15
6.640
5
0
5 1.320
3
0
3
3.680
YY1222 Y32
0
5Y12 1.320Y22 3Y32 0 3Y22 3.680Y32 0
1 2
G
3 4
1 1
1 5
ij
2 ①
3
④
5 ②1
③ 4
k
e
kiei
k
e ji
kiej
k
e jj
例题
例题 10
(2)各单元刚度矩阵
k
(1)
k (1) ii
k (1) ji
k (1) ij
k (1) jj
k
(2)
k (2) ii
k (2) ji
k (2 ij
k (2 jj
) )
P
(5)最大动弯矩
M D max
Pl 4
2
2
MDmax (kN m) 图
例8
试求刚架的自振频率和主振型,其横梁为无限刚性。设质量集中在楼层上,第一、 二、三层的质量分别为2m 、m、 m 。层间侧移刚度分别为k 、 、 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l3
0
0
6EI l2
12EI l3
0
1 6EI
l2
EA 6EI
l
l2
0
2 EA l
0
6EI
k 2
TT
k
2 T
l2
12EI l3
0 0
4EI
l
6EI l2
6EI l2
12EI l3
3 0
2EI
l
0
0
6EI l2
0
EA l
0
0
EA l
0
0
6EI l 2
0
2EI 6EI
l
EA
0
l
0
1
0
12EI l3
2 6EI
l2
0
6EI l2
3 4EI l
(1) 求各单元单刚
例题
EA
l
k
1
0
0
0
12EI l3 6EI l2
0
6EI
l2
4EI
l
2 900 , cos 2 =0, sin 2 =1
k 2 k 1
例题
12 30 0 0
12EI
Psin
m
l
l
例题4
例题
(1)体系的自振频率
单位力作用下的 M 图
求
1 2
ll
•
2 3
l
l3
EI
3EI
自振频率
k m
1
m
3EI ml 3
P=1 l
l
M图
例题4
例题
(2)简谐荷载的频率
6
(3)动力系数
1
1
2 2
1
1 1 6
2
36 35
(4)位移振幅
A
Yst
P
36 35
P•
l3 3EI
K 1 EA 0 1 0 1
l 0 0 0 0
0 1 0
1
x 3
1 0 1 0
K 2
EA
0
0
0
0
l 1 0 1 0
0
0
0
0
1 1 1 1
K 3 2EA 1 1 1 1
4l 1 1 1 1
1
1 1
1
例题5
1
① l
2
③
② l
例题
K
k
1
jj
kii3
kij1
k
3
ji
k
1
ji
kii1 kii2
1000EI
2
3
②
q ①
③l
y M,
1
4
x
l
例题
例题6
(1)由结构位移向量得出单元①的位移
1 ql2 0
1000EI
0
0
0
27l
5T
q
2 ②
①
3 ③l
(2)求单元①的固端力列阵
1
4
l
1
Fp 0
ql 2
ql2 12
0
ql 2
ql
2
T
12
例题
(3) F1 k1 1 Fp 1
EA
P=1 l
l
M图
例题4
例题
(5)体系稳定阶段动力弯矩幅值
MD
PM
36 35
PM
36 Pl 35
l M Dmax 图
例题5
例题
图示桁架,已知各单元整体坐标表示的单元刚度矩阵,试用后处理法求图示 桁架的结构总刚度矩阵,并写出引入支座条件后的总刚度矩阵(主元素置1法)
1 ① l
2
y ③
② l
M,
0 0 0 0
l
0
0
F1
EA
l
0
0
0
12EI l3
6EI l2
0
12EI l3
6EI l2
0
6EI
l2 4EI
l
0
6EI l2 2EI l
EA l 0
0 EA l 0
0
0
12EI
l3 6EI l2
0
12EI l3 6EI l2
0
6EI l2
2EI
0
0
l
0
ql2
1000EI
k
2
ji
kij3 kij2
kii2
k
3
jj
2
3
4
2 4
K
0 0
2
4
2
4
2 0 0 4
2 1 0 1 4
0 10 1 0 1
2 4 2 4
1 0 00
2 4 2 4
1 0
2 1 4 2
4
2
4
2
4
0 EA
0
l
2
4
2
4
例题5
1
① l
2
③
② l
例题
引入支座条件后
l
EA
0
00
2(0,0) ①
3(1,2) 2kN
4m
②③
3kN
y M,
1(0,0)
x
4m
例题3
例题
(1) 提取整体坐标系下单元的杆端位移
0
1
0 0.09524
0.25689
(2) 单元坐标系下单元的杆端位移
0
1
1
0 0.09524
0.25689
例题3 (3) 求杆端力
例题
EA
2.1104
l
l2
0
0 4EI l
例题
12EI
l3
k 2
0
6EI
l 2
0
6EI
l2
EA l
0
0
4EI
l
(2) 求总刚,叠加计算
EA l
12EI l3
k
k 1
k 2
0
6EI
l 2
0
EA 12EI
l
l3
6EI
l2
6EI
l2
6EI
l2
8EI
l
例题
例题2 图示结构用矩阵位移法计算时,求结点3的等效荷载列阵。
102 52.5
l
4
1 0 1 0 0 5kN
F 1 K 1
1
EA
0
l 1
0 0
0
0
0 1 0
0
0 0
0
0.09524
0.25689
0 5kN
0
例题
例题4
图示结构,已知=/6(为自振频率),EI=常数,杆长为l,不计阻 尼.求(1)体系的自振频率;(2)体系稳态阶段动力弯矩幅值并画 出MDmax图.
q=2kn/m
2
②
3m
① 3m
3
P=8kn ③
y M,
x
1
4
6m
例题2
例题
(1) 求各单元的固端力向量
2
Fp 0
6
6066T NhomakorabeaU2 1
2
3
4
5
6T
3
Fp 0
4
6
0
4
6T ;U3 0
0
0
4
5
6T
(2) 结点 3(4,5,6)
0 0
P3E 2 6 6
6 6
4 4
0 0
1
Fp
27l
6EI
l2
5
4EI
l
ql 2 1000EI
0
354EI l2
172EI l
0
354EI l2
182EI l
T
Fp
1
例题7
例题
图示结构,忽略梁的自重,集中质点的重量 W=4kN,P=2kN,
EI=9×104kN.m2,电机转速n=600r/min.求梁的最大位移,并
0
0
0
3
K
0
0
2 1 0 0 4
0
l0
EA
0
0l
2 4
2
4
0
0
EA
0
0
l
EA
0
2
00
2 1
2
4
4
4
0
2 4
0
0
2 4
2
4
例题
例题6
求图示刚架单元①在局部坐标下的杆端力列阵。已知各杆E,A, I,l 均为常数,已求得结构位移向量为
ql2 0 0 0 27l 0 5 27l 0 19 0 0 0T
(1) 求各单元单刚
1 00 ,
例题
k 1 k 1
0
EA
l
0
0
k 1
EA
l
0
0
0
0
12EI l3
6EI l2
0
12 l
EI
3
6EI l2
0
0
6EI l2 4EI
l
0
6EI l2 2EI l
12 3
EA 0 l
0
0
0 0
12EI l3
6EI l2
0
6EI l2
0 2EI
P3E 3
0
0
6 6
例题2
(3)等效荷载列阵
