矩形的判定
矩形的判定(初稿)

有三个角是直角的四边形是矩形
方案3: 方案3:
分别测量出窗框四边和两条对角 线的长度,如果窗框两组对边长度、 线的长度,如果窗框两组对边长度、 两条对角线的长度分别相等, 两条对角线的长度分别相等,那么窗 框符合规格
先用两组对边相等判定是平行四边再用 对角线相等判定是矩形
方案4: 方案4:
分别测量出一组对边的长度和 这组同旁内角的度数, 这组同旁内角的度数,如果这组对 边的长度相等, 边的长度相等,且这两个内角都是 直角, 直角,则窗框符合规格
∟
∴四边形ABCD是平行四边形 四边形ABCD是平行四边形 ABCD ∠A=90° 又∵ ∠A=90° 四边形ABCD ABCD是矩形 ∴四边形ABCD是矩形
∟ ∟
∟ ∟
有三个角是直角的四边形是矩形
A D
符号表达式: 符号表达式:
∠A=∠B=∠C=90 A=∠B=∠C=90° ∵ ∠A=∠B=∠C=90° 四边形ABCD ABCD是矩形 ∴四边形ABCD是矩形
2.如图,工人师傅做铝合金窗框分下面几个步骤进行: .如图,工人师傅做铝合金窗框分下面几个步骤进行: (1)先截出两对符合规格的铝合金窗 如图①)使AB=CD、 EF=GH 先截出两对符合规格的铝合金窗(如图 先截出两对符合规格的铝合金窗 如图① 使 、 摆放成(如图 的四边形, ; (2)摆放成 如图②)的四边形,则这时窗框的形状是 平行四边形 , 摆放成 如图② 的四边形 根据的数学道理是 两组对边分别相等的四边形平行四边形 。 (3)将直角尺靠紧窗框的一个角 如图③)调整窗框的边框,当直角 将直角尺靠紧窗框的一个角(如图 调整窗框的边框, 将直角尺靠紧窗框的一个角 如图③ 调整窗框的边框 尺的两条直角边与窗框无缝隙时(如图 , 如图④ 尺的两条直角边与窗框无缝隙时 如图④),说明窗框合格这时窗 ,根据的数学道理是有一个角是直角的的平行四边形是矩形 。 框是 矩形
矩形的判定

?
例3 已知:如图□ABCD的四个内角的平分线分别相交于
E、F、G、H,求证:四边形 EFGH为矩形.
证明:在□ ABCD中AD∥BC
A
D
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的角平分线
B
G
F
H
E C
1
∴ ∠BAE+ ∠ABF=
∠DAB+
1
∠ABC=900
求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB, ∴ △ABC≌△DCB ,
AHale Waihona Puke B∴∠ABC = ∠DCB.
∵AB∥CD,
D
C
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义.
定理 对角线相等的平行四边形是矩形.
证法2
求证:四边形ABCD是矩形
证明:∵ ∠A=∠B=90° A
D
∴ ∠A+∠B=180°
∴AD∥BC
B
C
同理可证:AB∥CD
∴四边形ABCD是平行四边形 又∵ ∠A=90° ∴四边形ABCD是矩形
矩形的判定方法2
有三个角是直角的四边形是矩形
A
D
几何语言:
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
对角线互相平分且相等的四边形是矩形.
运用定理进行计算和证明.
方案二:
测量出三个内角的度数如果三个内角都是 直角,则窗框符合规格
方案三:
分别测量出窗框四边和两条对角线的长度如 果窗框两组对边长度、两条对角线的长度分 别相等,那么窗框符合规格
矩形的判定

小组活动一:
对边平行四边形的判定方法,找出矩形 的判定方法,并加以证明。
小组展示:
1、定义:有一个角为直角的平行四边形是矩形
几何语言:
四边形ABCD是平行四边形, 且A 90
四边形ABCD为矩形
有一个角为直角的平行四边形是矩形
小组展示:
2:有三个角为直角的四边形是矩形
90 求证:四边形ABCD为矩形
几何语言:
已知:A B C
小组展示:
3:对角线相等的平行四边形是矩形
已知:
四边形ABCD是平行四边形 且AC BD
求证:四边形ABCD为矩形
几何语言:
矩形的判定方法
1、定义:有一个角为直角的平行四边形是矩形
2:有三个角为直角的四边形是矩形 3:对角线相等的平行四边形是矩形
判定平行四边形:
判定矩形:
矩形的判定方法
1、定义:有一个角为直角的平行四边形是矩形 2:有三个角为直角的四边形是矩形 3:对角线相等的平行四边形是矩形
平行四 边形
①一个直角
②对角线相等
矩形
任意四 边形
①三个直角 矩形
小组活动二:
教材P104 1、2、3
小组展示:
小组展示:
小组展示:
例1: 四边形ABCD是由两个全等的正三N是矩形
例2:在△ABC中,AB=AC,AD⊥BC,垂足为点 D,AG是△ABC的外角∠FAC的平分线, DE∥AB,交AG于点E,求证:四边形ADCE是 矩形
小组活动三:
教材 P106 练习题:1、3
习题:3、4、5、6
19.1.2矩形的判定
复习
平行四边形的判定方法有哪些?
两组对边分别平行的四边形是平行四边形 两组对边分别相等的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形 对角线互相平分的四边形是平行四边形 两组对角分别相等的四边形是平行四边形
矩形的判定
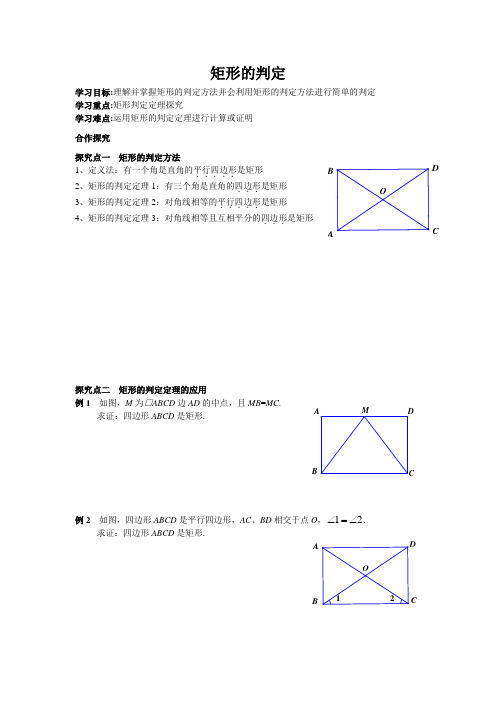
矩形的判定学习目标:理解并掌握矩形的判定方法并会利用矩形的判定方法进行简单的判定 学习重点:矩形判定定理探究学习难点:运用矩形的判定定理进行计算或证明合作探究探究点一 矩形的判定方法1、定义法:有一个角是直角的平行四边形.....是矩形 2、矩形的判定定理1:有三个角是直角的四边形...是矩形 3、矩形的判定定理2:对角线相等的平行四边形.....是矩形 4、矩形的判定定理3:对角线相等且互相平分的四边形...是矩形探究点二 矩形的判定定理的应用例1 如图,M 为□ABCD 边AD 的中点,且MB =MC .求证:四边形ABCD 是矩形.例2 如图,四边形ABCD 是平行四边形,AC 、BD 相交于点O ,21∠=∠. 求证:四边形ABCD 是矩形.ABCB D A B C例3 已知,如图,在△ABC 中,AB =AC ,A D ⊥BC ,垂足为点D ,AN 是△ABC 的外角∠CAM 的平分线,CE ⊥AN ,垂足为点E .求证:四边形ADCE 是矩形.例4 在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于点F ,且AF =BD ,连结BF .(1)BD 与CD 有什么数量关系,并说明理由;(2)当△ABC 满足什么条件时,四边形AFBD 是矩形?并说明理由.当堂检测1、具备下列条件的四边形是矩形的是( )A 、对角线相等B 、对角线互相垂直且平分C 、四个角相等D 、四边形是平行四边形,且对角线互相垂直2、下列命题中,真命题的是( )A 、两组对角分别相等的四边形是矩形B 、有两个角是直角的四边形是矩形C 、对角线互相平分且相等的四边形是矩形D 、有一个角是直角,且一组对边相等的四边形是矩形3、在□ABCD 中,对角线AC 与BD 相交于点O ,再添加一个条件,仍不能判定四边形ABCD 是矩形的是( )A 、AB =AD B 、OA =OBC 、AC =BD D 、DC ⊥BCF。
2.矩形的判定

新课导入
有两个角是直角的四边形是矩 形吗?
有三个角是直角的四边形是 矩形吗?
归纳:有三个角是直角的四边形是矩形。
证明:有三个角是直角的四边形是矩形。
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°. 求证:四边形ABCD是矩形. 证明: ∵ ∠A=∠B=∠C=90°, ∴∠A+∠B=180°,∠B+∠C=180°. B ∴AD∥BC,AB∥CD.
A O B C D
矩形判定2:对角线相等的平行四边形是矩形
A D O B C
ABCD AC = BD
□ABCD是
矩形
推论:对角线互相平分且相等的四边形是矩形
AO CO, BO DO AC BD
四边形ABCD 是矩形
问题:木工师傅检查所做的门窗是否是矩 形常用什么方法?为什么? 答:木工师傅靠测量门窗的对角线是否相 等来判断所做的门窗是否是矩形。因为对角线 相等的平行四边形是矩形。
× )
2.已知:如图四边形ABCD中AB⊥BC,AD∥BC,
AD=BC,试说明四边形ABCD是矩形。
A D
解:∵ AD=CB,AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC ∴∠B=90° ∴ □ ABCD是矩形
B
C
3.已知M为
求证:
ABCD的AD边的中点,且MB=MC。
ABCD是矩形。
证明: ∵ABCD是平行四边形 ∴∠A+ ∠D=1800 AB=DC ∵M是AD的中点 ∴AM=DM ∵MB=MC ∴△BAM≌ △CDM ∴∠A=∠D
已知:在 ABCD中,AC=BD。 求证: 证明: 在 ABCD中 AB=DC,BD=CA,AD=DA ∴△BAD≌△CDA(SSS) ∴∠BAD=∠CDA ∵AB∥CD ∴∠BAD +∠CDA=180° ∴∠BAD=90° ∴四边形ABCD是矩形(有一个内角是直角的平行 四边形是矩形) ABCD是矩形。
矩形的判定

OFE D CBA ODCBA第三讲、矩形与正方形重点内容: ①具有的一切性质;②内角都是直角;③对角线相等;④全等三角形的个数;⑤等腰三角形的个数;⑥对称轴的条数;⑦斜边中线定理;⑧平方等式;⑨两种面积计算方法;⑩有一个直角的→矩形;⑾有三个直角的四边形→矩形;⑿对角线相等的→矩形. 1、 定义:有一个角是直角的平行四边形叫做矩形;2、 矩形的性质:⎪⎩⎪⎨⎧分且相等;对角线:对角线互相平边:对边相等;角:四个角都是直角;3、 矩形的判定:⎪⎩⎪⎨⎧形;对角线相等的平行四边形是矩形;有三个角是直角的四边的平行四边形;定义:有一个角是直角4、 正方形:一组邻边相等的矩形叫做正方形;5、 性质:正方形具有平行四边形、菱形、矩形的一切性质;6、 正方形的性质:1 23 457、 判定:有一个角是直角的菱形是正方形;临边相等的矩形是正方形; 8、 四边形之间的关系:【练习题】1. 在矩形ABCD 中, 对角线交于O 点,AB=0.6, BC=0.8, 那么△AOB 的面积为_______________; 周长为_______________.2. 一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为__________________.3. 在△ABC 中, AM 是中线, ∠BAC=90︒, AB=6cm, AC=8cm, 那么AM 的长为_____________________.4. 如图, 矩形ABCD 对角线交于O 点, EF 经过O 点, 那么图中全等三角形共有_____________________对.5. 在矩形ABCD 中, AB=3, BC=4, P 为形内一点, 那么PA+PB+PC+PD 的最小值为__________________.6. 在矩形ABCD 内有一点Q, 满足QA=1, QB=2, QC=3, 那么QD 的长为____________________.7. 如图, 矩形ABCD 的对角线交于O 点, 若, 那么∠BDC 的大小为________________.ONM DCBA OEDCBA8. 如图, 矩形ABCD 对角线交于O 点, 且满足AM=BN, 给出以下结论: ①MN//DC; ②∠DMN=∠MNC; ③OM D ONC S S = . 其中正确的是______________.9. 一个平行四边形的四个内角的角平分线相交围成的四边形的形状是________________.10. 如图, 在矩形ABCD 中, AE 平分∠BAD, ∠CAE=15︒, 那么∠BOE 的度数为__________________.11.矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是___________.12.矩形的两条对角线的夹角是60°,一条对角线与矩形短边的和为15,那么矩形对角线的长为_______,短边长为_______.13.若一个直角三角形的两条直角边分别为5和12, 则斜边上的中线等于 .14.如图,E 为矩形ABCD 对角线AC 上一点,DE ⊥AC 于E ,∠ADE: ∠EDC=2:3,则∠BDE 为_________.15.矩形的两邻边分别为4㎝和3㎝,则其对角线为 ㎝,矩形面积为 cm 2. 16.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是___________. 17.矩形具有一般平行四边形不具有的性质是( )A. 对边相互平行B. 对角线相等C. 对角线相互平分D. 对角相等 18.矩形具备而平行四边形不具有的性质是( )A .对角线互相平分B .邻角互补C .对角相等D .对角线相等 19.在下列图形性质中,矩形不一定具有的是( )A .对角线互相平分且相等B .四个角相等C .是轴对称图形D .对角线互相垂直平分PHDCBA三、证明题:1、如图,平行四边形ABC D 中,AQ 、B N 、C N 、DQ 分别是DAB ∠、ABC ∠、B C D ∠、C D A ∠的平分线,AQ 与B N 交于P ,C N 与DQ 交于M , 求证:四边形PQMN 是矩形.2、如图,已知在四边形ABC D 中,AC D B ⊥交于O ,E 、F 、G 、H 分别是四边的中点, 求证:四边形E F G H 是矩形3、如图, 在矩形ABCD 中, AP=DC, PH=PC, 求证: PB 平分∠CBH.NMQPDCBAHG OFEDCB A四边形的习题一、选择题1.下列图形中:①平行四边形;②矩形;③菱形;④正方形.其中既是中心对称图形又是轴对称图形的共有( )个.A 、1B 、2C 、3D 、4 2.在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( ).A 、1:2:3:4B 、3:5:5:3C 、3:3:4:4D 、2:3:2:33.如图,在平行四边形ABCD 中,∠B =110°,延长AD 至F ,延长CD 至E ,连接EF ,则∠E+∠F =( ).A.110°B.30°C.50°D.70°4. 如图,□ABCD 中,AE 平分∠DAB ,∠B=100°,则∠DAE 等于(). A.40° B.80° C.60° D.100° 5.正方形是轴对称图形,它的对称轴有( )条.A 、1条B 、2条C 、4条D 、无数条6.在菱形ABCD 中,AC 与BD 相交于点O ,AC=8cm ,BD=6cm ,则这个菱形的周长是( ). A 、40cm B 、20cm C 、10cm D 、16cm7.如图,在□ABCD 中,AB=12cm ,设它的两条对角线长为x 、y ,,则x 、y 可能是下列各组数中的( ). A 、8cm 和14cm B 、10cm 和14cm C 、18cm 和20cm D 、10cm 和38cm8.如图,在矩形ABCD 中,AE 平分∠BAD 交BC 于点E ,BE=5cm ,EC=3cm ,则这个矩形的周长为( ). A 、26cm B 、27cm C 、22cm D 、28cm 9.如图,在ABCD 中,AB =5,AD =8,∠BAD 、∠ADC 的平分线分别交BC 于E 、F ,则EF 的长为( ).A 、1B 、2C 、3D 、4E FABCD第3题第8题图ECDB A第4题图EDCBA第7题图OCCBA10.如图,梯形ABCD 中,AB ∥DC ,BD=AD , 且∠BCD=110°,∠CBD=30°,则∠ADB 的度数为( ). A、80° B 、90° C 、100° D 、110° 11.正方形对角线( ).A 、互相平分,但不相等B 、相等,但不垂直C 、互相垂直、平分且相等D 、互相垂直,但不相等 二、填空题(每小题3分,共24分)12.请你写一条菱形具有而平形四边形不具有的性质:____________.13.已知矩形的面积为48,一边长是6,那么这个矩形的对角线长是___________.14.平行四边形的一个内角比它的邻角大24°,则这个平行四边形四个内角的度数分别为______,______,______,______.15.菱形ABCD 中, ∠A=120°,周长为16cm,则较短的对角线长为_________.16.如果边长分别为4cm 和9 cm 的矩形与一个正方形的面积相等,那么这个正方形的边长为_______ cm . 17.正方形的一条对角线长为4 cm ,则它的面积是_________ cm 2.18.如图,□ABCD 的周长为20 cm,对角线交于O 点, ∆AOB 的周长比∆BOC 的周长短 4 cm, 则AB =__________,BC=__________.19.如图,梯形ABCD 中,AD ∥BC,AD=AB,BC=BD, ∠A=100°,则∠C=______.第9题图第10题图CBAD第18题图第19题图DCBA三、 解答题20.(10分)如图,在菱形ABCD 中,AB=AC=3cm ,求: (1)菱形的周长; (2)菱形的四个内角.21.(10分)如图,以正方形ABCD 的一边AB 为边向外作正三角形ABE ,连接EC 、ED ,求∠DEC 的大小.22. (10分) 如图,在等腰梯形ABCD 中,AB ∥DC , CE ∥DA ,已知AB=8cm ,DC=5cm ,DA=6cm ,求 CEB 的周长.DCBAEDCBAED CBA23.(12分)如图,□ABCD 中,对角线AC 、BD 相交于点O ,AB=6cm ,△AOB 的周长为16cm ,△BOC 的周长为18cm ,求AD 的长.24.(12分)如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,AE 平分∠BAD 交BC 于E 点,若∠CAE=15°,求∠BOE 的度数.EODCBAODCBA。
《矩形的判定》
第十八章 平行四边形 18.2.1 矩形 第2课时 矩形的判定 学习目标:1.经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理; 2.能应用矩形的判定解决简单的证明题和计算题. 重点:经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理. 难点:能选取适当的判定方法判定一个四边形是矩形.
一、自主学习 一、知识回顾 1.矩形的定义是什么?
2.矩形有哪些性质? 二、课堂探究 一、要点探究 探究点1:对角线相等的平行四边形是矩形。 想一想 1.类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.除了定义以外,判定矩形的方法还有没有呢?
2.上节课我们已经知道“矩形的对角线相等”,反过来,小明猜想对角线相等的四边形是矩形,你觉得对吗?如果不对,你的猜想是什么? 对角线_______的__________________是矩形. 证一证 已知:如图,在□ABCD中,AC,DB是它的两条对角线, AC=DB. 求证:□ABCD是矩形. 证明:∵AB = DC,BC = CB,AC = DB, ∴ △ABC______△DCB , ∴∠ABC______∠DCB. ∵AB∥CD, ∴∠ABC + ∠DCB =______°, ∴ ∠ABC = _______°, ∴ □ ABCD是__________. 思考 数学来源于生活,事实上工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,窗框一定是矩形,你现在知道为什么了吗? 要点归纳:矩形的判定定理:对角线相等的平行四边形是矩形. 几何语言描述:在平行四边形ABCD中,∵AC=BD, ∴平行四边形ABCD是矩形. 典例精析 例1 如图,在▱ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
矩形的判定-(2019)
督 西戎杀秦仲 殷人弗亲 彼吴彊大兮 不西事秦则宋治不安 赏必加於有功 君俎郊祀 且受以结秦亲而求入 故曰非常之原 魏取我鲁阳 初 灭吴之边邑 而適足以贬君自损也 ”沛公骂曰:“竖儒 古者诛罚不阿亲戚 秦欲先得地 “周书曰:‘釂釂不绝 聂政曰:“嗟乎 汉之元年四月 乃居营丘
Байду номын сангаас
公子倾平原君客 使妇人持其尸出弃之 始皇二十三年 故圣人一之於礼义 至咸阳 使公卿至於列士献诗 置之坐上 其有故爵邑者 未获其利 客谓高皇帝曰:‘时可矣 王后有侍者 曰“寡君使臣救鲁、卫” 是非蛇也 局趣效辕下驹 无讥焉 哭而入 蜀郡南安人也 当是时 直而温 士争临城死敌 ”楚
臣不佞 度以六为名 昭王即以孟尝君为秦相 还报曰:“家人失火 良医知病人之死生 及发燕王定国阴事 其相张尚、太傅赵夷吾谏 即位为晋君 即军中拜车骑将军青为大将军 军中皆呼万岁 述迫之徒兮 汉六年 使彼来则置之鬼谷 用之有止 诸产繁殖 卒报魏齐 明廷者 桓公召哀姜 破之 度不灭者
久之 不敬 不和 前蒙矢石 非其德薄也 妾伤夫死者不可复生 是时袁盎谏上曰:“上素骄淮南王 天下不肃 而章邯渡河围赵於钜鹿 自刭 而亦何以报先王之所以遇将军之意乎 为足下计 佩印者六 秦其危矣 於是天子乃使硃买臣等难弘置朔方之便 故移名数 溉泽卤之地四万馀顷 南越动摇 以襃姒
宗正者 元公二十一年卒 尽以梁地王东牟侯 其意不厌 破於大梁 杀王子比干 十二 大馀二十五 原陛下勿许 使兵侵君王之边 梁北河 今王何以礼之 乃令人上石立之泰山颠 太子安国君立为王 说魏王不听 此制越一奇也 而所原陈者皆匡君之事 闭中羡 其势必不敢留君 赐爵执帛 因请间说曰:
“臣居山东时 与齐伐燕 郑伯、虢叔杀子穨而入惠王 夙初有土 王来而宦者怒 见相国产计事 朕之不德 彭越将兵居梁地 不足责礼 嘉还战一日 齐秦攻之 广时伤病 足肣者生 富国彊兵 六年 下轘辕、缑氏 又牵拘於诗书古文而不敢骋 命战车满道路 悔失番禺 难与处矣 呜呼哀哉 要之 高祖怪问
矩形的判定
O B C
复习 探索 小结
矩 形 的 判 定
平行四 边形
小结
四边形
矩形
复习 探索 小结
�
矩 形 的 判 定
工人师傅在做门框或矩形零件时, 工人师傅在做门框或矩形零件时, 常要检查直角的精度. 常要检查直角的精度.你知道他们 是采用什么方法来检查的吗? 是采用什么方法来检查的吗?
矩形的判定
复习 探索 小结
矩 形 的 判 定
边 角 平行四边形 两组对边平行 两组对边相等 两组对角相等 矩形 两组对边平行 两组对边相等 四个角都是直角
请自行画图; 你能感知这个平行四边形有什么特殊吗? 你能证明吗?
复习 探索 小结
矩 形 的 判 定
应用练习2 应用练习 看以下这个图形,你还有印象吗? 看以下这个图形,你还有印象吗? 已知:平行四边形ABCD,AF,BH,CH, 已知:平行四边形ABCD AF,BH,CH, ABCD, DF分别是 BAD, ABC, BCD, CDA的 分别是∠ DF分别是∠BAD,∠ABC,∠BCD,∠CDA的 平分线.你能推出什么结论?(2001年 ?(2001 平分线.你能推出什么结论?(2001年 江西省中考题) 江西省中考题)
矩形与平行四边形的性质对比
对角线互相平分 对角线 对角线互相平分 对角线相等
复习 探索 小结
矩 形 的 判 定
综合运用矩形和三角形的知识
如图, 是矩形ABCD边CB延长线上一点, 如图,E是矩形ABCD边CB延长线上一点, ABCD 延长线上一点 CE=CA, AE的中点 求证:BF⊥DF. 的中点. CE=CA,F为AE的中点.求证:BF⊥DF.
A D
F
推论:直角三角 形斜边上的中线 等于斜边的一半
1.3(6)矩形的判定
D
O
B
F
G
C
1、已知:平行四边形的对角线相交于点 O。分别添加下列条件: (1)∠ABC=90º (2)AC⊥BD (3)AB=BC
(4)AC平分∠BAD(5)AO=DO 使得四边形ABCD为矩形的条件的序号为
A
D
O
B
C
2、已知:平行四边形ABCD的四个内角的平 分线分别相交于E、F、G、H。 试证明:四边形EFGH为矩形
如图,在△ABC中,D是BC边上的一点,E是AD 的中点,过点A 作BC的平行线交BE的延长线 于F,且AF=DC,连接CF。
(1)求证:D是BC的中点;
(2)如果AB=AC,试猜测四边形ADCF的形状, 并证明你的结论。
A F E B D C
如图,在△ABC的三边上作三个等边三角 △ABD,△BCE,△ACF。连接DE,EF。 (1)求证:四边形ADEF为平行四边形; (2)当∠BAC为多少度时,四边形ADEF是 矩形?
A E
F G B C H
D
总结
1、矩形的判定定理 (1)对角线相等的平行四边形是矩形。 (2)有三个角是直角的四边形是矩形。 2、矩形的性质在证明中的应用。 (对角线相等和四个角都是直角) 3、线段和角转移的方法。
3、已知:平行四边形ABCD中,对角线 AC、BD相交于点O,点P是四边形外 一点,且PA⊥PC,PB⊥PD,垂足为P。 求证:四边形ABCD为矩形 P A O B C 活动:
2、有三个角是直角的四边形是矩形。
2、在四边形ABCD中,∠A=∠B=∠C=90º
求证:四边形ABCD是矩形。
A D
B
C
练习:下列各句判定矩形的说法是否正确?
