R进制数间的转换
计算机数值转换

教学内容:数制的概念以及转教学目标:掌握进制概念以及转换。
教学重点和难点:1、数值、字符等信息在计算机中的表示形式。
2、十进制与二进制转换。
教学过程:一、数制1.数制的表示方法:为了区别不同进制数,一般把具体数用括号括起来,在括号的右下角标上相应表示数制的数字2.基数:所使用的不同基本符号的个数3.权:是其基数的位序次幂1、十进制、二进制、十六进制、八进制概念(1)十进制:由0~9数字组成权:10i-计数时按逢十进一的规则进行用(345.59)10或54.11D表示(2)二进制:由0、1数字组成权:2i-计数时按逢二进一的规则进行用(10110.11)2或10110.11B表示(3)十六进制:由0~9、A、B、C、D、E、F数字组成权:16i计数时按逢十六进一的规则进行用(1A3F.CF)16或1A3F.16H表示(4)八进制:由0、1、2、3、4、5、6、7数字组成权:8i计数时按逢八进一的规则进行用(34.76)8或34.76O表示2、按权展开基本公式:举例:(1098)10=1×103+0×102+9×101+8×100(2C.4B)16=2×161+C×160+4×16-1+B×16-2(101.11)2=1×22+0×21+1×20+1×2-1+1×2-2基本公式:B=A0RI+A1RI-1+…+ANR0+AN+1R-1+…说明:(A0,A1,……AN+1)表示各位上的数字Ri为权3、进位计数的特点1)有一个基数R,数字中使用0,1,2,……(R-1)个符号2)每位有固定的权3)位序的排列法:从小数点处算起,由小数点向左,规定位序为0,1,2……;由小数点向右,规定位序为-1,-2,……4)采用“逢R进一的”的进位方法5)对任何一种进位计数制表示的数都可以写出其权展开的多项式之和二、十进制数与R进制数的转换一)十进制数与二进制数的转换1、二进制转换为十进制:按权展开法举例:(101101.11)2=1×25+0×24+1×23+1×22+0×21+1×20+1×2-1+1×2-2=32+8+4+1+0. 5+0. 25=45+0. 75=(45. 75)102、十进制转换为二进制整数部分:除2取余法、倒读。
不同进制之间的转换_大学计算机基础 (Windows 7 +Office 2010)_[共2页]
![不同进制之间的转换_大学计算机基础 (Windows 7 +Office 2010)_[共2页]](https://img.taocdn.com/s3/m/47745abf011ca300a7c39018.png)
大学计算机基础(Windows 7+Office 2010)141.3.2 不同进制之间的转换1.二进制、八进制和十六进制数转换为十进制数 转换原则:利用按权展开式(1-1),相加求和。
例1.1 将二进制数101011.11转换成十进制数。
2101234522121212120212021)11.101011(--⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==32 + 8 + 2 + 1 + 0.5 + 0.25=(43.75)10例1.2 将八进制数234.5转换成十进制数。
1010128)625.156(625.042412885848382)5.234(=+++=⨯+⨯+⨯+⨯=-例1.3 将十六进制数2E4.C 转换成十进制数。
(2E4. C )16=2×162+14×161+4×160+12×16-1=512+224+4+0.75=(740.75)10如上述例子一样,利用式(1-1)可以将R 进制数转换为十进制数。
2.十进制数转换为二进制、八进制和十六进制数 转换原则:将整数部分和小数部分分别转换,再合并。
(1)整数部分采用“除基(R )取余法”。
其中基R 为2、8或16等,余数按先后顺序由低位向高位排列,即先得的余数离小数点近,后得余数离小数点远(当然都在小数点左面)。
(2)小数部分采用“乘基(R )取整法”。
其中基R 为2、8或16等,所取的整数按先后顺序由高位向低位排列,即先取的整数离小数点近,后取的整数离小数点远(都在小数点右面)。
例1.4 将十进制数58.6875转换成二进制数。
整数部分:余数2 58— a 00 低位 2 29— a 11 2 14— a 20 27— a 31 2 3— a 4121— a 510 高位小数部分:(注意,整数部分已经取走,每次只把去掉整数的小数部分乘以2,直到小数部分为0或精度达到要求为止。
) 0.6875⨯ 2高位 a -1 — 11.3750⨯ 2a -2 — 00.7500 ⨯ 2a -3 — 11.5000 ⨯ 2低位 a -4 — 11.0000。
计算机数制及转化
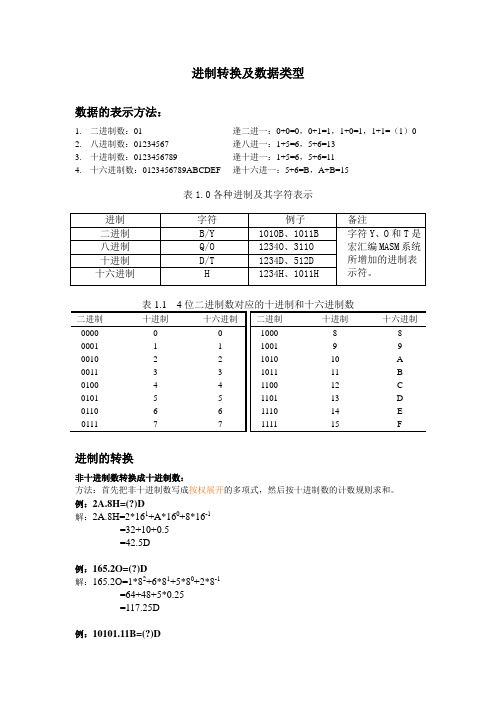
进制转换及数据类型数据的表示方法:1.二进制数:01 逢二进一:0+0=0,0+1=1,1+0=1,1+1=(1)02.八进制数:01234567 逢八进一:1+5=6,5+6=133.十进制数:0123456789 逢十进一:1+5=6,5+6=114.十六进制数:0123456789ABCDEF 逢十六进一:5+6=B,A+B=15表1.0各种进制及其字符表示进制的转换非十进制数转换成十进制数:方法:首先把非十进制数写成按权展开的多项式,然后按十进制数的计数规则求和。
例:2A.8H=(?)D解:2A.8H=2*161+A*160+8*16-1=32+10+0.5=42.5D例:165.2O=(?)D解:165.2O=1*82+6*81+5*80+2*8-1=64+48+5*0.25=117.25D例:10101.11B=(?)D解:10101.11B=1*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2=16+0+4+0+1+0.5+0.25=21.75D十进制数转换其它进制数:1.整数转换方法:整数转换,采用基数连除法。
把十进制整数N 转换成R 进制数的步骤:1) 将N 除以R ,记下所得的商和余数2) 将上一步所得的商再除以R ,记下所得商和余数 3) 重复做第2步直到商为04) 将各个余数转换成R 进制的数码,并按照和运算过程相反的顺序把各个余数排列起来,即为R 进制数。
例:427D=(?)H 解:427D=1ABH 例:427D=(?)O 解:427D=653O 例:11D=(?)B 解:11D=1011B2.纯小数转换纯小数转换,采用基数连乘法。
把十进制的纯小数M 转换成R 进制数的步骤: 1) 将M 乘以R ,记下整数部分2) 将上一步乘积中的小数部分再乘以R ,记下整数部分3) 重复做第2步,直到小数部分为0或者满足精度要求为止4) 将各步求得的整数转换成R 进制的数码,并按照和运算过程相同的顺序排列起来,即为所求的R 进制数。
不同数制之间的转换的教学方法探讨

3 2的下 方 写 1 , 计算 5 1 — 3 2 = 1 9 , 继续 1 9 > 1 6 , 得 1 , 继 续 计 算 1 9 — 1 6 = 3 , 因为 3 < 8 , 于是 在位 权 8的下 方 写 O , 继 续 2 基 数 < 4 , 权 值 4的下 方继续 为 O , 继续 比较 2和 1 , 得 到 定 义 :基 数是 指 该 进制 中允 许选 用 的基 本 数码 的个 比较 3
余取 整 的 方法 到 加 减计 算 的过 渡 ,使 学 生 更 容 易理 解 二进 制 等 数 制
的概 念 , 更 简 单 的完 成 数 制 之 间 的转 换 。 关键 词 : 二 进制 位权 新 方 法
1数 制 的 由来 开求 和 , 就 实现 了 R进制 转换 为十进 制。 早在 我 国古代《 周易 》 当中就有 二进 制 方法 的体 现 , 1 9 根 据 十进制 的权值 展开 , 如 1 2 5 = 1 X 1 0 + 2 X 1 0 ’ + 5 X 世 纪 爱 尔兰 逻辑 学 家乔 治布 尔 对逻辑 命 题 的思考 过 程 转 1 0 。 = 1 2 5 , 可 以得 到 R进制 的转换 如下 : 化 为对 符号 “ 0 ” “ 1 ” 的某种 代数 演算。被 誉 为 2 0世纪第 三 ( 1 0 1 1 0 ) B = ( 1×2 +0×2 3 +1×2 2 +1×2 + 0×2 0 ) D =( 1 6 + 4 次科技 革命 重要 标 志之~ 的计 算机 的发 明 与应 用 , 推动 了 2 ) D =( 2 2 ) D 二进制 的发展 。 数 字计 算机只 能识别 和 处理 由“ 0 ” “ 1 ” 符 号 + 4 . 2 十 进 制 转 换 为 二 进 制 串组成 的代码 。 其运 算模 式正是 二 进制 , 二进 制是 逢 2进 例 如将( 1 1 5) D 转 换 成 二 进制 , 首 先 根 据 二 进 制 的权 位 的进 位制 。0 、 1是基 本算符 。因为 它只使用 0 、 1两 个数 值 规律 , 写 出权 值排 列 : 8 4 2 1 , 所 写权值 大小 的判断 条件是 字符号 , 非常简单 方便 , 易于 用 电子 方式 实现。 看 1 1 5的大小要 介于最 左边 两个权 值 之 间 ,即 1 2 8和 6 4 其 中进 位 方式 计 数 的数 制 称 为进 位计 数制 。 日常 生 所 以该权 值排 列如 下 : 1 2 8, 6 4 , 3 2 , 1 6 , 8 , 4 , 2 , 1 。 然 活中, 人们 最 习惯 使 用 的数 据 是 十 进 制 ( 用符号 D表示 , 之间 , 后在权 值排 列 的下 方 对应 的数 值进 行 大小 比较 , 1 1 5比权 如7 8 。 ,表 示 数 7 8是 十进 制 数 ) ,但 生 活 中也 有 其他 进 , 小 的时候 写 0 , 跳 转到 下 一位 , 继 续 用 差 制, 如八 进 制( 用符号 O 表示) 、 十 六 进 制( 用符 号 H表 示) 。 值 大 的时候 写 1
进制的转换

时向老师汇报,其他同学不允许在讨论区发表。课堂讨论期间, PPT模板下载:/moban/ /hangye/ 节日PPT模板:/jieri/
/sucai/ PPT背景图片:/beijing/
/hangye/ 节日PPT模板:/jieri/
/sucai/ PPT背景图片:/beijing/
/tubiao/ 优秀PPT下载:/xiazai/
/powerpoint/ Word教程: /word/
/powerpoint/ Word教程: /word/
/excel/ 资料下载:/ziliao/
/kejian/ 范文下载:/fanwen/
/shiti/ 教案下载:/jiaoan/
/tubiao/ 优秀PPT下载:/xiazai/
/powerpoint/ Word教程: /word/
行业PPT模板: PPT素材下载: PPT图表下载: PPT教程: Excel教程:
/excel/
/sucai/ PPT背景图片:/beijing/
/tubiao/ 优秀PPT下载:/xiazai/
/powerpoint/ Word教程: /word/
/excel/ 资料下载:/ziliao/
(CD8)16=12×162 + 13×161 +8×160=(3288)10
PPT模板下载:/moban/
/hangye/ 节日PPT模板:/jieri/
/sucai/ PPT背景图片:/beijing/
/shiti/ 教案下载:/jiaoan/
行业PPT模板: PPT素材下载: PPT图表下载: PPT教程: Excel教程: PPT课件下载: 试卷下载: PPT论坛:
进位计数制
进制转换——精选推荐

进制转换进制转换对照表(0~255) - ⼗进制,⼗六进制,⼋进制,⼆进制Dec Hex Oct Bin 0 1 2 3 4 5 6 7 8 9101112131415 0123456789ABCDEF000001002003004005006007010016017 00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111Dec Hex Oct Bin 161718192021222324252610 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 020 021 022 023 024 025 026 027 030 031 032 033 034 03500010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111Dec Hex Oct Bin 3233343536373839404142434445464722232425262728292A2B2C2D2E2F040041042043044045046047050051052053054055056057 00100000 00100001 0010001000100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111Dec Hex Oct Bin 4849505152535455565758596061626330313233343738393A3B3C3D3E3F060061062063064065066067070071072073074075076077 00110000 00110001 00110010 00110011 00110100 00110101 00110110 0011011100111010 00111011 00111100 00111101 00111110 00111111Dec Hex Oct Bin 64656667686970 40414243444546100101102103104105106 01000000 01000001 01000010 01000011 01000100 010001018384858650515253545556120121122123124125126 01010000 01010001 01010010 01010011 01010100 01010101 01010110Dec Hex Oct Bin 969798996263646566140141142143144145146 01100000 01100001 01100010 01100011 01100100 01100101 01100110Dec Hex Oct Bin 112113114115116117118707172161162163164165166 ******** 01110001 01110010 01110011 01110100 01110101 01110110 717273747576777879 4748494A4B4C4D4E4F114115116117 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111 8788899091929394955758595A5B5C5D5E133134135136137 ******** 01011000 01011001 01011010 01011011 01011100 01011101 01011110 01011111 1031041051061071081091101116768696A6B6C6D152153154155156157 ******** 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111 1191201211221231241251261277778797A7B7C171172173174175176177011101110111100001111001011110100111101101111100011111010111111001111111Dec Hex Oct Bin128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 80 8182838485868788898A8B8C202203204205206207210211212213214215216217 10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 10001100 10001101 10001110 10001111148 149 150 151 152 153 154 155 156 157 158 159 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F 220 221227230231232233234235236237 10010000 10010001 10010010 10010011 10010100 10010101 10010110 10010111 10011000 10011001 10011010 10011011 10011100 10011101 10011110 10011111Dec Hex Oct Bin 160161162163169 170 171 172 173 174 175 A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF 240 241 242 243 244 245 246254255256257 10100000 10100001 10100010 10100011 10100100 10100101 10100110 10100111 10101000 10101001 10101010 10101011 10101100 10101101 10101110 10101111Dec Hex Oct Bin 176177178179180181182183184189 190 191 B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF 260 261 262 263 264 265 266 267 270 271 272 27310110000101100011011001010110011101101001011010110110110101101111011100010111001101110101011101110111100101111011011111010111111Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 C0 C1C2C3C4C5C6C7C8C9CACBCCCD303304305306307310311312313314315316317 11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111 208214 215 216 217 218 219 220 221 222 223 D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF 320 321 322 323331332333334335336337 11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010111 11011000 11011001 11011010 11011011 11011100 11011101 11011110 11011111 224225226227228229230236 237 238 239 E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF 340 341 342 343 344 345 346 347 350 351357 11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111 240241242243244245246247248249250251252F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 37711110011111101001111010111110110111101111111100011111001111110101111101111111100111111011111111011111111⼀:简述:进位计数制:是⼈们利⽤符号来计数的⽅法。
用计算器进行小数进制转换的方法
�
• •
例3:将十进制数2107.36579转换成十六进制 数,保留小数后2位。转换方法如下: 计算, 2107.36579×162×16-2
•
=539485.64224×16-2
•
•
•
≈539486×16-2 -2 =(83B5E)H×16
=(83B.5E)H
� �
•
• •
2、将R进制数转化成十进制数z.x的方法 将R进制数(z.x)R转化成十进制数(z.x)D的方法如下, 这个方法与十进制数转化成R进制数的方法略有不同。 1) 如果R进制数(z.x)R的小数部分有i 位,首先将小数 部分完全转换成整数ZR 。即将(z.x)R的小数点向右移 动 i 位。 2)利用计算器将整数ZR转换成十进制数整数ZD 。 3)利用计算器实现最终转换(z.x)D=ZD·R-i ,即将十进 制整数ZD乘以R-i,就得到最终结果了! 将上述的转换操作过程用数学形式表示如下: (z.x)R·Ri·R-i =ZR·R-i =ZD ·R-i =(z.x)D 。
• •
� �
例4:将八进制数(4073.273 221 52)O 转换成十进制,保留小数后5位。转换方法如 下:
•
•
(4073.273 221 52)O
=(4073.273 221 52)O×88×8-8
•
=(407 327 322 152)O×8-8
• •
=35 355 731 050×8-8 ≈2107.36579
�
• •
例1:将十进制数2107.36579转换成二进制数, 保留小数后8位。转换方法如下: 2107.36579×28×2-8 =539485.64224×2-8
•
【计算机基础】信息编码与进制转换
• ASCII码(美国信息交换标准代码) ASCII 码使用指定的7 位或8 位二进制数组合 来表示128 或256 种可能的字符。 如:A的ASCII码为65,对应的二进制数为 0100• ASCII码在计算机内部是二进制数,用户为 了方便,将其转换为十进制使用。用数字 代表字符。可以对字符大小进行比较。 • 对字符大小比较实质上是对ASCII码进行比 较
在电子技术中每个基数都对应这一种状态。 十进制有个十个基数,用电子技术实现10种状态很困难。 二进制数中有两个基数,要表示两种状态在物理技术上很容易实现。 如电压的高和低,电容的充电和放电等,正好用二进制数中的两个数 码表示。
• 可靠性
二进制数中只有两种状态,所以在传递过程中抗干扰能力强。计算机 工作(鉴别信息)的可靠性高。
权 权 权 权 权
表示相对小数点 的位置 不同数位上的数具有不同的权值10i。 基数(进制)
1. 十进制(Decimal)的特点
数字符号:0,1,…,9 基数:10 进(借)位规则为:逢十进一(借一为十)
2.二进制(Binary)的特点
数字符号:0,1
基数:2
进(借)位规则:逢二进一(借一为二)
将余数自下而上组合, 得 (307)10 = 307D= (100110011)2
对于小数,用取积的整数
将(0.6875)10转换成二进制数。 (对小数用2去乘,取整数) 积的整数部分 0.68752=1.375 1 0.3752=0.75 0 0.752=1.5 1 0.52=1.0 1 所以,(0.687 5)10 =(0.1011)2。
3. 八进制(Octonal)的特点
数字符号:0,1,2,3,4,5,6,7 基数:8 进(借)位规则为:逢八进一(借一为八)
进制转换(简介)
例:将十六制数2A转换为十进制数 2AH=2*161+A*160=32+10*1=42
其它进制转换为十进制
例:八进制数372转换为十进制数 372O=3*82+7*81+2*80=3*64+7*8+2*1=250
例:十六进制数2C8H转换为十进制数 12C8H=1*163+2*162+C*161+8*160
1区号为20位号为832将区位号2083转换为十六进制表示为1453h31453h2020h3473h得到国标码3473h43473h8080hb4f3h得到机内码为b4f3h汉字国标gb231280d常用字次常用字罕见字三个等级汉字的机内码a前者各字节的最高位二进制值各为1而后者为0b前者各字节的最高位二进制值各为0而后者为1c前者各字节的最高位二进制值各为10而后者为01d前者各字节的最高位二进制值各为01而后者为10国标码1一个汉字的国标码需用2字节存储其每个字节的最高二进制位的值分别为解析国标码两个字节的最高位都为0机内码两个字节的最高位都为1
汉字国标GB2312-80
汉字国标码(GB2312-80)把汉字分成________。 A)简化字和繁体字两个等级 B)一级汉字,二级汉字和三级汉字三个等级 C)一级常用汉字,二级次常用汉字两个等级 D)常用字,次常用字,罕见字三个等级
汉字的机内码
2、一个汉字的机内码与国标码之间的差别是 ________。 A)前者各字节的最高位二进制值各为1,而后者为0 B)前者各字节的最高位二进制值各为0,而后者为1 C)前者各字节的最高位二进制值各为1、0,而后者 为0、1
进制转换
在高速发展的现代社会,计算机浩浩荡荡地成为了人们生活中不可缺少的一部分,帮助人们解决通信,联络,互动等各方面的问题。
今天我就给大家讲讲与计算机甚至日常生活有密切相关的“进制转换”问题。
我们以(25.625)(十)为例讲解一下进制之间的转化问题。
1. 十-----> 二给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
那么:十转二示意图要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1“将商继续除以2,直到商为0……最后将所有余数倒序排列”好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:被除数计算过程商余数6 6/2 3 03 3/2 1 11 1/2 0 1(在计算机中,÷用 / 来表示)2. 二----> 十二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制" ^ " 为次方第0位 0 * 2^0 = 0第1位 0 * 2^1 = 0第2位 1 * 2^2 = 4第3位 0 * 2^3 = 0第4位 0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位 0 * 2^7 = 0 +---------------------------100用横式计算为:0 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 + 0 * 2 ^ 3 + 0 * 2 ^ 4 + 1 * 2 ^ 5 + 1 * 2 ^ 6 + 0 * 2 ^ 7 = 1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1 *2 ^ 2 + 1 * 2 ^ 5 + 1 * 2 ^ 6 = 1003. 十----> 八10进制数转换成8进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习2
将十六进制数(5A0B.0C)16转换成二进制数
转换过程:
5
A
0
B
.0
C
010 101 000 1011 .0000 110 1 0 0 0
转换结果: ( 5A0B.0C)16 =(101101000001011。000011)2
二进制数转成八进制数
二进制数转成十六进制数
以二进制数小数点为中心,向两端每三位分成一组,然后每一组二 “采用421规则” 进制数下写出对应的八进制数码,最高位或最低位不足时,用0补 齐,并将小数点垂直落到八进制数中。
例1:将二进制数(10101.0001011)
转换过程:
2
转换成八进制数
小数点 为中点,
0 10
101
001 01 0
1 2
111
011 . 001
3 . 1
011 100
7
3
4
转换结果:
(1010110101.1011101)2=(1265.564)8
练习2
例:将二进制数(10110101011.011101)
转换过程:
2
转换成十六进制数
001 110 0101. 0111 010 0 1 0
2 D 5 . 7 4
110 100
6
6
4
转换结果: (1010110101.1011101)2=(1265.564)8
二进制数转成十六进制数
“四位并一位”
以二进制数小数点为中心,向两端每四位截成一组,然后每一组 二进制数下写出对应的十六进制数码,最高位或最低位不足时, 用0补齐,并将小数点垂直落到十六进制数中。
例:将二进制数(10101111011.0011001011)
3
A
C
D
.A
1
001 101 110 1 0 0
1101 .1010 000 1
练习
转换结果: (3ACD.A1)16 =(11101011001101.10100001)2
例1
将八进制数(2754.41)8转换成二进制数
转换过程:
2
7
5
4
.4
1
010 111
转换结果: (2754.41)8
101 100 .100 001
“三位并一位”
以二进制数小数点为中心,向两端每三位截成一组,然后每一组 二进制数下写出对应的八进制数码,最高位或最低位不足时,用0 补齐,并将小数点垂直落到八进制数中。
例:将二进制数(1010110101.1011101)
转换过程:
2
转换成八进制数
001 01 0
1 2
110
101 . 101
5 .5
转换结果: (10110101011.011101)2 =(2D5.74)16
转换过程:
2
转换成十六进制数
010 011 1011. 1 1 0011
练习 5 7 B . 3
001 110 0 0
2 C
转换结果: (10101111011.0011001011)2 =(57B.32C)16
练习1
将二进制数(1010111011.0010111)2 转换成八进制数 转换过程:
. 000
101
1 00
练习
2
5
. 0
5
4
转换结果: (10101.0001011)2 =(25.054)8
一、八进制数转换为二进制数
23 = 8
1位八进值数恰好与3位二进制数相对应
“一位拆三位”
每一位八进制数展成三位二进制数,不足三位者补 0。 采用421规则
例1:将八进制数(4675.21) 转换成二进制数
8
转换过程:
4
6
7
5
.2
100 110 111
转换结果: (4675.21)8
101 .010 001
=(100110111101.010001)2
十六进制数转成二进制数
24 = 16
1位八进值数恰好与4位二进制数相对应
“一位拆四位”
例:将十六进制数(3ACD.A1)
转换过程:
16转换成二进制数
