2000年高考试题分类汇编动量与机械能综合
动量守恒和机械能守恒高考题剖析

高考复习指导动量守恒和机械能守,I:亘高考题剖析陈丽红,王嫣(河北师范大学物理科学与信息工程学院,河北石家庄050016)摘要:动量守恒定律和机械能守恒定律历来是高考物理试题的热点和难点。
本E),2003,--2007年高考物理试题中部分动量守恒定律和机械能守恒定律的典型题为例,进行解析,剖析易错点及成因,并分析试题特点。
关键词:高考物理试题;动量守恒定律;机械能守恒定律中图分类号:G633.7文献标识码:A文章编号:1009-010X(2008)04-0018-03动量守恒定律与机械能守恒定律历来是高考物理试题的热点和难点。
以下我们分析2003.2007年全国高考试卷中关于“动量守恒定律与机械能守恒定律”的典型试题,并进行归纳总结。
一、典型试题分析与学生主要易错点及成因例1.2003年卷22题r介子衰变的方程为K—,7r一+,r ro,其中K一介子和7r一介子.为带负电的基元电荷,矿介子不带电。
一个K—介子沿垂直于磁场的方向射入匀强磁场中,其轨迹A为圆弧A P,衰变后产生仃.介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径R。
.和R,之比为2:1。
矿介子的轨迹未画出。
如图1.由此可知^V 仃-介子的动量与矿介子的动量大小之比为( A.1:l B.1:2C.1:3D.1:6P××朗1)×眷××解析:K-介子衰变符合动量守恒,令m k…m m o分别表示K一、仃’、矿介子的质量,仇、”一、铀分别表示它们的速度,则由动量守恒可知,掣庐玎w o一舰Ⅳ一……①令风、R一分别表示K一和仃一的运动半径,由洛仑兹力和牛顿运动定律可知ev口=m k芒…”②儿^ev_B=m一譬…一③n一把②③代人①可得旦』上=导/7/桫0J易错点及成因:给了K’介子衰变却不知道用动量守恒求解,列不出动量守恒的式子①。
其原因是对动量守恒的适用条件理解不透。
例2.2004年2卷25题柴油打桩机的重锤由气缸、活塞等若干部件组成,气缸与活塞间有柴油与空气的混合物。
高考物理动量守恒定律试题(有答案和解析)

高考物理动量守恒定律试题(有答案和解析)一、高考物理精讲专题动量守恒定律1.如图所示,在倾角30°的斜面上放置一个凹撸B,B 与斜面间的动摩擦因数36μ=;槽内靠近右侧壁处有一小物块A(可视为质点),它到凹槽左侧壁的距离d =0.1m ,A 、B 的质量都为m=2kg ,B 与斜面间的最大静摩擦力可认为等于滑动摩摞力,不计A 、B 之间的摩擦,斜面足够长.现同时由静止释放A 、B,经过一段时间,A 与B 的侧壁发生碰撞,碰撞过程不计机械能损失,碰撞时间极短,g 取210/m s .求:(1)释放后物块A 和凹槽B 的加速度分别是多大?(2)物块A 与凹槽B 的左侧壁第一次碰撞后瞬间A 、B 的速度大小;(3)从初始位置到物块A 与凹糟B 的左侧壁发生第三次碰撞时B 的位移大小. 【答案】(1)(2)v An =(n-1)m∙s -1,v Bn ="n" m∙s -1(3)x n 总=0.2n 2m 【解析】 【分析】 【详解】(1)设物块A 的加速度为a 1,则有m A gsin θ=ma 1, 解得a 1=5m/s 2凹槽B 运动时受到的摩擦力f=μ×3mgcos θ=mg 方向沿斜面向上; 凹槽B 所受重力沿斜面的分力G 1=2mgsin θ=mg 方向沿斜面向下; 因为G 1=f ,则凹槽B 受力平衡,保持静止,凹槽B 的加速度为a 2=0 (2)设A 与B 的左壁第一次碰撞前的速度为v A0,根据运动公式:v 2A0=2a 1d 解得v A0=3m/s ;AB 发生弹性碰撞,设A 与B 第一次碰撞后瞬间A 的速度大小为v A1,B 的速度为v B1,则由动量守恒定律:0112A A B mv mv mv =+ ;由能量关系:2220111112222A AB mv mv mv =+⨯ 解得v A1=-1m/s(负号表示方向),v B1=2m/s2.一质量为的子弹以某一初速度水平射入置于光滑水平面上的木块并留在其中,与木块用一根弹性良好的轻质弹簧连在一起,开始弹簧处于原长,如图所示.已知弹簧被压缩瞬间的速度,木块、的质量均为.求:•子弹射入木块时的速度;‚弹簧被压缩到最短时弹簧的弹性势能.【答案】22()(2)Mm aM m M m++b【解析】试题分析:(1)普朗克为了对于当时经典物理无法解释的“紫外灾难”进行解释,第一次提出了能量量子化理论,A正确;爱因斯坦通过光电效应现象,提出了光子说,B正确;卢瑟福通过对粒子散射实验的研究,提出了原子的核式结构模型,故正确;贝克勒尔通过对天然放射性的研究,发现原子核有复杂的结构,但没有发现质子和中子,D错;德布罗意大胆提出假设,认为实物粒子也具有波动性,E错.(2)1以子弹与木块A组成的系统为研究对象,以子弹的初速度方向为正方向,由动量守恒定律得:解得:.2弹簧压缩最短时,两木块速度相等,以两木块与子弹组成的系统为研究对象,以木块的初速度方向为正方向,由动量守恒定律得:解得:由机械能守恒定律可知:.考点:本题考查了物理学史和动量守恒定律3.如图所示,在光滑的水平面上放置一个质量为2m的木板B,B的左端放置一个质量为m的物块A,已知A、B之间的动摩擦因数为μ,现有质量为m的小球以水平速度0υ飞来与A物块碰撞后立即粘住,在整个运动过程中物块A始终未滑离木板B,且物块A和小球均可视为质点(重力加速度g).求:①物块A相对B静止后的速度大小;②木板B至少多长.【答案】①0.25v0.②216v Lgμ=【解析】试题分析:(1)设小球和物体A碰撞后二者的速度为v1,三者相对静止后速度为v2,规定向右为正方向,根据动量守恒得,mv0=2mv1,① (2分)2mv1=4mv2② (2分)联立①②得,v2=0.25v0.(1分)(2)当A在木板B上滑动时,系统的动能转化为摩擦热,设木板B的长度为L,假设A刚好滑到B的右端时共速,则由能量守恒得,③ (2分)联立①②③得,L=考点:动量守恒,能量守恒.【名师点睛】小球与 A碰撞过程中动量守恒,三者组成的系统动量也守恒,结合动量守恒定律求出物块A相对B静止后的速度大小;对子弹和A共速后到三种共速的过程,运用能量守恒定律求出木板的至少长度.4.装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击.通过对一下简化模型的计算可以粗略说明其原因.质量为2m、厚度为2d的钢板静止在水平光滑桌面上.质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿.现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示.若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度.设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞不计重力影响.【答案】【解析】设子弹初速度为v0,射入厚度为2d的钢板后,由动量守恒得:mv0=(2m+m)V(2分)此过程中动能损失为:ΔE损=f·2d=12mv20-12×3mV2(2分)解得ΔE=13mv20分成两块钢板后,设子弹穿过第一块钢板时两者的速度分别为v1和V1:mv1+mV1=mv0(2分)因为子弹在射穿第一块钢板的动能损失为ΔE损1=f·d=mv2(1分),由能量守恒得:1 2mv21+12mV21=12mv20-ΔE损1(2分)且考虑到v1必须大于V1,解得:v1=13(26v0设子弹射入第二块钢板并留在其中后两者的共同速度为V2,由动量守恒得:2mV 2=mv 1(1分) 损失的动能为:ΔE′=12mv 21-12×2mV 22(2分) 联立解得:ΔE′=13(1)22+×mv 2因为ΔE′=f·x (1分), 可解得射入第二钢板的深度x 为:(2分)子弹打木块系统能量损失完全转化为了热量,相互作用力乘以相对位移为产生的热量,以系统为研究对象由能量守恒列式求解5.(1)恒星向外辐射的能量来自于其内部发生的各种热核反应,当温度达到108K 时,可以发生“氦燃烧”。
高考物理新力学知识点之动量真题汇编含答案解析(3)

高考物理新力学知识点之动量真题汇编含答案解析(3)一、选择题1.人的质量m=60kg,船的质量M=240kg,若船用缆绳固定,船离岸1.5m时,人可以跃上岸.若撤去缆绳,如图所示,人要安全跃上岸,船离岸至多为(不计水的阻力,两次人消耗的能量相等,两次从离开船到跃上岸所用的时间相等)()A.1.5m B.1.2m C.1.34m D.1.1m2.如图所示,光滑绝缘水平轨道上带正电的甲球,以某一水平速度射向静止在轨道上带正电的乙球,当它们相距最近时,甲球的速度变为原来的15.已知两球始终未接触,则甲、乙两球的质量之比是A.1:1B.1:2C.1:3D.1:43.如图所示,质量m1=10kg的木箱,放在光滑水平面上,木箱中有一个质量为m2=10kg 的铁块,木箱与铁块用一水平轻质弹簧固定连接,木箱与铁块一起以v0=6m/s的速度向左运动,与静止在水平面上质量M=40kg的铁箱发生正碰,碰后铁箱的速度为v=2m/s,忽略一切摩擦阻力,碰撞时间极短,弹簧始终在弹性限度内,则A.木箱与铁箱碰撞后瞬间木箱的速度大小为4m/sB.当弹簧被压缩到最短时木箱的速度大小为4m/sC.从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹力对木箱的冲量大小为20N·s D.从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹性势能的最大值为160J4.有人设想在遥远的宇宙探测时,给探测器安上反射率极高(可认为100%)的薄膜,并让它正对太阳,用光压为动力推动探测器加速。
已知某探测器在轨道上运行,阳光恰好垂直照射在薄膜上,若膜面积为S,每秒每平方米面积获得的太阳光能为E,探测器总质量为M,光速为c,则探测器获得的加速度大小的表达式是(光子动量为hpλ=)()A.2EScMB.22ESc MC.EScMD.2EScMh5.如图,光滑水平面上有两辆小车,用细线相连,中间有一个被压缩的轻弹簧,小车处于静止状态。
烧断细线后,由于弹力的作用两小车分别向左、右运动。
“动量、机械能”综合复习导航

归类分析 “ 动量 、 机械能” 综合题 主要有 以下 四种类 型 , 本
文以这 四类综合题 为例 进行剖析 , 探究分 析思路 , 总
结 解题 方法 .
1 .在 重 力作 用 下的 “ 动量 、 械 能” 机 综合 问题
3 .理清 动量守恒 与机械 能守恒 、 能量守恒综 合
小为 , 根据 A、 、 B C组成的系统动量守恒 和机械能
3 = m 2
2
守恒 , ( + B B=7 ( (R一 寺 T., 有 A ) = = , g V' + I2 4 U
()当 弹簧 再 次恢 复 为 原 长 时 , 的 速 度 最 大 , 2 C
化 , 总动 量不 变 ( 的机 械 能 可 能 变 化 )有 时 整 个 但 总 .
用隔离法处理 , 有时还需 要交叉 使用整 体法 和隔离 法. 几个物体相互作用过程 中, 往往涉及 动量的迁移
和能量 的转 移 、 转化 , 解题 中要 注 意物 理 过程 的分 析 , 建 立 清晰 的物理 情景 , 于从 题 目提 供 的背 景材 料 中 善
全 过程 . 当然 , 需 要 考 虑 单 个 物 体 、 一 过 程 , 采 若 某 则
知识提要
1 .应用 动量 定 理和 动 量 守恒 定 律 时应 注 意 矢 量
性( 表达式为矢量式) 同时性( 、 同时刻 的动量 、 冲量才 能求和)相对性( 、 速度相对于同一参照物) . 2 用 动 量守 恒定 律 时 , 先要 找 到 临界 状态 , .运 首 然后列式. 系统动量守 恒, 指任意一个时刻 的总动量 都等于初状 态下 的总动量, 管系统 中的状态在 变 尽
第八关 动力学、动量和能量观点在力学中的应用-高考物理专题复习及典型试题

第八关动力学、动量和能量观点在力学中的应用1.动量和能量综合应用例 1 (多选)如图甲所示,质量M=0.8kg的足够长的木板静止在光滑的水平面上,质量m=0.2kg的滑块静止在木板的左端,在滑块上施加一水平向右、大小按图乙所示随时间变化的拉力F,4 s后撤去力F.若滑块与木板间的动摩擦因数μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,则下列说法正确的是()A.0∼4s时间内拉力的冲量共为3.2N⋅sB.t=4s时滑块的速度大小为9.5m/sC.木板受到滑动摩擦力的冲量共为2.8N⋅sD.木板的速度最大为2m/s练习1-1如图所示,带有圆管轨道的长轨道水平固定,圆管轨道竖直(管内直径可以忽略),底端分别与两侧的直轨道相切,圆管轨道的半径R=0.5 m,P点左侧轨道(包括圆管)光滑,右侧轨道粗糙.质量m=1 kg的物块A以v0=10 m/s的速度滑入圆管,经过竖直圆管轨道后与直轨道上P处静止的质量M=2 kg的物块B发生碰撞(碰撞时间极短),碰后物块B在粗糙轨道上滑行18 m后速度减小为零.已知物块A、B与粗糙轨道间的动摩擦因数均为μ=0.1,取重力加速度大小g=10 m/s2,物块A、B均可视为质点.求:(1)物块A滑过竖直圆管轨道最高点Q时受到管壁的弹力;(2)最终物块A静止的位置到P点的距离.2.综合分析多过程问题例2如图所示,有一个可视为质点的质量为m=1 kg的小物块,从光滑平台上的A点以v0=2 m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=3 kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.4 m,C点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g取10 m/s2.求:(1)小物块到达C点时的速度大小;(2)小物块刚要到达圆弧轨道末端D点时对轨道的压力;(3)要使小物块不滑出长木板,木板的长度L至少多大.练习2-1如图所示,半径为R的四分之一光滑圆弧轨道竖直固定在水平地面上,下端与水平地面在P点相切,一个质量为2m的物块B(可视为质点)静止在水平地面上,左端固定有水平轻弹簧,Q点为弹簧处于原长时的左端点,P、Q间的距离为R,PQ段地面粗糙、动摩擦因数为μ=0.5,Q点右侧水平地面光滑,现将质量为m的物块A(可视为质点)从圆弧轨道的最高点由静止开始下滑,重力加速度为g.求:(1)物块A沿圆弧轨道滑至P点时对轨道的压力大小;(2)弹簧被压缩的最大弹性势能(未超过弹性限度);(3)物块A最终停止位置到Q点的距离.课后检测1. 质量为1 kg的物体静止在水平面上,t=0时受到水平拉力F的作用开始运动,F随时间t 变化的关系图象如图所示.已知t=4 s时物体刚好停止运动,取g=10m/s2,以下判断正确的是()A.物体所受摩擦力为3 NB.t=2 s时物体的速度最大C.t=3 s时物体的动量最大D.物体的最大动能为2 J2. 粗糙水平地面上的物体,在一个水平恒力作用下做直线运动,其v-t图象如图所示,下列物理量中第1 s内与第2 s内相同的是()A.摩擦力的功B.摩擦力的冲量C.水平恒力的功D.水平恒力的冲量3. 如图所示,质量均为m的两带电小球A与B,带电荷量分别为+q、+2q,在光滑绝缘水平桌面上由静止开始沿同一直线运动,当两带电小球运动一段时间后A球速度大小为v,在这段时间内,下列说法正确的是()A.任一时刻B的加速度比A的大B.两球均做加速度增大的加速运动C.两球组成的系统电势能减少了mv2,但动能和电势能之和不变D.两球动量均增大,且总动量也增大4.如图所示,质量为m、带有半圆形轨道的小车静止在光滑的水平地面上,其水平直径AB 的长度为2R,现将质量也为m的小球从距A点正上方为h的位置由静止释放,然后由A点ℎ(不计空气阻力),则() 进入半圆形轨道后从B点冲出,在空中上升的最大高度为12A.小球冲出B点后做斜上抛运动B.小球第二次进入轨道后恰能运动到A点C.小球第一次到达B点时,小车的位移大小是RmgℎD.小球第二次通过轨道克服摩擦力所做的功等于125.光滑水平面上放有质量分别为2m和m的物块A和B,用细线将它们连接起来,两物块中间加有一压缩的轻质弹簧(弹簧与物块不相连),弹簧的压缩量为x.现将细线剪断,此刻物块A的加速度大小为a,两物块刚要离开弹簧时物块A的速度大小为v,则()A.物块B的加速度大小为a时弹簧的压缩量为x3xB.物块A从开始运动到刚要离开弹簧时位移大小为23mv2C.物块开始运动前弹簧的弹性势能为32D.物块开始运动前弹簧的弹性势能为3mv26. “飞针穿玻璃”是一项高难度的绝技表演,曾度引起质疑.为了研究该问题,以下测量能够得出飞针在穿越玻璃的时间内,对玻璃平均冲击力大小的是()A.测出玻璃厚度和飞针穿越玻璃前后的速度B.测出玻璃厚度和飞针穿越玻璃所用的时间C.测出飞针质量、玻璃厚度和飞针穿越玻璃所用的时间D.测出飞针质量、飞针穿越玻璃所用时间和穿越玻璃前后的速度7.如图,立柱固定于光滑水平面上O点,质量为M的小球a向右运动,与静止于Q点的质量为m的小球b发生弹性碰撞,碰后a球立即向左运动,b球与立柱碰撞能量不损失,所有碰撞时间均不计,b球恰好在P点追到a球,Q点为OP间中点,则a、b球质量之比M:m=()A.3:5B.1:3C.2:3D.1:28. (多选)如图,在光滑的水平面上有一个长为L的木板,小物块b静止在木板的正中间,小物块a以某一初速度v0从左侧滑上木板.已知物块a、b与木板间的摩擦因数分别为μa、μb,木块与木板质量均为m,a、b之间的碰撞无机械能损失,滑动摩擦力等于最大静摩擦力.下列说法正确的是()mv02A.若没有物块从木板上滑下,则无论v0多大整个过程摩擦生热均为13B.若μb<2μa,则无论v0多大,a都不会从木板上滑落μa gL,则ab一定不相碰C.若v0≤√32D.若μb>2μa,则a可能从木板左端滑落9.(多选)如图所示,甲、乙两个小滑块(视为质点)静止在水平面上的A、B两处,B处左侧水平面光滑,右侧水平面粗糙.若甲在水平向右的拉力F=kt(其中k=2N/s)的作用下由静止开始运动,当t=3s时撤去力F,随后甲与乙发生正碰而粘合在一起,两滑块共同滑行2.4m后停下,已知甲的质量为1kg,两滑块与粗糙水平面间的动摩擦因数均为0.75,取g=10m/s2,则()A.0∼3s内,力F的冲量大小为18N⋅sB.撤去力F时甲的速度大小为9m/sC.两滑块正碰后瞬间的速度大小为4.5m/sD.乙的质量为0.5kg10. 如图所示,质量为M的木块位于光滑水平面上,在木块与墙壁之间用轻质弹簧连接,当木块静止时刚好位于A点,现有一质量为m的子弹以水平速度v0射向木块并嵌入其中(作用时间极短),求:(1)当木块回到A点时的速度大小;(2)从开始到木块回到A点的过程中,墙壁对弹簧的冲量.11. 如图所示,一轻质弹簧的一端固定在小球A上,另一端与小球B接触但未连接,该整体静止放在离地面高为H=5m的光滑水平桌面上.现有一小球C从光滑曲面上离桌面ℎ= 1.8m高处由静止开始滑下,与小球A发生碰撞(碰撞时间极短)并粘在一起压缩弹簧推动小球B向前运动,经一段时间,小球B脱离弹簧,继续在水平桌面上匀速运动一段时间后从桌面边缘飞出.小球均可视为质点,忽略空气阻力,已知m A=2kg,m B=3kg,m C=1kg,g=10m/s2.求:(1)小球C与小球A碰撞结束瞬间的速度;(2)小球B落地点与桌面边缘的水平距离.12. 如图所示,在水平桌面上放有长度为L=2m的木板C,C上右端是固定挡板P,在C 中点处放有小物块B,A、B的尺寸以及P的厚度皆可忽略不计.C上表面与固定在地面上半径为R=0.45m的圆弧光滑轨道相切,质量为m=1kg的小物块A从圆弧最高点由静止释放,设木板C与桌面之间无摩擦,A、C之间和B、C之间的滑动摩擦因数均为μ,A、B、C(包含挡板P)的质量相同,开始时,B和C静止,(g=10m/s2)(1)求滑块从释放到离开轨道受到的冲量大小;(2)若物块A与B发生碰撞,求滑动摩擦因数μ应满足的条件;(3)若物块A与B发生碰撞(设为完全弹性碰撞)后,物块B与挡板P发生碰撞,求滑动摩擦因数μ应满足的条件.13.一质量为m的烟花弹获得动能E后,从地面竖直升空.当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为E,且均沿竖直方向运动.爆炸时间极短,重力加速度大小为g,不计空气阻力和火药的质量.求:(1)烟花弹从地面开始上升到弹中火药爆炸所经过的时间;(2)爆炸后烟花弹向上运动的部分距地面的最大高度.14. 如图所示,水平光滑地面上有两个静止的小物块A和B(可视为质点),A的质量m=1.0 kg,B的质量M=4.0 kg,A、B之间有一轻质压缩弹簧,且A、B间用细线相连(图中未画出),弹簧的弹性势能E p=40 J,弹簧的两端与物块接触但不固定连接.水平面的左侧有一竖直墙壁,右侧与倾角为30°的光滑斜面平滑连接.将细线剪断,A、B分离后立即撤去弹簧,物块A与墙壁发生弹性碰撞后,A在B未到达斜面前追上B,并与B相碰后结合在一起向右运动,g取10 m/s2,求:(1)A与弹簧分离时的速度大小;(2)A、B沿斜面上升的最大距离.15. 如图所示,半径R1=1 m的四分之一光滑圆弧轨道AB与平台BC在B点平滑连接,半径R2=0.8 m的四分之一圆弧轨道上端与平台C端连接,下端与水平地面平滑连接,质量m =0.1 kg的乙物块放在平台BC的右端C点,将质量也为m的甲物块在A点由静止释放,让其沿圆弧下滑,并滑上平台与乙相碰,碰撞后甲与乙粘在一起从C点水平抛出,甲物块与平台间的动摩擦因数均为μ=0.2,BC长L=1 m,重力加速度g取10 m/s2,不计两物块的大小及碰撞所用的时间,求:(1)甲物块滑到B点时对轨道的压力大小;(2)甲和乙碰撞后瞬间共同速度的大小;(3)粘在一起的甲、乙两物块从C点抛出到落到CDE段轨道上所用的时间.16. 如图所示,一圆心为O、半径为R的光滑半圆轨道固定在竖直平面内,其下端和粗糙的水平轨道在A点相切,AB为圆弧轨道的直径.质量分别为m、2m的滑块1、2用很短的细线连接,在两滑块之间夹有压缩的短弹簧(弹簧与滑块不固连),滑块1、2位于A点.现剪断两滑块间的细线,滑块1恰能过B点,且落地点恰与滑块2停止运动的地点重合.滑块1、2可视为质点,不考虑滑块1落地后反弹,不计空气阻力,重力加速度为g,求:(1)滑块1过B点的速度大小;(2)弹簧释放的弹性势能大小;(3)滑块2与水平轨道间的动摩擦因数.17. 汽车A在水平冰雪路面上行驶.驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B.两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5 m,A车向前滑动了2.0 m.已知A和B的质量分别为2.0×103 kg和1.5×103 kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小g=10 m/s2.求:(1)碰撞后的瞬间B车速度的大小;(2)碰撞前的瞬间A车速度的大小.。
高考物理新力学知识点之动量真题汇编及答案(5)
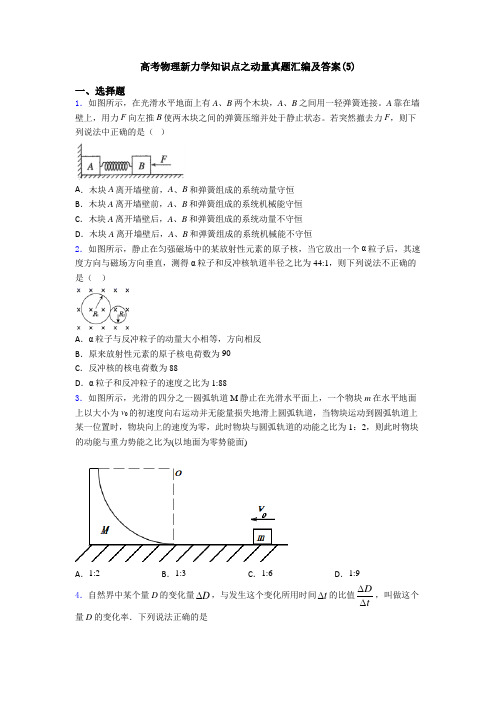
高考物理新力学知识点之动量真题汇编及答案(5)一、选择题1.如图所示,在光滑水平地面上有A 、B 两个木块,A 、B 之间用一轻弹簧连接。
A 靠在墙壁上,用力F 向左推B 使两木块之间的弹簧压缩并处于静止状态。
若突然撤去力F ,则下列说法中正确的是( )A .木块A 离开墙壁前,A 、B 和弹簧组成的系统动量守恒 B .木块A 离开墙壁前,A 、B 和弹簧组成的系统机械能守恒C .木块A 离开墙壁后,A 、B 和弹簧组成的系统动量不守恒D .木块A 离开墙壁后,A 、B 和弹簧组成的系统机械能不守恒2.如图所示,静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,则下列说法不正确的是( )A .α粒子与反冲粒子的动量大小相等,方向相反B .原来放射性元素的原子核电荷数为90C .反冲核的核电荷数为88D .α粒子和反冲粒子的速度之比为1:883.如图所示,光滑的四分之一圆弧轨道M 静止在光滑水平面上,一个物块m 在水平地面上以大小为v 0的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆弧轨道上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为1:2,则此时物块的动能与重力势能之比为(以地面为零势能面)A .1:2B .1:3C .1:6D .1:94.自然界中某个量D 的变化量D ∆,与发生这个变化所用时间t ∆的比值Dt∆∆,叫做这个量D 的变化率.下列说法正确的是A.若D表示某质点做平抛运动的速度,则Dt∆∆是恒定不变的B.若D表示某质点做匀速圆周运动的动量,则Dt∆∆是恒定不变的C.若D表示某质点做竖直上抛运动离抛出点的高度,则Dt∆∆一定变大.D.若D表示某质点的动能,则Dt∆∆越大,质点所受外力做的总功就越多5.下列说法正确的是( )A.速度大的物体,它的动量一定也大B.动量大的物体,它的速度一定也大C.只要物体的运动速度大小不变,物体的动量就保持不变D.物体的动量变化越大则该物体的速度变化一定越大6.“天津之眼”是一座跨河建设、桥轮合一的摩天轮,是天津市的地标之一.摩天轮悬挂透明座舱,乘客随座舱在竖直面内做匀速圆周运动.下列叙述正确的是()A.摩天轮转动过程中,乘客的机械能保持不变B.在最高点,乘客重力大于座椅对他的支持力C.摩天轮转动一周的过程中,乘客重力的冲量为零D.摩天轮转动过程中,乘客重力的瞬时功率保持不变7.如图所示,光滑绝缘水平轨道上带正电的甲球,以某一水平速度射向静止在轨道上带正电的乙球,当它们相距最近时,甲球的速度变为原来的15.已知两球始终未接触,则甲、乙两球的质量之比是A.1:1B.1:2C.1:3D.1:48.如图所示,一内外侧均光滑的半圆柱槽置于光滑的水平面上.槽的左侧有一竖直墙壁.现让一小球(可认为质点)自左端槽口A点的正上方从静止开始下落,与半圆槽相切并从A点进入槽内,则下列说法正确的是()A.小球离开右侧槽口以后,将做竖直上抛运动B.小球在槽内运动的全过程中,只有重力对小球做功C.小球在槽内运动的全过程中,小球与槽组成的系统机械能守恒D.小球在槽内运动的全过程中,小球与槽组成的系统水平方向上的动量守恒9.如图所示,一质量为2kg的物块B,静止在光滑水平面上,左侧固定一水平轻质弹簧,另一质量为3kg的物块A向右以5m/s的速度撞击弹簧,整个撞击过程中,两物块的速度始终在一条直线上,弹簧始终在弹性限度内,下列说法正确的是()A.物块A的最终速度大小为3m/sB.物块B的最终速度大小为5m/sC.弹簧的最大弹性势能为15JD.若其他条件不变而仅增大物块A的质量,则物块B的最终速度可能为12m/s10.如图所示,撑杆跳尚是运动会中的一个重要比赛项目。
2024年高考真题分类汇编专题07动量
2024年高考真题分类汇编专题07动量1.(2024全国甲卷考题)7.蹦床运动中,体重为60kg 的运动员在0=t 时刚好落到蹦床上,对蹦床作用力大小F 与时间t 的关系如图所示。
假设运动过程中运动员身体始终保持竖直,在其不与蹦床接触时蹦床水平。
忽略空气阻力,重力加速度大小取210m /s 。
下列说法正确的是()A.0.15s t =时,运动员的重力势能最大B.0.30s t =时,运动员的速度大小为10m /s C .1.00s t =时,运动员恰好运动到最大高度处D.运动员每次与蹦床接触到离开过程中对蹦床的平均作用力大小为4600N 【答案】BD【解析】根据牛顿第三定律结合题图可知0.15s t =时,蹦床对运动员的弹力最大,蹦床的形变量最大,此时运动员处于最低点,运动员的重力势能最小,故A 错误;根据题图可知运动员从0.30s t =离开蹦床到 2.3s t =再次落到蹦床上经历的时间为2s ,根据竖直上抛运动的对称性可知,运动员上升时间为1s,则在 1.3s t =时,运动员恰好运动到最大高度处,0.30s t =时运动员的速度大小101m/s 10m/s v =⨯=故B 正确,C 错误;同理可知运动员落到蹦床时的速度大小为10m/s ,以竖直向上为正方向,根据动量定理()F t mg t mv mv ⋅∆-⋅∆=--,其中0.3st ∆=代入数据可得4600NF =根据牛顿第三定律可知运动员每次与蹦床接触到离开过程中对蹦床的平均作用力大小为4600N ,故D 正确。
受到的合力大小始终不变 B.该过程中系统能量守恒,,312v v ≠ D.在图乙位置,该过程中系统动能和电势能相互转化,能量守恒,对整个系统分析可知系统0,故动量守恒;当三个小球运动到同一条直线上时,根据对称性可知细线受到1和2的电场力大小相等,方向相反,从静止状态开始运动,瞬间受到的合力不为0,故该过程中小球)m M mM+ B.子弹在木块中运动的时间为【答案】(1)tan Nmamg F θ=+;(2)①330N ∙s,方向竖直向上;②0.2m【解析】(1)敏感球受向下的重力mg 和敏感臂向下的压力F N 以及斜面的支持力N ,则由牛顿第二定律可知()N tan mg F maθ+=解得tan mamg F θ=+(2)4m/s;(3)0.250.4μ≤<(1)对小球摆动到最低点的过程中,由动能定理在最低点,对小球由牛顿第二定律2T v F mg mL-=点,则从第一次碰撞到第二次碰撞之间,A、B A A 1B B 11343v x k v x k +==+114323k k +=-=0,即AB2m m =v '。
《动量、机械能》综合运用检测题
D 下滑 的过程 中系统 的动 量守 恒 。 .
D 石 板 的质量 越大 , . 石板 获得 的动量 就越小 。 2 一 个 质量 为 0 3 g的弹性 小球 , . .k 在光 滑水 平 面上 以 6 s的 度垂 直撞 到墙 上 , m/ 速 碰撞 后 小
20 0 8年 第 3期 ( 下半 月)
大小 相 等 。
C P对Q 的压 力 的 冲 量 方 向 垂 直 于 斜 面 向 下 。 .
D. F的冲量 等于 物体动 量 的变化量 。 力
血
图 1
C 石板 的 质 量 越 大 , 板 所 受 到 的 打击 力 . 石
就越 小 。 ,
5如 图 2 示 , . 所 斜劈 M 放 在 光滑水 平 面上 , 物 块 放 在斜劈 上 , 、 之 间无摩擦 , M 现将 系统
维普资讯
Vo - 6 NO 3 2 l2 . 1 ( 3 2 0 X) . 0 8 .5 . 4
理
教
学
探
讨
第2 6卷 总 第 3 2 1 期
20 0 8年 第 3期 ( 下半 月)
o Ph is Te c ig f ysc a hn
球 沿相 反方 向运 动 , 弹后速 度大 小与碰 撞前 相 反
同。 则碰 撞 前后小 球 速 度 变化 量 的 大小 A v和碰 撞 过程 中墙 对小球 做 功的大 小 w 为 ( )
A. v = 0 A 。
C. = 0 W 。
BA . v= 1 m/ 。 2 s
历年(2020-2024)全国高考物理真题分类(动量守恒定律及其应用)汇编(附答案)
历年(2020-2024)全国高考物理真题与模拟题分类(动量守恒定律及其应用)汇编一、多选题1.(2023ꞏ浙江)下列说法正确的是( )A .利用电容传感器可制成麦克风B .物体受合外力越大,则动量变化越快C .利用红外传感器可制成商场的自动门D .若物理问题牛顿运动定律不适用,则动量守恒定律也不适用2.(2021ꞏ山东)如图所示,载有物资的热气球静止于距水平地面H 的高处,现将质量为m 的物资以相对地面的速度0v 水平投出,落地时物资与热气球的距离为d 。
已知投出物资后热气球的总质量为M ,所受浮力不变,重力加速度为g ,不计阻力,以下判断正确的是( )A .投出物资后热气球做匀加速直线运动B .投出物资后热气球所受合力大小为mgC .1m d M ⎛=+ ⎝D .d = 3.(2021ꞏ湖南)如图(a ),质量分别为m A 、m B 的A 、B 两物体用轻弹簧连接构成一个系统,外力F 作用在A 上,系统静止在光滑水平面上(B 靠墙面),此时弹簧形变量为x 。
撤去外力并开始计时,A 、B 两物体运动的a t -图像如图(b )所示,1S 表示0到1t 时间内A 的a t -图线与坐标轴所围面积大小,2S 、3S 分别表示1t 到2t 时间内A 、B 的a t -图线与坐标轴所围面积大小。
A 在1t 时刻的速度为0v 。
下列说法正确的是( )A .0到1t 时间内,墙对B 的冲量等于m A v 0B . m A > m BC .B 运动后,弹簧的最大形变量等于xD .123S S S -=4.(2020ꞏ全国)水平冰面上有一固定的竖直挡板,一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0 kg 的静止物块以大小为5.0 m/s 的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0 m/s 的速度与挡板弹性碰撞。
专题06 动量、机械振动与机械波(原卷版)-2023年高考物理二模试题分项汇编(浙江专用)
专题06 动量、机械振动与机械波(原卷版)一、单选题(本大题共9小题)1. (2023年浙江省十校联盟高考物理第三次联考试卷)物理规律往往有一定的适用条件,我们在运用物理规律解决实际问题时,需要判断使用的物理规律是否成立。
如图所示,站在车上的人用锤子连续敲打小车。
初始时,人、车、锤都静止,假设水平地面光滑,关于这一物理过程,下列说法正确的是( )A. 连续敲打可使小车持续向右运动B. 人、车和锤组成的系统机械能守恒C. 人、车和锤组成的系统动量和机械能都不守恒D. 人、车和锤组成的系统动量守恒但机械能不守恒2. (2023年浙江省金华市十校高考物理联考试卷)掷冰壶又称冰上溜石,是以队为单位在冰上进行的一种投掷性竞赛项目,被大家喻为冰上的“国际象棋”,是冬奥会比赛项目。
在某次冰壶比赛中,运动员利用红壶去碰撞对方静止的蓝壶,两者在大本营中心发生对心碰撞,如图(bb)所示。
碰撞前后两壶做直线运动的vv−tt 图线如图(cc)中实线所示,其中红壶碰撞前后的图线平行,两冰壶质量相等,则( )A. 两壶发生了弹性碰撞B. 碰后蓝壶的速度可能为0.9mm/ssC. 碰后蓝壶移动的距离为2mmD. 碰后红壶还能继续运动2ss3. (2023年浙江省宁波市镇海中学高考物理模拟试卷(选择考))发光实心弹力球因其弹性好深受小朋友喜爱。
一小朋友将弹力球(可视为质点)抛出,落到水平面(足够大)上前瞬间的速度大小为vv0,与水平方向夹角αα=37∘。
弹力球与水平面碰撞的过程中,受到摩擦力的大小等于其重力的16、弹力的大小等于其重力的2倍。
设每次碰撞前、后弹力球竖直方向的速度大小保持不变,不计空气阻力。
已知sin37∘=0.6,cos37∘=0.8,重力加速度为gg。
则弹力球( )A. 第1次碰后离开水平面瞬间,速度方向与水平面间的夹角大于45∘B. 第2、3次落地点间的距离为0.48vv02ggC. 与水平面碰撞4次后停止运动D. 与水平面碰撞过程中受到合力的冲量保持不变4. (2023年浙江省强基联盟高考物理统测试卷(2月份))如图所示,是博物馆珍藏的古代青铜“鱼洗”的复制品,注入适量水后,有节奏地摩擦鱼洗双耳,会发出嗡嗡声,盆内水花四溅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年高考动量与机械能综合试题汇编
(2005年理综②)25.(20分)质量为M的小物块A静止在高为h的水平桌面的边缘,质量为m的小物
块B沿桌面向A运动并以速度v0与之发生正碰(碰撞时间极短).碰后A离开桌面,其落地点离出发
点的水平距离L. 求B后退的距离.已知B与桌面间的动摩擦因数为μ. 重力加速度为g.
解:设t为A从离开桌面到落地、所经历的时间,v1表示刚碰后A的速度,v2表示刚碰后B的速度.碰
后A离开桌面做平抛运动,有:
2
2
1
gth
tvL1
由碰撞中A、B系统动量守恒得:
210
mvMvmv
设B后退的距离为l,由功能关系:
2
2
2
1
mvmgl
由以上各式得:20)2(21vhgmMLgl
(2005年理综③)25.(20分)如图所示,一对杂技演员
(都视为质点)乘秋千(秋千绳处于水平位置)从A点由
静止出发绕O点下摆,当摆到最低点B时,女演员在极
短时间内将男演员沿水平方向推出,然后自己刚好能回
到高处A. 求男演员落地点C与O点的水平距离s. 已知
男演员质量m1和女演员质量m2之比21mm=2,秋
千的质量
不计,秋千的摆长为R,C点比O点低5R.
解:设分离前男女演员在秋千最低点B的速度为v0,由
机械能守恒得:
2
02121
)(21)(vmmgRmm
设刚要分离时男演员速度的大小为v1,方向与v0相同;女演员速度的大小为v2,方向与v0相反,
由动量守恒可知:
2211021
)(vmvmvmm
分离后男演员做平抛运动,设男演员从被推出到落在C点所需的时间为t,根据题给的条件,由
运动学规律得:
2
2
1
4gtR
tvs1
根据题给的条件,女演员刚好回到A点,由机械能守恒定律得:
2
222
2
1
vmgRm
已知212mm,由以上各式得:s=8R
(2005年天津理综)24.(18分)如图所示,质量mA为4.0kg的木板A放在水平面C上,木板与水平面
间的动摩擦因数μ为0.24. 木板右端放着质量mB为1.0kg的小物块B(视为质点),它们均处于静止
状态.木板突然受到水平向右的12N·s的瞬时冲量I作用开始运动,当小物块滑离木板时,木板的动
能EkA为8.0J,小物块的动能EkB为0.50J,重力加速度取10m/s2,求:
(1)瞬时冲量作用结束时木板的速度v0;
(2)木板的长度L.
A B C O R
s
5R
A
B
C
L
解:设水平向右为正方向,有:0vmIA
得:v0=3.0m/s
(2)设小物块滑离木板时A、B的速度大小分别为vA、vB,则由EkA=8.0J,
EkB=0.50J得:
vA=2m/s,vB=1m/s
这段过程对A、B系统由动量定理得:0)(vmvmvmftABBAA
其中f为A与地面的摩擦力:)(gmmfBA
解得:t=0.25s
这段过程对A、B发生的位移分别为:
625.0)(210tvvs
AA
m
125.0)0(21tvs
BB
m
所以木板的长度50.0BAssLm
(2005年广东物理)18.(17分)
如图所示,两个完全相同的质量为m的木板A、B置于水平地面上,它们的间距s=2.88m,质量为2m、
大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平面之间的动
摩擦因数为μ2=0.10,最大静摩擦力可认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给C
施加一个水平向右、大小为mg52的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,要使
C最终不脱离木板,没块木板的长度至少为多少?
解:设A、C之间的滑动摩擦力大小为f1,A与水平地面之间的滑动摩擦力大小为f2
由22.01,10.02
所以mgfmgF25211
且gmmfmgF)2(5222
所以一开始A和C保持相对静止,在F作用下向右加速运动,有:
2
12
)2(21)(vmmsfF
A、B两板的碰撞瞬间,动量守恒:
21
)(vmmmv
碰撞结束后到三个物体达到共速的过程中,设木板向前移动的位移为s1,选三个物体构成的系统
为研究对象,外力之和为零,则:
321
)2()(2vmmmvmmmv
设A、B系统与水平地面之间的滑动摩擦力大小为f3,对A、B系统由动能定理得:
A B
C
F
s
222
31311
221221mvmvsfsf
其中gmmmf)2(23
对C物体,由动能定理:
212
3111
221221)2()2(mvmvslfslF
由以上各式代入数据计算得:3.0lm
(2005年江苏物理)18.(16分)如图所示,三个质量均为m的弹性小球用两根长为L的轻绳连成一条直
线而静止在光滑的水平面上。现在、给中间的小球B一个水平的初速度v0,方向与绳垂直,小球相互
碰撞时无机械能损失,轻绳不可伸长。求:
(1)当小球A、C第一次相碰时,小球B的速度;
(2)当三个小球再次处在同一直线上时,小球B的的速度;
(3)运动过程中小球A的最大动能EkA和此时两根绳的夹角θ;
(4)当三个小球处在同一直线上时,绳中的拉力F的大小。
解:(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到
对称性及绳子的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB,由动量守恒定律得:
Bmvmv30
得:30vvB
(2)当三个小球再次处在同一直线上时,由动量守恒定律和能量守恒定律得:
ABmvmvmv20
222
02212121AB
mvmvmv
解得:30vvB,320vvA
(3)当小球A的动能最大时,小球B的速度为零,设此时小球A、C的速度大小为u,两根绳的夹角
θ,由动量守恒定律和能量守恒定律得:
2
sin0mvumv
22
0
22121mumv
解得:小球A的最大动能2041mvEkA
此时两根绳的夹角90
(4)小球A、C均以半径L绕小球B做圆周运动,当三个小球在同一直线上时,以小球B为参考系
(小球B的加速度为零,为惯性参考系),小球A、C相对于小球B的速度均为0vvvvBA
所以,此时绳中的拉力为LvmLvmF202
(2005年春季理综)24.(18分)下雪天,卡车在笔直的高速公路上匀速行驶.司机突然发现前方停着
一辆故障车,他将刹车踩到底,车轮被抱死,但卡车仍向前滑行,并撞上故障车,且推着它共同滑行
了一段距离l后停下.事故发生后,经测量,卡车刹车时与故障车距离为L,撞车后共同滑行的距离
l=258L.假定两车轮胎与雪地之间的动摩擦因数相同.已知卡车质量M为故障车质量m的4倍.
⑴设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,求v1∶v2;
⑵卡车司机至少在距故障车多远处采取同样的紧急刹车措施,事故就能免于发生.
C B A
L v0 L
解:(1)卡车与故障车相撞的过程它们构成的系统动量守恒:
21
)(vmMMv
所以4:5:)(:21MmMvv
(2)设卡车刹车时的速度大小为v0,从开始刹车到与故障车相撞的过程中,由动能定理得:
202
1
212
1
MvMvfL
卡车与故障车相撞的过程它们构成的系统动量守恒:
21
)(vmMMv
相撞以后对卡车与故障车根据动能定理得:
2
2
)(210vmMfl
所以卡车的至少刹车距离为s应满足:
2
0
2
1
0Mvfs
由以上各式解得:Ls5.1
