化工原理课后习题答案第4章传热习题解答
化工原理第四章传热过程超详细讲解

例4-12 在其他条件(K,Cp,M1,M2)不变时, 并→逆,求T2, t1。 解:利用并流求得有关常数: Φ=KAΔtm=-M1Cp1ΔT’=M2Cp2Δt’
设热阻集中在保温层:则
则一米管年损失的热量:
W=J/s
年损失的价值:
一米管道耗保温材料体积:V= ∴年折旧费用:
总费用: 求导,求极值:
28.356
复杂系数一元三次方程,用试差法求解:
设D=0.4 时,左=62.8≈右=63 ∴δ=D-0.1/2=(0.4-0.1)/2=0.15 m
作业:P142 (4、5)
∴ A (t1 t 2) At
R=δ/λ—热阻
2 多层平面壁,如耐火砖——绝热砖——建筑砖组成三层复合 壁,对各层分别应用单层导热公式有:
一层:
(1)
二层:
(2)
三层:
(3)
∵平面壁:A1=A2=A3=A ∵稳定传热Φ1=Φ2=Φ3=Φ则有:
t1-t4=Δt=
…(4)
…(5)
讨论:(1) ①+②得:
(4)潜热 Q潜 mH m nH n
(J/mol*K)
式中:ΔHm和ΔHn分别为质量和摩尔相变潜热 (单位分别为: J/kg;J/mol)
§2 传导传热(热传导,导热) 一、定义:传导传热——发生在固体、静止或滞流流体中,因分
子的振动或自由电子的运动而传递热量的方式。
二、导热方程—付立叶定律:
故将对流传热扩展为:对流给热——流体与壁面 之间的传热。由于壁面附近的流体为滞流,因此:对 流给热包括湍流主体的对流传热和壁附近滞流层的热 传导,为描述此复杂的给热过程的速率,特提出对流 给热机理(模型),其要点为:
a.湍流主体以对流方式传热,温度一致, 即忽略湍流主体的热阻。
化工原理_大题第四章

第四章 习题2. 燃烧炉的内层为460mm 厚的耐火砖,外层为230mm 厚的绝缘砖。
若炉的内表面温度t1为1400℃,外表面温度t3为100℃。
试求导热的热通量及两砖间的界面温度。
设两层砖接触良好,已知耐火砖的导热系数为t 0007.09.01+=λ,绝缘砖的导热系数为t 0003.03.02+=λ。
两式中t 可分别取为各层材料的平均温度,单位为℃,A 单位为W/(m·℃)。
解:设两砖之间的界面温度为2t ,由23121212t t t t b b λλ--=,得222331223140010094946010/(0.90.000723010/(0.30.0003)22t t t Ct t t t ----=⇒=++⨯+⨯⨯+⨯热通量2121689/14009490.40/0.970.00072t t q W m -==+⎛⎫+⨯ ⎪⎝⎭3.直径为mm mm 360⨯φ,钢管用30mm 厚的软木包扎,其外又用100mm 厚的保温灰包扎,以作为绝热层。
现测得钢管外壁面温度为-110℃,绝热层外表面温度10℃。
已知软木和保温灰的导热系数分别为0.043和0.07W/(m ·℃),试求每米管长的冷量损失量。
解:每半管长的热损失,可由通过两层圆筒壁的传热速率方程求出:1332112211ln ln 22t t Q r r Lr r πλπλ-=+1100101601160ln ln2 3.140.043302 3.140.000760--=+⨯⨯⨯⨯25/W m =-负号表示由外界向体系传递的热量,即为冷量损失。
4.蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层,设外层的平均直径为内层的两倍。
其导热系数也为内层的两倍。
若将二层材料互换位置,假定其他条件不变,试问每米管长的热损失将改变多少?说明在本题情况下,哪一种材料包扎在内层较为适合?解:设外层的平均直径为2m d ,内层平均直径为1m d ,则212m m d d =且212λλ=。
化工原理课后习题答案

第一章流体流动1.某设备上真空表的读数为 13.3×103 Pa,试计算设备内的绝对压强与表压强。
已知该地区大气压强为 98.7×103 Pa。
解:由绝对压强 = 大气压强–真空度得到:设备内的绝对压强P绝= 98.7×103 Pa -13.3×103 Pa=8.54×103 Pa设备内的表压强 P表 = -真空度 = - 13.3×103 Pa2.在本题附图所示的储油罐中盛有密度为 960 ㎏/㎥的油品,油面高于罐底 6.9 m,油面上方为常压。
在罐侧壁的下部有一直径为 760 mm 的圆孔,其中心距罐底 800 mm,孔盖用14mm的钢制螺钉紧固。
若螺钉材料的工作应力取为39.23×106 Pa ,问至少需要几个螺钉?分析:罐底产生的压力不能超过螺钉的工作应力即P油≤σ螺解:P螺 = ρgh×A = 960×9.81×(9.6-0.8) ×3.14×0.762150.307×103 Nσ螺 = 39.03×103×3.14×0.0142×nP油≤σ螺得 n ≥ 6.23取 n min= 7至少需要7个螺钉4. 本题附图为远距离测量控制装置,用以测定分相槽内煤油和水的两相界面位置。
已知两吹气管出口的距离H = 1m,U管压差计的指示液为水银,煤油的密度为820Kg/㎥。
试求当压差计读数R=68mm时,相界面与油层的吹气管出口距离h。
分析:解此题应选取的合适的截面如图所示:忽略空气产生的压强,本题中1-1´和4-4´为等压面,2-2´和3-3´为等压面,且1-1´和2-2´的压强相等。
根据静力学基本方程列出一个方程组求解解:设插入油层气管的管口距油面高Δh在1-1´与2-2´截面之间P1 = P2 + ρ水银gR∵P1 = P4,P2 = P3且P3 = ρ煤油gΔh , P4 = ρ水g(H-h)+ ρ煤油g(Δh + h)联立这几个方程得到ρ水银gR = ρ水g(H-h)+ ρ煤油g(Δh + h)-ρ煤油gΔh 即ρ水银gR =ρ水gH + ρ煤油gh -ρ水gh 带入数据1.0³×10³×1 - 13.6×10³×0.068 = h(1.0×10³-0.82×10³)h= 0.418m6. 根据本题附图所示的微差压差计的读数,计算管路中气体的表压强p。
化工原理课后习题答案传热习题解答
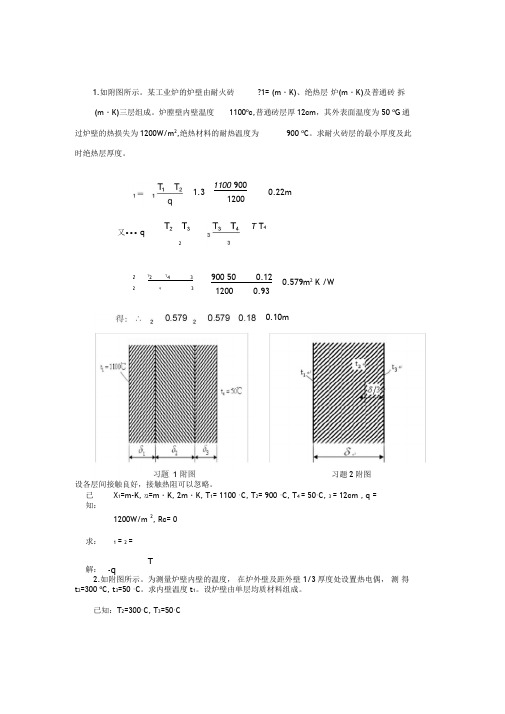
1.如附图所示。
某工业炉的炉壁由耐火砖 ?1= (m ・K)、绝热层 炉(m ・K)及普通砖 拆(m ・K)三层组成。
炉膛壁内壁温度1100o c,普通砖层厚12cm ,其外表面温度为 50 o G 通过炉壁的热损失为1200W/m 2,绝热材料的耐热温度为 900 o C 。
求耐火砖层的最小厚度及此时绝热层厚度。
设各层间接触良好,接触热阻可以忽略。
已知:X 1=m-K, ?2=m ・K, 2m ・K, T 1= 1100 °C, T 2= 900 °C, T 4 = 50°C, 3 = 12cm , q = 1200W/m 2, Rc= 0求:1 =2 =解: T-q2.如附图所示。
为测量炉壁内壁的温度, 在炉外壁及距外壁 1/3厚度处设置热电偶, 测 得t 2=300 o C, t 3=50 °C 。
求内壁温度t 1。
设炉壁由单层均质材料组成。
已知:T 2=300°C, T 3=50°C1100 90012000.22m又••• q900 50 0.12 12000.930.579m 2 K /W1.32T T 42 T 2T 4 3 2q30.10m习题2附图其中 r i =30mm , r 2=60mm , r 3=160mm 所以2 100 10丄ln60丄in 型0.043 300.076025W/m负号表示由外界向系统内传热,即为冷量损失量。
4.蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层,设外层的平均直径为内 层的两倍。
其导热系数也为内层的两倍。
若将二层材料互换位置,假定其它条件不变, 试问每米管长的热损失将改变多少说明在本题情况下,哪一种材料包扎在内层较为合适解:设外层平均直径为d m,2,内层平均直径为d m,1,则d m,2= 2d m,1 且 ?2=2 入由导热速率方程知bbbb5 b 1 S m12S m21 d m1L2 1 2d m1 L4 1两层互换位置后Qttd m 丄所以q_1.25求: T i =T i = 2(T 2— T 3)+T 3=3 X (300-50)+56= 800 °C3.直径为60 X 3mml 的钢管用30mm 厚的软木包扎,其外又用 100mm 厚的保温灰包扎, 以作为绝热层。
化工原理 第四章 传热-例题

t2 −t1 30−15 = 0.176 = P= T −t1 100−15 1
T −T2 100−40 R= 1 = = 4.0 t2 −t1 30−15
查 附 22,ϕ∆t = 0.92 图 录
∴∆tm =ϕ∆t ∆tm,逆 = 0.92×43.7 = 40.20C
又冷却水终温提到350C, 逆流时: 100 →40
35← 35 ←15 65 25
65−25 ∆ m,逆 = t = 41.90C 65 ln 25
解: (1)求以外表面积为基准时的传热系数 取钢管的导热系数λ=45W/m·K, 冷却水测的污垢热阻Rs1=0.58×10-3 m2·K/W CO2侧污垢热阻Rs2=0.5×10-3 m2·K/W 则:
1 1 bd1 d1 1 d1 = +R1 + +R 2 + s s K α d2 α2 d2 λdm 1
100→40
30 ← 15
70 25
t t ∆ 2 −∆ 1 70−25 = t ∴∆ m,逆 = = 43.70C 70 t ∆2 ln ln 25 t ∆1
并流时:
热流体 : 100→40 冷流体 :
15→30
85 10
∆t2 −∆ 1 85−10 t 0 ∆ m,并 = t = ∆2 t 85 = 35 C ln ln ∆1 t 10
解:此题为单层圆筒壁的热传导问题。 已知条件: 蒸汽导管外表面的半径 r2=0.426/2=0.213m = 温度 t2=177℃ 保温层的外表面的半径 r3=0.213+0.426=0.639m + = 温度 t3=38℃ 由:
t 2 − t3 Q= ln r3 r2 2π l λ
可得每米管道的热损失为:
化工原理习题解答(第二版)(祁存谦)习题解

祁存谦丁楠吕树申《化工原理》习题解答第1章流体流动第2章流体输送第3章沉降过滤第4章传热第5章蒸发第6章蒸馏第7章吸收第9章干燥第8章萃取第10章流态化广州中山大学化工学院(510275)2008/09/28第1章 流体流动1-1.容器A 中气体的表压力为60kPa ,容器B 中的气体的真空度为Pa 102.14⨯。
试分别求出A 、B 二容器中气体的绝对压力为若干Pa 。
该处环境大气压等于标准大气压。
(答:A,160kPa ;B,88kPa )解:取标准大气压为kPa 100,所以得到:kPa 16010060=+=A P ;kPa 8812100=-=B P 。
1-2.某设备进、出口的表压分别为 12kPa -和157kPa ,当地大气压为101.3kPa ,试求此设备进、出口的压力差为多少Pa 。
(答:169kPa -) 解:kPa 16915712-=--=-=∆出进P P P 。
1-3.为了排除煤气管中的少量积水,用如图示水封设备,水由煤气管道上的垂直支管排出,已知煤气压力为10kPa (表压)。
问水封管插入液面下的深度h 最小应为若干? (答:m 02.1)解:m 02.18.910101033=⨯⨯=∆=g P H ρ习题1-3 附图1-4.某一套管换热器,其内管为mm,25.3mm 5.33⨯φ外管为mm 5.3mm 60⨯φ。
内管流过密度为3m 1150kg -⋅,流量为1h 5000kg -⋅的冷冻盐水。
管隙间流着压力(绝压)为MPa 5.0,平均温度为C 00,流量为1h 160kg -⋅的气体。
标准状态下气体密度为3m 1.2kg -⋅,试求气体和液体的流速分别为若干1s m -⋅?( 答:1L s m11.2U -⋅=;1g s 5.69m U -⋅= )习题1-4 附图解:mm 27225.35.33=⨯-=内d ,m m 5325.360=⨯-=外d ;对液体:122s m 11.2027.011503600/500044/-⋅=⨯⨯⨯===ππρ内d m A V u l l l l l ; 对气体:0101P P =ρρ⇒3560101m kg 92.51001325.1105.02.1-⋅=⨯⨯⨯==P P ρρ,()224内外内外D d A A A g -=-=π()2322m 1032.10335.0053.04⨯=-=π,13s m 69.592.51032.13600/160/--⋅=⨯⨯===ggg gg g A m A V u ρ。
化工原理习题解答(第二版)(祁存谦)习题解
祁存谦丁楠吕树申《化工原理》习题解答第1章流体流动第2章流体输送第3章沉降过滤第4章传热第5章蒸发第6章蒸馏第7章吸收第9章干燥第8章萃取第10章流态化广州中山大学化工学院(510275)2008/09/28第1章 流体流动1-1.容器A 中气体的表压力为60kPa ,容器B 中的气体的真空度为Pa 102.14⨯。
试分别求出A 、B 二容器中气体的绝对压力为若干Pa 。
该处环境大气压等于标准大气压。
(答:A,160kPa ;B,88kPa )解:取标准大气压为kPa 100,所以得到:kPa 16010060=+=A P ;kPa 8812100=-=B P 。
1-2.某设备进、出口的表压分别为 12kPa -和157kPa ,当地大气压为101.3kPa ,试求此设备进、出口的压力差为多少Pa 。
(答:169kPa -) 解:kPa 16915712-=--=-=∆出进P P P 。
1-3.为了排除煤气管中的少量积水,用如图示水封设备,水由煤气管道上的垂直支管排出,已知煤气压力为10kPa (表压)。
问水封管插入液面下的深度h 最小应为若干? (答:m 02.1)解:m 02.18.910101033=⨯⨯=∆=g P H ρ习题1-3 附图1-4.某一套管换热器,其内管为mm,25.3mm 5.33⨯φ外管为mm 5.3mm 60⨯φ。
内管流过密度为3m 1150kg -⋅,流量为1h 5000kg -⋅的冷冻盐水。
管隙间流着压力(绝压)为MPa 5.0,平均温度为C 00,流量为1h 160kg -⋅的气体。
标准状态下气体密度为3m 1.2kg -⋅,试求气体和液体的流速分别为若干1s m -⋅?( 答:1L s m 11.2U -⋅=;1g s 5.69m U -⋅= )习题1-4 附图解:mm 27225.35.33=⨯-=内d ,m m 5325.360=⨯-=外d ;对液体:122s m 11.2027.011503600/500044/-⋅=⨯⨯⨯===ππρ内d m A V u l l l l l ; 对气体:0101P P =ρρ⇒3560101m kg 92.51001325.1105.02.1-⋅=⨯⨯⨯==P P ρρ,()224内外内外D d A A A g -=-=π()2322m 1032.10335.0053.04⨯=-=π,13s m 69.592.51032.13600/160/--⋅=⨯⨯===ggg gg g A m A V u ρ。
化工原理上第4章传热4
总发射系数 C12
C0 11
1
1
1 1
1
1 2
C1 C2 C0
一般形式:
12
C12A(1T010
)4
( T2 100
)
4
φ :角系数 (总能量被壁面拦截分率)。 φ =f (两壁面形状,大小,相对位置,距离等) 几种简单情况的角系数(见P285表4.5.2,图4.5.5)
0.64
L d0
液体沸腾传热及其影响因素 沸腾: 沸腾时,液体内部有气泡产生,
气泡产生和运动情况,对h影响极大。
沸腾分类: ① 按设备尺寸和形状不同
池式沸腾(大容积饱和沸腾)
强制对流沸腾(有复杂的两相流) ② 按液体主体温度不同
过冷沸腾:液体主体温度t < ts, 气泡进入液体主体后冷凝。
本节解决的问题:
(1)何谓热辐射 (2)辐射传热的基本概念、特点 (3)辐射传热的基本规律 (4)辐射传热的传热量计算
吸收辐射能
发射辐射能
4.5.1 辐射传热基本概念 (1) 热辐射
绝对温度大于0的物体,都不停地以电磁波的形式向外辐射能量。 同时不断吸收来自外界的辐射能。 物体以电磁波的形式向外发射能量的过程,称为热辐射。 一定波长内(0.4-40μm,主要是可见光和红外光) ,具有热效应。
4.5.5 复合传热与设备热损失的计算
(1) 复合传热
指:同时存在两种以上传热方式的综合传热现象。
例:设备表面的热损失,对流 + 热辐射
间壁换热过程中,对流 + 导热
(2) 设备热损失计算 热损失: c (对流) R (辐射)
化工原理答案
30 C,另测得距加热器平壁外表面250mm处的温4-1图所示。
试求加热器平壁外表面温度。
解t 2 75C , t s 30C 计算加热器平壁外表面温度t !,0.16W/(m C )加1T叫250itri|Tiii|jt l7575 30 0.25 0.05 0.160.16t i竺 0.250.0575 300C习题4-1附图【4-2】有一冷藏室,其保冷壁是由 30mm 厚的软木做成的。
软木的热导率 入=0.043第四章传 热热传导【4-1】有一加热器,为了减少热损失,在加热器的平壁外表面,包一层热导率为0.16W/(m •C )、厚度为00mm 的绝热材料。
已测得绝热层外表面温度为t l t 2 t 2 t 3b iW/(m •C )。
若外表面温度为28 C,内表面温度为3 C,试计算单位表面积的冷量损失。
解 已知 t 1 3C , t 2 28C ,=0.043W/(m C ), b 0.03m ,则单位表面积的冷量损失为0.043 2qt 1 t 23 28 35.8 W/ mb0.03【4-3】用平板法测定材料的热导率,平板状材料的一侧用电热器加热,另一侧用冷水冷却,同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2,材料的厚度为 0.02m 。
现测得电流表的读数为 2.8A ,伏特计的读数为 140V ,两侧温度分别为280 C 和100 C,峠肚面帜 /-2KA t 002m- I -I4OV试计算该材料的热导率。
解根据已知做图热传导的热量Q IV 2.8 140 392WAQ(t l t 2 ) bQb 392 0.02 A(t i t 2)0.02(280 100)2.18W/ m °C【4-4】燃烧炉的平壁由下列三层材料构成:耐火砖层,热导率 习题4-3附图入 =1.05W/(m •C ),厚 度b 230mm ;绝热砖层,热导率 疋0.151W/(m •C );普通砖层,热导率疋0.93W/(m •C )。
化工原理第四章习题答案
化工原理第四章习题答案化工原理第四章习题答案第一题:题目:某化工过程中,一种物质A在液相中的浓度随时间的变化满足以下动力学方程:d[A]/dt = k[A]^2,其中k为常数。
若初始时刻A的浓度为[A]0,求A 的浓度随时间的变化规律。
解答:根据题目中给出的动力学方程,我们可以得到d[A]/[A]^2 = kdt。
两边同时积分,得到∫d[A]/[A]^2 = ∫kdt。
对左边进行积分,得到-1/[A] = kt + C1,其中C1为积分常数。
整理得到[A] = -1/(kt + C1)。
由于初始时刻A的浓度为[A]0,所以代入初始条件得到[A]0 = -1/(k(0) + C1),解得C1 = -1/[A]0。
将C1代入[A] = -1/(kt + C1)中,得到[A] = -1/(kt - 1/[A]0)。
第二题:题目:某反应A + B → C的速率方程为r = k[A][B],其中k为常数。
若初始时刻A和B的浓度分别为[A]0和[B]0,求A和B的浓度随时间的变化规律。
解答:根据速率方程r = k[A][B],我们可以得到d[A]/dt = -k[A][B]和d[B]/dt = -k[A][B]。
将两个方程进行整理,得到d[A]/[A] = -k[B]dt和d[B]/[B] = -k[A]dt。
两边同时积分,得到∫d[A]/[A] = -k∫[B]dt和∫d[B]/[B] = -k∫[A]dt。
对左边进行积分,得到ln[A] = -k[B]t + C2和ln[B] = -k[A]t + C3,其中C2和C3为积分常数。
取指数,得到[A] = e^(-k[B]t + C2)和[B] = e^(-k[A]t + C3)。
由于初始时刻A和B的浓度分别为[A]0和[B]0,所以代入初始条件得到[A]0 = e^C2和[B]0 = e^C3,解得C2 = ln[A]0和C3 = ln[B]0。
将C2和C3代入[A] = e^(-k[B]t + C2)和[B] = e^(-k[A]t + C3)中,得到[A] = [A]0e^(-k[B]t)和[B] = [B]0e^(-k[A]t)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题1. 如附图所示。
某工业炉的炉壁由耐火砖λ1=1.3W/(m·K)、绝热层λ2=0.18W/(m·K)及普通砖λ3=0.93W/(m·K)三层组成。
炉膛壁内壁温度1100oC ,普通砖层厚12cm ,其外表面温度为50 oC 。
通过炉壁的热损失为1200W/m 2,绝热材料的耐热温度为900 oC 。
求耐火砖层的最小厚度及此时绝热层厚度。
设各层间接触良好,接触热阻可以忽略。
已知:λ1=1.3W/m·K,λ2=0.18W/m·K,λ3=0.93W/m·K,T 1=1100 oC ,T 2=900 oC ,T 4=50oC ,3δ=12cm ,q =1200W/m 2,Rc =0求: 1δ=?2δ=? 解: ∵δλTq ∆=∴1δ=m q T T 22.0120090011003.1211=-⨯=-λ 又∵33224234332322λδλδδλδλ+-=-=-=T T T T T T q∴W K m q T T /579.093.012.01200509002334222⋅=--=--=λδλδ 得:∴m 10.018.0579.0579.022=⨯==λδ习题1附图 习题2附图2. 如附图所示。
为测量炉壁内壁的温度,在炉外壁及距外壁1/3厚度处设置热电偶,测得t 2=300 oC ,t 3=50 oC 。
求内壁温度t 1。
设炉壁由单层均质材料组成。
已知:T 2=300oC ,T 3=50oC求: T 1=? 解: ∵δλδλ31323T T T T q -=-=∴T 1-T 3=3(T 2-T 3)T 1=2(T 2-T 3)+T 3=3×(300-50)+50=800 oC3. 直径为Ø60×3mm 的钢管用30mm 厚的软木包扎,其外又用100mm 厚的保温灰包扎,以作为绝热层。
现测得钢管外壁面温度为–110oC ,绝热层外表面温度10oC 。
已知软木和保温灰的导热系数分别为0.043和0.07 W/(m·o C ),试求每米管长的冷量损失量。
解:圆筒壁的导热速率方程为()23212131ln 1ln 12r r r r t t LQλλπ+-=其中 r 1=30mm ,r 2=60mm ,r 3=160mm 所以()2560160ln 07.013060ln 043.01101002-=+--=πLQ W/m 负号表示由外界向系统内传热,即为冷量损失量。
4. 蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层,设外层的平均直径为内层的两倍。
其导热系数也为内层的两倍。
若将二层材料互换位置,假定其它条件不变,试问每米管长的热损失将改变多少?说明在本题情况下,哪一种材料包扎在内层较为合适?解:设外层平均直径为d m,2,内层平均直径为d m,1,则 d m,2= 2d m,1 且 λ2=2λ1 由导热速率方程知 11111122114522λππλπλλλb Ld t Ld bL d b tS bS b t Q m m m m m ⨯⨯∆=+∆=+∆=两层互换位置后 11111122λππλπλbLd t Ld bL d b tQ m m m ⨯∆=+∆='所以25.145=='='q q Q Q即 q q 25.1='互换位置后,单位管长热损失量增加,说明在本题情况下,导热系数小的材料放在内层较适宜。
5. 在长为3m ,内径为53mm 的管内加热苯溶液。
苯的质量流速为172kg/(s·m 2)。
苯在定性温度下的物性数据:μ=0.49mPa·s;λ=0.14 W/(m·K);c p =1.8kJ/(kg·oC )。
试求苯对管壁的对流传热系数。
已知:L =3m ,d =53mm ,G=172 kg/(s·m 2),被加热苯物性,μ=0.49mPa·s,λ=0.14 W/(m·K);c p =1.8kJ/(kg·oC )求: α 解: Re =431086.11049.0172053.0⨯=⨯⨯=-μdG> 410 3.614.01049.0108.1Pr 33=⨯⨯⨯==-λμp c >0.76.56053.03==d L >40 故可用N u =0.023Re 0.8Pr 0.4公式 4.08.044.08.03.6)1086.1(053.014.0023.0Pr Re 023.0⨯⨯⨯⨯==dλα=330W/m 2·o C 6. 在常压下用列管换热器将空气由200 oC 冷却至120 oC ,空气以3kg/s 的流量在管外壳体中平行于管束流动。
换热器外壳的内径为260mm ,内径Ø25×2.5mm 钢管38根。
求空气对管壁的对流传热系数。
已知:T 1=200 oC ,T 2=120 oC ,空气q m =3kg/s 走管外壳程,D=260mm ,n =38,d =25mm 求: α解: 空气平均温度C T T t m ︒=+=+=1602120200221 查160 o C 空气:ρ=0.815kg/m 3,μ=2.45×10-5Pa·s,Pr =0.682,λ=0.0364W/m·Km nd D nd D d n D d n D S A de 036.0025.03826.0025.03826.0)44(44222222=⨯+⨯-=+-=+-⨯==ππππ s m kg A q G m ⋅=⨯-⨯==222/1.87)025.03826.0(785.03331029.11045.21.87036.0Re ⨯=⨯⨯==-μdeG>104 K m W d⋅=⨯⨯⨯⨯==24.08.034.08.0/254682.0)1029.1(036.00364.0023.0Pr Re 023.0λα7. 油罐中装有水平蒸汽管以加热罐内重油,重油的平均温度t m =20oC ,蒸汽管外壁温度t w =120oC ,管外径为60mm 。
已知在定性温度70 oC 下重油的物性数据:ρ=900kg/m 3;c p =1.88kJ/(kg·oC );λ=0.174 W/(m·oC );运动黏度ν=2×10-3m 2/s ;β=3×10-41/ oC 。
试问蒸汽对重油的热传递速率为多少,(单位为kW/m 2)?已知:水平管加热外部重油,d =60mm , t m =20oC ,t w =120oC ,70oC 下,ρ=900kg/m 3;c p =1.88kJ/(kg·oC );λ=0.174 W/(m·oC ),ν=2×10-3m 2/s ;β=3×10-4/ oC 。
求: q=?解: 属大容积自然对流,9.15)102(06.0)20120(81.9103233423=⨯⨯-⨯⨯⨯=∆=--νβtd g Gr 4331094.1174.09001021088.1Pr ⨯=⨯⨯⨯⨯===-λρλμv c c p p541009.31094.19.15Pr ⨯=⨯⨯=Gr 查教材可得:A =0.54,b =0.25 C m W Gr dAb ︒=⨯⨯⨯==225.05/9.36)1009.3(060.0174.054.0Pr)(λα 23/1069.3)20120(9.36)(m W t t q m w ⨯=-⨯=-=α8. 室内水平放置两根表面温度相同的蒸汽管,由于自然对流两管都向周围空气散失热量。
已知大管的直径为小管直径的10倍,小管的(GrPr )=109。
试问两管路单位时间、单位面积的热损失比值为多少?解:∵3Pr d Gr ∝⋅∴129323211101010Pr)()(Pr)(=⨯=⋅=⋅Gr d d Gr 查表6-5,两者均在3区域,A=0.135,31=b ∵b Gr dq Pr)(1⋅∝∴1)1010(10]Pr)(Pr)([3191213121122121=⨯=⋅⋅==-Gr Gr d d q q αα 9. 饱和温度为100oC 的水蒸气在长3m 、外径为0.03m 的单根黄铜管表面上冷凝。
铜管竖直放置,管外壁的温度维持96 oC ,试求:(1)每小时冷凝的蒸汽量;(2)又若将管子水平放,冷凝的蒸汽量又为多少?已知:t s =100oC ,t w =96 oC ,L =3m ,d =0.03m 求: (1)W 竖放;(2)W 水平 解: 查100o C ,水,r =2258kJ/kg C t t t w s m ︒=+=+=982961002 查98 oC ,水,ρ=960kg/m 3,μ=0.290cp ,λ=0.682W/m·K(1) 设凝液为层流,则竖放时 K m W tL gr ⋅⨯=⎪⎪⎭⎫⎝⎛∆⋅⋅=234132/1042.713.1μλρα 验5441022581029.0431042.744Re 333=⨯⨯⨯⨯⨯⨯⨯=∆=-r t L μα<2000计算有效 s kg r t d L r Q q m /1072.3102258403.014.331042.7333-⨯=⨯⨯⨯⨯⨯⨯=∆==πα (2) 水平放,仍设层流02.203.0364.064.04141=⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛='d L αα ∴K m W ⋅⨯=⨯⨯='243/1050.11042.702.2α∵α∞m q∴s kg q q m m /1051.71072.302.233--⨯=⨯⨯='='αα 验5.341029.031051.744Re 33=⨯⨯⨯⨯=⋅'=--μL q m <2000计算有效10. 在列管式换热器中用冷水冷却油。
水的直径为Ø19×2mm 的列管内流动。
已知管内水侧对流传热系数为3490 W/(m 2·oC ),管外油侧对流传热系数为258 W/(m 2·oC )。
换热器在使用一段时间后,管壁两侧均有污垢形成,水侧污垢热阻为0.00026m 2·oC/ W ,油侧污垢热阻为0.000176 m 2·o C/ W 。
管壁导热系数λ为45 W/(m 2·oC ),试求:(1)基于管外表面积的总传热系数;(2)产生污垢后热阻增加的百分数。
解:(1)总传热系数K 0ii i Si m S d d d d R d d b R K αλα000011++++=15349019151900026.0171945002.0000176.025811⨯+⨯+⨯++=2080048.01==W/(m 2·oC )(2)产生污垢后热阻增加百分数为%8.11%100151900028.0000176.00048.0151900026.0000176.0=⨯⎪⎭⎫ ⎝⎛⨯+-⨯+11. 热气体在套管换热器中用冷水冷却,内管为Ø25×2.5mm 钢管,热导率为45W/(m·K)。
