简支梁计算例题
结构力学计算题及结构力学练习题含答案

结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学,以下是一篇结构力学计算题及练习题,包括答案的示例。
结构力学计算题题目:一简支梁AB,跨度为4米,受到均布荷载q=2 kN/m,梁的截面惯性矩I=1.2×10^6 mm^4,弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤:1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式:\[ M_{max} = \frac{ql^2}{8} \]代入已知数据:\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式:\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据:\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案:梁的最大弯矩Mmax为4 kN·m,最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD,长度为3米,受到集中力F=5 kN作用在自由端,梁的截面惯性矩I=1.5×10^6 mm^4,弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax为5 kN·m,最大挠度y_max为0.013 mm。
2. 一连续梁EF,跨度为6米,分为两段,每段长度为3米,中间有一支点G。
梁上受到均布荷载q=1.5kN/m,梁的截面惯性矩I=2×10^6 mm^4,弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案:支点G的反力为4.5 kN,中间梁段的最大弯矩为2.25 kN·m。
简支梁计算示例

1.一座五梁式装配钢筋砼简支梁桥的主梁和横隔梁截面如下图1、图2所示,主梁长19.96m ,计算跨径19.5m ,主梁翼缘板刚性连接。
40C 的弹性模量210m N105.23E ⨯=,跨中截面惯性矩4c m 06626.0I =,跨中单位长度质量m kg 1083.51m 3c ⨯=,试计算5号梁5cq m ,50q m 以及在公路-Ⅰ级车道荷载作用下的跨中最大弯矩、最大剪力及支点截面最大剪力。
图1(单位:cm )图2(单位:cm )解:一、5号梁荷载横向分布系数计算1、杠杆原理法(1)绘出5号梁的横向分布影响线:(如图示)10.8751.60.8(2)在5号梁的横向分布影响线上进行最不利加载(如图示)m 50q =1/2(∑ηi )=1/2×0.875=0.4382、刚性横梁法(1)求5号梁的横向分布影响线:(以桥跨中心为坐标原点建立坐标系:如图示)∑a i 2=a 12+ a 22 +a 32 +a 42+ a 52=2×(3.22+1.62)=25.6η51= 1/n-a 5×a 1/∑a i 2=1/5-3.2×3.2/25.6=-0.2η55= 1/n+a 3×a 7/∑a i 2=1/5+3.2×3.2/25.6=0.6绘出5号梁的横向分布影响线(2)在5号梁的横向分布影响线上进行最不利加载:绘出加载图0.875η1=(480-20)/480*0.6=0.575η2=(480-200)/480*0.6=0.35η3=(480-330)/480*0.6=0.1875η4=-30/480*0.6=-0.0375 ?m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575)=0.556m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575-0.0375)=0.538 ?二.内力计算1、恒载内力)(222x l gxx gx x glM x -=⨯-⨯=)2(22x l ggx gl Q x -=-=g=1.583*103kg/m=1.583/9.8*103=16.15kN/m各计算截面的剪力和弯矩值如下表:5号梁恒载内力2、活载内力计算课程设计中要计算简支桥基频,公式为:cc m EI l f 22π=再根据计算基频选择冲击系数。
3节装配式钢筋混凝土简支梁设计例题
(2)分析梁内是否需要配置剪力钢筋
跨中: 0.50×10-
3ftdbh0=0.50×103×1.39×180×1381=172.76kN 支点:
0kN.500 V ×1d ,l 0/2 3 ft( 1 dbhk 0=3 ) 0 ( N .0 5.05 5 × 1 10 3 3) ×f 0 1c .b 3d 90 ×10 h V 8d 0,0 × 1( 7 450k .10 ) 0=N 17 81.4
Sv 12320.56106(V2'20.6p) fcu,kbh02
1.01.10.56106(20.61.56) 3018014126 6623
17m 5 m
14
现取跨中部分箍筋的间距为170mm
则满足规范Sv=170mm<h0/2=750mm及 400mm
配箍率 验sv 算1 2 : 8 5 1 .3 0 0 7 0 .0 3% 3 sm v in 0 .1% 8
在支座中心向跨径方向长度相当于不小于 一倍梁高范围内,箍筋间距不宜大于 100mm,取Sv=100mm。
15
弯起钢筋及斜筋设计
设焊接钢筋骨架的架立钢筋HRB335级为 2Ф22,钢筋中心至梁受压一般上缘距离为 as′=56mm,c=43mm.
计算第一排弯起钢筋Asb1时,对于简支梁和 连续梁近边支点梁段,取用距支点中心h/2 处由弯起钢筋承担的那部分剪力值Vsb1;
12
箍筋设计
钢筋混凝土梁应设置直径不小于8mm或1/4 主筋直径的箍筋。其配筋率ρsv,R235钢筋 不应小于0.18%,
现初步选用φ 8的双肢箍筋 n=2;Asv1=50.3mm2。 Asv=nAsv1=2×50.3=100.6mm2
计算简单梁在集中荷载作用下的支座反力

起的该量值的代数和。
B 叠加原理的适用条件: 结构处于弹性限度内和小变
形条件下;荷载和某量值的关系 q 是线性关系。
B
例题 1、求下图所示简支梁的支座反力RA、RB。
40KN A
10KN B
2m 2m 2m
6m
解:1)、取整体为研究对象,作受力图
2)、列平衡方程、求解 (1)∑mA=0,RB×6﹣40 ×2-1 0 ×4=0,解之, RB=20KN(↑) (2)∑mB=0,RA ×6-40 ×4-10 × 2=0,解之, RA=30KN (↑)
HA MA
RA
例 2 求图示结构的支座反力。 解:取AB 杆为研究对象画受力图。 由 ∑X = 0 :
HA=0 由 ∑MA = 0 :
由 ∑Y = 0 :
HA
RA
RB
2.3.4叠加原理
P
A
P
A
A
=+
叠加原理:
q
结构在多个荷载作用下的某
B 一量值(反力、内力、变形等)的
大小等于各个荷载单独作用时所引
∑ Y=0,
YA-P=0, YA=P=10KN (↑)
∑ X=0,
XA=0
∑ MA=0,
MA-P×3=0
MA=P×3= 10×3=30KN·M(方向同图示)
3)、校核(只能判断公式中的计算正误,不能 确认平衡方程本身是否列对)。
三、课堂练习
1、求图示梁的支座反力
解法一: 1)、取梁整体研究,作受力图
3)校核 ∵ ∑ Y= RA + RB –40-10=0 ∴计算无误(只有支反
力无误,才有可能作的内 力图正确)
40KN A
10KN B
预应力混凝土简支梁计算
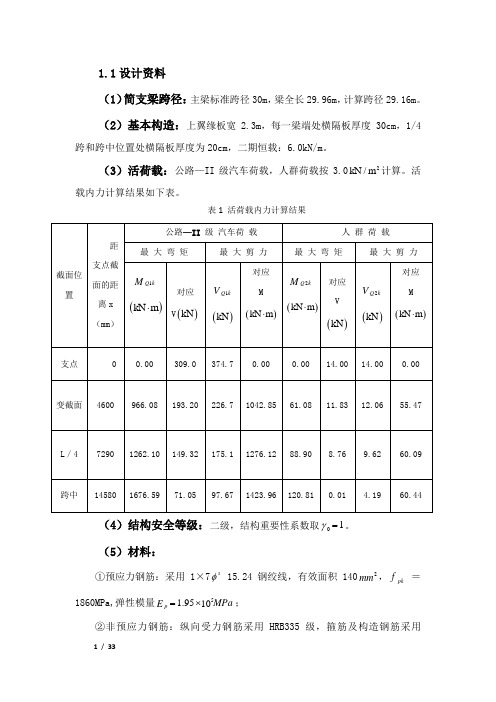
表1 活荷载内力计算结果1.1设计资料(1)简支梁跨径:主梁标准跨径30m ,梁全长29.96m ,计算跨径29.16m 。
(2)基本构造:上翼缘板宽2.3m ,每一梁端处横隔板厚度30cm ,1/4跨和跨中位置处横隔板厚度为20cm ,二期恒载:6.0kN/m 。
(3)活荷载:公路—II 级汽车荷载,人群荷载按3.02kN /m 计算。
活载内力计算结果如下表。
(4)结构安全等级:二级,结构重要性系数取01γ=。
(5)材料:①预应力钢筋:采用1×7s φ 15.24钢绞线,有效面积1402mm ,pkf =1860MPa,弹性模量51.9510p MPa E =⨯;②非预应力钢筋:纵向受力钢筋采用HRB335级,箍筋及构造钢筋采用HRB335,R235级;③混凝土:C50,43.4510c MPa E =⨯,抗压强度标准值32.4ck MPa f =,抗压强度设计值22.4cd MPa f =;抗拉强度标准值 2.65tk MPa f =,抗拉强度设计值1.83td MPa f =。
(6)施工方法:采用后张法两端同时张拉,预应力孔道采用塑料波纹管;(7)设计要求:按全预应力混凝土或部分预应力混凝土A 类构件设计。
1.2主梁尺寸主梁各部分尺寸如下图所示。
1.3主梁全截面几何特性1)主梁翼缘有效宽度'f b ,取下列三者中的最小值: (1)简支梁计算跨径的l/3,即l/3=29160/3=9720mm ; (2)相邻两梁的平均间距,对于中梁为2300mm ;(3)()'b 612b h f h ++,式中b 为梁腹板宽度,b h 为承托长度,这里b h =0,'h f 为受压区翼缘处板的厚度, 'h f 可取跨中截面议板厚度的平均值,即'h f ≈(1000×180+800×120/2)/1000=228mm 。
所以有()'b 612b h f h ++=200+6×0+12×228=2936mm 。
例题-简支梁内力计算

ql/2 -ql/2
剪力图
ql2/8
弯矩图
2
2、计算截面内力 距离A支座为x的任一截面上的弯矩和剪 力(内力)分别用Mx、Vx表示。
q R1 A R2 x
Mx Vx
由∑Fy=0,得到R2-Vx- qx=0பைடு நூலகம்
Vx= ql/2-qx
对x截面取矩,由∑Mx=0,得到Mx+ qx×x/2-R2×x=0
3、绘制内力图
Mx= qlx/2-qx2/2
横坐标表示x,纵坐标表示内力(弯矩或剪力,即为内力图。
线分布荷载q的合力为ql力臂合力点到a点的距离为l2荷载对a点的力矩为qlql2qx距离a支座为x的任一截面上的弯矩和剪力内力分别用m表示
简支梁内力计算
已知简支梁跨度为l、分布荷载q。求截面弯矩和剪力分布。
〖解〗
R1
1、求支座约束反力
A
三个约束反力分别用R1、R2、R3表示。 R2
q B
l
R3
由静力平衡条件:∑Fx=0 得到R1=0;
对A点取力矩,力矩等于力×力臂。反力R1、 R2 的力臂为0; 反力R3 的力臂为l,对A点的力矩为-R3 l;线分布荷载q的合力为ql
力臂(合力点到A点的距离)为l/2,荷载对A点的力矩为 ql2/2 。
由∑MA=0,0+0- R3 l+ ql2/2=0
得到R3=ql/2
1
∑Fy=0,得到R2= R3 = ql/2
钢筋混凝土矩形截面简支梁计算
4Φ20钢筋混凝土矩形截面简支梁,截面尺寸b×h =200mm ×450mm , 计算跨度L 0=6m ,承受均布线荷载:活荷载:楼面板2kN/m ,屋面板1.5 kN/m.永久荷载标准值:钢筋混凝土的重度标准值为25kN/m 3,故梁自重标准值为25×0.2×0.45=2.25 kN/m 。
墙自重18×0.24×3=12.96 kN/m ,楼板:25×0.08×2.25=4.5kN/m. 楼盖板25×0.06×2.25=3.375kN/m.查表得f c =12.5N/mm 2,f t =1.3N/mm 2,f y =360N/mm 2,ξb =0.550,α1=1.0,结构重要性系数 γ0=1.0,可变荷载组合值系数Ψc=0.71.计算弯矩设计值M故作用在梁上的恒荷载标准值为:g k =2.25+12.96+4.5+3.375=23.085kN/m简支梁在恒荷载标准值作用下的跨中弯矩为:M gk =1/8g k l 02=1/8×23.085×62=103.88kN.m简支梁在活荷载标准值作用下的跨中弯矩为:M qk =1/8q k l 02=1/8×62×(2+1.5*0.4)=11.7kN·m由恒载控制的跨中弯矩为:γ0(γG M gk + γQ Ψc M qk )=1.0×(1.35×103.88+1.4×0.7×11.7)=151.70kN·m由活荷载控制的跨中弯矩为:γ0(γG M gk +γQ M qk ) =1.0×(1.2×13.88+1.4×11.7)=141.03kN·m取较大值得跨中弯矩设计值M =151.70kN·m 。
1.确定截面有效高度h 0假设纵向受力钢筋为单层,则h 0=h -35=450-35=415mm假设纵向受力钢筋为单层,则h 0=h -35=450-35=415mm2.计算x ,并判断是否为超筋梁=4.15-((4.152-2*151.70*106/1.1*12.5*200))^0.5=166.03mm<0.518*415=214.97不属超筋梁。
钢筋混凝土简支梁挠度计算算例
钢筋混凝土简支梁挠度计算算例编写 王行耐某装配式钢筋混凝土T 形截面简支梁,计算跨径L=19.5m ,跨中截面尺寸b=24cm 、h=100cm 、b i =178cm 、h i =12cm ,配置HRB400钢筋(12φ32,A s =96.516cm 2),跨中截面恒载弯矩标准值M GK =912.52kN.m ,汽车荷载弯矩标准值(包括冲击力)M Q1K =859.57kN.m ,冲击系数(1+μ)=1.19,人群荷载弯矩标准值M Q2K =85.44kN.m 。
试验算此梁跨中截面裂缝宽度。
解:荷载短期效应作用下的跨中截面挠度按下式近似计算:BMl f 2485⋅= 其中:荷载短期效应组合mkN M M M M KQ K Q GK S .59.1503 44.85)19.1/(51.8597.052.912 )1/(7.021=+⨯+=+++=μL=19.50m=19.5×105mmcr s cr s cr B B M M M M B B 02201⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=0B 为全截面抗弯刚度,B 0=0.95E c J 0,按全截面参加工作计算,取f b '=1780mm ,Es α=E S /E 0=2×105/3×104≈6.67,换算截面重心至受压缘的距离'0y =386.2mm , 至受拉缘的距离0y =1000-386.2=613.8mm 。
换算截面惯性矩0J =5.9881×1010mm 4,对受拉边缘的弹性抵抗矩000/y J W == 5.9881×1010/613.8=9.7557×107mm 3,换算截面重心以上部分面积对重心轴的面积矩为:S 0 =240×386.22/2+(1780-240)×120×(386.2-120/2)=78179812.8mm 2取E C =3.0×104MPa ,将以上数据代入公式得B 0=0.95×104×5.9881×1010=17.0661×1014N.mm 2B cr 为开裂截面的抗弯刚度,B cr =E c J cr ,开裂截面的换算截面几何特征值,按有关公式计算求得:混凝土受压区高度x 0=247.2mm换算截面惯性矩J cr =3.5202×1010mmB cr =3.0×104×3.5202×1010=10.5607×1014N.mm开裂弯矩 0W f M tk cr γ=γ=2S 0/W 0=2×78179812.8/9.7557×107=1.6028,tk f =2.01MPa ,代入上式得:M cr =1.6028×2.01×9.7557×107=310.29×106N.mm=310.29kN.mM s =1503.59kN.m将以上数据代入公式得mmkN B B M M M M B B cr s cr s cr .10738.10 105607.10100061.1759.150329.314159.150329.314100061.17 114141422140220⨯=⨯⨯⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=荷载短期效应作用下跨中截面挠度为: mm B Ml f s 2.5310738.10195001059.150348548514262=⨯⨯⨯⋅=⋅= 长期挠度为:mm L mm f f s l 19.121600/195001610/2.852.536.1==>=⨯==θη应设置预拱度,预拱度值按结构自重和1/2可变作用频遇值计算的长期挠度值之和采用。
例20-1 图20-10(a)所示简支梁AB,试计算C 、B截面上的内力
68 例20-1 图20-10(a )所示简支梁AB ,试计算C 、B 截面上的内力(B 截面是指无限接近于B 截面并位于其左侧的截面)。
解 首先计算其约束反力,设其方向如图20-10(a )所示。
由平衡方程得:0=∑A m 02=⋅+⋅--l Y lP m BP Y B 25=0=∑B m 02=⋅+-⋅-lP m l Y AP Y A 23-=这里Y A 为负,说明它的方向设反了。
下面计算C 截面的内力。
假想将梁在C 截面截开,如果保留左段,可先设剪力Q C 与弯矩M C 皆为正,它们的方向必然如图20-10(b )所示。
在图20-10(b )中将Y A 的正确方向画出,这时,由平衡方程得:∑=0Y 0=--C A Q Y P Q C 23-=00=∑m 04=+-⋅C A M m lY Pl M C 813=弯矩M C 得正号,说明原先假定正弯矩的转向是对的,同时又表示该截面的弯矩是正弯矩。
而剪力Q C 得负号,说明剪力的方向设反了,实际上为负剪力。
最后再计算B 截面的内力。
将梁假想在B 截面截开,并选右段为研究对象,设Q B与M B 皆为正,由平衡方程得BM (BC 图 20-1069∑=0Y P Y Q B B 25-=-=00=∑m 00=⋅+B B Y M 0=B M例 20-2 切刀在切割棒料时,若刀刃上的切割力在垂直方向的分力为P [图20-11(a )],切刀的伸出长度为l ,试作切刀伸出部分的剪力图和弯矩图。
解 首先将刀杆简化为一个受集中力P 作用的悬臂梁[图20-11(b )]。
以自由端为坐标原点,在建立梁的剪力和弯矩方程时,取距原点为x 的任意截面[图20-11(b )],并研究截面左边的一段梁。
由于其上的外力为已知,故无需先求支座反力。
按前述方法,可得到该截面上的剪力和弯矩分别为: P Q -= Px M -=由于梁上除P 力外,再没有其它的载荷,因而这两个方程式(a )、(b )对于全梁的各横截面,即在0≤x ≤l 的范围内均适用。
简支梁计算例题
简支梁计算例题设计任务:设计一个简支梁,已知梁的跨度L=6米,梁的截面尺寸为b×h=200×400毫米,承受均布荷载设计值q=70kN/m(包括自重),混凝土强度等级为C25,纵向受拉钢筋采用HRB400级钢筋,箍筋采用HPB300级钢筋。
1. 计算梁所受总弯矩M:M = qL²/ 8 = 70 ×6²/ 8 = 255 kN·m2. 计算梁的截面面积A:A = b ×h = 200 ×400 = 80000 mm²3. 计算梁的截面模量W:W = α×A ×fcm = 1.1 ×80000 ×30 = 2640000 N·mm4. 计算梁的抗弯承载力Mu:Mu = fcmw = 30 ×2640000 = 79200000 N·mm > M = 25500000 N·mm5. 计算梁的纵筋数量:由M/mho²+fyAs/s ≤fcd得出As ≥M/(mho²+ fy/s),其中fy为HRB400级钢筋的抗拉强度设计值,取值为360N/mm²。
通过计算得出As≥8176mm²,选用2Φ28的钢筋,As=12568mm²。
6. 计算箍筋数量:根据构造要求,选用Φ8@200的箍筋,每米长度内布置箍筋数量为n=1×100/200+1=2个。
7. 验算裂缝宽度:根据规范要求,裂缝宽度不应超过Wmax=0.3mm。
根据M/γfW≤Wmax,其中γf为受拉或受压区纵向普通钢筋的配筋率,取值为As/(bho),通过计算得出W≤Wmax。
8. 绘制施工图,标明梁的跨度、截面尺寸、纵向钢筋和箍筋的位置和规格。
结论:根据以上计算和验算,该简支梁的设计满足要求,可以用于实际工程中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简支梁计算例题
(原创实用版)
目录
1.引言:简支梁的概述
2.简支梁的计算方法
3.计算例题
4.总结
正文
【引言】
简支梁是一种常见的梁式结构,主要用于承受横向载荷。
在工程设计中,简支梁的计算是必不可少的环节。
本文将介绍简支梁的计算方法,并通过例题进行具体讲解。
【简支梁的计算方法】
简支梁的计算主要包括以下几个步骤:
1.确定梁的材料和截面形状
2.计算截面的惯性矩和截面模量
3.计算梁的弯曲应力和弯矩
4.根据梁的稳定性条件,确定梁的允许载荷
【计算例题】
假设有一根简支梁,材料为普通钢筋混凝土,截面为矩形,长为 4 米,宽为 0.2 米。
现需要计算该梁在承受最大弯矩时,允许的载荷。
首先,计算截面的惯性矩和截面模量。
矩形截面的惯性矩 I=(b*h^3)/12=(0.2*4^3)/12=0.0267m^4,截面模量 W=I/(b*h)
=0.0267/(0.2*4)=0.0334m^2。
其次,计算梁的弯曲应力和弯矩。
假设最大弯矩为 M,根据弯矩公式M=F*L/4,其中 F 为梁的允许载荷,L 为梁的长度。
代入已知数值,得到M=F*4/4=F。
由于简支梁在弯曲时,弯曲应力σ=M/W,所以σ=F/W。
最后,根据简支梁的稳定性条件,确定梁的允许载荷。
假设梁的允许弯矩为 M",根据简支梁的稳定性条件 M"=2*W*σ",其中σ"为梁的允许弯曲应力。
代入已知数值,得到 M"=2*0.0334*0.6=0.04m^2。
因此,该梁在承受最大弯矩时,允许的载荷为 F=M"=0.04m^2。
【总结】
通过以上例题,我们可以看出简支梁的计算过程主要包括确定梁的材料和截面形状、计算截面的惯性矩和截面模量、计算梁的弯曲应力和弯矩以及根据梁的稳定性条件确定梁的允许载荷。
