2016年高考(232)甘肃省兰州一中2016届高三12月月考
2016届甘肃省兰州市高三实战考试数学(文)试题(扫描版)讲解

2016年兰州市高三实战考试 文科数学试题答案及评分参考12.解析:∵()2f x ax b '=+∴(0)0f b '=>又∵对于任意实数x 都有0)(≥x f ,∴0a ≥且240b ac -≤∴24b ac ≤,∴0c >∴(1)112(0)f a b c a c f b b +++==+≥+≥' 二、填空题13. 14. 4 15. 16. ①或③ 三、解答题17. 解:(Ⅰ)设等差数列{}n a 的公差是d .∵()382726a a a a d +-+==-, ∴d =-3.∴2712723a a a d +=+=-,解得11a =-.∴数列{}n a 的通项公式为 32n a n =-+. ……………6分 (Ⅱ)∵数列{}n n a b +是首项为1,公比为q 的等比数列,∴1n n n a b q -+=,即132n n n b q --++=, ∴132n n b n q -=-+.所以21[147(32)](1)n n S n q q q -=++++-+++++(31)21(1)2n n n q q q --=++++⋯+ 故当1q =时,()231322n n n n nS n -+=+=; ……………11分 当1q ≠时,()31121nn n n q S q--=+-. ……………12分 18. 解:(Ⅰ)12月中旬市民到户外的时间可能是11日、12日、13日、14日、15日、16日、17日、18日、19日、20日,共10种情况;12月中旬市民不适合进行户外活动的时间有13日、14日、19日、20日,共4种情况.设“12月中旬市民不适合进行户外活动”为事件A ,则 42()105P A == 所以12月中旬市民不适合进行户外活动的概率为25…………6分 (Ⅱ)该游客在12月中旬来此城市旅游,想连续游玩两天,到此城市的时间可能为:{11,12}、{12,13}、{13,14}、{14,15}、{15,16}、{16,17}、{17,18}、{18,19}、{19,20},共9种情况,连续两天都适合旅游的时间为:{11,12}、{15,16}、{16,17}、{17,18},共4种情况.设“适合旅游的时间”为事件B ,则4()9P B =所以游客在12月中旬来此城市旅游,想连续游玩两天,适合旅游的概率为49…12分 19. 解:(Ⅰ)证明:连结OP ,因PA PB =,O 为AB 的中点故OP AB ⊥.∵侧面PAB ⊥底面ABCD ∴OP 平面ABCD∴OP OD ⊥,OP OC ⊥∵OD PC ⊥,∴OD ⊥平面OPC ,∴OD OC ⊥, …………4分 又∵OP OC ⊥,故OC ⊥平面OPD所以OC PD ⊥. …………6分 (Ⅱ)在矩形ABCD 中,由(Ⅰ)得OD OC ⊥,所以2AB AD =,故1AD =.∵侧面PAB ⊥底面ABCD ,底面ABCD 为矩形∴DA ⊥平面PAB CB ⊥平面PAB DPA ∆≌CPB ∆ ∴DPA ∠为直线PD 与平面PAB 所成的角 ∴DPA ∠=30,CPB ∠=30,PA PB == 连接PO ,则PO ⊥AB ,所以PO ⊥平面ABCD ∴PO 为四棱锥的-P ABCD 的高 在PAB ∆中,2AB =,PA PB ==∴PO =∴1112333P ABCD ABCD V PO S -=⋅=⨯=………………12分 20. 解:(Ⅰ)由122c a c a =⇒=,所以22224,3a c b c ==, 将点3(1,)2P 的坐标代入椭圆方程得21c =,故所求椭圆方程为22143x y += ………………5分(Ⅱ)当1l 与2l 中有一条直线的斜率不存在,则另一条直线的斜率为0,此时四边形 的面积为6S =,若1l 与2l 的斜率都存在,设1l 的斜率为k ,则2l 的斜率为1k-.∴直线1l 的方程为(+1y k x =),设11(,)A x y ,22(,)B x y ,联立22(1)143y k x x y =+⎧⎪⎨+=⎪⎩,消去y 整理得,2222(43)84120k x k x k +++-= 4222=644(34)(412)1441440k k k k ∆-+-=+>∴2122843k x x k +=-+, 212241243k x x k -⋅=+,∴122||43x x k -=+∴212212(1)|||43k AB x x k +=-=+ ………………8分 同理可得得 2212(1)||34k CD k +=+, ∴2222172(1)||||2(43)(34)k S AB CD k k +=⋅=+⋅+,令2(0,)k t =∈+∞, ∴22272(1)6(122512)6(43)(34)122512t t t tS t t t t +++-==+⋅+++,66288661249491225t t=-≥-=++ ∴288[,6)49S ∈ 综上可知,四边形ABCD 面积的取值范围是288[,6]49.………………12分21. 解:(I)因为11ln )(--+-=xaax x x f 所以222111)(x ax ax x a a x x f -+--=-+-=' ),0(+∞∈x 令111,0)('-=ax f ,可得两根分别为 因为2.10<<a ,所以0111>>-a, 当)1,0(∈x 时,此时()0<'x f ,函数)(x f 单调递减;)11,1(-∈a x 时,此时()0>'x f ,函数)(x f 单调递增;),11(+∞-∈a x 时,此时0)(<'x f ,函数)(x f 单调递减 ……………… 5分(II)因为)21,0(41∈=a ,由(I)知,,)2,0(311∉=-a,当)1,0(∈x 时,,0)('<x f 函数)(x f 单调递减;当)2,1(∈x 时,0)(>'x f ,函数)(x f 单调递增, 所以)(x f 在)2,0(上的最小值为21)1(-=f 由于“对任意)2,0(1∈x ,存在]2,1[2∈x ,使)()(21x g x f ≥等价于()x g 在]2,1[上的最小值不大于)(x f 在)2,0(上的最小值21-” (*) ………………8分又]2,1[,4)()(22∈-+-=x b b x x g ,所以①当1<b 时,因为025)1()]([min >-==b g x g 此时与(*)矛盾②当21≤≤b 时,因为04)]([2min ≥-=b x g 同样与(*)矛盾③当2>b 时,因为b g x g 48)2()]([min -==,且当2>b 时,048<-b ,解不等式2148-≤-b ,可得817≥b 所以实数b 取值范围),817[+∞ ………………12分 22. 解: (I)因为DE 是圆O 的直径, 所以2BED EDB π∠+∠=又BC DE ⊥,所以2CBD EDB π∠+∠=AB 切圆O 于点B , 得DBA BED ∠=∠所以CBD DBA ∠=∠ ………………5分 (II)由(I)知BD 平分CBA ∠, 则3BA AD BC CD==,又BC =,从而AB =所以4AC ==, 所以3AD =, 由切割线定理得2AB AD AE =⋅ ,所以26AB AE AD== 故3DE AE AD =-=即圆O 的直径为3. ………………10分.23. 解:(Ⅰ)由322x y ⎧=-⎪⎪⎨⎪=⎪⎩得直线l的普通方程为30x y +-=又由ρθ=得圆C的直角坐标方程为220x y +-=即22(5x y +=. ………………5分(II)把直线l 的参数方程代入圆C 的直角坐标方程,得22(3)()522-+=,即240t -+=由于(24420∆=-⨯=>,故可设12,t t 是上述方程的两实数根,所以12t t +=124t t ⋅=又直线l 过点P ,A 、B 两点对应的参数分别为1t 、2t所以1212PA PB t t t t +=+=+= ………………10分24. 解:(I )当4a =时,|1|||5x x a -+-≥等价为1255x x <⎧⎨-+≥⎩或1435x ≤<⎧⎨≥⎩或4255x x >⎧⎨-≥⎩解得0x ≤或5x ≥所以不等式()5f x ≥的解集为{|x 0x ≤或5x ≥} ………………5分 (II )因为()|1||||(1)()||1|f x x x a x x a a =-+-≥---=-所以min ()|1|f x a =-要使()4f x ≥对a R ∈恒成立,则须|1|4a -≥即可所以3a ≤-或5a ≥即实数a 的取值范围是{|a 3a ≤-或5a ≥} ………………10分。
2016届高三12月月考数学(理)试卷
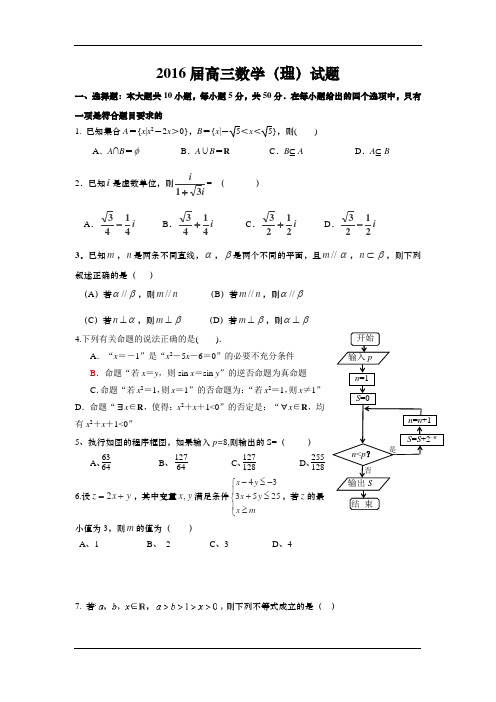
2016届高三数学(理)试题一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1. 已知集合A ={x |x 2-2x >0},B ={x |-5<x <5},则( )A .A ∩B =φ B .A ∪B =RC .B ⊆AD .A ⊆B 2.已知i 是虚数单位,则ii 31+= ( )A .i 4143- B .i 4143+ C .i 2123+ D .i 2123- 3.已知m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,则下列叙述正确的是( )(A )若//αβ,则//m n (B )若//m n ,则//αβ (C )若n α⊥,则m β⊥ (D )若m β⊥,则αβ⊥ 4.下列有关命题的说法正确的是( ).A .“x =-1”是“x 2-5x -6=0”的必要不充分条件B .命题“若x =y ,则sin x =sin y ”的逆否命题为真命题C .命题“若x 2=1,则x =1”的否命题为:“若x 2=1,则x ≠1”D .命题“∃x ∈R ,使得:x 2+x +1<0”的否定是:“∀x ∈R ,均有x 2+x +1<0”5、执行如图的程序框图,如果输入p=8,则输出的S=( )A 、6364B 、 12764C 、127128D 、2551286.设2z x y =+,其中变量,x y 满足条件433525x y x y x m -≤-⎧⎪+≤⎨⎪≥⎩,若z 的最小值为3,则m 的值为( )A 、1B 、 2C 、3D 、4 7. 若则下列不等式成立的是( )8.一机器元件的三视图及尺寸如右图示(单位:dm ),则该组合体的体积为(A) 80 dm 3 (B) 88 dm 3 (C) 96 dm}3 (D) 112 dm 39.已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ,其中b R ∈ ,若函数()()y f x g x =- 恰有4个零点,则b 的取值范围是(A )7,4⎛⎫+∞⎪⎝⎭ (B )7,4⎛⎫-∞ ⎪⎝⎭ (C )70,4⎛⎫ ⎪⎝⎭ (D )7,24⎛⎫⎪⎝⎭10.设函数f (x )在R 上存在导函数f '(x ),对∀x ∈R ,f (-x )+f (x )=x 2,且在(0,+∞)上, f '(x )>x .若有f (2-a )-f (a )≥2-2a ,则实数a 的取值范围为 A .(-∞,1]B .[1,+ ∞)C .(-∞,2]D .[2,+∞)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. 11.若非零向量a ,b 满足a b a b +=-,则a ,b 的夹角的大小为__________. 12. 已知正项等比数列{}n a 的前n 项和n S ,若352651,20,64,q a a a a S >+===则 .13.已知函数()3sin 2cos f x x x x =+-的图像在点A (0x ,0()f x )处的切线斜率为3,则0tan x 的值是________.14.设0,a b >>1,若4121a b a b +=+-,则的最小值为 .15.有下列4个命题:①若函数()f x 定义域为R ,则()()()g x f x f x =--是奇函数;②若函数()f x 是定义在R 上的奇函数,R x ∈∀,()(2)0f x f x +-=,则()f x 图像关于x =1对称;③已知x 1和x 2是函数定义域内的两个值(x 1<x 2),若12()()f x f x >,则()f x 在定义域内单调递减;④若()f x 是定义在R 上的奇函数, (2)f x +也是奇函数,则()f x 是以4为周期的周期函数. 其中,正确命题是 (把所有正确结论的序号都填上).三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.16.(本小题满分12分)已知向量,),23,(cos ),1,(sin m x n x =-= m )()(∙+=n m x f (1)当x ∈[0,2π]时,求函数y =f (x )的值域;(2)锐角三角形ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,若5,a b ==(),.2B f a c =求边17.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且22n n S a =-;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T .18(本题满分12分).如图,一简单几何体ABCDE 的一个面ABC 内接于圆O, G 、H 分别是AE 、BC 的中点,AB 是圆O 的直径,四边形DCBE 为平行四边形,且DC ⊥平面ABC. (I )证明:GH //平面ACD ;(II )若AC=BC=BE =2,求二面角O-CE-B 的余弦值.19(本小题满分12分)已知函数的图象如图所示·(I)求f (x)在R 上的单调递增区间;(II )设是函数y=f(x)的一个零点,求的值.20.(本小题满分13分)如图,在四棱锥P —ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA=PD=2,PA ⊥PD ,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AB=BC=1,O 为AD 中点。
问题5.4 如何顺畅求解复杂数列的求和问题-2017届高三数学跨越一本线(解析版)

2017届高三数学跨越一本线精品问题四:如何顺畅求解复杂数列的求和问题数列求和是历年高考命题的热点,数列求和的方法取决于其通项公式的形式,基本思路是将其转化为等成数列、等比数列的求和问题或通过裂项求和进行求解. 一、公式法公式法是数列求和的最基本的方法.也是数列求和的基础.其他一些数列的求和可以转化为等差或等比数列的求和.利用等比数列求和公式,当公比是用字母表示时,应对其是否为1进行讨论. 【例1】设}{n a 为等差数列,n S 为数列}{n a 的前n 项和,已知77=S ,7515=S ,n T 为数列}{nS n的前n 项和,求n T .【分析】利用等差数列的求和找1a 、d 的等式,解出1a 、d ,判断数列}{nS n的类型,在用公式求解.【点评】(1)直接应用公式求和时,要注意公式的应用范围,如当等比数列公比为参数(字母)时,应对其公比是否为1进行讨论.(2)几类可以使用公式求和的数列①等差数列、等比数列以及由等差数列、等比数列通过加、减构成的数列,它们可以使用等差数列、等比数列的求和公式求解.②奇数项和偶数项分别构成等差数列或者等比数列的,可以分项数为奇数和偶数时,分别使用等差数列或等比数列的求和公式.③等差数列各项加上绝对值,等差数列乘以(-1)n.【小试牛刀】【2017届重庆巴蜀中学高三文12月月考】已知数列{a }n 满足130n n a a ++=,243a =-,则{a }n 的前10项的和等于( ) A.106(13)--- B.101(13)9-- C.103(13)-- D.103(13)-+ 【答案】C【解析】设由题设可知数列是公比为31-,首项是4的等比数列.故其前10项和为)31(3311)311(4101010--=+-=S ,应选C. 二、分组法将数列的每一项拆成多项,然后重新分组,将一般的数列求和问题转化成特殊数列求和问题.运用这种方法的关键是将通项变形.“合项”法是利用加法的交换律和结合律将“不规则和”转化为“规则和”,化繁为简.【例2】 【 2016届河北省衡水中学高三二调】已知数列{}n a 中,121a a ==,且21n n a a +-=,则数列{}n a 的前100项和为( )A .2550B .2600C .2651D .2652 【分析】分偶数项与奇数项分别求和【解析】由题易知数列{}n a 奇数项与偶数项分别组成一1,1为首项,公差为1的等差数列,所以不难得到前100项的和.()()1005015050150255022S ++=+=,故选A .【点评】某些数列的求和是将数列分解转化为若干个可求和的新数列的和或差,从而求得原数列的和,这就要通过对数列通项结构特点进行分析研究,将数列的通项合理分解转化.特别注意在含有字母的数列中对字母的讨论.【小试牛刀】【2017届江西吉安市一中高三理上段考】已知数列{}n a 满足:当()11,,p q p q N p q *+=∈<时,2pp q a a +=,则{}n a 的前10项和10S =( )A .31B .62C .170D .1023 【答案】B【解析】12510110295622262S a a a a a a =++++++=+++=.三、裂项相消法此类变形的特点是将原数列每一项拆为两项之后,其中中间的大部分项都互相抵消了.只剩下有限的几项.注意:○1余下的项前后的位置前后是对称的.○2余下的项前后的正负性是相反的.常用的裂项方法: 【 例3】【2017届辽宁葫芦岛普通高中高三理上学期考试】在等差数列{}n a 中,公差0d ≠,17a =,且2a ,5a ,10a 成等比数列.⑴求数列{}n a 的通项公式及其前n 项和n S ; ⑵若15n n n b a a +=⋅,求数列{}n b 的前n 项和n T .【分析】⑴由2510 a a a ,,成等比数列⇒()7d +()()27974d d +=+⇒2d =⇒25n a n =+⇒()272562n n nS n n ++==+;⑵由⑴可得()()5511252722527n b n n n n ⎛⎫==- ⎪+⋅+++⎝⎭⇒5111111527991125271449n nT n n n ⎛⎫=-+-+-=⎪+++⎝⎭…+. 【解析】⑴∵2510 a a a ,,成等比数列,∴()()()277974d d d ++=+,又∵0d ≠,∴2d =. ∴25n a n =+,()272562n n nS n n ++==+.⑵由⑴可得()()5511252722527n b n n n n ⎛⎫==-⎪+⋅+++⎝⎭, ∴5111111527991125271449n nT n n n ⎛⎫=-+-+-= ⎪+++⎝⎭…+. 【点评】(1)裂项相消法求和的原理及注意问题①原理:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和. ②注意:在相加抵消过程中,有的是依次抵消,有的是间隔抵消,特别是间隔抵消时要注意规律性. ③一般地,若{a n }为等差数列,则求数列⎩⎨⎧⎭⎬⎫1a n a n +1的前n 项和可尝试此方法,事实上,1a n a n +1=d da n a n +1=a n +1-a nda n a n +1=1d ·⎝ ⎛⎭⎪⎫1a n -1a n +1.(2)用裂项法求和的裂项原则及规律(1)裂项原则:一般是前边裂几项,后边就裂几项直到发现被消去项的规律为止.(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项. 常见式的裂项【小试牛刀】【2016届湖南省长沙明德中学高三上第三次月考】数列1,12+,123++,…,1123n++++的前n 项和n S = ( ) A .311n n -+ B .21n n + C .31n n + D .43nn + 【答案】B四、错位相减法若数列{}n a 是等差数列,数列{}n b 是等比数列,由这两个数列的对应项的乘积组成的新数列{}n n a b ,当求数列的前n 项和时,常常采用将{}n n a b 各项乘以{}n b 的公比q ,并向后错一项与原{}n n a b 的同次项对应相减的方法.错位相减法实际上是把一个数列求和问题转化为等比数列求和的问题. 注意:○1 要考虑 当公比q 为1时为特殊情况 , ○2错位相减时要注意末项. 【例4】【2017届江西鹰潭一中高三理上学期月考】设数列{}n a 的前n 项和为n S ,已知11a =,12n n n a S n++=(*n N ∈). (1)证明:数列n S n ⎧⎫⎨⎬⎩⎭是等比数列; (2)求数列{}n S 的前n 项和n T .【分析】(1)利用12n n n a S n ++=,11n n n a S S ++=-,推导出121n n S S n n +=+,由此能证明n S n ⎧⎫⎨⎬⎩⎭是等比数列;(2)由已知条件推导出12n nS n-=,由此利用错位相减法能求出数列{}n S 的前n 项和n T .【点评】错位相减法求和的适用条件及关注点(1)适用条件:如果一个数列的各项由一个等差数列的各项和一个等比数列对应项乘积组成,那么这个数列的前n 项和可用此法来求.即求数列{a n ·b n }的前n 项和,其中{a n },{b n }分别是等差数列和等比数列. (2)关注点:①要善于识别题目类型,特别是等比数列公比为负数的情形;②在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”,以便于下一步准确地写出“S n -qS n ”的表达式.【小试牛刀】【2016届重庆市巴蜀中学高三上学期一诊模拟】已知数列{}n a 的首项11=a ,且满足)(0)1(11*++∈=+-N n a a a n n n .(1)求数列{}n a 的通项公式;(2)设nnn a c 3=,求数列{}n c 的前n 项和n S .【答案】(1)n a n 1=;(2)4334)12(1+⨯-=+n n n S . 【解析】(1)整理得1111=-+nn a a , 所以数列1{}na 是以首项为1,公差为1的等差数列,所以n n a n=-+=)1(11,所以n a n 1=.(2)由(1)知,n n n c 3⋅=,n n n S 333323132⨯+⋅⋅⋅+⨯+⨯+⨯=,①143233)1(3332313+⨯+⨯-+⋅⋅⋅+⨯+⨯+⨯=n n n n n S ,②①-②有132333332+⨯-+⋅⋅⋅+++=-n n n n S , 解得:4334)12(1+⨯-=+n n n S . 五. 数列{|a n |}的前n 项和问题【例5】在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列. (Ⅰ)求d ,a n ;(Ⅱ)若d <0,求|a 1|+|a 2|+…+|a n |. 【解析】 (Ⅰ)由题意得5a 3·a 1=(2a 2+2)2, 即d 2-3d -4=0.故d =-1或4.所以a n =-n +11,n ∈N *或a n =4n +6,n ∈N *, (Ⅱ)设数列{a n }的前n 项和为S n . 因为d <0,由(1)得d =-1,a n =-n +11. ∴S n =-12n 2+212n ,当n ≤11时,|a 1|+|a 2|+|a 3|+…+|a n |=S n =-12n 2+212n .当n ≥12时, |a 1|+|a 2|+|a 3|+…+|a n |=-S n +2S 11=12n 2-212n +110.综上所述,|a 1|+|a 2|+|a 3|+…+|a n |=⎪⎪⎩⎪⎪⎨⎧∈≥+-∈≤+-**N N n n n n n n n n ,12,11022121,11,2212122. 【点评】 (Ⅰ)本题求解用了分类讨论思想,求数列{|a n |}的和时,因为a n 有正有负,所以应分两类分别求和.(Ⅱ)常出现的错误:①当n ≤11时,求{|a n |}的和,有的学生认为就是S 11=110;②当n ≥12时,求{|a n |}的和,有的学生不能转化为2(a 1+a 2+…+a 11)-(a 1+a 2+…+a n ),导致出错. 求数列{|a n |}的前n 项和一般步骤如下: 第一步:求数列{a n }的前n 项和;第二步:令a n ≤0(或a n ≥0)确定分类标准; 第三步:分两类分别求前n 项和; 第四步:用分段函数形式下结论;第五步:反思回顾:查看{|a n |}的前n 项和与{a n }的前n 项和的关系,以防求错结果.【牛刀小试】【2016届浙江宁波效实中学高三上期中考试】数列{}n a 的前n 项和为26n S n n =-,则2a = ;数列{}n a 的前10项和1210a a a +++= .【答案】3-,58.【解析】当1n =时,115a S ==-,当2n ≥时,2216(1)6(1)27n n n a S S n n n n n -=-=---+-=-, ∴22273a =⨯-=-,∴1210113531131397949582a a a ++++=+++++⋅⋅⋅+=+⨯=+=. 【迁移运用】1.【2017届云南曲靖一中高三理上学期月考】已知等差数列{}n a 的前n 项和为n S ,又知101ln eS xdx =⎰,2011S =,则30S 为( )A .21B .30C .48D .50 【答案】B 【解析】1012010103020301ln (ln )|12()()30eeS xdx x x x S S S S S S ==-=⇒-=+-⇒=⎰,故选B.2.【2017届河北武邑中学高三周考】设曲线()n y x x N *=∈与x 轴及直线1x =围成的封闭图形的面积为n a ,设1n n n b a a +=,则122012b b b +++=( )A .5031007 B .20112012 C.20122013 D .20132014【答案】A【解析】由题意可得111+==⎰n dx x a n n ,则2111)2)(1(11+-+=++==+n n n n a a b n n n ,则122012b b b +++=10075032014121220121113121=-=+-++⋅⋅⋅+-n ,应选A. 3. 已知函数f (n )=⎩⎪⎨⎪⎧n 2当n 为奇数时,-n 2当n 为偶数时,且a n =f (n )+f (n +1),则a 1+a 2+a 3+…+a 100等于( )A .0B .100C .-100D .10 200【答案】B4.【2016届学年江西省新余一中等校高三联考模拟】已知数列}{n a 的前n 项和为n n S n -=2,令2cosπn a b n n =,记数列}{n b 的前n 项为n T ,则(2015=T ) A .2011- B .2012- C .2013- D .2014- 【答案】D【解析】根据题意有22n a n =-,所以有(22)cos2n n b n π=-,所以2015020608010040260T =-+++-++++-+201240262014=-=-,故选D .5.【2016届学年江西省新余一中等校高三联考模拟】数列{}n a 的通项公式是()()121--=n a nn ,则该数列的前100项之和为A .200-B .100-C .200D .100 【答案】D【解析】根据题意有1001357921197199250100S =-+-+-+--+=⨯=,故选D .6. 设f (x )=4x4x +2,若S =f (12 015)+f (22 015)+…+f (2 0142 015),则S =________.【答案】1 007【解析】∵f (x )=4x4x +2,∴f (1-x )=41-x41-x +2=22+4x ,∴f (x )+f (1-x )=4x 4x +2+22+4x =1.S =f (12 015)+f (22 015)+…+f (2 0142 015), ① S =f (2 0142 015)+f (2 0132 015)+…+f (12 015),②①+②得,2S =[f (12 015)+f (2 0142 015)]+[f (22 015)+f (2 0132 015)]+…+[f (2 0142 015)+f (12 015)]=2 014,∴S =2 0142=1 007.7.【 2017届安徽百校论坛高三上学期联考】已知函数{}n a 满足11123n n n a a a +++=+,且11a =,则数列21n a ⎧⎫⎨⎬+⎩⎭的前20项和为 . 【答案】7808.【2017届湖南长沙一中高三月考】数列{a }n 满足113a =,对任意n N *∈,21n n n a a a +=+,则2016111n n a =+∑的整数部分是 . 【答案】2【解析】因为21n n n a a a +=+,所以11111(1)1n n n n n a a a a a +==-++,即11111n n n a a a +=-+,所以 2016112232016201712017111111111()()()1n n a a a a a a a a a ==-+-++-=-+∑,所以2016111n n a =+∑的整数部分是2. 9.【2017届安徽淮北一中高三上学期四模】已知数列{}n a 的前n 项和为n S ,满足()12213,2,2412n n n a a S S S ++==+=+, 则数列{}n a 的前n 项和n S =__________.【答案】254n n+【解析】()21241n n n S S S +++=+化为()()21112n n n n S S S S +++---=,即2112n n a a ++-=,故n a 为等差数列,公差为113,22d a ==,所以254n n n S +=.10.【2016届甘肃省兰州一中高三12月月考】数列{}n a 的通项为(1)(21)sin 12n n n a n π=-+⋅+,前n 项和为n S ,则100S = . 【答案】200【解析】由已知可得13sin122a π=-+=-;25sin 11a π=+=;337sin182a π=-+=;49sin 211a π=+=;5511sin1102a π=-+=-;613sin 311a π=+=;7715sin 1162a π=-+=;分析可知偶数项均为1,所以前100项中偶数项的和为15050⨯=. 分析可知相邻两项奇数项的和为6,所以前100项中奇数项的和为5061502⨯=. 10050150200S ∴=+=.11.已知数列{a n }满足a 1=1,a n +1·a n =2n(n ∈N *),则S 2 012= 。
2016届高三12月月考数学(理)试卷
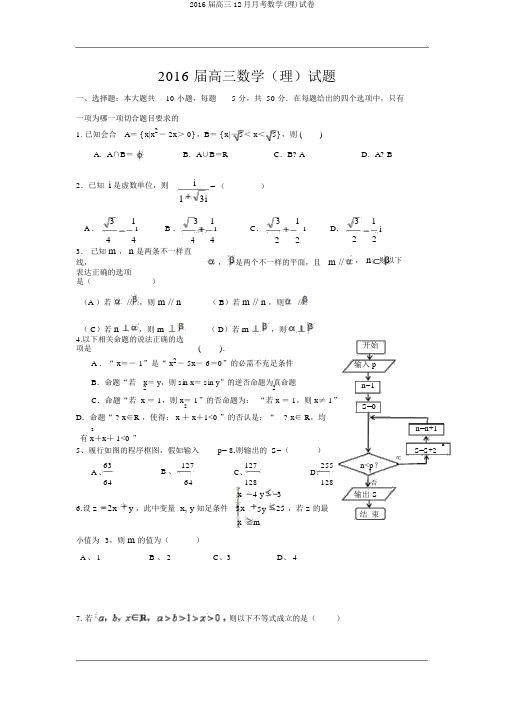
2016 届高三数学(理)试题一、选择题:本大题共10 小题,每题 5 分,共 50 分.在每题给出的四个选项中,只有一项为哪一项切合题目要求的1. 已知会合A= { x|x2- 2x> 0} ,B= { x|-5< x<5} ,则 ()A.A∩B=B.A∪B=R C.B? A2.已知i是虚数单位,则i= ()13i31B .31C.31D.A .i4i2i44423.已知m,n是两条不一样直线,,是两个不一样的平面,且m //表达正确的选项是()(A )若//,则 m // n( B)若m // n,则//( C)若n,则 m( D)若m,则4.以下相关命题的说法正确的选项是().A .“ x=- 1”是“ x2- 5x- 6=0”的必需不充足条件B.命题“若x= y,则 sin x= sin y”的逆否命题为真命题22C.命题“若 x = 1,则 x= 1”的否命题为:“若 x = 1,则 x≠ 1”2D.命题“ ? x∈R,使得: x + x+1<0 ”的否认是:“? x∈R,均D.A? B3 1i2 2,n,则以下开始输入 pn=1S=02+x+ 1<0 ”n=n+1有 x- n 5、履行如图的程序框图,假如输入p= 8,则输出的 S=()S=S+2是63B 、127127255n<p?A 、64C、D、?64128128否x 4 y3输出 S 6.设z2x y ,此中变量 x, y 知足条件3x5y25 ,若z的最结束x m小值为3,则m的值为()A 、 1B 、 2C、3D、 47. 若则以下不等式成立的是()8.一机器元件的三视图及尺寸如右图示(单位:dm),则该组合体的体积为3(A)80 dm(B)88 dm 3(C)96 dm} 33(D) 112 dm2x ,x2,9.已知函数 f x22函数 g x b f 2 x ,此中 b R ,若函数x, x2,y f x g x 恰有4个零点,则 b 的取值范围是(A)7,( B),7(C)0,7(D)7,2 444410.设函数 f( x)在 R 上存在导函数 f (x),对x∈ R,f( -x)+f( x)=x 2,且在( 0,+∞)上, f (x)>x.如有f(2-a)-f(a)≥2-2a,则实数a的取值范围为A.(-∞,1]B.[1,+∞)C.(-∞,2]D.[2,+ ∞)二、填空题:本大题共 5 小题,每题 5 分,共 25 分.把答案填在答题卡的相应地点.11.若非零向量 a , b 知足a b a b ,则a,b的夹角的大小为__________.12.已知正项等比数列 { a n} 的前 n 项和 S n,若q 1,a3 a520, a2a664,则S5.13.已知函数f ( x) 3x sin x 2cos x 的图像在点A(x0,f (x0))处的切线斜率为3,则tanx0的值是________.14.设a 0,b,若 a b 2,则41的最小值为.a b115.有以下 4 个命题:①若函数 f ( x) 定义域为则 g(x) f (x) f ( x) 是奇函数;R ,②若函数 f ( x) 是定义在 R 上的奇函数 , xR , f (x) f (2 x) 0,则 f (x) 图像对于 x =1对称 ;③已知 x 1 和 x 2 是函数定义域内的两个值(x 1<x 2),若 f ( x 1 ) f (x 2 ) ,则 f ( x) 在定义域内单一递减;④若 f ( x) 是定义在 R 上的奇函数 , f ( x 2) 也是奇函数 ,则 f ( x) 是以 4 为周期的周期函数.此中 ,正确命题是(把全部正确结论的序号都填上) .三、解答题:本大题共6 小题,共 75 分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定地区内.16.(本小题满分 12 分)已知向量 , m(sin x, 1), n (cos x, 3), f (x)(m n) m2(1) 当 x ∈ [0, ] 时,求函数 y = f(x)的值域;2(2) 锐角三角形 ABC 中, a ,b , c 分别为内角 A , B ,C 的对边,若 5a 4 2c,b 7 2,f ( B ) 3 2,求边 a, c.2 1017.(本小题满分 12 分)已 知 数 列 { a n } 的 前 n 项 和 为 S n , 且 S n 2a n2 ; 数 列 { b n } 满 足 b 1 1 ,bn 1b n 2 . n N * .(Ⅰ)求数列 { a n } , {b n } 的通项公式;(Ⅱ)记 c n a n b n , n N * .求数列 { c n } 的前 n 项和 T n .18(此题满分 12 分).如图,一简单几何体 ABCDE 的一个面 ABC 内接于圆 O, G 、H 分别是 AE 、BC 的中点, AB 是圆 O 的直径, 四边形 DCBE 为平行四边形,且 DC 平面 ABC.( I )证明 :GH//平面 ACD ;( I I )若 AC=BC=BE =2,求二面角 O-CE-B 的余弦值 .19(本小题满分 12 分)已知函数的图象如图所示·(I)求 f( x)在 R 上的单一递加区间;( II )设是函数y=f(x)的一个零点,求的值.20.(本小题满分13 分)如图,在四棱锥P—ABCD中,侧面 PAD⊥底面 ABCD,侧棱 PA=PD= 2 ,PA⊥ PD,底面 ABCD 为直角梯形,此中 BC∥ AD, AB⊥ AD, AB=BC=1, O为 AD中点。
2024-2025学年甘肃省兰州市高三上学期12月月考数学检测试题(含答案)

注意事项2024-2025学年甘肃省兰州市高三上学期12月月考数学检测试题:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.2.答卷前,考生务必将自己的姓名、班级填写在答题卡上.3.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号框涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号框.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.第Ⅰ卷(选择题)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知复数z 满足()43i 12i z -=+,则z =()B.25 C.152.已知集合{}12A x x =-≤≤,{}1B x a x a =-≤≤+,则“1a =”是“A B ⊆”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3.若正项等差数列{}n a 的前n 项和为n S ,20100S =,则1011a a ⋅的最大值为()A.9B.16C.25D.504.在ABC △中,6BC =,4AB =,π2CBA ∠=,设点D 为AC 的中点,点E 在BC 上,且0AE BD ⋅=,则BC AE ⋅=()A.16B.12C.8D.4-5.已知定义在R 上的函数()f x 在(),2-∞内为减函数,且()2f x +为偶函数,则()1f -,()4f ,112f ⎛⎫⎪⎝⎭的大小为()A .()()11142f f f ⎛⎫-<< ⎪⎝⎭B .()()11412f f f ⎛⎫<-< ⎪⎝⎭C .()()11412f f f ⎛⎫<<- ⎪⎝⎭D .()()11142f f f ⎛⎫-<< ⎪⎝⎭6.近年来,人们越来越注意到家用冰箱使用的氟化物的释放对大气臭氧层的破坏作用.科学研究表明,臭氧含量Q 与时间t (单位:年)的关系为0etaQ Q -=,其中0Q 是臭氧的初始含量,a 为常数.经过测算,如果不对氟化物的使用和释放进行控制,经过280年将有一半的臭氧消失.如果继续不对氟化物的使用和释放进行控制,再.经过n 年,臭氧含量只剩下初始含量的20%,n 约为()(参考数据:ln 20.7≈,ln10 2.3≈)A .280B.300C.360D.6407.已知角α,β满足()11cos ,cos cos 34βααβ=+=,则()cos 2αβ+=()A.13B.14C.16D.188.南宋数学家杨辉在《解析九章算法・商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关,如图是一个三角垛,最顶层有1个小球,第二层有3个,第三层有6个,第四层有10个, ,设第n 层有n a 个球,则12320251111a a a a ++++的值为()A .40442023B .20231012C .20222023D .20251013二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.)9.设a ,b ,c ,d 为实数,且0a b c d >>>>,则下列不等式正确的有()A.2c cd< B.a c b d-<- C.ac bd< D.c d a b>10.已知()sin()f x A x ωϕ=+(0A >,0ω>,π02ϕ<<)的部分图象如图所示,则()A.()f x 的最小正周期为πB.()f x 的图象可由2cos2y x =的图象向右平移π12个单位得到C.()f x 在5π5π,126⎛⎫- ⎪⎝⎭内有3个极值点D.()f x 在区间11π,2π6⎡⎤⎢⎥⎣⎦11.已知三次函数()32f x ax bx cx d =+++有三个不同的零点1x ,2x ,()3123x x x x <<,函数()()1g x f x =-也有三个零点1t ,2t ,()3123t t t t <<,则()A.23b ac >B.若1x ,2x ,3x 成等差数列,则23bx a=-C.1313x x t t +<+ D.222222123123x x x t t t ++=++第Ⅱ卷(非选择题)三、填空题(本大题共3小题,每小题5分,共15分.)12.已知()1e xf x x x+=-,则曲线()y f x =在点()()1,1f --处的切线方程为__________.13.已知数列{}n a 满足()123232n a a a na n n ++++=+ ,则66a =____________.14.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC △ABC △的周长6,2322a bcAB AC -⋅= ,则A 的最大值为____________.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(13分)已知数列{}n a 满足11a =,23a =,数列{}n b 为等比数列,且满足11()n n n n b a a b -=++.(1)求数列{}n a 的通项公式;(2)数列{}n b 的前n 项和为n S ,若________,记数列{}n c 满足,,,,n n n a n c b n ⎧⎩=⎨为奇数为偶数,求数列{}n c 的前2n 项和2n T .在①2322S S =-,②2b ,32a ,4b 成等差数列,③6126S =这三个条件中任选一个补充在第(2)问中,并对其求解.16.(15分)如图,在三棱锥P ABC -中,PA ⊥平面ABC ,AC BC ⊥.(1)求证:平面PAC ⊥平面PBC ;(2)若5AC =,12BC =,三棱锥P ABC -的体积为100,求二面角A PB C --的余弦值.17.(15分)如图,四边形OACB 中,a ,b ,c 为ABC △的内角A ,B ,C 的对边,且满足sin sin 2cos cos sin cos B C B CA A+--=.(1)证明:2b c a +=;(2)若b c =,设AOB θ∠=(0π)θ<<,22OA OB ==,求四边形OACB 面积的最大值.18.(17分)已知动点(,)P x y 与定点(1,0)F 的距离和P 到定直线:2l x =的距离的比是常数2,记点P 的轨迹为曲线C .(1)求曲线C 的标准方程;(2)设点(1,0)F '-,若曲线C 上两点M ,N 均在x 轴上方,且//FM F N ',FM F N '+=求直线FM 的斜率.19.(17分)若将对于任意x ,y ∈R 总有()()()()2f x y f x y f x f y ++-=的函数称为“类余弦型”函数.(1)已知()f x 为“类余弦型”函数,且()0f x >,()1728f =,求()1f 的值;(2)在(1)的条件下,若数列:()()()*21n a f n f n n =+-∈N ,求10012222log log log 333a a a++⋯+的值;(3)若()g x 为“类余弦型”函数,且()00g >,对任意非零实数t ,总有()1g t >.设有理数1x ,2x 满足21x x >,判断()2g x 与()1g x 的大小关系,并给出证明.一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题高三数学答案目要求的.)二、多选题(本大题共3小题,每小题6分,共18分.全部选对的得6分,部分选对的得部分分,第9题答对一个选项得2分;第10、11题答对一个选项得3分,有选错的得0分.)题号91011答案ADABDABD三、填空题(本大题共3小题,每小题5分,共15分.)12.3+y 30x +=;13.13366;14.π3四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(13分)【解析】(1)因为11()n n n n b a a b ++-=,11a =,23a =,令1n =得122b b =,又数列{}n b 为等比数列,所以公比为2,即12n n b b +=,则12n n a a +-=,所以数列{}n a 是以1为首项2为公差的等差数列,所以21n a n =-……………6分(2)由(1)知数列{}n b 为公比为2的等比数列若选①,由2322S S =-得()1111122242b b b b b +=++-,所以12b =,则2nn b =若选②,由2b ,32a ,4b 成等差数列得3244a b b =+,即112820b b +=,所以12b =,则2nn b =若选③,由6126S =得61(12)12612b -=-,所以12b =,则2nn b =所以21,,2,,n nn n c n -⎧=⎨⎩为奇数为偶数,数列{}n c 的奇数项是以1为首项4为公差的等差数列,偶数项是以4为首项4为公比的等比数列,所以()()32121242n n n a a a b b T b -++⋅⋅⋅++++⋅⋅⋅+==2(1)4(14)4(41)4=22143n n n n n n n ---+⨯+-+-………………13分题号12345678答案DACABCCD16.(15分)【解析】(1)证明:由题意得PA ⊥平面ABC ,因为BC ⊂平面ABC ,所以PA BC ⊥,又因为AC BC ⊥,PA ,AC ⊂平面PAC ,所以BC ⊥平面PAC ,又因为BC ⊂平面PCB ,所以平面PAC ⊥平面PBC .……………6分(2)因为5AC =,12BC =,AC BC ⊥,所以1125302ABC S =⨯⨯=△,又因为三棱锥P ABC -的体积为100,即,得1100303PA =⨯⨯10PA =,由题意可得以A 为原点,分别以平行于BC ,及AC ,AP 所在直线为x,y,z 轴建立空间直角坐标系,如图,则125100100n PB x y z n AP z ⎧⋅=+-=⎪⎨⋅==⎪⎩,令5x =-,得12y =,0z =,则()5,12,0n =- ,设平面PBC 的一个法向量为(),,m a b c =,则125100120m PB a b c m CB a ⎧⋅=+-=⎪⎨⋅==⎪⎩,令2b =,得0a =,1c =,则()0,2,1m = ,设二面角A PB C --为θ,则·cos cos ,65m n n m m n θ====.所以锐二面角A PB C --的余弦值为65.……………15分17.(15分)【解析】证明sin sin 2cos cos sin cos B C B CA A+--=,∴sin cos sin cos 2sin cos sin cos sin B A C A A B A C A +=--,sin cos cos sin sin cos cos sin 2sin B A B A C A C A A ∴+++=,sin()sin()2sin A B A C A ∴+++=,sin sin 2sin C B A ∴+=,2b c a ∴+=.…………………7分(2)因为2b c a +=,b c =,所以a b c ==,所以ABC △为等边三角形,所以21sin 24OACBOAB ABC SS S OA OB AB θ=+=⋅+△△()22sin 2cos 4OA OB OA OB θθ=++-⋅sin 4θθ=-+π2sin 3θ⎛⎫=- ⎪⎝⎭ (),π0θ∈,∴ππ2π,333θ⎛⎫-∈- ⎪⎝⎭,当且仅当ππ32θ-=,即π56θ=时取最大值,OACB S的最大值为2.…………………15分18.(17分)【解析】(12=,整理化简得,2212x y +=,所以曲线C 的标准方程为2212x y +=.……………6分(2)由题意,直线FM ,F N '的斜率都存在,设FM F N k k k '==,则直线F N '的方程为()1y k x =+,分别延长NF ',MF 交曲线C 于点N ',M ',设()11,N x y ,()22,N x y ',联立()22112y k x x y =+⎧⎪⎨+=⎪⎩,即()2222124220k x k x k +++-=,则2122412k x x k +=-+,21222212k x x k -=+,根据对称性,可得FM F N ='',则FM F N NN +=='')22112k k +==+,即)22112k k +=+k =,所以直线FM 的斜率为.…………………17分19.(17分)【解析】(1)令0x y ==则,()()()20020f f f +=,又()0f x >,故()01f =.令1x =,1y =,则()()()()20211f f f f +=,则()()22511016f f =>故()514f =……………5分(2)令x n =,1y =,n +∈N ,则()()()()()511212f n f n f n f f n ++-==,()()()()21221f n f n f n f n +-=--⎡⎤⎣⎦,即12n n a a -=又13a =,所以数列n a 为以2为公比,3为首项的等比数列,即13.2n n a -=,则10012222099log log log 0129910049503332a a a ++++=++++=⨯= ……………11分(3)由题意得:函数()g x 定义域为R ,定义域关于原点对称,令0x y ==,有()()()20020g g g +=又()00g >,故()01g =.令0x =,y 为任意实数则()()()()20g y g y g g y +-=即()()g y g y =-,故()g x 是偶函数因为()()()()2g x y g x y g x g y ++-=又因为当0x ≠时,()1g x >所以当0x ≠时,有()()()22g x g y g y >所以()()()2g x y g x y g y ++->2x ,1x 为有理数,不妨设111p x q =,222p x q =令N 为2x ,1x ,分母的最小公倍数且1a x N =,2bx N=,a ,b 均为自然数,且a b <,设n n C g N ⎛⎫= ⎪⎝⎭,()101g g N ⎛⎫=< ⎪⎝⎭,则01c c <令n x N =,1y N =,则112n n n g g g N N N+-⎛⎫⎛⎫⎛⎫+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即112n n n C C C +-+>,()1112n n n n n n n C C C C C C C +-->-=+->,故数列{}n C 单调递增则()()21g x g x >,又()g x 是偶函数,所以有()()21g x g x >…………………17分。
甘肃省兰州第一中学2024-2025学年高三上学期12月月考数学试题(含答案)

兰州一中高三年级11月月考试题高三数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.2.答卷前,考生务必将自己的姓名、班级填写在答题卡上.3.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号框涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号框.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.第Ⅰ卷(选择题)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知复数z 满足()43i 12i z -=+,则z =()B.25 C.152.已知集合{}12A x x =-≤≤,{}1B x a x a =-≤≤+,则“1a =”是“A B ⊆”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3.若正项等差数列{}n a 的前n 项和为n S ,20100S =,则1011a a ⋅的最大值为()A.9B.16C.25D.504.在ABC △中,6BC =,4AB =,π2CBA ∠=,设点D 为AC 的中点,点E 在BC 上,且0AE BD ⋅=,则BC AE ⋅=()A.16B.12C.8D.4-5.已知定义在R 上的函数()f x 在(),2-∞内为减函数,且()2f x +为偶函数,则()1f -,()4f ,112f ⎛⎫⎪⎝⎭的大小为()A .()()11142f f f ⎛⎫-<< ⎪⎝⎭B .()()11412f f f ⎛⎫<-< ⎪⎝⎭C .()()11412f f f ⎛⎫<<- ⎪⎝⎭D .()()11142f f f ⎛⎫-<< ⎪⎝⎭6.近年来,人们越来越注意到家用冰箱使用的氟化物的释放对大气臭氧层的破坏作用.科学研究表明,臭氧含量Q 与时间t (单位:年)的关系为0etaQ Q -=,其中0Q 是臭氧的初始含量,a 为常数.经过测算,如果不对氟化物的使用和释放进行控制,经过280年将有一半的臭氧消失.如果继续不对氟化物的使用和释放进行控制,再.经过n 年,臭氧含量只剩下初始含量的20%,n 约为()(参考数据:ln 20.7≈,ln10 2.3≈)A .280B.300C.360D.6407.已知角α,β满足()11cos ,cos cos 34βααβ=+=,则()cos 2αβ+=()A.13B.14C.16D.188.南宋数学家杨辉在《解析九章算法・商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关,如图是一个三角垛,最顶层有1个小球,第二层有3个,第三层有6个,第四层有10个, ,设第n 层有n a 个球,则12320251111a a a a ++++的值为()A .40442023B .20231012C .20222023D .20251013二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.)9.设a ,b ,c ,d 为实数,且0a b c d >>>>,则下列不等式正确的有()A.2c cd< B.a c b d-<- C.ac bd< D.c d a b>10.已知()sin()f x A x ωϕ=+(0A >,0ω>,π02ϕ<<)的部分图象如图所示,则()A.()f x 的最小正周期为πB.()f x 的图象可由2cos2y x =的图象向右平移π12个单位得到C.()f x 在5π5π,126⎛⎫- ⎪⎝⎭内有3个极值点D.()f x 在区间11π,2π6⎡⎤⎢⎥⎣⎦11.已知三次函数()32f x ax bx cx d =+++有三个不同的零点1x ,2x ,()3123x x x x <<,函数()()1g x f x =-也有三个零点1t ,2t ,()3123t t t t <<,则()A.23b ac >B.若1x ,2x ,3x 成等差数列,则23bx a=-C.1313x x t t +<+ D.222222123123x x x t t t ++=++第Ⅱ卷(非选择题)三、填空题(本大题共3小题,每小题5分,共15分.)12.已知()1e xf x x x+=-,则曲线()y f x =在点()()1,1f --处的切线方程为__________.13.已知数列{}n a 满足()123232n a a a na n n ++++=+ ,则66a =____________.14.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC △ABC △的周长6,2322a bcAB AC -⋅= ,则A 的最大值为____________.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(13分)已知数列{}n a 满足11a =,23a =,数列{}n b 为等比数列,且满足11()n n n n b a a b -=++.(1)求数列{}n a 的通项公式;(2)数列{}n b 的前n 项和为n S ,若________,记数列{}n c 满足,,,,n n n a n c b n ⎧⎩=⎨为奇数为偶数,求数列{}n c 的前2n 项和2n T .在①2322S S =-,②2b ,32a ,4b 成等差数列,③6126S =这三个条件中任选一个补充在第(2)问中,并对其求解.16.(15分)如图,在三棱锥P ABC -中,PA ⊥平面ABC ,AC BC ⊥.(1)求证:平面PAC ⊥平面PBC ;(2)若5AC =,12BC =,三棱锥P ABC -的体积为100,求二面角A PB C --的余弦值.17.(15分)如图,四边形OACB 中,a ,b ,c 为ABC △的内角A ,B ,C 的对边,且满足sin sin 2cos cos sin cos B C B CA A+--=.(1)证明:2b c a +=;(2)若b c =,设AOB θ∠=(0π)θ<<,22OA OB ==,求四边形OACB 面积的最大值.18.(17分)已知动点(,)P x y 与定点(1,0)F 的距离和P 到定直线:2l x =的距离的比是常数2,记点P 的轨迹为曲线C .(1)求曲线C 的标准方程;(2)设点(1,0)F '-,若曲线C 上两点M ,N 均在x 轴上方,且//FM F N ',FM F N '+=求直线FM 的斜率.19.(17分)若将对于任意x ,y ∈R 总有()()()()2f x y f x y f x f y ++-=的函数称为“类余弦型”函数.(1)已知()f x 为“类余弦型”函数,且()0f x >,()1728f =,求()1f 的值;(2)在(1)的条件下,若数列:()()()*21n a f n f n n =+-∈N ,求10012222log log log 333a a a++⋯+的值;(3)若()g x 为“类余弦型”函数,且()00g >,对任意非零实数t ,总有()1g t >.设有理数1x ,2x 满足21x x >,判断()2g x 与()1g x 的大小关系,并给出证明.兰州一中高三年级11月月考试题高三数学答案一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)二、多选题(本大题共3小题,每小题6分,共18分.全部选对的得6分,部分选对的得部分分,第9题答对一个选项得2分;第10、11题答对一个选项得3分,有选错的得0分.)题号91011答案ADABDABD三、填空题(本大题共3小题,每小题5分,共15分.)12.3+y 30x +=;13.13366;14.π3四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(13分)【解析】(1)因为11()n n n n b a a b ++-=,11a =,23a =,令1n =得122b b =,又数列{}n b 为等比数列,所以公比为2,即12n n b b +=,则12n n a a +-=,所以数列{}n a 是以1为首项2为公差的等差数列,所以21n a n =-……………6分(2)由(1)知数列{}n b 为公比为2的等比数列若选①,由2322S S =-得()1111122242b b b b b +=++-,所以12b =,则2nn b =若选②,由2b ,32a ,4b 成等差数列得3244a b b =+,即112820b b +=,所以12b =,则2nn b =若选③,由6126S =得61(12)12612b -=-,所以12b =,则2nn b =所以21,,2,,n nn n c n -⎧=⎨⎩为奇数为偶数,数列{}n c 的奇数项是以1为首项4为公差的等差数列,偶数项是以4为首项4为公比的等比数列,所以()()32121242n n n a a a b b T b -++⋅⋅⋅++++⋅⋅⋅+==2(1)4(14)4(41)4=22143n n n n n n n ---+⨯+-+-………………13分题号12345678答案DACABCCD16.(15分)【解析】(1)证明:由题意得PA ⊥平面ABC ,因为BC ⊂平面ABC ,所以PA BC ⊥,又因为AC BC ⊥,PA ,AC ⊂平面PAC ,所以BC ⊥平面PAC ,又因为BC ⊂平面PCB ,所以平面PAC ⊥平面PBC .……………6分(2)因为5AC =,12BC =,AC BC ⊥,所以1125302ABC S =⨯⨯=△,又因为三棱锥P ABC -的体积为100,即,得1100303PA =⨯⨯10PA =,由题意可得以A 为原点,分别以平行于BC ,及AC ,AP 所在直线为x,y,z 轴建立空间直角坐标系,如图,则125100100n PB x y z n AP z ⎧⋅=+-=⎪⎨⋅==⎪⎩,令5x =-,得12y =,0z =,则()5,12,0n =- ,设平面PBC 的一个法向量为(),,m a b c =,则125100120m PB a b c m CB a ⎧⋅=+-=⎪⎨⋅==⎪⎩,令2b =,得0a =,1c =,则()0,2,1m = ,设二面角A PB C --为θ,则·cos cos ,65m n n m m n θ====.所以锐二面角A PB C --的余弦值为65.……………15分17.(15分)【解析】证明sin sin 2cos cos sin cos B C B CA A+--=,∴sin cos sin cos 2sin cos sin cos sin B A C A A B A C A +=--,sin cos cos sin sin cos cos sin 2sin B A B A C A C A A ∴+++=,sin()sin()2sin A B A C A ∴+++=,sin sin 2sin C B A ∴+=,2b c a ∴+=.…………………7分(2)因为2b c a +=,b c =,所以a b c ==,所以ABC △为等边三角形,所以21sin 24OACBOAB ABC SS S OA OB AB θ=+=⋅+△△()22sin 2cos 4OA OB OA OB θθ=++-⋅sin 4θθ=-+π2sin 3θ⎛⎫=- ⎪⎝⎭ (),π0θ∈,∴ππ2π,333θ⎛⎫-∈- ⎪⎝⎭,当且仅当ππ32θ-=,即π56θ=时取最大值,OACB S的最大值为2.…………………15分18.(17分)【解析】(12=,整理化简得,2212x y +=,所以曲线C 的标准方程为2212x y +=.……………6分(2)由题意,直线FM ,F N '的斜率都存在,设FM F N k k k '==,则直线F N '的方程为()1y k x =+,分别延长NF ',MF 交曲线C 于点N ',M ',设()11,N x y ,()22,N x y ',联立()22112y k x x y =+⎧⎪⎨+=⎪⎩,即()2222124220k x k x k +++-=,则2122412k x x k +=-+,21222212k x x k -=+,根据对称性,可得FM F N ='',则FM F N NN +=='')22112k k +==+,即)22112k k +=+k =,所以直线FM 的斜率为.…………………17分19.(17分)【解析】(1)令0x y ==则,()()()20020f f f +=,又()0f x >,故()01f =.令1x =,1y =,则()()()()20211f f f f +=,则()()22511016f f =>故()514f =……………5分(2)令x n =,1y =,n +∈N ,则()()()()()511212f n f n f n f f n ++-==,()()()()21221f n f n f n f n +-=--⎡⎤⎣⎦,即12n n a a -=又13a =,所以数列n a 为以2为公比,3为首项的等比数列,即13.2n n a -=,则10012222099log log log 0129910049503332a a a ++++=++++=⨯= ……………11分(3)由题意得:函数()g x 定义域为R ,定义域关于原点对称,令0x y ==,有()()()20020g g g +=又()00g >,故()01g =.令0x =,y 为任意实数则()()()()20g y g y g g y +-=即()()g y g y =-,故()g x 是偶函数因为()()()()2g x y g x y g x g y ++-=又因为当0x ≠时,()1g x >所以当0x ≠时,有()()()22g x g y g y >所以()()()2g x y g x y g y ++->2x ,1x 为有理数,不妨设111p x q =,222p x q =令N 为2x ,1x ,分母的最小公倍数且1a x N =,2bx N=,a ,b 均为自然数,且a b <,设n n C g N ⎛⎫= ⎪⎝⎭,()101g g N ⎛⎫=< ⎪⎝⎭,则01c c <令n x N =,1y N =,则112n n n g g g N N N+-⎛⎫⎛⎫⎛⎫+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即112n n n C C C +-+>,()1112n n n n n n n C C C C C C C +-->-=+->,故数列{}n C 单调递增则()()21g x g x >,又()g x 是偶函数,所以有()()21g x g x >…………………17分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年高考(232)甘肃省兰州一中2016届高三12月月考 兰州一中2015-2016-1学期高三年级12月月考试题 语文 第卷 阅读题 一、现代文阅读(9分,每小题3分) 阅读下面的文字,完成1-3题。 司马迁与班固 司马迁作《史记》,完成于汉武帝末年。班固作《汉书》,书未成而因与外戚窦宪的关系,死于狱中,事在汉和帝永元四年(公元92年)。一属西汉,一属东汉,相去公元元年各约90年。今日看来,这两部书好像联袂而出。其实它们间隔了大约180年,等于我们现在距离清嘉庆朝的时间。 《史记》为私人著作,《汉书》则经皇帝看过,有国史的色彩。司马迁自称成一家之言和藏之名山,已和班固作书的宗旨不同。况且《史记》是通史,《汉书》是断代史。两位史家的个性癖好不同,这也使他们在取材行文之间,有相当的出入。在公元前90年和公元90年,中国的史家和思想家所处的社会环境已有大幅度的变化。其中一个关键在于,汉武帝用董仲舒之建议,罢斥百家,独尊儒术。我们在这里要特别指出的是,董仲舒之尊儒,并不是以尊儒为目的,而是为了树立一种统一帝国的正统思想,他坦白地承认提倡学术,旨在支持当时政权。武帝之置五经博士、立学校之官、策贤良,都根据此宗旨着眼,从此中国庞大的文官集团,有了他们施政的正统逻辑。司马迁和董仲舒同时代,他读书不受这种政策的影响。而到了班固生活的年代,正规的儒家思想已有一百多年的基础。 司马迁和班固一样,自称是周公和孔子的信徒。可是今日我们一打开《史记》,随意翻阅三五处,即可以体会到带着一种浪漫主义和个人主义的作风,爽快淋漓,不拘形迹,无腐儒气息。他自称少负不羁之才,长无乡曲之誉,应当是一种真实的写照。他所崇奉的士为知己用,女为悦己容也可以说是源于儒家道德,可是这立场就已经和经过正统限制的所谓儒家不同了。 《史记》里写荆轲和高渐离饮酒击筑,又歌又泣,旁若无人,已近于董仲舒所说的邪辟。并且项羽是汉高祖刘邦的死对头,而《史记》里的《项羽本纪》排列在《高祖本纪》之前(若在后代必称项酋伪楚,而本纪只能降格为载记)。文中又把项羽写成一个虽暴躁却又浑憨可爱的角色,其英雄末路,令人怜惜。与之相较,刘邦反像一个伪君子。 《史记》除了《刺客列传》之外,还有《滑稽列传》《日者列传》和《龟策列传》,可谓涉及九流三教,有呈现整个社会之剖面的样子。班固书里虽有《东方朔传》,却不再缕列非正派或下流的文化资料。 也因其如此,司马迁就受到班固的指责。《汉书》里就有《司马迁传》,内中批评他又其是非颇缪于圣人,论大道则先黄老而后六经,序游侠则退处士而进奸雄,述货殖则崇势利而羞贱贫,此其所蔽也。 这些地方还不足以表现班固的正统思想,最使我们看出他的作品在历史上是属于罢斥百家,独尊儒术之后的产物的,乃是《汉书》卷二十《古今人表》。这表里列有1931位古代名人,包括传奇中的人物如女娲氏、有巢氏,《论语》中有名的孔门弟子,《春秋》中的国君等,至秦亡为止。由显善昭恶的原则按上上至下下区分为三等九则。内中得上上圣人者十四人,包括三皇五帝,以周公、孔子殿后。仲尼之外即再无圣人,孟子也只与颜渊、管仲同属上中仁人。老子与商鞅、申子、墨翟、韩非都属中上,与孙膑、白起一流。刺客荆轲则为中中,和孟尝 君、吕不韦同品。而下下愚人里既有蚩尤、共工、三苗,也有倾国倾城的褒姒和妲己。秦始皇虽焚书坑儒,班固只贬之为中下,因为他下面还有二世胡亥列入下中,宦官赵高列入下下。 因此,我们也可以推想出世俗观念中儒家的拘泥,并不一定是孔子和他门徒的真性格。那些呆 板多方面的样子,还是后人所造,其目的在维持文官集团的紧凑。总算还是中国读书人的运气好,得有太史公司马迁在兰台令班固之前写作,否则没有《史记》,径由《汉书》开二十三史之端,中国史学的传统,必更趋向文以载道的方针,更缺乏百家殊方的真实性和生动活泼了。 (选自黄仁宇《赫逊河畔谈中国历史》,有删改) 1.关于《史记》和《汉书》的表述,下列理解符合原文意思的一项是(3分) A.《史记》完成于汉武帝末年,《汉书》完成于汉和帝永元四年,一属西汉,一属东汉,成书年代相差约180年。 B.《史记》为私人著作,而《汉书》则经皇帝看过,带有国史的色彩,因此《汉书》在编修上要比《史记》更为严谨和准确。 C.司马迁的成一家之言藏之名山的宗旨和班固作《汉书》的宗旨有很大不同,这就决定了《史记》是通史,《汉书》是断代史。 D.汉武帝用董仲舒之建议,罢斥百家,独尊儒术,司马迁的思想并未受此影响,而班固则不同,这 也是《史记》和《汉书》风格差异的重要原因。 2.下列理解和分析,不符合原文意思的一项是(3分) A.董仲舒之尊儒,并不是以尊儒为目的,其真正目的在于树立一种统一帝国的正统思想,支持当时政权。班固受其影响,并呈现于《汉书》的创作中。 B.司马迁和班固都认同儒家思想,但是个人气质的巨大差异使得《史记》和《汉书》文风差异明显,司马迁带着一种浪漫主义和个人主义的作风。 C.《史记》和《汉书》在对待项羽的态度上差异明显,《史记》里的《项羽本纪》排列在《高祖本纪》之前,这在《汉书》中是不可能出现的。 D.《史记》里的人物涉及三教九流各色人等,如日者(占卜的人),而《汉书》秉持官方正统思想,较少记录不符合正统观念的人物。 3.根据原文内容,下列理解和分析不正确的一项是(3分) A.班固在《汉书·司马迁传》中表达了对司马迁的看法是非颇缪于圣人,他认为《史记》的叙史观念有悖于圣人之道。 B.《汉书》里的卷二十《古今人表》按照官方正统观念把历史人物分为三等九则,内中得上上圣人者十四人,仲尼之后即再无圣人,表现了极强的独尊儒术的态度。 C.我们现在所看到的孔子及其门徒的形象,多半出于汉朝独尊儒术以后的历史典籍,这些形象并不是他们的真实形象。 D.《史记》中把项羽刻画成一个虽暴躁却又浑憨可爱的末路英雄的形象,与之相比,刘邦反像一个伪君子,这样的描述在《汉书》中是不可能出现的。 二、古代诗文阅读(39分) (一)文言文阅读(17分) 阅读下面的文言文,完成4-7题。 安守忠,字信臣 ,并州晋阳人。晋天福八年,以守忠为牙内指挥使,领绣州刺史。周显德四年春,改鞍辔库使。会淮南初下命守忠驰往宣谕时藩臣骄蹇遇朝使多简傲守忠抗以正礼无所辱命。未几,改卫州刺史。 宋初,入为左卫将军。蜀平,太祖知远俗苦苛虐,南郑为走集之地,故特命守忠知兴元府以抚绥之。四年,改汉州刺史。时寇难甫平,使车旁午,公帑不足,守忠出私钱以给用。每遣使,太祖必戒之曰:安守忠在蜀,能律己以正,汝行见之,当效其为人也。开宝五年,知辽州。民有阴召并寇谋内应者,事泄,守忠悉斩以徇。九年,命将征太原,守忠受诏与孙晏宣由辽州入,既而与路罗寨监押马继恩遇,乃相与会兵入贼境,燔寨四十余,获牛羊数千。 雍熙二年,改知易州,徙夏州。每西戎犯边,战无不捷。淳化二年,徙知雄州。方与僚佐宴饮,有军校谋变,擐甲及阍,阍者仓卒入白。守忠言笑自若,徐顾坐客曰:此辈酒狂尔,擒之可也。人服其量焉。明年,加耀州观察使,兼判雄州。未几,召还,条陈边事,敷奏称旨,赐钱五百万。五年,又知沧州。至道初,移雄州。三年,复知沧州,拜感德军节度观察留后。徙宋州,兼制置营田使。威德兼著,吏民不忍其去。咸平三年,入觐,遣还未行,暴卒,年六十九,赠太尉。 守忠谨悫淡薄,为治简静。太祖居藩日,素相厚善,及受禅后,每优任之,守忠处之益谦。从征太原,多与谋略,人罕知之者。所至藩郡,乐施予,丰宴犒,且喜与士大夫游从,故时论多与之。 (选自《宋史·安守忠传》,有删改) [注]并:指并州,现在的山西太原一带。 4.对文中画波浪线部分的断句,正确的一项是(3分) A.会淮南初下/命守忠驰往宣谕时/藩臣骄蹇/遇朝使多简傲/守忠抗以正礼/无所辱命 B.会淮南初下/命守忠驰往宣谕/时藩臣骄蹇/遇朝使多/简傲守忠抗以正礼/无所辱命 C.会淮南初下/命守忠驰往宣谕时/藩臣骄蹇/遇朝使多/简傲守忠抗以正礼/无所辱命 D.会淮南初下/命守忠驰往宣谕/时藩臣骄蹇/遇朝使多简傲/守忠抗以正礼/无所辱命 5.下列对文中加点词语的相关内容的解说,不正确的一项是(3分) A.淳化:是宋太宗的年号。历代帝王凡遇到天降祥瑞或内讧外忧,遇到大事、要事,往往要更改一下年号。 B.兼:兼任,同时监管之意。同时表示兼职、代理的词语,还有假领摄署权陟行等等。 C.赠:是古代朝廷为表彰已死大臣的功绩,追授 给死者的一种官职或称号,也称追赠;其余还有赠官、赠典等。 D.受禅:上古时期的禅让制度,最早记载于《尚书》之中。后来中国的帝王更替,也有以受禅之名,行夺权之实的。 6.下列对原文有关内容的概括和分析,不正确的一项是(3分) A.安守忠在蜀地任职时,为官清廉。由于战争刚刚平息 ,满目疮痍,民生凋敝,库藏的钱财不足,他就用自己的钱来贴补。 B.安守忠军事才能卓越,战功显赫。征伐太原,燔寨四十余,获牛羊数千,但因不是主帅,所以很少有人知道他参与了谋略。 C.安守忠改任雄州知州,处惊不变。面对军校的阴谋叛变,不仅有胆,而且有识,从容面对,在谈笑之间消除了祸端。 D.安守忠在太祖登基后,深受重用。他跟随太祖南征北战,因冷静诚实地处理政务,太祖不仅厚待,而且优先任用。 7.把文中画横线的句子翻译成现代汉语。(8分) 民有阴召并寇谋内应者,事泄,守忠悉斩以徇。(4分) 所至藩郡,乐施予,丰宴犒,且喜与士大夫游从,故时论多与之。(4分) (二)古代诗歌阅读(12分)
