第章习题解答
络筒-习题解答(最完整)

文档第一章络筒习题解答(最完好)1.络筒工序的目的及工艺要求是什么?目的:① 改变纱线的卷装,增添纱线卷装的容纱量,提升后继工序的生产率。
②检查纱线直径,除去纱线上的疵点和杂质,改良纱线质量。
工艺要求:① 卷绕张力适合,颠簸小,不损害纱线原有的物理机械性能。
② 筒子卷绕容量大,成形优秀,利于储藏和运输。
③ 筒子的形状和构造应保证后道工序的顺利退绕。
④ 染色用筒子构造均匀。
⑤ 纱线接头小而牢。
2.络筒机的主要构成部分及各部分的作用是什么?①主要构成部分:气圈破碎器、张力装置、清纱装置、捻接器、槽筒、传动系统。
② 各部分作用:气圈破碎器:也叫气圈控制器,改变气圈形状,改良纱线张力颠簸。
预清纱器:除去纱线上的杂质和较大的纱疵。
张力装置:给纱线施加张力。
捻接器:形成无结接头。
电子清纱器:对纱线的疵点(粗节、细节、双纱等)进行检测,并剪断。
张力传感器:连续感觉纱线张力,经反应控制,对张力进行自动调理。
槽筒:使筒子做展转运动,将纱线卷入,带动纱线做导纱运动,使筒子成形。
传动系统:用来传动槽筒等运动零件,达成络筒。
3.筒子卷绕的方式有哪几种?各样卷绕方式的特色是什么?筒子卷绕的方式有摩擦传动卷绕和锭轴传动卷绕。
摩擦传动卷绕的特色:短纤维纱线络筒采纳。
槽筒由电动机传动,安装在筒锭握臂上的筒子紧压在槽筒上,依赖槽筒的摩擦作用绕自己的轴线展转,卷绕纱线;槽筒表面的沟槽作为导纱器指引纱线作来去的导纱运动,使纱线均匀地络卷到筒子表面。
锭轴传动卷绕的特色:长丝纱线络筒采纳。
筒子的展转靠锭轴带动,导纱器的来去导纱运动能够与锭轴联动,也可独自传动。
文档4. 筒子成形由哪两种基本运动构成?达成两种运动的方式是什么?筒子成形由导纱运动和展转运动构成。
摩擦传动卷绕机构中, 安装在筒锭握臂上的筒子紧压在槽筒上, 依赖槽筒的摩擦作用绕自己的轴线展转, 卷绕纱线;槽筒表面的沟槽作为导纱器指引纱线作来去的导纱运动, 使纱线均匀地络卷到筒子表面。
编译原理第3章 习题解答

第3章习题解答1.构造正规式1(0|1)*101相应的DFA.[答案]先构造NFA确定化0 1X AA A ABAB AC ABAC A ABYABY AC AB重新命名,令AB为B、AC为C、ABY为D0 1X AA A BB C BC A DD C B转化成DFA:============================================================== 2.将下图确定化:[答案]0 1S VQ QUVQ VZ QUQU V QUZVZ Z ZV ZQUZ VZ QUZZ Z Z重新命名,令VQ为A、QU为B、VZ为C、V为D、QUZ为E、Z为F。
0 1S A BA C BB D EC F FD FE C EF F F转化为DFA:================================================================ 3.把下图最小化:[答案](1)初始分划得Π0:终态组{0},非终态组{1,2,3,4,5}对非终态组进行审查:{1,2,3,4,5}a {0,1,3,5}而{0,1,3,5}既不属于{0},也不属于{1,2,3,4,5} ∵{4} a {0},所以得新分划 (2)Π1:{0},{4},{1,2,3,5} 对{1,2,3,5}进行审查: ∵{1,5} b {4}{2,3} b {1,2,3,5},故得新分划 (3)Π2:{0},{4},{1, 5},{2,3} {1, 5} a {1, 5}{2,3} a {1,3},故状态2和状态3不等价,得新分划 (3)Π3:{0},{2},{3},{4},{1, 5} 这是最后分划了 (4)最小DFA :======================================= 4.构造一个DFA ,它接收Σ={0,1}上所有满足如下条件的字符串:每个1都有0直接跟在右边。
第一章习题答案

第⼀章习题答案第⼀章思考题答案1.基于总线结构的计算机系统通常由哪5个部分构成?并简述各部分的主要作⽤。
解答:1.中央处理器CPU(central processor unit)或称微处理器(microprocessor unit)中央处理器具有算术运算、逻辑运算和控制操作的功能,是计算机的核⼼。
2.总线总线是把计算机各个部分有机地连接起来的导线,是各个部分之间进⾏信息交换的公共通道。
3.存储器(memory)存储器的功能是存储程序、数据和各种信号、命令等信息,并在需要时提供这些信息。
4.输⼊输出(I/O)接⼝外部设备与CPU之间通过输⼊输出接⼝连接。
5.输⼊输出(I/O)设备输⼊设备是变换输⼊信息形式的部件。
它将⼈们熟悉的信息形式变换成计算机能接收并识别的信息形式。
输出设备是变换计算机的输出信息形式的部件。
它将计算机处理结果的⼆进制信息转换成⼈们或其他设备能接收和识别的形式,如字符、⽂字、图形等。
2.试举例说明计算机进⾏加法运算的⼯作过程。
解答:⽰例如下:inta,b,c;c=a+b;⼯作过程简述:a,b,c都为内存中的数据,CPU⾸先需要从内存中分别将a,b的值读⼊寄存器中,然后再执⾏加法运算指令,加法运算的结果暂存在寄存器中,因此还需要执⾏数据存储指令,将运算结果保存到内存中,因此像上例中的C语⾔语句,实际上需要经过两条数据读取指令,⼀条加法运算指令,⼀条数据存储指令才能完成。
3.“冯·诺依曼型结构”计算机与哈佛结构计算机的差别是什么?各有什么优缺点?解答:冯·诺依曼结构计算机具有以下⼏个特点:①有⼀个存储器;②有⼀个控制器;③有⼀个运算器,⽤于完成算术运算和逻辑运算;④有输⼊和输出设备,⽤于进⾏⼈机通信;⑤处理器使⽤同⼀个存储器存储指令和数据,经由同⼀个总线传输。
哈佛结构计算机:①使⽤两个独⽴的存储器模块,分别存储指令和数据,每个存储模块都不允许指令和数据并存;②具有⼀条独⽴的地址总线和⼀条独⽴的数据总线,利⽤公⽤地址总线访问两个存储模块(程序存储模块和数据存储模块),公⽤数据总线则被⽤来完成程序存储模块或数据存储模块与CPU 之间的数据传输;③两条总线由程序存储器和数据存储器分时共⽤。
电工学课后第1-6章习题答案
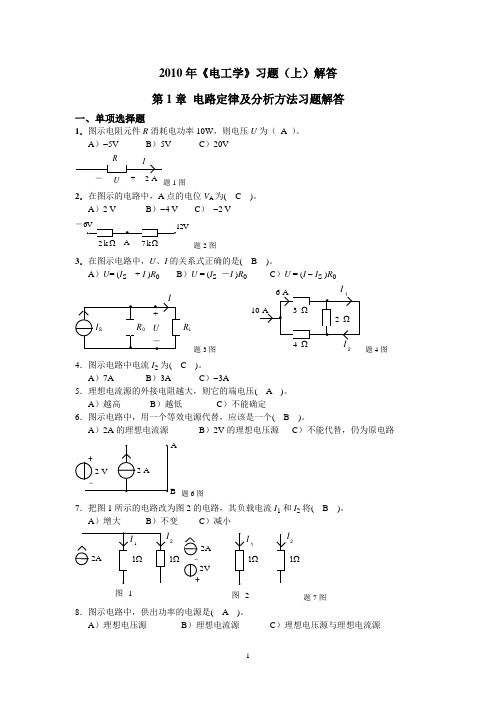
2010年《电工学》习题(上)解答 第1章 电路定律及分析方法习题解答一、单项选择题1.图示电阻元件R 消耗电功率10W ,则电压U 为( A )。
A )-5V B )5V C )20VUR 题1图2.在图示的电路中,A 点的电位V A 为( C )。
A )2 V B )-4 V C ) -2 V- 2 k 7 k ΩΩ题2图3.在图示电路中,U 、I 的关系式正确的是( B )。
A )U = (I S + I )R 0 B )U = (I S -I )R 0 C )U = (I - I S )R 0R L题3图I 2题4图4.图示电路中电流I 2为( C )。
A )7AB )3AC )-3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A )越高 B )越低 C )不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A )2A 的理想电流源 B )2V 的理想电压源 C )不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( B )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源 B )理想电流源C )理想电压源与理想电流源U4VS题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3 B )3和3 C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用 B )不可以用 C )有条件地使用11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )-18VB )18VC )-6VU I SS+题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。
运筹学教程(第三版)习题答案(第一章)

b 3/2 1
c x1 0 1 0
d x2 1 0 0
0 x3 5/14
0 x4 -3/4
-2/14 10/35 -5/14d+2/14c 3/14d-10/14c
School of Management
运筹学教程
第一章习题解答
之间时最优解为图中的A点 当c/d在3/10到5/2之间时最优解为图中的 点 ; 当 在 到 之间时最优解为图中的 c/d大于 且c大于等于 时最优解为图中的 点;当c/d 大于5/2且 大于等于 时最优解为图中的B点 大于等于0时最优解为图中的 大于 小于3/10且 d大于 时最优解为图中的 点 ; 当 c/d大于 大于0时最优解为图中的 小于 且 大于 时最优解为图中的C点 大于 5/2且c小于等于 时或当 小于 小于等于0时或当 小于3/10且d小于 时最优解 小于0时最优解 且 小于等于 时或当c/d小于 且 小于 为图中的原点。 为图中的原点。
page 7 14 March 2012
School of Management
运筹学教程
第一章习题解答
对下述线性规划问题找出所有基解, 1.3 对下述线性规划问题找出所有基解,指出哪 些是基可行解,并确定最优解。 些是基可行解,并确定最优解。
max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0( j = 1, L , 6) ,
School of Management
数电第3章习题及解答

第3章习题及解答3.1分析图P3.1所示电路的逻辑功能,写出输出逻辑表达式,列出真值表,说明电路完成何种逻辑功能。
F图P3.1题3.1 解:根据题意可写出输出逻辑表达式,并列写真值表为:B A AB F +=该电路完成同或功能3.2 分析图P3.3所示电路的逻辑功能,写出输出1F 和2F 的逻辑表达式,列出真值表,说明电路完成什么逻辑功能。
A B CF F 12图P3.3题3.3 解:根据题意可写出输出逻辑表达式为:=+AC⊕=F+⊕ABBCFCBA12列写真值表为:该电路构成了一个全加器。
3.5 写出图P3.5所示电路的逻辑函数表达式,其中以S3、S2、S1、S0作为控制信号,A,B作为数据输入,列表说明输出Y在S3~S0作用下与A、B的关系。
图P3.5题3.5 解:由逻辑图可写出Y的逻辑表达式为:AS+⊕=+ABY+SSBBSAB321图中的S3、S2、S1、S0作为控制信号,用以选通待传送数据A、B,两类信号作用不同,分析中应区别开来,否则得不出正确结果。
由于S3、S2、S1、S0共有16种取值组合,因此输出Y和A、B之间应有16种函数关系。
列表如下:3.7 设计一个含三台设备工作的故障显示器。
要求如下:三台设备都正常工作时,绿灯亮;仅一台设备发生故障时,黄灯亮;两台或两台以上设备同时发生故障时,红灯亮。
题3.7 解:设三台设备为A 、B 、C ,正常工作时为1,出现故障时为0; F 1为绿灯、F 2为黄灯、F 3为红灯,灯亮为1,灯灭为0。
根据题意可列写真值表为:求得F 1、F 2、F 3的逻辑表达式分别为:C A C B B A F C AB C B A BC A F ABC F ++=++==321;;根据逻辑表达式可画出电路图(图略)。
3.9 设计一个组合逻辑电路,该电路有三个输入信号ABC ,三个输出信号XYZ,输入和输出信号均代表一个三位的二进制数。
电路完成如下功能:当输入信号的数值为0,1,2,3时,输出是一个比输入大1的数值;当输入信号的数值为4,5,6,7时,输出是一个比输入小1的数值。
线性代数(第一~三章)习题解答
习 题 一1.解:(1)31542的逆序数=2+0+2+1+0=5(2)264315的逆序数=1+4+2+1+0+0=8 (3)54321的逆序数=4+3+2+1=10(4))12)(32(135)2)(22(246---n n n n =1+2+3+…(2n -1)=2)1(+n n 2.解:四阶行列式中含有31a 的项可表示为42142143121)1()1(j j j j j j a a a a τ-,其中421,,j j j 为2,3,4的全排列。
故带有负号的项有:43312412a a a a -,44312213a a a a -,42312314a a a a -3.解:xx x x x x 347165423112展开式中含有4x 的项必须每行都取含x 的项相乘,即41863x x x x x =⋅⋅⋅=,含有3x 的项为x x x x x x ⋅⋅⋅-+⋅⋅⋅-2)1(763)1()1324()4231(ττ3128x -=4.证明:(反证法)假设该行列式不为零,则不为零的元素的个数≥n ,从而为零的元素的个数≤n n -2,与已知行列式中有n n -2个以上元素为零矛盾。
所以该行列式为零。
5.解:(1)2456323652-=⨯-⨯=+ (2)))(())((22222222b ab a b a b ab a b a ba b a b ab a b ab a ++--+-+=+-+++-33b a +=3332)(b b a =--(3)022=bababa (4)45500251190221242513122113-=-----r r r r (5)3711107403112311740532224332453213312213=-----↔-----r r r r r r r r(6)))((0))((0111121212222c b a a c a c c b a a b a b bca ar r r r abc c acb bbca a ++--++-------- 0)(10)(101))(()()(232=++++-----c b a c b a bca aa c ab ac r a b r 提取提取(7)43123524323556485437r r r r --23214123524031102115437r r r r r r -+--3524010002111400---24100011302410000111000524343231-按第一行展开--++-r r r r r r22411=-按第三列展开 (8)132141873754169521321r r r r r ---1226400622069521321r r ---2312226400622043101321r r r r ----346400240043101321r r -----16400240043101321=---(9)4321c c c c xa b c a x c b b c x a c b a x +++----xa b x c b a a x c x c b a bc x x c b a cb a xc b a --++--++--++-++131214 )(r r r r r r x c b a ----++ 提取cx b a a b c a b x a c cb bc a x c b a x c b a -------------++0001)(4223c c c c ++c x b c a x ca c ab x cb c b a x b c a x ca b c a x c b a --+----+----+---+---++-++000001)( 432c c c --cx b c a x c a c a b x cx a b ca b c a x c b a --+----+---++-++-++00000001)( 按第一列展开cx b c a x ca c ab xc x a b x c b a --+-------++--++0|00)())()()(()1()321(x a c b c b a x b c a x x c b a +-++---+----++-=τ ))()()((x c b a x b a c x c a b x c b a ----------++=6.解:(1) 证明:cb a a cb c b a cba cb a ++++++222并提取公因式321c c c ++c b a a b c b a ba++++++21211c)b 2(ac b a c b a bac b a c c c c ++++++--00001)(213123)(2c b a ++=(2)bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++5行列式性质bz ay by ax az by ax bx az ay bx az bz ay ax +++++++bz ay by ax bx by ax bx az bz bxaz bz ay by ++++++ 提取公因式bz ay by ax z by ax bx az y bxaz bz ay xa +++++++bzay by ax xby ax bx az z bx az bz ay yb ++++++5行列式性质ay by ax zax bx az y az bz ay x a ++++bz by ax zby bx az ybx bz ay x a ++++bz ay ax xby ax az zbxaz ay y b ++++bz ay by x by ax bx z bxaz bz y b +++y by ax z x bx az y zbzay x a +++2+++00bz ay y xby ax x zbxaz z yb +++25行列式性质y ax z x azy z ay x a 2+y by z x bx y zbzx a 2+ayy x ax x zazz yb 2+bz y x by x zbxz y b 2yxzx z y zy x a 3+++00zy x y xzx z yb 3 1223,c c c c ↔↔第二个行列式y xzx z y z y xb a )(33+ (3)用数学归纳法①当1=n 时,1)11(22x x x D n +===,命题成立;②设k n ≤时命题成立,即k k x k D )1(+=,则1+=k n 时,)1()1(22222100020000002100002100002+⨯+=k k n x x x x x x x x x D=kk x x x x x x x x x x⨯210002000000210000210000222222kk x x x x x x x ⨯-210020000020000122221212)1(22--⋅-+⋅=-=k k k k kx x x k x D x xD 11)2()22(+++=-+k k x k x k k n x n )1(+=综合①、②可得对一切自然数n ,都有n n x n D )1(+=. 7.解:(1)1444414444144441 =n D),,3,2(1n i r r i =+14444144441434343434 ----n n n n)34()34(--n n 提取1444414444141111 )34(,3,2 4 1-=-n ni r r i 300030000301111---)34()3(1--=-n n(2)121212555333321321321321---=n n n n n n n n Dni i c i ,3,2=提取2222224442223213213211111!---n n n n n n n∏≤<≤-nj i j i n 122)(! 式行列利用范德蒙(3)递推法nn n n a a a a a a a a D -------=-+11000010000001100001100001132211112r r +nn n a a a a a a a ------11000100000011000010000113221D n展开按第一列nn n a a a a a a a ------11001000000110000100001143321a -11-a 1Dnn 2=(4)nnn n n n nnn d c d c d c b a b a b a D 111111112----=行取第一行和第拉普拉斯定理n 2nn nnd c b a .11111111----n n n n d c d c b a b a22)( --n n n n n D c b d a 421111))((-------n n n n n n n n n D c b d a c b d a 可得类似111133331111)())((d c b a c b d a c b d a c b d a n n n n n n n n -------∏=-ni i i i i c b d a 1)((5)na xxxx a x xx x a x x x x a3211,2,1 1-=-+n i c c i inn n a a x x x a x x a a x x x a a x x x a -------- 000000 00 00 001332212,1, 1 -=--n n i r r i ixa a a x x a x a a a x x a a a x xx a n n n n -------------1132321212 000 000002000 020 00∏∏=-+=---+-ni i i n n i i a a x x x a n 2111)2()1()( 展开列按第 ∏∏=-=-++-ni i i ni i x a a x x a 211)2()(8.解:(1)计算系数行列式232142234321212r r r r D --=51050321430-=----5321032143031-+--r r 210321200=-101312173237323211r r r r D --=01240310211=----2321242274331212r r r r D --=311050331450r r -----31105033160r r ----302321342734321112r r r r D --==----5503215303131103215305r r +---101103212005=-- 所以方程组有唯一解011==D D x , 322==D Dx , 133-==DD x (2)计算系数行列式4352323211431121----=D 101110740064112132141312------++r r r r r r 10111010402021104424123------++-r r r r r r6114022111=---展开按c 43513232114711231----=D 24232143r r r r r r +-+01212901919114700610--- 324241212919190610)1(r r c +----+展开按60121290121006101413122224312322211731131r r r r r r D --+----=1421505440001041131c c -------11501440001040131-----390144000104013134---+r r 3900104131)1(434---+展开按c3131r r +303900104001)1(43-=--+41523232174313213--=D 141312223r r r r r r ---2510541042201321-------2423225105410211013212)2(r r r r r -+--------提取06003300211013212----- 0603302112C 1----展开按36=- 13522232714331214--=D 141312223r r r r r r ---5110441024203121-------2423251104410121031212)2(r r r r r -+--------提取61003200121031212----- 613201212C 1----展开按18= 所以方程组有唯一解1011==D D x , 522-==D D x , 633-==D D x , 344==DDx (3)计算系数行列式5733856155334231=D 343214131222716043307160423133r r r r r r r r r r ++--------17004330150042312004330150001013124---r r r r 64310)1(20204331502331=-⨯+展开按展开按r C3412125738856855364233r r r r D --=24232123230856831304233r r r r r r -++----0100270831301303--13123442320833013)1(r r r r r -+---+展开按600203913-=--57838581556342312=D 022435713022043507130423131131224---------展开按c r r r r r r11420720253232313---+r r r r r 提取12-58338861563343313=D 020453736020045307360433131131224---------展开按c r r r r r r 6=87338561653332314=D 220533316220053303160323131131224---------展开按c r r r r r r122275)1(3220533750212121=-⨯++展开按c r r所以方程组有唯一解111-==D D x , 222-==D D x , 133==D D x , 244==DDx9.解:(1)λλλλ--=3111211D 1232rr c c --λλλλλ----3321022132122332021---+---λλλλλλλ展开按r )2)(2()22)(2()3)(2(2---=--+--=λλλλλλλλ)1()2(2+--=λλ当0=D 时,即时=-或12λλ=,齐次方程组有非零解. (2)324124122-+--=λλλD 32423601221212---+-----λλλλλr r c cλλλλλλλ--+--+-----2460)1(3223621展开按r [])6)(4)(1()23)(2()6(32-+---++--=λλλλλλ)4)(2)(3(241423-++-=+-=λλλλλλ+-当0=D 时,即时=或-或423λλλ=-=,齐次方程组有非零解.习 题 二1. 解:(1)⎪⎪⎪⎭⎫ ⎝⎛---=+776491056532B AB (2)⎪⎪⎪⎭⎫ ⎝⎛------=-4332412332E AB T2.解:(1)⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--000046696432 (2)⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛834231413121342(3)()⎪⎪⎪⎭⎫ ⎝⎛----=-⎪⎪⎪⎭⎫ ⎝⎛-339226113113321 (4)()2321113-=⎪⎪⎪⎭⎫⎝⎛--(5)⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛------777468505642531432321234643755467 (6)()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321333231232221131211321x x x a a a a a a a a a x x x()⎪⎪⎪⎭⎫⎝⎛++++++=321333223113332222112331221111x x x x a x a x a x a x a x a x a x a x a)()()(233332233113233222222112133112212111x a x x a x x a x x a x a x x a x x a x x a x a ++++++++=3.解:⎪⎪⎪⎭⎫ ⎝⎛---=210143321TA , ⎪⎪⎭⎫ ⎝⎛=234112T B(1)⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=112143213142210143321B A T(2)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛=124113213142031234112A B T(3)⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛==1165511210143321234112)(TT T A B AB4.解:从321321,,,,x x x y y y 到的线性变换可表示为:⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321y y y A x x x ,其中⎪⎪⎪⎭⎫ ⎝⎛---=352143231A ;从321321,,,,y y y z z z 到的线性变换可表示为:⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321z z z B y y y ,其中⎪⎪⎪⎭⎫ ⎝⎛=231341652B ,所以从321321,,,,x x x z z z 到的线性变换可表示为:=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321z z z AB x x x ⎪⎪⎪⎭⎫ ⎝⎛---352143231⎪⎪⎪⎭⎫ ⎝⎛231341652=⎪⎪⎪⎭⎫ ⎝⎛321z z z ⎪⎪⎪⎭⎫ ⎝⎛--312823111⎪⎪⎪⎭⎫ ⎝⎛321z z z 所以,从321321,,,,x x x z z z 到的线性变换为: ⎪⎩⎪⎨⎧+-=++=+-=32823 321332123211z z z x z z z x z z z x5.解:(1)E A A A f 43)(2+-=⎪⎪⎭⎫ ⎝⎛--=2321⎪⎪⎭⎫ ⎝⎛--2321-3⎪⎪⎭⎫ ⎝⎛--2321E 4+=⎪⎪⎭⎫⎝⎛8008 (2) 2201310111)(2--=--=x x x x x x f=--=E A A A f 22)(2⎪⎪⎭⎫ ⎝⎛0211⎪⎪⎭⎫ ⎝⎛0211⎪⎪⎭⎫ ⎝⎛-02112E 2-⎪⎪⎭⎫⎝⎛---=01216.(1)∵222))(()(B BA AB A B A B A B A +++=++=+ ∴要使2222)(B AB A B A ++=+,则必须AB BA = (2) ∵22))((B BA AB A B A B A -+-=-+∴要使22))((B A B A B A -=-+,则必须0=+-BA AB ,即AB BA = (3) 当AB BA =时,用数学归纳法证明kk k B A AB =)(①1=k 时,显然kk k B A AB =)(2=k 时,222)()()()(B A B AB A B AB A ABAB AB AB k =====,所以kk k B A AB =)(②设n k =时,有kk k B A AB =)(,则1+=n k 时B BA B A B A B A AB B A AB AB AB AB n n n n n n n n K)()()()()()(1!-+=====B AB B A n n )(1-=21)(B A B A n n -=11)(++===n n n n B A B AB A可见,1+=n k 时,也有k k k B A AB =)(所以,当AB BA =时,对一切正整数k 都有 k k k B A AB =)(7.解:(1) ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛----111122221111n n n n n(2) ∵⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--100123122∴⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--为奇数为偶数n n n 2312 10012312 (3) ∵⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1002101211001100112,⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1002101211001100113⎪⎪⎪⎭⎫⎝⎛100110011⎪⎪⎪⎭⎫⎝⎛=100310331 =⎪⎪⎪⎭⎫ ⎝⎛41001100113100110011⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛100110011⎪⎪⎪⎭⎫ ⎝⎛=100310331⎪⎪⎪⎭⎫⎝⎛100110011 ⎪⎪⎪⎭⎫ ⎝⎛=100410641 ∴⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫⎝⎛100102)1(1100110011n n n n n8.证明:∵A 、B 为对称矩阵,∴=T A A ,=TB B(1) ∵ AC C C A C AC C T T T T T T T ==)()(∴ AC C T是对称矩阵(2) ∵ ABABA A B A B A ABABA TT T T T T ==)(∴ ABABA 是对称矩阵(3) ∵E E AA TT ==-)(1,=T A A∴==--T T T A A AA )()(11A A E A A T 11)(--== ∴ 11)(--=A A T ∴ 1-A 是对称矩阵9.解:(1) ∵027342≠=∴⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-23477342173421⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫⎝⎛-23472173421(2) ∵01cos sin sin cos cos sin 22≠=+=-θθθθθθ∴ ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--θθθθθθθθsin cos cos sin 11sin cos cos sin 1⎪⎪⎭⎫⎝⎛-=θθθθsin cos cos sin (3) ∵232132643321532r r r r --01320321110≠-=---- ∴⎪⎪⎪⎭⎫⎝⎛643321532可逆 又∵0643211==A , 3633112=-=A , 2432113-==A 2645321=-=A , 3635222-==A , 1433223=-=A 1325331-==A , 1315232-=-=A , 1213233==A ∴⎪⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛-1121331206433215323323133222123121111A A A A A A A A A(4) ⎪⎪⎪⎭⎫⎝⎛-------=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛-----11133131121212113123233323133222123121111A A A A A A A A A(5) ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛----1212335123240634332311(6) 把⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1000210032104321D 分块为⎪⎪⎭⎫ ⎝⎛B C A 0, 其中⎪⎪⎭⎫ ⎝⎛=1021A ,⎪⎪⎭⎫ ⎝⎛=1021B ,⎪⎪⎭⎫⎝⎛=3243C , 则01≠==B A D ,∴矩阵D 可逆。
第三章 习题解答-2.0
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
通信原理 第3章 习题解答
习题解答3-1、 填空题(1) 在模拟通信系统中,有效性与已调信号带宽的定性关系是( 已调信号带宽越小,有效性越好),可靠性与解调器输出信噪比的定性关系是(解调器输出信噪比越大,可靠性越好)。
(2) 鉴频器输出噪声的功率谱密度与频率的定性关系是(功率谱密度与频率的平方成正比),采用预加重和去加重技术的目的是(提高解调器输出信噪比)。
(3) 在AM 、DSB 、SSB 、FM 等4个通信系统中,可靠性最好的是(FM ),有效性最好的是(SSB ),有效性相同的是(AM 和DSB ),可靠性相同的是(DSB 、SSB )。
(4) 在VSB 系统中,无失真传输信息的两个条件是:(相干解调)、(系统的频率特性在载频两边互补对称)。
(5) 某调频信号的时域表达式为)10sin 5102cos(1036t t ππ+⨯,此信号的载频是(106)Hz ,最大频偏是(2500)Hz ,信号带宽是(6000)Hz ,当调频灵敏度为5kHz/V 时,基带信号的时域表达式为(t π310cos 5.0)。
3-2、 根据题3-2图(a )所示的调制信号波形,试画出DSB 及AM 信号的波形图,并比较它们分别通过包络检波器后的波形差别。
解:设载波t t s c ωsin )(=,(1)DSB 信号)()()(t s t m t s D SB =的波形如题3-2图(b ),通过包络后的输出波形为题3-2图(c)。
(2)AM 信号t t m m t s c AM ωsin )]([)(0+=,设max 0)(t m m >,波形如题3-2图(d ),通过包络后的输出波形为题3-2图(e)。
结论:DSB 解调信号已严重失真,故对DSB 信号不能采用包络检波法;而AM 可采用此法恢复。
题3-2图(a )题3-2图(b)、(c)、(d)和(e)3-3、 已知调制信号)4000cos()2000cos()(t t t m ππ+=,载波为t π410cos ,进行单边带调制,试确定该单边带信号的表示式,并画出频谱图。
第9-10章习题解答
第九章 电磁感应§9-1 电源 电动势 §9-2 电磁感应定律 §9-3 动生电动势§9-4 感生电动势和感生电场 §9-5 自感和互感 §9-6 磁场的能量§9-7 位移电流 麦克斯韦方程组9.1 法拉第电磁感应定律指出:通过回路所圈围的面积的磁通量发生变化时,回路中就产生感应电动势。
哪些物理量的改变会引起磁通量的变化?9.2 若感应电流的方向与楞次定律所确定的方向相反,或者说,法拉第定律公式中的负号换成正号,会导致什么结果?9.3 有人说,楞次定律告诉我们“感应电流的磁通总是原磁通相反的”,你认为对吗?为什么?解答:不对,阻碍并不是相反。
9.4 L 值是否有负值?M 值是否有负值?怎样理解负值的物理意义? 9.5 有两个相隔距离不太远的线圈,如何放置才能使其互感系数为零? 9.6 存在位移电流,是否必存在位移电流的磁场?9.7 半径为a 的圆线圈置于磁感强度为B 的均匀磁场中,线圈平面与磁场方向垂直,线圈电阻为R ;当把线圈转动使其法向与B 的夹角060=θ时,线圈中通过的电荷与线圈面积及转动所用的时间的关系是( ) A 、与线圈面积成正比,与时间无关; B 、与线圈面积成正比,与时间成正比; C 、与线圈面积成反比,与时间成正比; D 、与线圈面积成反比,与时间无关。
答案:A9.8 如图9-8所示,长度为 的直导线ab 在均匀磁场B 中以速度υ移动,直导线ab 中的电动势为A 、B υ B 、sin B υαC 、cos B υαD 、0 答案:D9.9 在感生电场中,电磁感应定律可写成i k d d dtεΦ=⋅=⎰E l,式中k E 为感生电场的电场强度;此式表明( ) A 、闭合回路 上的k E 处处相等; B 、感生电场是保守场;C 、感生电场的电场线不是闭合曲线;D 、感生电场是涡旋藏。
答案:D9.10 若尺寸相同的铁环与铜环所包围的面积中穿过磁通量的变化率相同,则在这两个环中( )A 、感应电动势不同,感应电流相同;B 、感应电动势和感应电流都相同;C 、感应电动势和感应电流都不同;D 、感应电动势相同,感应电流不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 组合逻辑电路分析与设计 2-1 图2-5是两个CMOS逻辑门的内部结构图,试说出逻辑门的名称,并写出输出函数表达式,画出其逻辑符号。
解 图2-5(a)电路实现与门功能,输出函数表达式为F=AB,其逻辑符号如图2-1(a)所示。图2-5(b)电路实现A和B的或非运算,输出函数表达式为FAB,逻辑符号如图2-1(b)所示,其中,输入信号B所接输入端的小圆圈表示取非操作。
2-2 已知74S00是2输入四与非门,IOL=20mA,IOH =1mA,IIL=2mA,IIH=50μA;7410是3输入三与非门,IOL=16mA,IOH =,IIL=,IIH=40μA。试分别计算74S00和7410的扇出系数。理论上,一个74S00逻辑门的输出端最多可以驱动几个7410逻辑门,一个7410逻辑门的输出端最多可以驱动几个74S00逻辑门
解 74S00驱动74S00:OHIHI/I1mA/50A20, OLILI/I20mA/2mA10。所以,
74S00的扇出系数NO=10。
7410驱动7410:OHIHI/I0.4mA/40A10,OLILI/I16mA/1.6mA10。所以,
7410的扇出系数NO=10。
74S00驱动7410:OH(74S00)IH(7410)I/I1mA/40A25,
QQ36 AB+VQQQQF1245DD QQ12 FABQQQQ
+V3456
DD
(a) (b) 图2-5 CMOS逻辑门内部结构图
F≥1ABA
B&F
(a) (b) 图2-1 OL(74S00)IL(7410)I/I20mA/1.6mA12。所以,74S00可以驱动12个7410的输入端。
7410驱动74S00:OH(7410)IH(74S00)I/I0.4mA/50A8,
OL(7410)IL(74S00)I/I16mA/2mA8,所以,7410可以驱动8个74S00的输入端。
2-3 图2-7中的逻辑门均为TTL门。试问图中电路能否实现1FAB,2FAB,
3FABBC的功能要求说明理由。
解 图2-7(a)需要确定在与非门输出信号驱动下,三极管能否实现非门功能。 当与非门输出低电平(约)时,由于三极管的BEV0.7V(三极管的导通电压),所以
三极管截止,集电极电阻(1k)上的压降为0,F1输出高电平(+5V)。
当与非门输出高电平(约)时,三极管导通,VBE=,基极电流为
BOHBEBI(VV)/R(3.6V0.7V)/10k0.29mA 三极管的基极饱和电流为(设三极管饱和输出电压VCES=)
BSCSCCCESCII/(VV)/R(5V0.2V)/501k0.096mAg 由于IB>IBS,三极管饱和,F1输出低电平()。 综上所述,三极管实现非门功能。整个电路是一个与非-非结构,实现与运算1FAB。
图2-7(b)所示电路中,当与非门输出高电平()时,三极管导通,导通后的三极管的VBE基本上被钳制在,把与非门输出电平也下拉到,多余的高电平由逻辑门内部的输出电路负担,逻辑门输出电流过大。不仅造成逻辑门输出电平错误,而且容易损坏器件。所以,该电路结构是不正确的。
图2-7(c)所示电路是两个集电极开路与非门的输出信号采用“线与”连接的结构。该电路存在的问题是,缺少集电极开路门输出端必须的上拉电阻和上拉电源。所以,该电路不能实现3FABBC。
&A1B10KFβ=50+5V1K &A
2
B
10KF
β=50
+5V1K
&
& A
B
C3F
(a) (b) (c) 图2-7 2-4 试用OC与非门实现逻辑函数FACABCACD,假定不允许反变量输入。 解 用OC与非门及其线与功能实现的逻辑函数形式为“与非-与”。通过卡诺图化简求取最简“与非-与”表达式时,应该圈0,先写出最简或与式,然后变换成“与非-与”形式。电路如图2-8所示。
2-5 某组合逻辑电路如图2-9(a)所示 (1) 写出输出函数F的表达式; (2) 列出真值表; (3) 对应图2-9(b)所示输入波形,画出输出信号F的波形; (4) 用图2-9(c)所示与或非门实现函数F(允许反变量输入)。
解 (1)图2-9(a)中的两个三态门分时操作,当控制输入变量E=0时,三态与门工作,输出信号FAB;当E=1时,三态非门工作,输出FAB。综合上述情况,输出函数为FEABEABgg。
(2)输出函数F的真值表如表2-4所示。 (3)输出信号的波形如图2-10(a)所示。
A EN
EN
B
E≥1&1F 1ABEF
&
≥1
(a) (b) (c) 图2-9
F(AB)(CD)(AC) ABCDAC ABCDAC ABCDACLLLLLLLLLLLLggLLLLLLL最简或与式最简或非-或非式最简与或非式最简与非-与式
&
& A
B
F
+EC
RL
CD
& CA
图2-8 (4)用与或非门实现逻辑函数时,需要先将函数化简为最简与或非式,采用卡诺图圈0化简(a)中求得的函数F,得到最简或与式为FA(EB)(EB)gg,经变换后得到最简与或非式为FAEBEB,用图2-9(c)所示与或非门实现该表达式时,应正确处理多余的逻辑门和多余的输入端,实现函数F的电路如图2-10(b)所示。
2-6 写出图2-11所示电路的输出函数表达式,说明该电路的逻辑功能和每个输入变量和输出变量的含义。
解 由逻辑门构成的组合逻辑电路的输出函数表达式容易求得,只要按照信号传输路径,从输入端写到输出端即可。
100101102103YEN(AAXAAXAAXAAX) 该电路是一个带使能端的四选一数据选择器(MUX),使能端EN低电平有效,选择输入端(地址输入端)是A1A0,数据输入端是X0~X3,Y是数据输出端。当EN1时,MUX无效,输出信号Y总是0;当EN0时,Y输出A1A0选中的Xi。
&≥1
1 =1&≥1AB F
SSS123 S0
图2-12 图2-11
&≥1
A1
A01
1
1X1
X0
X3
X2
EN
Y
表2-4 真值表 EAB F 000 0 001 1 010 0 011 0 100 1 101 0 110 0 111 0
ABEF
&≥1A
111
EB1
EB
00
F
(a) (b) 图2-10 2-7 列表说明图2-12所示电路中,当S3S2S1S0作为控制信号时,F与A、B的逻辑关系。 解 首先写出函数F的表达式
3210FSABSABSBSBA
该电路是在S3S2S1S0控制下的函数发生器,在不同的S3S2S1S0取值下,F是A、B不同的逻辑函数,可以实现常量0、1输出;单变量输出(原变量或反变量形式);与、与非、或、或非、异或、同或等逻辑功能,具体逻辑功能如表2-5所示。函数发生器是计算机CPU的基本功能,是CPU中算术逻辑单元(ALU)的重要组成部分。 2-8 译码器74154构成的逻辑电路如图2-13所示,写出输出函数的最小项表达式。
解 74154是4线-16线全译码器,输出信号低电平有效。16个译码输出变量是4个编码输入变量的所有最大项iiYM(i=0~15),利用这个特点可以实现四变量的逻辑函
数。图2-13所示电路的输出函数F的表达式为
019119111315019119111315019119111315911
F(W,X,Y,Z)YYYYYYYY MMMMMMMM (MMMM)(MMMM) mm WXYZWXYZg
图2-13 YZWXF&&≥1A Y741543AY8Y6212Y7Y2Y0Y913Y311Y5Y11510AY14YYYG0YY24A
11
G 图2-14
01
32
Y
YYY AA10 BA DEC3
1
0
2D
MUXD
YDD7 5A4A6ADD2D0D1 BACF(A,B,C)01
32
Y
YYY AA10 BC
DEC
表2-5 S3S2S1S0 F S3S2S1S0 F 0000 A 1000 AB
0001 AB 1001 AB
0010 AB 1010 B
0011 1 1011 AB
0100 AB 1100 0
0101 B 1101 AB
0110 ABe 1110 AB
0111 AB 1111 A
