初中最难几何题
初中数学经典几何题难及答案分析
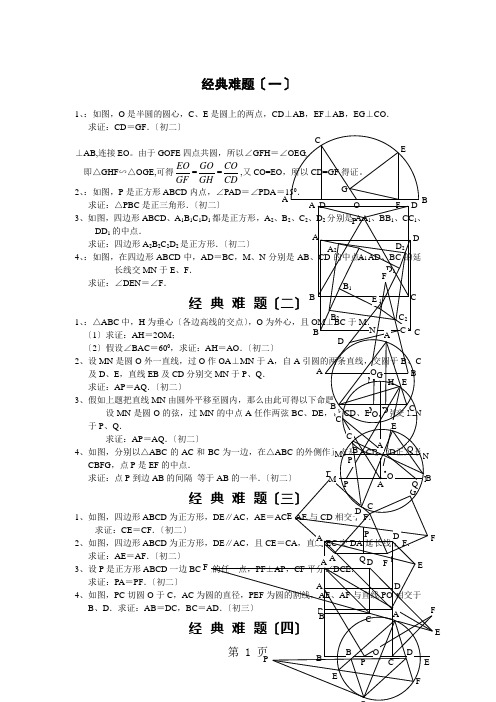
经典难题〔一〕1、:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.〔初二〕⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.3、如图,四边形ABCD、A1B1CDD1的中点.求证:四边形A2B2C2D24、:如图,在四边形ABCD中,长线交MN于E、F.求证:∠DEN=∠F.1、:△ABC中,H〔1〕求证:AH=2OM;〔2〕假设∠BAC=6002、设MN是圆O外一直线,过及D、E,直线EB及CD求证:AP=AQ.〔初二〕3、假如上题把直线MN设MN是圆O的弦,过于P、Q.求证:AP=AQ.4、如图,分别以△ABC的ACCBFG,点P是EF的中点.求证:点P到边AB的间隔1、如图,四边形ABCD求证:CE=CF.〔初二〕2、如图,四边形ABCD求证:AE=AF.〔初二〕3、设P是正方形ABCD一边求证:PA=PF.〔初二〕4、如图,PC切圆O于C,ACB、D.求证:AB=DC,BCGCE1、:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.〔初二〕2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .〔初二〕 3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .〔初三〕4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .〔初二〕经典难题〔五〕1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA=300,∠EBA =200,求∠BED 的度数. 经典难题〔一〕⊥AB,连接EO 。
初中难度几何题100道

初中教师转正必做100题第一题:已知:ABCAE⊥,ABBAC,BCCF⊥,AE、CF相交∆外接于⊙O,︒=∠60于点H,点D为弧BC的中点,连接HD、AD.∆为等腰三角形求证:AHD第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE.CE=求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC . 求证:BC AD =第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB . 求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB ,求ACD ∠.BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =,求证:222BD BC AB =+.B D第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D.求证:四边形ABCD为平行四边形第八题:已知:在ABC=OBC,︒∠10OCA.∠20AB=,︒∆中,AC==∠80A,︒求证:OBAB=CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形.第十题:已知:正方形ABCD 中,E 、F 为AD 、DC 的中点,连接BE 、AF ,相交于点P ,连接PC .求证:BC PC =第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFD.EB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =. 求证:︒=∠60ACB .A第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠, 求证:AB CD AD =+.AB第十四题:已知:ABC ∆中,BC AB =,D 是AC 的中点,过D 作BC DE ⊥于E ,连接AE ,取DE 中点F ,连接BF . 求证:BF AE ⊥.AC第十五题:已知:ABC ∆中,︒=∠24A ,︒=∠30C ,D 为AC 上一点,CD AB =,连接BD . 求证:AC BD BC AB ⋅=⋅.AC第十六题:已知:ABCD 与1111D C B A 均为正方形,2A 、2B 、2C 、2D 分别为1AA 、1BB 、1CC 、1DD 的中点.求证:2222D C B A 为正方形.A第十七题:如图,在ABC ∆三边上,向外做三角形ABR 、BCP 、CAQ ,使︒=∠=∠45CAQ CBP ,︒=∠=∠30ACQ BCP ,︒=∠=∠15BAR ABR .求证:RQ 与RP 垂直且相等.Q第十八题:如图,已知AD 是⊙O 的直径,D 是BC 中点,AB 、AC 交⊙O 于点E 、F ,EM 、FM 是⊙O 的切线,EM 、FM 相交于点M ,连接DM . 求证:BC DM .B第十九题:如图,三角形ABC 内接于⊙O ,两条高AD 、BE 交于点H ,连接AO 、OH 。
初中数学几何题(超难)及答案分析

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
初中数学几何题超难及答案分析-七年级几何题超难
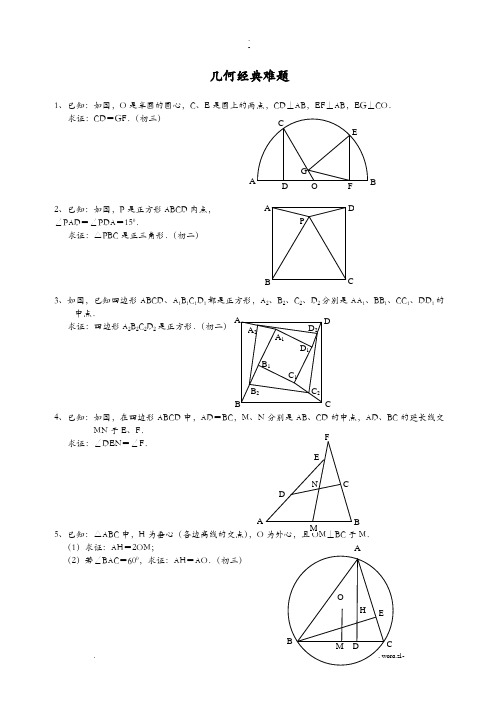
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点) (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FGCE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E EP13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB C B D AFPDECBA. -18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH⊥AB,连接EO。
初中难度几何题100道 (1)

初中教师转正必做100题第一题: (4)第二题: (5)第三题: (6)第四题: (7)第五题: (8)第六题: (9)第七题: (10)第八题: (11)第九题: (12)第十题: (13)第十一题: (14)第十二题: (15)第十三题: (16)第十四题: (17)第十五题: (18)第十六题: (19)第十七题: (20)第十八题: (21)第十九题: (22)第二十题: (23)第二十一题: (24)第二十二题: (25)第二十三题: (26)第二十四题: (27)第二十五题: (28)第二十六题: (29)第二十七题: (30)第二十八题: (31)第二十九题: (32)第三十题: (33)第三十一题: (34)第三十二题: (35)第三十三题: (36)第三十四题: (37)第三十五题: (38)第三十六题: (39)第三十七题: (40)第三十八题: (41)第三十九题: (42)第四十题: (43)第四十一题: (44)第四十二题: (45)第四十三题: (46)第四十五题: (48)第四十六题: (49)第四十七题: (50)第四十八题: (51)第四十九题: (52)第五十题: (53)第五十一题: (54)第五十二题: (55)第五十三题: (56)第五十四题: (57)第五十五题: (58)第五十六题: (59)第五十七题: (60)第五十八题: (61)第五十九题: (62)第六十题: (63)第六十一题: (64)第六十二题: (65)第六十三题: (66)第六十四题: (67)第六十五题: (68)第六十六题: (69)第六十七题: (70)第六十八题: (71)第六十九题: (72)第七十题: (73)第七十一题: (74)第七十二题: (75)第七十三题: (76)第七十四题: (77)第七十五题: (78)第七十六题: (79)第七十七题: (80)第七十八题: (81)第七十九题: (82)第八十题: (83)第八十一题: (84)第八十二题: (85)第八十三题: (86)第八十四题: (87)第八十五题: (88)第八十六题: (89)第八十七题: (90)第八十九题: (92)第九十题: (93)第九十一题: (94)第九十二题: (95)第九十三题: (96)第九十四题: (97)第九十五题: (98)第九十六题: (99)第九十七题: (100)第九十八题: (101)第九十九题: (102)第一百题: (103)第一题:已知:ABCAE⊥,ABCF⊥,AE、CF相交BAC,BC∆外接于⊙O,︒=∠60于点H,点D为弧BC的中点,连接HD、AD.∆为等腰三角形求证:AHD第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE 于点E,连接CE,且AC=AE.CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC .求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB . 求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB ,求ACD ∠.B D第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =,求证:222BD BC AB =+.DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D.求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA . 求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形.第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC.PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFD .EB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =. 求证:︒=∠60ACB .A第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠, 求证:AB CD AD =+.AB第十四题:已知:ABC ∆中,BC AB =,D 是AC 的中点,过D 作BC DE ⊥于E ,连接AE ,取DE 中点F ,连接BF . 求证:BF AE ⊥.AC第十五题:已知:ABC ∆中,︒=∠24A ,︒=∠30C ,D 为AC 上一点,CD AB =,连接BD . 求证:AC BD BC AB ⋅=⋅.A第十六题:已知:ABCD 与1111D C B A 均为正方形,2A 、2B 、2C 、2D 分别为1AA 、1BB 、1CC 、1DD 的中点.求证:2222D C B A 为正方形.A第十七题:如图,在ABC ∆三边上,向外做三角形ABR 、BCP 、CAQ ,使︒=∠=∠45CAQ CBP ,︒=∠=∠30ACQ BCP ,︒=∠=∠15BAR ABR .求证:RQ 与RP 垂直且相等.Q第十八题:如图,已知AD是⊙O的直径,D是BC中点,AB、AC交⊙O于点E、F,EM、FM 是⊙O的切线,EM、FM相交于点M,连接DM.DM .求证:BCB第十九题:如图,三角形ABC 内接于⊙O ,两条高AD 、BE 交于点H ,连接AO 、OH 。
(完整版)初中数学几何题(超难)及答案分析

,求证:≤n d A l n g s i n th e i r b e i n g GF GH CD,从而得出△PBC 是正三角形分别找其中点F,E.连接C F 与A E 并延长相交于l l t h i n g s i n th e i r b e i n g a r e g o o d f o r s o 4.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
5.(1)延长AD 到F 连BF ,做OG ⊥AF,又∠F=∠ACB=∠BHD ,可得BH=BF,从而可得HD=DF ,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB ,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证。
dAllirbeinndAllthing22heirbeingaregoandAllthitheirbeingaregl l t h i n g s i n th ei r b e i n g a r e g o o d f o r s o 12.证明:作CQ ⊥PD 于Q ,连接EO ,EQ ,EC ,OF ,QF ,CF ,所以PC 2=PQ•PO (射影定理),又PC 2=PE•PF ,所以EFOQ 四点共圆,∠EQF=∠EOF=2∠BAD ,又∠PQE=∠OFE=∠OEF=∠OQF ,而CQ ⊥PD ,所以∠EQC=∠FQC ,因为∠AEC=∠PQC=90°,故B 、E 、C 、Q 四点共圆,所以∠EBC=∠EQC=1/2∠EQF=1/2∠EOF=∠BAD ,∴CB ∥AD ,所以BO=DO ,即四边形ABCD 是平行四边形,∴AB=DC ,BC=AD .13.顺时针旋转△ABP 600 ,连接PQ ,则△PBQ 是正三角形。
初中几何100题--高难度版
初中竞赛几何必做100题第一题:已知:ABCAE⊥,ABCF⊥,AE、CF相交BAC,BC∆外接于⊙O,︒=∠60于点H,点D为弧BC的中点,连接HD、AD.∆为等腰三角形.求证:AHD第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE.CE .求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC . 求证:BC AD =.B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB . 求证:BC AB ⊥.AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB ,求ACD ∠.BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =,求证:222BD BC AB =+.DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D.求证:四边形ABCD为平行四边形.第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA . 求证:OB AB =.CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形.第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC.PC .求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFD .EB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =. 求证:︒=∠60ACB .第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠. 求证:AB CD AD =+.AB第十四题:已知:ABC ∆中,BC AB =,D 是AC 的中点,过D 作BC DE ⊥于E ,连接AE ,取DE 中点F ,连接BF . 求证:BF AE ⊥.A第十五题:已知:ABC ∆中,︒=∠24A ,︒=∠30C ,D 为AC 上一点,CD AB =,连接BD . 求证:AC BD BC AB ⋅=⋅.A第十六题:已知:ABCD 与1111D C B A 均为正方形,2A 、2B 、2C 、2D 分别为1AA 、1BB 、1CC 、1DD 的中点.求证:2222D C B A 为正方形.A第十七题:如图,在ABC ∆三边上,向外做三角形ABR 、BCP 、CAQ ,使︒=∠=∠45CAQ CBP ,︒=∠=∠30ACQ BCP ,︒=∠=∠15BAR ABR .求证:RQ 与RP 垂直且相等.Q第十八题:如图,已知AD是⊙O的直径,D是BC中点,AB、AC交⊙O于点E、F,EM、FM 是⊙O的切线,EM、FM相交于点M,连接DM.DM .求证:BCB第十九题:如图,三角形ABC 内接于⊙O ,两条高AD 、BE 交于点H ,连接AO 、OH 。
2025年九年级中考数学三轮重难题型专项突破课件:重难题型三 几何最值问题
A.3 5
B.6 5
5
BD的最小值是(
5
C.5 3
B )
D.10
【解析】过点D作DH⊥AB于点H,过点C作CM⊥AB
于点M.∵BE⊥AC,∴∠AEB=90°,∵tan A= =2,
设AE=a,BE=2a,则AB= 5a,sin∠ABE=
∴HD=
5
,
5
当D′E⊥AB时,PD+PE的值最小.
类型二:根据两点之间线段最短求最值
(安徽2023T10)
2.(2023·安徽第10题4分)如图,E是线段AB上一点,△ADE和△BCE是位于
直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,
则下列结论错误的是( A )
A.PA+PB的最小值为3 3
的长为FG+GH+HE的最小值.在Rt△AMN中,AM=8,AN=6,∴MN
=10.在Rt△AEF中,AE=2,AF=4,∴EF=2 5.∴四边形EFGH周长的最
小值为10+2 5.
9.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边
的垂直平分线,P是直线m上的一动点,则△APC周长的最小值为( A )
1
∴∠BAD=30°,BD= BC=1,
2
连接CF,由△ABC,△BEF都是等边三角形,
易证得△BAE≌△BCF(SAS),∴∠BCF=∠BAD=30°,
∴点F与点C的连线与CB始终成30°,
°,DE为∠ADC的平分线,F为DE上一动点,G为CF的中点,连接AG,
则AG的最小值是( B )
A.2
ቤተ መጻሕፍቲ ባይዱ
初中数学几何题(超难)及答案分析(最新整理)
第 1 页 共 15 页几何经典难题1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初三)
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150. 求证:△PBC是正三角形.(初二)
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的
中点.求证:四边形A2B2C2D2是正方形.(初二)
4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.
5、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M. (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO.(初三)
APCDB
AF
G
CE
BOD
D2
C2B
2
A2
D1
C1
B1
CB
DAA1
ANFECD
MB
·A
DHEMCBO第 2 页 共 15 页
P
CGFBQ
A
DE
6、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初三)
7、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初三 )
8、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)
·GAODB
EC
QP
NM
·O
QP
B
D
EC
NM·
A第 3 页 共 15 页
9、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)
10、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)
初中数学经典几何题及答案
经典难题〔一〕1、:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.〔初二〕求证:△PBC是正三角形.3、如图,四边形ABCD、A1B1CC1、DD1的中点.求证:四边形A2B2C2D24、:如图,在四边形ABCD延长线交MN于E、F求证:∠DEN=∠F.1、:△ABC中,H〔1〕求证:AH=2OM;〔2〕假设∠BAC=6002、设MN是圆O外一直线,过及D、E,直线EB及CD求证:AP=AQ.〔初二〕3、如果上题把直线MN设MN是圆O的弦,过于P、Q.求证:AP=AQ.4、如图,分别以△ABC的ACCBFG,点P是EF求证:点P到边AB1、如图,四边形ABCD求证:CE=CF.〔初二〕2、如图,四边形ABCD求证:AE=AF.〔初二〕3、设P是正方形ABCD一边求证:PA=PF.〔初二〕4、如图,PC切圆O于C,AC于B、D.求证:AB=DC,1、:△ABC是正三角形,P求:∠APB的度数.〔初二〕2、设P是平行四边形ABCD求证:∠PAB =∠PCB .〔初二〕3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .〔初三〕4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .〔初二〕 经典难题〔五〕1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC2、:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数. 经典难题〔一〕答案1.如以下图做GH ⊥AB,连接EO 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中最难几何题
引言
几何学是数学的一个分支,研究空间和图形的性质、关系和变换。在初中阶段,学
生开始接触几何学,并学习一些基本的几何知识和技巧。然而,有一些几何题目对
于初中生来说可能会比较困难。本文将介绍一些初中最难的几何题目,并探讨解决
这些题目的方法。
最难的几何题目
题目1:相似三角形
已知直角三角形ABC中,∠B=90°,AB=3cm,BC=4cm。点D位于AC上,且AD=2cm。
若∠CDB=∠ABC,则求BD的长度。
解析:
首先我们可以利用勾股定理求出AC的长度:
AC² = AB² + BC² = 3² + 4² = 9 + 16 = 25
所以AC = √25 = 5 cm
由于∆ABC为直角三角形,所以AD也是AC的高线。
根据相似三角形性质可得:
BD/CD = AB/AC
代入已知值可得:
BD/CD = 3/5
又已知∠CDB=∠ABC,所以∆BCD与∆BAC相似。
根据相似三角形性质可得:
CD/BC = AC/AB
代入已知值可得:
CD/4 = 5/3
解方程可得:
CD = 20/3 cm
所以BD = BC - CD = 4 - 20/3 = 12/3 - 20/3 = -8/3 cm
由于BD是线段的长度,所以BD的长度不能为负数。因此,这个题目没有解。
题目2:平行线与三角形
已知平行线l₁和l₂分别与直线AB和AC相交于点D和E,且DE=5cm,BD=7cm,
CE=9cm。若∠BAC=90°,求两条平行线的距离。
解析:
首先我们可以利用勾股定理求出AD的长度:
AD² = AB² + BD² = BC² + CE²
代入已知值可得:
AD² = 7² + 9² = 49 + 81 = 130
所以AD = √130 cm
由于∆ABC为直角三角形,所以AD也是AC的高线。
根据平行线性质可得:
DE // BC
根据相似三角形性质可得:
DE/BC = AD/AC
代入已知值可得:
5/BC = √130/(7+9)
解方程可得:
BC ≈ 0.6 cm
所以两条平行线的距离为0.6 cm。
解决难题的方法
1. 理解几何原理
对于初中最难的几何题目,首先要理解几何原理。几何学是一门基础学科,其中的
原理和定理是解决问题的关键。通过深入理解几何原理,我们可以更好地应用这些
原理来解决复杂的几何问题。
2. 灵活运用几何知识
在解决难题时,需要将已学过的几何知识灵活运用。有时候,一个问题可能需要结
合多个几何概念和定理来解决。因此,在学习过程中要注重对各种几何知识的掌握,
并能够将它们灵活运用到实际问题中。
3. 多做练习题
练习是提高解题能力的关键。通过多做练习题,可以熟悉各种类型的几何问题,并
掌握相应的解题方法和技巧。同时,练习也可以帮助培养思维逻辑和分析问题的能
力,提高解决难题的能力。
总结
初中最难的几何题目对于学生来说可能会比较困难,但只要掌握了相应的几何原理
和解题方法,就能够解决这些难题。通过理解几何原理、灵活运用几何知识和多做
练习题,学生可以提高解决难题的能力,并在几何学中取得更好的成绩。希望本文
的介绍对于初中生学习几何学有所帮助。
