第一章 《数的整除》复习
数的整除复习

数的整除复习一.知识梳理1、整数:“零”既不是正整数,也不是负整数 2、整除:整数a 除以整数b ,如果除得的商正好是整数而没有余数,我们就说a 能被b 整除,或者说b 能整除a 。
3、因数和倍数:归纳:一个数的因数是有限的。
一个数的倍数的个数是无限的。
一个数的因数通常是成对出现的。
最小的因数是1,最大的因数是它本身。
最小的倍数是它本身,没有最大的倍数。
4、区别除尽和整除:除尽:最后结果是一个有限数;整除:最后结果是一个整数。
5、偶数与奇数如果一个整数能被2整除,称该整数为偶数。
如果一个整数不能被2整除,称该整数为奇数。
整数的分类⎩⎨⎧偶数奇数 整数正整数 零 负整数 自然数 条件: 除数、被除数都是整数 被除数除以除数,商是整数而且余数为零一个数的倍数是无限的,最小的倍数是它本身定义:整数a 能被整数b 整除,a 叫做b 的倍数,b 就叫做a 因数(也称为约数) 一个整数的因数的个数是有限的,最小的因数是1,最大的因数是它本身 因数倍数6、能被2、3、5整除的数的特征:7、素数、合数:我们把只含有因数1如果除了1分解素因数的方法:8、公因数与最大公因数如果两个整数只有公因数19、公倍数和最小公倍数:例题解析例1、填空题(1)有一个直角三角形,两条直角边是两个质数,长度和是18分米,这个三角形的面积是( )平方分米。
(2)一堆苹果,已知比50个多,比70个少,把它们可以平均分成两堆,也可以平均分成三堆,还可以平均分成五堆,这堆苹果有()个(3)六年级同学站队,每排5人多2人,每排6人多3人,每排7人则差2人,六年级学生人数不超过150人,那么他们应是( )人。
(4)某长途汽车站向北线每20分钟发一辆汽车,向南线每15分钟发一辆汽车,如果同时向两线发车,至少要经过( )分钟又同时发车。
巩固练习:(1)一盒铅笔可以平均分给2、3、5、6个小朋友,这盒铅笔最少有()人。
(2)一筐梨,按每份2个梨分多1个,每份3个多2个,每份5个多4个,筐里至少有()个梨。
初中数学复习第一讲 数的整除
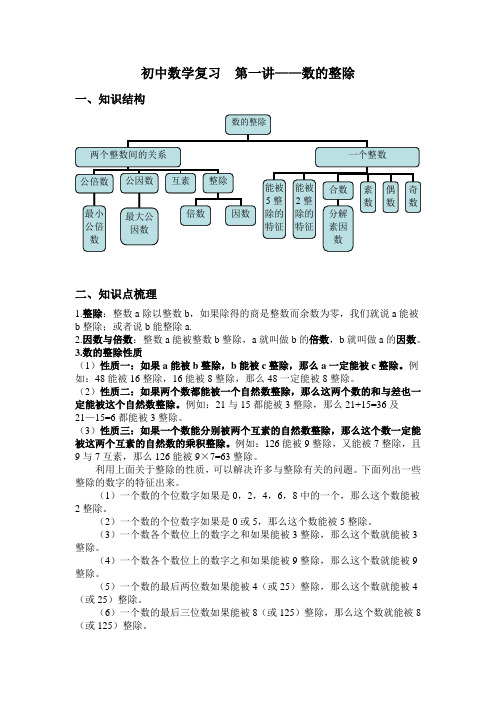
初中数学复习第一讲——数的整除一、知识结构二、知识点梳理1.整除:整数a除以整数b,如果除得的商是整数而余数为零,我们就说a能被b整除;或者说b能整除a.2.因数与倍数:整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数。
3.数的整除性质(1)性质一:如果a能被b整除,b能被c整除,那么a一定能被c整除。
例如:48能被16整除,16能被8整除,那么48一定能被8整除。
(2)性质二:如果两个数都能被一个自然数整除,那么这两个数的和与差也一定能被这个自然数整除。
例如:21与15都能被3整除,那么21+15=36及21—15=6都能被3整除。
(3)性质三:如果一个数能分别被两个互素的自然数整除,那么这个数一定能被这两个互素的自然数的乘积整除。
例如:126能被9整除,又能被7整除,且9与7互素,那么126能被9×7=63整除。
利用上面关于整除的性质,可以解决许多与整除有关的问题。
下面列出一些整除的数字的特征出来。
(1)一个数的个位数字如果是0,2,4,6,8中的一个,那么这个数能被2整除。
(2)一个数的个位数字如果是0或5,那么这个数能被5整除。
(3)一个数各个数位上的数字之和如果能被3整除,那么这个数就能被3整除。
(4)一个数各个数位上的数字之和如果能被9整除,那么这个数就能被9整除。
(5)一个数的最后两位数如果能被4(或25)整除,那么这个数就能被4(或25)整除。
(6)一个数的最后三位数如果能被8(或125)整除,那么这个数就能被8(或125)整除。
4.奇数与偶数:能被2整除的整数叫做偶数,不能被2整除的整数叫做奇数。
5.素数和合数:一个正整数,如果只有1和它本身两个因数,这样的数叫做素数,也叫做质数;如果除了1和它的本身以外还有别的因数,这样的数叫做合数。
1既不是素数,也不是合数。
6.分解素因数:每个合数都可以写成几个素数相乘的形式,其中每个素数都是这个合数的因数,叫做这个合数的素因数。
第一章 数的整除精讲

第一章数的整除1.1 整数和整除的意义重点概念:1.在数物体的时候,用来表示物体个数的数1,2,3,4,5,……,叫做整数2.在正整数1,2,3,4,5,……,的前面添上“—”号,得到的数—1,—2,—3,—4,—5,……,叫做负整数3. 零和正整数统称为自然数4.正整数、负整数和零统称为整数5.整数a除以整数b,如果除得的商正好是整数而没有余数,我们就说a能被b整除,或者说b能整除a。
运用巩固:1. 判断下列哪一个算式的被除数能被除数整除,并说明谁能被谁整除?谁能整除谁?11÷4 49÷7 8÷32.问题2:2.6÷1.3 = 2 ,能不能说2.6能被1.3整除?为什么?1.2 因数和倍数重点概念:1.如果整数a能被整数b整除,a就叫做b倍数,b就叫做a的因数2.倍数和因数是相互依存的3.一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身4.一个数的倍数的个数是无限的,其中最小的倍数是它本身运用巩固:1.填空:1)2的倍数有(从小到大写出5个)2)5的倍数有(从小到大写出5个)3)既是2的倍数又是5的倍数有(从小到大写出5个)2.一个整数的倍数有多少个?它有没有最大或最小的倍数?如果有,分别是什么?1.3能被2,5整除的数重点概念:1.个位数字是0,2,4,6,8的数都能被2整除2.整数可以分成奇数和偶数,能被2整除的数叫做偶数,不能被2整除的数叫做奇数3.在正整数中(除1外),与奇数相邻的两个数是偶数4.在正整数中,与偶数相邻的两个数是奇数5.个位数字是0,5的数都能被5整除6. 0是偶数运用巩固:1.简述:1).偶数,奇数的特征:2).整数的分类:3).能被2整除的整数的特征:4).能5整除的整数的特征:5).能被10整除的整数的特征:1.4 素数、合数与分解素因数重点概念:1.只含有因数1及本身的整数叫做素数或质数2.除了1及本身还有别的因数,这样的数叫做合数3. 1既不是素数也不是合数4.奇数和偶数统称为正整数,素数、合数和1统称为正整数5.每个合数都可以写成几个素数相乘的形式,这几个素数都叫做这个合数的素因数6.把一个合数用素因数相乘的形式表示出来,叫做分解素因数。
数的整除复习教案

既是奇数,又是合数的最小的一个数是( 9 ); 既是偶数,又是合数的最小的一个数是( 4 );
既不是质数,又不是合数的一个数是( 1 );
(2)能被3和5同时整除的最小三位数是(105),最大
三位数是(990); (3)小于10的所有质数的和是( 17 )。
?
练习
二、判断下面各题的正误
(1)自然数中只有质数和合数。
(× )
√ (2)最小的质数是自然数中全部偶数的最大公约数。( )
× (3)所有的偶数都是合数,所有的奇数都是质数。 ( )
(4)因为a÷b=8,所以 a一定是b的倍数。
(× )
(5)把153分解质因数是:153=3 × 51
(× )
?√ (6)在1-100的自然数中,有25个质数,74个合数。( )
你知道吗
(1) 1
?
38÷2=19
你知道吗
38的约数有:1 2 19 38
2的约数有: 1
2
19的约数有: 1 19
?
你知道吗
38 =2×19
?
你知道吗
除尽 整除
公倍数
最小公倍数
公约数
最大公约数
?
练习
一、填空
(1)在自然数中,既是质数,又是偶数的数是( 2 ); 既是质数,又是奇数的最小的一个数是( 3 );
数的整除整理复习

数的整除整理复习数的整除是小学数学中的一个重要内容,同时也是许多其他数学学科的基础知识。
在学习这一知识点时,需要掌握如何判断一个数是否能够被另一个数整除,并学会运用相关的计算方法,以便在实际问题中进行运用。
一、基本概念1.1 什么是整除一个整数a能被另一个整数b整除,是指存在另一个整数x,使得a = b × x。
用数学符号表示为:b | a (读作b整除a),即b是a的因数(或因子),a是b的倍数。
例如,4 | 12,表示4是12的因数,12是4的倍数,即12能被4整除。
1.2 整数的因数和倍数一个整数可以被其他整数整除,这意味着这个整数可以被其他整数整除,这些整数就是这个整数的因数。
例如,正整数12的因数为1、2、3、4、6、12。
一个整数的倍数是指能够被这个整数整除的数。
例如,12的倍数有12、24、36,即任何正整数n × 12都是12的倍数。
1.3 两个以上整数的公共因数对于两个以上的整数,如果它们有一个共同的因子,那么这个因子称为它们的公共因数。
例如,20和30的公共因数是1、2、5、10。
如果两个数没有公共因数(除1以外),那么它们称为互质数。
二、整除的判定方法判定一个数是否能被另一个数整除,常用的方法有以下几种:2.1 因数分解法因式分解法是指将一个数分解为若干个质因数的乘积,然后将这个数的因子全部列出来,再判断这个数是否能够被给定的整数整除。
对于一个正整数n,若其能分解为若干个质因数的乘积,其表达式为n = p1^k1 × p2^k2 × ... × pn^kn,则它的所有因子为p1^i1 × p2^i2 × ... × pn^in,其中0 ≤ i1 ≤ k1, 0 ≤ i2 ≤k2, …, 0 ≤ in ≤ kn。
例如,判断72是否能被8整除,我们先将72分解为2^3 × 3^2,再列出72的所有因子为1、2、3、4、6、8、9、12、18、24、36、72,经过检查,发现8是72的一个因子,因此72能够被8整除。
数的整除复习(吴正宪)

《数的整除复习》课堂实录(吴正宪)师:同学们今天这一节课我们要做一节有关数的整除的综合复习课,大家看到课前我在黑板上零零散散的贴出了这么多卡片,那么这些卡片上写的都是有关数的整除中的一些有关数的概念,那么我不知道当我们把这些知识学完以后,今天的复习第一件事我们能不能根据这些有关数的概念它的意义和他们之间的联系,把这些零零散散的概念做一次梳理,你认为哪个概念最重要你可以举例说明也可以呢根据他内在的联系和你认为他的数学概念把它整理一个比较系统的知识网络图,这事原来干过吗?没干过。
今天我们一起来试一试好不好!我不知道你们怎么分组,四人以小组还是怎么样分你们自己结合好不好?你认为哪个概念最重要它的概念下面又可以派生出哪些新的概念,那我们把这些做一个整理,好吗?把时间先给同学们,下面就自愿结合按照你们的老规矩,开始。
学生分组整理小组汇报生1:我们小组觉得整除是最重要的。
师:整除最重要是吗?那么整除最重要的你要把它先第一个出来是吗?那这样我就先把它放在最重要的位置。
生1:整除它还可以分为奇数和偶数。
师:整除还可以分为奇数和偶数?奇数和偶数是从整除这个角度去分的吗?同学们摇头呢!有意见呢!你选一位同学。
生1:赵俊艺师:赵俊艺有不同看法。
生2:我觉得整除它可以分为因数和倍数。
师:你为什么在整除下面分得出因数和倍数?生2:因为整除一个数,因数然后乘以倍数等于一个数,那么这个数可以除以因数等于倍数。
师:那么我的问题是,假如说数a能够被数b整除的话,那么想一想数a和数b一定有一个什么样的关系?你同意吗?生2:同意师:谁是谁的倍数?生2:a是b的倍数师:接着生2:b是a的因数师:你们同意这意见吗?生:同意师:她的意见说在整除的前提下一定会产生一种概念,什么?师生齐声:因数和倍数师:你为什么不同意她的意见呢?她说把奇数和偶数分出来就行了,你们可以有些讨论吗?生2:我觉得偶数和奇数应该不算在整除里面,它应该是数的名称。
师:偶数和奇数是在什么前提下产生的?它跟谁有关系?跟整除有关系没错,在具体点,我们怎么确定这个概念呢?是跟整除有关系,能在具体点吗?在什么情况下我就认定它是偶数了?生2:能被2整除的师:接下来,说完整,老说一半生2:能被2整除的那些自然数都是偶数生2:不能被2整除的那么就是奇数师:那你的意思偶数和奇数一定和一个重要的数有关系,是吗?师:和谁?生2:2师:同意吗?师:她说能被2整除的就是?生:偶数师:不能被2整除的就是?生:奇数师:那好,这样啊,你既然提出来了这个问题我把这2先补充到这里好不好,我先假如说补充到这里,那么跟它有关系的赶快拿啊,偶数和奇数学生拿卡片师:你认为他们有关系,是这个意思吗?能被2整数和不能被2整除的,对吗?他们的关系你们同意吗?生:同意师:他们认为在整除的前提下一定有一对非常重要的概念,是什么?一起说生:倍数和因数师:你们认可不认可这样的观点?生1:认可师:那赶快找出来学生找卡片师:这样啊,既然跟它有关系我帮你们放在上面好不好粘贴卡片因数、倍数师:你们的意思就是说当数a能被数b整除的时候,数a就是数b的倍数,那么数b就是数a的因数,是这意思吗?生:是师:接下来继续说,因数还能接着往下说吗?生:有公因数和公倍数,那么赶快跳出来啊学生找卡片师:又在下面的前提下产生了公因数和公倍数,你认为应该贴在哪里就贴下来,不同意见的赶快上来啊学生贴卡片师:贴在着跟他有关系是不是啊,你认为倍数和公倍数有关系,是吗?师:他认为因数公因数有关系,是吗?还有吗?生:还有最大公因数和最小公倍数师:那么你们的意思就是说因数可以引出公因数这个概念,对吗?生:对师:那请问什么叫公因数?生:公因数就2个数共有的因数叫做公因数师:共有的因数对不对?生:对师:那什么叫最大公因数啊?生:就是2个数最大的公因数师:几个数公有的因数,其中最大的一个是它的什么?生:最大公因数师:那你们能接着把这段概念总结完吗?生:2个数公共倍数就做公倍数,其中最小的一个就叫做最小公倍数师:同意吗?生:同意师:你们这么一说还挺有道理,的确,从因数当中我们可以引出公因数的概念,还可以引出最大公因数的概念,是这样吧?那么,从倍数当中我们可以引出公倍数的概念,那么其中最小的一个是最小公倍数,有没有意见?师:接下来还有这么多的概念那,你有不同意见,那你可以上来啊。
16-第15次课:数的整除章节复习一
例5、某数被2除余1,被3除余2,被4除余3,被5除余4,满足以上条件的数有多少个?求最小的一个.
例6、求两个自然数,使它们的和为84,它们的最大公约数为12.
练习:
两个合数的最大公因数是3,最小公倍数是30,则这两个数分别是多少?
4、课堂检测:
2.如果一个正整数除以5,商是2,余数是3,那么这个正整数是______.
3.能够被4整除的数是不是一定能被2整除_______.
4.既是60的因数,又是3的倍数的数有哪几个____________________.
5.个位数是2的倍数的数一定能被2整除,那么个位数为3,6,9的数是否都能被3整除呢?_____(是或不是).
分解素因数:
1.一个正整数,如果只有1和它本身两个因数,这样的数叫做素数,也叫做质数;如果除了1和它本身外还有别
的因数,这样的数叫做合数.
2.1既不是素数也不是合数.正整数又可以分为1,素数和合数三类.
3.每个合数都可以写成几个素数相乘的形式,其中每个素数都是这个合数的因数,叫做这个合数的素因数.把一
6.下列哪些数有因数2,哪些数有因数5?
12, 27, 25, 30, 51, 60, 75, 96, 186, 225
有因数2:____________________________________.
有因数5:____________________________________.
7、正整数可以分为、和合数三类.
8、素数有个因数,合数至少有个因数,1有个因数.
9、1到20的正整数中,素数有.
10、最小的素数是,最小的合数是.
11、1既不是也不是,唯一的一个既是偶数又是素数的数是.
第1章数的整除【真题训练】-2020年六年级数学上册单元复习一遍过(沪教版)原卷版
第1章数的整除【真题训练】考试时间90分钟 满分100分一、填空题(本大题共有14题,每题2分,共28分)1.(2019南模初中10月考1) 最小的自然数是.2.(2019曹杨二附10月考1)在515,5.6,87,9,5---+中,是非负正整数的是. 3.(2019大同初中10月考7)4.8÷3=1.6,填“能”或“不能”)说3能整除4.84.(2019晋元附校测试10)有一个数,它既是a 的倍数,又是a 的因数,这个数是__________.5.(2019松江九亭10月考1)写出既能被2整除又能被5整除的最小的两位__________.6.(2019中国中学10月考6)三位数75□能同时被2、3整除,那么□可以是。
7.(2019松江九亭10月考11)18的因数有__________,18的素因数有__________。
8.(2019徐教院附中10月考13)36的因数:___________________,50以内9的倍数:____________.9.(浦东四署2019期中11)一个三位数,百位是最小的合数,十位是最小的素数,且能被2和5整除,这个数是.10. (奉贤2019期中19)规定一个新运算:对于不小于3的正整数n ,(n )表示不是n 的因数的最小正整数,如5的因数是1和5,所以(5)=2;再如8的因数是1、2、4和8,所以(8)=3等等,请你在理解这种新运算的基础上,求(6)+(24)=.11.(黄浦2016期中9) 24与18的最大公因数是,最小公倍数是。
12.(闵行2016期中10)已知M=2⨯3⨯5 ,N=2⨯2⨯3,则M 和N 的最小公倍数是______.13.(浦东四署2015期中9)最小合数的倒数是.14.(黄浦2016期中18)数学家歌德巴赫通过研究下面一系列等式,作出了一个著名的猜想. 4=2+2; 12=5+7;6=3+3; 14=3+11=7+7;8=3+5; 16=3+13=5+11;10=3+7=5+5; 18=5+13=7+11;……通过这组等式,你发现的规律是(请用文字语言表达).二.选择题(本大题共有4个小题,每题3分,共12分)15.(2019上南中学10月考1)下列关于“1”的叙述不正确的是()A.1是最小的自然数;B.1既不是素数,也不是合数;C.1是奇数;D.1能整除任何一个正整数.16.(2019上南中学10月考3)下列说法正确的是()A.任何整数的因数至少有2个;B.一个数的因数都比这个数的倍数小;C.连续两个自然数相加的和一定是奇数;D.8是因数,12是倍数.17.(2019进才北12月考1)下列说法正确的是()A. 一个整数不是正整数就是负整数B. 一个正整数不是素数就是合数C. 一个正整数不是奇数就是偶数D. 一个正整数的最大因数不是它的最小倍数.18.(2019闵行实验西校10月考5)下列语句错误的是()①2.5能被5整除;②因为4÷2=2,所以4是倍数,2是因数;A=2×3×5×B,B>1,则B一定是A的因素;④两个整数的公倍数一定能被这两个数整除;A.1个;B.2个;C.3个;D.4个.三、解答题(本大题共有6题,每题5分,共30分)19.(2019浦东四署10月考19)把下列各数填入指定的圈内(每个数只能使用一次).1,2,4,5,12,24,30,40,52,60,10020.(2019大同初中10月考21)把下列各数填在适当的内:9,0,0.23, -53, 559, 26, -1正整数负整数自然数21.三位数B2A能同时被2、3、5整除,求字母A、B.22.求出100以内是9的倍数的所有偶数的和.23.杨浦2015期中19)用短除法求45与27的最大公因数和最小公倍数。
01-六年级数的整除复习
教学目标理解整除的意义;因数与倍数;素数、合数、分解素因数.重点、难点素数、最小公倍数与最大公因数;考点及考试要求利用短除法分解素因数、求最大公因数与最小公倍数.教学内容一、知识点回顾与重点题型讲解第一章:数的整除1. 零和正整数统称为自然数。
正整数、零、负整数统称为整数。
重点题型:1. 在8,-10,0,0.25,-50,73,100,-8.5中,正整数有,自然数有,整数有2.最小的自然数是提高:非负整数,如小于3的非负整数有2. 整数a除以整数b,如果除得的商是整数而余数为零,我们就说a能被b整除,或者说b能整除a。
用式子表示:如果 a÷b=c(其中a、b,c都为整数)称a能被b整除或b能整除a。
(区分两种表述)重点题型:1. 下列各组数中,第一个数能被第二个数整除的是,第二个数能整除第一个数的是12和24;39和13;54和27;46和4;17和51;84和72. 12÷3=4,那么能被整除;能整除3. 整除的条件:1)除数,被除数都为整数2)被除数除以除数,商是整数而且余数为零。
重点题型:小明认为2.5能被5整除。
这种说法对吗?4. 整数a被整数b整除,a叫b的倍数(mutiple),b叫a的因数(factor)(也称为约数)因数和倍数是相互依存的。
重要结论:一个整数的因数的个数是的(填:无限或有限),其中最小的因数是,最大的因数是。
一个整数的倍数的个数是的(填:有限或无限),其中最小的倍数是,一个整数最大的倍数。
重点题型:1. 因为4÷2=2,所以4是倍数,2是因数,这种说法对吗?2. 一个整数的最大因数减去这个正整数的最小倍数,所得的差一定()A <0B =0C >0D 不等于03. 会求一个数的因数:如求105的因数4. 会求一个数的倍数:如求7的倍数(写出5个)5. 任何一个正整数至少有两个因数。
( )6. 如果一个数既是12的因数,又是12的倍数,那么这个数一定是。
261第一章数的整除知识点
第一章数的整除知识点的整理2不是整数.例如:12,0,—7都是整数. 1.5,注意:“3个字换,4个字不换”.(3)数a除以数b,如果商是整数或有限小数,我们就说a能被b除尽;或者说b能除尽a.如果商是无限循环小数,我们就说a不能被b除尽;或者说b除不尽a.例题1 下列哪一个算式的被除数能被除数整除?10÷3 48÷8 6÷4●解:∵10÷3=3.3∴10不能被3除尽,或3除不尽10.∵48÷8=6∴48能被8整除,或8能整除48.∵6÷4=1.5一般情况下,大数是小数的倍数,小数是大数的因数.例题2 分别写出16和13的因数.解:16的因数有1,2,4,8,16.13的因数有1,13.☆求因数的方法:用除法,从1开始试到这个数本身.☆一个整数的因数有有限个,其中最小的因数是1,最大的因数是它本身.例题3 写出2和5的倍数.解:2的倍数有2,4,6,8,10,…5的倍数与5,10,15,20,25,…☆求倍数的方法:用乘法,从这个数本身开始,找它的2倍,3倍,…☆一个整数的倍数有无数个,最小的倍数是它本身,最大的倍数是没有.合数: 4, 6, 8, 9, 10, 12, 14, 15,…☆2是最小的素数,唯一的偶素数. 4是最小的合数.9是最小的奇合数.☆1既不是素数,也不是合数.这样正整数又可以分成1、素数和合数三类.☆100以内的素数有2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,解:29,37是素数.(它们不是2,3,5,7的倍数)☆素因数既是素数,也是合数的因数.例题5 把60分解素因数.解:602235=⨯⨯⨯注意:60的素因数有2,2,3,5. 共4个.☆用短除法分解素因数(1)用2,3,5,7,…作为除数去试商. (2)直到商为素数.(3)将除数和商一起从小到大写成连乘的形式.解:∴18和30的最大公因数为236⨯=.☆最大公因数=公有素因数的乘积例题7 求48和60的最大公因数.(短除法)解:∴48和60的最大公因数为22312⨯⨯=.☆用公有素因数作为除数,连续去除直到商互素.最大公因数=所有除数的乘积. 602302155318233=⨯⨯30235=⨯⨯486022430212153546和7的最大公因数为1.例题8 求18和30的最小公倍数.(分解素因数法)解:∴18和30的最小公倍数为233590⨯⨯⨯=.☆最小公倍数=公有素因数和剩余素因数连乘的积.例题9 求36和48的最小公倍数.(短除法)解:∴36和48的最小公倍数为22337252⨯⨯⨯⨯=.☆用公有素因数作为除数,连续去除直到商互素.最小公倍数=所有6和7的最小公倍数为6×7=42.拓展 求三个整数的最小公倍数例题 求8,12和30的最小公倍数.8,12和30的最小公倍数为2×2×3×2×1×5=120.☆先用三个数的公因数2;再用两个数的公因数2,3;直到任意两 个商都互素,把所有的除数和商都相乘.18233=⨯⨯30235=⨯⨯36842184229213738123024615223153215。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 《数的整除》复习
知识点:
1、数的整除
2、写出因数与分解素因数的区别;
3、互素的两个数的最大公因数与最小公倍数
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧最小公倍数公倍数最大公因数公因数互素倍数因数
整除整数间的关系整除的数的特征能被整除的数的特征能被整除的数的特征能被分解素因数合数素数
奇数
偶数
一个整数------------532------1
练习选讲:
一、填空题:
(i)统称为自然数。
(ii)在正整数中,(有或没有)最大的数;(有或没有)最小的数。
(iii)2.8÷2=1.4,(能或不能)说2整除2.8。
(iv)16的因数从小到大有。
(v)20以内的正整数中,3的倍数从小到大有。
(vi)正整数按照数的奇偶性可分为奇数和偶数两类,若a >3,且a是奇数,与a相邻奇数是。
(vii)的数称为素数,
的数称为合数。
写出20以内的所有素数,
写出20以内的所有的合数。
(viii)分解素因数:72=。
(ix)16和24的最大公因数是。
在20以内2和3的公倍数有。
(x)一堆苹果,比50个多,比70个少,把它们可以平均分成两堆,也可以平均分成三堆,还可以平均分成五堆。
这堆苹果有个,还可以分成堆。
二、判断题:
(i)20能整除4()。
(ii)1既是奇数也是偶数()。
(iii)1既不是素数也不是合数()。
(iv)合数不都是偶数,素数不都是奇数()。
(v)52=13×4,13和4都是52的因数。
()。
(vi)因为52=13×4;所以我们说13和4的公倍数只有52一个。
()
(vii)互素的两个数一定都是素数()。
(viii)两个素数一定互素()。
(ix)两个数的积一定是这两个数的公倍数()。
(x)两个数的最小公倍数一定是这两个数的最大公因数的倍数()。
三、选择题:
(i)48全部因数共有()个。
(A)9个(B)8个(C)10个(D)12个
(ii)在14=2×7中,2和7都是14的()。
(A)素数(B)互素数(C)素因数(D)公因数
(iii)a和b是互素数,它们的最小公倍数是()。
(A)a (B)b (C)1 (D)ab
(iv)一间长方形的房屋装修时用正方形的地砖正好铺满,那么这间房屋的长和宽都应该是正方形边长的倍数,正方形地砖的边长应该是长方形的长和宽的()。
(A)公因数(B)最大公因数(C)公倍数(D)最小公倍数
(v)一个汽车站内有两路公共汽车,甲路汽车每隔a分钟发一次车,乙路汽车每隔b分钟发一次车,这两路汽车同时发车后,紧接的下次又同时发车的时间是a和b的()。
(A)公因数(B)最大公因数(C)公倍数(D)最小公倍数
四、用短除法求出下列各组数的最大公因数和最小公倍数:(i)42和63 (iii)8和20
五、某学校同学做操,把同学们分成10人一组,14人一组,18人一组,正好分完,并且知道这个学校学生的人数超过1000人,这个学校至少有多少个学生?
六、理解总结题:
先把42和30分解素因数,再回答下面的问题:
(i)42=。
30=。
(ii)42和30全部公有的素因数有。
(iii)42和30各自独有的素因数有。
(iv)42和30的最大公因数是。
(v)42和30的最小公倍数是。
(vi)通过以上解答,你能总结的是。
七、我们设a为大于3的正偶数,那么紧邻它而比它小的偶数可以表示为a-2,紧邻它而比它大的偶数可以表示为a+2,因为a+(a-2)+(a+2)=3a,所以我们可以说三个连续的偶数之和一定能被3整除。
试用上面的方法说明“三个连续的正整数之和能被3整除”。
