概率积分法公式
概率论公式汇总
Pn ( k ) C n p k q n k
k
， k 0,1,2, , n 。
第二章
随机变量及其分布
基本事件 随机事件A P ( A) 随机变量X ( ) a X b F (b) F (a )
设离散型随机变量 X 的可能取值为 Xk(k=1,2,…)且取各个值的概率，即事 件(X=Xk)的概率为 P(X=xk)=pk，k=1,2,…， （1）离散 型随机变 量的分布 律 则称上式为离散型随机变量 X 的概率分布或分布律。有时也用分布列的形 式给出：
P ( A)
（10）加法 公式 （11）减法 公式
L( A) 。其中 L 为几何度量（长度、面积、体积） 。 L ()
P(A+B)=P(A)+P(B)-P(AB) 当 P(AB)＝0 时，P(A+B)=P(A)+P(B) P(A-B)=P(A)-P(AB) 当 B A 时，P(A-B)=P(A)-P(B) 当 A=Ω时，P( B )=1- P(B) 定义 设 A、B 是两个事件，且 P(A)>0，则称
德摩根率： i 1
A A
i i 1
i
A B A B， A B A B
设 为样本空间， A 为事件，对每一个事件 A 都有一个实数 P(A)，若满 足下列三个条件： 1° 0≤P(A)≤1， 2° P(Ω) =1 （7）概率 的公理化 定义 3° 对于两两互不相容的事件 A1 ， A2 ，…有
P(A)= ( 1 ) ( 2 ) ( m ) = P( 1 ) P( 2 ) P( m )
设任一事件 A ，它是由 1 , 2 m 组成的，则有
概率论核心概念及公式
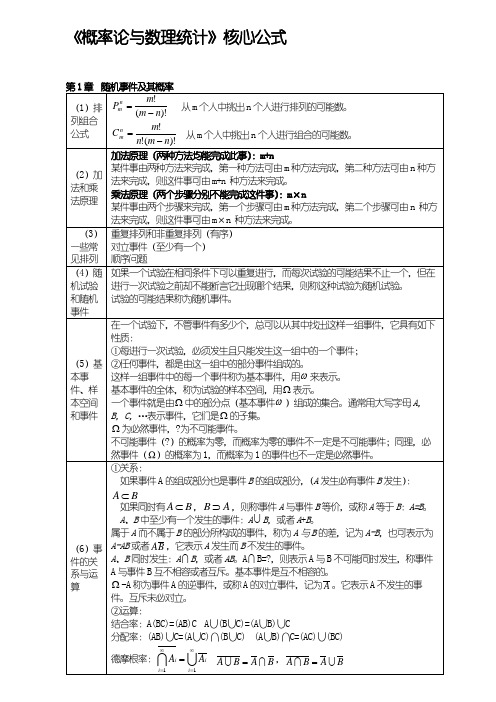
②运算：
结合率：A(BC)=(AB)C A∪(B∪C)=(A∪B)∪C
分配率：(AB)∪C=(A∪C)∩(B∪C) (A∪B)∩C=(AC)∪(BC)
德摩根率： ，
（7）概率的公理化定义
设 为样本空间， 为事件，对每一个事件 都有一个实数P(A)，若满足下列三个条件：
若 ，则 的分布函数为
。。
参数 、 时的正态分布称为标准正态分布，记为 ，其密度函数记为
， ，
分布函数为
。
是不可求积函数，其函数值，已编制成表可供查用。
Φ(-x)＝1-Φ(x)且Φ(0)＝ 。
如果 ~ ，则 ~ 。
。
（6）分位数
下分位表： ；
上分位表： 。
（7）函数分布
离散型
已知 的分布列为
，
的分布列（ 互不相等）如下：
，
若有某些 相等，则应将对应的 相加作为 的概率。
连续型
先利用X的概率密度fX(x)写出Y的分布函数FY(y)＝P(g(X)≤y)，再利用变上下限积分的求导公式求出fY(y)。
第三章 二维随机变量及其分布
（1）联合分布
离散型
如果二维随机向量 （X，Y）的所有可能取值为至多可列个有序对（x,y），则称 为离散型随机量。
。其中L为几何度量（长度、面积、体积）。
（10）加法公式
P(A+B)=P(A)+P(B)-P(AB)
当P(AB)＝0时，P(A+B)=P(A)+P(B)
（11）减法公式
P(A-B)=P(A)-P(AB)
当B A时，P(A-B)=P(A)-P(B)
概率论核心概念及公式全
2° A n Bi ，P(A) 0 ，
i 1
则
公式
P(Bi / A)
P(Bi )P( A / Bi )
n
，i=1，2，…n。
P(Bj )P(A/ Bj )
j 1
此公式即为贝叶斯公式。
①两个事件的独立性
设事件 A 、B 满足P(AB) P(A)P(B) ，则称事件 A 、B 是相互独立的。 若事件 A 、B 相互独立，且P(A) 0 ，则有
P(B | A) P( AB) P( A)P(B) P(B)
P( A)
P( A)
若事件 A 、B 相互独立，则可得到 A 与B 、A 与B 、A 与B 也都相互
F (x) x f (x)dx ，
则称 X 为连续型随机变量。 f (x) 称为 X 的概率密度函数或密度函数，
简称概率密度。
密度函数具有下面 4 个性质：
1° f (x) 0 。
2° f (x)dx 1。
（3）离 P(X x) P(x X x dx) f (x)dx 散与连 积分元 f (x)dx 在连续型随机变量理论中所起的作用与P(X xk) pk 续型随 在离散型随机变量理论中所起的作用相类似。
机试验 一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试
和随机 验为随机试验。
事件 试验的可能结果称为随机事件。
在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，
它具有如下性质：
①每进行一次试验，必须发生且只能发生这一组中的一个事件；
②任何事件，都是由这一组中的部分事件组成的。
(整理)概率论公式大全
第一章随机事件和概率（1）排列组合公式从m个人中挑出n个人进行排列的可能数。
从m个人中挑出n个人进行组合的可能数。
（2）加法和乘法原理加法原理（两种方法均能完成此事）：m+n某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n 种方法来完成，则这件事可由m+n 种方法来完成。
乘法原理（两个步骤分别不能完成这件事）：m×n某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n 种方法来完成，则这件事可由m×n 种方法来完成。
（3）一些常见排列重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题（4）随机试验和随机事件如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。
试验的可能结果称为随机事件。
（5）基本事件、样本空间和事件在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：①每进行一次试验，必须发生且只能发生这一组中的一个事件；②任何事件，都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件，用来表示。
基本事件的全体，称为试验的样本空间，用表示。
一个事件就是由中的部分点（基本事件）组成的集合。
通常用大写字母A，B，C，…表示事件，它们是的子集。
为必然事件，Ø为不可能事件。
不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω）的概率为1，而概率为1的事件也不一定是必然事件。
（6）事件的关系与运算①关系：如果事件A的组成部分也是事件B的组成部分，（A发生必有事件B发生）：如果同时有，，则称事件A与事件B等价，或称A等于B：A=B。
A、B中至少有一个发生的事件：A B，或者A+B。
属于A而不属于B的部分所构成的事件，称为A与B的差，记为A-B，也可表示为A-AB或者，它表示A发生而B不发生的事件。
概率统计公式大全(复习重点)
第一章随机事件和概率（1）排列组合公式)!(!nmmP nm-=从m个人中挑出n个人进行排列的可能数。
)!(!!nmnmC nm-=从m个人中挑出n个人进行组合的可能数。
（2）加法和乘法原理加法原理（两种方法均能完成此事）：m+n某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n 种方法来完成，则这件事可由m+n 种方法来完成。
乘法原理（两个步骤分别不能完成这件事）：m×n某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n 种方法来完成，则这件事可由m×n 种方法来完成。
（3）一些常见排列【重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题（4）随机试验和随机事件如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。
试验的可能结果称为随机事件。
（5）基本事件、样本空间和事件在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：①每进行一次试验，必须发生且只能发生这一组中的一个事件；②任何事件，都是由这一组中的部分事件组成的。
^这样一组事件中的每一个事件称为基本事件，用ω来表示。
基本事件的全体，称为试验的样本空间，用Ω表示。
一个事件就是由Ω中的部分点（基本事件ω）组成的集合。
通常用大写字母A，B，C，…表示事件，它们是Ω的子集。
Ω为必然事件，Ø为不可能事件。
不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω）的概率为1，而概率为1的事件也不一定是必然事件。
（6）事件的关系与运算①关系：如果事件A的组成部分也是事件B的组成部分，（A发生必有事件B发生）：BA⊂如果同时有BA⊂，AB⊃，则称事件A与事件B等价，或称A等于B：A=B。
A、B中至少有一个发生的事件：A B，或者A+B。
概率公式大全
第一章随机事件和概率第二章随机变量及其分布第三章二维随机变量及其分布第四章随机变量的数字特征第六章样本及抽样分布单正态总体均值和方差的假设检验公式整理1．随机事件及其概率吸收律：A AB A A A A =⋃=∅⋃Ω=Ω⋃)( AB A A A AA =⋃⋂∅=∅⋂=Ω⋂)()(AB A B A B A -==-反演律：B A B A =⋃ B A AB ⋃=n i in i iA A 11=== ni in i iA A 11===2．概率的定义及其计算)(1)(A P A P -=若B A ⊂ )()()(A P B P A B P -=-⇒对任意两个事件A ， B , 有 )()()(AB P B P A B P -=- 加法公式：对任意两个事件A , B ， 有)()()()(AB P B P A P B A P -+=⋃ )()()(B P A P B A P +≤⋃)()1()()()()(2111111n n nnk j i kjinj i jini i n i i A A A P A A A P A A P A P A P -≤<<≤≤<≤==-+++-=∑∑∑3．条件概率 ()=A B P )()(A P AB P 乘法公式())0)(()()(>=A P A B P A P AB P()())0)(()()(12112112121>=--n n n n A A A P A A A A P A A P A P A A A P 全概率公式∑==ni i AB P A P 1)()( )()(1i ni i B A P B P ⋅=∑=Bayes 公式)(A B P k )()(A P AB P k =∑==n i i i k k B A P B P B A P B P 1)()()()(4．随机变量及其分布 分布函数计算)()()()()(a F b F a X P b X P b X a P -=≤-≤=≤<5．离散型随机变量 (1) 0 – 1 分布1,0,)1()(1=-==-k p p k X P k k（2) 二项分布 ),(p n B 若P ( A ） = pn k p p C k X P k n kk n ,,1,0,)1()( =-==-*Possion 定理0lim >=∞→λn n np有,2,1,0!)1(lim ==---∞→k k ep p C kkn n k nk n n λλ（3) Poisson 分布 )(λP,2,1,0,!)(===-k k ek X P kλλ6．连续型随机变量 (1） 均匀分布 ),(b a U⎪⎩⎪⎨⎧<<-=其他,0,1)(b x a ab x f ⎪⎪⎩⎪⎪⎨⎧--=1,,0)(a b a x x F（2) 指数分布 )(λE⎪⎩⎪⎨⎧>=-其他,00,)(x e x f x λλ⎩⎨⎧≥-<=-0,10,0)(x e x x F xλ （3） 正态分布 N (μ ， σ 2 ）+∞<<∞-=--x e x f x 222)(21)(σμσπ⎰∞---=xt t ex F d 21)(222)(σμσπ*N (0，1) — 标准正态分布+∞<<∞-=-x ex x 2221)(πϕ+∞<<∞-=Φ⎰∞--x t e x xt d 21)(22π7.多维随机变量及其分布二维随机变量（ X ，Y ）的分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),(边缘分布函数与边缘密度函数⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()(⎰+∞∞-=dv v x f x f X ),()(⎰⎰∞-+∞∞-=yY dudv v u f y F ),()(⎰+∞∞-=du y u f y f Y ),()(8. 连续型二维随机变量（1） 区域G 上的均匀分布，U （ G ）⎪⎩⎪⎨⎧∈=其他,0),(,1),(Gy x A y x f(2）二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+------y x ey x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9. 二维随机变量的 条件分布0)()()(),(>=x f x y f x f y x f X X Y X0)()()(>=y f y x f y f Y Y X Y⎰⎰+∞∞-+∞∞-==dy y f y x f dy y x f x f Y Y X X )()(),()(⎰⎰+∞∞-+∞∞-==dx x f x y f dx y x f y f X X Y Y )()(),()()(y x f Y X )(),(y f y x f Y =)()()(y f x f x y f Y X X Y = )(x y f X Y )(),(x f y x f X =)()()(x f y f y x f X Y Y X = 10.随机变量的数字特征数学期望∑+∞==1)(k k k p x X E⎰+∞∞-=dx x xf X E )()(随机变量函数的数学期望 X 的 k 阶原点矩)(k X E X 的 k 阶绝对原点矩)|(|k X E X 的 k 阶中心矩)))(((k X E X E - X 的 方差)()))(((2X D X E X E =- X ，Y 的 k + l 阶混合原点矩)(l k Y X E X ，Y 的 k + l 阶混合中心矩()l k Y E Y X E X E ))(())((--X ，Y 的 二阶混合原点矩)(XY EX ，Y 的二阶混合中心矩 X ，Y 的协方差()))())(((Y E Y X E X E --X ,Y 的相关系数XY Y D X D Y E Y X E X E ρ=⎪⎪⎭⎫⎝⎛--)()())())((( X 的方差D （X ） =E (（X — E (X )）2))()()(22X E X E X D -=协方差()))())(((),cov(Y E Y X E X E Y X --=)()()(Y E X E XY E -=())()()(21Y D X D Y X D --±±= 相关系数)()(),cov(Y D X D Y X XY =ρ⎰∞---=xt t ex F d 21)(222)(σμσπ＊N (0,1） — 标准正态分布+∞<<∞-=-x e x x 2221)(πϕ+∞<<∞-=Φ⎰∞--x t e x xt d 21)(22π7.多维随机变量及其分布二维随机变量（ X ,Y )的分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),(边缘分布函数与边缘密度函数⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()(⎰+∞∞-=dv v x f x f X ),()(⎰⎰∞-+∞∞-=yY dudv v u f y F ),()(⎰+∞∞-=du y u f y f Y ),()(8. 连续型二维随机变量（1） 区域G 上的均匀分布，U （ G ）⎪⎩⎪⎨⎧∈=其他,0),(,1),(Gy x A y x f(2）二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+------y x ey x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9。
概率公式大全
随机变量的的概率为分布律p(X=xk)=pk, k=1,2, ；••则称上式为离散型随机变量的概率分布或分布律。
有时也用分布列的形式给出:显然分布律应满足下列条件:(1) ；；(2)。
(2)连续型设是随机变量的分布函数，若存在非负函数，对任意实数，有随机变量的分布密度则称为连续型随机变量。
称为的概率密度函数或密度函数，简称概率密度。
密度函数具有下面4个性质:(3)离散与在离散型随机变量理论中所起积分元在连续型随机变量理论中所起的作用与连续型随机的作用相类似。
变量的关系(4)分布函设为随机变量；是任意实数；则函数称为随机变量X的分布函数，本质上是一个累积函数。
可以得到X落入区间的概率。
分布函数表示随机变量落入区间(-a, x］内的概率。
分布函数具有如下性质:是单调不减的函数，即时，有；，即是右连续的;4i 1i 1P(B A)P(B) P(A) 对任意两个事件A, B,有P(B A)P(B) P(AB)加法公式：对任意两个事件A, B,有P(A B) P(A) P(B) P(AB)P(A B)P(A) P(B)P(AA j AQ(1)n1P(A i A 2A n ) 3 .i 1i 11 i j n1 i j k n条件概率P B AP(AB) P(A)乘法公式P(AB) P(A)P B A (P(A) 0)P(AA A n )P(A)P A A 1PA nAAA 1 1全概率公式P(A)nP(AB i )P(B i ) P(A B i )公式整理P(A) 1 P(A)吸收律：A AAAB)AA A(AB) AA (A A BAB A (AB)反演律：AB A^BAB A BnnnnA iAi 1i 1 i 1i 11.随机事件及其概率2 •概率的定义及其计算AP(AA j )(P(AA 2A n 1)0)nP( A)nP(A i )nP(BJP(A B k )~nP(B i )P(AB i )i 14 .随机变量及其分布分布函数计算P(a X b) P(X b) P(X a)F(b) F(a)5 .离散型随机变量 (1)0 -1分布P(X k) p k (1 p)1k , k 0,1⑵二项分布 B(n,p)若 P ( A ) = pP(X k) c ：p k (1 p)n k , k 0,1, ,n*Possion 定理lim np nnk若 limC n P n (1 P n )n e 一有nk!k 0,1,2,⑶ Poisson 分布 P()kP(X k) e —, k 0,1,2,k!6 .连续型随机变量 (1)均匀分布U(a,b),a x b f(x) b aBayes 公式P(B k A)P(AB k ) P(A)0,0, 其他F(x)(2)指数分布E()f(x)0, 其他F(x)0, x 0 1 e x, x 0(3)正态分布N ( , 2 )(x f(x))2 2厂1 x F(x) (2)(t )2e F dt* N (0,1)—标准正态分布1(x)、2 °~2(x)、2t2 'dt7•多维随机变量及其分布二维随机变量(X，丫)的分布函数x yF(x, y) f(u,v)dvdu 边缘分布函数与边缘密度函数xF X (x) f (u, v)dvdu f x(x) f (x,v)dvyF Y(y) f (u,v)dudvf v(y) f (u, y)du8.连续型二维随机变量0,10.随机变量的数字特征数学期望E(X) X k P kk 1E(X) xf (x)dx随机变量函数的数学期望kx 的k 阶原点矩E(x )kx 的k 阶绝对原点矩E(| x | ) kx 的k 阶中心矩E((x E(x)))(1)区域G 上的均匀分布，U ( G )1 f(x, y) A ，0,(x, y) G 其他(2)二维正态分布f(x,y)(x 1)22 (x 1)(y2)212 (y 2)22 29.二维随机变量的条件分布f(x,y)f x (x )f Y|x (yx ) f x (x) f x (x) f Y (y)f x|Y (xy)fY|x(yx)f Y (y) f xY (x y)f(x, y)dy f (x, y)dx f(x, y f Y (y) f(x, y) f x (x)f Y (y)f x|Y (x y) f Y (y)dy f Y|x (yx)f x (x)dxf Yx (yx)f x (x)f Y (y) f xY (x|y) f Y (y)f x (x)2X 的方差 E((X E(X))2) D(X) X ，丫的k + l 阶混合原点矩E(X k Y l ) X ,Y 的k + l 阶混合中心矩E (X E(X))k (Y E(Y))1X ,Y 的 二阶混合原点矩 E(XY) X ,Y 的二阶混合中心矩X ，丫的协方差E(X E(X))(Y E(Y))X ,Y 的相关系数X 的方差D (X) =E ((X - E(X))2)2 2D(X) E(X ) E (X)协方差E(XY) E(X)E(Y)1D(X Y) D(X) D(Y)2(t )2e 2 2dt* N (0,1)— 标准正态分布x 2E (X E(X))(YE(Y))、D(X )e (Y)XYcov(X,Y)E (X E(X))(Y E(Y))相关系数XYcov(X,Y) D(X) ." D(Y)F(x)1 x1 e 2dt27•多维随机变量及其分布二维随机变量(X，丫)的分布函数x yF(x,y) f(u,v)dvdu边缘分布函数与边缘密度函数xF X(x) f (u,v)dvduf x(x) f (x,v)dvyF Y(y) f (u,v)dudvf v(y) f (u, y)du8.连续型二维随机变量(1)区域G上的均匀分布，U ( G )1f(x,y) A，(x，y) G0, 其他(2)二维正态分布f(x,y) f x(x)f Y|x(yx) f x(x) 0f Y(y)f xY(xy) f y(y) 0f x(x) f(x, y)dy f x|Y(x y) f y (y)dy f Y(y) f (x, y)dx f Y|x(yx)f x(x)dx f x,Y(xy) gf Yx (yx)fx(x)f(x,y)12 1 2、、1 2(x J 22~ 乙1(y 2)22~2(X 1)(y 2)1 29.二维随机变量的条件分布f Y(y)f Y(y)10.随机变量的数字特征数学期望E(X) X k P kk 1E(X) xf (x)dx随机变量函数的数学期望kX 的k 阶原点矩E(X )X 的k 阶绝对原点矩E(| X |k )X 的k 阶中心矩E((X E(X))k )2X 的方差 E((X E(X)) ) D(X)k lX ,Y 的k + l 阶混合原点矩E(X Y ) X ,Y 的k + l 阶混合中心矩k l E (X E(X)) (Y E(Y))X ,Y 的 二阶混合原点矩 E(XY) X ,Y 的二阶混合中心矩 X ,Y 的协方差 E(X E(X))(Y E(Y))X ,Y 的相关系数 (X_E(X))(Y_E(Y))、,D(X)\D(Y)X 的方差D (X) =E ((X - E(X))2) f Y|x (yx ) f(x, y)f x (x) f xY (x|y)f Y (y) f x (x)XYD(X) E(X2) E2(X) 协方差cov(X,Y) E (X E(X))(Y E(Y))E(XY) E(X)E(Y)1-D(X Y) D(X) D(Y)2相关系数cov(X,Y)XY.D(X).“D(Y)。
概率公式大全
第一章随机事件和概率第二章随机变量及其分布第三章二维随机变量及其分布第四章随机变量的数字特征第五章大数定律和中心极限定理第六章样本及抽样分布第七章参数估计第八章假设检验单正态总体均值和方差的假设检验公式整理1．随机事件及其概率吸收律：AAB A AA A =⋃=∅⋃Ω=Ω⋃)( AB A A A AA =⋃⋂∅=∅⋂=Ω⋂)(反演律：B A B A =⋃ B A AB ⋃= 2．概率的定义及其计算若B A ⊂ )()()(A P B P A B P -=-⇒对任意两个事件A , B , 有 )()()(AB P B P A B P -=- 加法公式：对任意两个事件A , B , 有)()1()()()()(2111111n n nnk j i kjinj i jini i n i i A A A P A A A P A A P A P A P -≤<<≤≤<≤==-+++-=∑∑∑3．条件概率()=A B P)()(A P AB P 乘法公式()())0)(()()(12112112121>=--n n n n A A A P A A A A P A A P A P A A A P 全概率公式Bayes 公式4．随机变量及其分布 分布函数计算 5．离散型随机变量 (1) 0 – 1 分布 (2) 二项分布 ),(p n B 若P ( A ) = p *Possion 定理有,2,1,0!)1(lim ==---∞→k k ep p C kkn n k nk nn λλ(3) Poisson 分布 )(λP 6．连续型随机变量 (1) 均匀分布 ),(b a U (2) 指数分布 )(λE (3) 正态分布 N ( , 2 ) *N (0,1) — 标准正态分布 7.多维随机变量及其分布二维随机变量( X ,Y )的分布函数 边缘分布函数与边缘密度函数 8. 连续型二维随机变量(1) 区域G 上的均匀分布，U ( G ) (2)二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+------y x ey x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9. 二维随机变量的 条件分布10.随机变量的数字特征 数学期望随机变量函数的数学期望X 的 k 阶原点矩)(k X E X 的 k 阶绝对原点矩)|(|k X E X 的 k 阶中心矩)))(((k X E X E - X 的 方差)()))(((2X D X E X E =- X ,Y 的 k + l 阶混合原点矩)(l k Y X E X ,Y 的 k + l 阶混合中心矩 X ,Y 的 二阶混合原点矩)(XY EX ,Y 的二阶混合中心矩 X ,Y 的协方差 X ,Y 的相关系数 X 的方差D (X ) =E ((X - E (X ))2)协方差相关系数)()(),cov(Y D X D Y X XY =ρ*N (0,1) — 标准正态分布 7.多维随机变量及其分布二维随机变量( X ,Y )的分布函数 边缘分布函数与边缘密度函数 8. 连续型二维随机变量(1) 区域G 上的均匀分布，U ( G ) (2)二维正态分布+∞<<-∞+∞<<∞-⨯-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+------y x ey x f y y x x ,121),(2222212121212)())((2)()1(21221σμσσμμρσμρρσπσ9. 二维随机变量的 条件分布10.随机变量的数字特征 数学期望随机变量函数的数学期望X 的 k 阶原点矩)(k X E X 的 k 阶绝对原点矩)|(|k X E X 的 k 阶中心矩)))(((k X E X E - X 的 方差)()))(((2X D X E X E =- X ,Y 的 k + l 阶混合原点矩)(l k Y X E X ,Y 的 k + l 阶混合中心矩 X ,Y 的 二阶混合原点矩)(XY EX ,Y 的二阶混合中心矩 X ,Y 的协方差X ,Y 的相关系数 X 的方差D (X ) =E ((X - E (X ))2)协方差 相关系数)()(),cov(Y D X D Y X XY =ρ。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
⑴ 应用概率积分法进行地表任意点A(x，y)下沉值W(x，y)的数学表达式如下：
W（X，Y）=Wcm·CX·Cy= m ·q· C 0 Sα·CX·Cy
CX=1[rxe02dλ—rlxe02dλ]
Cy=1[120ryedλ—220rLyedλ]
m —— 采出煤层厚度；
q —— 地表下沉系数；
α —— 煤层倾角；
CX 、 CY —— 分别为待求点在走向和倾向主断面上投影点处的下沉分布系数；
l、 L 一一 分别为采区拐点平移后走向长度及倾斜方向在地表的计算开采宽度；
r，r 1，r 2 —— 分别为走向、下山、上山的主要影响半经；
(2) 地表任意点倾斜值i(x，y)φ (沿指定的φ方向)
iφ=ix Cy cosφ+iy CX s i nφ
iφ+90= —ix Cys i nφ—iy CX cosφ
ix 、iy——分别为待求点沿走向和倾向主断面上投影点处迭加后的倾斜变形值，mm/m；
(3) 地表任意点的曲率变形K
φ
Kφ= Kx Cy cos2φ+Ky CX s i n2φ+WiicmyXsin2φ
Kφ+90= Kx Cy sin2φ+Ky CX cos2φ-WiiCmyXsin2φ
Kx、ky——分别为待求点沿走向及倾向在主断面投影处迭加后的曲率值。
（4）地表任意点沿指定方向φ的水平移动值uφ
uφ=ux Cy cosφ+uy CX s i nφ
uφ+90= —ux Cy cosφ+uy CX sinφ
ux 、uy———分别为待求点沿走向和倾向在主断面投影点处迭加后的水平移动值，
mm。
(5) 地表任意点的水平变形εφ (沿指定方向)
εφ=εx Cy cos2φ+εy CX s i n2φ+ [(ux iy + uy ix)/Wcm] sinφ·cosφ
εφ+90 =εx Cy sin2φ+εy CX cos2φ- [(ux iy + uy ix)/Wcm] sinφ·cosφ
εx 、εy———分别为待求点沿走向和倾向在主断面投影点处迭加后的水平变形值，
mm/m。
上述公式即为概率积分法计算各种移动与变形的基本公式。