非线性分析中弧长法的简介
opensees弧长法

opensees弧长法摘要:1.OpenSees 简介2.OpenSees 弧长法的定义和原理3.OpenSees 弧长法的应用4.OpenSees 弧长法的优点与局限性正文:1.OpenSees 简介OpenSees 是一款开源的土木工程计算软件,主要用于结构分析和设计。
它基于有限元方法,可以模拟各种复杂的结构和材料。
OpenSees 具有灵活、易用的特点,可以进行线性静力分析、模态分析、屈曲分析、响应谱分析等多种计算。
此外,OpenSees 还提供了丰富的接口和工具,方便与其他软件进行数据交换和二次开发。
2.OpenSees 弧长法的定义和原理OpenSees 弧长法是一种基于有限元方法的结构分析方法,主要用于求解结构在非线性荷载作用下的响应。
弧长法的基本思想是将结构的位移- 时间曲线划分为若干个弧段,通过对每个弧段的积分,求解结构的累积位移、速度和加速度等响应参数。
在OpenSees 中,弧长法通过定义一个函数来描述结构的位移- 时间关系。
该函数可以是线性的、非线性的或者是分段线性的。
在求解过程中,OpenSees 采用自适应时间步长控制,以保证计算精度和效率。
3.OpenSees 弧长法的应用OpenSees 弧长法广泛应用于土木工程领域,尤其是结构动力学分析和地震响应分析。
以下是一些典型的应用场景:(1)求解结构的周期、频率和振型;(2)分析结构在地震作用下的响应,包括峰值地面加速度、地面位移等;(3)评估结构在极端荷载作用下的性能,如屈曲、滑移等;(4)进行结构动力修改,如减震措施等。
4.OpenSees 弧长法的优点与局限性优点:(1)适用范围广,可以处理各种复杂的结构和材料;(2)计算精度高,可以模拟非线性和动态响应;(3)计算效率高,采用自适应时间步长控制;(4)易于与其他软件接口,方便进行数据交换和二次开发。
CAE软件操作小百科(36)

CAE软件操作小百科(36)作者:王峰来源:《计算机辅助工程》2017年第02期1如何利用Abaqus进行非线性屈曲分析弧长法是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一,可用于跳跃失稳问题的研究,也可以用于分支屈曲的后屈曲研究. 分支屈曲的后屈曲分析不能直接在分支屈曲后面研究,而是要给一个初始缺陷,使力学响应呈连续状态(非线性).Abaqus根据分支屈曲模型取线性组合、根据静力分析结果或直接指定等3种方法定义初始缺陷. 若已知初始缺陷,则一般采用第一种方法.(1)特征屈曲分析(分析步选择Buckle). (2)将这些特征屈曲模态添加到理想的几何体中,作为初始缺陷(见图1,菜单栏中选择Model→Edit Keywords). Abaqus通过节点标签输入初始缺陷(imperfection),但是软件不会去确认2个模型的兼容性,所以要特别注意节点标号的一致性. 一般来说因数w在第1阶模态最大,而且w一般取结构几何参数的倍数,如壳的厚度的0.1倍等. (3)利用弧长法进行非线性分析(分析步选择Static,Riks).2如何在Abaqus中建立弹簧单元在Abaqus中建立弹簧单元一般有2种方法:定义Spring单元和定义Wire Feature.方法一:定义Spring单元. 在Abaqus/CAE中进入Interaction模块,在菜单栏中选择Special→Springs/Dashpots→Manager,进入弹簧阻尼单元管理器,可以选择创建两点弹簧或者接地弹簧,见图2. 点击Continue按钮可以对弹簧刚度、位置和自由度进行设置.方法二:定义Wire Feature. (1)创建Wire Feature. 在Abaqus/CAE中进入Interaction模块,在工具条中选择(Create Wire Feature),在弹出的对话框中点击“+”,选择两点创建Wire Feature. (2)为Wire Feature赋予属性. 在Interaction模块下点击工具条中的Create Connector Section,将Connection Category选为Basic,Translational type选为Cartesian,并点击Continue;在弹出的Create Connector Section对话框中设置弹簧的属性,见图3. (3)在Interaction模块下点击工具条中的Create Connector Assignment赋予属性.需要注意的是,虽然2种方法的作用一致,但是方法二在一些情况下使用更加方便,即方法二可以同时定义3个方向的刚度,而且可以模拟非线性弹簧,此外还可以同时定义线性或非线性阻尼等,这对于分析带有减振装置的复杂结构十分便捷.3Abaqus接触问题分析Abaqus/Standard 的接触对由主面(master surfer)和从面(slave surfer)构成. 在模拟过程中,接触方向总是主面的法线方向,从面上的节点不会穿越主面,但主面上的节点可以穿越从面. 在定义主面和从面时要注意以下问题.(1)主从面的定义.1)选择刚度较大的面作为主面,此处的刚度不仅要考虑材料特性,也要考虑结构刚度. 刚体必须作为主面,从面则必须是柔体上的面(可以是施加了刚体约束的柔体). 2)主面不能由节点构成,并且必须连续. 如果相对滑动形式为有限滑移,则主面在发生接触的部位必须是光滑的(即不能有尖角). 3)如果为有限滑移,则整个分析过程中尽量不要让从面节点落到主面之外,更不要落到主面的背面,否则收敛会出现问题.(2)滑移形式.有限滑移要求主面是光滑的,否则会出现收敛问题. 如果主面在发生接触的部位存在尖角或凹角,应该在此尖角处把主面分为2部分分别定义. 对于由单元构成的主面,Abaqus 会自动进行平滑处理. 对于小滑移的接触对,Abaqus/Standard在分析的开始就确定了从面节点与主面的关系,在整个分析过程中这种接触关系不会再发生变化.(3)接触面间的几何尺寸位置和Adjust参数. 如果不特别设置,Abaqus会直接根据模型尺寸位置判断从面和主面的距离,从而确定二者的接触状态,这就要求建模时模型尺寸必须非常精确. 一般情况下,模型尺寸往往会存在误差,可以应该利用Adjust参数调整从面节点的初始坐标. 如果从面节点与主面的距离小于这个参数,Abaqus将调整这些节点的初始坐标,使其与主面的距离为0(刚好接触).(4)收敛问题.在进行接触分析时,难免会遇到收敛问题(往往是因为模型中有问题),例如存在刚体位移、过约束、接触定义不当等,这时应该查看MSG文件,然后采取相应措施.(摘自同济大学郑百林教授《CAE操作技能与实践》课堂讲义)(待续)。
第三章 非线性分析

第三章非线性分析在工程结构实际中,常常会遇到许多不符合小变形假设的问题,例如板和壳等薄壁结构在一定载荷作用F,尽管应变很小,甚至未超过弹性极限,但是位移较大,材料微单元会有较大的刚体转动位移。
这时平衡条件应如实地建立在变形后的位形上,以考虑变形对平衡的影响。
同时应变表达式也应包括位移的二次项。
这样,结构的几何形变关系将是非线性的。
这种由于大位移和大转动引起的非线性问题称为几何非线性问题。
在涉及几何非线性问题的有限元方法中,可以采用两种不同的表达格式来建立有限元方程。
一种格式是所有静力学和运动学变量总是参考于初始位形的完全拉格朗日格式,即在整个分析过程中参考位形保持不变。
而另一种格式中,所有静力学和运动学的变量参考于每一载荷步增量或时间步长开始的位形,即在分析过程中参考位形是不断被更新的,这种格式就称为更新的拉格朗日格式。
下面将分别具体讨论大变形情况下应变和应力度量,几何非线性有限元方程的建立以及系数矩阵的形成。
在涉及几何非线性问题的有限元方法中,可以采用两种不同的表达格式来建立有限元方程。
一种格式是所有静力学和运动学变量总是参考于初始位形的完全拉格朗日格式,即在整个分析过程中参考位形保持不变。
而另一种格式中,所有静力学和运动学的变量参考于每一载荷步增量或时间步长开始的位形,即在分析过程中参考位形是不断被更新的,这种格式就称为更新的拉格朗日格式。
下面将分别具体讨论大变形情况下应变和应力度量,几何非线性有限元方程的建立以及系数矩阵的形成。
第三章非线性分析的数值计算方法3.1概述非线性问题一般包括三类:材料非线性、几何非线性和边界非线性;而在许多实际的结构中,常常是三种非线性问题的融合,因此其解析方法能够得到的解答是十分有限的。
对于非线性问题的求解,可以采用有限元分析的方法,因此非线性方程组的解法也就成为非线性问题有限元分析涉及的基本问题,也就是通常所说的非线性分析的数值计算方法I”。
常用的有Newton—Raphson法(简称N-R)和弧长法。
AnsysWorkbench工程应用之——结构非线性(上):几何非线性(3)——屈曲

AnsysWorkbench工程应用之——结构非线性(上):几何非线性(3)——屈曲本文可能是您能在网络上找到得有限元计算屈曲最详细最接地气得文章。
图惜原本计划将屈曲写入几何非线性一文,后来发现内容太多,所有拎出来单独做一个专题。
在屈曲计算中,特别是非线性屈曲计算中,很多初学者也和图惜一样,有很多疑问,此文将针对初学者常见的问题做通俗详细的解读,其中一定有您想要的答案。
1 屈曲的概念结构失稳即屈曲,最常见的便是压杆失稳现象。
压杆稳定示意图如下,在稳定点之前,支反力呈线性增长,逐渐达到一个极值,之后支反力降低,这个极值便是屈曲极限。
屈曲极限往往远小于材料的屈服强度,屈曲分析的目的在于找出结构的屈曲极限,分析出结构的安全载荷、或对结构进行相应优化设计提高屈曲极限。
分析屈曲有两类方法,一类是线性特征值屈曲,用于计算理想线性屈曲极限,一类是非线性分析,用于计算零件因初始缺陷、材料、几何、接触等引起的非线性屈曲,而非线性分析又分为前屈曲分析和后屈曲分析。
很多结构设计是以理想线性屈曲极限除以一个安全系数作为设计依据,但是如果要探究结构的实际屈曲极限,有必要进行非线性屈曲分析。
特征值模态只是结构的线性特征,是结构在受荷载情况下能量最小的变形模式,不是真实变形。
最终采用大变形方法计算得到的结果才是结构真正的破坏状态。
2 线性屈曲在Ansys Workbench中,进行线性屈曲分析的是特征值屈曲模块。
线性特征值屈曲分析通过提取线性系统的刚度矩阵的奇异特征值,以获得结构临界失稳载荷以及失稳模态。
线性特征值屈曲分析不考虑初始结构缺陷与非线性因素的影响,计算较快,计算精度不如非线性屈曲,特别是对于复杂模型。
但是计算的特征值对结构稳定性评价有一定帮助,例如,求解出密集排列的负载乘数,则表明该结构对初始缺陷敏感;求解出稀松排列的负载乘数,则表明该结构对初始缺陷不敏感。
需要强调的是,线性特征值屈曲计算得到的失稳模态变形结果,并不是真实结构失稳后的结构最大位移。
弧长法

弧长法的一点资料对于许多物理意义上不稳定的结构可以应用弧长方法(ARCLEN)来获得数值上稳定的解,应用弧长方法时,请记住下列考虑事项:1、弧长方法仅限于具有渐进加载方式的静态分析。
2、程序由第一个子步的第一次迭代的载荷(或位移)增量计算出参考弧长半径,公式为:参考弧长半径=总体载荷(或位移)/NSBSTP。
NSBSTP是NSUBST 命令中指定的子步数。
3、选择子步数时,考虑到较多的子步导致求解时间过长,因此理想情况是选择一个最佳有效解所需的最小子步数。
有时需要对子步数进行评诂,按照需要调整再重新求解。
4、弧长方法激活时,不要使用线搜索(LNSRCH)、预测(PRED)、自适应下降(NROPT,ON)、自动时间分步(AUTOTS,TIME,DELTIM)或时间积分效应(TIMINT)。
5、不要使用位移收敛准则(CNVTOL,U)。
使用力的收敛准则(CNVTOL,F)。
6、要用弧长方法帮助缩短求解时间时,单一子步内最大平衡迭代数应当小于或等于15。
7、如果一个弧长求解在规定的最大迭代次数内没能收敛,程序将自动进行二分且继续分析或者采用最小弧长半径(最小半径由NSUBST(NSUBST)和MINARC (ARCLEN)定义)。
8、一般地,不能应用这种方法在确定载荷或位移处获得解,因为这个载荷或者位移值随获得的平衡态改变(沿球面弧)。
注意图1-4中给定的载荷仅用作一个起始点。
收敛处的实际载荷有点小。
类似地,当在一个非线性屈曲分析中应用弧长方法在某些已知的范围内确定一个极限载荷或位移的值可能是困难的。
通常不得不通过尝试-错误-再尝试调整参考弧长半径(使用NSUBST)来在极限点处获得一个解。
此时,应用带二分法(AUTOTS)的标准NEWTON-RAPHSON迭代来确定非线性载荷屈曲临界负载的值可能会更方便。
9、通常应当避免和弧长方法一起使用JCG或者PCG求解器(EQSLV),因为弧长方法可能会产生一个负定刚度矩阵(负的主对角线),导致求解失败。
弧长法基本原理
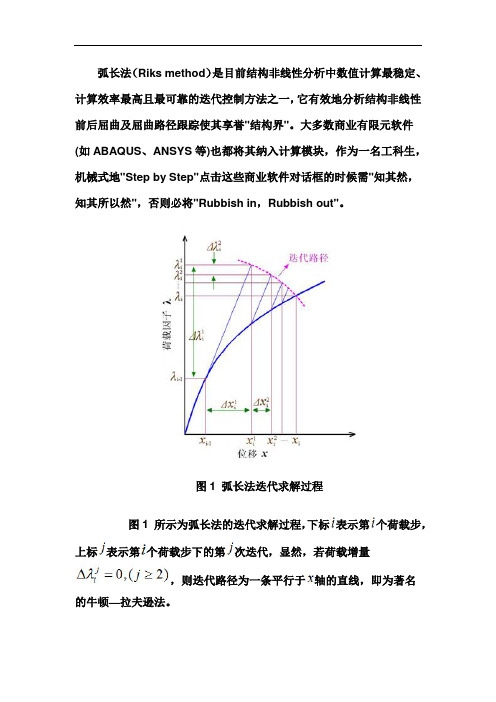
弧长法(Riks method)是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一,它有效地分析结构非线性前后屈曲及屈曲路径跟踪使其享誉"结构界"。
大多数商业有限元软件(如ABAQUS、ANSYS等)也都将其纳入计算模块,作为一名工科生,机械式地"Step by Step"点击这些商业软件对话框的时候需"知其然,知其所以然",否则必将"Rubbish in,Rubbish out"。
图1 弧长法迭代求解过程图1 所示为弧长法的迭代求解过程,下标表示第个荷载步,上标表示第个荷载步下的第次迭代,显然,若荷载增量,则迭代路径为一条平行于轴的直线,即为著名的牛顿—拉夫逊法。
设第个荷载步收敛于,那么对于第个荷载步来说,需要进行次迭代才能达到新的收敛点。
外部参照力,在ABAQUS需要用户以外荷载的形式输入,因此,作用在结构上的真实力大小为。
由于牛顿—拉夫逊法在迭代过程中,以荷载控制(或位移控制)时,荷载增量步(或位移增量步)为常数,它无法越过极值点得到完整的荷载—位移曲线,事实上,也只有变化的荷载增量步才能使求解过程越过极值点。
从图1中可以看出,弧长法的荷载增量步是变化的,可以自动控制荷载,但这又使原方程组增加了一个多余的未知量,因此需要额外补充一个控制方程,即:(1)该控制方程说明,其迭代路径是以上一个荷载步收敛点为圆心半径为的圆弧,所以称为弧长法。
通常用户需指定初始弧长半径或固定的弧长半径,当设定了初始弧长半径时,根据收敛速率,一般按式(2)计算,其中为荷载步期望收敛迭代次数,一般取6, 为上一荷载步的迭代次数,大于10时取10。
(2)1. 当时,根据上一个荷载步收敛结束时的构形,得到用于第个荷载步收敛计算的切线刚度矩阵,即图1中的蓝色平行线的斜率。
通过式(2)可得相应的切线位移。
(3)(4)(5)很容易由式(5)求得,但不能确定其符号,而的符号决定了跟踪分析是向前还是返回,因此非常重要。
弧长法算法

矩阵不是正定的,则节点荷载 ∆f i +1 = − ∆f i 。 2.1.2、 弧长法的具体实现方法 在实际计算中,先进行矩阵正定性判别,利用 Lancsoz 方法,进行两步 Lancsoz 过程, 得到相应的 Ritz 值 θ 1 ,θ n 。因为 θ 2 ≈ λ n , λ n 为刚度矩阵最小的特征值。如果 θ 2 < 0 ,则 认为刚度矩阵为非正定。 弧长法程序模块由三个子程序组成: 1:subroutine ArcLeng(TotalP,TotalU,F,ArcL),功能:弧长法迭代核心程序 2:subroutine Judge(PD,GK),功能:判断刚度矩阵的正定性 3:subroutine Solve(GK,Gload,Gdisp),功能:求解迭代方程组
《高等数值分析》课程研究
数值误差“吃掉” ,最后没有出现有些文献中声称的那样明显的效果,因此,在这个预处理 方法上, 还需要一些讨论。 以 Hilbert 矩阵为例, 在双精度下, 当矩阵 n>5 时, 预处理 Lanczos 的结果精度对普通高斯消去已经没有什么优势了。 因此,我认为基于 Lancsoz 方法求解的尝试没有取得预想效果,需要用新的方法代替。 2.2.2、A3 预处理技术 取预处理矩阵 M=A3,即取原矩阵的三条主对角线元素为预处理矩阵,对原矩阵进行预 处理。为了比较其效果,这里以 Hilbert 矩阵为例,比较其效果。 方程 Hx = b , H 为 Hilbert 矩阵,分别用普通高斯消去法和预处理后的消去法得到结 果~ x ,记误差为 b − A~ x
r (i ) ⋅ r (i ) = S 2
∆u ( i +1) (∆u ( i +1) + 2r ( i ) ) = 0
几何非线性大作业荷载增量法和弧长法程序设计汇编完整

几何非线性大作业荷载增量法和弧长法程序设计汇编(可以直接使用,可编辑优秀版资料,欢迎下载)几何非线性大作业荷载增量法和弧长法程序设计系(所):建筑工程系学号:姓名:焦联洪培养层次:专业硕士指导老师:吴明儿2021年6月19日一、几何非线性大作业(Newton-Raphson法)用荷载增量法(Newton-Raphson法)编写几何非线性程序:(1)用平面梁单元,可分析平面杆系(2)算例:悬臂端作用弯矩。
悬臂梁最终变形形成周长为悬臂梁长度的圆。
1.1 Newton-Raphson算法基本思想图1.1 Newton-Raphson算法基本思想1.2 悬臂梁参数基本参数:L=2m, D=0.03m, A=7.069E-4m2, I=3.976E-08m4 ,E=2.0E11N/m2图1.2 悬臂梁单元信息将悬臂梁分成10个单元,如图1.2所示2.1 MATLAB输入信息材料信息单元信息约束信息(0为约束,1为放松)荷载信息(FX,FY,M)节点信息2.2 求解过程运用ABAQUS和MATLAB进行求解对比:图1.3 加载图图1.4 ABAQUS变形图图1.5 MATLAB变形曲线ABAQUS和MATLAB变形对比,最终在理论荷载作用下都弯成了一个圆,其直径为0.64716m,与理论值相对比值为:(0.64716-0.642)/0.642=0.00804.非常接近。
2.3 加载点荷载位移曲线图1.5 加载点Y方向的荷载位移曲线加载点的最大竖向位移,相对比值(1.4525-1.45246)/1.45246=2.75395E-05。
完全相同,说明MATLAB的计算结果很好。
二、几何非线性大作业(弧长法)用弧长法编写几何非线性程序,分析荷载位移全过程曲线:1) 用平面梁单元,可分析平面杆系结构2) 算例(1)受集中荷载的拱:考察拱的矢跨比、荷载位置对荷载位移曲线的影响。
(2)其他有复杂平衡路径的结构3) 将结果与相关文献进行对比1.1 弧长法基本思想图2.1 弧长法基本思想1.2 拱基本参数拱参数:L=100m, A=0.32m2 ,I=1m4 ,E=1.0e7N/m2,F=-5000N,拱曲线y=5×sin(3.1415926*x/L)将拱结构分成25个单元,如图2所示图2.2 拱单元信息2.1 MATLAB输入信息材料信息单元信息约束信息(0为约束,1为放松)荷载信息(FX,FY,M)节点信息2.2 运用ANSYS和MATLAB进行求解对比(两端铰接)ANSYS中模型:图2.3 ANSYS模型图2.4 MATLAB和ANSYS变形图2.3 加载点荷载位移曲线图2.5 加载点荷载位移曲线ANSYS求得的极限承载力3042.53,对应位移3.00142 MATLAB求得的极限承载力3043.8, 对应位移3.0768 相对误差分别为0.0417%,2.45%,模拟效果比较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非线性分析弧长法的读书报告
1.弧长法的原理
弧长法属于双重目标控制方法,即在求解过程中同时控制荷载因子和位移增量的步长。
其基本的控制方程为:
{}{}{}{}222l P P T T ∆=∆+∆∆ϕλδδ (1)
式中:
λ∆为荷载因子增量数值
ϕ为荷载比例系数,用于控制弧长法中荷载因子增量所占的比重
l ∆为固定的半径
在求解过程中,荷载因子增量λ∆在迭代中是变化的,下列非线性静力平衡的迭代求解公式中存在n 个未知数,即
()[]{}{}(){}j i j i j
i j i
F P K δλ
δδδ-=++1
1
210,,=i (2)
这样,在弧长法中一共存在1+n 个未知数,根据约束方程:
{}{}{}{}222l P P T T ∆=∆+∆∆ψλδδ
即为附加的控制方程,问题才能得到解答,此时,可以根据ψ值的取值分为两种弧长法,其中,0≠ψ时的弧长法称为球面弧长法,0=ψ时的弧长法称为柱面弧长法。
1.1球面弧长法
如下图所示,根据图中所示来说明弧长法的求解策略:
在第j 步荷载增量第i 次迭代分析中,结构的位移增量}{1j
i +δδ可由式(2)来计算,即
}
{)]([)}({)]([})
{)}(({)]([)})({}{}{()]([)})
({}{()]([}
{1111111111P K K P K F P P K F P K j i j i j i j i j i j i j i j i j i j i j i j i j i j i j i -+-+-+-+-++-=
--=-+=-=δδλδψδδλδψδδδλλδδλδδδ (3) 由于刚度矩阵不对称以及带宽被改变,通常情况下直接联立求解式(1)和式(3)中1+n 个变量相当困难。
通常,将式(3)中}{1j
i +δδ分解为两个部分,即
j
i p j i j i g j i 1
111}{}{}{+++++=δδδλδδδδ (4)
式中,)}({)]([}{11j i j i j i g K δψδδδ-+-= (5) 说明j i j 1}{+δδ的第一项j i g 1}{+δδ为采用荷载控制的标准切线刚度迭代求解的 结果;
P K j i j i p 11)]([}{-+=δδδ (6)
说明j i j 1}{+δδ的第二项j i p 1}{+δδ为考虑荷载}{P 下按当前结构刚度)]([j i K δ计算出来的位移增量。
至此,式(4)中仍有j i 1+δλ为未知量,现在只有借助控制方程(1)来求解。
第i 次迭代结束后相应于迭代初始点(上图中1-j 点)的位移增量}{1+∆i δ为
}{}{}{11+++∆=∆i i i δδδδ
(7)
将(7)式代入控制方程(1)式,并考虑迭代前后弧长保持不变,故得到:
}
{}{)(}{}{}{}{)(}{}{22111222P P P P l T
j i j i T j i T j i j i T j i ψλδδψλδδ+++∆+∆∆=∆+∆∆=∆ (8)
式中:
j i λ∆与j i 1+∆λ分别为第i 次迭代前后荷载因子相对于迭代初始点(上图中1-j
点)的增量,它们有如下关系:
j i j i j i 11+++∆=∆δλλλ
(9)
将(4)代入(9)中,可得:
(10)
式中:
}{}{}{}{211p p A T j i p T
j i p ψδδδδ+∙=++
}{}{2)}{}({}{2211p p B T j i j i g j i T j i p ψλδδδδδ∆∙++∆∙=++
22211}{}{)()}{}({)}{}({l p p C T j i j i g j i T j i g j i ∆-∆++∆+∆=++ψλδδδδδδ
由此,可通过解上述一元二次方程得到何在因子的增量j i 1+δλ,从而进一步确定当前的荷载水平和位移向量,即
j i j i j i j j i 1101++++=∆+=δλλλλλ
(11) }
{}{}{}{}{1101j
i j i j i j j i ++++=∆+=δδδδδδ
(12)
1.2柱面弧长法
经过研究发现,荷载比例系数ψ对于最终分析结果的影响是有限的,尤其是结构非线性成都较高时,这种影响甚微。
令0=ψ,从而减少程序中的未知数和提高求解效率。
于是把从原先所谓的“球面弧长法”简化为“柱面弧长法”,结构的控制方程则简化成:
{}{}2l T ∆=∆∆δδ (13)
0)(121=+∙+∙++C B A j i j i δλδλ。
