北师大版初中数学八年级上册期末测试题3

合集下载

2021年北师大版八年级数学上册期末测试卷及答案【完整】

2021年北师大版八年级数学上册期末测试卷及答案【完整】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．估计101+的值在（）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间2．一次函数24y x =+的图像与y 轴交点的坐标是（）A ．（0，-4）B ．（0，4）C ．（2，0）D ．（-2，0）3．已知a ，b 满足方程组51234a b a b +=⎧⎨-=⎩则a+b 的值为（） A ．﹣4 B ．4 C ．﹣2 D ．24．如果一次函数y=kx+b （k 、b 是常数，k ≠0）的图象经过第一、二、四象限，那么k 、b 应满足的条件是（）A ．k ＞0，且b ＞0B ．k ＜0，且b ＞0C ．k ＞0，且b ＜0D ．k ＜0，且b ＜05．下列说法中，错误的是（）A ．不等式x ＜5的整数解有无数多个B ．不等式x ＞－5的负整数解集有有限个C ．不等式－2x ＜8的解集是x ＜－4D ．－40是不等式2x ＜－8的一个解6．欧几里得的《原本》记载，形如22x ax b +=的方程的图解法是：画Rt ABC ∆，使90ACB ∠=，2a BC =，AC b =，再在斜边AB 上截取2a BD =.则该方程的一个正根是（）A ．AC 的长B ．AD 的长C ．BC 的长D ．CD 的长7．如图，在▱ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）A．6 B．12 C．18 D．248．如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（）A．80°B．60°C．50°D．40°9．如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是（）A．310B．103C．9 D．9210．正比例函数y=kx（k≠0）的函数值y随着x增大而减小，则一次函数y=x+k的图象大致是（）A． B．C． D．二、填空题（本大题共6小题，每小题3分，共18分）1．若a-b=1，则222--的值为____________．a b b2．已知34(1)(2)x x x ---=1A x -+2B x -，则实数A=__________． 3．在△ABC 中，AB=15，AC=13，高AD=12，则ABC ∆的周长为____________．4．如图，▱ABCD 中，AC 、BD 相交于点O ，若AD=6，AC+BD=16，则△BOC 的周长为________．5．如图，菱形ABCD 中，∠B ＝60°，AB ＝3，四边形ACEF 是正方形，则EF 的长为__________．6．如图，在平行四边形ABCD 中，连接BD ，且BD ＝CD ，过点A 作AM ⊥BD 于点M ，过点D 作DN ⊥AB 于点N ，且DN ＝32，在DB 的延长线上取一点P ，满足∠ABD ＝∠MAP ＋∠PAB ，则AP ＝________.三、解答题（本大题共6小题，共72分）1．解方程组：4311213x y x y -=⎧⎨+=⎩2．先化简，再求值：（a ﹣2b ）（a+2b ）﹣（a ﹣2b ）2+8b 2，其中a=﹣2，b=12．3．已知22a b -=，且1a ≥，0b ≤．（1）求b 的取值范围（2）设2m a b =+，求m 的最大值．4．如图，△ABC 与△DCB 中，AC 与BD 交于点E ，且∠A=∠D ，AB=DC（1）求证：△ABE ≌DCE ；（2）当∠AEB=50°，求∠EBC 的度数．5．已知：如图所示，AD 平分BAC ∠，M 是BC 的中点，MF//AD ，分别交CA 延长线，AB 于F 、E ．求证：BE=CF ．6．在“母亲节”前期，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销售量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍．（1）求降价后每枝玫瑰的售价是多少元？（2）根据销售情况，店主用不多于900元的资金再次购进两种鲜花共500枝，康乃馨进价为2元/枝，玫瑰进价为1.5元/枝，问至少购进玫瑰多少枝？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、C2、B3、B5、C6、B7、B8、D9、A10、A二、填空题（本大题共6小题，每小题3分，共18分）1、12、13、32或424、145、36、6三、解答题（本大题共6小题，共72分）1、53xy=⎧⎨=⎩．2、4ab，﹣4．3、（1）12b-≤≤；（2）24、略（2）∠EBC=25°5、略.6、（1）2元；（2）至少购进玫瑰200枝.。

北师大版初中数学八年级上册期末试题(山东省菏泽市

2017-2018学年山东省菏泽市单县八年级（上）期末数学试卷一、选择题（本题共10小题，每小题3分，共30分）下面各题给出的四个选项中，只有一坝是正确的，请将正确选项的代号填写在第Ⅱ卷相应的横线上．1．（3分）下列命题是真命题的是（）A．有两边及一角对应相等的两个三角形全等B．底角相等的两个等腰三角形全等C．若a+b＝0，则|a|＝|b|D．角不是轴对称图形2．（3分）如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠P AE．则说明这两个三角形全等的依据是（）A．SAS B．ASA C．AAS D．SSS3．（3分）如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）A．甲B．乙C．丙D．丁4．（3分）如图，直线a∥b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有（）A．4个B．3个C．2个D．1个5．（3分）如果分式与的值相等，那么x的值是（）A．9B．7C．5D．36．（3分）下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（）A．①B．②C．③D．④7．（3分）如图，在△OBC中，延长BO到D，延长CO到A，要证明OD＝OA，则应添加条件中错误的是（）A．△ABC≌△DCB B．OB＝OC，∠A＝∠DC．OB＝OC，AB＝DC D．∠A＝∠D，∠ABC＝∠DCB 8．（3分）如图，将△ABC纸片沿DE折叠，使点A落在四边形BCDE外点A'的位置，则下列结论正确的是（）A．∠1+∠2＝∠A B．∠1+∠2＝2∠A C．∠1﹣∠2＝∠A D．∠1﹣∠2＝2∠A9．（3分）某服装店用10000元购进一批某品牌夏季衬衫若干件，很快售完；该店又用14700元钱购进第二批这种衬衫，所进件数比第一批多40%，每件衬衫的进价比第一批每件衬衫的进价多10元，求第一批购进多少件衬衫？设第一批购进x件衬衫，则所列方程为（）A．﹣10＝B．+10＝C．﹣10＝D．+10＝10．（3分）如图，在△ABC中，AB＝AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）A．BC B．CE C．AD D．AC二、填空题（本題共10小题，每小题3分，共30分）请将答案填写在第Ⅱ卷相应的横线上11．（3分）某校调查了20名男生某一周参加篮球运动次数，调查结果如表所示，那么这20名男生该周参加篮球运动次数的平均数是次．12．（3分）已知＝，则的值为．13．（3分）如图，在直角三角形ABC中，∠C＝90°，∠B＝42°，点E是BC 上一点，EF⊥AB于点F，若EC＝EF，则∠AEC的度数为．14．（3分）若等腰三角形的周长为10cm，其中一边长为2cm，则该等腰三角形的底边长为．15．（3分）在一次射击训练中，某位选手五次射击的环数分别为5，8，7，6，9，则这位选手五次射击环数的方差为．16．（3分）化简÷的结果为．17．（3分）如图，已知△ABC≌△DEF，DF∥BC，且∠B＝60°，∠F＝40°，点A在DE上，则∠BAD的度数为．18．（3分）一组数据1、3、4、5、x、9的众数和中位数相同，那么x的值是．19．（3分）关于x的分式方程有增根，则m的值为．20．（3分）如图，四边形ABDC，∠A＝110°，若点D在AB、AC的垂直平分线上，则∠BDC的度数为．三、解答题（满分60分）21．（8分）如图，点E，F在AB上，AD＝BC，∠A＝∠B，AE＝BF．求证：△ADF≌△BCE．22．（10分）某公司共25名员工，下表是他们月收入的资料．（1）该公司员工月收入的中位数是元，众数是元．（2）根据上表，可以算得该公司员工月收入的平均数为6276元．你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．23．（10分）如图，在Rt△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，DE⊥AC于点E，BF∥DE交CD于点F．求证：DE＝BF．24．（12分）解答下列各题．（1）解方程＝1﹣；（2）化简：（1+）÷．25．（10分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1＝42°，求∠BDE的度数．26．（10分）甲、乙两个工程队均参与某筑路工程，先由甲队筑路60公里，再由乙队完成剩下的筑路工程，已知乙队筑路总公里数是甲队筑路总公里数的倍，甲队比乙队多筑路20天．（1）求乙队筑路的总公里数；（2）若甲、乙两队平均每天筑路公里数之比为5：8，求乙队平均每天筑路多少公里．2017-2018学年山东省菏泽市单县八年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共10小题，每小题3分，共30分）下面各题给出的四个选项中，只有一坝是正确的，请将正确选项的代号填写在第Ⅱ卷相应的横线上．1．（3分）下列命题是真命题的是（）A．有两边及一角对应相等的两个三角形全等B．底角相等的两个等腰三角形全等C．若a+b＝0，则|a|＝|b|D．角不是轴对称图形【分析】利用三角形全等的判定、绝对值的定义、轴对称的性质分别判断后即可确定正确的选项．【解答】解：A、有两边及一角对应相等的两个三角形不一定全等，错误，是假命题；B、底角相等的两个等腰三角形不一定全等，错误，是假命题；C、若a+b＝0，则|a|＝|b|，正确，是真命题；D、角是轴对称图形，错误，是假命题，故选：C．【点评】本题考查了三角形全等的判定、绝对值的定义、轴对称的性质，解题的关键是了解有关的性质及定义，难度不大．2．（3分）如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠P AE．则说明这两个三角形全等的依据是（）A．SAS B．ASA C．AAS D．SSS【分析】在△ADC和△ABC中，由于AC为公共边，AB＝AD，BC＝DC，利用SSS定理可判定△ADC≌△ABC，进而得到∠DAC＝∠BAC，即∠QAE＝∠P AE．【解答】解：在△ADC和△ABC中，，∴△ADC≌△ABC（SSS），∴∠DAC＝∠BAC，即∠QAE＝∠P AE．故选：D．【点评】本题考查了全等三角形的应用；这种设计，用SSS判断全等，再运用性质，是全等三角形判定及性质的综合运用，做题时要认真读题，充分理解题意．3．（3分）如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）A．甲B．乙C．丙D．丁【分析】首先比较平均数，平均数相同时选择方差较小的运动员参加．【解答】解：∵＝＞＝，∴从甲和丙中选择一人参加比赛，∵＝＜＜，∴选择甲参赛，故选：A．【点评】此题考查了平均数和方差，正确理解方差与平均数的意义是解题关键．4．（3分）如图，直线a∥b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有（）A．4个B．3个C．2个D．1个【分析】根据射线DF⊥直线c，可得与∠1互余的角有∠2，∠3，根据a∥b，可得与∠1互余的角有∠4，∠5．【解答】解：∵射线DF⊥直线c，∴∠1+∠2＝90°，∠1+∠3＝90°，即与∠1互余的角有∠2，∠3，又∵a∥b，∴∠3＝∠5，∠2＝∠4，∴与∠1互余的角有∠4，∠5，∴与∠1互余的角有4个，故选：A．【点评】本题主要考查了平行线的性质以及余角的综合应用，解决问题的关键是掌握：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．5．（3分）如果分式与的值相等，那么x的值是（）A．9B．7C．5D．3【分析】根据题意列出方程，求出方程的解即可得到x的值．【解答】解：根据题意得：＝，去分母得：2x+6＝4x﹣8，解得：x＝7，经检验x＝7是分式方程的解，故选：B．【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．6．（3分）下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（）A．①B．②C．③D．④【分析】利用作一个角等于已知角；作一个角的平分线；作一条线段的垂直平分线；过直线外一点P作已知直线的垂线的作法进而判断得出答案．【解答】解：①作一个角等于已知角的方法正确；②作一个角的平分线的作法正确；③作一条线段的垂直平分线缺少另一个交点，作法错误；④过直线外一点P作已知直线的垂线的作法正确．故选：C．【点评】此题主要考查了基本作图，正确把握作图方法是解题关键．7．（3分）如图，在△OBC中，延长BO到D，延长CO到A，要证明OD＝OA，则应添加条件中错误的是（）A．△ABC≌△DCB B．OB＝OC，∠A＝∠DC．OB＝OC，AB＝DC D．∠A＝∠D，∠ABC＝∠DCB【分析】根据全等三角形的判定和性质，一一判断即可．【解答】解：A、正确．∵△ABC≌△DCB，∴AC＝BD，∠OCB＝∠OBC，∴OB＝OC，∴OA＝OD，故选项正确．B、正确．在△AOB和△DOC中，，∴△AOB≌△DOC，∴AO＝OD．故选项正确．C、错误．SSA无法判断三角形全等，故选项错误．D、正确．可以证明△ABC≌△DCB，由A可知正确．故选：C．【点评】本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于基础题，中考常考题型．8．（3分）如图，将△ABC纸片沿DE折叠，使点A落在四边形BCDE外点A'的位置，则下列结论正确的是（）A．∠1+∠2＝∠A B．∠1+∠2＝2∠A C．∠1﹣∠2＝∠A D．∠1﹣∠2＝2∠A【分析】根据折叠的性质和三角形的外角的性质解答即可．【解答】解：∵△A′DE是△ADE沿DE折叠得到，∴∠A′＝∠A，∵∠1＝∠A+∠3，∠3＝∠A′+∠2，∴∠1＝∠A+∠A′+∠2，∴∠1﹣∠2＝2∠A，故选：D．【点评】本题考查的是三角形的外角性质和图形的翻折变换，理清图中角与角的关系是解决问题的关键．9．（3分）某服装店用10000元购进一批某品牌夏季衬衫若干件，很快售完；该店又用14700元钱购进第二批这种衬衫，所进件数比第一批多40%，每件衬衫的进价比第一批每件衬衫的进价多10元，求第一批购进多少件衬衫？设第一批购进x件衬衫，则所列方程为（）A．﹣10＝B．+10＝C．﹣10＝D．+10＝【分析】根据题意表示出衬衫的价格，利用进价的变化得出等式即可．【解答】解：设第一批购进x件衬衫，则所列方程为：+10＝．故选：B．【点评】此题主要考查了由实际问题抽象出分式方程，正确找出等量关系是解题关键．10．（3分）如图，在△ABC中，AB＝AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）A．BC B．CE C．AD D．AC【分析】如图连接PC，只要证明PB＝PC，即可推出PB+PE＝PC+PE，由PE+PC ≥CE，推出P、C、E共线时，PB+PE的值最小，最小值为CE的长度．【解答】解：如图连接PC，∵AB＝AC，BD＝CD，∴AD⊥BC，∴PB＝PC，∴PB+PE＝PC+PE，∵PE+PC≥CE，∴P、C、E共线时，PB+PE的值最小，最小值为CE的长度，故选：B．【点评】本题考查轴对称﹣最短问题，等腰三角形的性质、线段的垂直平分线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．二、填空题（本題共10小题，每小题3分，共30分）请将答案填写在第Ⅱ卷相应的横线上11．（3分）某校调查了20名男生某一周参加篮球运动次数，调查结果如表所示，那么这20名男生该周参加篮球运动次数的平均数是4次．【分析】加权平均数：若n个数x1，x2，x3，…，x n的权分别是w1，w2，w3，…，w n，则（x1w1+x2w2+…+x n w n）÷（w1+w2+…+w n）叫做这n个数的加权平均数，依此列式计算即可求解．【解答】解：（2×2+3×2+4×10+5×6）÷20＝（4+6+40+30）÷20＝80÷20＝4（次）．∴这20名男生该周参加篮球运动次数的平均数是4次．故答案为：4．【点评】本题考查的是加权平均数的求法．本题易出现的错误是求2，3，4，5这四个数的平均数，对平均数的理解不正确．12．（3分）已知＝，则的值为．【分析】设a＝13k，b＝5k，分别代入所求分式可得结论．【解答】解：∵＝，∴设a＝13k，b＝5k，则＝＝＝，故答案为：．【点评】本题主要考查的是比例的性质的应用，掌握比例的性质是解题的关键．13．（3分）如图，在直角三角形ABC中，∠C＝90°，∠B＝42°，点E是BC 上一点，EF⊥AB于点F，若EC＝EF，则∠AEC的度数为66°．【分析】由Rt△AEF≌Rt△AEC（HL），推出∠AEF＝∠AEC，由∠FEC＝∠B+∠FEB＝132°，可得∠AEC＝∠FEC解决问题；【解答】解：∵EF⊥AB，∴∠AFE＝∠C＝90°，在Rt△AEF和Rt△AEC中，，∴Rt△AEF≌Rt△AEC（HL），∴∠AEF＝∠AEC，∵∠FEC＝∠B+∠FEB＝132°，∴∠AEC＝∠FEC＝66°，故答案为66°【点评】本题考查全等三角形的判定和性质、三角形的外角的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．14．（3分）若等腰三角形的周长为10cm，其中一边长为2cm，则该等腰三角形的底边长为2cm．【分析】分为两种情况：2cm是等腰三角形的腰或2cm是等腰三角形的底边，然后进一步根据三角形的三边关系进行分析能否构成三角形．【解答】解：若2cm为等腰三角形的腰长，则底边长为10﹣2﹣2＝6（cm），2+2＜6，不符合三角形的三边关系；若2cm为等腰三角形的底边，则腰长为（10﹣2）÷2＝4（cm），此时三角形的三边长分别为2cm，4cm，4cm，符合三角形的三边关系；故答案为：2cm．【点评】此题考查了等腰三角形的两腰相等的性质，同时注意三角形的三边关系：三角形任意两边之和大于第三边．15．（3分）在一次射击训练中，某位选手五次射击的环数分别为5，8，7，6，9，则这位选手五次射击环数的方差为2．【分析】运用方差公式S2＝[（x1﹣）2+（x2﹣）2+…+（x n﹣）2]，代入数据求出即可．【解答】解：五次射击的平均成绩为＝（5+7+8+6+9）＝7，方差S2＝[（5﹣7）2+（8﹣7）2+（7﹣7）2+（6﹣7）2+（9﹣7）2]＝2．故答案为：2．【点评】本题考查了方差的定义．一般地设n个数据，x1，x2，…x n的平均数为，则方差S2＝[（x1﹣）2+（x2﹣）2+…+（x n﹣）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．16．（3分）化简÷的结果为﹣．【分析】分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘．【解答】解：÷＝×＝﹣，故答案为：﹣．【点评】本题主要考查了分式的乘除法，分式乘除法的运算，归根到底是乘法的运算，当分子和分母是多项式时，一般应先进行因式分解，再约分．17．（3分）如图，已知△ABC≌△DEF，DF∥BC，且∠B＝60°，∠F＝40°，点A在DE上，则∠BAD的度数为20°．【分析】先由△ABC≌△DEF，根据全等三角形的性质得出∠B＝∠E＝60°，∠C＝∠F＝40°，由DF∥BC，得出∠1＝∠C，等量代换得到∠1＝∠F，那么AC∥EF，于是∠2＝∠E＝60°．由三角形内角和定理求出∠BAC＝180°﹣∠B﹣∠C＝80°，于是∠BAD＝∠BAC﹣∠2＝20°．【解答】解：∵△ABC≌△DEF，∴∠B＝∠E＝60°，∠C＝∠F＝40°，∵DF∥BC，∴∠1＝∠C，∴∠1＝∠F，∴AC∥EF，∴∠2＝∠E＝60°．∵∠BAC＝180°﹣∠B﹣∠C＝180°﹣60°﹣40°＝80°，∴∠BAD＝∠BAC﹣∠2＝80°﹣60°＝20°．故答案为：20°．【点评】本题考查了全等三角形的性质，平行线的判定与性质，三角形内角和定理，求出∠2＝∠E＝60°是解题的关键．18．（3分）一组数据1、3、4、5、x、9的众数和中位数相同，那么x的值是4．【分析】众数是数据中出现次数最多的数，中位数是数据从小到大排列后，中间的数（或中间的两数的平均数）就是中位数．【解答】解：数据共有6个，中位数应是从业到大排列后的第3个和第4个数据的平均数，由题意知，第4个数可能是4或5，当是4时，中位数是4，当是5时，中位数是4.5，由题意知，x只能是4时，才能满足题意．故填4．【点评】本题结合众数和中位数的知识来确定未知数的值．19．（3分）关于x的分式方程有增根，则m的值为4．【分析】分式方程去分母转化为整式方程，由分式方程有增根得到x﹣1＝0，求出x的值，代入整式方程计算即可求出m的值．【解答】解：去分母得：7x+5x﹣5＝2m﹣1，由分式方程有增根，得到x﹣1＝0，即x＝1，把x＝1代入整式方程得：12﹣5＝2m﹣1，解得：m＝4，故答案为：4【点评】此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．20．（3分）如图，四边形ABDC，∠A＝110°，若点D在AB、AC的垂直平分线上，则∠BDC的度数为140°．【分析】连接AD，根据线段的垂直平分线性质得出BD＝AD，DC＝AD，推出∠B＝∠BAD，∠C＝∠CAD，求出∠BAC＝∠BAD+∠CAD＝∠B+∠C＝110°，即可求出答案．【解答】解：连接AD，∵点D在AB、AC的垂直平分线上，∴BD＝AD，DC＝AD，∴∠B＝∠BAD，∠C＝∠CAD，∵∠BAC＝110°＝∠BAD+∠CAD，∴∠B+∠C＝110°，∴∠BDC＝360°﹣（∠B+∠C）﹣∠BAC＝360°﹣110°﹣110°＝140°，故答案为：140°．【点评】本题考查了四边形的内角和定理，等腰三角形的性质和判定，线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．三、解答题（满分60分）21．（8分）如图，点E，F在AB上，AD＝BC，∠A＝∠B，AE＝BF．求证：△ADF≌△BCE．【分析】根据全等三角形的判定即可求证：△ADF≌△BCE【解答】解：∵AE＝BF，∴AE+EF＝BF+EF，∴AF＝BE，在△ADF与△BCE中，∴△ADF≌△BCE（SAS）【点评】本题考查全等三角形的判定，解题的关键是求证AF＝BE，本题属于基础题型．22．（10分）某公司共25名员工，下表是他们月收入的资料．（1）该公司员工月收入的中位数是3400元，众数是3000元．（2）根据上表，可以算得该公司员工月收入的平均数为6276元．你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．【分析】（1）根据中位数的定义把这组数据从小到大排列起来，找出最中间一个数即可；根据众数的定义找出现次数最多的数据即可；（2）根据平均数、中位数和众数的意义回答．【解答】解：（1）共有25个员工，中位数是第13个数，则中位数是3400元；3000出现了11次，出现的次数最多，则众数是3000．故答案为3400；3000；（2）用中位数或众数来描述更为恰当．理由：平均数受极端值45000元的影响，只有3个人的工资达到了6276元，不恰当；【点评】此题考查了中位数、众数、平均数，掌握中位数、众数、平均数的定义是解题的关键，将一组数据从小到大依次排列，把中间数据（或中间两数据的平均数）叫做中位数，平均数＝总数÷个数，众数是出现次数最多的数据．23．（10分）如图，在Rt△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，DE⊥AC于点E，BF∥DE交CD于点F．求证：DE＝BF．【分析】根据角平分线的定义得到∠1＝∠2，根据角平分线的性质得到DE＝BD，∠3＝∠4，由平行线的性质得到3＝∠5，于是得到结论．【解答】证明：∵CD平分∠ACB，∴∠1＝∠2，∵DE⊥AC，∠ABC＝90°∴DE＝BD，∠3＝∠4，∵BF∥DE，∴∠4＝∠5，∴∠3＝∠5，∴BD＝BF，∴DE＝BF．【点评】本题考查了角平分线的性质，平行线的性质，等腰三角形的判定和性质，熟练掌握角平分线的性质是解题的关键．24．（12分）解答下列各题．（1）解方程＝1﹣；（2）化简：（1+）÷．【分析】（1）根据解分式方程的步骤和方法解方程即可；（2）根据分式的混合运算的法则计算即可．【解答】解：（1）方程两边都乘（x﹣2）得，2x＝x﹣2+1，解这个一元一次方程得，x＝﹣1经检验可知，x＝﹣1是原方程的解所以原方程的解为x＝﹣1；（2）（1+）÷＝（）×（＝×＝a﹣1．【点评】本题考查了解分式方程，分式的混合运算，熟练掌握解分式方程的步骤和方法是解题的关键．25．（10分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1＝42°，求∠BDE的度数．【分析】（1）根据全等三角形的判定即可判断△AEC≌△BED；（2）由（1）可知：EC＝ED，∠C＝∠BDE，根据等腰三角形的性质即可知∠C 的度数，从而可求出∠BDE的度数；【解答】解：（1）证明：∵AE和BD相交于点O，∴∠AOD＝∠BOE．在△AOD和△BOE中，∠A＝∠B，∴∠BEO＝∠2．又∵∠1＝∠2，∴∠1＝∠BEO，∴∠AEC＝∠BED．在△AEC和△BED中，，∴△AEC≌△BED（ASA）．（2）∵△AEC≌△BED，∴EC＝ED，∠C＝∠BDE．在△EDC中，∵EC＝ED，∠1＝42°，∴∠C＝∠EDC＝69°，∴∠BDE＝∠C＝69°．【点评】本题考查全等三角形，解题的关键是熟练运用全等三角形的性质与判定，本题属于中等题型．26．（10分）甲、乙两个工程队均参与某筑路工程，先由甲队筑路60公里，再由乙队完成剩下的筑路工程，已知乙队筑路总公里数是甲队筑路总公里数的倍，甲队比乙队多筑路20天．（1）求乙队筑路的总公里数；（2）若甲、乙两队平均每天筑路公里数之比为5：8，求乙队平均每天筑路多少公里．【分析】（1）根据甲队筑路60公里以及乙队筑路总公里数是甲队筑路总公里数的倍，即可求出乙队筑路的总公里数；（2）设乙队平均每天筑路8x公里，则甲队平均每天筑路5x公里，根据甲队比乙队多筑路20天，即可得出关于x的分式方程，解之经检验后即可得出结论．【解答】解：（1）60×＝80（公里）．答：乙队筑路的总公里数为80公里．（2）设乙队平均每天筑路8x公里，则甲队平均每天筑路5x公里，根据题意得：﹣＝20，解得：x＝0.1，经检验，x＝0.1是原方程的解，∴8x＝0.8．答：乙队平均每天筑路0.8公里．【点评】本题考查了分式方程的应用，解题的关键是：（1）根据数量关系列式计算；（2）找准等量关系，列出分式方程．。

北师大版八年级数学上册期末试卷及答案【完整版】

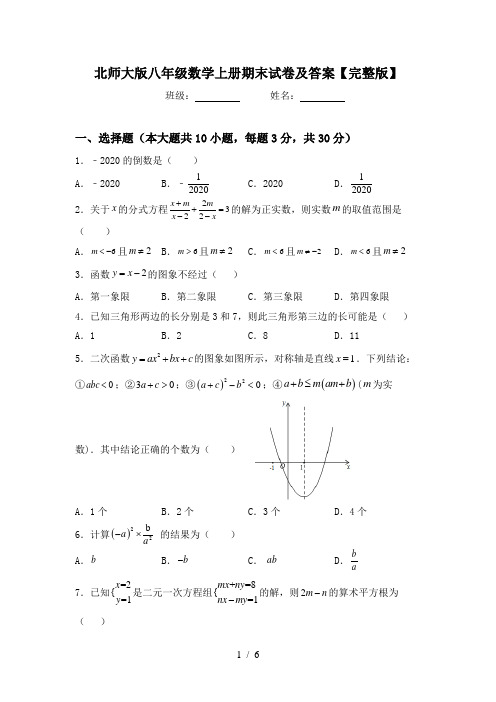
北师大版八年级数学上册期末试卷及答案【完整版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．﹣2020的倒数是（）A ．﹣2020B ．﹣12020C ．2020D ．12020 2．关于x 的分式方程2322x m m x x++=--的解为正实数，则实数m 的取值范围是（） A ．6m <-且2m ≠ B ．6m >且2m ≠ C ．6m <且2m ≠- D ．6m <且2m ≠3．函数2y x =-的图象不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）A ．1B ．2C ．8D ．115．二次函数2y ax bx c =++的图象如图所示，对称轴是直线1x =．下列结论：①0abc <；②30a c +>；③()220a c b +-<；④()a b m am b +≤+(m 为实数)．其中结论正确的个数为（）A ．1个B ．2个C ．3个D ．4个 6．计算()22b a a -⨯的结果为（） A ．bB ．b -C ． abD ．b a 7．已知=2{=1x y 是二元一次方程组+=8{ =1mx ny nx my -的解，则2m n -的算术平方根为（）A ．±2B ．2C ．2D ．48．如图，小华剪了两条宽为1的纸条，交叉叠放在一起，且它们较小的交角为60，则它们重叠部分的面积为（）A ．1B ．2C 3D ．23 39．如图，在正方形ABCD 中，AB =9，点E 在CD 边上，且DE =2CE ，点P 是对角线AC 上的一个动点，则PE +PD 的最小值是（）A ．310B ．103C ．9D ．9210．如图，已知在△ABC ，AB ＝AC ．若以点B 为圆心，BC 长为半径画弧，交腰AC 于点E ，则下列结论一定正确的是（）A ．AE ＝ECB ．AE ＝BEC ．∠EBC ＝∠BACD ．∠EBC ＝∠ABE二、填空题（本大题共6小题，每小题3分，共18分）1．因式分解：2()4()a a b a b ---＝________.2．已知菱形ABCD 的面积是12cm 2，对角线AC ＝4cm ，则菱形的边长是______cm ．3．因式分解：a 2-9=_____________．4．如图，把△ABC 绕点C 按顺时针方向旋转35°，得到△A ’B ’C ，A ’B ’交AC 于点D ，若∠A ’DC=90°，则∠A= °.5．如图,E 、F 分别是平行四边形ABCD 的边AB 、CD 上的点,AF 与DE 相交于点P,BF 与CE 相交于点Q,若215APD S cm ∆=，225BQC S cm ∆=，则阴影部分的面积为__________2cm ．6．如图△ABC 中，分别延长边AB 、BC 、CA ，使得BD=AB ，CE=2BC ，AF=3CA ，若△ABC 的面积为1，则△DEF 的面积为________.三、解答题（本大题共6小题，共72分）1．解方程：2142242x x x x +-+--=1．2．先化简，后求值：（5a 5a （a ﹣2），其中a=12+2．3．已知5a 2+的立方根是3，3a b 1+-的算术平方根是4，c 13分．（1）求a ，b ，c 的值；（2）求3a b c -+的平方根．4．在Rt△ABC中，∠BAC=90°,D是BC的中点，E是AD的中点．过点A作AF ∥BC交BE的延长线于点F（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF 的面积．5．已知平行四边形ABCD，对角线AC、BD交于点O，线段EF过点O交AD于点E，交BC于点F．求证：OE=OF．6．某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒的售价比乙种羽毛球多15元，王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球，共花费255元．（1）该网店甲、乙两种羽毛球每筒的售价各是多少元？（2）根据消费者需求，该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒，且甲种羽毛球的数量大于乙种羽毛球数量的35，已知甲种羽毛球每筒的进价为50元，乙种羽毛球每筒的进价为40元．①若设购进甲种羽毛球m筒，则该网店有哪几种进货方案？②若所购进羽毛球均可全部售出，请求出网店所获利润W（元）与甲种羽毛球进货量m（筒）之间的函数关系式，并说明当m为何值时所获利润最大？最大利润是多少？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、D3、B4、C5、C6、A7、C8、D9、A10、C二、填空题（本大题共6小题，每小题3分，共18分）1、()()()22a b a a -+-23、（a+3）（a ﹣3）4、55.5、406、18三、解答题（本大题共6小题，共72分）1、x=12、43、（1）a=5，b=2，c=3 ；（2）±4.4、（1）证明略；（2）证明略；（3）10．5、略.6、（1）该网店甲种羽毛球每筒的售价为60元，乙种羽毛球每筒的售价为45元；（2）①进货方案有3种，具体见解析；②当m=78时，所获利润最大，最大利润为1390元．。

北师大版八年级数学上册期末测试卷及完整答案

1 / 6 北师大版八年级数学上册期末测试卷及完整答案班级：姓名：

一、选择题（本大题共10小题，每题3分，共30分） 1．2020的相反数是（）

A．2020 B．2020 C．12020 D．12020 2．若关于x的方程3m(x＋1)＋5＝m(3x－1)－5x的解是负数，则m的取值范围是（） A．m＞－54 B．m＜－54 C．m＞54 D．m＜54 3．已知x+y＝﹣5，xy＝3，则x2+y2＝（） A．25 B．﹣25 C．19 D．﹣19 4．若关于x的方程333xmmxx=3的解为正数，则m的取值范围是（）

A．m＜92 B．m＜92且m≠32 C．m＞﹣94 D．m＞﹣94且m≠﹣34 5．已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长（） A．4 B．16 C．34 D．4或34 6．如图，有一块直角三角形纸片，两直角边6cmAC，8cmBC．现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于

（） A．2cm B．3cm C．4cm D．5cm 2 / 6

7．下列说法中错误的是（） A．12是0.25的一个平方根 B．正数a的两个平方根的和为0

C．916的平方根是34 D．当0x时，2x没有平方根 8．如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1等于（）

A．132° B．134° C．136° D．138° 9．如图，在四边形ABCD中，ADBC∥，90D，4AD，3BC．分别以点A，C为圆心，大于12AC长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（）

A．22 B．4 C．3 D．10 10．如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，

则∠A的大小为（） A．150° B．130° C．120° D．100° 二、填空题（本大题共6小题，每小题3分，共18分）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级（上）数学期末复习测试卷2
班级姓名
一、选择题（
每小题只有一个正确的选项，每小题2分，共30分）

1、分别顺次连结 ①等腰梯形；②矩形；③菱形；④对角线相等的四边形“各边中点所构
成的四边形”中，为菱形的是（）
A．① B．② C．①②③ D．①②④
2、下图所列图形中是轴对称，但不是中心对称图形的有（）

A．1个 B．2个 C．3个 D．4个
3、将△ABC向右平移3个单位后得到△A′B′C′，若点A的坐标是（－2，3），则
点A′的坐标是（）
A．（1，3） B．（－2，6） C．（－5，3） D．（－2，0）

4、一个直角三角形的两条直角边分别是5和12，则斜边是（）
A．13 B．12 C．15 D．10
5、下列说法中正确的是（）
A．四个角相等的四边形是矩形 B．四个角相等的四边形是正方形
C．对角线垂直的四边形是菱形 D．四条边相等的四边形是正方形
6、一段导线，在0℃时的电阻为2欧，温度每增加1℃，电阻增加0.008欧，那么电阻R欧
表示为温度t℃的函数关系为（）
A、R=2992.1t B、 R=2008.0t C、 R=2008.2t D、 R=22t
7、点P(m+3，m+1)在直角坐标系的x轴上，则点P的坐标为（）
A．（0，2） B．（2，0） C．（4，0） D．（0，-2）

8、计算82的结果是（）
A．4 B．4 C．2 D．±4
9、已知一个多边形的的内角和为1080º，则这个多边形的边数是（）
A．5 B．6 C． 7 D． 8

10、若532yxba与xyba2425是同类项，则（）

A．12xy B．21xy C．02xy D．31xy
11、设方程组.433,1byxabyax的解是.1,1yx那么ba,的值分别为（）
A、;3,2 B、;2,3 C、;3,2 D、.2,3
12、关于关于yx、的方程组5m212y3x4m113y2x的解也是二元一次方程2073myx的解，
则m的值是（）
A、0 B、1 C、2 D、21
13、如果点P(m，1+2m)在第二象限，那么m的取值范围是（）

A．210m B．021m C．0m D．21m
14.甲、乙两人参加植树活动，两人共植树20棵，已知甲植树数是乙的1.5倍．如果设甲
植树x棵，乙植树y棵，那么可以列方程组．（）

（A）yxyx5.2,20 （B）yxyx5.1,20 （C）yxyx5.1,20 （D）5.1,20yxyx

15、下列函数中，是一次函数的有（）
(1)（1）y＝x; (2)4xy； (3)y＝2x－1； (4)y＝1x ； (5)y＝x2－1中，
A．4个 B．3个 C．2个 D．1个
二、填空题（每小题2分，共20分）
1．若一个数的算术平方根是8，则这个数的立方根是．
2．已知点P1（a，3）与P2（－2，－3）关于x轴对称，则______a；与P1关于原点对称
的点P3的坐标是__________．

3．一个多边形的每个外角都等于60º，这个多边形是边形．
4．菱形的两条对角线长为6和8，则菱形的面积是，周长是．
5、已知x＜1，则12x-x2化简的结果是．
6、对于函数4)4(kxky当k_______时，它是正比例函数；当k_______时，它是一次
函数.
7、在□ABCD中，对角线AC与BD相交于点O，在不添加任何辅助线和字母的情况下，请
添加一个条件，使□ABCD变为矩形，需添加的条件是．（写出
一个即可）

8、拖拉机开始工作时，油箱中有油28升，如果每小时耗油4升，那么油箱中的剩余油量y
（升）和工作时间x（时）之间的函数关系式是．
9、如图2，菱形ABCD中，∠ADC=120°，AB=10,则BD=________,AC=__________,
菱形ABCD的面积=________

10、如图5，等腰梯形ABCD中，AD//BC,AB=AD=DC
B=45,1AE
，则梯形ABCD的周长=____________，梯形ABCD的面积________

三、解答题(共50分)
1．计算：（每小题4分，共24分）

（1）25)15(45220212 （2）81632426

2．解方程组：（1）156356yxyx （2）153752yxyx
（3）14329mnnm （4）232)21(3)1(4yxyyx
3．（4分）已知：如图，在Rt△OAB中，∠OAB＝90°，OA＝AB＝6cm，将△OAB绕点O沿逆时
针方向旋转90°得到Rt△OA1B1．
（1）直接写出线段OA1的长度和∠AOB1的度数；
（2）连结AA1，则四边形OAA1B1是平行四边形吗？请说明理由．

图2
B
O
A
C

图5
E
A
D

B
C
4、（4分）蜡烛燃烧，每小时耗去4.8厘米，已知蜡烛原来的长度为24厘米，设燃烧x小时后剩下的长度
为y厘米．（1）写出y与x之间的函数关系式；（2）经过多长时间后，蜡烛点完？

6、（6分）如图，已知AB∥DC，AE⊥DC，AE = 12，BD = 15，AC = 20，求梯形ABCD的面积．

7、（8分）如图，已知△ABC中，AB=AC，AD是∠BAC的平分线，AE是∠BAC的外角平分线，CE⊥AE于点E。
（1）、求证：四边形ADCE为矩形；
（2）、求证：四边形ABDE为平行四边形。
A

B
C
D

E
F