泊松分布
泊松分布函数

泊松分布函数
泊松分布函数是一个在统计学中应用非常广泛的概率分布函数,它具有非常实用的特性,更是随机变量分析中的重要性能指标。
本文就泊松分布函数的定义,性质以及应用三方面,进行系统的介绍。
### 1.定义
泊松分布函数又称泊松概率分布,它是 Lamoré1919提出的,它是描述连续独立随机变量分布的概率分布函数。
简单的说,泊松分布函数可以用来描述随机变量的概率分布情况,其定义如下:设 X 为一个取 k 个正整数值的独立随机变量,并且有固定的参数令 X概率密度函数为
$$f(x)= frac{mu^x}{x!}e^{-mu},x=0,1,2,ldots k$$ 其中,μ为 X期望值,k 为最大取值。
### 2.性质
泊松分布函数具有以下特性:
(1)均值和方差:泊松分布函数的均值μ和方差μ都是μ。
(2)最小值:泊松分布函数的最小值为0。
(3)最大值:当X取正无穷时,泊松分布函数的最大值为0。
### 3.应用
泊松分布函数主要应用于描述何种连续独立随机变量的概率分
布情况,例如:
(1)医疗:用来预测一定时间段内的某种疾病的发病率;
(2)交通:用来预测交通流量随时间变化的概率;
(3)教育:用来预测每一类学生的成绩分布等等。
因此,泊松分布函数是一个很有用的概率函数,不仅在统计学中得到了广泛的应用,而且在日常生活中也有所涉及。
泊松分布的母函数

泊松分布的母函数泊松分布是一种离散概率分布,它描述了在一定时间或空间内发生某一事件的次数分布规律。
泊松分布的母函数是一种重要的工具,可以用来求解泊松分布的各种性质和应用。
本文将介绍泊松分布的母函数及其应用。
一、泊松分布的定义泊松分布是一种描述在一定时间或空间内某一事件发生次数的概率分布。
它的概率函数为:P(X=k)=e^(-λ) * λ^k / k!其中,X表示事件发生的次数,λ为单位时间或单位空间内事件发生的平均次数。
这个平均值也被称为泊松分布的参数。
k为事件发生的次数,k可以是任意非负整数。
泊松分布在实际生活中有很多应用,比如研究电话呼叫中心的来电次数、研究交通事故的发生次数等等。
二、泊松分布的母函数泊松分布的母函数是指:G(s)=E(s^X)=∑(k=0,∞)(s^k * e^(-λ) * λ^k / k!) 其中,E(s^X)表示事件发生次数的期望值。
s为一个实数,G(s)是s的函数。
这个母函数可以用来求解泊松分布的各种性质和应用。
为了简化计算,我们可以将泊松分布的概率函数变形:P(X=k)=e^(-λ) * λ^k / k! = (λ/k) * e^(-λ) * (λ^(k-1) / (k-1)!)然后,我们将这个式子代入泊松分布的母函数中:G(s)=∑(k=0,∞)(s^k * e^(-λ) * λ^k / k!)=e^(-λ) * ∑(k=0,∞)(s^k * (λ^k / k!))=e^(-λ) * ∑(k=0,∞)(s^k * (λ/k) * (λ^(k-1) / (k-1)!)) =e^(-λ) * λ * ∑(k=1,∞)(s^k * (λ^(k-1) / (k-1)!))=e^(-λ) * λ * ∑(k=0,∞)(s^(k+1) * (λ^k / k!))=e^(-λ) * λ * E(s^(X+1))可以看出,泊松分布的母函数可以表示为泊松分布的期望值E(s^(X+1))的函数。
二项分布、泊松分布的关系

二项分布、泊松分布的关系二项分布和泊松分布是概率论中两个重要的离散概率分布。
它们在实际问题中经常被用来描述随机事件的发生情况,尤其是在计算事件发生次数的概率时。
本文将从概念定义、特点、应用场景等方面介绍二项分布和泊松分布的关系。
一、概念定义1. 二项分布:简单来说,二项分布是指在n次独立重复试验中,成功事件发生的次数服从的概率分布。
其中,每次试验只有两个可能的结果,成功和失败,成功事件发生的概率为p,失败事件发生的概率为1-p。
这些独立重复试验的结果是互相独立的,且每次试验的成功概率不变。
2. 泊松分布:泊松分布是指在一定时间或空间范围内,某事件发生的次数服从的概率分布。
泊松分布的特点是事件发生的概率是相等的,且事件之间是独立的。
泊松分布的参数λ表示单位时间或单位空间内事件发生的平均次数。
二、特点对比1. 参数不同:二项分布的参数是试验次数n和成功概率p,而泊松分布的参数是事件发生的平均次数λ。
2. 取值范围不同:二项分布的取值范围是0到n,表示成功事件发生的次数;泊松分布的取值范围是0到无穷大,表示事件发生的次数。
3. 分布形态不同:二项分布呈现出明显的对称性,随着试验次数的增加,其形态逐渐趋于正态分布;泊松分布呈现出右偏的形态,随着参数λ的增大,其形态逐渐趋于对称。
三、关系解释1. 二项分布是泊松分布的一个特例:当试验次数n趋于无穷大,成功概率p趋于0,使得λ=np保持不变时,二项分布近似于泊松分布。
这是因为在大量独立重复试验中,每次试验成功的概率很小,但整体成功的次数还是有一定规律可循的,符合泊松分布的特点。
2. 泊松分布是二项分布的极限情况:当试验次数n趋于无穷大,成功概率p趋于0,使得λ=np保持不变时,二项分布近似于泊松分布。
这是因为泊松分布是用来描述单位时间或单位空间内事件发生次数的概率,当试验次数趋于无穷大时,单位时间或单位空间内事件发生次数也趋于无穷大,符合泊松分布的特点。
四、应用场景1. 二项分布的应用场景:二项分布常用于描述离散的二元事件,比如抛硬币的结果、赌博中的输赢、商品的合格率等。
泊松分布
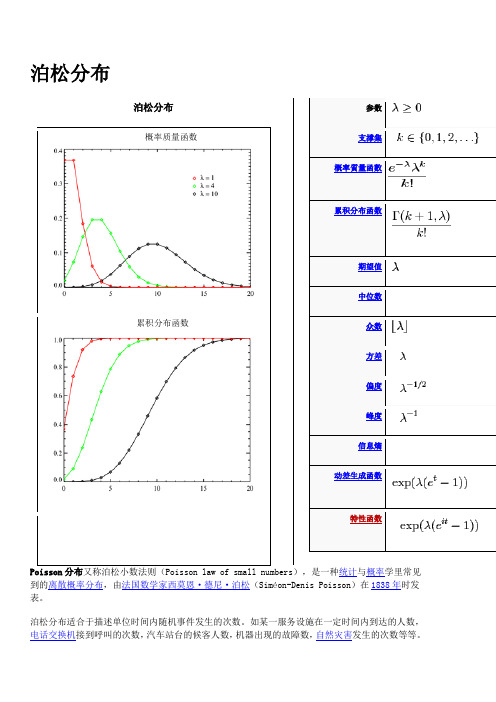
泊松分布泊松分布概率质量函数累积分布函数参数支撑集概率質量函數累积分布函数期望值中位数众数方差偏度峰度信息熵动差生成函数特性函数Poisson分布又称泊松小数法则(Poisson law of small numbers),是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
泊松分布适合于描述单位时间内随机事件发生的次数。
如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数等等。
泊松分布的概率质量函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
性质服从泊松分布的随机变量,其数学期望与方差相等,同为参数λ: E(X)=V(X)=λ•动差生成函数:泊松分布的来源在二项分布的伯努力试验中,如果试验次数n很大,二项分布的概率p很小,而乘积λ= n p比较适中,则事件出现的次数的概率可以用泊松分布来逼近。
这在现实世界中是很常见的现象,如DNA 序列的变异、放射性原子核的衰变、电话交换机收到的来电呼叫、公共汽车站候车情况等等。
证明如下。
首先,回顾e的定义:二项分布的定义:如果令p = λ / n, n趋于无穷时P的极限:[编辑]最大似然估计给定n个样本值k i,希望得到从中推测出总体的泊松分布参数λ的估计。
为计算最大似然估计值, 列出对数似然函数:对函数L取相对于λ的导数并令其等于零:解得λ从而得到一个驻点(stationary point):检查函数L的二阶导数,发现对所有的λ与k i大于零的情况二阶导数都为负。
因此求得的驻点是对数似然函数L的极大值点:[编辑]例子对某公共汽车站的客流做调查,统计了某天上午10:30到11:47来到候车的乘客情况。
假定来到候车的乘客各批(每批可以是1人也可以是多人)是互相独立发生的。
泊松分布 超几何分布

泊松分布超几何分布泊松分布和超几何分布是概率论中常见的两种离散概率分布,它们在实际问题中具有广泛的应用。
本文将分别介绍泊松分布和超几何分布的定义、特点以及应用领域。
一、泊松分布泊松分布是一种描述单位时间内随机事件发生次数的概率分布。
它的定义如下:在单位时间内随机事件发生的次数服从泊松分布,如果事件发生的概率在不同时间段内相等,并且相互独立。
泊松分布的特点是只有一个参数λ,表示单位时间内事件平均发生的次数。
泊松分布的概率质量函数为:P(X=k)=e^(-λ)*(λ^k)/k!,其中e为自然对数的底数。
泊松分布的应用非常广泛。
例如,在电话交换机的研究中,可以使用泊松分布来描述单位时间内呼叫到达的次数;在客流量预测中,可以使用泊松分布来描述单位时间内到达某个地点的人数;在信号传输中,可以使用泊松分布来描述单位时间内出现的误码数等。
二、超几何分布超几何分布是描述从有限总体中抽取固定数量样本中成功次数的概率分布。
它的定义如下:从总体中随机抽取n个样本,其中包含m 个成功的样本和N-m个失败的样本,那么超几何分布表示样本中成功次数的概率分布。
超几何分布的特点是有三个参数:总体中成功的样本数m,总体中失败的样本数N-m,以及抽取的样本数量n。
超几何分布的概率质量函数为:P(X=k)=(C(m,k)*C(N-m,n-k))/C(N,n),其中C(a,b)表示从a个元素中选取b个元素的组合数。
超几何分布的应用也非常广泛。
例如,在质量控制中,可以使用超几何分布来描述从一批产品中抽取固定数量的样本中不合格品的数量;在样本调查中,可以使用超几何分布来描述从总体中抽取一定数量的样本中满足某个条件的样本数量等。
泊松分布和超几何分布在实际问题中的应用是相互补充的。
泊松分布适用于描述单位时间内事件发生的次数,而超几何分布适用于描述从有限总体中抽取样本中成功次数。
在实际问题中,可以根据具体情况选择使用泊松分布还是超几何分布来建立概率模型。
泊松分布的方差

泊松分布的方差引言:泊松分布是一种重要的离散概率分布,常用于描述单位时间内某一事件发生次数的概率分布。
其最显著的特征是均值(即期望值)和方差相等。
本文将详细探讨泊松分布的方差及其计算方法。
一、泊松分布的定义与特性泊松分布是一种离散型概率分布,其定义如下:P(X=k)= (e^(-λ) * λ^k)/ k!其中,k表示某一事件发生的次数,λ为单位时间内该事件的平均发生次数,e为自然对数的底数。
泊松分布的期望值和方差均等于λ。
二、方差的定义与计算方法方差是描述一个概率分布中离散程度的指标。
对于泊松分布的方差,可以使用以下公式进行计算:Var(X) = λ三、方差公式的推导与解释泊松分布的方差公式的推导可以通过以下步骤完成:1. 先计算泊松分布的期望值,即λ;2. 计算泊松分布的方差:Var(X) = E(X^2) - [E(X)]^2= Σ(k^2 * P(X=k)) - [Σ(k * P(X=k))]^2= Σ(k^2 * (e^(-λ) * λ^k)/ k!) - [(Σ(k * (e^(-λ) * λ^k)/ k!)]^2= Σ((k * (k-1) * e^(-λ) * λ^k)/ k!) + Σ(λ * e^(-λ) * λ^k / k) - [(Σ(λ * e^(-λ) * λ^k/ k!)]^2= λ(λ+1) - λ^2= λ方差公式的解释为泊松分布的性质之一,即方差等于其期望值。
这意味着在泊松分布中,事件的发生次数的离散程度与其平均发生次数相等。
四、泊松分布方差的应用泊松分布的方差在实际应用中具有重要意义。
以下是一些常见的应用场景:1. 电话呼叫中心的接待员接收到来电的数量;2. 网络服务器接收到请求的数量;3. 股票交易所在某一时间段内的交易数量;4. 道路上的交通事故发生数量等。
在这些场景中,泊松分布的方差可以帮助我们分析和预测事件的发生频率及其离散程度,进而进行合理的资源分配和决策。
泊松分布例题及解析
泊松分布例题及解析
当在一个呼叫中心,每小时平均接到10个电话。
在接下来的一个小时内,恰好接到5个电话的概率是多少?
解答:
要解决这个问题,我们可以使用泊松分布公式:
P(X = k) = (e^(-λ) * λ^k) / k!
其中:
- P(X = k) 是恰好获得k个事件发生的概率
- e 是自然对数的底数(约为2.71828)
- λ是在给定时间段内事件平均发生的速率
- k 是我们感兴趣的事件数量
在这个例子中,λ被设定为10(每小时的平均呼叫数量),而k是5(所期望的呼叫数量)。
让我们将这些值代入公式中:
P(X = 5) = (e^(-10) * 10^5) / 5!
计算阶乘:
5! = 5 * 4 * 3 * 2 * 1 = 120
现在我们来计算概率:
P(X = 5) = (2.71828^(-10) * 10^5) / 120 ≈0.037833
因此,在接下来的一个小时内,恰好接到5个电话的概率约为0.037833,或者说是3.78%。
注意:泊松分布通常用于建模在固定的时间或空间间隔内事件发生的数量,给定事件的平均发生率。
它假设事件是独立且以恒定速率发生的。
1。
泊松分布矩估计
泊松分布矩估计泊松分布又称负二项分布,其中“泊”指大海,“松”即木材。
泊松分布是由二项分布推广得到的,在学习的过程中我们常常会用到它。
今天我们就来研究泊松分布。
1.为了简化论证,我们把研究对象集合成一个集合。
2.数据随机样本的基本概念,简单的说就是“ n个随机变量的集合,而每个随机变量的期望值为它们的算术平均数的平方根”。
数据的分布形状有点像板块,可以想象出来:我们把这种分布叫做正态分布,而把介于这两种分布之间的随机分布叫做伪随机分布。
3.泊松分布的矩估计公式: r(X) = n(x- e)X(其中e是参数)。
此外,我们还需要知道另外两个重要的统计量:方差和标准差。
其中,E是一个矩,是每个变量的均值; X是某个正态分布的期望,而样本中所有变量的分布都是服从于正态分布的。
4.泊松分布的特征根,泊松分布的特征根有三个,它们分别是u=-1, v=-2, w=-4。
为什么要求它们的符号呢?因为我们在建立正态分布函数的时候只需要一个。
比如说,把y=3代入我们刚才的结果,然后带入定义式,就可以得到-3,所以-3是的特征根。
也可以通过数学工具求特征根。
数据符号: t-1; t-2; t-3; t+1; t+2; t+3;t+4;特征根符号: f+1; f+2; f+3; f+4; 5.泊松分布的三个特征根只有在自变量是标准正态分布或者两个参数的分布服从正态分布时才存在,否则特征根为0。
5.9点法6.泊松分布不满足正态分布。
(1)如果所有观测值服从正态分布,且标准差服从正态分布,则认为是泊松分布; (2)若观测值中大部分是服从正态分布的,但小部分不是,那么原来认为是泊松分布的现在就可能认为是其他分布。
泊松分布联合分布律
泊松分布联合分布律泊松分布是离散随机变量的一种概率分布,可以用来描述单位时间(或空间)内随机事件发生的次数。
泊松分布的概率质量函数如下:P(X=k) = (e^(-λ) * λ^k) / k!其中,X表示随机变量的取值,k表示随机事件发生的次数,λ表示在单位时间(或空间)内平均发生的次数,e是自然对数的底数。
接下来我们考虑两个泊松分布随机变量X和Y,它们的参数分别为λX和λY。
我们可以求出它们的联合分布律。
首先,我们定义一个事件A,它表示随机变量X的取值为i (X=i),同时随机变量Y的取值为j(Y=j)。
我们可以表示事件A的概率为P(X=i, Y=j)。
然后,我们可以用X的概率质量函数和Y的概率质量函数来表示事件A的概率。
P(X=i, Y=j) = P(X=i) * P(Y=j)根据泊松分布的概率质量函数,我们可以将上式展开为:P(X=i, Y=j) = ((e^(-λX) * λX^i) / i!) * ((e^(-λY) * λY^j) / j!)接下来,我们可以用以上公式来计算任意的联合概率。
我们也可以计算出X和Y的边缘分布,即X和Y分别的概率分布。
对于X来说,它的边缘分布可以用如下公式表示:P(X=i) = Σ P(X=i, Y=j) = Σ ((e^(-λX) * λX^i) / i!) * ((e^(-λY) *λY^j) / j!)其中,Σ是求和符号,表示对所有可能的Y=j进行求和。
同样地,对于Y来说,它的边缘分布可以用如下公式表示:P(Y=j) = Σ P(X=i, Y=j) = Σ ((e^(-λX) * λX^i) / i!) * ((e^(-λY) *λY^j) / j!)其中,Σ是求和符号,表示对所有可能的X=i进行求和。
通过以上的联合分布律和边缘分布律,我们可以计算出泊松分布随机变量X和Y之间的一系列联合概率和边缘概率。
这些概率可以用来研究和分析随机事件发生的次数之间的相关性和依赖关系。
泊松分布的证明
泊松分布的证明泊松分布是概率论中常见的一种离散概率分布,描述了一段固定时间内,某事件发生次数的概率分布情况。
下面将从数学推导的角度证明泊松分布的性质。
设事件发生的平均次数为λ(λ > 0),即在一单位时间内发生某事件的次数平均为λ,我们要求在一段固定时间内发生该事件的次数为n的概率,即P(X = n)。
现在,我们开始推导:1.首先,我们要确定事件发生次数的分布情况,也就是找到事件的概率质量函数p(x)。
考虑单位时间内事件发生的概率为λ,那么在一个长度为t的时间段内(t单位时间内,每个单位时间是独立的),我们可以将其分割成n个单位时间段,每个单位时间段内事件发生的概率仍然是λ。
所以,假设每个单位时间段内事件发生的概率为p,则p的取值范围为0到1。
2.接下来,我们需要确定事件发生次数为n的概率。
考虑在t单位时间内事件发生n次的情况,假设每个单位时间段内事件发生的概率为p,则n次事件发生的概率为p^n。
但这只是考虑了某一个特定的事件发生次数为n的情况,而事实上,在t单位时间内事件发生的次数可以有很多种可能。
我们需要考虑所有可能的组合情况。
3.组合问题。
接下来,我们需要考虑组合问题。
对于t单位时间内事件发生n次的情况,我们可以将其视为n个单位时间段,每个单位时间段内事件发生或不发生。
所以,对于t单位时间内的事件发生情况,我们有2^n种可能性,且每种可能性的概率相同,即每种可能性的概率为p^n * (1-p)^(t-n)。
4.最后的求和。
由于每种可能性的概率相同,我们只需要将所有可能性的概率求和,即得到在t单位时间内事件发生次数为n的概率。
考虑到t单位时间内,总共可能发生的次数为0到t,我们可以将其表示为一个求和形式:P(X = n) = ∑ [p^n * (1-p)^(t-n)]上式中的求和符号对应的是事件发生次数的所有可能性,即从0到t。
5.结果化简。
将上式中的概率公式进行化简,可以得到泊松分布的概率质量函数:P(X = n) = e^(-λ) * λ^n / n!其中,e是自然对数的底数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一家商店采用科学管理, 例1 一家商店采用科学管理,由该商店过去 的销售记录知道, 的销售记录知道,某种商品每月的销售数可 的泊松分布来描述, 以用参数λ=5的泊松分布来描述,为了以 的泊松分布来描述 95%以上的把握保证不脱销,问商店在月底 以上的把握保证不脱销, 以上的把握保证不脱销 至少应进某种商品多少件 某种商品多少件? 至少应进某种商品多少件? 解: 设该商品每月的销售数为X, 设该商品每月的销售数为 已知X服从参数 的泊松分布. 已知 服从参数λ=5的泊松分布 的泊松分布 设商店在月底应进某种商品 某种商品m件 设商店在月底应进某种商品 件, 的最小的m 求满足 P(X≤m)>0.95 的最小的 .
泊松分布
欧阳顺湘 北京师范大学珠海分校 2005.5.15
一、泊松分布的定义及图形特点 设随机变量X所有可能取的值为 设随机变量 所有可能取的值为0 , 1 , 所有可能取的值为 2 , … , 且概率分布为: 且概率分布为:
P(X = k) = e
−λ
λ
, k= ,12L , 0,, L k!
k
P{ X = k } ≈
λk
k!
e
−λ
,
k = 0,1,2,...
• Example In his book, Feller discusses the statistics of flying bomb hits in the south of London during the Second World War. • Assume that you live in a district of size 10 blocks by 10 blocks so that the total district is divided into 100 small squares. How likely is it that the square in which you live will receive no hits if the total area is hit by 400 bombs?
>0 是常数,则称 其中 λ 是常数 则称 X 服从参数为 的 λ 泊松分布,记作 记作X~P(λ ). 泊松分布 记作
泊松分布的图形特点: 泊松分布的图形特点:X~P( ) λ
二、二项分布与泊松分布 历史上, 历史上,泊松分布是作为二项分布的近 似,于1837年由法国数学家泊松引入的 . 年由法国数学家泊松引入的 在实际中, 在实际中,许多随机现象服从或近 似服从泊松分布. 似服从泊松分布
• • • • • • • • • •
用 X 表示落入该小区内的炸弹数,则 X~B(400,1/100) n=400, p=1/100 因此 P(X=0)=(99/100)^400 用Poisson分布近似计算。。 X近似服从参数为 4 =np=400*1/100的Poisson 分布 即 X~P(4) 因此 P(X=0)=exp(-4) P(X=0)=(99/100)^400 可以计算(99/100)^400= 0.01795055328 exp(-4)= 0.01831563889
三、泊松分布产生的一般条件 在自然界和人们的现实生活中, 在自然界和人们的现实生活中,经常要遇 到在随机时刻出现的某种事件. 到在随机时刻出现的某种事件.我们把在随机 时刻相继出现的事件所形成的序列, 时刻相继出现的事件所形成的序列,叫做随机 事件流. 事件流. 若事件流具有平稳性、无后效性、普通性, 若事件流具有平稳性、无后效性、普通性, 则称该事件流为泊松事件流(泊松流) 则称该事件流为泊松事件流(泊松流). 下面简要解释平稳性、无后效性、普通性. 下面简要解释平稳性、无后效性、普通性. 平稳性
∞
−5 k
这一讲,我们介绍了泊松分布 这一讲,我们介绍了泊松分布 n重贝努里试验中稀有事件出现的次数近 重贝努里试验中稀有事件出现的次数近 重贝努里试验中稀有事件 似地服从泊松分布. 似地服从泊松分布 我们给出了泊松分布产生的一般条件 泊松分布在管理科学、 泊松分布在管理科学、运筹学以及自然 科学的某些问题中都占有重要的地位 .
平稳性: 平稳性: 在任意时发生k次(k≥0)的 的 概率只依赖于区间长度而与区间端点无关. 概率只依赖于区间长度而与区间端点无关 无后效性: 无后效性: 在不相重叠的时间段内, 在不相重叠的时间段内,事件的发生是相 互独立的. 互独立的 普通性: 普通性: 如果时间区间充分小, 如果时间区间充分小,事件出现两次或 两次以上的概率可忽略不计. 两次以上的概率可忽略不计
我们把在每次试验中出现概率很小的事 稀有事件. 件称作稀有事件 件称作稀有事件 如地震、火山爆发、特大洪水、 如地震、火山爆发、特大洪水、意外事故等等
由泊松定理, 重贝努里试验中 重贝努里试验中稀有事件 由泊松定理,n重贝努里试验中稀有事件 出现的次数近似地服从泊松分布. 出现的次数近似地服从泊松分布
例如
粒子数; 一放射性源放射出的 α粒子数; 某电话交换台收到的电话呼叫数; 某电话交换台收到的电话呼叫数; 到某机场降落的飞机数; 到某机场降落的飞机数 一个售货员接待的顾客数; 一个售货员接待的顾客数 一台纺纱机的断头数; … 一台纺纱机的断头数 都可以看作泊松流. 都可以看作泊松流
对泊松流,在任意时间间隔 对泊松流,在任意时间间隔(0,t)内,事件 内 事件 (如交通事故 出现的次数服从参数为 λ的 如交通事故)出现的次数服从参数为 t 如交通事故 称为泊松流的强度. 泊松分布 . λ 称为泊松流的强度
进货数
销售数
的最小的m. 求满足 P(X≤m)>0.95 的最小的 也即 P(X>m) ≤ 0.05
∞ −5 k
e 5 ≤ 0.05 或 ∑ ! k=m+ 1 k
查泊松分布表得
e 5 ∑ k! ≈0.032, k= 10
于是得 m+1=10,
∞
−5 k
e 5 ∑ k! ≈0.068 k=9
m=9件 件
泊松定理: 泊松定理: 是一个正整数, 设 是一个正整数, ,则有
−λ
limC p ( − pn) = 1 e
n→ ∞ k n k n
n−k
λ
, k= , ,2L , 01 , L k!
k
设随机变量X 由此可知 设随机变量 n~B(n, p), (n=0, 1, = 2,…), 且n很大,p很小,记λ=np,则 很大, 很小 很小, 很大 ,
