翼型厚度对风力机翼型气动特性的影响
机翼的几何外形和气动力和气动力矩

2.2超音速翼型的升力 如图是超音速以小迎角绕双弧翼型的流动
当α <δ ,前缘上下均受压缩,形 成强度不同的斜激波;当α>δ ,上
面形成膨胀波 ,下面形成斜激波;
经一系列膨胀波后,由于在后缘处 流动方向和压强不一致,从而形成 两道斜激波,或一道斜激波一族膨 胀波。由于上翼面压强低于下翼面, 因此形成升力。
垂直于翼面)和摩擦切应力(与翼面相切),它们将产生一 个合力R,合力的作用点称为压力中心,合力在来流方向的分 量为阻力X,在垂直于来流方向的分量为升力Y。
N ( p cos sin )ds A ( cos p sin )ds
R
A2 N 2
1.4
翼型的空气动力系数
1.3 低速翼型的低速气动特性概述
(4)随着迎角的增大,驻点逐渐后移,最大速度点越靠近前 缘,最大速度值越大,上下翼面的压差越大,因而升力越大。 (5)气流到后缘处,从上下翼面平顺流出,因此后缘点不一
定是后驻点。
1.5 低速翼型的低速气动特性概述
翼型绕流气动力系数随迎角的变化曲线 一个翼型的气动特性,通常用曲线表示。有升力系数
S c pj c
1. 2 机翼的平面几何参数
展弦比:翼展b和平均几何弦长cpj的比值叫做展弦比,用λ表 示,其计算公式可表示为:
b c pj
展弦比也可以表示为翼展的平方于机翼面积的比值。
b2 S
展弦比越大,机翼的升力系数越大,但阻力也增大。高速飞 机一般采用小展弦比的机翼。 根梢比:根梢比是翼根弦长c0与翼尖弦长c1的比值,一般用η
表示,
c0 c1
1.2 机翼的平面几何参数
梢根比:梢根比是翼尖弦长c1与翼根弦长c0的比值,一般用ξ 表示,
NACA0018翼型锯齿襟翼气动性能的数值研究

Modeling and Simulation 建模与仿真, 2021, 10(2), 578-585Published Online May 2021 in Hans. /journal/moshttps:///10.12677/mos.2021.102058NACA0018翼型锯齿襟翼气动性能的数值研究于永迪上海理工大学,上海收稿日期:2021年4月26日;录用日期:2021年5月17日;发布日期:2021年5月25日摘要以NACA0018翼型作为基础翼型,选取θ = 30˚, 60˚, 90˚三种不同锯齿角度以及d/h = 0.6, 0.8, 1三种不同深度的锯齿襟翼研究锯齿几何参数对翼型气动性能的影响。
同时通过改变入口速度研究不同雷诺数下锯齿襟翼对性能的影响。
结果表明,锯齿襟翼角度对翼型气动性能影响较小;随着锯齿深度的增加,翼型升阻比降低;随着入口雷诺数的增大,翼型升力逐渐增加,阻力逐渐降低,但增大幅度有所减缓;当格尼襟翼上开锯齿后,原本格尼襟翼后交替脱落的管状涡结构,由于气体从锯齿间隙通过并形成一对流向涡,与格尼襟翼固有的脱落涡掺混耗散,形成破碎的小结构,减弱尾迹流动不稳定性,降低翼型阻力,随着开齿深度的增加,涡核集中区域逐渐向襟翼附近前移,涡的掺混、消散更快。
关键词锯齿襟翼,气动性能,尾迹涡,数值计算,LiutexNumerical Investigation on AerodynamicPerformance of NACA0018 Airfoil Serrated Gurney FlapYongdi YuUniversity of Shanghai for Science and Technology, ShanghaiReceived: Apr. 26th, 2021; accepted: May 17th, 2021; published: May 25th, 2021AbstractWith NACA0018 airfoil as the basic airfoil, three kinds of serrated Gurneyflap with different angles of 30˚, 60˚ and 90˚ and different depths of d/h = 0.6, 0.8 and 1 were selected to study the effects of于永迪the serrated geometrical parameters on the aerodynamic performance of the airfoil. At the same time, the performance of the serrated Gurneyflap under different Reynolds numbers was studied by changing the inlet velocity. The results show that the angle of the serrated flaps has little effect on the aerodynamic performance of the airfoil. With the increase of sawtooth depth, the lift-drag ratio of airfoil decreases. With the increase of Reynolds number, the airfoil lift increases gradually and the drag decreases gradually, but the increase rate slows down. When the sawtooth is opened on the Gurney flap, the original tubular vortex structure which falls off alternately after the Gur-ney flap passes through the serrated gap and forms a convective vortex, which is mixed with the inherent shedding vortex of the Gurney flap to form a broken small structure, which weakens the wake flow instability and reduces the airfoil resistance. The concentration region of vortex core gradually moves forward near the flap, and the mixing and dissipation of vortex are faster. KeywordsSerrated Gurney Flap, Aerodynamic Performance, Wake Vortex, Numerical Computation,LiutexThis work is licensed under the Creative Commons Attribution International License (CC BY 4.0)./licenses/by/4.0/1. 引言近些年来,利用垂直轴风力机(VAWT)捕捉低速和复杂的城市地区风能,是风能利用技术的研究热点之一。
风力机叶片翼型气动特性模型

15 90
机械科学与技术
第 29卷
1 基础理论 在流体力学 中, N av ier-Stokes方程之 所以强大
是因为它能对所有的流体状态给出 一个完整的描
述, 但是它的缺点在于计算成本高。在本论文中, 当 非压缩性粘性的紊流经过风机翼型时, 流体的粘性 作用只有在翼型表面很薄的一层区域显得重要, 在 这一层很薄的区域中 N av ier-Stokes方程可以近似处 理为边界层方程。而在边界层之外, 流体可以做非 粘性处理, 利用非粘性模型进行计算。 1 1 非粘性流体模型
流的强度是假定稳定的并且作为未知数, 则流函数 可写成
n
j= 1
0, j
2
ln( |
j
r-
r0
| ) ds0
( 3)
翼型周围的流函数是自由流体作用和每个面元
上涡流 0ds作用的叠加。自由流体部分的流函数为 =V y
式中: V 为水平来流的速度。因此, 最终二维翼型
周围任意点的流函数可以写成
n
=u
yi - v
非粘性流体模型的建立主要有两种方法。一种
是涡格法, 另一种是面元法。面元法也有许多种, 主 要差别在于翼型表面处用来代表速度势流的奇点以
及 Ku tta条件 ( 用来使方程组收敛 ) 的选择。本论文 中用了线性涡流分布, 能够在较少的面元下获得足 够的计算精度 [ 5 ] 。面元方法的主要 假设是流体非 压缩性的, 非旋转的 ( 势流 )。这两项假设极大简化 了流体运动的控制方程。在二维条件下, 翼型的表 面被分为片状的直线段, 每个直线段代表一个面元, 每个面元通过两个端点 ( 面元两端 ) 和一个控制点 ( 面元中心 ) 定义, 强度为 0的涡流置于每个面元控 制点上。每个面元上涡流强度是 = 0 ds0, ds0 是面 元的长度。如果某个面元上涡流放在控制点 r0, 则 该位置上涡流部分的流函数是
naca0018垂直轴风力机叶片参数

文章主题:naca0018垂直轴风力机叶片参数1. 简介naca0018垂直轴风力机叶片参数是指在设计和制造垂直轴风力机时,采用的叶片设计参数。
这些参数包括叶片的形状、材料、长度、厚度等,它们对风力机的性能和效率有着重要影响。
2. 叶片形状naca0018垂直轴风力机叶片采用NACA(National Advisory Committee for Aeronautics)空气动力学剖面的设计。
NACA空气动力学剖面是根据翼型在空气中的流动特性而设计的一种理论曲线,其特点是厚度和弯曲都被数学公式所描述,能够满足风力机叶片对气流的要求,具有良好的气动性能和叶片传动特性。
3. 叶片材料naca0018垂直轴风力机叶片通常采用玻璃钢、碳纤维等轻质高强材料制成,以保证叶片的强度和刚度,同时又能够减轻叶片自身的重量,降低风力机的整体质量,从而提高风力机的启动性能和运行效率。
4. 叶片长度和厚度naca0018垂直轴风力机叶片的长度和厚度也是制定设计参数时需要考虑的重要因素。
合理的长度和厚度可以使风力机在各种风速下都能够获得较高的效率,同时还要考虑到叶片的结构强度和振动问题,以确保叶片在恶劣环境下能够安全可靠地运行。
5. 个人观点与理解在对naca0018垂直轴风力机叶片参数进行全面评估后,我认为这些参数的合理选择对于风力机的性能和效率至关重要。
通过优化叶片形状、材料、长度和厚度等参数,可以最大程度地提高风力机的能量转换效率,降低风能资源的利用成本,同时也能够降低对环境的影响,实现可持续发展。
总结回顾在本文中,我们对naca0018垂直轴风力机叶片参数进行了全面的评估,并深入探讨了叶片形状、材料、长度和厚度等设计参数的重要性。
合理选择这些参数,对于提高风力机的性能和效率具有重要意义。
我们还共享了个人的观点和理解,强调了对可再生能源的重视和应用前景。
通过对这些参数深入研究和了解,相信我们能够更好地设计和制造高性能的垂直轴风力机,推动清洁能源产业的发展,实现绿色和可持续能源的利用。
基于Kriging模型的风力机翼型优化设计及气动性能分析

基于Kriging模型的风力机翼型优化设计及气动性能分析目录一、内容概括 (2)1.1 研究背景与意义 (2)1.2 国内外研究现状 (4)1.3 研究内容与方法 (5)二、Kriging模型的基本原理及实现 (6)2.1 Kriging插值方法 (8)2.2 Kriging模型的参数优化 (9)2.3 Kriging模型的应用实例 (11)三、风力机翼型优化设计方法 (12)3.1 风力机翼型设计的基本理论 (14)3.2 基于Kriging模型的翼型优化设计流程 (15)3.3 风力机翼型设计参数敏感性分析 (16)四、翼型气动性能分析 (18)4.1 翼型气动性能基本理论 (20)4.2 气动性能参数计算方法 (21)4.3 气动性能测试与分析 (23)五、Kriging模型应用于翼型优化设计实例 (25)5.1 实例翼型的选取 (26)5.2 翼型优化设计过程 (27)5.3 优化结果分析与验证 (29)六、基于Kriging模型的翼型优化设计结果对比分析 (30)6.1 不同Kriging模型插值精度对比 (31)6.2 优化前后翼型气动性能对比 (32)6.3 优化分析结果的可视化展示 (33)七、Kriging模型在翼型优化设计中的局限性及改进措施 (34)7.1 Kriging模型存在的局限性 (34)7.2 改进措施与展望 (36)八、结论 (38)8.1 研究成果总结 (39)8.2 研究创新点 (40)8.3 研究不足与展望 (41)一、内容概括本章节概述了基于Kriging模型的风力机翼型优化设计及气动性能分析的研究背景及意义。
Kriging模型作为一种高效的全局优化方法,在处理复杂、多维的黑箱函数优化问题时表现出显著的优势,是当前工程设计中广泛采用的手段之一。
本研究旨在通过引入Kriging模型,结合高效的优化算法,对风力机翼型进行优化设计,并进一步分析优化设计的风力机翼型在不同气流条件下的气动性能,力求提升风能转换效率,减少设计时间和费用。
风力机的基本参数与理论.
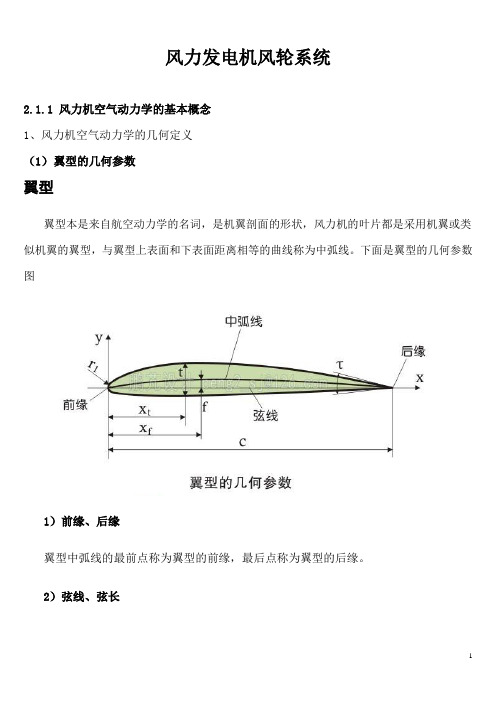
风力发电机风轮系统2.1.1 风力机空气动力学的基本概念1、风力机空气动力学的几何定义(1)翼型的几何参数翼型翼型本是来自航空动力学的名词,是机翼剖面的形状,风力机的叶片都是采用机翼或类似机翼的翼型,与翼型上表面和下表面距离相等的曲线称为中弧线。
下面是翼型的几何参数图1)前缘、后缘翼型中弧线的最前点称为翼型的前缘,最后点称为翼型的后缘。
2)弦线、弦长连接前缘与后缘的直线称为弦线;其长度称为弦长,用c表示。
弦长是很重要的数据,翼型上的所有尺寸数据都是弦长的相对值。
3)最大弯度、最大弯度位置中弧线在y坐标最大值称为最大弯度,用f表示,简称弯度;最大弯度点的x坐标称为最大弯度位置,用x f表示。
4)最大厚度、最大厚度位置上下翼面在y坐标上的最大距离称为翼型的最大厚度,简称厚度,用t表示;最大厚度点的x坐标称为最大厚度位置,用x t表示。
5)前缘半径翼型前缘为一圆弧,该圆弧半径称为前缘半径,用r1表示。
6)后缘角翼型后缘上下两弧线切线的夹角称为后缘角,用τ表示。
7)中弧线翼型内切圆圆心的连线。
对称翼型的中弧线与翼弦重合。
8)上翼面凸出的翼型表面。
9)下翼面平缓的翼型表面。
(2)风轮的几何参数1)风力发电机的扫风面积风轮旋转扫过的面积在垂直于风向的投影面积是风力机截留风能的面积,称为风力机的扫掠面积,下图是一个三叶片水平轴风力机的扫掠面积示意图。
下图是一个四叶片的H型升力垂直轴风力发电机的扫掠面积示意图。
根据前面两表可由所需发电功率估算出风力机所需的扫风面积,例如200W的升力型垂直轴风力发电机工作风速为6m/s,全效率按25%计算所需扫风面积约为6.2m2,如果工作风速为10m/s则所需扫风面积约为1.4m2即可;例如10kW的升力型垂直轴风力发电机工作风速为10m/s,全效率按30%计算所需扫风面积约为56m2,如果工作风速为13m/s则所需扫风面积约为25m2即可。
按高风速设计的风力机体积小成本相对低些,但必须用在高风速环境,例如把一台设计风速为10m/s的风力机放在风速为6m/s的环境工作,其功率会下降80%;按风速6m/s设计的风力机风轮会很大,虽在6m/s时运行很好,但遇大风易超速损坏电机,为抗强风时需增加结构强度使成本大大增加。
风力机的工作原理和气动特性

1. 空气动力学的基本知识
1.1 升力和阻力 物体在空气中运动或者空气
流过物体时,物体将受到空气的 作用力,称为空气动力。
通常空气动力由两部分组成:一部 分是由于气流绕物体流动时,在物体表 面处的流动速度发生变化,引起气流压 力的变化,即物体表面各处气流的速度 与压力不同,从而对物体产生合成的压 力;另一部分是由于气流绕物体流动时, 在物体附面层内由于气流粘性作用产生 的摩擦力。将整个物体表面这些力合成 起来便得到一个合力.这个合力即为空 气动力。
升力是使风力机有效工作的力,而
阻力则形成对风轮的正面压力。为了使 风力机很好的工作,就需要叶片具有这 样的翼型断面,使其能得到最大的升力 和最小的阻力,也就是要求具有很大的
升阻比K。
雷诺数是一个无量纲数。雷 诺数愈小的流动。粘性作用愈大; 雷诺数愈大的流动,粘性作用愈 小,雷诺数增加。由于翼型附面 层气流粘性减小,最大升力系数 增加,最小阻力系数减小,因而 升阻比增加。
样.则叶片各处的实际攻角都将不同,这样除了攻
角接近最佳值的一小段叶片升力较大外,其它部分 所得到的升力则由于攻角偏离最佳值而不理想。
所以这样的叶片不具备良好的气动力特
性。为了在沿整个叶片长度方向均能获得有 利的攻角数值,就必须使叶片每一个截面的 安装角随着半径的增大而逐渐减小。在此情 况下,有可能使气流在整个叶片长度均以最 有利的攻角吹向每一叶片元.从而具有比较 好的气动力性能。而且各处受力比较均匀, 也增加了叶片的强度。这种具有变化的安装 角的叶片称为螺旋浆型叶片,而那种各处安 装角均相同的叶片称为平板型叶片。显然, 螺旋桨型叶片比起平板型叶片来要好得多。
图中示出空气流过一块平板的情形,平板面与 气流方向形成一个夹角 a ,a称为攻角。由于平板上 方和下方的气流速度不同(上方速度大于下方速度), 因此平板上、下方所受的压力也不同(下方压力大干 上方压力 ),总的舍力F即为平饭在流动空气中所受 到的空气动力,其方向垂直于板面。
雷诺数对低速对称翼型气动性能的影响

雷诺数对低速对称翼型气动性能的影响史广泰;李振朋【摘要】基于CFD软件,采用k-ω SST湍流模型,研究了不同雷诺数对低速对称翼型NACA0012、NACA0015和NACA0018气动性能的影响,以及同一雷诺数下翼型相对厚度对翼型气动性能的影响.比较了翼型NACA0012、NACA0015和NACA0018的升力系数和阻力系数的计算值与试验值,得出了和试验值最接近的翼型,总结了对称翼型升力系数、阻力系数和升阻比的变化规律,确定了对称翼型最佳攻角.结果显示,低速对称翼型相对厚度越大,气动性能越好;雷诺数越小,黏性越大,越先发生边界层分离;翼型NACA0018的计算值和试验值最接近;翼型NACA0018的最佳攻角为10°.【期刊名称】《新技术新工艺》【年(卷),期】2013(000)009【总页数】5页(P18-22)【关键词】低速对称翼型;雷诺数影响;气动特性;数值模拟【作者】史广泰;李振朋【作者单位】兰州理工大学风能技术研究中心,甘肃兰州730050;兰州理工大学风能技术研究中心,甘肃兰州730050【正文语种】中文【中图分类】TK83目前,用于风力机叶片的翼型有2类:1)航空翼型及其修型,如NACA系列;2)风力机专用翼型,如美国NREL的S系列,瑞典FFA的W系列和荷兰的DU系列等。
在垂直轴风力机中,由于对其翼型的研究相对于水平轴风力机来说较少,且其翼型必须满足升力系数大、阻力系数小,以及阻力系数要对称于零升力角等特性[1];所以,实际中,NACA的4位数系列对称翼型是经常使用的翼型。
NACA的4位数系列翼型是美国NACA最早建立的一个低速翼型系列,与早期的其他翼型相比,有较高的升力系数和较低的阻力系数。
本文采用Fluent软件,对NACA0012、NACA0015和 NACA0018翼型的气动性能进行了数值模拟计算。
1 数值计算1.1 湍流模型通过对不同湍流模型数值模拟的尝试和比较,本文采用了k-ω的SST湍流模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
采用数值方法对两种不同厚度的 NREL 风力
机专用翼型 S827、S828 进行数值模拟研究 ,分析
从图 8中可看出 ,入流攻角 α在 - 5°~0°范 的升阻比 ,这是因为由于翼型厚度的增加 ,翼型前 围时 , S827 翼型的上下表面压力系数都较 S828 缘曲率较大 ,导致流管在前缘变细 ,翼型上表面流 低 ,由于 S827翼型吸力面压力很低 ,使得翼型上 线挤拢 ,流速加大 ,表面静压降低 ,由流体力学原 下面的压差较大 ,反而具有较高的升阻比 。当入 理可知 ,加速减压运动流体不容易分离 ,使得翼型 流攻角 α在 5°~10°范围时 , S827 翼型上下面的 表面边界层流体主要为附着流 ,流体流动效率较 压力系数高 ,压力面与吸力面压差较大 ,具有较高 高 ,从而产生较大的升阻比 。
从图中可看出 ,在 - 2°~10°攻角范围内 ,使 用 k - w SST湍流模型得到的二维翼型计算结果 与试验值吻合较好 ,说明该湍流模型可有效地用 于本文的数值模拟研究 。
3 计算结果及分析
图 1 S832翼型网格局部放大
从图中可看出 ,在翼型前缘和尾缘对网格进 行了局部加密 。第一层网格线距翼型表面最近距 离为弦长的 10 - 5倍 ,计算域的外边界离翼型表面 为 12倍弦长 ,这种网格划分保证了在近壁面处复 杂流动的计算精度 。
k - w SST湍流模型是 M eter F. R 在 W ilcox
提出的 k - w模型的基础上 ,结合 k - ε湍流模型
的优点发展起来的 ,它利用函数 F1 将 k - ε和 k
- w二方程模式结合起来 ,再利用混合函数 F2 改
进涡团粘性系数
μ t
在壁面逆压流动区域的结果
,
充分发挥了 k - ε模型处理自由流 , k - w 模型处
图 8 给出了通过数值模拟所获得的 S827、 S828两种翼型表面压力系数分布对比图 。
( a) α = - 5° ( b) α = 5° ( c)α = 15° 图 5 不同攻角下 S827流速分布
( a) α = - 5° ( b) α = 5° ( c)α = 15° 图 6 不同攻角 S828流速分布
Effects of Aerofo il Th ickness on A irfo il Aerodynam ic Character istics
L I Chang , L IANG W u2ke , J IN Xue2hong,WANG Xue2tao (Xi′an University of Technology , Xi′an 710048 , China)
34 FLU ID MACH INERY Vol138, No12, 2010
( a) α = - 5°( S827) ( b) α = 5°( S827) ( c)α = 15°( S828) 图 7 S827、S828部分攻角流线
本文 采 用 数 值 计 算 方 法 对 NREL 系 列 中 S832以及弯度相近 ,相对厚度不同的 S827、S828 三种翼型进行数值模拟 ,通过与 NREL 的试验结 果进行比较 ,验证所采用的数值方法的可行性 ,分
2 数值研究方法
2. 1 湍流模型 k - w SST两方程模型为 [ 3 ] :
3. 1 翼型厚度对翼型气动特性的影响 图 3为 S827、S828翼型在攻角 α = - 5°~15°
时的升力 、阻力系数数值计算结果的比较 ,图 4为
这两种翼型的升阻比随攻角变化的曲线 。由图 3
可知 ,随着入流攻角的增大 , S827、S828 翼型的
升 、阻力系数都逐渐增大 ,对同一攻角 , S827翼型 具有相对较大的升力系数 , 最大升力系数为 1. 308,出现在 15°攻角附近 ; S828 翼型最大升力系
- βρω2
+2(1 -
F1
)ρσω2
1 ω
5k 5xj
5ω 5xj
(3)
收稿日期 : 2009—09—07 修稿日期 : 2009—10—10
32 FLU ID MACH INERY Vol138, No12, 2010
式中 β、γ、σk 、σω ———模型参数 F1 、F2 ———混合函数
图 7是两种翼型在部分攻角下的流体运动轨 迹图 ,从图上可明显看出 ,在 5°攻角时 , S828翼型 流体流动未发生分离 ,而 S827翼型绕流已开始与 翼型吸力面分离 ,在 15°攻角时 , S827翼型吸力面 分离加大 ,形成明显的涡流 。 3. 3 翼型厚度对压力系数分布的影响
翼型上下表面的压力分布会影响翼型的升阻 比大小 ,翼型压力面压力越大 ,吸力面压力越小 , 翼型的升阻比越大 。
υ t
=
m
ax
(
a1 k
a1ω;ΩF2
)
;
a1
= 0.
31
(1)
Dρk Dt
=
5 5xj
[
(μ +σkμt )
5k 5xj
]
+τij
5ui 5xj
- β3 ρωk
(τij = - ρu——′—i u—′j ) ( 2)
Dρω Dt
=
5 5xj
[
(μ
+σωμt
)
5ω 5xj
]
+
υγτij t
5ui 5xj
数较升力系数增加的程度要大 ,同时 ,随着翼型厚
度的增加 ,翼型最佳升阻比减小 ,但最佳升阻比对
2010年第 38卷第 2期 流 体 机 械
33
应的攻角范围较宽 ,利于提高工作效率 。
图 3 S827、S828 升力 、阻力系数随攻角的变化 图 4 S827、S828 升阻比随攻角的变化
3. 2 翼型厚度对流态分布的影响 图 5、6 分别为 S827、S828 翼型在 - 5°、0°、
5°、15°攻角下的速度分布 ,由图可知 S827翼型出 流动分离现象较早 , 在 5°附近出现流动分离现 象 , S828翼型在 8°附近出现流动分离现象 。通过 对比图 5、6可看出 ,随着翼型厚度的增加 ,翼型分 离点前移速度较慢 ,涡分布范围较小 ;厚度相对较 小的翼型分离点前移速度较快 ,涡的分布范围较 大 ,使得阻力系数增大较快 ,这一点可从图 3得到 解释 。此外随着翼型厚度的增大 ,翼型上表面速 度加大致使摩擦阻力上升 ,翼型压差阻力增大 ,使 得翼型的最大升阻比较小 。
数为 1. 21, 出现在 14°攻角附近 。由图 4 可知 ,
S827翼型最佳升阻比达到最大约为 41. 95,对应
的最佳攻角为 6°; S828翼型最大升阻比约为 44,
对应的最佳攻角为 7°。 S827翼型较 S828翼型有 较宽的大升阻比攻角范围 。
针对所计算的翼型 ,在小攻角下随着翼型厚
度的增加 ,翼型升 、阻力系数都显著增加 ,阻力系
理壁面约束流动的特长 。
2. 2 数值方法
本文采用 Fluent前处 理软 件 Gambit2. 0 对
S832翼型进行几何建模 ,计算网格为 C型结构化
网格 ,网格数为 58600,其中翼型表面分布了 189
个节点 ,图 1是网格的局部放大 。
验数据 [ 6 ]进行比较 ,如图 2所示 。
图 2 S832 升力 、阻力系数随攻角的变化
厚度对翼型气动特性的影响 ,计算条件为 : R e = 3. 0 ×106 ,攻角 α = - 5°~15°,所选翼型参数如表
所示 1[ 7 ] 。
表 1 所选翼型的主要参数
翼型名称 采用弦长 ( cm ) 相对弯度 ( % ) 相对厚度 ( % )
S827
100
2. 2
Байду номын сангаас21
S828
100
2. 3
16
Abstract: Based on the k2w SST turbulence model , two airfoils of different thickness are simulated at R e = 3 ×106 , the aerody2 nam ic characteristics of airfoil w ith different thicknesses at the attack angle of - 5°~15°are investigated. The unsteady numerical results show that : the effect of the different aerofoil thickness is obvious to the aerodynam ic performance , at a small angle of at2 tack range , the greater thickness leads to the large lift2drag ratio , at large angle of attack , larger thickness can imp rove the lift2 drag ratio, broaden the scope of the angle of attack of the high lift2drag ratio , effectively imp rove the flow separation characteris2 tics. Key words: k2w SST turbulence model; aerofoil thickness; aerodynam ic performance; separated flow
