综上可知,若 f (x )的最小值为 1,则 a 的取值范围是[2,+∞).
2-a
a
高中数学选修本(理科)几种常见函数的导数
几种常见函数的导数 ●教学目标 (一)教学知识点 1.公式1 C ′=0(C 为常数) 2.公式2 (x n )′=nx n -1(n ∈Q ) 3.公式3 (sin x )′=cos x 4.公式4 (cos x )′=-sin x 5.变化率 (二)能力训练要求 1.掌握四个公式,理解公式的证明过程. 2.学会利用公式,求一些函数的导数. 3.理解变化率的概念,解决一些物理上的简单问题. (三)德育渗透目标 1.培养学生的计算能力. 2.培养学生的应用能力. 3.培养学生自学的能力. ●教学重点 四种常见函数的导数C ′=0(C 为常数),(x n )′=nx n -1(x ∈Q ),(sin x )′=cos x ,(cos x )′=-sin x . ●教学难点 四种常见函数的导数的内容,以及证明的过程,这些公式由导数定义导出的. ●教学方法 建构主义式 让学生自己根据导数的定义来推导公式1、公式2、公式3、公式4,公式2中先证n ∈N *的情况. ●教学过程 Ⅰ.课题导入 [师]我们上一节课学习了导数的概念,导数的几何意义.我们是用极限来定义函数的导数的,我们这节课来求几种常见函数的导数.以后可以把它们当作直接的结论来用. Ⅱ.讲授新课 [师]请几位同学上来用导数的定义求函数的导数. 1.y =C (C 是常数),求y ′. [学生板演]解:y =f (x )=C ∴Δy =f (x +Δx )-f (x )=C -C =0 x y ??=0 y ′=C ′=x y x ??→?0lim =0,∴y ′=0. 2.y =x n (n ∈N *),求y ′. [学生板演]解:y =f (x )=x n ∴Δy =f (x +Δx )-f (x )=(x +Δx )n -x n
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记 1.函数的平均变化率是什么? 答:平均变化率为 = ??=??x f x y x x f x x f x x x f x f ?-?+=--)()()()(111212 注1:其中x ?是自变量的改变量,可正,可负,可零。 注2:函数的平均变化率可以看作是物体运动的平均速度。 2、导函数的概念是什么? 答:函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 3.平均变化率和导数的几何意义是什么? 答:函数的平均变化率的几何意义是割线的斜率;函数的导数的几何意义是切线的斜率。 4导数的背景是什么? 答:(1)切线的斜率;(2)瞬时速度;(3)边际成本。 5、常见的函数导数和积分公式有哪些? 函数 导函数 不定积分 y c = 'y =0 ———————— n y x =()*n N ∈ 1'n y nx -= 1 1n n x x dx n +=+? x y a =()0,1a a >≠ 'ln x y a a = ln x x a a dx a =? x y e = 'x y e = x x e dx e =? log a y x =()0,1,0a a x >≠> 1 'ln y x a = ———————— ln y x = 1'y x = 1 ln dx x x =? sin y x = 'cos y x = cos sin xdx x =? cos y x = 'sin y x =- sin cos xdx x =-? 6、常见的导数和定积分运算公式有哪些?
高二数学选修2-2导数12种题型归纳(中等难度)汇编
导数题型分类解析(中等难度) 一、变化率与导数 函数)(0x f y =在x 0到x 0+x ?之间的平均变化率,即)('0x f =0 lim →?x x y ??=0lim →?x x x f x x f Δ)()Δ(00-+,表示函数)(0x f y =在x 0点的斜率。注意增量的意义。 例1:若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则000 ()() lim h f x h f x h h →+-- 的值为( ) A .'0()f x B .'02()f x C .' 02()f x - D .0 例2:若' 0()3f x =-,则000()(3) lim h f x h f x h h →+--=( ) A.3- B .6- C .9- D .12- 例3:求0lim →h h x f h x f ) ()(020-+ 二、“隐函数”的求值 将)('0x f 当作一个常数对)(0x f 进行求导,代入0x 进行求值。 例1:已知()()232 f x x x f '+=,则()='2f 例2:已知函数()x x f x f sin cos 4+?? ? ??'=π,则??? ??4πf 的值为 . 例3:已知函数)(x f 在R 上满足88)2(2)(2 -+--=x x x f x f ,则曲线)(x f y =在点))1(,1(f 处的切线方程为( ) A. 12-=x y B. x y = C. 23-=x y D. 32+-=x y 三、导数的物理应用 如果物体运动的规律是s=s (t ),那么该物体在时刻t 的瞬间速度v=s ′(t )。 如果物体运动的速度随时间的变化的规律是v=v (t ),则该物体在时刻t 的加速度a=v′(t )。 例1:一个物体的运动方程为2 1t t s +-=其中s 的单位是米,t 的单位是秒,求物体在3秒末的瞬时速度。 例2:汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( ) 四、基本导数的求导公式 A . B . C . D .
高中数学导数及其应用电子教案
高中数学导数及其应用一、知识网络 二、高考考点 1、导数定义的认知与应用; 2、求导公式与运算法则的运用; 3、导数的几何意义; 4、导数在研究函数单调性上的应用; 5、导数在寻求函数的极值或最值的应用; 6、导数在解决实际问题中的应用。
三、知识要点 (一)导数 1、导数的概念 (1)导数的定义 (Ⅰ)设函数在点及其附近有定义,当自变量x在处有增量△x(△x可 正可负),则函数y相应地有增量,这两个增量的比 ,叫做函数在点到这间的平均变化率。如果 时,有极限,则说函数在点处可导,并把这个极限叫做在点 处的导数(或变化率),记作,即 。 (Ⅱ)如果函数在开区间()内每一点都可导,则说在开区间() 内可导,此时,对于开区间()内每一个确定的值,都对应着一个确定的导数,这样在开区间()内构成一个新的函数,我们把这个新函数叫做在开区间() 内的导函数(简称导数),记作或,即 。 认知: (Ⅰ)函数的导数是以x为自变量的函数,而函数在点处的导数 是一个数值;在点处的导数是的导函数当时的函数值。 (Ⅱ)求函数在点处的导数的三部曲: ①求函数的增量;
②求平均变化率; ③求极限 上述三部曲可简记为一差、二比、三极限。 (2)导数的几何意义: 函数在点处的导数,是曲线在点处的切线的斜率。 (3)函数的可导与连续的关系 函数的可导与连续既有联系又有区别: (Ⅰ)若函数在点处可导,则在点处连续; 若函数在开区间()内可导,则在开区间()内连续(可导一定连续)。 事实上,若函数在点处可导,则有此时, 记 ,则有即在点处连续。 (Ⅱ)若函数在点处连续,但在点处不一定可导(连续不一定可导)。 反例:在点处连续,但在点处无导数。
(word完整版)高中数学导数练习题(分类练习)讲义
导数专题 经典例题剖析 考点一:求导公式。 例1. ()f x '是3 1()213 f x x x = ++的导函数,则(1)f '-的值是 。 解析:()2'2 +=x x f ,所以()3211'=+=-f 答案:3 考点二:导数的几何意义。 例 2. 已知函数()y f x =的图象在点(1 (1))M f ,处的切线方程是1 22 y x =+,则(1)(1)f f '+= 。 解析:因为21= k ,所以()2 1 1'=f ,由切线过点(1 (1))M f ,,可得点M 的纵坐标为25,所以()2 5 1=f ,所以()()31'1=+f f 答案:3 例3.曲线32 242y x x x =--+在点(1 3)-,处的切线方程是 。 解析:443'2 --=x x y ,∴点(1 3)-,处切线的斜率为5443-=--=k ,所以设切线方程为b x y +-=5,将点(13)-,带入切线方程可得2=b ,所以,过曲线上点(13)-,处的切线方程为:025=-+y x 答案:025=-+y x 点评:以上两小题均是对导数的几何意义的考查。 考点三:导数的几何意义的应用。 例4.已知曲线C :x x x y 232 3 +-=,直线kx y l =:,且直线l 与曲线C 相切于点 ()00,y x 00≠x ,求直线l 的方程及切点坐标。
解析:Θ直线过原点,则()000 ≠= x x y k 。由点()00,y x 在曲线C 上,则02 030023x x x y +-=,∴ 2302 00 0+-=x x x y 。又263'2+-=x x y ,∴ 在() 00,y x 处曲线C 的切线斜率为()263'02 00+-==x x x f k ,∴ 2632302 0020+-=+-x x x x , 整理得:03200=-x x ,解得:2 3 0=x 或00=x (舍),此时,830- =y ,41-=k 。所以,直线l 的方程为x y 4 1 -=,切点坐标是?? ? ??-83,23。 答案:直线l 的方程为x y 41- =,切点坐标是?? ? ??-83,23 点评:本小题考查导数几何意义的应用。解决此类问题时应注意“切点既在曲线上又在切线上”这个条件的应用。函数在某点可导是相应曲线上过该点存在切线的充分条件,而不是必要条件。 考点四:函数的单调性。 例5.已知()132 3 +-+=x x ax x f 在R 上是减函数,求a 的取值范围。 解析:函数()x f 的导数为()163'2 -+=x ax x f 。对于R x ∈都有()0'a 时,函数()x f 在R 上存在增区间。所以,当3->a 时,函数()x f 在 R 上不是单调递减函数。 综合(1)(2)(3)可知3-≤a 。
高二数学导数及其应用练习题及答案
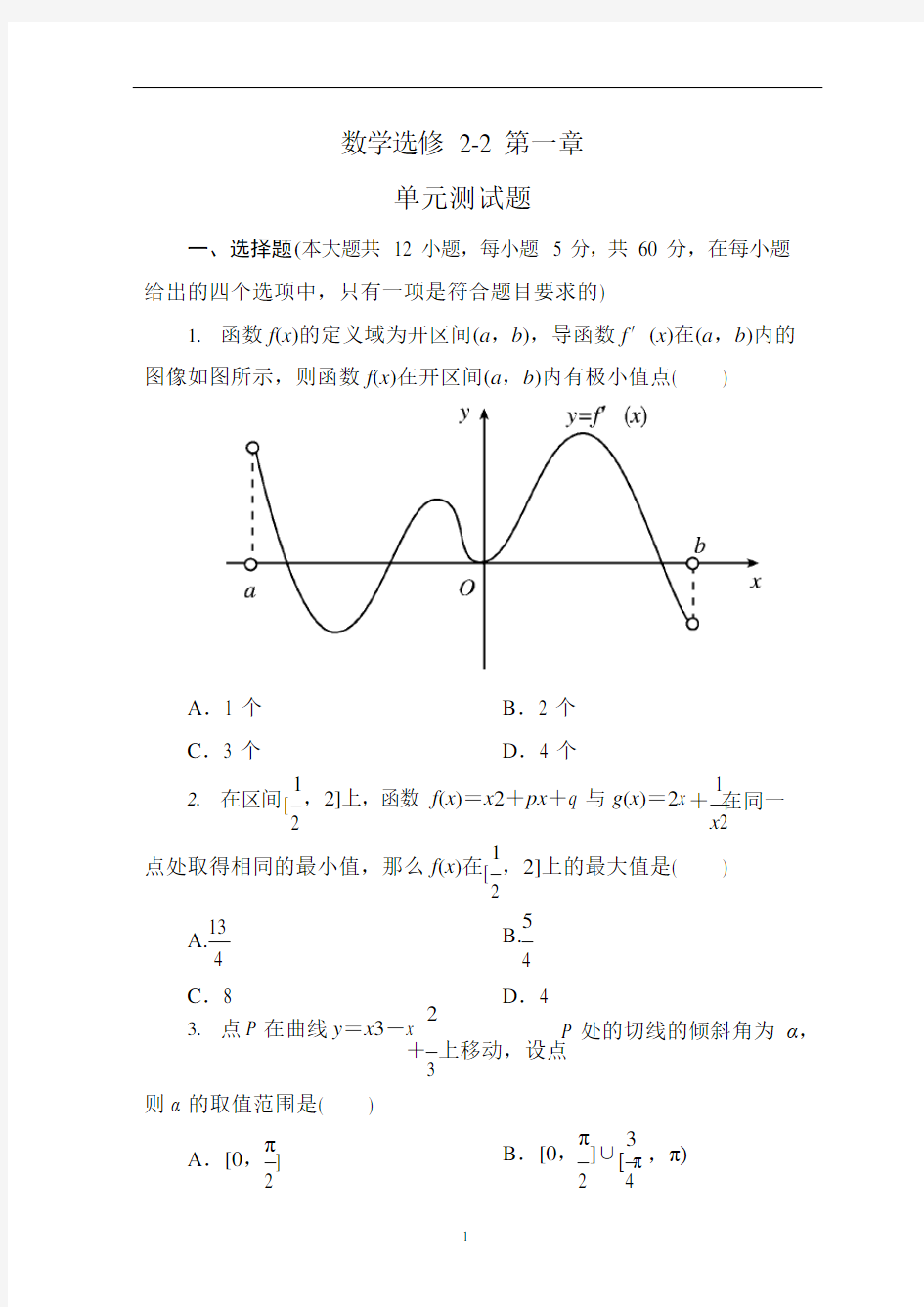
(数学选修1-1)第一章 导数及其应用 [提高训练C 组]及答案 一、选择题 1.若()sin cos f x x α=-,则'()f α等于( ) A .sin α B .cos α C .sin cos αα+ D .2sin α 2.若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象是( ) 3.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数a 的 取值范围是( ) A .),3[]3,(+∞--∞ B .]3,3[- C .),3()3,(+∞--∞ D .)3,3(- 4.对于R 上可导的任意函数()f x ,若满足'(1)()0x f x -≥,则必有( ) A . (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C. (0)(2)2(1)f f f +≥ D. (0)(2)2(1)f f f +> 5.若曲线4 y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( ) A .430x y --= B .450x y +-= C .430x y -+= D .430x y ++= 6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示, 则函数)(x f 在开区间),(b a 内有极小值点( A .1个 B .2个 C .3个 D .4个 二、填空题 1.若函数()()2 f x x x c =-在2x =处有极大值,则常数c 的值为_________;
2.函数x x y sin 2+=的单调增区间为 。 3.设函数())(0)f x ??π=+<<,若()()f x f x '+为奇函数,则?=__________ 4.设3 2 1()252 f x x x x =- -+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的 取值范围为 。 5.对正整数n ,设曲线)1(x x y n -=在2x =处的切线与y 轴交点的纵坐标为n a ,则 数列1n a n ?? ? ?+?? 的前n 项和的公式是 三、解答题 1.求函数3(1cos 2)y x =+的导数。 2.求函数y = 3.已知函数3 2 ()f x x ax bx c =+++在2 3 x =-与1x =时都取得极值 (1)求,a b 的值与函数()f x 的单调区间 (2)若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围。 4.已知23()log x ax b f x x ++=,(0,)x ∈+∞,是否存在实数a b 、,使)(x f 同时满足下列 两个条件:(1))(x f 在(0,1)上是减函数,在[)1,+∞上是增函数;(2))(x f 的最小值是1,若存在,求出a b 、,若不存在,说明理由. (数学选修1-1)第一章 导数及其应用 [提高训练C 组] 一、选择题 1.A ' ' ()sin ,()sin f x x f αα==
高中数学《导数的概念及几何意义》公开课优秀教学设计
《导数的概念及几何意义》教学设计 教材内容分析 本节课的教学内容选自人教社普通高中课程标准实验教科书( A 版)数学选修2-2第一章第一节的《变化率与导数》,《导数的概念及几何意义》是在学习了函数平均变化率以后,过渡到瞬时变化率,从而得出导数的概念,再从平均变化率的几何意义,迁移至瞬时变化率即导数的几何意义。 导数是微积分的核心概念之一,是从生产技术和自然科学的需要中产生的,它深刻揭示了函数变化的本质,其思想方法和基本理论在在天文、物理、工程技术中有着广泛的应用,而且在日常生活及经济领域也日渐显示出其重要的功能。 在中学数学中,导数具有相当重要的地位和作用。 从横向看,导数在现行高中教材体系中处于一种特殊的地位。它是众多知识的交汇点,是解决函数、不等式、数列、几何等多章节相关问题的重要工具, 它以更高的观点和更简捷的方法对中学数学的许多问题起到以简驭繁的处理。 从纵向看,导数是函数一章学习的延续和深化,也是对极限知识的发展, 同时为后继研究导数的几何意义及应用打下必备的基础, 具有承前启后的重要作用。 学生学情分析 学生在高一年级的物理课程中已经学习了瞬时速度,因此,先通过求物体在某一时刻的平均速度的极限去得出瞬时速度, 再由此抽象出函数在某点的平均变化率的极限就是瞬时变化率的的模型, 并将瞬时变化率定义为导数,这是符合学生认知规律的. 而在第一课时平均变化率的学习中,课本给出了一个思考,观察函数 )(x f y 的图像,平均变化x y 表示什么?这个思考为研究导数的几何意义埋下 了伏笔。因此,在将瞬时变化率定义为导数之后, 立即让学生继续探索导数的几何意义,学生会对导数的几何意义有更为深刻的认识。 教学目标 1、知识与技能目标会从数值逼近、几何直观感知,解析式抽象三个角度认识导数的含义,应用导数的定义求简单函数在某点处的导数, 掌握求导数的基本步骤,初步学会求解 简单函数在一点处的切线方程。 2、过程与方法目标 通过动手计算培养学生观察、分析、比较和归纳能力,通过问题的探究体会逼近、类比、以及用已知探求未知、从特殊到一般的数学思想方法。 3、情感态度与价值观
高中数学选修2-2导数--导数的运算(解析版)
高中数学选修2-2导数--导数的运算(解析版) 1.若f (x )=sin π 3 -cos x ,则f ′(α)等于( ) A .Sin α B .Cos α C .sin π3+cos α D .cos π 3+sin α [答案] A [解析] ∵f (x )=sin π 3 -cos x ,∴f ′(x )=sin x ,∴f ′(α)=sin α,故选A. 2.设函数f (x )=x m +ax 的导数为f ′(x )=2x +1,则数列{1 f (n ) }(n ∈N *)的前n 项和是( ) A.n n +1B .n +2n +1C.n n -1 D .n +1n [答案] A [解析] ∵f (x )=x m +ax 的导数为f ′(x )=2x +1,∴m =2,a =1,∴f (x )=x 2+x , ∴f (n )=n 2+n =n (n +1),∴数列{1 f (n ) }(n ∈N *)的前n 项和为: S n =11×2+12×3+13×4+…+1 n (n +1)=????1-12+????12-13+…+????1n -1n +1 =1-1n +1=n n +1 ,故选A. 3.已知二次函数f (x )的图象如图所示,则其导函数f ′(x )的图象大致形状是( ) [答案] B [解析] 依题意可设f (x )=ax 2+c (a <0,且c >0),于是f ′(x )=2ax ,显然f ′(x )的图象为直线,过原点,且斜率2a <0,故选B. 4.已知函数f (x )的导函数为f ′(x ),且满足f (x )=2xf ′(e)+ln x ,则f ′(e)=( ) A .e - 1B .-1C .-e - 1 D .-e [答案] C [解析] ∵f (x )=2xf ′(e)+ln x ,∴f ′(x )=2f ′(e)+1x ,∴f ′(e)=2f ′(e)+1 e , 解得f ′(e)=-1 e ,故选C.
2021年高中数学选修本(理科)复合函数的导数(1)
2021年高中数学选修本(理科)复合函数的导数(1) 教学目的: 1.理解掌握复合函数的求导法则. 2.能够结合已学过的法则、公式,进行一些复合函数的求导 3.培养学生善于观察事物,善于发现规律,认识规律,掌握规律,利用规律. 教学重点:复合函数的求导法则的概念与应用 教学难点:复合函数的求导法则的导入与理解 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 内容分析: 复合函数的导数是导数的重点,也是导数的难点. 要弄清每一步的求导是哪个变量对哪个变量的求导.求导时对哪个变量求导要写明,可以通过具体的例子,让学生对求导法则有一个直观的了解 教学过程: 一、复习引入: 1. 常见函数的导数公式: ;;; 2.法则1 )()()]()(['''x v x u x v x u ±=±. 法则2 [()()]'()()()'()u x v x u x v x u x v x '=+, 法则3 ' 2''(0)u u v uv v v v -??=≠ ??? 二、讲解新课: 1.复合函数: 由几个函数复合而成的函数,叫复合函数.由函数与复合而成的函数一般形式是,其中u 称为中间变量. 2.求函数的导数的两种方法与思路: 方法一:22[(32)](9124)1812x y x x x x '''=-=-+=-; 方法二:将函数看作是函数和函数复合函数,并分别求对应变量的导数如下: , 两个导数相乘,得 232(32)31812u x y u u x x ''==-=-, 从而有 对于一般的复合函数,结论也成立,以后我们求y ′x 时,就可以转化为求y u ′和u ′x 的
高中数学-导数的概念及运算练习
高中数学-导数的概念及运算练习 1.y =ln 1 x 的导函数为( ) A .y ′=-1 x B .y ′=1 x C .y ′=lnx D .y ′=-ln(-x) 答案 A 解析 y =ln 1x =-lnx ,∴y ′=-1 x . 2.(·东北师大附中摸底)曲线y =5x +lnx 在点(1,5)处的切线方程为( ) A .4x -y +1=0 B .4x -y -1=0 C .6x -y +1=0 D .6x -y -1=0 答案 D 解析 将点(1,5)代入y =5x +lnx 成立,即点(1,5)为切点.因为y ′=5+1x ,所以y ′|x =1=5+1 1=6. 所以切线方程为y -5=6(x -1),即6x -y -1=0.故选D. 3.曲线y =x +1 x -1在点(3,2)处的切线的斜率是( ) A .2 B .-2 C.12 D .-12 答案 D 解析 y ′=(x +1)′(x -1)-(x +1)(x -1)′(x -1)2=-2 (x -1)2,故曲线在(3,2)处的切线的斜率k = y ′|x =3=-2(3-1)2=-1 2 ,故选D. 4.一质点沿直线运动,如果由始点起经过t 秒后的位移为s =13t 3-32t 2 +2t ,那么速度为零的时刻是( ) A .0秒 B .1秒末 C .2秒末 D .1秒末和2秒末 答案 D 解析 ∵s=13t 3-32t 2+2t ,∴v =s ′(t)=t 2 -3t +2. 令v =0,得t 2 -3t +2=0,t 1=1或t 2=2. 5.(·郑州质量检测)已知曲线y =x 2 2-3lnx 的一条切线的斜率为2,则切点的横坐标为( ) A .3 B .2 C .1 D.12 答案 A
最新高中数学选修1-1《导数及其应用》知识点讲义
第三章 导数及其应用 1 一、变化率与导数 2 ()()()()()()()() 000000000000000 10,0lim lim lim . x x x x x y f x x x x x y y x x x x x y x x f x x f x y x x y x x f x y f x x f x f x x ?→?→=?→==??≠??+???→=+?-?=??=+?-=?'''、定义:设在处取得一个增量. 函数值也得到一个增量称 为从到的平均变化率.若当时时,有极限存在,则称此极限值为函数在处的瞬时变化率,记为,也称为函 数在处的导数,记作或, 即 3 4 ()0y f x x x ==说明:导数即为函数在处的瞬时变化率. 5 6 7 ()()00. PT x f x P PT f x k ?→='2、几何意义:时,Q 沿图像无限趋近于点时,切线的斜率.即 8 9 ()()()()003==lim lim . x x f x x f x y y f x y f x y x x ?→?→+?-?==??''''、导函数(简称为导数)称为导函数,记作,即 10 二、常见函数的导数公式 11 1若()f x c =(c 为常数),则()0f x '=; 12 2 若()f x x α=,则1()f x x αα-'=; 13 3 若()sin f x x =,则()cos f x x '= 14 4 若()cos f x x =,则()sin f x x '=-; 15 5 若()x f x a =,则()ln x f x a a '= 16 6 若()x f x e =,则()x f x e '= 17
高中数学选修2-2第一章导数测试题
选修2-2第一章单元测试 (一) 时间:120分钟 总分:150分 一、选择题(每小题5分,共60分) 1.函数f (x )=x ·sin x 的导数为( ) A .f ′(x )=2x ·sin x +x ·cos x B .f ′(x )=2x ·sin x -x ·cos x C .f ′(x )=sin x 2x +x ·cos x D .f ′(x )=sin x 2x -x ·cos x 2.若曲线y =x 2+ax +b 在点(0,b )处的切线方程是x -y +1=0,则( ) A .a =1,b =1 B .a =-1,b =1 C .a =1,b =-1 D .a =-1,b =-1 3.设f (x )=x ln x ,若f ′(x 0)=2,则x 0=( ) A .e 2 B .e C.ln2 2 D .ln2 4.已知f (x )=x 2+2xf ′(1),则f ′(0)等于( ) A .0 B .-4 C .-2 D .2 5.图中由函数y =f (x )的图象与x 轴围成的阴影部分的面积,用定积分可表示为( ) A. ???-33f (x )d x B.??1 3f (x )d x +??1-3f (x )d x C. ???-31f (x )d x D. ???-3 1f (x )d x -??13f (x )d x 6.如图是函数 y =f (x )的导函数的图象,给出下面四个判断:
①f (x )在区间[-2,-1]上是增函数; ②x =-1是f (x )的极小值点; ③f (x )在区间[-1,2]上是增函数,在区间[2,4]上是减函数; ④x =2是f (x )的极小值点. 其中,所有正确判断的序号是( ) A .①② B .②③ C .③④ D .①②③④ 7.对任意的x ∈R ,函数f (x )=x 3+ax 2+7ax 不存在极值点的充要条件是( ) A .0≤a ≤21 B .a =0或a =7 C .a <0或a >21 D .a =0或a =21 8.某商场从生产厂家以每件20元的价格购进一批商品,若该商品零售价定为P 元,销售量为Q ,则销量Q (单位:件)与零售价P (单位:元)有如下关系:Q =8 300-170P -P 2,则最大毛利润为(毛利润=销售收入-进货支出)( ) A .30元 B .60元 C .28 000元 D .23 000元 9.函数f (x )=-x e x (a f (b ) D .f (a ),f (b )大小关系不能确定 10.函数f (x )=-x 3+x 2+x -2的零点个数及分布情况为( ) A .一个零点,在? ? ? ??-∞,-13内
高中数学导数及其应用
高中数学导数及其应用 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
高中数学导数及其应用 一、知识网络 二、高考考点 1、导数定义的认知与应用; 2、求导公式与运算法则的运用; 3、导数的几何意义; 4、导数在研究函数单调性上的应用; 5、导数在寻求函数的极值或最值的应用; 6、导数在解决实际问题中的应用。 三、知识要点 (一)导数 1、导数的概念 (1)导数的定义 (Ⅰ)设函数在点及其附近有定义,当自变量x在处有增量△x(△x可正可负),则函数y相应地有增量,这两个增量的比 ,叫做函数在点到这间的平均变化率。如
在点处的导数(或变化率),记作,即 。 (Ⅱ)如果函数在开区间()内每一点都可导,则说在开区间 ()内可导,此时,对于开区间()内每一个确定的值,都对应着一个确定的导数,这样在开区间()内构成一个新的函数,我们把这个新函数叫做在开区间()内的导函数(简称导数),记作或,即 。 认知: (Ⅰ)函数的导数是以x为自变量的函数,而函数在点处的导数是一个数值;在点处的导数是的导函数当时的函数值。 (Ⅱ)求函数在点处的导数的三部曲: ①求函数的增量; ②求平均变化率;
③求极限 上述三部曲可简记为一差、二比、三极限。 (2)导数的几何意义: 函数在点处的导数,是曲线在点处的切线的斜率。 (3)函数的可导与连续的关系 函数的可导与连续既有联系又有区别: (Ⅰ)若函数在点处可导,则在点处连续; 若函数在开区间()内可导,则在开区间()内连续(可导一定连续)。 事实上,若函数在点处可导,则有此时,
高中数学导数讲义完整版
高中数学导数讲义完整版 第一部分 导数的背景 一、导入新课 1. 瞬时速度 问题1:一个小球自由下落,它在下落3秒时的速度是多少? (2 2 1gt s =,其中g 是重力加速度). 2. 切线的斜率 问题2:P (1,1)是曲线2 x y =上的一点,Q 是曲线上点P 附近的一个点,当点Q 沿曲线逐渐向点P 趋近时割线PQ 的斜率的变化情况. 3. 边际成本 问题3:设成本为C ,产量为q ,成本与产量的函数关系式为103)(2 +=q q C ,我们来研究当q =50时,产量变化q ?对成本的影响. 二、小结: 瞬时速度是平均速度 t s ??当t ?趋近于0时的极限;切线是割线的极限位置,切线的斜率是割线斜率x y ??当x ?趋近于0时的极限;边际成本是平均成本 q C ??当q ?趋近于0时的极限. 三、练习与作业: 1. 某物体的运动方程为2 5)(t t s =(位移单位:m ,时间单位:s )求它在t =2s 时的速度. 2. 判断曲线2 2x y =在点P (1,2)处是否有切线,如果有,求出切线的方程. 3. 已知成本C 与产量q 的函数关系式为522 +=q C ,求当产量q =80时的边际成本. 4. 一球沿某一斜面自由滚下,测得滚下的垂直距离h (单位:m )与时间t (单位:s )之间的函数关系为2 t h =,求t =4s 时此球在垂直方向的瞬时速度. 5. 判断曲线2 2 1x y = 在(1,21)处是否有切线,如果有,求出切线的方程. 6. 已知成本C 与产量q 的函数关系为742 +=q C ,求当产量q =30时的边际成本.
导数的运算-高中数学知识点讲解
导数的运算1.导数的运算 【知识点的知识】 1、基本函数的导函数 ①(为常数) C=0 C ②()=() x n nx n﹣1 n R ③()= sinx cosx ④()=﹣ cosx sinx ⑤()= e e x x ⑥()=()* (>0且1) a a lna a a x x ⑦= [log x)] a 11 (log e)(a>0且a 1) ?* = ???? a lnx ⑧=1.? 2、和差积商的导数 ① [ (f x)g(x)]=f (x )g(x) ② [ (f x)﹣g(x)]=f(x)﹣g(x) ③ [ (f x)g(x)]=f(x)(g x)(f x)g(x) ?(?) ④[?(?)]′=[?′(?)?(?)― ?(?)?′(?)] . [?(?)2]
3、复合函数的导数 设,则 y=(u t),t=(v x)y(x)=u(t)v(x)=u[(v x)]v(x) 1/ 3
【典型例题分析】 题型一:和差积商的导数 典例 1:已知函数,为的导函数,则(f x)=asinx bx 3 (4a R,b R)f (x)(f x)(2014)(﹣2014)(2015)﹣(﹣2015)=() f f f f A.0 B.2014 C.2015 D.8 f (x)=acosx 3bx 2 解:, ∴f (﹣x)=aco(s ﹣x ) 3(b ﹣x) 2 ∴为偶函数; f (x) f ( 2015)﹣f (﹣2015)=0 ∴()(﹣) f 2014 f 2014 =asi(n)b asi(n﹣)(b﹣)=; 2014 ? 20143 4 2014 2014 3 4 8 (f2014)(f﹣2014)f(2015)﹣(f ﹣2015)=8 故选D. 题型二:复合函数的导数 典例 2:下列式子不正确的是() A.B.=()=﹣(lnx﹣2x ) 3x 2 cosx 6x sinx 1?―2?ln2 ????C.()=D.()′= 2sin2x 2cos2x ??????―???? ?2 解:由复合函数的求导法则 对于选项,成立,故正确; A (3x 2 cosx )=6x﹣sinx A
高中数学-导数的概念几何性质及应用
高中数学 导数及其应用学案 类型一:利用导数研究函数的图像 例2、若函数的导函数... 在区间上是增函数,则函数在区间上的图象 可能是( ) (A) (B) (C) (D) 练习1.如右图:是f (x )的导函数, 的图象如右图所示,则f (x )的图象只可能是( ) (A ) (B ) (C ) (D ) ()y f x =[,]a b ()y f x =[,]a b )(/x f 例1、设a <b,函数y=(x-a)2(x-b)的图象可能是( ) a b a b a o o y o y o y
2.设f '(x )是函数f (x )的导函数,y =f '(x )的图象如右图所示,则y =f (x )的图象最有 可能的是 ( ) A . B . C . D . 类型二:导数几何意义的应用 例3、(1)求曲线在点处的切线方程。(2)求抛物线y=2x 过点5,62?? ??? 的切线方程 32151,09425217257.1..76444644y x y ax x a B C D ==+ ----练习:若存在过点()的直线和都相切,则等于()A.-1或-或或-或 7.曲线y =x 2-2x +a 与直线y =3x +1相切时,常数a 的值是________. 类型三:利用导数研究函数的单调性 例4、已知a ,b 为常数,且a ≠0,函数f (x )=-ax+b+axlnx ,f(e)=2(e=2.71828…是自然对数的底数). (I )求实数b 的值; (II )求函数f (x )的单调区间; 21x y x =-()1,1
例5、已知函数f(x)= ax 1x 2 ++在(-2,+∞)内单调递减,求实数a 的取值范围. 练习:若函数y =3 1x 3-21ax 2+(a -1)x +1在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,试求实数a 的取值范围 类型四:导数与极值 ()ln 6x f x x = 例、求函数的极值。 ()3227310,f x x ax bx a x a b =+++=-例、已知在有极值,求常数的值。 练习1、已知f(x)=x 3+ax 2 +(a+6)x+1有极大值和极小值,则a 的取值范围是( ) (A )-1<a <2 (B )-3<a <6 (C )a <-1或a >2 (D )a <-3或a >6 2、直线y =a 与函数f(x)=x 3-3x 的图象有相异的三个公共点,则求a 的取值范围。 类型五:导数与最值 例8、已知函数f(x)=(x-k)e x . (1)求f(x)的单调区间;
人教版高中数学(理科)选修导数的概念(二)
●课题 §3.1.2 导数的概念(二)——瞬时速度 ●教学目标 (一)教学知识点 物体在时刻t的瞬时速度的概念. (二)能力训练要求 1.掌握用极限给瞬时速度下的精确的定义. 2.会运用瞬时速度的定义,求物体在某一时刻的瞬时速度. 3.理解足够小、足够短的含义. (三)德育渗透目标 1.培养学生解决实际问题的能力. 2.平均速度与瞬时速度是互相联系、辩证统一的,培养学生联系的、辩证统一的思想. 3.培养学生严谨的科学态度. ●教学重点 知道了物体的运动规律,用极限来定义物体的瞬时速度,学会求物体的瞬时速度. ●教学难点 理解物体的瞬时速度的定义. ●教学方法 启发式 由高中物理上给瞬时速度下的定义,以及进行直观的描述,如何利用已学过的极限知识,进行精确地刻划呢?让学生自己根据极限的定义,来定义物体的瞬时速度. ●教学过程 Ⅰ.课题导入 [师]我们物理中学习直线运动的速度时,已经学习了物体的瞬时速度的有关知识,现在我们从数学的角度重新来认识一下瞬时速度. Ⅱ.讲授新课 [师]物理课本上瞬时速度是如何定义的? [生]运动物体经过某一时刻(某一位置)的速度,叫做瞬时速度. [师]那怎么来理解瞬时速度?物理课本上有具体的阐述吗? [生]有,要确定物体在某一点A处的瞬时速度,从A点起取一小段位移AA1,求出物体在这段位移上的平均速度,这个平均速度可以近似地表示物体经过A点的瞬时速度. [师]那一小段的位移AA1,有什么要求吗?是不是越小越好? [生]是越小越好,当位移足够小时,物体在这段时间内运动可认为是匀速的,所得的平均速度就等于物体经过A点的瞬时速度了. [师]我们现在已经了解了一些关于瞬时速度的知识,现在已经知道物体做直线运动时,它的运动规律用函数表示为s=s(t),也叫做物体的运动方程或位移公式,现在有两个时刻t0,t0+Δt,现在问从t0到t0+Δt这段时间内,物体的位移、平均速度各是多少? [生]位移为s(t0+Δt)-s(t0) 平均速度为 t t s t t s ?- ? +) ( ) ( (一边讲一边老师板书) [师]根据对瞬时速度的直观描述,当位移足够小,现在位移由时间t来表示,也就是说时间足够短时,平均速度就等于瞬时速度.怎么来刻划时间足够短呢?现在是从t0到t0+
高中数学导数及其应用
高中数学导数及其应用 一、知识网络 二、高考考点?1、导数定义的认知与应用; ?2、求导公式与运算法则的运用; ? 3、导数的几何意义; ?4、导数在研究函数单调性上的应用; 5、导数在寻求函数的极值或最值的应用; 6、导数在解决实际问题中的应用。??三、知识要点? (一)导数?1、导数的概念?(1)导数的定义 (Ⅰ)设函数在点及其附近有定义,当自变量x在处有增量△x(△x可正可负),则函数y相应地有增量,这两个增量的比 ,叫做函数在点到这间的平均变化率。如果
时,有极限,则说函数在点处可导,并把这个极限叫做在点处的导数(或变化率),记作 ,即 。 ?(Ⅱ)如果函数在开区间()内每一点都可导,则说在开区间()内可导,此时,对于开区间()内每一个确定的值 ,都对应着一个确定的导数 ,这样在开区间()内构成一个新的函数,我们把这个新函数叫做在开区间( )内的导函数(简称导数),记作或, 即。??认知: (Ⅰ)函数的导数是以x为自变量的函数,而函数在点处的导数是一个数值;在点处的导数是的导函数当 时的函数值。 (Ⅱ)求函数在点处的导数的三部曲: ①求函数的增量 ;? ②求平均变化率; ③求极限?上述三部曲可简记为一差、二比、三极限。?? (2)导数的几何意义:?函数在点处的导数,是曲线在点 处的切线的斜率。? (3)函数的可导与连续的关系 函数的可导与连续既有联系又有区别:?(Ⅰ)若函数在点处可导,则在点处连续;?若函数在开区间()内可导,则在开区间()内连续(可
导一定连续)。??事实上,若函数在点处可导,则有 此 时,? ? ? ?记 ,则有即在点处连续。?(Ⅱ)若函数在点处连续,但在点处不一定可导(连续不一定可导)。?反例:在点处连续,但在点处无导数。 事实上,在点处的增量?当 时,, ;?当时,, 由此可知,不存在,故在点处不可导。??2、求导公式与 求导运算法则 (1)基本函数的导数(求导公式) 公式1 常数的导数:(c为常数),即常数的导数等于0。??公式2 幂函 数的导数:。? 公式3 正弦函数的导数:。??公式4 余弦函数的导数: ??公式5 对数函数的导数:? (Ⅰ); ?(Ⅱ)
高中数学-导数的计算练习
高中数学-导数的计算练习 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.下列求导运算正确的是 A .211()1x x x '+=+ B .21 (log )ln 2 x x '= C .3(3)3log x x x '= D .2 (cos )2sin x x x x '=- 【答案】B 【解析】因为211()x x '=- ,所以A 项应为2 11x -;由1(log )ln a x x a '=知B 项正确;由()ln x x a a a '=可知C 项错误;D 项中,2 2 (cos )2cos sin x x x x x x '=-,所以D 项是错误的,综上所述,正确选项为B . 2.已知函数3 ()f x x =在点P 处的导数值为3,则P 点的坐标为 A .(2,8)-- B .(1,1)-- C .(2,8)--或(2,8) D .(1,1)--或(1,1) 【答案】D 3.已知函数()f x 的导函数为()f x ',且满足()(1)2ln xf f x x ='+,则(1)f '等于 A .e - B . 1- C .1 D .e 【答案】B 【解析】∵函数()f x 的导函数为()f x ',且满足()(1)2ln (0)f x x xf x ='+>, ∴1 ()1()2f x f x '='+ ,把1x =代入()f x '可得(1)2(1)1f f '='+,解得(1)1f '=-.故选B . 4.曲线e x y =在点2 (2,e )处的切线与坐标轴所围成的三角形的面积为 A .2e 2 B .23e C .26e D .29e 【答案】A
高中导数经典知识点及例题讲解
高中导数经典知识点及 例题讲解 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
§ 1.1 变化率与导数 1.1.1 变化率问题 自学引导 1.通过实例分析,了解平均变化率的实际意义. 2.会求给定函数在某个区间上的平均变化率. 课前热身 1.函数f (x )在区间[x 1,x 2]上的平均变化率为Δy Δx =________. 2.平均变化率另一种表示形式:设Δx =x -x 0,则Δy Δx =________,表示函数 y =f (x )从x 0到x 的平均变化率. 1.f (x 2)-f (x 1)x 2-x 1 答 案 2. f (x 0+Δx )-f (x 0) Δx 名师讲解 1.如何理解Δx ,Δy 的含义 Δx 表示自变量x 的改变量,即Δx =x 2-x 1;Δy 表示函数值的改变量,即Δy =f (x 2)-f (x 1). 2.求平均变化率的步骤 求函数y =f (x )在[x 1,x 2]内的平均变化率. (1)先计算函数的增量Δy =f (x 2)-f (x 1). (2)计算自变量的增量Δx =x 2-x 1. (3)得平均变化率Δy Δx =f x 2-f x 1 x 2-x 1 . 对平均变化率的认识 函数的平均变化率可以表现出函数在某段区间上的变化趋势,且区间长度越小,表现得越精确.如函数y =sin x 在区间[0,π]上的平均变化率为0,而在 [0,π2]上的平均变化率为sin π 2-sin0 π2-0 =2π. 在平均变化率的意义中,f (x 2)-f (x 1)的值可正、可负,也可以为零.但Δx =x 2-x 1≠0.