气泡动力学非线性分析
第七章----沸腾换热

g
根据以上 8 个假设从边界层微分方程组推出努 塞尔的简化方程组,从而保持对流换热理论的 统一性。同样的,凝结液膜的流动和换热符合
边界层的薄层性质。
以竖壁的膜状凝结为例: x 坐标为重力方向,如 图所示。 在稳态情况下,凝结液膜流动的微分方程组为 :
u v x y 0 u u dp 2u v ) l g l 2 l (u x y dx y t t 2t u v al 2 y y x
gr hV 1.13 l l( t s t w )
2 l 3 l 1/ 4
(4)当是水平圆管及球表面上的层流膜状凝结时, 其平均表面传热系数为:
水平管:
gr hH 0.729 d( t t ) s w l
2 l 3 l
g
tw ts
特点:壁面上有一层液膜,凝结放出的
相变热(潜热)须穿过液膜才能传到冷
却壁面上, 此时液膜成为主要的换热
热阻
(2)珠状凝结
定义:凝结液体不能很好地湿润壁 面,凝结液体在壁面上形成一个个 小液珠的凝结形式,称珠状凝结。
g
tw ts
特点:凝结放出的潜热不须穿过液膜的阻力即 可传到冷却壁面上。
考虑假定(5) 膜内温度线性分布,即热量 转移只有导热
t t u v 0 x y
只有u 和 t 两个未知量,于是,上面得方 程组化简为:
2u l g l y 2 0 2 t a 0 l 2 y
边界条件: y 0 时, u 0, t t w
计算方法:对于竖壁紊流膜状换热,沿整个
壁面上的平均表面传热系数
自适应变分模态分解算法在高温高压水空化特性分析中的应用

自适应变分模态分解算法在高温高压水空化特性分析中的应用目录1. 内容简述 (2)1.1 背景与研究意义 (2)1.2 文献综述 (3)1.3 研究目标与内容 (4)2. 高温高压水空化现象及特征 (5)2.1 空化现象的物理机制 (6)2.2 高温高压水空化特性 (7)2.3 传统分析方法的局限性 (8)3. 自适应变分模态分解算法简介 (9)3.1 变分模态分解算法原理 (10)3.2 自适应策略的引入 (11)3.3 算法优势及应用前景 (12)4. AVMD应用于高温高压水空化特性分析 (14)4.1 数据采集与预处理 (15)4.2 AVMD参数选择及模型构建 (16)4.3 空化特性特征提取与分析 (17)4.3.1 空化频率谱分析 (18)4.3.2 空化强度特征提取 (20)4.3.3 空化发展趋势分析 (21)4.4 相关性研究 (23)5. 结果与讨论 (24)5.1 空化频率谱及强度特征 (25)5.2 高温高压下空化规律分析 (27)5.3 AVMD算法的有效性和适用性 (28)6. 结论与展望 (30)6.1 研究结论 (31)6.2 未来研究方向 (32)1. 内容简述本文重点研究自适应变分模态分解算法在高温高压水空化特性分析中的应用。
简要介绍了高温高压环境下的水空化现象及其重要性,指出水空化特性的准确分析对于相关领域的研究和实际应用至关重要。
阐述了自适应变分模态分解算法的基本原理和优势,包括其在处理复杂非线性、非平稳信号方面的能力。
通过理论分析和实验研究相结合的方式,探讨了如何将自适应变分模态分解算法应用于高温高压水空化特性的分析过程中。
通过分解水空化过程中的复杂信号,提取出具有物理意义的模态分量,进一步揭示水空化的内在规律和特性。
通过对比分析验证了自适应变分模态分解算法的有效性和优越性,展望了其在相关领域的应用前景。
1.1 背景与研究意义随着现代工业技术的飞速发展,高温高压水(HPW)系统的应用日益广泛,特别是在能源、化工、石油及航天等领域。
偏微分方程(本科生数学基础课教材)

偏微分方程(本科生数学基础课教材)微分方程是一种非常重要的数学方法,它可以处理定义在一定空间中的未知变量和已知变量间的关系。
本科生数学基础课教材中涉及到了一些偏微分方程的知识,本文将深入的介绍下偏微分方程的内容。
1. 什么是偏微分方程偏微分方程(partial differential equation,简称PDE)是指表示未知函数的某个变量的函数序列的方程,其中的变量的某些部分可能被某些定义的函数所限定。
这种方程反映了区域内任意函数的可能存在的连续性及其求解时某些变量之间的约束性关系。
偏微分方程在微分几何,动力学系统,电磁学,偏微分方程的变分技术,稳定性理论,普朗克力学,热传导,流体动力学等数学领域都有着广泛的应用。
2. 偏微分方程的基本概念偏微分方程的基本概念是函数的求导和积分,是变分法的基础。
它以熟悉概念为基础,将导数和积分结合起来,形成一种新的数学形式。
它所求解的未知函数,都是在空间和时间两个方面连续发展变化的,或者说,同时考虑空间和时间函数和现象之间的关系。
3. 常见的偏微分方程偏微分方程一般分为四类,其中常见的有波动方程,Poisson方程,拉普拉斯方程,Kelvin-Voigt方程,吉普斯梅尔方程,马太偏微分方程等。
(1)波动方程:它是一个非线性的偏微分方程,其解的特殊情况可表示为解析解,常见的波速等作为特例。
(2)Poisson方程:它是一个双曲型偏微分方程,可以用于描述在两个或多个方向上具有对称性的繁杂系统或一维系统中热或电荷的分布。
(3)拉普拉斯方程:它可以用于求解变分问题,它本身也是一个偏微分方程问题,可用来求解几何和物理系统中的路径长度,其求解结果为变函数。
(4)Kelvin-Voigt方程:它可以引用细胞膜的抗冲击性能的偏微分方程,在本科教材中可以用来求解组织在生物学上产生渐进延迟的情况。
(5)吉普斯梅尔方程:它是一类非线性偏微分方程,通常用来描述热传导,晶体振动和流体动力学在狭义上的应用。
【国家自然科学基金】_系统动力学分析_基金支持热词逐年推荐_【万方软件创新助手】_20140803
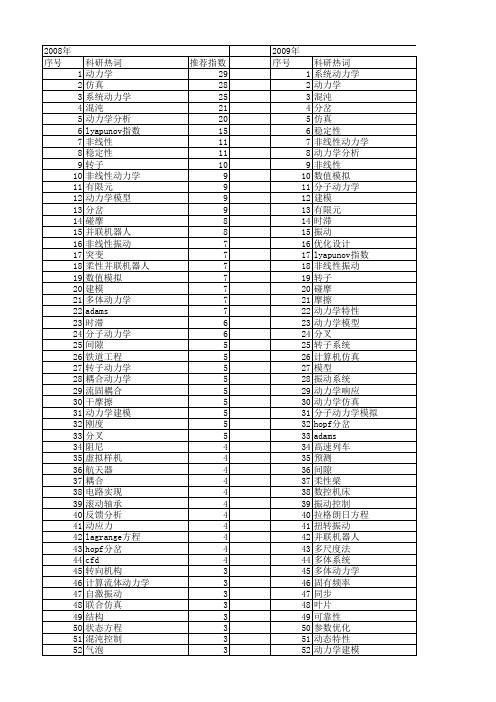
3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 系统动力学 动力学 混沌 分岔 仿真 稳定性 非线性动力学 动力学分析 非线性 数值模拟 分子动力学 建模 有限元 时滞 振动 优化设计 lyapunov指数 非线性振动 转子 碰摩 摩擦 动力学特性 动力学模型 分叉 转子系统 计算机仿真 模型 振动系统 动力学响应 动力学仿真 分子动力学模拟 hopf分岔 adams 高速列车 预测 间隙 柔性梁 数控机床 振动控制 拉格朗日方程 扭转振动 并联机器人 多尺度法 多体系统 多体动力学 固有频率 同步 叶片 可靠性 参数优化 动态特性 动力学建模
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
非光滑 阻尼 运动学 轮腿复合 耦合动力学 耦合 粒子群算法 符号动力学 突变 空间算子代数 空气动力学 神经网络 球齿轮 灵敏度分析 滑行力 混沌同步 流固耦合 气动弹性 模拟 模态分析 机电耦合 有限元法 有限元分析 数值仿真 振动与波 弹性动力学 干摩擦 周期运动 周期解 可持续发展 变结构控制 双面约束 动态响应 动力响应 分岔图 内共振 供应链 不对中 lagrange方程 齿轮动力学 颤振 预反射 面齿轮传动 非线性系统 非线性动力系运动认知 运动特性 输流管道
硅粉流化床中颗粒浓度信号非线性分析

新兴学科, F u e分析划时代的发展结果。与 Fu 是 or r i o—
tr i 分析相 比, 波分析在时域 和频域都具有 良好的局 e 小 部化特性 以及 具 有 多分 辨 率 ( ut rsli ) 特 m l.eo tn 的 i uo
性[ 。因此 , 1 ] 小波变换 作 为一 种数 学理论 和方法在科
Z mm /
5 O
10 0
10 5
2O O
20 5
第1 期
硅粉流化床 中颗粒浓度信号非线性分析
表 2 不 同小 波基 函数 信号 重构 的 误差
3 5
2 实验数 据处理与分 析
2 1 重构误差分析 .
2 11 最佳 小波函数 ..
小波基函数有许 多不 同类 型 的小波族 , 们 的性 它
更好 的对称性 , 此小波 函数 的支撑宽度 :N一1其 滤波 6 ; 器长度为 6 其正则性 : N; 对于重构小 波 函数 , 在节点上
 ̄ 5m Xl0m 1 m 0 m的有机玻璃管和开孔率为 5 0 O 的气
体分布板构成 。供气系统包括 风机 、 稳压罐 、 流量调节 阀、 转子流量计 。P 4 V A型 颗粒 测速 仪 系统 由光 纤探
头、 信号放大转换仪 、C机和采样软件等组成 。 P
学技术界 引起 了越来越多的关注和重视 。在工程 应用
中的压力降、 壁效应、 气泡相的不均匀分布, 使床层 的
空 隙率在空间上具有不 均匀性 ; 另一方面 , 由于气泡在 床层 中的运动具有 不确定性 , 使局部空隙率在 时间上 也 具有不 均匀性[ 3 2] - 。随着计 算机技术和非线性 理论 的不 断发展 , 各种非线性 分析方法 已被应用 于分 析气
水下爆炸载荷下舰船响应与毁伤研究综述

第25卷第5期水下无人系统学报 Vol. 25No. 5 2017年12月 JOURNAL OF UNMANNED UNDERSEA SYSTEMS Dec. 2017收稿日期: 2017-09-30; 修回日期: 2017-11-10.基金项目: 国家自然科学基金项目(51479204、51409253、51679246).作者简介: 金 键(1990-), 男, 在读博士, 主要研究方向为舰船抗爆抗冲击.[引用格式] 金键, 朱锡, 侯海量, 等. 水下爆炸载荷下舰船响应与毁伤研究综述[J]. 水下无人系统学报, 2017, 25(5): 396-409.【编者按】现代舰船的生命力和战斗力受到鱼、水雷等水中兵器的严重威胁, 开展水下爆炸载荷下舰船响应与毁伤研究具有十分重要的现实意义。
水下爆炸载荷下舰船的响应与毁伤过程是复杂的非线性动态过程, 属大变形、强非线性问题, 涉及流体力学、气泡动力学、爆炸力学、塑性力学、塑性动力学、结构力学、断裂力学、结构振动学、水弹性力学及计算机应用等众多学科及相互之间的交叉。
目前对水下爆炸的基本过程、物理现象和载荷特性的研究较为成熟, 对复杂边界条件下的水下爆炸过程和载荷特性的研究也有了长足的进展, 而水下爆炸载荷下舰船动响应过程、毁伤机理问题还有待进一步研究。
在受到水中兵器的攻击情况下, 如何根据舰船动响应过程与毁伤机理合理选取材料、设置优化结构是舰船防护中亟待解决的问题。
在国内, 朱锡教授带领的舰船抗爆抗冲击技术研究团队在舰船防护装甲材料、舰船防护结构设计方法、舰船结构防护/承载/隐身多功能一体化等方向有深入研究, 取得了一批原创性成果。
目前团队承担着武器装备预研项目、国防973项目、国家自然科学基金重点项目等多项国家级项目的研究与研制任务。
本刊特邀其团队成员金键博士系统梳理了水下爆炸下舰船响应与毁伤问题, 以综述形式呈现, 旨在让读者对水下爆炸的过程、分类和载荷特征、舰船动响应过程和毁伤机理以及研究方法和研究趋势有清晰的了解与认识。
球形贮箱内液体横向晃动问题的系统辨识与参数化等效建模

0引言液体晃动现象普遍存在于人们的生活与生产中,液体晃动导致的安全和稳定性问题长期影响着各充液系统应用行业技术的发展。
对于受外部干扰作用的贮箱内液体晃动产生的动态非平衡晃动力和晃动力矩的研究,在交通运输[1-4]、液体能源储存[5-6]和航空航天[7-13]等工程领域受到学者们的普遍关注。
建立液体晃动系统的力学模型是研究液体晃动特性的重要手段。
传统单摆模型研究中,包光伟[14]针对平放式贮箱内的液体晃动特性建立单摆模型来对其进行描述;苗楠等[15]对单摆模型各个参数插值建立航天液体燃料晃动模型,并进行了变充液比工况下的输出响应仿真验证。
质量-弹簧模型研究中,刘嘉一等[16]利用建立的三维质量-弹簧模型计算了水平载荷时的液体作用力;岳宝增等[17]在解析带柔性附件充液航天器耦合特性时将液体晃动等效为球摆模型。
此类传统等效力学模型具有计算量小和效率高的优点,但是简化假设较多,制约了传统力学模型描述液体高阶晃动模态时的完整性,且可控、可调参数的数目较少,使其准确性也受到了限制。
近年来涌现出的各类新型模型有复合模型[18]、运动脉动球模型(moving pulsating ball model ,MPBM )[19]、深度学习预测模型[20]、幅度组合模型[21]和参数化模型[22-23],以上模型对液体晃动系统的特性表达精度较传统等效力学模型有了较大提高,其中参数化模型不仅可控、可变参数多,而且描述高阶晃动模态时精准度高。
文献[22-23]中的参数化模型均是在传统等效单摆模型的基础上对模型进行参数确定方法的优化,尽管比传统等效模型有所提升,但受限于传统力学模型框架结构单一的特点而无法对液体复杂工况下的晃动行为进行描述。
动力学系统建模需对研究对象进行系统辨识和参数估计,测量实验和CFD 模拟实验均可获得系统的输入、输出响应,但实验测量法[24-26]往往存在实验误差,且相似比选取不恰当时模拟实际工况程度较低或成本高,而CFD 数值模拟方法[27-30]成本低、适用性强和准确性高,且对液体晃动系统进行激励输入时准确无延迟。
lsdyna简介

LS-DYNA 简介ANSYS学习2009-02-17 20:03:54 阅读444 评论0 字号:大中小1.1 LS-DYNA 简介LS-DYNA 是世界上最著名的通用显式动力分析程序,能够模拟真实世界的各种复杂问题,特别适合求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成型等非线性动力冲击问题,同时可以求解传热、流体及流固耦合问题。
在工程应用领域被广泛认可为最佳的分析软件包。
与实验的无数次对比证实了其计算的可靠性。
由J.O.Hallquist主持开发完成的DYNA程序系列被公认为是显式有限元程序的鼻祖和理论先导,是目前所有显式求解程序(包括显式板成型程序)的基础代码。
1988年J.O.Hallquist创建LSTC公司,推出LS-DYNA程序系列,并于1997年将LS-DYNA2D、LS-DYNA3D、LS-TOPAZ2D、LS-TOPAZ3D 等程序合成一个软件包,称为LS-DYNA。
LS-DYNA的最新版本是2004年8月推出的970版。
ANSYS/LS-DYNA的前后处理器是ANSYS/PRE-POST,求解器LS-DYNA,是全世界范围内最知名的有限元显式求解程序。
LS-DYNA在1976年由美国劳伦斯·利沃莫尔国家实验室(Lawrence Livermore National Laboratory)J.O.Hallquist博士主持开发,时间积分采用中心差分格式,当时主要用于求解三维非弹性结构在高速碰撞、爆炸冲击下的大变形动力响应,是北约组织武器结构设计的分析工具。
LS-DYNA 的源程序曾在北约的局域网Pubic Domain公开发行,因此在广泛传播到世界各地的研究机构和大学。
从理论和算法而言,LS-DYNA是目前所有的显式求解程序的鼻祖和理论基础。
1988年,J.O.Hallquist创建利沃莫尔软件技术公司(Livermore Software Technology Corporation),LS-DYNA开始商业化进程,总体来看,到目前为止在单元技术、材料模式、接触算法以及多场耦合方面获得非常大的进步。
