Τ
希腊字母表

α Α 阿尔法
β Β 贝塔
γ Γ 伽马
δ Γ 德尔塔
ε Δ 艾普西隆
δ Ε 泽塔
λ Ν 纽
μ Ξ 克西
ν Ο 奥米克戎
π Π 派
ξ Ρ 柔
ζ 西格马
ε Ζ 伊塔
ζ Θ西塔
η Η约塔
θ Κ卡帕
ι Λ拉姆塔
κ Μ谬
η Σ陶
υ Τ宇普西隆
θ Φ斐
χ Υ希
ψ Φ普西
ω ω奥米伽
常用数学符号读法大全

常用数学符号读法大全大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon艾普西隆Ζζ zeta zeta截塔Ηη eta eta艾塔Θθ theta θita西塔Ιι iotaiota 约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mumiu 缪Νν nuniu 纽Ξξ xiksi 可塞Οο omicron omikron奥密可戎∏π pipai 派Ρρ rho r ou 柔∑σ sigma sigma西格马Ττ tautau 套Υυ upsilon jupsilon 衣普西隆Φφ phifai 斐Χχ chi k hai 喜Ψψ psi psa i 普西Ωω omega omiga欧米伽1 Α α alpha a:lf 阿尔法角度;系数2 Β β beta bet 贝塔磁通系数;角度;系数3 Γ γ gamma ga:m 伽马电导系数(小写)4 Δ δ delta delt 德尔塔变动;密度;屈光度5 Ε ε epsilon ep`silon 伊普西龙对数之基数6 Ζ ζ zeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数7 Η η eta eit 艾塔磁滞系数;效率(小写)8 Θ θ thet θit 西塔温度;相位角9 Ι ι iot aiot 约塔微小,一点儿10 Κ κ kappa kap 卡帕介质常数11 ∧ λ lambda lambd 兰布达波长(小写);体积12 Μ μ mu mju 缪磁导系数;微(千分之一);放大因数(小写)13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派圆周率=圆周÷直径=3.141617 Ρ ρ rho rou 肉电阻系数(小写)18 ∑ σ sigma `sigma 西格马总和(大写),表面密度;跨导(小写)19 Τ τ tau tau 套时间常数20 Υ υ upsilon jup`silon 宇普西龙位移21 Φ φ phi fai 佛爱磁通;角22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速;介质电通量(静电力线);角24 Ω ω omega o`miga 欧米伽欧姆(大写);角速(小写);角小写大写读法α Α 阿尔法β Β 贝塔γ Γ ga马δ Δ 德尔塔ε Ε 伊普西龙ζ Ζ 截塔η Η 依塔θ Θ 西塔ι Ι 约塔κ Κ 卡帕λ ∧兰嘛达μ Μ 缪ν Ν 纽ξ Ξ 克赛ο Ο 奥密克戎π∏ 派ρ Ρ 肉σ ∑ 西格马τ Τ 套υ Υ 宇普西龙φ Φ Fai(四声)χ Χ 西ψ Ψ 普赛ω Ω 欧米伽。
希腊字母中英对照表
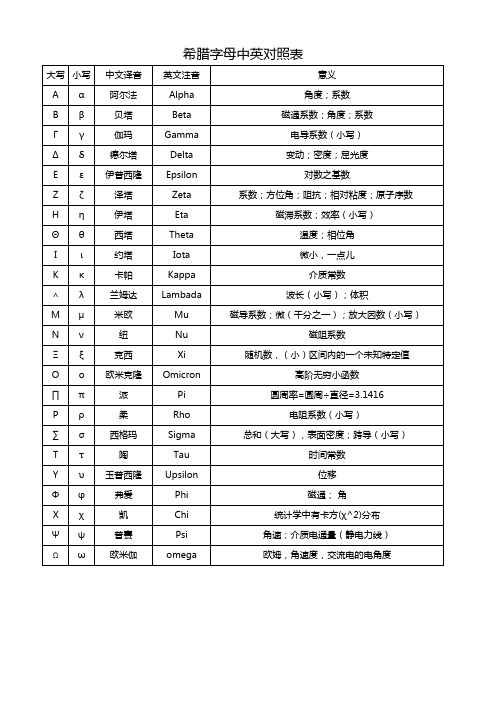
希腊字母中英对照表
大写小写中文译音英文注音意义
Aα阿尔法Alpha角度;系数
Bβ贝塔Beta磁通系数;角度;系数
Γγ伽玛Gamma电导系数(小写)
Δδ德尔塔Delta变动;密度;屈光度
Εε伊普西隆Epsilon对数之基数
Ζζ泽塔Zeta系数;方位角;阻抗;相对粘度;原子序数 Ηη伊塔Eta磁滞系数;效率(小写)
Θθ西塔Theta温度;相位角
Ιι约塔Iota微小,一点儿
Κκ卡帕Kappa介质常数
∧λ兰姆达Lambada波长(小写);体积
Μμ米欧Mu磁导系数;微(千分之一);放大因数(小写) Νν纽Nu磁阻系数
Ξξ克西Xi随机数,(小)区间内的一个未知特定值
Οο欧米克隆Omicron高阶无穷小函数
∏π派Pi圆周率=圆周÷直径=3.1416
Ρρ柔Rho电阻系数(小写)
∑σ西格玛Sigma总和(大写),表面密度;跨导(小写)
Ττ陶Tau时间常数
Υυ玉普西隆Upsilon位移
Φφ弗爱Phi磁通; 角
Χχ凯Chi统计学中有卡方(χ^2)分布
Ψψ普赛Psi角速;介质电通量(静电力线)
Ωω欧米伽omega欧姆,角速度,交流电的电角度。
希腊字母表及其读音与意义

希腊字母表及其读音与意义二:有关希腊语希腊语是印欧语系独立的一支,作为古希腊文明的载体,作为文学、哲学、科学、宗教等众多领域使用的语言,它的灿烂光辉举世罕见。
古希腊语是极少数至今仍然在世界范围内被学习和使用的古典语言之一。
“希腊”的中文名字不是来自英语Greece,而是来自Hellas这个诗歌语汇。
此举与希腊这个艺术的国度是多么相称啊!讲希腊语的民族在大约4000年前从巴尔干半岛来到希腊半岛及附近地区。
他们的语言分化为4种方言:伊奥里亚、爱奥尼亚、阿卡迪亚-塞浦路斯和多利安方言。
著名的《荷马史诗》——《伊利亚特》和《奥德赛》是大约公元前9世纪的作品,使用的是爱奥尼亚方言。
由爱奥尼亚方言发展为雅典语——古希腊语的主要形式和共同语Koine的基础。
《圣经》的《旧约全书》在公元前3-公元前2世纪译为Koine;《新约全书》则是直接用Koine写作的。
信仰东正教的人们现在还在使用这种古典语言的《圣经》。
现在使用希腊语的国家包括希腊、塞浦路斯、意大利、阿尔巴尼亚、土耳其等,以希腊语为母语的人有1500多万。
我们对希腊字母并不陌生,数学、物理、生物、天文学等学科都广泛使用希腊字母。
读过初中的人对“阿尔法”、“贝塔”、“伽玛”……早已耳熟能详。
《新约》里, 神说:“我是阿拉法,我是俄梅嘎。
我是始,我是终。
”在希腊字母表里,第一个字母是“阿尔法”(阿拉法),代表开始;最后一个字母是“欧美噶”(俄梅嘎),代表终了。
这正是《新约》用希腊语写作的痕迹。
罗马帝国时代,希腊语是继拉丁语之后的第二语言。
它在教育领域的地位至今仍然在欧美国家的大学里延续。
希腊字母并不神秘,就像阿拉伯文、俄文字母一样,只是符号不同,标音的性质是一样的。
阿拉伯文没有元音字母。
希腊字母是世界上最早的有元音的字母。
俄文、新蒙文等使用的基里尔字母和格鲁吉亚语字母都是由希腊字母发展而来,学过俄文的人使用希腊字母会觉得似曾相识。
希腊字母进入了许多语言的词汇中,如delta(三角洲)这个国际语汇就来自希腊字母Γ,因为Γ是三角形。
数学符号

序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Θ θ kappa kap 卡帕11 Ι ι lambda lambd 兰布达12 Κ κ mu mju 缪13 Λ λ nu nju 纽14 Μ μ xi ksi 克西15 Ν ν omicron omik`ron 奥密克戎16 Ξ π pi pai 派17 Ο ξ rho rou 肉18 Π ζ sigma `sigma 西格马19 Ρ η tau tau 套20 υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Σ χ chi phai 西23 Τ ψ psi psai 普西24 Υ ω omega o`miga 欧米伽希腊字母的正确读法是什么?1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Κ θ kappa kap 卡帕11 ⅸι la mbda lambd 兰布达12 Μ κ mu mju 缪13 Ν λ nu nju 纽磁阻系数14 Ξ μ xi ksi 克西15 Ο ν omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ξ rho rou 肉18 ∑ ζ sigma `sigma 西格马19 Σ η tau tau 套20 Τ υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Υ χ chi phai 西23 Φ ψ psi psai 普西角速;24 Χ ω omega o`miga 欧米伽希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΓδ:德尔塔DelteΔε:艾普西龙Epsilonδ :捷塔ZetaΕε:依塔EtaΘζ:西塔ThetaΗη:艾欧塔IotaΚθ:喀帕Kappaⅸι:拉姆达LambdaΜκ:缪MuΝλ:拗NuΞμ:克西XiΟν:欧麦克轮Omicron∏π:派PiΡξ:柔Rho∑ζ:西格玛SigmaΣη:套TauΤυ:宇普西龙UpsilonΦθ:fai PhiΥχ:器ChiΦψ:普赛PsiΧω:欧米伽Omega数学符号大全2008年01月29日星期二 15:25因为自然科学的讨论经常要用到数学,但用文本方式只能表达L!t d5w x r ^ |$s Y 左右结构的数学公式,上下结构、根式、指数等都很难表达。
希腊字母的读法

希腊字母的读法序号大写小写英文注音国际音标注音中文读音意义1 Α α alpha a:lf 阿尔法角度;系数2 Β β beta bet 贝塔磁通系数;角度;系数3 Γ γ gamma ga:m伽马电导系数(小写)4 Γ δ delta delt德尔塔变动;密度;屈光度5 Δ ε epsilon ep`silon伊普西龙对数之基数6 Ε δ zeta zat截塔系数;方位角;阻抗;相对粘度;7 Ζ ε eta eit艾塔磁滞系数;效率(小写)8 Θ ζthetζit西塔温度;相位角9 Η ηiotaiot约塔微小,一点儿10 Κ θ kappa kap卡帕介质常数11 ∧ι lambda lambd兰布达波长(小写);体积12 Μ κ mu mju缪磁导系数;微(千分之一);放大因数13 Ν λ nu nju纽磁阻系数14 Ξ μ xi ksi克西15 Ο νomicron omik`ron奥密克戎16 ∏ π pi pai派圆周率=圆周÷直径=3.14159 26535 8979317 Ρ ξ rho rou肉电阻系数(小写)18 ∑ ζ sigma `sigma西格马总和(大写),表面密度;跨导(小写)19 Σ η tau tau套时间常数20 Τ υ upsilon jup`silon宇普西龙位移21 Φ θ phi fai佛爱磁通;角22 Υ χ chi phai西23 Φ ψ psi psai普西角速;介质电通量(静电力线);角24 Χ ω omega o`miga欧米伽欧姆(大写);角速(小写);角再附送希腊字母的读法αΑalpha ['?lfa]βΒbeta ['bi:ta / 'beita]γΓgamma ['g?ma]δΓdelta ['delta]εΔepsilon ['epsilan / ep'sailan]δΕzeta ['zi:ta]εΖeta ['i:ta / 'eita]ζΘtheta ['ζita]ηΗiota [ai'outa]θΚkappa ['k?pa]ιΛlamda ['l?mda]κΜmu [mju:]λΝnu [nju:]μΞxi [ksai / gzai / zai]νΟomicron [ou'maikran]πΠpi [pai]ξΡrho [rou]ζsigma ['sigma]ηΣtau [tau]υΤupsilon ['ju:psilon / ju:p'sailan]o 是反c 。
希腊字母表
序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Κ θ kappa kap 卡帕11 ∧ι lambda lambd 兰布达12 Μ κ mu mju 缪13 Ν λ nu nju 纽‵14 Ξ μ xi ksi 克西15 Ο ν omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ξ rho rou 肉18 ∑ ζ sigma `sigma 西格马19 Σ η tau tau 套20 Τ υ upsilon jup`silon 宇普西龙21 Φ θ phi f ai 佛爱22 Υ χ chi phai 西23 Φ ψ psi psai 普西24 Χ ω omega o`miga 欧米伽Α α alpha ['Alf E]Β β beta ['bi:tE,'beitE]Γ γ gamma ['gAmE]Γ δ delta ['deltE]Δ ε epsilon [ep'sailEn,'epsilEn]Ε δ zeta ['zi:tE]Ζ ε eta ['i:tE,'eitE]Θ ζ theta ['Wi:tE]Η η iota [ai'outE]Κ θ kappa ['kApE]∧ι lambda ['lAmdE]Μ κ mu [mju:]Ν λ nu [nju:]Ξ μ xi [gzai,ksai,zai]Ο ν omicron [ou'maikrEn]∏ π pi [pai]Ρ ξ rho [rou]∑ ζ sigma ['sigmE]Σ η tau [tR:]Τ υ upsilon [ju:p'sailEn,'ju:psilEn]Φ θ phi [f ai]Υ χ chi [kai]Φ ψ psi [psai]Χω omega ['oumigE]a b c d e f g h i j k l m n o p q r s t u v w x y zαβζ/θδεθγεηηδθι κλνπθξζηπθππμγδA B C D E F G H I J K L M N O P Q R S T U V W X Y ZΑΒ/ΚΓΔΦΓΖΗΣΕΚΛΜΝΟΠΚΡΣΤΦΤΤΞΓΕps ch sh ck th ΣΖςρζρθθζΘεκπλεύζηεεκπλεύζηεθεεμπνεύσεεκπλευζκέλνεκπλεπζκέλνοev&ovcridci)VInspiration拉丁文动词inspiroInspiration theopneusto默示一词译自希腊文theopneustos,意思是「神呼气」(提后三16)inspiration,έκπλευζε默示άή净化Καζαξηζκός灵感Έκπλευζε迷狂υγχέεη crazily模仿Μίκεζες预言Πξόβιεψε是圣灵的工作。
数学符号——精选推荐
数学符号、希腊字母:α——阿尔法β——贝塔γ——伽马Δ——德尔塔ξ——可sei ψ——可赛ω——奥秘噶µ——⽶哟λ——南⽊打σ——西格玛τ——套φ——fai2、数学运算符:∑—连加号∏—连乘号∪—并∩—补∈—属于∵—因为∴—所以√—根号‖—平⾏⊥—垂直∠—⾓⌒—弧⊙—圆∝—正⽐于∞—⽆穷∫—积分≈—约等≡—恒等3、三⾓函数:sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体序号⼤写⼩写英⽂注⾳国际⾳标注⾳中⽂注⾳1 Αα alpha a:lf 阿尔法2 Ββ beta bet 贝塔3 Γγ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Εε epsilon ep`silon 伊普西龙6 Ζζ zeta zat 截塔7 Ηη eta eit 艾塔8 Θθ thet θit 西塔9 Ιι iot aiot 约塔10 Κκ k appa kap 卡帕11 Λλ lambda lambd 兰布达12 Μ µ mu mju 缪13 Νν nu nju 纽14 Ξξ xi ksi 克西15 Οο omicron omik`ron 奥密克戎16 Ππ pi pai 派17 Ρρ rho rou ⾁18 Σσ sigma `sigma 西格马19 Ττ tau tau 套20 Υυ upsilon jup`silon 宇普西龙21 Φφ phi fai 佛爱22 Χχ c hi phai 西23 Ψψ psi psai 普西1 Αα alpha a:lf 阿尔法2 Ββ beta bet 贝塔3 Γγ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Εε epsilon ep`silon 伊普西龙6 Ζζ zeta zat 截塔7 Ηη eta eit 艾塔8 Θθ thet θit 西塔9 Ιι iot aiot 约塔10 Κκ kappa kap 卡帕11 ∧λ lambda lambd 兰布达12 Μ µ mu mju 缪13 Νν nu nju 纽磁阻系数14 Ξξ xi ksi 克西15 Οο omicron omik`ron 奥密克戎16 ∏π pi pai 派17 Ρρ rho rou ⾁18 ∑ σ sigma `sigma 西格马19 Ττ tau tau 套20 Υυ upsilon jup`silon 宇普西龙21 Φφ phi f ai 佛爱22 Χχ chi phai 西23 Ψψ psi psai 普西⾓速;24 Ωω omega o`miga 欧⽶伽希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΔδ:德尔塔DelteΕε:艾普西龙Epsilonζ:捷塔ZetaΖη:依塔EtaΘθ:西塔ThetaΙι:艾欧塔IotaΜµ:缪MuΝν:拗NuΞξ:克西XiΟο:欧麦克轮Omicron∏π:派PiΡρ:柔Rho∑σ:西格玛SigmaΤτ:套TauΥυ:宇普西龙UpsilonΦφ:fai PhiΧχ:器ChiΨψ:普赛PsiΩω:欧⽶伽Omega数学符号⼤全2008年01⽉29⽇星期⼆ 15:25因为⾃然科学的讨论经常要⽤到数学,但⽤⽂本⽅式只能表达L!t d5w x r ^ |$s Y 左右结构的数学公式,上下结构、根式、指数等都很难表达。
希腊字母与英文字母对照表
中文 注音
阿尔法 贝塔 德尔塔 泽塔 伊塔 西塔 约塔 兰姆达 谬 纽 塞 欧米克隆 派 柔 西格玛 陶 弗艾 角度;系数
数
学
意
思
磁通系数;角度;系数;晶体三极管放大倍数 电导系数(小写) 变动;密度;屈光度 系数;方位角;阻抗;相对粘度;原子序数 磁滞系数;效率(小写) 温度;相位角 微小,一点儿 介质常数 波长(小写);体积 微(千分之一);放大因数(小写) 磁阻系数
英 文 字 母
a b g d e z h u i k l m n j o p r s t y f x c v
古 希 腊 语 名 称
?ι θ α β ?η α γ ?κ κ α δ ?ι η α ?ψ η ι ν λ δ ?η α ?η α ζ ?η α η ?η α θ ?π π α κ υ (现为κ η ) λ υ (现为λ η ) μ η ?κ η θ ξ ν λ πη ξ ω ζ ?γ κ α η α υ ?ψ η ι ν λ θη χ η ψη ω κ ?γ α
英语名称 现 代 希 腊 语 发 音
Alpha Beta Gamma Delta Epsilon Zeta Eta Theta Iota Kappa Mu Nu Xi Omicron Pi Rho Sigma Tau Upsilon Phi Chi Psi Omega [a] [v] [ð] [e] [z] [i] [ζ ] [i] [l] [m] [n] [ks]
玉普塞隆 位移
/i/,/e/前为[ç],其 凯 馀为[x] [ps] [o] 普赛 欧米伽 角速;介质电通量(静电力线) 欧姆(大写);角速(小写);角
深圳市顺涛科技有限公司制
常用希腊字母与英文字母对照表
希腊字母表
序 号 大 写 小 写 英文注音 国际音标 英文 中文 1 Α α alpha a:lfa a 阿尔法 2 Β β beta beta b, v 贝塔 3 Γ γ gamma ga:m g, gh, y 伽马 4 Γ δ delta delta d, dh, th 戴尔塔 5 Δ ε epsilon ep`silon e 艾普西龙 6 Ε δ zeta zeta z 截塔 7 Ζ ε eta eta e, i 艾塔 8 Θ ζ theta θita th 西塔 9 Η η iot jot i 约塔 10 Κ θ kappa kap k 卡帕 11 Λ ι lambda lamda l 兰姆达 12 Μ κ mu mju m 缪 13 Ν λ nu nju n 纽 14 Ξ μ xi ksi x, ks 克西 15 Ο ο omicron omik`ron o 奥密克戎 16 Π π pi pai p 派 17 Ρ ρ rho rou r 柔 18 ζ sigma `sigma s 西格马 19 Σ η lon jup`silon u, y, v, f 宇普西龙 21 Φ θ phi fai ph, f 法爱 22 Υ χ chi khi ch, kh 奇 23 Φ ψ psi psai ps 帕赛 Χ 24 ω omega o`miga o 欧米伽 sinh / 双曲正弦 其实一般写作:sh 读作 赛恩(爱区) cosh / 双曲余弦 其实一般写作:ch 读作 扣赛恩(爱区) tanh / 双曲正切 其实一般写作:th 读作 天卷(爱区) coth / 双曲余切 其实一般写作:cth 扣天卷(爱区) sech / 双曲正割 读作 西看(爱区) csch / 双曲余割 读作 扣西看(爱区)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2002年第9期 数学学习与研究
△=一12<0.方程无解.
当b=7时。关于Y的方程可化为
) 一5) +4=O.
解这个方程,得Y.=4,),:=1,
.・.
+ =3, ・ =2,
.・.
:
!
一
3z+2=0为所求的一元二次方
程.
三、变用——验根求根
例4已知方程
2z:一6 +m一3:0
有两个非负整数根。求两根及m的值.
分析注意由“非负整数”条件引发
的讨论.
解设方程的两根为X.、 ,,则
.+ =3, . :!
.
又 l、 为非负整数,且 l+ :=3,
所以 .、 !的值为1,2或0,3.
当X。、 的值为1,2 ̄,-j-, =2,
解得m=7.
当 .、 的值为o,3 ̄,-j-,旦 =0,
解得m=3.
因此,方程的两根为1,2时,m的值为
7;
方程的两根为0.3时.m的值为3.
例5已知关于 的方程
一
2(k+1) +k:+2k一1=0 ①
(1)求证:对于任意实数k,方程①总
有两个不相等的实数根.
(2)如果a是关于Y的方程
,一 一( ,+ 一2k)y+( .一 )( !一 )=o ②
的根,其中 .、z:为方程①的两个实数根,
求代数式
( 1
一
)÷ ・
的值.(2001年北京市海淀区中考题)
解(1)证明:
-
.
’
△=[一2(k+1)]:一4(k +2k一1)
=
8>0
.
・
.
对任意实数k,方程①总有两个不
相等的实数根.
(2)’.’ l+ !=2(k+1),
.
XI 3=k:+2k一1
,
.
’
. l+ :~2k=2,
( l—k)( !一k)=一1,
.
-
.
方程②为Y!一2y一1=0.
又’.’n是方程②的根,
.・.
a
:
一
2a一1=0.
.
・
.
a≠O,a+1≠O,a =2a+1,
.・.
c 一 ÷ ・ =一÷.
韦达定理的几个推论及应用
(云南省广南一中663300) 王 瑜
九义教材《代数》第三册介绍了一元
二次方程的两根之和与两根之积与系数的
关系,由此可联想到两根之差,两根之比与
系数有什么关系呢?本文对这两个问题进
行探究。可得如下的推论.
推论1设 ., :是一元二次方程
・
25・
维普资讯 http://www.cqvip.com
2002年第9期 数学学习与研究
OAt::+6 +C=0f nso)
的两根,则 一 :I= ,
其中△=b 一4ac.
证明利用韦达定理易证
推论2如果一元二次方程
:+ +C=0(nSO)
的两根之比为k,则kb =(1+k):∞
证明设 .、 ,是方程
!+ +C=0(nSO)
的两个实数根.则
:
,
1 l+ 2 一
I c
[XIX2
消去方程组中的 。, :,得
kb:=(1+k):nc.
推论3若 ., :为任意实数,则
4 l 2≤( l+ :):.
证明略.
下面谈谈这几个推论的应用.
例1设 。, :是关于 的方程
+(2m+1) +(,7l一2):=0
的两个实数根,当m取什么值时,
( .一 :):=157(1995年江西省中考题)
解‘.‘( l— 2):=15,
由推论1.得
,二 :l5
. 1
.・.
20m一15=15,即m= D.
例2 已知开向下的抛物线
Y=n戈:+ +c
与 轴交于 、Ⅳ两点(点Ⅳ在点 的右
侧),并且 和Ⅳ两点的横坐标分别是
:
一
2 一3=0
.
26.
的两根.点 是抛物线与Y轴的交点,
/_MKN不小于9O。.
(1)求点 和点Ⅳ的坐标;
(2)求系数n的取值范围.
(2000年甘肃省初中升学考试题)
解(1)‘.’ 一2x一3=0的两根是
l=3, 2=一l,
.‘.
M(一l,0),Ⅳ(3,0).
(2)‘.’ MKN ̄>90。,
当/_MKN=90。时.
OK2=I OMI・I ONI
.
.
・
.
C=
压
当/_MKN>90。时.
则C< .即c≤压
由于 (一l,0),N(3,0),
.・.
MN=4, =l,...b=2a.
n
由推论l,得:4= 等 ,
.・.16口:=4a 一4ac’...
n=一
÷.
又...c≤ ,...n≥一拿.
又抛物线开口向下,
.・.
一
≤n<o.
例3 已知关于 的一元二次方程
5 一2 +5q=O(pSO)有两个相等的
实数根,若方程 + +q=0的两个实数
根是 ., :且I 。I<I :I,求 的值.
(1998年山东省普通高中招生统一考试
题)
解・.・关于 的一元二次方程
5x 一2 36px+5q=0
有两个相等的实数根,
.
・
.
△=(一2 ) 一4×5×5q
=
24,o=一100q=0.
维普资讯 http://www.cqvip.com
2002年第9期 数学学习与研究
・‘・
q ,
.・.
方程 +px+p=0变为
+ + :=o
.
由推论2,得:
kp =(1 :×l× .
又‘.‘P≠O.整理,得
6k:一13k+6=0
.
.・.
吾 = .
又‘.‘I I I<I I,
. 一
三
一 一
3‘
例4如果抛物线
y=一 +2(m—1) +(m+1)
与 轴相交于 、 两点.且点 在 轴的
正半轴上, 点在 轴的负半轴上, 的
长是n,OB的长是b,若t7,:b=3:l,求m的
值,并写出抛物线的解析式.(1999年南京
市中考试题)
解依题意,得k=一3.
由推论2,得:
一
3[2(m—1)]
=
(1—3):X(一1)X(m+1). 整理,得3m:一7m+2=O, .・.m.:2,m:: , .・.抛物线的解析式为 Y=一 !+2 +3或 ,4 4 Y 一 +了‘ 例5已知实数 、),、 满足 =6—3y和 +3y一2xy+2 :=O 试求 !、 的值.(1998年上海市“鹏 欣杯”竞赛题) 解由已知条件,得 +3y=6, 2xy=( +3y)+2z:=6+2 , .‘. ・(3y)=9+3。:. 由推论3,得: 4(9+3: )≤6:. 整理.得12z ≤O,.・.:=0. 将:=0代人已知条件解得 =3,Y=l,故 、 =3 =9. 例6正数 、),、 ,A、B、C满足条件: +A=y+B=:+C=后,求证: + ),+Cz<k . (第2l届全国苏联数学竞赛题) 证明 ‘.‘正数 、Y、。, 、 、C满足条 件: +A=Y+B=。+C=k. 由推论3,得: 4Ax≤ :,4By≤ :,4Cz< ̄k!, .・.Ax≤} :,By< ̄lk"-, ≤÷ :, .・.Ax+By+c:≤} <k , 故 + y+Cz<k . 例7设实数x,y、:解方程组 f2 +3),+。=l3 (1) 【4 :+9 +:。一2 +15y+3z=82 (2) (1992年“友谊杯”国际数学邀请赛试题) 解由(1)得 2 +(3),+3)=16一:, (1)+(2),得:
(2 ):+(3),+3):=一:!一4 +104,
.・.
[2 +(3),+3)] 一2(2x)(3),+3)
:一: 一4 +104
.
・
.
(2 )(3),+3)= :一14z+76.
由推论3,得:
4(z:一14z+76)≤(16一:):,
整理,得3(:一4) ≤O,
.
‘
.
=4.
将:=4代人(1)、(2),解得
=
3.Y=1.
f =3
故原方程组的解是{Y=1.
【 =4
・
27・
维普资讯 http://www.cqvip.com
