一元一次方程的应用(同步)(一)
一元一次方程应用题(行程问题一)(人教版)(含答案).docx
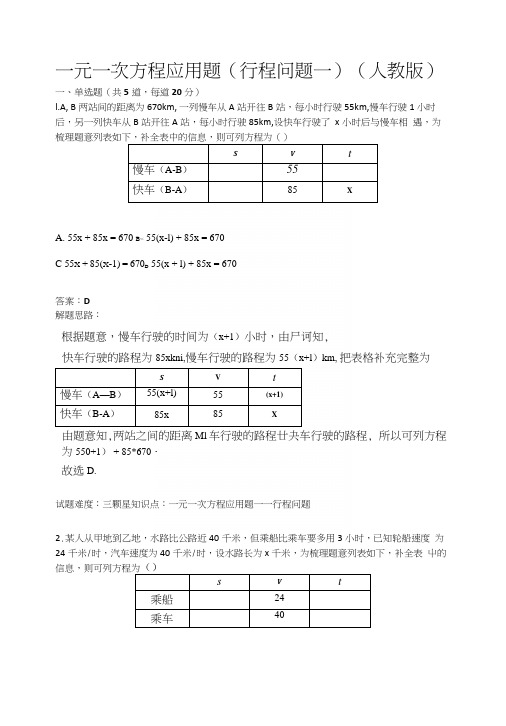
一元一次方程应用题(行程问题一)(人教版)一、单选题(共5道,每道20分)l.A, B两站间的距离为670km, 一列慢车从A站开往B站,每小时行驶55km,慢车行驶1 小时后,另一列快车从B站开往A站,每小时行驶85km,设快车行驶了x小时后与慢车相遇,为梳理题意列表如下,补全表中的信息,则可列方程为()S V t慢车(A-B)55快车(B-A)85 XA. 55x + 85x = 670 B< 55(x-l) + 85x = 670C 55X +85(X-1)=670D 55(x + l) + 85x = 670答案:D解题思路:根据题意,慢车行驶的时间为(x+1)小时,由尸诃知,快车行驶的路程为85xkni,慢车行驶的路程为55(x+l)km, 把表格补充完整为S V t慢车(A—B)55(x+l) 55 (x+1)快车(B-A)85x 85 X由题意知,两站之间的距离Ml车行驶的路程廿夬车行驶的路程, 所以可列方程为550+1) + 85*670・故选D.试题难度:三颗星知识点:一元一次方程应用题一一行程问题2.某人从甲地到乙地,水路比公路近40千米,但乘船比乘车要多用3小时,已知轮船速度为24千米/时,汽车速度为40千米/时,设水路长为x千米,为梳理题意列表如下,补全表屮的s V t乘船24乘车40x - x-40 x - x-40———3 = ——+ 3 = A. 2440 B. 2440— -3 = x+40— 4-3 =x + 40C. 24 40D. 24 40答案:C解题思路:根据题意,公路的长为(x+40)km,由r = ±可表达从甲地到乙地,乘船和乘车的时间.把表格补充完整为s V t乘船X24X 24乘车(x+40) 40 x+40 40根据题意,乘船比乘车要多用3小时,所以可列方程为召-3=呼・24 40故选C.试题难度:三颗星知识点:一元一次方程的应用一一行程问题3.小明家离学校1200米,其中有一段上坡路,另一段为下坡路.他去学校共用了16分钟,假设小明上坡路的平均速度为3千米/时,下坡路的平均速度为5千米/时.若设小明上坡用了xs V t上坡 3下坡 5A 3X +5(16-X)=1200B 3x4-5(16-x) = 1.23.上+ )4 = 1 200 3•兰+ 5・J = 1.2 C 60 60 D.60 60答案:D解题思路:根据题意,下坡用了(16-x)分钟,由尸诃知,上坡的路程为3--km,下坡的路程为5-l^km,60 60把表格补充完整为S V t上坡3上60 3X60下坡 5 16-兀60 516—x60根据总路程为「2千米,所以可列方程为垢+ 5.罟“2. 故选D.试题难度:三颗星知识点:一元一次方程的应用一一行程问题4.甲、乙两人从A地到B地,同时出发,甲比乙每小时多走1千米,若甲每小时走10千米, 结果甲比乙早到半小时,求A, B之间的距离.设A, B:H千米)y(千米小时)讣时)甲X10 乙XX X1X+ — =2B. 10 X 1A.io _10-1 10 + 1 2X X 1 X X,1 C.W_ 10-1 2『0一104-1 ~r —2 答案:C 解题思路:因为甲比乙每小时多走1千米,甲的速度为10千米小时, 所以乙的速度为(10-1)千米小时.再根据r = 2表达甲和乙的时间.V把表格补充完整为H千米)诃千米小时)X小时)甲X10X 10乙X10-1X 10-1画线段图如下:三A乙根据甲比乙早到半小时,说明甲的时间比乙的时间少半小时, 即甲的时间等于乙的时间减去半小时,因此可列方程为2 =亠-2・10 10-1 2故选C.试题难度:三颗星知识点:一元一次方程应用题5.A, B两地相距64千米,甲从B地出发,每小吋行14千米,乙从A地出发,每小吋行18 千米.若甲在前、乙在后,两人同时同向而行,则经过多长时间乙超过甲10千米?设经过xH千米)M千米外时)K小时)甲14乙18A 18x-14x = 64B 18x-14x = 10 c 14X + 64_18X = 1O D 18x-64-14x = 10答案:D解题思路: 因为两人同时出发,到相遇时时间相同,均为X小时. 再根据尸讥表达甲和乙的路程.把表格补充完整为3(千米}V(千米小时)氏小吋)甲14.Y 14 X乙18.v 1S X画线段图如下,14x1S.Y根据题意画图分析,乙超过甲10千米时,乙的路程比甲的路程多(64亠10)千米, 所以可列方程为18x-14x = 64+10,即18x-64-14x=10. 注意:甲是从B地岀发,乙是从月地岀发的.故选D.试题难度:三颗星知识点:一元一次方程应用题64。
人教版七年级数期末复习(一元一次方程的应用)教案教学设计导学案课时作业同步练习试卷含答案解析2021

一元一次方程的应用【目标导航】1.通过利润利率问题、行程问题等实际问题的分析,使学生掌握如何用方程来解决一些生活中的实际问题;2.引导学生积极探索思考,培养学生分析问题和用方程解决实际问题的能力;3.让学生在问题情境中感受数学的应用价值,从而产生对数学学习的浓厚兴趣.【要点梳理】列一元一次方程解应用题的一般步骤 1.审题;2.根据题意恰当的设出未知数;3.分析问题,找出等量关系并列出方程;4.求出所列方程的解;5.检验解的合理性;6.做出答案.【应用举例】一、和差倍分问题:父亲今年32岁,儿子今年8岁,几年后父亲的年龄是儿子年龄的3倍? 答案:解:设x 年后父亲的年龄是儿子年龄的3倍 32+x=3(8+x),解得:x=4. 二、数字问题:有一个两位数,它的十位上的数字比个位上的数字大5,并且这个两位数比它的两个数字之和的7倍还要大3,求这个两位数. 答案:解:设个位数为x,十位数为(x+5) 10(x+5)+x=7(x+x+5)+3, x=4, 这个两位数是:94 三、等积问题:一个长为20m ,宽为15m ,高为5m 的长方体盒子盛满水倒进棱长为15m 的正方体盒子,求水的高度. 答案:解:设水的高度是:xm. 151520155x ⨯⨯=⨯⨯203x =答:水高203m. 四、行程问题 1.(2011广西崇左)元代朱世杰所著《算学启蒙》里有这样一道题:“良马日行两百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”,请你回答:良马___________天可以追上驽马. 答案:20.解:设良马x 天可以追上驽马,根据题意,得240x =150(12+x ).解得x =20.所以良马20天可以追上驽马.2.甲、乙两人骑自行车同时从相距65km 的两地同时出发,已知甲比乙每小时多骑2.5km , (1)若两人相向而行,2小时相遇,求乙的速度?(2)若两人同向而行,甲经过几小时追上乙? 答案: 解:(1)设:两人相向而行乙的速度每小时xkm. 2(x+x+2.5)=65, x=30答:乙的速度每小时30 km 。
2019秋浙教版数学七年级上册同步测试试题:5.4 一元一次方程的应用

5.4 一元一次方程的应用第1课时和差倍分、行程和日历等问题知识点1.和差倍分1.甲有图书60册,乙有图书36册,若要使甲、乙两人的图书一样多,则甲应给乙图书(B)A.11本B.12本C.13本D.14本【解析】设甲应给乙x本图书,由题意,得60-x=36+x,解得x=12,即甲应给乙图书12本.2.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,则中型汽车有(C)A.13辆B.14辆C.15辆D.16辆【解析】设该停车场内停放的中型汽车有x辆,则小型汽车有(50-x)辆.列方程,得6x+4×(50-x)=230,解得x=15,则该停车场内停放的中型汽车有15辆.3.连州某旅行社组织甲、乙两个旅游团分别到西安、北京旅游,已知这两个旅游团共有55人,甲旅游团的人数比乙旅游团的人数的2倍少5人,问:(1)若设乙旅游团的人数为x,请用含x的代数式表示甲旅游团的人数;(2)甲、乙两个旅游团各有多少人?解:(1)甲旅游团有(2x-5)人;(2)由题意,得2x-5+x=55,解得x=20,∴2x-5=35(人).答:甲旅游团有35人,乙旅游团有20人.知识点2.行程问题4.两地相距600 km,甲、乙两车分别从两地同时出发相向而行,甲车比乙车每小时多走10 km,4 h后两车相遇,则乙车的速度是(A)A.70 km/h B.75 km/hC.80 km/h D.85 km/h【解析】设乙车的速度为x km/h,则甲车的速度为(x+10) km/h,根据题意,得4(x+x+10)=600,解得x=70.5.一列匀速前进的火车,从它进入320 m长的隧道到完全通过隧道共用了18 s,隧道顶部一盏固定的小灯灯光在火车上照了10 s,则这列火车的长为(B)A.190 m B.400 mC.380 m D.240 m【解析】设这列火车的长为x m,根据题意得320+x18=x10,解得x=400,即这列火车长为400 m.6. 为了参加2019年杭州马拉松比赛,爸爸与小明在足球场进行耐力训练,他们在400 m 的环形跑道上同一起点沿同一方向同时出发进行绕圈跑,爸爸跑完一圈时,小明才跑完半圈,4 min时爸爸第一次追上小明,请问:(1)小明与爸爸的速度各是多少?(2)再过多少分钟后,爸爸在第二次追上小明前两人相距50 m?解:(1)设小明的速度为x m/min,则爸爸的速度为2x m/min,根据题意,得4(2x-x)=400,解得x=100,则2x=200.答:小明的速度为100 m/min,爸爸的速度为200 m/min;(2)设再经过y分钟后,爸爸在第二次追上小明前两人相距50 m,①爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多跑了50 m,根据题意,得200y-100y=50,解得y=1 2;②爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多跑了350 m,根据题意,得200y-100y=350,解得y=72.答:再过12或72分钟后,爸爸在第二次追上小明前两人相距50 m.知识点3.日历问题7.[2018秋·丰台区期末]如图1,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,这7个数的和不可能的是(C)图1A.63 B.70C.96 D.105【解析】设“H”型框中的正中间的数为x,则其他6个数分别为x-8,x-6,x-1,x +1,x+6,x+8,这7个数之和为x-8+x-6+x-1+x+1+x+x+6+x+8=7x.由题意得A.7x=63,解得x=9,能求得这7个数;B.7x=70,解得x=10,能求得这7个数;C.7x=96,解得x=967,不能求得这7个数;D.7x=105,解得x=15,能求得这7个数.【易错点】行程问题中忽视两种情形需要分类讨论.8.A,B两地相距900 km,甲、乙两车分别从A,B两地同时出发,相向而行,已知甲车的速度为110 km/h,乙车的速度为90 km/h,则当两车相距100 km时,甲车行驶的时间是(D)A.4 h B.4.5 hC.5 h D.4 h或5 h【解析】设当两车相距100 km时,甲车行驶的时间为x h,根据题意,得900-(110+90)x=100或(110+90)x-900=100,解得x=4或x=5.第2课时图形的面积、体积变形等问题知识点1.图形的面积1.用两根长12 cm的铁丝分别围成正方形和长与宽之比为2∶1的长方形,则长方形和正方形的面积依次为(B)A.9 cm2和8 cm2B.8 cm2和9 cm2C.32 cm2和36 cm2D.36 cm2和32 cm2【解析】∵用长12 cm的铁丝围成正方形,∴正方形的边长为3 cm,故正方形面积为9 cm2,∵用长12 cm的铁丝围成长与宽之比为2∶1的长方形,∴设宽为x cm,则长为2x cm,故2(2x+x)=12,解得x=2,则长为4 cm,宽为2 cm,故长方形面积为8 cm2.2.两个正方形,大正方形的边长比小正方形的边长长3 cm,大正方形的周长是小正方形周长的2倍,则这两个正方形的面积分别是(C)A.4 cm2和1 cm2B.16 cm2和1 cm2C.36 cm2和9 cm2D.8 cm2和1 cm2【解析】设小正方形的边长为x cm,则大正方形的边长为(x+3)cm,由题意,得2×4x =4(x +3),解得x =3,即小正方形的边长为3 cm ,大正方形的边长为6 cm ,故小正方形的面积为9 cm 2,大正方形的面积为36 cm 2.3.如图1所示,宽80 cm 的长方形图形由8个完全相同的小长方形组成,求每一个小长方形的长和宽.图1解:设小长方形的宽为x cm ,则长为(80-x )cm ,依题意,有2(80-x )=3x +80-x ,解得x =20,∴长为60 cm.答:小长方形的长为60 cm ,宽为20 cm.知识点2.等积变形4.圆柱A 的底面直径为40 mm ,圆柱B 的底面直径为30 mm ,高为60 mm ,已知圆柱B 的体积是圆柱A 的体积的3倍,则圆柱A 的高为( B )A .45 mmB.454 mm C .90 mm D .20 mm【解析】 设圆柱A 的高为x mm ,由题意,得π×⎝ ⎛⎭⎪⎫4022·x ×3=π×⎝ ⎛⎭⎪⎫3022×60,解得x =454.5.把直径6 cm ,长16 cm 的圆钢锻造成半径为4 cm 的圆钢,锻造后的圆钢的长为__9__cm.【解析】 设锻造后的圆钢的长为x cm ,则V =πr 2h =π×(6÷2)2×16=π×42·x ,解得x =9.故锻造后的圆钢的长为9 cm.6.把一个长、宽、高分别为9 cm ,6 cm ,4 cm 的长方体铁块和一个棱长为6 cm 的正方体铁块熔化,炼成一个底面直径为25 cm 的圆柱体.原长方体铁块的体积是__216__cm 3,原正方体铁块的体积是__216__cm 3,设要熔炼的圆柱体的高为x cm ,则圆柱体的体积是__432__cm 3,因此可列方程为__π×⎝ ⎛⎭⎪⎫2522x =432__. 【解析】 根据题意,得原长方体铁块的体积是9×6×4=216 cm 3;原正方体铁块的体积是63=216 cm 3;则圆柱体的体积是216+216=432 cm 3;可列方程为π×⎝ ⎛⎭⎪⎫2522x =432. 7.如图2所示,一个长方体容器里装满了果汁,长方体的长为12 cm ,宽为8 cm ,高为24 cm ,用果汁将旁边的圆柱体玻璃杯倒满.已知杯子的内径为6 cm ,高为18 cm ,这时长方体容器内的果汁高度是多少?(π取3.14,结果精确到0.01 cm)图2解:圆柱的体积为π×⎝ ⎛⎭⎪⎫622×18=162π≈508.68 cm 3, 设长方体内果汁的高度为x ,则12×8×x =12×8×24-508.68,解得x ≈18.70.答:这时长方体容器内的果汁高度是18.70 cm.8.在一个底面直径为5 cm ,高为18 cm 的圆柱形杯内装满水,将杯内的水倒入一个底面直径为6 cm ,高为13 cm 的圆柱形瓶内,问能否完全装下?若装不下,那么杯内的水还有多高?若未能装满,瓶内的水面离瓶口的距离是多少?解:底面直径5 cm 、高18 cm 的圆柱形瓶内体积为π×⎝ ⎛⎭⎪⎫522×18=450π4, 底面直径6 cm 、高13 cm 的圆柱形玻璃体积为π×(6÷2)2×13=117π,∵117π>450π4,∴未能装满.设瓶内的水面离瓶口的距离是x cm ,则π×(6÷2)2×x =117π-450π4,解得x =0.5.答:未能装满,瓶内的水面离瓶口的距离是0.5 cm.【易错点】面对复杂情况列方程时读不懂题意,找不出相互关系及等量关系.9.在环行自行车赛场内,甲、乙、丙三人骑自行车进行训练,他们的速度分别是甲每分钟23圈,乙每分钟34圈,丙每分钟12圈,他们同时出发,起点如图3所示(甲从A 点出发,沿圆周逆时针运动;乙从B 点出发,沿圆周逆时针运动;丙从C 点出发,沿圆周顺时针运动),则出发后__5__min 三人第一次相遇.图3【解析】设出发后x min后三人第一次相遇,由甲和乙相遇得:23x+14+16=34x,解得x=5,此时,甲逆时针行驶了23×5=103圈,当出发5 min后,丙顺时针行驶了12×5=52圈,13+12=56,此时,甲、乙、丙恰好第一次相遇.第3课时劳动力调配、工程、销售等问题1.知识点1.劳动力调配某服装厂有工人54人,每人每天可加工上衣8件,或裤子10条,应怎样分配人数,才能使每天生产的上衣和裤子配套?设x人做上衣,则做裤子的人数为__(54-x)__人,根据题意,可列方程为__8x=10(54-x)__,解得x=__30__.2.有一个专项加工茶杯的车间,一个工人每小时平均可以加工杯身12个,或者加工杯盖15个,车间共有90人.安排加工杯身的人数为多少时,才能使生产的杯身和杯盖正好配套?直接设元法:设安排加工杯身的人数为x,则加工杯盖的为__(90-x)__人,每小时加工杯身__12x__个,杯盖__15(90-x)__个,则可列方程为__12x=15(90-x)__,解得x=__50__.间接设元法:设共加工杯身x个,共加工杯盖x个,则加工杯身的工人为__x12__人,加工杯盖的工人为__x15__人,则可列方程为__x12+x15=90__.解得x=__600__.故加工杯身的工人为__50__人.3.一个车间加工轴杆和轴承,每人每天平均可以加工轴杆12根或者轴承16个,1根轴杆与2个轴承为一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?解:设x个人加工轴杆,则(90-x)个人加工轴承,根据题意,得12x×2=16(90-x),去括号,得24x =1 440-16x ,移项合并,得40x =1 440,解得x =36.则调配36个人加工轴杆,54个人加工轴承,才能使每天生产的轴承和轴杆正好配套. 知识点2.工程问题4.某项工作甲单独做4天完成,乙单独做6天完成,若甲先做一天,然后甲、乙共同完成此项工作,设甲一共做了x 天,所列方程为( C )A.x +14+x 6=1B.x 4+x +16=1C.x 4+x -16=1D.x 4+14+x +16=15.一项工程,甲队单独完成需要20天,乙队单独完成需要30天,如果先由甲队单独做5天,则剩下部分由甲、乙两队合作完成还需要的天数是( A )A .9B .10C .12D .15【解析】 设甲、乙两队合作完成还需要的天数是x ,根据题意可得120×5+⎝ ⎛⎭⎪⎫120+130x =1,解得x =9. 6.学校图书管理员整理一批图书,由一个人做要80 h 完成,现在计划由一部分人先做8 h ,再增加2人和他们一起做16 h 完成这项工作.假设这些人的工作效率相同,则应该先安排多少人工作8 h?解:设应先安排x 人工作,根据题意得8x 80+16(x +2)80=1,解得x =2. 答:应先安排2人工作.知识点3.商品销售7.小陈妈妈做儿童服装生意,在“六一”这一天上午的销售中,某规格童装以每件60元的价格卖出,盈利20%,求这种规格童装每件的进价.解:设这种规格童装每件的进价为x元,根据题意,得(1+20%)x=60,解得x=50.答:这种规格童装每件的进价为50元.【易错点】解决销售问题需要弄清利润、利润率、打折、进价、售价等之间的关系.8.互联网“微商”经营已成为大众创业新途径,某微商平台上一件物品标价为300元,实际进价为200元,若想获利20%,则这件商品的折扣应为(B)A.七折B.八折C.九折D.八五折【解析】商品利润率为20%,则利润应是200×20%=40元,则售价是200+40=240(元).设该商品销售应按x折销售,则300x=240,解得x=0.8,即八折.故选B.第4课时银行利息问题知识点1.银行利息1.小明将前年春节所得的压岁钱买了一个某银行的两年期的理财产品,该理财产品的年回报率为4.5%,银行告知小明今年春节他将得到利息288元,则小明前年春节的压岁钱为(B)A.6 400元B.3 200元C.2 560元D.1 600元【解析】设本金是x元,由题意,得4.5%x×2=288,解得x=3 200,即小明前年春节的压岁钱为3 200元.2.某人存入5 000元参加三年期储蓄(免征利息税),到期后本息和共得5 417元,那么这种储蓄的年利率为(C)A.2.58% B.2.68%C.2.78% D.2.88%【解析】设这种储蓄的年利率为x,由题意,得5 000+5 000×3x=5 417,解得x=2.78%.3.小明的爸爸买了利率为3.96%的3年期债券,到期后可获得本息共1 678.2元,则小明的爸爸买债券花了(A)A.1 500元B.1 600元C.1 700元D.1 800元4.国家规定存款利息的纳税办法:利息税=利息×20%.银行一年定期储蓄的年利率为2.25%,今年小刚取出一年到期的本金及利息时,交了18元的利息税,则小刚一年前存入银行的钱为(C)A.2 400元B.1 800元C.4 000元D.4 400元【解析】设小刚一年前存入银行的钱为x元,根据题意,得2.25%×20%x=18,解得x=4 000.故小刚一年前存入银行的钱为4 000元.5.某人以两种形式共储蓄了800元,一种储蓄的年利率为10%,另一种储蓄的年利率为11%,一年到期去提取,他共得到利息85元5角,问两种储蓄他各存了多少钱?解:设他第一种存了x元,则第二种存了(800-x)元,则有10%x+11%(800-x)=85.5,解得x=250,800-x=550(元),答:第一种存了250元,第二种存了550元.6.小刚的妈妈有一笔一年期的定期储蓄,年利率为2.25%,利息税率为20%,到期纳税后的利息为180元,小刚的妈妈存入的本金是多少元?解:设小刚的妈妈存入的本金是x元,由题意,得2.25%x(1-20%)=180,解得x=10 000.答:小刚的妈妈存入的本金是10 000元.知识点2.其他问题7.[2017·道里区校级模拟]七年级(2)班有46人报名参加文学社或书画社.已知参加文学社的人数比参加书画社的人数多10人,两社都参加的有20人,则参加书画社的有__28__人.【解析】设参加书画社的有x人,根据题意,得(46+20-x)-x=10,解得x=28.8.七年级二班有45人,已知参加文学社的人数比参加书画社的人数多5人,两个社都参加的有20人,两个社都不参加的有10人,问只参加书画社的有多少人?解:设参加书画社的有x人,根据题意,得(45+20-10-x)-x=5,解得x=25,25-20=5.答:只参加书画社的有5人.【易错点】没有弄清“本金、利率、存期、利息、利息税、本息和”之间的关系导致的错误.9.小彬将一笔压岁钱按一年定期储蓄存入“少儿银行”,年利率为10%,到期后将本金和利息取出,并将其中的50元捐给“希望工程”,剩余的又全部按一年定期存入,这时存款的年利率已下调到上次存款时年利率的一半,这样到期后可得本金和利息共63元.你能算出小彬的这笔压岁钱是多少吗?(“少儿银行”不缴纳利息税)解:设这笔压岁钱为x元,依据题意得出[x(1+10%)-50]×(1+5%)=63,解得x=100.答:小彬的这笔压岁钱是100元.。
一元一次方程的应用题100道

一元一次方程的应用题100道一元一次方程的应用题用方程解决问题(1)---------比例问题与日历问题1、甲、乙、丙三种货物共有167吨,甲种货物比乙种货物的2倍少5吨,丙种货物比甲种货物的多3吨,求甲、乙、丙三种货物各多少吨?2、有蔬菜地975公顷,种植青菜、西红柿和芹菜,其中青菜和西红柿的面积比是3∶2,种西红柿和芹菜的面积比是5∶7,三种蔬菜各种的面积是多少公顷?3、甲、乙、丙三村集资140万元办学,经协商甲、乙、丙三村的投资之比是5:2:3。
问他们应各投资多少万元?4、建筑工人在施工中,使用一中混凝土,是由水、水泥、黄沙、碎石搅拌而成的,这四种原料的重量的比是0.7:1:2:4.7,搅拌这种混凝土2100千克,分别需要水、水泥、黄沙、碎石多少千克?5、小名出去旅游四天,已知四天日期之和为65,求这四天分别是哪几日?6、XXX在日历上任意找出一个数,发现它连同上、下、左、右的共5个数的和为85,请求出XXX找的数。
7日历上同一竖列上3日,日期之和为75,第一个日期是几号?用方程解决问题(2)---------调配问题1、甲车队有15辆汽车,乙车队有28辆汽车,现调来10辆汽车分给两个车队,使甲车队车数比乙车队车数的一半多2辆,应分配到甲乙两车队各多少辆车?2、某班女生人数比男生的还少2人,如果女生增加3人,男生减少3人,那么女生人数等于男生人数的,那问男、女生各多少人?3、某车间有工人85人,平均每人天天可加工大齿轮16个或小齿轮10人,又知二个大齿轮和三个小齿轮配套一套,问应若何放置劳力使生产的产物刚好成套?4、某同学做数学题,如果每小时做5题,就可以在预定时间完成,当他做完10题后,解题效率提高了60%,因而不但提前3小时完成,而还多做了6道,问原计划做几题?几小时完成?5、XXX在生果店花18元,买了XXX和橘子共6千克,XXX每千克3.2元,橘子每千克2.6元,XXX买了苹果和橘子各多少千克?6、甲仓库有煤200吨,乙仓库有煤80吨,假如甲仓库天天运出15吨,乙仓库天天运进25吨,问多少天后两仓库存煤相称?7、两个水池共贮有水50吨,甲池用去水5吨,乙池注进水8吨后,这时甲池的水比乙池的水少3吨,甲、乙水池原来各有水多少吨?8、某队有55人,每人每天平均挖土2.5方或运土3方,为合理安排劳力,使挖出的土及时运走,应如何分配挖土和运土人数?用方程解决问题(3)---------盈亏问题事情量与折扣问题1.用化肥多少千克给一块麦田施肥,每亩用6千克,还差17千克;每亩用5千克,还多3千克,这块麦田有多少亩?2.毕业生在礼堂入座,1条长凳坐3人,有25人坐不下;1条长凳坐4人,正好空出4条长凳,则共有多少名毕业生?长凳有多少条?3.将一批货色装入一批箱子中,假如每箱装10件,还剩下6件;假如每箱装13件,那末有一只箱子只装1件,这批货色和箱子各有多少?4.有一次数学比赛共20题,划定做对一题得5分,做错或不做的题每题扣2分,XXX得了86分,问XXX 对了几题?5.修一条路,A队单独修完要20天,B队单独修完要12天。
一元一次方程的应用(配套问题)省公开课一等奖全国示范课微课金奖PPT课件

5x=3(48-x),
解得x=18,48-x=30
所以天天安排3 用白铁皮做罐头盒,每张铁皮可制盒 身25个,或制盒底40个,一个盒身与两个 盒底配成一套.现在有36张白铁皮,用多少 张制盒身,多少张制盒底,可使盒身与盒 底恰好配套?。
第9页
分析:本题配套关系是:盒身数:盒 底数=1:2. 解:设用x张白铁皮制盒身,(36-x)张 制盒底,则共制盒身25x个,共制盒底 40(36-x)个,依据题意,得 2×25x=40(36-x) 解得x=16,36-x=20 所以用16张制盒身,20张制盒底恰好 使盒身与盒底配套.
解得x=3,5-x=2 所以用3立方米做桌面,2立方米做桌腿, 恰能配成方桌.共可做150张方桌.
第12页
请你来试一试: 1.某车间有28名工人,生产一个螺栓和螺 帽,平均每人每小时能生产螺栓12个或螺 帽18个,两个螺栓要配三个螺帽,应分配多 少人生产螺栓,多少人生产螺帽,才能使生 产螺栓和螺帽刚好配套? 2.某服装厂要生产某种型号学生校服,已 知3m长某种布料可做上衣2件或裤子3条, 一件上衣和一条裤子为一套,库内存这种 布料600m,应怎样分配布料做上衣和做 裤子才能恰好配套?
第10页
例4一张方桌由1个桌面、4条桌腿组成, 假如1立方米木料能够做方桌桌面50个或 做桌腿300条,现有5立方米木料,那么 用多少立方米木料做桌面、多少立方米 木料做桌腿,做出桌面和桌腿,恰好配 成方桌?能配成多少方桌?
第11页
分析:本题配套关系是:桌面:桌腿=1: 4,即一个桌面需要4个桌腿. 解:设用x立方米做桌面,(5-x)立方米做 桌腿,则可做桌面50x个,做桌腿300(5x)条.依据题意,得 4×50x=300(5-x),
第13页
一元一次方程应用题专项练习

一元一次方程应用题专项练习(一)配套问题1.有某种三色冰淇淋50克,咖啡色、红色和白色配料的比是2:3:5,这种三色冰淇淋中咖啡色、红色和白色配料分别是多少克?2、某粮库装粮食,第一个仓库是第二个仓库存粮的3倍、如果从第一个仓库中取出20吨放入第二个仓库中,第个仓库中的粮食是第一个中的二。
向每个仓库各有多少粮食3.食品安全是关乎民生的问题,在食品中添加过量的添加剂对入体有害,但适量的添加剂对人体无害且有利于食品的储存和运输,某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?4、某车间有16名工人,每人每天可加工甲柝中零件5个或乙种零件4个.在这6名工人中,一部分人加工甲中零件,其余的加工乙种零件.已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.若此车间一共获利1440元,求这一天有几个工人加工甲种零件.5、某家具厂有60名工人,加工某种由一个桌面和四条桌腿的桌子,工人每天美人可以加工3个桌面或6个桌腿。
怎么分配加工桌面和桌腿的人数,オ能使每天生产的桌面和桌腿配套?(二)工程类问题1.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做。
则甲、乙一起做还需多少小时才能完成工作?2、一件工程,甲独做需15天完成、乙独倣需12天完成、现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成、问乙还要几天才能完成全部工程?3.一个替水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单独开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?4、一项工程甲单独做需要10天,乙需要12天,丙单独倣需要15天,甲、丙先做3天后,甲因事离去,乙参与工作,向还需几天完成?5、某中学修整草场,如果让初一学生单独工作,需要7.5小时完成;如果让初二学生单独做,需要5小时完成.如果让初一、初二学生一起工作1小时,再由初二学生单独完成剩余部分,共需多少时间完成?7、一批文稿,如果甲抄30小时完成,乙抄20小时完成,现由甲抄3小时后该为乙抄余下部分,问乙尚需抄多少小时?(三)利润类问题1.某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是多少2.某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在六一儿童节举行文具优惠售卖活动,铅笔按原价打8折出售圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求两种笔各卖了多少支?3、某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%(1)求这款空调每台的进价:(利润率=售价一进价)(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?4、现在对某商品降价百分之十促销,为了使销售总金额不变,销售量要比按原价销售时增加百分之几?5、工艺商场安标价销售某种工艺品时,每件可获利45元按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等,该工艺品每件的进价、标价分别是多少元?6、两件商品都卖120元,其中一件赢利25%,另一件亏本20%,则两件商品卖出后总共是盈利还是亏损?盈利或亏损多少?7.某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是多少?(一)行程问题1甲、乙两人在400米长的环形跑道上跑步,甲分钟跑240米,乙每分钟跑200米。
精品 2014年一元一次方程应用题 行程问题 同步讲义+同步练习
第 7 页 共 8 页
七年级数学同步讲义
(3) 3( x 2) 1 4 x (2 x 1)
(4)
x4 x 2 (x 5) 5 2
13.甲、乙两站相距 245km,一列慢车由甲站开出,速度为 50km/h;同时,一列快车由乙站开出,速度 为 70km/h,两车同向而行,快车在慢车的后面,经过几小时快车可以追上慢车?
第 6 页 共 8 页
七年级数学同步讲义
一元一次方程应用题测试题 满分:100 分 时间:20 分钟 姓名: B.由 3x-2 =2x + 1 得 x= 3 D.由-2x= 3 得 x= - 得分: 1.下列变形错误的是( ) A.由 x + 7= 5 得 x+7-7 = 5-7 ; C.由 4-3x = 4x-3 得 4+3 = 4x+3x 2.下列解方程去分母正确的是( A.由 )
第 8 页 共 8 页
(2)当 x=-3 时,代数式 (2 m) x 2m 3 的值是-7,当 x 为何值时,这个代数式的值是 1?
5.如果方程
1 x4 x2 的解与方程 4 x (3a 1) 6 x 2a 1 的解相同,求式子 a 的值 . 8 a 3 2
第 3 页 共 8 页
例 5.一只轮船,在甲、乙两地之间航行,顺水用 8 小时,逆水比顺水多 30 分钟,一直轮船在静水中速 度为每小时 26km,求水流的速度?
例 6.已知有 A、B、C 三个码头,BC 相距 24km,某船从 B 顺水而下到达 A 后,立即逆水而上到达 C.共用 8 小时,已知水流速度 5km/h,船在静水中的速度为 20km/h,求 A、B 之间的距离。
1 6
5.6-应用一元一次方程---追赶小明--同步练习题-含答案
北师大版数学七年级上册第五章一元一次方程 5.6 应用一元一次方程---追赶小明同步练习题1.一辆汽车以每小时80千米的速度匀速行驶,则该汽车行驶x小时,所走的路程为______千米;若该汽车行驶了s千米,则该汽车行驶的时间是_____小时.2.甲、乙二人骑车从A,B两地同时出发相向而行,x小时后两人相遇.已知甲每小时行18千米,乙每小时行20千米,则A,B两地之间的距离可表示为___________千米.3.小明和小刚家距离900 m,两人同时从家出发相向而行,5 min后两人相遇,小刚每分钟走80 m,小明每分钟走()A.80 m B.90 m C.100 m D.110 m4.甲、乙二人练习赛跑,甲每秒跑7米,乙每秒跑6.5米.乙先跑5米后,甲开始跑.设x秒后甲追上乙,则下列方程中不正确的是()A.7x=6.5x+5 B.7x-5=6.5 C.(7-6.5)x=5 D.6.5x=7x-55.A,B两地相距480千米,一列慢车从A地开出,每小时行驶70千米,一列快车从B地开出,每小时行驶90千米,根据上述条件回答:(1)两车同时开出,相向而行,x小时相遇,则由条件列出方程为________________.(2)两车同时开出,相背而行,x小时后两车相距620千米,由条件列出方程为____________________.(3)慢车先开1小时,同向而行,快车开出x小时后追上慢车,则由条件列出方程为_____________________.6.甲、乙两地间的铁路经过技术改造后,列车在两地间的运行速度从100 km/h提高到120 km/h,运行时间缩短了2 h.设甲、乙两地间的路程为x km,可得方程________________.7.甲、乙两人骑自行车同时从相距65千米的两地相向而行,2小时后相遇.若乙每小时比甲少骑2.5千米,则乙每小时骑()A.20千米B.17.5千米C.15千米D.12.5千米8.明明与父亲早上去公园晨练,父亲从家跑步到公园需30分钟,明明只需20分钟,如果父亲比明明早出发5分钟,明明追上父亲需()A.8分钟B.9分钟C.10分钟D.11分钟9.某同学骑车从学校到家每分钟行1.5千米.某天回家时,速度提高到每分钟2千米,结果提前5分钟回到家.设原来从学校到家之间需骑x分钟,则列方程为()A.1.5x=2(x+5) B.1.5x=2(x-5) C.1.5(x+5)=2x D.1.5(x-5)=2x10.甲、乙两人练习百米赛跑,甲的速度是6.5 m/s,乙的速度是7 m/s.若乙让甲先跑1 s,则乙追上甲需()A.14 s B.13 s C.7.5 s D.6.5 s11.学校到县城有28千米,除乘公共汽车外,还需步行一段路程.公共汽车的速度为36千米/时,步行的速度为4千米/时,全程共需1小时.求步行和乘车所用时间各是多少?设步行所用时间为x小时,列方程得()A.36x+4(1-x)=28 B. 36x+41-x=28C.36(1-x)+4x=28 D.36+4=28 x12.轮船在静水中速度为每小时20 km,水流速度为每小时4 km,从甲码头顺流航行到乙码头,再返回到甲码头,共用5 h(不计停留时间),则甲、乙两码头间的距离是() A.16 km B.24 km C.32 km D.48 km13.一环形跑道长400米,小明跑步每秒行5米,爸爸骑自行车每秒行15米,两人同时同地反向而行,经过__ __秒两人首次相遇.14.京津城际铁路开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试运行时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶了40千米,那么这次试车时由北京到天津的平均速度是多少?15.小明家离学校2.7千米,一天早上上学,小明已走28分钟时,妈妈发现小明上学忘带数学书了,这时爸爸立即骑自行车带上数学书去追赶小明.已知小明上学每分钟走60米,爸爸骑车每分钟走200米,请问小明爸爸能否赶在小明到学校前把书送到小明手上?16.王力骑自行车从A地到B地,陈平骑自行车从B地到A地,两人都沿同一公路匀速前进,已知两人在上午8时同时出发,到上午10时,两人还相距36 km,到中午12时,两人又相距36 km.求A,B两地间的路程.17.已知小明骑车和步行的速度分别为240米/分,80米/分,小红每次从家步行到学校的时间相同.请你根据图中小红和小明的对话内容,求小明从家到学校的路程和小红从家步行到学校的时间.答案:1. 50s 802. (18+20)x3. C4. B5. (1) 70x+90x=480 (2) 70x+90x=620-480(2) 90x-70x=70+4806.x100-x120=27. C8. C9. B10. B11. C12. D13. 2014. 解:设试车时由北京到天津的平均速度为x千米/时.依题意得30+660x=3060(x+40),x=20015. 解:设小明爸爸追上小明用了x分钟.依题意得(200-60)x=28×60.x=12,因为2.7千米=2700米,所以2700÷60=45(分钟),因为28+12=40<45.所以小明爸爸能赶在小明到达学校前把书送到小明手中16. 解:设A,B两地间的路程为x km,依题意得:x-3610-8=x+3612-8,解得:x=10817. 解:设小明从家到学校的路程为x米.依题意得x240+4=x80-2.解得x=720,720240+4=7(分钟).所以小红从家步行到学校的时间是7分钟。
一元一次方程的实际应用题(含详细答案)
一元一次方程的实际应用题题型一:利率问题利率问题利息=本金×利率×期数本利和=本金十利息=本金×(1+利率×期数)利息税=利息×税率税后利息=利息一利息税=利息×(1-税率)税后本利和=本金+税后利息【总结】若利率是年利率,期数以“年”为单位计数,若是月利率,则期数以“月”为单位计数,解题时要注意.【例1】某人把若干元按三年期的定期储蓄存入银行,假设年利率为3. 69%,到期支取时扣除所得税实得利息2 103.3元,求存入银行的本金.(利息税为5%)【答案】设存入银行的本金为x元,根据题意,得()()%%3 3.69152103.3x⨯⨯⨯-=x⨯=0.1051652103.3x=,20000因此,存入银行的本金是20000元.【总结】利息=本金×利率×期数×利息税题型二:折扣问题利润额=成本价×利润率售价=成本价+利润额新售价=原售价×折扣【例2】小丽和小明相约去书城买书,请你根据他们的对话内容(如图),求出小明上次所买书籍的原价.--图641【分析】设小明上次购买书籍的原价是x元,由题意,得0.82012+=-,x xx=.解得160因此,小明上次所买书籍的原价是160元,【答案】160元.1:一件衣服按标价的八折出售,获得利润18元,占标价的10%,问该衣服的买入价?分析:本金:标价利率:-20%利息:成交价-标价=买入价+利润-标价解:设该衣服的买入价为x元x+18-18/10%=18/10%×(80%-1)当然,这道题这样解是一种方法,还可以按照我们常规的算术方法解来,倒也简单,因此,列方程解应用题是针对过程清楚的问题比较简单方便。
2. 一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?[分析]探究题目中隐含的条件是关键,可直接设出成本为X元进价折扣率标价优惠价利润X元8折(1+40%)X元80%(1+40%)X 15元等量关系:(利润=折扣后价格—进价)折扣后价格-进价=15解:设进价为X元,80%X(1+40%)—X=15,X=125答:进价是125元。
人教版七年级上册同步训练:第三章《一元一次方程》实际应用填空题提优一
同步训练:第三章《一元一次方程》实际应用填空题提优一1.某商场新进一批同型号的电脑,按进价提高40%标价(就是价格牌上标出的价格),此商场为了促销,又对该电脑打8折销售(8折就是实际售价为标价的80%),每台电脑仍可盈利420元,那么该型号电脑每台进价为元.2.在日历中圈出一竖列上相邻的3个数,使它们的和为42,则所圈数中最小的是.3.(按非课改要求命制)某服装店“六一”搞促销,店主将进价120元/件的童装按标价打八折出售,每价仍有40元利润,请问每件童装的标价是元.4.某商场购进一批运动服,每件售价120元,可获利20%,这种运动服每件的进价是元.5.某篮球运动员在一次篮球比赛中20投16中得30分,其中3分球2个,则他投中个2分球和个罚球(罚球命中1次得1分).6.某电脑公司在5月1日将500台电脑投放市场,经市场调研发现,该批电脑每隔10天平均日销售量减少2台,现准备用38天销售完该批电脑,则预计该公司5月1日至5月10日的平均日销售量是台.7.某种钢笔标价a元,若购20支及以上可按8折付款,甲买20支这种笔比乙买8支多用40元,则a=.8.一件运动衣按原价的八折出售时,售价是40元,则原价为元.9.民意商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,此商品进价为1000元,则商品的原价是元.10.杏花村现有手机188部,比2004年底的3倍还多17部,则该村2004年底有手机部.11.一家书店所有图书按八折销售,小华星期天在该书店买了几本书,共节省了8元,那么这几本书按原价应付元.12.销售某件商品可获利30元,若打9折每件商品所获利润比原来减少了10元,则该商品的进价是元.13.如图,是2005年6月份的日历,像图中那样竖着圈住三个数.如果圈住的三个数的和为36,则这三个数中最大的数为.14.某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券.(奖券购物不再享受优惠)消费金额x的范围(元)200≤x<400 400≤x<500 500≤x<700 …获得奖券的金额(元)30 60 100 …根据上述促销方法,顾客在该商场购物可获得双重优惠,如果胡老师在该商场购标价450元的商品,他获得的优惠额为元.15.下图是2004年6月份的日历,如图中那样,用一个矩形在日历中任意框出4个数,请用一个等式表示a、b、c、d之间的关系:.日一二三四五六1 2 3 4 56 7 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 2627 28 29 3016.汉江上游的某一牧场有162公顷,为了改善流域环境,把一部分牧场改为林场,改造后牧场面积是林场面积的20%,则退牧还林后,林场面积为公顷.17.某商品标价为800元,现按九折出售,仍可获利20%,则这种商品的进价为元.18.为了能有效地使用电力资源,我市供电部门最近进行居民峰谷用电试点,每天8:00至21:00用电每千瓦时0.55元(“峰电”价),21:00至次日8:00每千瓦时0.30元(“谷电”价).王老师家使用“峰谷”电后,五月份用电量为300千瓦时,付电费115元,则王老师家该月使用“峰电”千瓦时.19.某种货物的零售价为每件110元,若按八折(零售价的80%)出售,仍可获利10%,则该货物每件的进价为元.20.某商品的标价是1100元,打八折(按标价的80%)出售,仍可获利10%,则此商品的进价是元.21.用“84”消毒液配制药液,对白色衣物进行消毒,要求按1:200的比例进行稀释,现要配制此种药液4020克,则需“84”消毒液克.22.厦门日报1月24日报道了2003年非师范类大中专毕业生和研究生(厦门生源)的就业形势,其中关于研究生学历的工作岗位是供不应求.具体的情况是:实际需要研究生的人数比实际毕业的研究生的人数多1124人,它们之间的比是309:28.则实际需要研究生人,实际毕业的研究生人.23.下面是甲商场电脑产品的进货单,其中进价一栏被墨迹污染,读了进货单后,请你求出这台电脑的进价是元.24.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件元.25.某市开展“保护母亲河”植树造林活动.该市金桥村有1000亩荒山绿化率达80%,300亩良田视为已绿化,河坡地植树绿化率已达20%,目前金桥村所有土地的绿化率为60%,则河坡地有亩.参考答案1.解:设该型号电脑每台进价为x元,根据题意列方程得:(x+40%x)×0.8﹣x=420,解得:x=3500∴该型号电脑每台进价为3500元.2.解:设中间的数是x.则x+x﹣7+x+7=42,解得:x=14则最小的数是x﹣7=7故填:7.3.解:设童装的标价为x元.根据售价﹣进价=利润得:0.8x﹣120=40解得:x=200∴每件童装的标价是200元.4.解:设运动服每件的进价是x元,利润可表示为120﹣x,则120﹣x=20%x,解得x=100.故填100.5.解:设乔丹两分球投中x球2分球,罚球投中y球,根据题意得:,解得:.故答案为:10,4.6.解:设预计该公司5月1日至5月10日的平均日销售量是x台,根据题意得:10x+10(x﹣2)+10(x﹣4)+8(x﹣6)=500解得x=16,故填16.7.解:根据题意得:20×0.8a=8a+40,解得a=5,故填5.8.解:设原价为x元,则:x×0.8=40,解得:x=50(元)故填:50.9.解:设商品的原价是x元,则0.8x=1000(1+10%)解得x=1375则商品的原价是1375元.10.解:设该村2004年年底有手机x部,那么根据题意得:3x+17=188解得:x=57因此该村2004年底有手机57部.故填57.11.解:设原价是x元,则0.8x=x﹣8,解得:x=40.故这几本书按原价应付40元.12.解:设该商品的进价是x元,则(30+x)×0.9=30+x﹣10 解得x=70,则该商品的进价是70元.13.解:设中间一行的那个数是x,则上面的是x﹣7,下面的是x+7,根据题意得x+x﹣7+x+7=36,解得x=12,所以最大的数是19.14.解:胡老师获得的优惠额为450×(1﹣80%)+30=120(元).故答案为:120.15.解:对角线来看:a+d=b+c(答案不唯一).故答案为:a+d=b+c.16.解:设林场面积为x公顷.由题意得:162﹣x=20%x解得:x=135.∴退牧还林后,林场面积为135公顷.17.解:设进价为x元,则:x+x×20%=800×0.9,解得:x=600.故填600.18.解:设用峰电x千瓦时,则有0.55x+0.30×(300﹣x)=115,解得:x=100.∴王老师家该月使用“峰电”100千瓦时.19.解:设进价为x则:x×(1+10%)=110×80%解得x=80,故进价为80元.20.解:设进价为x元,那么1100×0.8=10%•x+x解得x=800.所以填800.21.解:设需“84”消毒液x克,则x:4020=1:201,解得x=20.故填20.22.解:设实际毕业的研究生人数是x人,则实际需要的研究生人数是(x+1124)人,根据题意得:(x+1124):x=309:28,解得x=112,则x+1124=1236则实际需要研究生1236人,实际毕业的研究生112人.23.解:设电脑的进价为x元,根据进货单可得:x+210=5850×0.8,解得:x=4470(元).故答案为:4470.24.解:设标价为x元,根据题意列方程:90%x﹣30=30×20%解得x=40,则标价是每件40元.25.解:由题意设河坡地有x亩,依题意得方程:1000×80%+300+x×20%=(1000+300+x)×60%,解得:x=800亩.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 20 同步课程˙一元一次方程的应用 一、如何设未知数 设未知数的方法一般来讲,有以下几种: (1)直接设未知数解应用题: 直接设未知数指题目问什么就设什么,它多适用于要求的未知数只有一个的情况; (2)间接设未知数解应用题: 设间接未知数,是指所设的不是所求的,而解得的间接未知数对确定所求的量起中介作用; (3)引入辅助未知数解应用题: 设辅助未知数,就是为了使题目中的数量关系更加明确,可以引进辅助未知数帮助建立方程.辅助未知数往往不需要求出,可以在解题时消去. 解应用题的方法多种多样,除此之外,还有运用逆推法解应用题、运用整体思想解应用题、运用图形图表法解应用题等等,单纯的背这些方法是没有意义的,关键还在于提高理解能力,大量练习,从而学会快速读懂题意,综合运用各种方法去求解问题.
二、列方程解应用题的步骤: ①审:审题,分析题中已知什么,求什么,明确各数量之间关系 ②设:设未知数(一般求什么,就设什么为x) ③找:找出能够表示应用题全部意义的一个相等关系 ④列:根据这个相等关系列出需要的代数式,进而列出方程 ⑤解:解所列出的方程,求出未知数的值 ⑥答:检验所求解是否符合题意,写出答案(包括单位名称)
一、 数字问题
数字问题是常见的数学问题。一元一次方程应用题中的数字问题多是整数,一般可设个位数字为a,十位数字为b,百位数字为c.十位数可表示为10b+a, 百位数可表示为100c+10b+a.然后抓住数字间或新数、原数之间的关系找等量关系列方程.
一元一次方程的应用(一) 同步练习 知识讲解 2 / 20 同步课程˙一元一次方程的应用 【例1】 一个三位数,三个数位上的和是17,百位上的数比十位上的数大7,个位上的数是十位上的数的3 倍。求这个数。
【例2】 一个六位数的最高位上的数字是1,如果把这个数字移到个位数的右边,那么所得的数等于原数的3倍,求原数。
【例3】 一个两位数,十位数字比个位数字的4倍多1,将这两个数字调换顺序所得的数比原数小63,求原数.
【例4】 一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得的两位数比原两位数大36,求原来的两位数.
模块二、调配(分配)与比例问题 调配与比例问题在日常生活中十分常见,比如合理安排工人生产,按比例选取工程材料,调剂人数或货物等。调配问题中关键是要认识清楚部分量、总量以及两者之间的关系。在调配问题中主要考虑“总量不变”;而在比例问题中则主要考虑总量与部分量之间的关系,或是量与量之间的比例关系。
【例5】 甲、乙两书架各有若干本书,如果从乙架拿100本放到甲架上,那么甲架上的书比乙架上所剩的书多5倍,如果从甲架上拿100本书放到乙架上,两架所有书相等。问原来每架上各有多少书?
【例6】 教室内共有灯管和吊扇总数为13个。已知每条拉线管3个灯管或2个吊扇,共有这样的拉线5条,求室内灯管有多少个? 3 / 20
同步课程˙一元一次方程的应用 【例7】 某车间22名工人参加生产一种螺母和螺丝。每人每天平均生产螺丝120个或螺母200个,一个螺丝要配两个螺母,应分配多少名工人生产螺丝,多少名工人生产螺母,才能使每天生产的产品刚好配套?
【例8】 苹果若干个分给小朋友,每人m个余14个,每人9个,则最后一人得6个。问小朋友有几人?
【例9】 出口1吨猪肉可以换5吨钢材,7吨猪肉价格与4吨砂糖的价格相等,现有288吨砂糖,把这些砂
糖出口,可换回多少吨钢材?
模块三 和差倍分问题 【例10】 玻璃缸里养了三个品种的金鱼,分别是“水泡”“朝天龙”“珍珠”.“水泡”的条数是“珍珠”的3倍;“朝天龙”的条数是“珍珠”的2倍,且“朝天龙”比“水泡”少1条,这三种金鱼各有几条呢?
【例11】 甲队有32人,乙队有28人,现从乙队抽x人到甲队,使甲队是乙队人数的2倍,依题意,列出方程为?
4 / 20
同步课程˙一元一次方程的应用 【例12】 汽车若干辆装运货物一批,若每辆汽车装3.5吨货物,这批货物就有2吨运不走;若每辆汽车装4吨货物,那么装完这批货物后,还可以装其他货物1吨,问汽车有多少辆?这批货物有多少吨?
【例13】 ⑴ 甲仓库有粮120吨.乙仓库有粮90吨.从甲仓库调运 吨到乙仓库,调剂后甲仓库存粮 是乙仓库的一半. ⑵ 甲乙两个圆柱体容器,底面积比为53∶,甲容器水深20cm,乙容器水深10cm,再往两个容 器注入同样多的水,使两个容器的水深相等,这时水深多少厘米?
【例14】 某公司有甲乙两个工程队,甲队人数比乙队人数的23多28人.现因任务需要,从乙队调走20人到甲队,这时甲队人数是乙队人数的2倍,则甲乙两队原来的人数分别是多少人?
【例15】 甲、乙、丙三条铁路共长1191千米,甲铁路长比乙铁路的2倍少189千米,乙铁路长比丙铁路少8 千米,求甲铁路的长.
【例16】 某区中学生足球联赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分,在这次足球联赛中,猛虎足球队踢平的场数是所负场数的2倍,共得17分.试问该队胜了几场?
【例17】 一次数学测验中,小明认为自己可以得满分,不料卷子发下来一看得了96分,原来是由于粗心把一个题目的答案十位与个位数字写颠倒了,结果自己的答案比正确答案大了36,而正确答案的个位数字是十位数字的2倍.正确答案是多少? 5 / 20
同步课程˙一元一次方程的应用 【例18】 初一(1)班有学生60名,其中参加数学小组的有36人,参加英语小组的人数比参加数学小组的人数少5人,并且这两个小组都不参加的人数比两个小组都参加的人数的14多2人,则同时参加这两个小组的人数是( ). A.16 B.12 C.10 D.8
【例19】 电影票有10元、15元、20元三种票价,班长用500元买了30张电影票,其中票价为20元的比票价为10元的多多少张?
【例20】 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的13,另一根露出水面的长度是它的15.两根铁棒长度之和为55cm,此时木桶中水的深度是 cm.
【例21】 牧羊人赶着一群羊寻找一个草长得茂盛的地方,一个过路人牵着一只肥羊从后面跟了上来,他对牧羊人说:“你赶的这群羊大概有100只吧!”牧羊人答道:“如果这群羊增加一倍,再加上原来这群羊的一半,又加上原来这群羊一半的一半,连你这只羊也算进去,才刚好凑满100只.”问牧羊人的这群羊共有多少只? 6 / 20
同步课程˙一元一次方程的应用 【例22】 一批树苗按下列方法分给各班:第一班取100棵和余下的110,第二班取200棵和余下的110,……最后树苗全部被取完且各班树苗数都相等.求树苗总数和班级数.
【例23】 有粗细不同的两支蜡烛,细蜡烛之长时粗蜡烛之长的2倍,细蜡烛点完需1小时,粗蜡烛点完需2小时,有一次停电,将这样的两支未使用过的蜡烛同时点燃,来电时,发现两支蜡烛所剩的长度一样,问停电的时间有多长?
【例24】 在环保竞赛中,某校代表队的平均分是88分,其中女生的平均成绩比男生高10%,而男生的人数比女生多10%.试问男、女生的平均成绩各是多少?
模块四 行程问题 行程问题中有三个基本量:路程、时间、速度。关系式为:①路程=速度×时间;②速度=;③时
间=。
可寻找的相等关系有:路程关系、时间关系、速度关系。在不同的问题中,相等关系是灵活多变的。如相遇问题中多以路程作相等关系,而对有先后顺序的问题却通常以时间作相等关系,在航行问题中很多时候还用速度作相等关系。
航行问题是行程问题中的一种特殊情况,其速度在不同的条件下会发生变化:①顺水(风)速度=静水(无风)速度+水流速度(风速);②逆水(风)速度=静水(无风)速度-水流速度(风速)。由此可得到航行问题中一个重要等量关系:顺水(风)速度-水流速度(风速)=逆水(风)速度+水流速度(风速)=静水(无风)速度。
7 / 20
同步课程˙一元一次方程的应用 【例25】 甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。 (1)慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇? (2)两车同时开出,相背而行多少小时后两车相距600公里? (3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里? (4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车? (5)慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车? 此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。故可结合图形分析。
【例26】 A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。 (1)甲、乙同时出发,背向而行,问几小时后他们相距351千米? (2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇? (3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时? (4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
追击问题 解决追击问题的一个最基本的公式:追击时间速度差追击的路程.于此相关的问题都可以应用这一公式进行解答. 【例27】 敌我两军相距32千米,敌军以每小时6千米的速度逃窜,我军同时以每小时16千米的速度追击在相距2千米的地方发生战斗,问战斗是从开始追击后几小时发生的?
