宁波三校联考高二下学期
浙江省宁波市九校高二下学期期末联考数学试卷-含答案
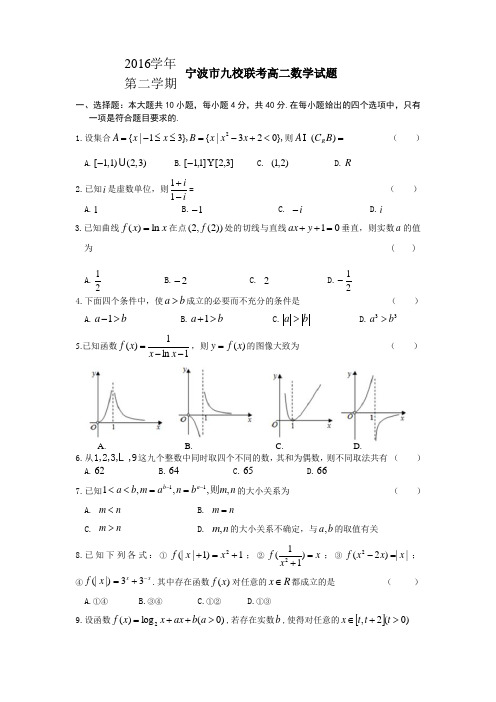
宁波市九校联考高二数学试题一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有 一项是符合题目要求的.1.设集合2{|13}{|320}A x x B x x x =-≤≤=-+<,,则=)(B C A R I( )A.[1,1)(2,3)-UB.]3,2[]1,1[Y -C. )2,1(D.R2.已知i 是虚数单位,则ii-+11= () A.1 B.1- C. i - D.i3.已知曲线x x f ln )(=在点))2(,2(f 处的切线与直线01=++y ax 垂直,则实数a 的值为 ( )A.21 B.2- C. 2 D.21-4.下面四个条件中,使a b >成立的必要而不充分的条件是 ( )A.1a b ->B.1a b +>C.a b >D.33a b > 5.已知函数1ln 1)(--=x x x f ,则)(x f y =的图像大致为 ( )A. B. C. D.6.从1,2,3,,9L 这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有 ( ) A.62 B.64 C.65 D.667.已知n m b n am b a a b ,,,,111则--==<<的大小关系为 ( )A. n m <B. n m =C. n m >D. n m ,的大小关系不确定,与b a ,的取值有关 8.已知下列各式:①1)1|(|2+=+x x f ;②x x f =+)11(2;③||)2(2x x x f =-; ④x x x f -+=33|)(|.其中存在函数)(x f 对任意的R x ∈都成立的是 ( )A.①④B.③④C.①②D.①③9.设函数)0(log )(2>++=a b ax x x f ,若存在实数b ,使得对任意的[])0(2,>+∈t t t x第二学期学年2016都有a x f +≤1|)(|,则t 的最小值是 ( ) A.2 B.1 C.43 D.3210.定义在R 上的可导函数)(x f 满足32)()(x x f x f =--,当(]0,∞-∈x 时,3)(2x x f <'实数a 满足1332)()1(23+-+-≥--a a a a f a f ,则a 的取值范围是 ( ) A.⎪⎭⎫⎢⎣⎡∞+,23 B.⎥⎦⎤⎝⎛∞-23, C. ⎪⎭⎫⎢⎣⎡∞+,21 D.⎥⎦⎤⎝⎛∞-21, 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.若,3log ,2log n m a a ==则=+n m a 2 ,用n m ,表示6log 4为 . 12.已知nxx )212(-的展开式中二项式系数和为64,则=n ,该展开式中常数项 为 .13.已知函数10,2,122,4)(≠>⎩⎨⎧>++≤+-=a a x a a x x x f x 且其中.若21=a 时方程b x f =)(有两个不同的实根,则实数b 的取值范围是 ;若)(x f 的值域为[)∞+,2,则实数a 的 取值范围是 . 14.函数xxee x x xf --+-=2)(3的奇偶性为 ,在R 上的增减性为 (填“单调递增”、“单调递减”或“有增有减”).15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为 . 16.已知ax a x x a x x x f 22|1||1|)(-+--+-+=)(0>x 的最小值为23,则实数=a . 17.已知函数)R b a b ax x x f ∈++=,()(2在区间(]1,0上有零点0x ,则)31914(00-+x x ab 的最大值是 .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.已知*∈N n ,(1)(2)(),n S n n n n =+++L 213(21)nn T n =⨯⨯⨯⨯-L .(Ⅰ)求 321321,,,,,T T T S S S ;(Ⅱ)猜想n S 与n T 的关系,并用数学归纳法证明.19.(Ⅰ)已知1021001210(21)(1)(1(1)x a a x a x a x -=+-+-++-L ),其中,1,2,10i a R i ∈=L .(i )求01210a a a a ++++L ;(ii )求7a .(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、 丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至 少有一人参加,且五人均能胜任这四个岗位.(i )若每人不准兼职,则不同的分配方案有几种?(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案 有几种? 20.已知R a ∈,函数)(x f 满足.12)2(22-+-=a ax x f x(Ⅰ)求)(x f 的解析式,并写出)(x f 的定义域; (Ⅱ)若)(x f 在]2,2[2212+--a aa 上的值域为[]0,1-,求实数a 的取值范围.21.已知函数()1e1xf x x-=-+. (Ⅰ)证明 当[]0,3x ∈时,xe x 911+≥-. (Ⅱ)证明 当[]2,3x ∈时, 0)(72<<-x f .22.已知1-<a ,函数)(|1|)(33R x ax x x x f ∈++-=. (Ⅰ)求函数)(x f 的最小值;(Ⅱ)已知存在实数),1(,≤<n m n m 对任意),,(0n m t ∈总存在两个不同的),,1(,21+∞∈t t 使得)()(2)(210t f t f t f ==-,求证:274≤-m n .2016学年第二学期宁波市九校联考高二数学参考答案一、选择题(本大题共10小题,每小题4分,共40分)BDCBA DCADD二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.12 ,2m n m + 12.6,60 13.)(49,2 ,),1()1,21[+∞⋃ 14.奇,单调递增 15.84 16.45 17.14410)31914()(,170002≥-+=--=x x x g ax x b 题:20000()()()ab g x a x ax g x ⋅=--[])()(000x g a x a x --≤343200000()1()44439x g x x x x ⋅≤=-+求导知其在11220,,,,,13333⎛⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥⎝⎦⎣⎦⎣⎦上分别递增、递减、递增,故 1441)}1(),31(max{=⋅⋅≤g ab g ab 其.)21,21,1(0时等号成立-=-==b a x方法2:三、解答题:本大题共5小题,共74分 18.(本小题满分14分)解:(Ⅰ)120,12,2332211======T S T S T S ; ……(3分)(Ⅱ)猜想:n n S T =(*n N ∈) ……(4分)证明:(1)当1n =时,11S T =; ……(6分) (2)假设当()*1n k k k N=≥∈且时,kk ST =,即(1)(2)()213(21)kk k k k k +++=⨯⨯⨯-L L ,……(8分) 则当1n k =+时200002002222200000011()493113=92()11313131(1)(1)942362362144ax b x x ab x ax b x ax b x x x x x +=-+-+⎡⎤≤=-=-≤⎢⎥⎣⎦g 可得则(-)(-)111)(12)(11)(1)(11)k S k k k k k k k k +=++++++-+++++L ( =(2)(3)(2)(21)(22)k k k k k ++++L=213(21)(21)(22)1k k k k k ⨯⨯⨯-⨯+++L =11213(21)(21)k k k k T ++⨯⨯⨯-+=L . ……(13分)即1+=k n 时也成立,由(1)(2)可知*n N ∈,n n S T =成立 ……(14分) 19.(本小题满分15分)解:(Ⅰ)(i )令,2=x 则10012103(59049)a a a a ++++=L 即.……(3分) (ii)令10210012101,(12),x y y a a y a y a y -=+=+++L 则 得77710215360.a C == …… (7分)(Ⅱ)(i ).2404425=⋅A C……(11分)(ii) ()114)))(((233233424324=-+-C C C CC ……(15分)20.(本小题满分15分)解:(Ⅰ)令20,xt =>则,log 2t x =则,1log 2)(log )(2222-+-=a t a t t f 即.1log 2)(log )(2222-+-=a x a x x f ……(5分) 定义域为()+∞,0 ……(7分) (Ⅱ))(x f 在]2,2[2212+--a aa 上的值域为[]0,1-等价于12)(22-+-=a ax x x g在区间]22,1[2+--a a a 上的值域为].0,1[- ……(9分)101+1y x ay x a x a =-⇒==⇒=-=令或由图可得2221a a a a ≤-+≤+ ……(13分)12a a ≤≤≤≤或 ……(15分)21.(本小题满分15分) 解(Ⅰ)证明 要证1e19xx-≥+, 也即证e 19xx ≤+. ……(2分) 令()e 91xF x x =--, 则()'e 9xF x =-. 令()'0F x >, 则2ln3x >. 因此, 当02ln3x ≤<时, 有()'0F x <, 故()F x 在[]0,2ln3上单调递减; 当2ln33x <≤时, 有()'0F x >, 故()F x 在[]2ln3,3上单调递增. ……(5分)所以, ()F x 在[]0,3上的最大值为()(){}max 0,3F F .又()00F =,()33e 280F =-<. 故()[]0, 0,3F x x ≤∈成立, 即[]e 19, 0,3xx x ≤+∈成立. 原命题得证. ……(7分) (Ⅱ) 证明 由 (I) 得 当[]2,3x ∈时, ()111e1191xf x x x x -=-≥-+++令()11191t x x x=-++, 则 ()()()()()()()()()()()[]22222222222199119'19911191917280, 2,3.191x x t x x x x x x x x x x x --+-+=-+⋅++=-=++++-=≥∈++(9分)所以, ()t x 在[]2,3上单调递增,即()()[]161622, 2,357567t x t x ≥=->-=-∈所以()f x 72->得证. ……(12分) 下证0)(<x f . 即证1+>x e x令),1()(+-=x e x h x则01)(>-='xe x h ,所以)(x h 在[]32,上单调递增, 所以,03)1()(2>-≥+-=e x e x h x ,得证. ……(15分)另证:要证7211911->+-+x x ,即证011892>+-x x , 令8)19(1189)(22--=+-=x x x x m 在[]32,上递增,所以01)2()(>=≥m x m 得证.22.(本小题满分15分)解:(1)⎩⎨⎧≥-+<+=++-=1,121,1|1|)(333x ax x x ax ax x x x f记)1(12)(),1(1)(321≥-+=<+=x ax x x f x ax x f则a x x f +=2'26)( , 因为 1-<a 则由6,0)('2ax x f -±==得 ……(2分) (i )时,即1616-<≤-≤-a a,上递增,在上递减,在),1[)()1,()(21+∞-∞x f x f 所以1)1()]([min +==a f x f ……(4分) (ii )时,即616-<>-a a,上递减,在)1,()(1-∞x f 递增,上递减,在在)6[)6,1[)(2∞+--a a x f , 所以1632)6()(2min --=-=aa a f x f综上,⎪⎩⎪⎨⎧-<≤-+-<--=16,16,1632)(mina a a aa x f……(6分) (2)不妨设,21t t <则由(1)知,若,16-<≤-a 则)(2x f 在),1(+∞上递增, 不满足题意,所以6-<a . ……(7分) 所以),6(),6,1(21+∞-∈-∈a t a t ,且 1632)6()(2min --=-=a a a f x f (i )>-+21a 1632--a a ,即⎩⎨⎧<<--<1)1(2)(22721x f x f a 时,由即 ⎩⎨⎧<+<-+1121x a ax ,解得121<<+x a ,即)1,21(0a t +∈ 所以)1,21(),(a n m +⊆,所以1,21≤+≥n a m ,所以2742<-≤-a m n ……(11分)(ii )≤-+21a 1632--a a ,即⎪⎩⎪⎨⎧->-<--<≤-)6(2)()1(2)(62272121a f x f f x f a 时,由 即⎪⎩⎪⎨⎧-->-++<-+163221121aa ax a ax ,解得63221a x a -<<+, 所以)632,21(),(a a n m -+⊆,所以632,21a n a m -≤+≥ 所以aa m n 21632---≤- 令]23,1(6∈=-u a ,则23113221632uu a a +-=--- 令231132)(u u u +-=ϕ,则0)11(32)(3'>-=u u ϕ 所以 231132)(u u u +-=ϕ在]23,1(∈u 递增,所以 274)23()(=≤ϕϕu ,所以 274)(≤≤-u m n ϕ. ……(15分)。
浙江省苍南县巨人中学等三校2013-2014学年高二下学期第二次联考数学试题 Word版含答案

高二下学期第二次联考数学试题温馨提示:考试时间110分钟,满分100分,请注意掌握时间。
一.选择题(本题有25小题,1—15每小题2分,16—25每小题3分,共60分.在每小题给出的四个选项中,只有一个正确答案) 1.已知集合{1,0},{1,2},A B ==则AB =( )A.{1, 0, 2}B.{1}C.{2}D.{0} 2.函数3log (1)y x =-的定义域为( )A.RB. (–∞,1)∪(1, ∞)C. (–∞,1)D. (1, ∞)3.在ΔABC 中,若3tan 4A =,则cos A =( ) A.35 B.45 C.45- D.45±4.sin 240°=( )A.23-B. 21C. 23D. 21-5.化简AC -BD +CD -AB 得( )A .AB B .C .BCD .06.已知平面向量(3,1)a =,(,3)b x =-,且a b ⊥,则x =( )A .3-B .1-C .1D .37.下列函数中,在(0,+∞)上是减函数的是( )A.x y 1=B.12+=x yC.x y 2=D.()⎩⎨⎧<->=0)0(x x x x y 8.将函数x y 2sin =的图像向左平移12π个单位,得到函数 )20)(2sin(πϕϕ<<+=x y 的图像,则ϕ=( )A.6π- B. 12π- C. 6π D. 12π9.已知43cos ,(,2)52πααπ=,则=+)4(cos πα ( )A.10B.10 C. 10-10-10.在ΔABC 中,已知A=120°,1=b ,2=c ,则=a ( )A.3B.325+C.7D.325-11.已知等差数列}{n a 中,716a =,14=a ,则10a =( )A.15B.30C.31D.6412.在等比数列{}n a 中,若12344,12,a a a a +=+=则78a a +=( )A.16B.28C.32D.10813.设集合{|10},{|}A x x B x x a =+>= ,若AB ¹Ф,则实数a 的取值范围是( )A.1a <-B.1a ?C.1a >-D.1a ?14.幂函数图像过点,则(4)f = ( )A. B.2D.1 15. 函数]5,1[,142∈+-=x x x y 的值域是………( )A ]61[,B ]13[,-C ),3[+∞-D ]63[,-16.“2230x x --<”是“3<x ”的 ( )A .充分不必要条件 B.必要不充分条件C .充分必要条件 D.既不充分也不必要条件 17.方程x x 28lg -=的根)1,(+∈k k x ,k ∈Z ,则k =( ) A .2 B .3 C .4D .518.函数)1,0(≠>-=a a a a y x 的图像可能是( )A. B. C. D. 19.已知下列命题中:(1)若k R ∈,且0kb =,则0k =或0b =, (2)若0a b ⋅=,则0a =或0b =(3)若不平行的两个非零向量b a ,,满足||||b a =,则0)()(=-⋅+b a b a (4)若a 与b 平行,则||||a b a b =⋅其中真命题的个数是( )A .0B .1C .2D .3 20.函数2()2cos ()14f x x π=+-是( ) A.最小正周期为2π的奇函数 B. 最小正周期为2π的偶函数 C.最小正周期为π的奇函数 D. 最小正周期为π的偶函数21.若sin α+sin β=75,cos α+cos β=-75,则cos(α-β)等于( )A .-2425 B.2425 C .-150D.15022.在数列*1111{},,(2,)21n n n a a a n n N a -==澄-中若,则2014a 等于( )A .21B .1C .2D .–1 23.已知{}n a ,{}n b 都是等比数列,那么( )A.{}n n b a +,{}n n b a ⋅都一定是等比数列B. {}n n b a +一定是等比数列,但{}n n b a ⋅不一定是等比数列C. {}n n b a +不一定是等比数列,但{}n n b a ⋅一定是等比数列D. {}n n b a +,{}n n b a ⋅都不一定是等比数列 24.设偶函数)sin()(ϕω+=x A x f (,0>A )0,0πϕω<<>的部分图象如图所示,△KLM为等腰直角三角形,∠KML =90°,KL =1,则1()6f 的值为( )A.43-B .14-C .12-D .4325.已知圆O 的半径为2,A B 、是圆上两点且AOB ∠=23π,MN 是一条直径,点C 在圆内且满足(1)OC OA OB λλ=+-(01)λ<<,则CM CN ⋅的最小值为( )A .-1B .-2C .-3D .-4试卷Ⅱ二.填空题(本题有5小题,每小题2分,共10分)26. 已知数列{}n a 前n 项和2n S n n =+,则12111098a a a a a ++++=___________ 27.在ABC ∆中.若1b =,c =23C π∠=,则a= 。
2010-2023历年浙江省宁波市八校高二下学期期末联考化学试卷(带解析)

2010-2023历年浙江省宁波市八校高二下学期期末联考化学试卷(带解析)第1卷一.参考题库(共20题)1.下列实验装置,其中按要求设计正确的是2.常温下,用0.10 mol·L-1 KOH溶液滴定10.00 mL 0.10mol·L-1H2C2O4(二元弱酸)溶液所得滴定曲线如图(混合溶液的体积可看成混合前溶液的体积之和)。
下列说法正确的是A.点①所示溶液中: c(H+)/c(OH—)=1012B.点②所示溶液中: c(K+)+c(H+)=c(HC2O4—)+c(C2O42-)+c(OH—)C.点③所示溶液中:c(K+)>c(HC2O4—)> c(H2C2O4)>c(C2O42-)D.点④所示溶液中:c(K+)+ c(H2C2O4)+ c(HC2O4—) +c(C2O42-)=0.10mol·L-1 3.下列事实不能用勒夏特列原理解释的是A.氯化铁溶液加热蒸干最终得不到氯化铁固体B.工业上合成氨采用较高的温度C.常温下,将1 mL pH=3的醋酸溶液加水稀释至100 mL,测得其pH<5 D.钠与氯化钾共融制备钾:Na(l)+KCl(l) K(g)+NaCl(l)4.下列判断正确的是①Ca(OH)2微溶于水,所以Ca(OH)2是弱电解质;②强电解质溶液的导电能力可能比弱电解质溶液导电能力弱;③液态氯化氢不导电,但它是电解质;④碳酸氢钠是弱酸的酸式盐,所以是弱电解质;⑤SO3溶于水后导电,所以SO3是电解质;⑥Cu能导电,但它不是化合物,所以Cu是非电解质A.②③B.②③⑥C.①④⑤⑥D.②③⑤5.一定量的Fe与过量的稀硫酸反应制取氢气,一定温度下为加快反应速率而又不影响氢气的量,可向其中加入A.CH3COOK固体B.Zn粉C.CuSO4晶体D.SO3固体6.(10分)某化学实验小组想要了解市场上所售食用白醋(主要是醋酸的水溶液)的准确浓度,现从市场上买来一瓶某品牌食用白醋,用实验室标准NaOH 溶液对其进行滴定。
2020-2021学年高二下学期期末考试联考地理试题(word版,含答案)

2020~2021学年第二学期期末三校联考高二地理第一卷单项选择题(每小题2分,共60分)我国国产科考破冰船“雪龙2”号历时5个多月,于2021年5月6日14时载着我国第37次南极科学考察队部分队员顺利返航,靠泊在上海外高桥港中国极地考察国内基地码头。
下图为该船考察期间所途径的部分地区示意图,据此完成1-3题。
1.在我国的南极科学考察站中,长城站位于中山站的()方向A.东北B.东南C.西北D.西南2.从图中可以读出,弗里曼特尔到蓬塔阿雷纳斯的最短距离大约为()A.110 km B.5500 km C.10 500 km D.15 500 km 3.“雪龙2”号返航结束时,下列说法可信的是()A.纽约(西五区)夜幕深沉B.东京(东九区)午饭刚刚开始C.莫斯科(东三区)夕阳西垂D.悉尼(东十区)华灯初上下图为某区域等高线地形图(单位:米),甲、乙两地建有养殖场,完成4-6题。
4.从图中可知()A.图中所示山峰的海拔可能为1044米B.乙地海拔可能为1025米C.图中陡崖最大相对高度可能为24米D.区域内最大高差超55米5.在②地可以看到()A.②②B.②②C.②②D.②②6.若图中建有一小型水库,甲养殖场濒临水库最高水位,则()A.水库最深可能接近10米B.水坝高度最低为15米C.库区水面大于1平方千米D.乙养殖场将污染水库印度尼西亚种植园的农民为开辟新耕地,一直有焚烧芭蕉的传统,随着种植园经济的发展,持续的毁林开荒导致“烧芭”产生的烟霾污染日益扩大,“烧芭”时节,本国及邻国新加坡烟霾污染严重,污染新加坡的烟雾主要来自苏门答腊岛的芭蕉燃烧,如图。
读图回答7-9题。
7.推测印度尼西亚“烧芭”的时间()A.12月—次年1月B.3—4月C.7—8月D.10月—11月8.新加坡降水丰富,但淡水资源匮乏,主要自然原因是()A.面积小,储水条件差B.地势低平,径流数少C.人口多,淡水需求大D.经济发达,污染严重9.苏门答腊岛产业发展方向,合理的是()A.大力推进乳畜业发展B.大力改进河网交通建设C.提升种植园农产品品质D.扩大耕地增加粮食产量图为长江、黄河、尼罗河、亚马孙河河流剖面图及水能蕴藏量表,完成10-12题。
浙江省宁波市高二数学下学期期末考试试题 文(含解析)

浙江省宁波市2021-2021学年高二数学下学期期末考试试题 文(含解析)新人教A版【试卷综评】本试卷试题要紧注重大体知识、大体能力、大体方式等当面的考察,覆盖面广,注重数学思想方式的简单应用,试题有新意,符合课改和教改方向,能有效地测评学生,有利于学生自我评判,有利于指导学生的学习,既重视双基能力培育,偏重学生自主探讨能力,分析问题和解决问题的能力,突出应用,同时对观看与猜想、阅读与试探等方面的考查。
着重考察学生大体知识与大体方式的应用,以大体运算为主,难度适中,立足于教材,大多数题是基础题。
选择题部份(共50分)一、选择题:本大题共10个小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1. 设集合{|ln(1)}A x y x ==+,{}2,1,0,1B =--,那么()R A B =( )A. }2{-B. {2,1}--C. }0,1,2{--D. {2,1,0,1}-- 【知识点】对数不等式的解法;交集、补集的概念.【答案解析】B 解析 :解:因为{|ln(1)}A x y x ==+因此10,x 即1,x则{|1}RA x x ,故()R A B ={2,1}--.应选:B.【思路点拨】先确信集合A 中的元素,再求RA,最后求出结果即可.2. 假设a 、b 为实数,那么“1ab <”是“10a b <<”的( )A. 充分而没必要要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【知识点】必要条件、充分条件与充要条件的判定. 【答案解析】B 解析 :解:假设a 、b 为实数,1ab <,令a=-1,b=1,ab=-1<1,推不出10a b <<,若10a b <<,可得b >0,∴0<ab <1,⇒ab <1,∴ab <1”是“10a b <<必要不充分条件,故选B .【思路点拨】令a=-1,b=1特殊值法代入,再依照必要条件和充分条件的概念进行判定.3.平面向量a 与b 的夹角为120,且a (2,0)=,b 1=,那么2=a +b ( )A.4B.C. 2D.【知识点】向量的数量积运算;向量的模的运算. 【答案解析】C 解析 :解:因为a (2,0)=,故2a ,因此cos1201bb a a ,而222224442b ba +b a +baa .应选:C.【思路点拨】下通过已知条件取得a和b a ,然后代入222a +b a +b即可.4. 已知直线,m l ,平面,αβ,且,m l αβ⊥⊂,给出以下命题,其中正确的选项是( )A. 若//αβ,那么m l ⊥B. 若αβ⊥,那么//m lC. 若m l ⊥,那么//αβD. 若//m l ,那么//αβ 【知识点】线面、面面位置关系的判定. 【答案解析】A 解析 :解: 关于A ∵ //αβ,m∴m,又∵l,∴m l ⊥,∴A 正确.关于B ∵αβ⊥,,m l αβ⊥⊂则m 与l 的位置关系是平行、相交、异面,故B 错误. 关于C ∵m l ⊥,,m l αβ⊥⊂则,αβ的位置关系是平行或相交,故C 错误. 关于D ∵//m l ,,m l αβ⊥⊂则αβ⊥.故D 错误. 应选:A.【思路点拨】利用直线与直线,直线与平面,平面与平面的位置关系一一判定,成立的证明,不成立的可举出反例.5.已知函数2()4f x x =-,()y g x =是概念在R 上的奇函数,当0x >时,2()log g x x =,那么函数()()f x g x ⋅的大致图象为( )A. B. C . D . 【知识点】函数图象的识别;函数的奇偶性和图象的关系.【答案解析】D 解析 :解:因为函数2()4f x x =-为偶函数,()y g x =是概念在R 上的奇函数,因此函数()()f x g x ⋅为奇函数,图象关于原点对称,因此排除A ,B .当x时,2()log g x x =>0,2()4f x x =-<0.因此现在()()f x g x ⋅<0.所以排除C . 故选D .【思路点拨】利用函数奇偶性的性质判定函数()()f x g x ⋅的奇偶性,然后利用极限思想判定,当x 时,函数值的符号.[6.数列{}n a 的首项为1,数列{}n b 为等比数列,且1n n n a b a +=,假设10116b b ⋅=则20a =( )A. 12B. 13 C. 1 D. 2 【知识点】等比数列的性质.【答案解析】A 解析 :解:由题意可得1111112a a b a ,,设等比数列{}n b 的公比为q ,那么91019101111b b b q b q4q6,解得191920133q b b q 2322,,即202013a a ,解得201.2a应选:A【思路点拨】由题意可得1112a b ,,代入1011b b 6可得193q 2,进而可得2020b ,a 的值.7. 将函数()2sin(2)4f x x π=+的图象向右平移(0)ϕϕ>个单位,再将图象上每一点的 横坐标缩短到原先的12倍,所得图象关于直线4x π=对称,那么ϕ的最小正值为( ) A .34π B .12πC .38πD .18π【知识点】三角函数图象的变换规律;三角函数的图象与性质.【答案解析】C 解析 :解:将函数()2sin(2)4f x x π=+的图象向右平移φ个单位所得图象的解析式()2sin[2(x )]2sin(2x 2)44f x ,再将图象上每一点的横坐标缩短到原先的12倍所得图象的解析式()2sin(4x 2)4f x 因为所得图象关于直线4x π=对称,因此当4x π=时函数取得最值,因此42kkZ442,整理得出3k Z28k ,当k=0时,φ取得最小正值为38π.故选:C .【思路点拨】依照三角函数图象的变换规律得出图象的解析式()2sin(4x 2)4f x ,再依照三角函数的性质,当4x π=时函数取得最值,列出关于φ的不等式,讨论求解即可.8. 已知抛物线1C :y x 22=的核心为F ,以F 为圆心的圆2C 交1C 于,A B 两点,交1C 的准线于,C D 两点,假设四边形ABCD 是矩形,那么圆2C 的方程为( )A. 22(1)12x y +-=B.22(1)16x y +-= C. 221()32x y +-= D. 221()42x y +-=【知识点】抛物线的简单性质;圆的标准方程.【答案解析】D 解析 :解:依题意,抛物线1C :y x 22=的核心为1F(0)2,,∴圆C2的圆心坐标为1F(0)2,,作图如下:∵四边形ABCD 是矩形,且BD 为直径,AC 为直径,1F(0)2,为圆C2的圆心, ∴点F 为该矩形的两条对角线的交点,∴点F 到直线CD 的距离与点F 到AB 的距离相等,又点F 到直线CD 的距离d=1,∴直线AB 的方程为:3y2,∴33)2,, ∴圆C2的半径2231r AF(30)()222,∴圆C2的方程为:221()42x y +-=,应选:D .【思路点拨】依题意知,圆C2的圆心坐标为1F(0)2,,且点F 为该矩形ABCD 的两条对角线的交点,利用点F 到直线CD 的距离与点F 到AB 的距离相等可求得直线AB 的方程为:3y2,从而可求得A 点坐标,从而可求得圆C2的半径,于是可得答案.9.已知正实数,a b 知足21a b +=,那么2214a b ab ++的最小值为( )A. 72 B. 4C. 16136D. 172【知识点】大体不等式在最值问题中的应用.【答案解析】D 解析 :解:22211142414a b a bab ab abab ab ,令t ab ,那么2214a b ab ++=114ab ab =114t t .∵正实数a ,b 知足2a+b=1,∴122ab ,∴10ab8<,由1y4t t 可得211y 400t t 8<,<时,1y 4t t 单调递减,∴15y2,∴2214a b ab++172.故选:D.【思路点拨】由题意,22211142414a b a bab ab abab ab ,令t ab ,那么2214a b ab ++=114ab ab =114t t .确信t 的范围及1y 4tt 单调递减,即可得出结论.10.已知概念在R 上的函数()f x 知足:()[)[)()()222,0,1,22,1,0,x x f x f x f x x x ⎧+∈⎪=+=⎨-∈-⎪⎩且,()252x g x x +=+,那么方程()()f xg x =在区间[]5,1-上的所有实根之和为( )A .7-B .6-C .8-D .0 【知识点】函数的零点与方程根的关系.【答案解析】A 解析 :解:∵()[)[)()()222,0,1,22,1,0,x x f x f x f x x x ⎧+∈⎪=+=⎨-∈-⎪⎩且∴22,0,1(2)2,1,0x x f x x x又()252x g x x +=+,∴1g x 22x (), ∴g x 22() 1x ,当x ≠2k-1,k ∈Z 时,上述两个函数都是关于(-2,2)对称,;由图象可得:方程()()f xg x =在区间[-5,1]上的实根有3个,12x 3x ,知足235x 4x <<,知足3230x 1x x 4<<,;∴方程()()f xg x =在区间[-5,1]上的所有实根之和为-7.故选:A .【思路点拨】将方程根的问题转化为函数图象的交点问题,由图象读出即可. 非选择题部份(共100分)二、填空题:本大题共7个小题,每题4分,共28分.把答案填在答题卷的相应位置.11. 已知函数2log ,0,()31,0,x x x f x x >⎧=⎨+≤⎩则1(())4f f 的值是___________ 【知识点】分段函数求值【答案解析】109解析 :解:211()log 244f ,因此2102319f ,则1(())4f f =109. 故答案为:109.【思路点拨】先求内层函数1()4f ,再求2f即可.12. 直线l 与圆222410x y x y ++-+=相交于A,B 两点,假设弦AB 的中点()2,3-,那么直线l 的方程为_____________【知识点】直线与圆相交的性质;直线的一样式方程.【答案解析】50x y 解析 :解:由圆222410x y x y ++-+=整理得 22124x y ,取得圆心的坐标为(12),, 由题意得:圆心C 与弦AB 中点的连线与直线l 垂直,∵弦AB 的中点为()2,3-,圆心C 的坐标为(12),,∴圆心与弦AB 中点的连线的斜率为32121,∴直线l 的斜率为1,又直线l 过()2,3-,那么直线l 的方程为y3x 2,即xy 50.故答案为:xy 50.【思路点拨】由圆的方程找出圆心C 的坐标,连接圆心与弦AB 的中点,依照垂径定理的逆定理取得此直线与直线l 垂直,依照两直线垂直时斜率的乘积为-1,由圆心与弦AB 中点的连线的斜率,求出直线l 的斜率,再由直线l 过AB 的中点,即可取得直线l 的方程.【典型总结】此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,两直线垂直时斜率知足的关系,垂径定理,和直线的点斜式方程,其中由垂径定理的逆定理取得圆心与弦AB 中点的连线与直线l 垂直是解此题的关键.13. 一个几何体的三视图如右图所示,那么该几何体的体积为 __ __【知识点】三视图求几何体的体积.【答案解析】223解析 :解:由三视图知几何体是正方体削去一个角,如图:∴几何体的体积311222V 212283233.故答案为:223.21 121正视图侧视图俯视图(第13题图)【思路点拨】依照三视图知几何体是正方体削去一个角,画出其直观图,把数据代入正方体与棱锥的体积公式计算.14.已知不等式组⎪⎩⎪⎨⎧≥-≥-≤+11yyxyx所表示的平面区域为D,假设直线kkxy3-=与平面区域D有公共点,那么k的取值范围为【知识点】简单线性计划的应用.【答案解析】1,03解析:解:知足约束条件⎪⎩⎪⎨⎧≥-≥-≤+11yyxyx的平面区域如图示:因为y=kx-3k过定点D(3,0).所以当y=kx-3k过点A(0,1)时,找到k=1 3当y=kx-3k过点B(1,0)时,对应k=0.又因为直线y=kx-3k与平面区域M有公共点.所以13≤k≤0.故答案为1,0 3.【思路点拨】此题考查的知识点是简单线性计划的应用,咱们要先画出知足约束条件⎪⎩⎪⎨⎧≥-≥-≤+11yyxyx的平面区域,然后分析平面区域里各个角点,然后将其代入y=kx-3k中,求出y=kx-3k对应的k的端点值即可.【典型总结】在解决线性计划的小题时,咱们经常使用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标一一代入目标函数⇒④验证,求出最优解.15.若是关于x 的不等式()0f x <和()0g x <的解集别离为(,)a b 和(11,b a ),那么称这两个不等式为对偶不等式。
浙江省苍南县巨人中学等三校2013-2014学年高二下学期第二次联考语文试题 Word版含答案

高二下学期第二次联考语文试题(考试时间:110分钟,分值:100 分,共 6 页)选择题部分一、选择题(共18题,每小题3分,共54分)1.下列词语中,加点字的读音全都正确的一项是A.漱.(sù)口愧煞.(shā)殉.(xùn)葬铺.(pù)面B.寥廓.(kuò)亘.(gâng)古梵.(fàn)文伺.(cì)候C.惊愕.(â)袖襟.(jīn)褶.(zhã)皱模.(mó)糊D.炮.(páo)烙蹒跚.(shān)惦.(diàn)记脑髓.(suǐ)2. 下列句子中没有别字的一项是A.你看,这些家俱都是你从前顶喜欢的东西,多少年我总是留着,为着纪念你。
B.他就把我的脚放在一张纸上,用铅笔在外沿上搔上两三次,跟着用他敏感的手指来回地摸我的脚趾。
C.她大约因为在别人祝福的时候,感到自身的寂漠,然而会不会含有别的什么意思呢?D.四百多年里,它剥蚀了古殿檐头浮夸的琉璃,淡退了门壁上炫耀的朱红。
3.依次填入下列句子横线处的词语,恰当的一项是①三十年的_________你还是找到这儿来了。
②离开了文化,无从寻觅和_________什么传统。
③满园子都是草木___________ 生长弄出的响动,窸窸窣窣窸窸窣窣片刻不息。
A.工夫琢磨竞相 B.功夫捉摸竞自C.功夫琢磨竞自 D.工夫捉摸竞相4.下列句子中加点的成语运用不恰当的一项是A.对联,是一种独特的文学样式,它要求形式上对仗整齐,内容上别具用心,好的对联看似信手拈来....,其实已凝聚了作者的智慧。
B.他先是反复思考,认真研究材料,然后执笔成文,又不厌其...详.的推敲修改。
C.李局长认真听取大家的意见和建议,多次修改了自己的方案,真是从善如流....。
D.这对分别多年的老同学在庙会上不期而遇....,他们决定好好庆祝庆祝。
5.下列句子没有语病的一项是A.在城市化进程中,由于措施不到位,一些古代建筑遭受了不同程度的破坏。
stage,point等名词后用where引导的定语从句
case, condition, situation, position, point, stage之青柳念文创作等名词后接where引出的定语从句小议不久前,下面这道题引发了我们对stage作先行词之后的定语从句引导词的问题以及其它近似定于从句的探讨,先看一道题:the conflict had developed into a stage ______ the two countries were gathering big troops on the border.(第二学期浙东北(zdb)三校期中联考高二英语试卷(.05))a. whereb.when c.which d. that本题到底是选a还是选b?关键问题在于对先行词stage 的懂得,根据《牛津高阶英汉双解词典》(第七版)简作(oald)的解析:stage: a period of state thatsb./sth. passes through while developing or makingprogress. 既可以懂得为事件“(停顿或停顿的)阶段,状态”; 又可以懂得为“时期”.而上题中作“阶段”或“时期”都懂得的通.再看stage的用法;*stage名词 n. [c]some girls are dancing on the stage. 一些女孩在舞台上跳舞.2.注意中心,活动舞台,场合3.(停顿的)阶段;时期a caterpillar must pass through the cocoon stage to become a butterfly.暗示这些意思时,当stage作先行词后有定语从句时,.例句:1.表地点: the stage where the girls are going to dance is in the gym.2.表时期: the stage when he is preparing for his study is really important.分歧的叙述:①当先行词为case,condition,situation,position,point,stage等名词,暗示情况、方面、处境时用关系副词where.②当先行词是case, condition, situation, position, point, stage 等名词时,暗示情况、方面、处境时,用关系副词where.但先行词是occasion时,用关系副词when.③当 situation, condition, stage, point,scenes 做先行词时,用 where 引导定语从句④先行词通常是 time, day, season, age, occasion 等时间名词时其后的定语从句用when引导.事实上, 当先行词 occasion, point, stage等名词是暗示时间节点的时候,其后的定语从句就用when引导,在从句中作时间状语. 例如:1. i can remember very few occasions when he had to cancel because of ill health.(oald)我记得他因健康欠安而自愿取消的情况绝无唯一.when引导定语从句,在从句中作时间状语.2.(·山东·26) occasions are quite rare___________i have the time to spend a day with my kids.a. whob. whichc. whyd. when答案选d.考察定语从句.此题关键是要根据句意断定是定语从句.句意为:我有时间和孩子们一起度过一天的机会很少.occasions 是先行词, 所选关系词在定语从句中要作时间状语, 故选d项3. we had reached the point when there was no money. 我们那时已到了没有一分钱的时刻.point暗示“某一阶段,关头”,所以其后用when 引导定语从句.4. there comes a point in your life when yourealize: who matters, who never did, who won't anymore5. china is now at a stage of accelerated industrialization and urbanization when the contradiction between economic growth and environmental protection is particularly prominent.中国今朝正处于工业化和城市化加速发展的阶段,此时经济增长和环境呵护之间的抵触十分突出.source: hard times call for green economy/by hu shaowei (china daily03/24/ page8)但更多情况是:position,situation, stage, case等,作先行词时,其后的定语从句应用where引导定语从句.如:1.oxford dictionary onlinemore examples introducing a clause with 'when ' can be found but it is hard to find an example with'where' after 'occasion'.2.it is the same with longman dictionary"under these conditions, where we see so much uncertainty with leadership succession, possible instability, we see no arms control, we see no confidence building measures, we see no disarmament, we see north korea refusing to return to thesixparty talks, we see the sinking of the cheonan and potential clashes in the west sea around the northern limit line. so a lot of people are justsaying this is just not the right time," pinkston said. voa news.it is the same with ' situation'."it moves from a situation where only those items on the permitted list can come into gaza to a situation where things come into gaza as a matter of course unless they are on the prohibited list.it allows us to facilitate the united nations projects for reconstruction in things like schools and hospital and water sanitation and so on." bbc news新闻 06213.we were put in a position in which(=where) we had either to accept we were less important, or fight the government.(人教版新课标高中英语必修1line25.p34)我们被置于这样一种地步,或者是自愿承认我们低人一等,或者是与政府作斗争.这是一个主从复合句,in which引导定语从句,修饰先行词position.4. can you think of a situation where you once felt embarrassed?你能设想起你曾有过感到很拮据的场合吗?5.he is the boss of the restaurant where (= in which) we often have lunch.6. the last thirty years have seen the greatest number of laws stopping our rights and progress until today we have reached a stage where we have almost no rights at all.(人教版新课标高中英语必修1 line1920 p34)注意:近些年来高考对关系副词where的考察趋于复杂化,从先行词为分明的“地点”发展为“恍惚的地点化”.事实上,当先行词暗示某事物发展的某个situation“情景”、stage“阶段”或某种程度时都可以用where引导定语从句.所以文章开首那道题答案为a.更多的列子如:1.(·福建·24)it’s helpful to put children ina situation ________they can see themselves differently.a. thatb.when c.which d. where2.(·浙江14)i have reached a point in my life_______i am supposed to make decisions of my own.a. whichb. wherec. howd. why3. an iraqi reporter during a news conference________threw his shoes at bush and called him a dog in arabic shocked the world.a. whob. wherec. whomd. which1.【解析】选d.考察定语从句.句意为:把孩子放在一个能使他们从别的一个角度认识自己的环境中对他们有益.当先行词是case, condition, situation, position, point, stage等名词暗示“情况, 方面, 处境”时, 关系副词用where.2. 【解析】选b.考察定语从句.句意为:我已经到了应该自己作决议的阿谁人生阶段.先行词point和定语从句被介词短语in my life隔开.当先行词是case, condition, situation, position, point, stage等名词暗示“情况、方面、处境”时, 定语从句用关系副词where引导.how不克不及用来引导定语从句; which在定语从句中作主语或宾语; why引导定语从句时先行词应为reason; 因此可解除选项a、c和d.3. 【解析】选d.考察定语从句.此题关键是要根据句意断定是定语从句.句意为:我有时间和孩子们一起度过一天的机会很少.occasions 是先行词, 所选关系词在定语从句中要作时间状语, 故选d项.近似的还有如:4.those successful deaf dancers think that da ncing is an activity ____sight matters more than hearing.a. whenb. whosec.which d. where这道题中的activity 做地点状语.选d4.【解析】选d:本题查核对定语从句的掌握和运用才能.句意为“那些失聪的成功舞蹈演员们认为,舞蹈是一种让人看胜过让人听的活动.”据句子布局断定,空缺处缺一引导定语从句的关联词,由于先行词activity在从句中担任地点状语故应该选择关系副词where,因此正确答案为d项.所以大部分的语法解析中提到当situation stage case point这四个词在定语从句中作先行词暗示抽象的地点时,其后的定语从句的引导词一般用where例如:1. the media can draw attention to situationwhere help is needed.2. we have reached a stagewhere we have almost no rights.3. today, we’ll discuss a number of caseswhere beginners of english fail to use thelanguage properly.4. we are just trying to reach a pointwhere both sides will sit down together and talk.5. their youngest child is at the stage where she can say individual words but not full sentences.操练:用适当的关系副词填空1. today, we’ll discuss a number of cases________ beginners of english fail to use the language properly.a.which b.asc.why d.where2. those successful deaf dancers think that dancing is an activity_______ sight matters more than hearing.a.when b.whose c .which d.where3. after graduation she reached a point in her career_______ she needed to decide what to do. a.that b.whatc.which d.where4. can you think out a situation _______ this word can be used?a.where b.whose c .which d.when5. her illness has developed to the point _______ nobody can cure her.a.that b.wherec.which d.what6. we're just trying to reaching a point _________ both sides will sit down together and talk.a. whenb.that c.where d. which答案及诠释:1. 答案d.解析:考察定语从句.先行词是cases,意思是:情况,状态,关系词在从句中作状语,先行词指地点,用where.2. 答案d.解析:考察的是定语从句.dancing is an activity后面是一个定语从句,修饰an activity,在定语从句中缺少状语,所以用where或in which.3. 答案d.解析:本题考察定语从句的引导词.在定语从句中,当先行词为point, case, situation等时,通常常使用关系副词where引导.4. 答案a.解析:本题考察定语从句的引导词.在定语从句中,当先行词为point, case, situation等时,通常常使用关系副词where引导.你能设想出这个单词被使用的场合吗?5. 答案b.解析:本题考察定语从句的引导词.在定语从句中,当先行词为point, case, situation等时,通常常使用关系副词where引导. 她的病发展到没人能治的地步.6.答案c.解析:本题考察定语从句的引导词.在定语从句中,当先行词为point, case, situation等时,通常常使用关系副词where引导.。
2018-2019学年浙江省宁波市九校联考高二(下)期末数学试卷(含答案)
高二(下)期末数学试卷一、选择题(本大题共10小题,共40.0分)1.已知集合A={x|-1≤x<2},B={x|0≤x<3},则A∩B=()A. {x|-1≤x<3}B. {x|0≤x<2}C. {x|0<x<2}D. {x|0<x<3}2.已知f(x)是定义在R上的函数,则下列函数中一定是偶函数的是()A. f(|x|)B. |f(x)|C. [f(x)]2D. [f(x)]33.“>1”是“0<a<1”的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4.已知,则( )A. B. C. D.5.若函数f(x)=在x=2处的切线与直线y=kx垂直,则实数k的值是()A. B. 2 C. -4 D. 46.若x(x+)n(n∈N*)的展开式中存在常数项,则n的值可以是()A. 9B. 10C. 11D. 127.下列函数f(x)中,满足“任意x1>0,x2>0,x1≠x2,且(x1-x2)[f(x1)-f(x2)]<0”的是()A. f(x)=-xB. f(x)=x3C. f(x)=ln xD. f(x)=2x8.存在函数f(x)满足定义域为(-∞,0)∪(0,+∞)的是()A. f(x+)=x+1B. f(x2)=x+1C. f(sin x)=x+1D. f(a x)=2x(a>0,a≠1)9.从,1,2,3…,20中选取四元数组(a1,a2,a3,a4),且满足a2-a1≥3,a3-a2≥4,a4-a3≥5,则这样的四元数组(a1,a2,a3,a4)的个数是()A. B. C. D.10.已知函数f(x)=e x-a+e-x+a(其中e是自然对数的底数).若3a=log3b=c,且c>1,则()A. f(a)<f(b)<f(c)B. f(b)<f(c)<f(a)C. f(a)<f(c)<f(b)D. f(c)<f(b)<f(a)二、填空题(本大题共7小题,共36.0分)11.设(x+2)10=a10x10+a9x9+…+a1x+a0,则a8=______;a9+a7+a5+a3+a1=______.12.已知方程log a(5x-3x)=x(a>0,a≠1),若2是方程的一个解,则a=______当a=2时,方程的解是______.13.已知函数f(x)=,则f(f())=______;方程f(f(x))=2的解集是______.14.已知函数,若的定义域为R,则实数a的取值范围是______:若的值域为则实数a的取值范围是______.15.甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中含有1门相同的选法有______ 种(用数字作答).16.已知函数f(x)=,若函数g(x)=f[f(x-1)]恰有3个不同的零点,则实数b的取值范围是______.17.已知定义在R上的偶函数f(x)的导函数为f′(x),若f(x)满足:当x>0时,xf′(x)+f(x)>1,f(1)=2019,则不等式f(x)≤1+的解集是______.三、解答题(本大题共5小题,共74.0分)18.已知袋中装有8只除颜色外,其它完全相同的球,其中有且仅有5只是黄色的.现从袋中一个一个地取出球,共取三次,记拿到黄色球的个数为X.(Ⅰ)若取球过程是无放回的,求事件“X=2”的概率;(Ⅱ)若取球过程是有放回的,求X的概率分布列及数学期望E(X).19.已知f(x)=4x3+ax+b(a,b∈R)的图象关于点(0,1)中心对称.(Ⅰ)求b的值;(Ⅱ)若对-l≤x≤1,不等式f(x)<0无解,求a的取值的集合.20.已知数列{a n}满足:a1=,且a n+1=a n2-2(n∈N*).(Ⅰ)求a2,a3的值;(Ⅱ)猜测通项公式a n的表达式,并用数学归纳法证明你的猜测.21.已知函数f(x)=(其中e是自然对数的底数),g(x)=1-ax2(a∈R).(Ⅰ)求函数f(x)的极值;(Ⅱ)设h(x)=f(x)-g(x),若a满足0<a<且ln2a+1>0,试判断方程h (x)=0的实数根个数,并说明理由.22.已知函数f(x)=ln(x+1)+ax2-x(a∈R).(Ⅰ)若对任意x≥0,都有f(x)≥0成立,求a的取值范围;(Ⅱ)证明:ln(1+)+ln(1+)+ln(1+)+…+ln(1+)≥81.答案和解析1.【答案】B【解析】解:∵A={x|-1≤x<2},B={x|0≤x<3};∴A∩B={x|0≤x<2}.故选:B.进行交集的运算即可.考查描述法表示集合的定义,以及交集的运算.2.【答案】A【解析】解:∵f(|-x|)=f(|x|);∴f(|x|)是偶函数.故选:A.根据偶函数的定义,f(|-x|)=f(|x|),从而得出f(|x|)一定是偶函数.考查偶函数的定义,以及偶函数的判断.3.【答案】C【解析】解:>1⇔a(a-1)<0⇔0<a<1,∴“>1”是“0<a<1”的充要条件.故选:C.>1⇔a(a-1)<0解出不等式即可判断出结论.本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.4.【答案】B【解析】【分析】本题考查了指数函数和对数函数的单调性运用,属基础题.由指数函数和对数函数的单调性易得log20.2<0,20.2>1,0<0.20.3<1,从而得出a,b,c的大小关系.【解答】解:a=log20.2<log21=0,b=20.2>20=1,∵0<0.20.3<0.20=1,∴c=0.20.3∈(0,1),∴a<c<b,故选B.5.【答案】D【解析】解:由f(x)=,得f′(x)=-,则f′(2)=-,∵函数f(x)=在x=2处的切线与直线y=kx垂直,∴-×k=-1,即k=4.故选:D.求出函数f(x)=的导函数,得到f′(2),再由两直线垂直与斜率的关系求得k值.本题考查利用导数研究过曲线上某点处的切线方程,考查两直线垂直与斜率的关系,是基础题.6.【答案】A【解析】【分析】本题考查了二项式定理的通项公式,考查了推理能力与计算能力,属于基础题.利用通项公式即可得出.【解答】解:x(x+)n(n∈N*)的展开式中通项公式:T k+1=x n-k=x n-4k.∵存在常数项,∴n-4k=-1,即n=4k+1,n,k∈N*.则n的值可以是9.故选A.7.【答案】A【解析】解:“任意x1>0,x2>0,x1≠x2,且(x1-x2)[f(x1)-f(x2)]<0”,说明函数f(x)是单调减函数,函数f(x)=-x是x>0上的减函数,函数f(x)=x3是增函数;函数f(x)=ln x是增函数;函数f(x)=2x是增函数;故选:A.利用函数的单调性的定义判断函数的单调性,然后判断选项的正误即可.本题考查函数的单调性的定义的应用,常见函数的单调性的判断,是基本知识的考查.8.【答案】A【解析】解:对于B,该函数定义域均为R,与题意不符,故B错误;对于C,当x=π时,f(sinπ)=f(0)=π+1,当x=2π时,f(sin2π)=f(0)=2π+1,违反了唯一性,故C错误;对于D,令t=a x,则x=log a t,即x∈R,故D错.故选:A.判断自变量有意义的范围是否符合(-∞,0)∪(0,+∞),排除B和D;依照函数的定义,判断定义域中的自变量是否有唯一与之相对应的函数值,排除C,故选A.本题考查函数的三要素中定义域和对应关系,属于基础题9.【答案】B【解析】解:将a1连同其右边的2个空位捆绑,a2连同其右边的3个空位捆绑,a3连同其右边的4个空位捆绑分别看作一个元素,四元数组(a1,a2,a3,a4)的个数相当于从11个元素中选取4个,故这样的四元数组(a1,a2,a3,a4)的个数是.故选:B.将a1连同其右边的2个空位捆绑,a2连同其右边的3个空位捆绑,a3连同其右边的4个空位捆绑分别看作一个元素,四元数组(a1,a2,a3,a4)的个数相当于从11个元素中选取4个,本题考查了计数原理,组合数的原理,考查了捆绑法的使用.属于中档题.10.【答案】C【解析】解:函数f(x)=e x-a+e-x+a=e x-a+,根据3a=log3b=c,可得a=log3c,b=3c,可得b>c>a.又函数f(x)=e x-a+e-x+a=e x-a+在(a,+∞)上单调递增,故有f(a)<f(c)<f(b),故选:C.由题意可得b>c>a,再根据函数f(x)=e x-a+在(a,+∞)上单调递增,可得f(a)、f(c)、f(b)的大小关系.本题主要考查指数函数的单调性的应用,属于基础题.11.【答案】180【解析】解:①T3==180x8.∴a8=180.②对(x+2)10=a10x10+a9x9+…+a1x+a0,令x=-1,则1=a10-a9+…-a1+a0,令x=1,则310=a10+a9+…+a1+a0,相减可得:a9+a7+a5+a3+a1=.故答案为:180,.①T3==180x8.可得a8.②对(x+2)10=a10x10+a9x9+…+a1x+a0,令x=-1,则1=a10-a9+…-a1+a0,令x=1,则310=a10+a9+…+a1+a0,相减可得:a9+a7+a5+a3+a1.本题考查了二项式定理的通项公式、赋值法,考查了推理能力与计算能力,属于基础题.12.【答案】4 1【解析】解:将方程的解x=2代入原方程,得到,即log a16=2,计算得a=±4,且a>0,故a=4;将a=2代入原方程,得,化为5x-3x=2x,计算得到x=1.故答案为4,1.将方程的解代入原方程,得到关于a的对数函数方程式,计算出a的值;将a=2带入原方程,再将对数函数式变为指数函数式,计算出x的值本题考查方程的解,指数函数与对数函数的计算,难度不大,属于基础题13.【答案】2 [0,1]∪{2}【解析】解:函数f(x)=,则f()=2,f(f())=f(2)=2;若x∈[0,1],则f(x)=2,方程f(f(x))=2,即为f(2)=2成立;若x∉[0,1],则f(x)=x,由f(x)=2,可得x=2,故答案为:2,[0,1]∪{2}.由分段函数的解析式,可得f(),可得所求值;讨论x∈[0,1],或x∉[0,1],解方程可得所求解集.本题考查分段函数的运用,求函数值和解方程,考查运算能力,属于基础题.14.【答案】[2,+∞); [0,2]【解析】【分析】本题考查函数定义域、值域的定义及求法,一元二次不等式ax2+bx+c≥0的解集为R时所满足的条件,以及子集的定义,属中档题.根据f(x)的定义域为R即可得出不等式的解集为R,从而得出,解出a的范围即可;根据f(x)的值域为[0,+∞)即可得出函数的值域包含集合[0,+∞),从而得出或a=0,解出a的范围即可.【解答】解:∵f(x)的定义域为R;∴不等式的解集为R;∴;解得a≥2;∴实数a的取值范围是[2,+∞);∵f(x)的值域为[0,+∞);∴的值域包含集合[0,+∞);∴或a=0;解得0≤a≤2;∴实数a的取值范围是[0,2].故答案为:[2,+∞);[0,2].15.【答案】24【解析】解:根据题意,分两步,①由题意可得,所有两人各选修2门的种数C42C42=36,②两人所选两门都相同的有为C42=6种,都不同的种数为C42=6,故只恰好有1门相同的选法有36-6-6=24种.故答案为:24.根据题意,分两步,①先求所有两人各选修2门的种数,②再求两人所选两门都相同与都不同的种数,进而由事件间的相互关系,分析可得答案.本题考查组合公式的运用,解题时注意事件之间的关系,选用直接法或间接法.16.【答案】(-∞,2-)【解析】解:当x<0时,f′(x)=-3x2+8x=-x(3x-8)<0,则f(x)在(-∞,0)上单调递减,此时f(x)>f(0)=b,令f(x-1)=m,当b≥0时,f(m)=0只有一解m=0,此时g(x)不可能有三个零点,故b<0,此时f(m)=0有两个根,一个为0,和一个负根m1,如下图所示,则f(x-1)=0或f(x-1)=m1,m1<0,显然f(x-1)=0有两个根,则f(x-1)=m1必然有一个根,由图象可知,要使f(x-1)=m1有一个根,则需b<m1,又,所以,∴,解得,∴.故答案为:.首先分析出b<0,则f(m)=0有两个根,一个为0,和一个负根m1,那么g(x)=f[f (x-1)]=0需满足f(x-1)=0或f(x-1)=m1,显然f(x-1)=0有两个根,由题意,f(x-1)=m1必然有一个根,则只需b<m1即可.本题考查函数的零点,复合函数问题一般利用换元法转化为简单函数,再将函数零点个数转化为两个函数图象的交点个数,利用数形结合思想求解.17.【答案】[-1,0]∪(0,1]【解析】解:当x>0时,x•f'(x)+f(x)>1,∴x•f'(x)+f(x)-1>0,令g(x)=xf(x)-x=x(f(x)-1),∴g′(x)=x•f'(x)+f(x)-1>0,∴g(x)在(0,+∞)上为增函数,∵f(x)为偶函数,∴g(x)为奇函数,且g(0)=0,∴g(x)在(-∞,0)上为增函数,∴g(x)在R上为增函数,∵f(x)≤1,x≠0∴|x|f(x)≤|x|+2018,即|x|f(x)-|x|≤2018,∴g(|x|)≤2018,∵g(1)=f(1)-1=2019-1=2018,∴|x|≤1,即-1≤x≤1,又x≠0,∴f(x)≤1的解集为[-1,0)∪(0,1],故答案为:[-1,0)∪(0,1].构造函数g(x)=xf(x)-x,根据导数和函数的单调性的关系,判断g(x)的单调性,根据单调性即可求出不等式的解集.本题主要考查利用函数的单调性求解函数不等式问题,属于中档题目.18.【答案】解:(Ⅰ)依题意,P(X=2)==;(Ⅱ)由题意可得,随机变量X~B(3,),X的可能的取值为0,1,2,3.P(X=k)=,(k=0,1,2,3).所以X的分布列为:X 0123P所以E(X)=0×1×+2×+=(或者E(X)=3×=).【解析】(Ⅰ)若取球过程是无放回的,则X服从超几何分布,根据P(X=k)=,(k=0,1,2,3)将k带成2即可得到概率;(Ⅱ)若取球过程是有放回的,则随机变量X~B(3,),X的可能的取值为0,1,2,3.P(X=k)=,(k=0,1,2,3).分别求出各X对应的概率,列出分布列,求出期望即可.本题考查了离散型随机变量的概率分布列,超几何分布,二项分布.离散型随机变量的期望,属于中档题.19.【答案】解:f(x)=4x3+ax+b(a,b∈R)(1)令g(x)=f(x)-b=4x3+ax,则:g(-x)=-g(x)所以:g(x)是奇函数,故g(x)的图象关于原点对称,所以:f(x)=g(x)+b的图象关于(0,b)对称,因为f(x)=4x3+ax+b(a,b∈R)的图象关于点(0,1)中心对称.所以:b=1(Ⅱ)由(1)知,f(x)=4x3+ax+1,由条件对-l≤x≤1,不等式f(x)<0无解,知f(-1)=-3-a≥0,f()=+≥0;解得:a=-3.又当-l≤x≤1时,f(x)=4x3-3x+1=4(x+1)(x-)2≥0,所以:a=-3,即a的取值的集合为:{-3}.【解析】(Ⅰ)构造新函数令g(x)=f(x)-b=4x3+ax,利用函数的性质可得g(x)是奇函数,可得b的值;(Ⅱ)若对-l≤x≤1,不等式f(x)<0无解,即不等式f(x)≥0有解,从而可得a的取值的集合.考查函数的性质问题,体现了转化的思想方法,属于中档题.20.【答案】解:(Ⅰ)a1=,可得a2=a12-2=;a3=a22-2=;(Ⅱ)猜测a n=2+2.运用数学归纳法证明:当n=1时,a1=2+2-1,等式成立;设n=k时,a k=2+2,当n=k+1时,a n+1=a k2-2=(2+2)2-2=2+2,即当n=k+1也成立,综上可得a n=2+2.n∈N*.【解析】(Ⅰ)分别令n=1,2,计算可得所求值;(Ⅱ)猜测a n=2+2.运用数学归纳法证明,注意由n=k成立,证明n=k+1也成立.本题考查数列的通项公式的求法,以及数学归纳法的运用,考查云南省能力和推理能力,属于基础题.21.【答案】解:(Ⅰ)易知,当x<0时,f′(x)>0,此时f(x)单调递增;当x>0时,f′(x)<0,此时f(x)单调递减,所以f(x)极大值=f(0)=1,但无极小值.(Ⅱ)因为,所以.因为,所以,于是,令h′(x)=0,此时,当x<0时,f′(x)<0,此时f(x)单调递减;当时,f′(x)>0,此时f(x)单调递增;所以.因为,所以,,又函数h(x)在R上连续,故h(x)有一个零点0,且在上也有一个零点;综上,方程h(x)=0有2个实数根.【解析】(Ⅰ)对f(x)求导数,判断单调性,进而求出极值;(Ⅱ)通过分类讨论,结合函数的单调性,零点存在性定理进行判断.本题考查函数极值、函数的零点个数问题.22.【答案】(Ⅰ)解:当a≤0时,f(1)=ln2+a-1≤1-1=0,不合题意;当a>0时,,令f′(x)=0,得x1=0,;若x2>0,则有f(x)在(0,x2)上单调递减,,不合题意;∴x2≤0,且f(0)=0;∴由解得,;∴a得取值范围是;(Ⅱ)证明:由(Ⅰ)知,当时,对∀x≥0,都有f(x)>0,即;∴,(k=2,3,4,…,2019);∵=;=10,∴=,>2×44.5-3-5=81.【解析】(Ⅰ)分类讨论,当a≤0时不合题意;当a>0时,对f(x)求导,通过导函数判断f(x)的增减区间与极小值,进而求出a的取值范围;(Ⅱ)利用时,f(x)≥0,对原式左边进行变形,有;分别计算和,进而得出结论.本题考查了利用导数求函数的极值,不等式得放缩,数列的求和,属难题.。
2022-2023学年浙江省宁波市九校高二下学期期末考联考数学试卷含详解
2022学年第二学期宁波市九校联考高二数学试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足i 1i z ⋅=+,则z 对应的点位于()A.第一象限 B.第二象限C.第三象限D.第四象限2.设集合(){},21xM x y y ==-,()π,cos ,442N x y y x x ⎧⎫==-≤≤⎨⎬⎩⎭,则M N ⋂中元素的个数为()A.2B.3C.4D.53.已知随机变量()211~,X N μσ,()222~,Y N μσ,它们的分布密度曲线如下图所示,则下列说法中正确的是()A.12μμ<,2212σσ< B.12μμ<,2212σσ>C.12μμ>,2212σσ< D.12μμ>,2212σσ>4.已知平面向量a ,b满足a b a b +=- ,则b a - 在a 上的投影向量为()A.a-r B.aC.b-D.b5.若1sin()43πα+=,(0,)απ∈,则cos 2=α()A.79-B.429±C.9D.9-6.在ABC 中,点O 满足2CO OB = ,过点O 的直线分别交射线AB ,AC 于点M ,N ,且AM mAB = ,AN nAC =,则2m n +的最小值为()A.83 B.103C.3D.47.已知()f x 是定义在R 上的奇函数,且()22f =,若对任意的1x ,()20,x ∈+∞,均有()()12121f x f x x x ->-成立,则不等式()11f x x -+>的解集为()A.()()2,02,-+∞B.()(),20,2-∞-C.()(),11,3-∞- D.()()1,13,-+∞ 8.三面角是立体几何的重要概念之一.三面角-P ABC 是指由有公共端点P 且不共面的三条射线PA ,PB ,PC 以及相邻两射线之间的平面部分所组成的空间图形.三面角余弦定理告诉我们,若APC α∠=,BPC β∠=,APB γ∠=,平面APC 与平面BPC 所成夹角为θ,则cos cos cos cos sin sin γαβθαβ-=.现已知三棱锥-P ABC ,PA =,3BC =,45APC ∠=︒,60BPC ∠=︒,90APB ∠=︒,则当三棱锥-P ABC 的体积最大时,它的外接球的表面积为()A.18πB.36πC.87π2D.117π2二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列等式成立的是()A.0!0= B.11A A mm n n n --=C.11(1)C (1)C mm n n n m +++=+ D.111C C C mm m n nn -+++=10.以下四个正方体中,满足AB ⊥平面CDE 的有()A. B.C. D.11.已知函数()f x 的定义域为R ,()21f x +是偶函数,()1f x -的图象关于点()3,3中心对称,则下列说法正确的是()A.()()2f x f x =+ B.()203f = C.()()24f x f k x +=-,Zk ∈ D.411()123k i f i k -==-∑,Zk ∈12.一个不透明的袋子中装有大小形状完全相同的红、黄、蓝三种颜色的小球各一个,每次从袋子中随机摸出一个小球,记录颜色后放回,当三种颜色的小球均被摸出过时就停止摸球.设=i A “第i 次摸到红球”,i B =“第i 次摸到黄球”,i C =“第i 次摸到蓝球”,i D =“摸完第i 次球后就停止摸球”,则()A .()329P D =B.()41227P D A =C.()11223n n n P D ---=,3n ≥ D.()312223n n n n n P D B C ----=,3n ≥三、填空题:本题共4小题,每小题5分,共20分.13.已知实数a ,b 满足25abm ==且1112a b +=,则m =______.14.现有一枚质地不均匀的硬币,若随机抛掷它两次均正面朝上的概率为12,则随机抛掷它两次得到正面、反面朝上各一次的概率为______;若随机抛掷它10次得到正面朝上的次数为ξ,则()E ξ=______.(第一空2分,第二空3分)15.已知函数()()ln 2e ,0234,0x a x f x x ax a x -⎧⎪-<=⎨-++-≥⎪⎩,若()f x 有4个零点,则实数a 的范围是______.16.已知平面向量a ,b ,()1,2i c i =满足22a b b ==⋅= ,1i c a -= ,则()1222R c b c b λλλ-+-∈ 的最小值为______.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且______,请从下列两个条件中任选一个填入上方的横线中作为已知条件,并解答本题(如果选择多个条件分别解答,则按第一个解答计分):①sinsin 2B C c a C +=;②()22234ABC S b c a =+- ,(1)求A ;(2)若D 为边BC 上一点,且2CD AD BD ==,试判断ABC 是锐角三角形、直角三角形还是钝角三角形,并说明理由.18.已知函数()sin cos (0)f x x x ωωω=+>的图象关于直线π8x =对称,且()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值.(1)求()f x 的单调增区间;(2)已知函数()()log 242xa g x a a =-+(0a >且1a ≠),对任意1ππ,42x ⎡⎤∈⎢⎣⎦,总存在[]21,2x ∈,使得()()12f x g x ≤,求实数a 的取值范围.19.航班正点率是指航空旅客运输部门在执行运输计划时,航班实际出发时间与计划出发时间较为一致的航班数量与全部航班数量的比率.人们常用航班正点率来衡量一个航空公司的运行效率和服务质量.现随机抽取10家航空公司,对其近一年的航班正点率和顾客投诉次数进行调查,得到数据如下:航空公司编号12345678910航班正点率i x /%82777776747371709169顾客投诉次数i y /次2158796874937212218125整理数据得:10153620iii x y=≈∑,102158150ii x =≈∑,102164810ii y =≈∑,101760i i x ==∑,101730i i y ==∑70≈.(1)(i )证明:样本相关系数niix ynx yr -=∑;(ii )根据以上数据计算样本相关系数(结果保留2位小数),并由此推断顾客投诉次数与航班正点率之间的线性相关程度(若0.81r ≤≤,则认为线性相关程度很强;若0.30.8r ≤<,则认为线性相关程度一般;若0.3r <,则认为线性相关程度很弱).(2)用一元线性回归模型对上表中的样本数据进行拟合,得到顾客投诉次数关于航班正点率的经验回归方程为5y x a=-+.现有一家航空公司拟通过加强内部管理来减少由于公司自身原因引起的航班延误次数,并希望一年内收到的顾客投诉不超过73次,试估计该公司的航班正点率应达到多少?参考公式:样本相关系数()()nii xxy y r --=∑.20.2023年4月23日是第28个“世界读书日”.为了倡导学生享受阅读带来的乐趣、尊重和保护知识产权,立德中学举办了一次阅读知识竞赛.初赛中每支队伍均要参加两轮比赛,只有两轮比赛均通过的队伍才能晋级.现有甲、乙两队参赛,初赛中甲队通过第一轮和第二轮的概率均为34,乙队通过第一轮和第二轮的概率分别为35,23,且各队各轮比赛互不影响.(1)记甲、乙两队中晋级的队伍数量为X ,求X 的分布列和数学期望;(2)经过激烈的比拼,甲、乙两队成功进入决赛争夺冠军.决赛共有两道抢答题.第一题中,某支队伍若抢到并答对则加10分,若抢到但答错则对方加10分.第二题中,某支队伍若抢到并答对则加20分,若抢到但答错则对方加20分.最终得分高的队伍获胜.假设两支队伍在每一题中抢到答题权的概率均为12,且每一题答对的概率分别与初赛中通过对应轮次的概率相等.各队各题作答互不影响.已知甲队获得了冠军,计算第二题是由甲队抢到答题权的概率.21.如图,四面体ABCD 中,平面ABC⊥平面BCD ,AB AC ⊥,AB AC ==1CD =,(1)若AD AB ⊥,证明:CD ⊥平面ABC ;(2)设过直线AD 且与直线BC 平行的平面为α,当BD 与平面ABC 所成的角最大时,求平面α与平面BCD 的夹角的余弦值.22.已知()1f x x =+,()22g x x =+.定义{},min ,,a a ba b b b a≤⎧=⎨≤⎩,设()()(){}min ,2m x f x t g x t=--,R t ∈.(1)若3t =,(i )画出函数()m x 的图象;(ii )直接写出函数()m x 的单调区间;(2)定义区间(),A p q =的长度()L A q p =-.若()*12N n B A A A n =⋃⋃⋃∈ ,(1)i j A A i j n =∅≤<≤ ,则()1()ni i L B L A ==∑.设关于x 的不等式()m x t <的解集为D .是否存在t ,使得()6L D =?若存在,求出t 的值;若不存在,请说明理由.2022学年第二学期宁波市九校联考高二数学试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足i 1i z ⋅=+,则z 对应的点位于()A.第一象限 B.第二象限C.第三象限D.第四象限【答案】A【分析】根据复数的除法运算法则,求出复数z ,即可求解.【详解】由i 1i z ⋅=+,得21i (1i)(i)=1i i iz ++-==--,所以1i z =+,在复平面内对应的点为(1,1)所以对应点位于第一象限.故选:A.2.设集合(){},21x M x y y ==-,()π,cos ,442N x y y x x ⎧⎫==-≤≤⎨⎬⎩⎭,则M N ⋂中元素的个数为()A.2B.3C.4D.5【答案】B【分析】在同一坐标系下画出两集合对应函数图象,交点个数即为交集元素个数【详解】对于函数21xy =-,当0x <时,01y <<;当0x ≥时,0y ≥.对于函数πcos,442y x x =-≤≤,222ππ,πx ⎡⎤∈-⎣⎦,则11y -≤≤且端点处取最大值.两函数图象在同一坐标系下大致如下,则两函数图象有3个交点,即M N ⋂中元素的个数为3个.故选:B3.已知随机变量()211~,X N μσ,()222~,Y N μσ,它们的分布密度曲线如下图所示,则下列说法中正确的是()A.12μμ<,2212σσ< B.12μμ<,2212σσ>C .12μμ>,2212σσ< D.12μμ>,2212σσ>【答案】B【分析】由图结合正态分布曲线特点可得答案.【详解】由图可得随机变量X 的均值比随机变量Y 的均值小,则12μμ<.又由图得,随机变量X 的分布比随机变量Y 的分布更加分散,则2212σσ>.故选:B4.已知平面向量a ,b满足a b a b +=- ,则b a - 在a 上的投影向量为()A.a-r B.aC.b- D.b【答案】A【分析】由已知可得0a b ⋅=,根据投影向量的定义及数量积的运算律求投影向量即可.【详解】由a b a b +=- 知:222222aa ab b a b b-= ,可得0a b ⋅= ,所以b a - 在a上的投影向量为22()a b a a a b a a a a a a⋅-⋅-⋅=⋅=- .故选:A 5.若1sin()43πα+=,(0,)απ∈,则cos 2=α()A.79-B.29±C.29D.29-【答案】D【分析】根据同角三角函数的关系结合角度范围可得22cos(43πα+=-,再根据二倍角公式可得sin[2()]4πα+,结合诱导公式可得cos 2α.【详解】因为(0,)απ∈,所以5(,)444πππα+∈,又13sin()sin 434ππα+=<,所以3(,)44ππαπ+∈,所以22cos()43πα+==-,所以cos 2sin(2sin[2()]2sin()cos()2444ππππααααα=+=+=++=9-故选:D6.在ABC 中,点O 满足2CO OB = ,过点O 的直线分别交射线AB ,AC 于点M ,N ,且AM mAB = ,AN nAC =,则2m n +的最小值为()A.83 B.103C.3D.4【答案】A【分析】利用共线定理的推论可得21133m n+=,然后妙用“1”可得.【详解】由题可知,0,0m n >>,因为AM mAB = ,AN nAC =,所以1AB AM m= ,1AC AN n = ,又2CO OB = ,所以22AO AC AB AO -=-,所以21213333AO AB AC AM AN m n=+=+,因为,,M O N 三点共线,所以21133m n+=,所以2144482(2)()3333333m n m n m n m n n m +=++=++≥+=,当且仅当43321133m nn mm n⎧=⎪⎪⎨⎪+=⎪⎩,即42,33m n ==时,等号成立.所以2m n +的最小值为83.故选:A7.已知()f x 是定义在R 上的奇函数,且()22f =,若对任意的1x ,()20,x ∈+∞,均有()()12121f x f x x x ->-成立,则不等式()11f x x -+>的解集为()A.()()2,02,-+∞B.()(),20,2-∞-C.()(),11,3-∞- D.()()1,13,-+∞【答案】D【分析】构造函数()()g x f x x =-,则()()g x f x x =-在()0,∞+上递增,判断()()g x f x x =-也是是定义在R 上的奇函数,可得()()g x f x x =-在(),0∞-上递增,分类讨论列不等式求解即可.【详解】因为对任意的1x ,()20,x ∈+∞,均有()()12121f x f x x x ->-成立,不妨设2x >1>0x ,则-1x 20x <,所以()()()()12121122f x f x x x f x x f x x ⇒-<--<-,构造函数()()g x f x x =-,则()()g x f x x =-在()0,∞+上递增,因为()f x 是定义在R 上的奇函数,所以()()g x f x x =-也是是定义在R 上的奇函数,所以()()g x f x x =-在(),0∞-上递增,不等式()11f x x -+>化为()()()11010f x x g x --->⇒->,因为()()()()()2222020220f f g g g =⇒-=⇒=⇒-=-=,则()()121231010x g x g x x x ->⎧->⎧⇒⇒>⎨⎨->->⎩⎩,或()()1212111010x g x g x x x ->-⎧->-⎧⇒⇒-<<⎨⎨-<-<⎩⎩;10x -=时,()00g =,不合题意;综上不等式()11f x x -+>的解集为()()1,13,-+∞ ,故选:D.8.三面角是立体几何的重要概念之一.三面角-P ABC 是指由有公共端点P 且不共面的三条射线PA ,PB ,PC 以及相邻两射线之间的平面部分所组成的空间图形.三面角余弦定理告诉我们,若APC α∠=,BPC β∠=,APB γ∠=,平面APC 与平面BPC 所成夹角为θ,则cos cos cos cos sin sin γαβθαβ-=.现已知三棱锥-P ABC ,PA =,3BC =,45APC ∠=︒,60BPC ∠=︒,90APB ∠=︒,则当三棱锥-P ABC 的体积最大时,它的外接球的表面积为()A.18πB.36πC.87π2D.117π2【答案】B【分析】作出图形,作BD PC ⊥,BM ⊥平面APC ,则θ∠=BDM ,先表示出13P ABC APC V S BM -=⋅ ,接着用条件表示成P ABC V PB -=⋅,要使三棱锥-P ABC 的体积最大,则PB PC ⋅最大,利用基本不等式得出3PBPC ==时,其体积最大,然后补全三棱锥成棱柱,根据棱柱外接球半径即可求解.【详解】由题知,45APC ∠=︒,60BPC ∠=︒,90APB ∠=︒,平面APC 与平面BPC 所成夹角为θ,作BD PC ⊥,BM ⊥平面APC ,则θ∠=BDM,由题意得13P ABC APC V S BM -=⋅,210cos cos cos 22cos sin sin 32322γαβθαβ-⨯-==-,()0,πθ∈,6sin 3θ=,62sin sin 32BM BD PB PB θβ=⋅==⋅⋅=⋅,13sin 22APC S PA PC PC α=⋅⋅=⋅ ,所以112322P ABC APC V S BM PC PB PB -=⋅=⋅⋅⋅=⋅ ,要使三棱锥-P ABC 的体积最大,则PB PC ⋅最大,在PBC 中,由余弦定理得,2221cos 22PB PC BC BPC PB PC+-∠==⋅⋅,整理得,229PB PC PB PC +-=⋅,2292PB PC PB PC PB PC +=⋅+≥⋅,即9PB PC ⋅≤,当且仅当3PBPC ==时,等号成立,则PA =,3PB PC BC ===,AB ===因为2222cos 22PA PC AC APC PA PC+-∠==⋅⋅,解得3AC =,所以222PC AC PA +=,222AC BC AB +=,即AC PC ⊥,AC BC ⊥,60BCP ∠=︒,所以补全三棱锥成棱柱,如下图,则四边形BCPD 是菱形,点O 为其外接球的球心,即AD 中点,所以3BP =,2cos30CD PC =⋅⋅︒=6AD ===,所以外接球半径为3,即三棱锥-P ABC 外接球的表面积为24π336π⨯=.故选:B【点睛】三棱锥外接球表面积问题,从以下几个角度分析:(1)面面角的定义以及辨析;(2)求解最值时,基本不等式的利用;(3)几何体割补法的应用;(4)数形结合思想的应用.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列等式成立的是()A.0!0= B.11A A mm n n n --=C.11(1)C (1)C mm n n n m +++=+ D.111C C C mm m n nn -+++=【答案】BC【分析】利用排列数、组合数公式对各选项逐一计算判断作答.【详解】根据阶乘的概念可知,0!1=,故A 错误;()()()111!!!!A A m m n nn n n n n m n m ---===--,故B 正确;因为11(1)!1!1C C (1)!()!1!()!1m m n n n n n n m n m m m n m m +++++===+-+-+,所以11(1)C (1)C m m n n n m +++=+,故C 正确;根据组合数的性质可知11C C C mm m n n n -++=,故D 错误;故选:BC10.以下四个正方体中,满足AB ⊥平面CDE 的有()A. B.C. D.【答案】BD【分析】根据直线与平面内的直线不垂直可判断AC ,根据直线与平面垂直的判定定理判断BD.【详解】对A ,CE AD ∥,π4DAB ∠=,AB ∴与CE 所成角为π4,故AB 与平面CDE 不垂直,故A 错误;对B ,在正方体中,ED ⊥平面ABD ,AB ⊂平面ABD ,所以AB ED ⊥,又AB CE ^,DE CE E ⋂=,,DE CE ⊂平面CDE ,所以AB ⊥平面CDE ,故B 正确;对C ,连接,AF BF ,如图,在正方体中,由正方体面上的对角线相等可知,ABF △为正三角形,所以π3BAF ∠=,又CE AF ∥,AB 与CE 所成的角为π3,所以AB 与平面CDE 不垂直,故C 不正确;对D ,连接,MB BN ,如图,因为AM ⊥平面CMEB ,EC ⊂平面CMEB ,所以AM EC ⊥,又BM EC ⊥,,BM AM M BM AM =⊂ ,平面AMB ,所以EC ⊥平面AMB ,又AB ⊂平面AMB ,所以EC AB ⊥,同理可得ED AB ⊥,再由,,EC ED E EC ED =⊂ 平面ECD ,所以AB ⊥平面CDE ,故D 正确.故选:BD11.已知函数()f x 的定义域为R ,()21f x +是偶函数,()1f x -的图象关于点()3,3中心对称,则下列说法正确的是()A.()()2f x f x =+ B.()203f =C.()()24f x f k x +=-,Z k ∈ D.411()123k i f i k -==-∑,Zk ∈【答案】BCD【分析】根据()21f x +是偶函数可得函数()f x 关于直线1x =对称,由()1f x -的图象关于点()3,3中心对称可得()f x 关于点(2,3)成中心对称,据此可推导出函数为周期函数,判断A ,再由函数的周期求出()20f 判断B ,由周期性及对称性可判断C ,由以上分析利用()()41411()4k ki i f i f i f k -===-∑∑求解可判断D.【详解】因为()21f x +是偶函数,所以(21)(21)f x f x -+=+,可得(1)(1)-+=+f x f x ,故()f x 关于直线1x =对称,因为()1f x -的图象关于点()3,3中心对称,所以()f x 关于点(2,3)成中心对称,所以(2)(2)6f x f x -++=,又由(1)(1)-+=+f x f x 可得()(2)f x f x -=+,所以(2)()6f x f x -+-=,即(2)()6f x f x ++=,所以(4)(2)6f x f x +++=,两式相减可得(4)()0f x f x +-=,即(4)()f x f x +=,所以4T =,故A 错误;由周期4T =,()20(4)(0)f f f ∴==,又(0)(4)6f f +=,所以(0)(4)3f f ==,即()203f =,故B 正确;由周期4T =,()4()f k x f x ∴-=-,Z k ∈,由()(2)f x f x -=+可得,()()24f x f k x +=-,Z k ∈,故C 正确;由上述分析可知(2)(4)3f f ==,又因为(1)(3)6f f +=,所以(1)(2)(3)(4)12f f f f +++=,所以()()41411()4123k ki i f i f i f k k -===-=-∑∑,故D 正确.故选:BCD【点睛】关键点点睛:当函数满足()()f a x f b x +=-时,函数()f x 关于直线2a bx +=对称,当函数满足()()2f a x f b x c ++-=时,函数关于点,2a b c +⎛⎫⎪⎝⎭成中心对称.12.一个不透明的袋子中装有大小形状完全相同的红、黄、蓝三种颜色的小球各一个,每次从袋子中随机摸出一个小球,记录颜色后放回,当三种颜色的小球均被摸出过时就停止摸球.设=i A “第i 次摸到红球”,i B =“第i 次摸到黄球”,i C =“第i 次摸到蓝球”,i D =“摸完第i 次球后就停止摸球”,则()A.()329P D =B.()41227P D A =C.()11223n n n P D ---=,3n ≥ D.()312223n n n n n P D B C ----=,3n ≥【答案】ACD【分析】AC 选项,求出n D 包含的事件数为()12322C n --,从而得到()n P D ,并计算出()3P D ;B 选项,计算出()41227P D A =,()113P A =,利用条件概率公式计算出答案,D 选项,表达出()31223n n n n n P D B C ---=,3n ≥,和()21233n n n n P B C ---=,3n ≥,利用条件概率公式得到答案.【详解】AC 选项,n D =“摸完第n 次球后就停止摸球”,有放回的摸n 次,有3n 种可能,若恰好摸球n 次就停止摸球,则恰好第n 次三种颜色都被摸到,即前()1n -次摸到2种颜色,第n 次摸到第三种颜色,共()12322C n --种情况,则()()1311222322C 3nn n nn P D----==-,3n ≥,()23222239P D -==,AC 正确;B 选项,事件41D A 表示第一次摸到红球,摸到第4次,摸球结束,若第2次或第3次摸到的球为红球,此时有12A 种情况,不妨设第2次摸到的球为红球,则第3次和第4次摸到的球为蓝球或黄球,有2种可能,故有122A 4=种情况,若第2次和第3次都没有摸到红球,则第2次和第3次摸到的球颜色相同,第4次摸到的球和第2,3次摸到的球颜色不同,故有22A 2=种情况,故()41426n D A =+=,其中摸4次球可能得情况有4381=种情况,故()41761228P D A ==,其中()113P A =,故()()()4141129P D A P D A P A ==,B 错误;D 选项,12n n n D B C --表示“第()2n -次摸到蓝球,第()1n -次摸到黄球,第n 次摸到红球,停止摸球”,则前()3n -次摸到的球时蓝球或红球,故有32n -种可能,故()31223n n n n n P D B C ---=,3n ≥,12n n B C --表示“在前n 次摸球中,第()2n -次摸到蓝球,第()1n -次摸到黄球”,故有23n -种可能,故()21233n n n n P B C ---=,3n ≥,则()312223n n n n n P D B C ----=,3n ≥,D 正确.故选:ACD【点睛】常见的条件概率处理方法,其一是用样本点数的比值处理,需要弄情况事件包含的样本点数,其二是用概率的比值处理,也可以缩小样本空间,从而确定概率,解决实际问题的关键在于分析情况基本事件.三、填空题:本题共4小题,每小题5分,共20分.13.已知实数a ,b 满足25a bm ==且1112a b +=,则m =______.【答案】100【分析】根据指数与对数的互化公式,表示出,a b ,再结合换底公式表示出1112a b +=,最后结合对数运算即可求解【详解】由25a bm ==可得2511log ,log log 2,log 5m m a m b m a b==⇒==,又1112a b +=,即1log 2log 5log 102m m m +==,所以1210m =,即100m =故答案为:10014.现有一枚质地不均匀的硬币,若随机抛掷它两次均正面朝上的概率为12,则随机抛掷它两次得到正面、反面朝上各一次的概率为______;若随机抛掷它10次得到正面朝上的次数为ξ,则()E ξ=______.(第一空2分,第二空3分)【答案】①.1##1-②.【分析】根据独立事件的乘法公式求出抛掷一枚硬币正面朝上概率p ,再由独立重复试验求出正面、反面朝上各一次的概率为,由二项分布的期望公式求期望.【详解】设这枚硬币正面朝上的概率为p ,反面朝上的概率为1p -,则两次正面朝上的概率为212p =,解得2p =,所以随机抛掷两次得到正面,反面朝上各一次的概率为()1222C 121122P p p ⎛⎫=-=⨯-= ⎪ ⎪⎝⎭.由题易知随机变量ξ服从二项分布ξ~102,2B ⎛⎫⎪ ⎪⎝⎭,则()102E ξ=⨯=.1;已知函数()()ln 2e ,0234,0x a x f x x ax a x -⎧⎪-<=⎨-++-≥⎪⎩,若()f x 有4个零点,则实数a 的范围是______.【答案】41,3⎛⎤ ⎥⎝⎦【分析】由题可得方程()ln e x a -=与方程22340,0x ax a x -++-=≥各有两个根,对于前者转化为函数()()ln ex g x -=图象与直线y a =有两个交点,后者由判别式结合韦达定理可得a 范围,综合后可得答案.【详解】当0x <时,()()()ln ,1ln ln ,10x x x x x ⎧-≤-⎪-=⎨---<<⎪⎩,则函数()()()()ln ln ln e ,1e1e,10x x x x x g x x x ----⎧=-<-⎪==⎨=--≤<⎪⎩在(),1-∞-上单调递减,在[)10-,上单调递增,据此可得()g x 大致图象如下,又()ln e x a -=方程的解的个数相当于函数()g x 图象与直线y a =交点个数,方程22340,0x ax a x -++-=≥最多2个根,()f x 有4个零点,则方程()ln e x a -=与方程22340,0x ax a x -++-=≥各有两个根.设方程22340,0x ax a x -++-=≥两根为12,x x ,则212121Δ41216041203430a a a a x x a x x a >⎧⎪=+->⎪⇒<≤⎨+=>⎪⎪=-≥⎩.故答案为:41,3⎛⎤ ⎥⎝⎦.【点睛】16.已知平面向量a ,b ,()1,2i c i =满足222a b a b ==⋅= ,1i c a -= ,则()1222R c b c b λλλ-+-∈ 的最小值为______.【答案】53-##35-+【分析】求出向量,a b的模及夹角,记1122,,2,,2OA a OB b OB b OC c OC c λ=====' ,得出对应点的轨迹,利用数形结合求最值.【详解】由||2||22a b b ==⋅=,即21cos ,2a b ⨯⨯= ,所以π,4a b = ,记1122,,2,,2OA a OB b OB b OC c OC c λ'=====,因为1i c a -= ,所以1C 在以A 为圆心,1为半径的圆上,2C 在以A '为圆心,2为半径的圆上,其中(2,0),(4,0)A A ',所以11222122222||||c B b c b c b c b C B C λλλλ-+-=-'+='+-,作A 关于直线l (OB所在直线)的对称圆,1C 的对称点记为3C ,知1(0,2)A ,则1232B C B C B C B C +=+'''',如图,由图可知,当132,,,,A C B C A ''共线时,32||||C B C B ''+存在最小值,因为111645,1,2A A A A r r '=+===',所以32||||C B C B ''+最小值为53-.故答案为:53-【点睛】关键点点睛:利用向量的的几何表示,原问题转化为求32||||C B C B ''+最小值,数形结合,利用共线线段最短得解.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且______,请从下列两个条件中任选一个填入上方的横线中作为已知条件,并解答本题(如果选择多个条件分别解答,则按第一个解答计分):①sin sin 2B C c a C +=;②()2224ABC S b c a =+- ,(1)求A ;(2)若D 为边BC 上一点,且2CD AD BD ==,试判断ABC 是锐角三角形、直角三角形还是钝角三角形,并说明理由.【答案】(1)π3A =(2)直角三角形,理由见解析【分析】(1)选①:利用诱导公式化简,再由正弦定理边化角,然后由二倍角公式化简可得;选②:根据面积公式和余弦定理列方程可解;(2)根据已知先得1233AD AB AC =+,然后平方,联立余弦定理求解可得2c b =,a =,然后可判断三角形形状.【小问1详解】若选①:πsinsin cos 222B C A A c c c +-== ,cos sin 2A c a C ∴=,sin cos sin sin 2A C A C ∴=,()0,π,sin 0C C ∈> ,cossin 2sin cos 222A A AA ∴==,π0,,cos 0222A A ⎛⎫∈> ⎪⎝⎭,1sin 22A ∴=,所以π26A =,解得π3A =.若选②:()2223332cos cos 442ABC S b c a bc A bc A =+-=⨯= ,31cos sin 22A bc A =,sin A A =,tan A ∴=,因为()0,πA ∈,故π3A =.【小问2详解】2CD BD AD ==Q ,212,,333AD a CD a BD a ∴===且2BD DC = 22AD AB AC AD ∴-=- ,即1233AD AB AC =+ ,222144999AD AB AC AB AC ∴=++⋅uuu r uu u r uuu r uu u r uuu r,22241429999a cb bc ∴=++,即222442a c b bc =++①,又由余弦定理得222a b c bc =+-②,联立①②可得2c b =,a =,从而222+=a b c ,故ABC 是直角三角形.18.已知函数()sin cos (0)f x x x ωωω=+>的图象关于直线π8x =对称,且()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值.(1)求()f x 的单调增区间;(2)已知函数()()log 242xa g x a a =-+(0a >且1a ≠),对任意1ππ,42x ⎡⎤∈⎢⎣⎦,总存在[]21,2x ∈,使得()()12f x g x ≤,求实数a 的取值范围.【答案】(1)()3πππ,πZ 88k k k ⎡⎤-++∈⎢⎥⎣⎦(2)2a ≥或112a ≤<.【分析】(1)由两角和的正弦公式化简,再由对称轴及在π0,6⎛⎫⎪⎝⎭上没有最小值求出解析式,由正弦型函数的单调性求单调区间即可;(2)根据存在性及任意性问题转化为()()12max max f x g x ≤,分别利用三角函数及对数型函数的性质求最值,解不等式即可.【小问1详解】()πsin cos 4f x x x x ωωω⎛⎫=+=+ ⎪⎝⎭.()f x 的图象关于直线π8x =对称.ππππ,Z 842k k ω∴+=+∈,解得82,Z k k ω=+∈.当π0,6x ⎛⎫∈ ⎪⎝⎭时,ππππ,4464x ω⎛⎫+∈+ ⎪⎝⎭.()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值.ππ3π642ω∴+≤,解得152ω≤.又0ω>,所以2ω=,所以()π24f x x ⎛⎫=+ ⎪⎝⎭.令()πππ2π22πZ 242k x k k -+≤+≤+∈,解得()3ππππZ 88k x k k -+≤≤+∈.所以()f x 的单调增区间为()3πππ,πZ 88k k k ⎡⎤-++∈⎢⎥⎣⎦.【小问2详解】任意1ππ,42x ⎡⎤∈⎢⎣⎦,均存在[]20,2x ∈,使得()()12f x g x ≤.()()12max max f x g x ∴≤.1ππ,42x ⎡⎤∈⎢⎣⎦Q .1π3π5π2,444x ⎡⎤∴+∈⎢⎣⎦.()m x 11a sin 1π24f x x ⎛⎫∴ +≤≤=⎪⎝⎭.又log ,242x a y t t a a ==-+Q (0a >且1a ≠)单调性相同,()()log 242x a g x a a ∴=-+在定义域上是增函数.()()()2max 2log 2421a g x g a a ∴==-+≥.21242a a a a >⎧∴⎨-+≥⎩或2010242a a a a <<⎧⎨<-+≤⎩2a ∴≥或112a ≤<.19.航班正点率是指航空旅客运输部门在执行运输计划时,航班实际出发时间与计划出发时间较为一致的航班数量与全部航班数量的比率.人们常用航班正点率来衡量一个航空公司的运行效率和服务质量.现随机抽取10家航空公司,对其近一年的航班正点率和顾客投诉次数进行调查,得到数据如下:航空公司编号12345678910航班正点率i x /%82777776747371709169顾客投诉次数i y /次2158796874937212218125整理数据得:10153620iii x y=≈∑,102158150ii x =≈∑,102164810ii y =≈∑,101760i i x ==∑,101730i i y ==∑70≈.(1)(i)证明:样本相关系数niix ynx yr -=∑;(ii )根据以上数据计算样本相关系数(结果保留2位小数),并由此推断顾客投诉次数与航班正点率之间的线性相关程度(若0.81r ≤≤,则认为线性相关程度很强;若0.30.8r ≤<,则认为线性相关程度一般;若0.3r <,则认为线性相关程度很弱).(2)用一元线性回归模型对上表中的样本数据进行拟合,得到顾客投诉次数关于航班正点率的经验回归方程为5y x a=-+.现有一家航空公司拟通过加强内部管理来减少由于公司自身原因引起的航班延误次数,并希望一年内收到的顾客投诉不超过73次,试估计该公司的航班正点率应达到多少?参考公式:样本相关系数()()nii xxy y r --=∑【答案】(1)(i )证明见解析;(ii )0.89-;顾客投诉次数与航班正点率之间的线性相关程度很强(2)76%.【分析】(1)(i )将()()1niii x x yy =--∑展开,结合平均数意义化简可得()()11nni ii ii i x xy y x y nx y ==--=-∑∑,然后分别用,i x x ,i x x 替代,i y y ,用,i y y 分别替代,i x x 可证;(ii )根据所给数据代入公式计算,然后可作出判断;(2)利用样本中心点求 a,然后根据回归方程解不等式可得.【小问1详解】(i )证明:()()()11ni i i i ni i i i x x x y x y x y y y x y===+----∑∑1111n n nni i i i i i i i x y x y x y x y=====--+∑∑∑∑1111nn nni i i i i i i i x y y x x y x y=====--+∑∑1)()ni i i x y y nx x ny nx y==--+∑1ni i i x y nx y ==-∑,在上式中分别用,i x x 替代,i y y ,得()22211nni i i i x xx nx ==-=-∑∑,同理,也有()2211nni ii i y yyn y ==-=-∑∑,故样本相关系数n i ix y nx yr -=∑.(ii )可知10117610i i x x ===∑,10117310i i y y ===∑.10110536201076731860i i i x y x y =∴-≈-⨯⨯=-∑,10222110581501076390ii xx =-≈-⨯=∑,1022211064810107311520ii y y =-≈-⨯=∑,1010iix yx yr -∴=∑620.8970=≈-≈-,故顾客投诉次数与航班正点率之间的线性相关程度很强.【小问2详解】557673453a x y =+=⨯+=$令545373ˆyx =-+≤,得76x ≥.即该公司的航班正点率应达到76%.20.2023年4月23日是第28个“世界读书日”.为了倡导学生享受阅读带来的乐趣、尊重和保护知识产权,立德中学举办了一次阅读知识竞赛.初赛中每支队伍均要参加两轮比赛,只有两轮比赛均通过的队伍才能晋级.现有甲、乙两队参赛,初赛中甲队通过第一轮和第二轮的概率均为34,乙队通过第一轮和第二轮的概率分别为35,23,且各队各轮比赛互不影响.(1)记甲、乙两队中晋级的队伍数量为X ,求X 的分布列和数学期望;(2)经过激烈的比拼,甲、乙两队成功进入决赛争夺冠军.决赛共有两道抢答题.第一题中,某支队伍若抢到并答对则加10分,若抢到但答错则对方加10分.第二题中,某支队伍若抢到并答对则加20分,若抢到但答错则对方加20分.最终得分高的队伍获胜.假设两支队伍在每一题中抢到答题权的概率均为12,且每一题答对的概率分别与初赛中通过对应轮次的概率相等.各队各题作答互不影响.已知甲队获得了冠军,计算第二题是由甲队抢到答题权的概率.【答案】(1)分布列见解析,7780(2)57【分析】(1)设“甲队晋级”为事件M ,“乙队晋级”为事件N ,求得9()16P M =,2()5P N =,得到X 的可能取值为0,1,2,求得相应的概率,出分布列,结合期望的公式,即可求解;(2)记事件A =“甲队获得冠军”,B =“该题由甲队抢到答题权”,结合条件概率的公式,即可求解.【小问1详解】解:设“甲队晋级”为事件M ,“乙队晋级”为事件N ,可得339()4416P M =⨯=,322()535P N =⨯=,则随机变量X 的可能取值为0,1,2,可得()922101116580P X ⎛⎫⎛⎫==-⨯-= ⎪ ⎪⎝⎭⎝⎭;()92924111116516580P X ⎛⎫⎛⎫==-⨯+⨯-= ⎪ ⎪⎝⎭⎝⎭.()929216540P X ==⨯=.所以随机变量X 的分布列为X012P21804180940则期望()214197701280804080E X =⨯+⨯+⨯=.【小问2详解】解:根据题意,设甲乙两队通过初赛的事件分布为12,A A ,可得12339322(),()4416535P A P A =⨯==⨯=,即甲乙进入决赛的概率分别为916和25,记事件A =“甲队获得冠军”,B =“该题由甲队抢到答题权”,可得()()()()()191393||21625160P A P B P A B P B P A B =+=⨯+⨯=,又由()()()199()(|)()21632P AB P AB P B P B P A B P B =⋅==⨯=,故()()()()()()9|532|937160P AB P B P A B P B A P A P A====.21.如图,四面体ABCD 中,平面ABC⊥平面BCD ,AB AC ⊥,AB AC ==1CD =,(1)若AD AB ⊥,证明:CD ⊥平面ABC ;(2)设过直线AD 且与直线BC 平行的平面为α,当BD 与平面ABC 所成的角最大时,求平面α与平面BCD 的夹角的余弦值.【答案】(1)证明见解析(2)217【分析】(1)利用面面垂直的性质定理证得⊥AE 平面BCD ,进而得到AE CD ⊥,从而利用线面垂直的判定定理依次证得AB ⊥平面ACD ,CD ⊥平面ABC ;(2)先由题意推得BD 与平面ABC 所成的角最大时DF 的值,再推得平面α与平面BCD 的夹角的平面角为AGE ∠,从而在Rt AEG △中求得所求.【小问1详解】过点A 作AE BC ⊥,垂足为E ,平面ABC⊥平面BCD ,平面ABC ⋂平面BCD BC =,AE BC ⊥,AE ⊂平面ABC ,AE ∴⊥平面BCD ,又CD ⊂平面BCD ,AE CD ∴⊥,AD AB ⊥ ,AB AC ⊥,AC AD A = ,AC AD ⊂ 平面ACD ,AB ∴⊥平面ACD ,又CD ⊂平面ACD ,AB CD ∴⊥,又,,AE AB A AE AB =⊂ 平面ABC ,故CD ⊥平面ABC .【小问2详解】过点D 作DF BC ⊥,垂足为F ,平面ABC⊥平面BCD ,平面ABC ⋂平面BCD BC =,DF BC ⊥,DF ⊂平面BCD ,DF ⊥∴平面ABC ,DBC ∴∠是BD 与平面ABC 所成的角,在ABC 中,AB AC ⊥,2AB AC ==,则2BC =,故sin sin CD BC DBC BDC=∠∠,即12sin sin DBC BDC =∠∠,则1sin sin 2DBC BDC ∠=∠,∴当sin 1BDC ∠=,即CD BD ⊥时,sin DBC ∠最大,且最大值为12,此时π6DBC ∠=,BD =,32DF =,记l α=I 平面BCD ,过点E 作EG l ⊥,垂足为G ,连接AG ,//BC αQ ,BC ⊂平面BCD ,l α=I 平面BCD ,//l BC ∴,故平面ADG 就是平面α,AE ^Q 平面BCD ,AE l ∴⊥,EG l ⊥Q ,EG AE E ⋂=,,EG AE ⊂平面AGE ,l ∴⊥平面AGE ,又AG ⊂平面AGE ,l AG ∴⊥,AGE ∴∠是平面α与平面BCD 的夹角,则π02AGE <∠<,又因为DF BC ⊥,//l BC ,所以//GE DF ,所以四边形DFEG 是平行四边形,故2GE DF ==,则在Rt AEG △中,2AG ==,所以平面α与平面BCD的夹角余弦值为cos GE AGE AG ∠===..22.已知()1f x x =+,()22g x x =+.定义{},min ,,a a b a b b b a≤⎧=⎨≤⎩,设()()(){}min ,2m x f x t g x t =--,R t ∈.(1)若3t =,(i )画出函数()m x 的图象;(ii )直接写出函数()m x 的单调区间;(2)定义区间(),A p q =的长度()L A q p =-.若()*12Nn B A A A n =⋃⋃⋃∈ ,(1)ijA Ai j n =∅≤<≤ ,则()1()nii L B L A ==∑.设关于x 的不等式()m x t <的解集为D .是否存在t ,使得()6L D =?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)(i )作图见解析;(ii )单调减区间为(),3-∞,()5,6,单调增区间为()3,5,()6,+∞(2)存在,3t =【分析】(1)(i )3t =时,(){}2min 31,1238m x x x x =-+-+,求出方程221238x x x -=-+的根,即可画出()m x 的图象;(ii )由()m x 的图象即可写出其单调区间;(2)由()min 1m x =得不等式()m x t <有解的必要条件是1t >,再对t 的值分情况讨论即可.【小问1详解】(i )若3t =,则()31f x t x -=-+,()()222621238g x t x x x -=-+=-+.(){}2min 31,1238m x x x x ∴=-+-+.令221238x x x -=-+,得15=x ,28x =.故函数()m x 的图象如图所示.(ii )由函数()m x 的图象可知()m x 的单调减区间为(),3-∞,()5,6,单调增区间为()3,5,()6,+∞.-【小问2详解】()min 1f x = ,()min 2g x =.()min 1m x ∴=.∴不等式()m x t <有解的必要条件是1t >.①当12t <≤时,如图①所示,令()m x t <,即()f x t <,得()1,21D t =-.()222L D t ∴=-≤,不符合题意.。
浙江省苍南县巨人中学等三校2013-2014学年高二下学期第二次联考生物试题 Word版含答案
高二下学期第二次联考生物试题一、选择题(本大题共35小题,每小题2分,共70分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.国家癌症研究中心最近公布了20种抗癌蔬菜,其中红薯位列榜首。
红薯的块状根中贮藏有丰富的多糖,下列属于红薯中的多糖的是A .蔗糖、麦芽糖B .果糖、糖元C .葡萄糖、纤维素D .淀粉、纤维素2.用纤维素酶除去植物细胞的细胞壁,而细胞膜成分却不受任何影响,这一现象体现酶的A .催化性B .专一性C .多样性D .高效性3.在细胞周期中,DNA 的复制发生在A .G 1期B .S 期C .G 2期D .M 期 4.在某细胞培养液中加入32P 标记的磷酸分子,一段时间内分离出细胞的ATP ,发现其含量变化不大,但部分A TP 的末端磷酸基团已带上放射性标记,该现象不能..说明 A .ATP 中远离A 的磷酸基团容易脱离B .部分32P 标记的A TP 是重新合成的C .ATP 是细胞内的直接能源物质D .该过程中ATP 既有合成又有分解5.对于多细胞生物而言,下列有关细胞生命历程的说法正确的是A .正常情况下,细胞分化是可逆的B .细胞癌变是所有细胞都要经历的一个阶段C .细胞衰老时细胞呼吸的速率减慢D .细胞凋亡是细胞癌变的结果6.需氧呼吸过程中与柠檬酸循环有关的酶分布在哪里?A .线粒体内膜B .细胞溶胶C .线粒体基质D .线粒体基质和线粒体内膜7.图甲表示酶催化反应过程的示意图,图乙表示在最适温度下该酶促反应生成氨基酸的量与时间的关系曲线。
下列叙述错误..的是A .图甲中b 表示二肽B .图甲中a 与b 结合后,a 的形状会发生变化图甲C.适当降低温度,图乙中得M值不变D.图乙中c-d段形成的主要原因是酶的数量有限8.下图表示生物体内的某化学反应,下列有关该反应的叙述中错误..的是A.需要ATP合成酶B.属于水解反应C.会有能量变化D.反应速率与温度有关9.测得苹果果实在一段时间内,CO2的释放量比O2的吸收量大,由此可以推断出果实A.需氧呼吸占优势B.需氧呼吸与厌氧呼吸消耗的葡萄糖相等C.厌氧呼吸占优势D.既进行厌氧呼吸又进行需氧呼吸10.探索温度对酶活性影响的实验,需进行如下步骤①取3支试管,编号并注入2mL淀粉溶液;②观察实验现象;③向各试管滴1滴碘液;④向各试管注入1mL唾液并摇匀,并在各自的温度下静置5min;⑤将3支试管分别放在37℃的温水、沸水和冰块中维持温度5min最合理的实验顺序应为A.①→②→③→④→⑤ B.①→③→②→④→⑤C.①→④→⑤→③→② D.①→⑤→④→③→②11.如图所示,科学家对单细胞伞藻的幼体嫁接,将甲的伞柄嫁接到乙的假根上,长出了伞帽。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年宁波三校联考高二下学期历史期末卷 命题学校:象山三中 审核学校:李惠利中学 卷I (60分) 一、单项选择题(每小题1.5分,共60分) 1.“事在四方,要在中央;圣人执要,四方来效。”下列选项体现这一思想的是 ( ▲ ) A.实行郡县制 B.废丞相、设内阁 C.实行宗法制 D.设军机处 2.著名历史学家钱穆曾说:“故中国政制之废丞相,统‘政府’于‘王室’之下,真不免为独裁专制之黑暗所笼罩者,其事乃起于明而完成于清,则相沿亦已六百年之久。”对其理解正确的是 ( ▲ ) A.明朝废丞相造成了皇权不断强化 B.在明朝以前政府并不完全直接统属于王室 C.明朝以前的政府采取集体决策方式 D.明清两代都形成了专制集权的社会 3.某人为了让弟弟顺利取得任官的机会,故意在分家时,将优厚的部分归于自己,让弟弟取得贫瘠的土地。乡里民众因此盛赞其弟“能让”,故推荐这位弟弟参加政府的任官考试。这个故事里的选官制度所依据的标准最早是何时产生的? ( ▲ ) A.春秋战国 B.两汉 C.魏晋 D.隋唐 4.柳宗元在《封建论》中说:“秦有天下,裂都会而为之郡邑,废侯卫而为守宰(宰:县令)……汉有天下,矫秦之枉,徇周之制,剖海内而立宗子,封功臣。……郡国居半,时则有叛国而无叛郡,秦制之得亦以明矣。”柳宗元这段话实际否定的是 ( ▲ ) A.西周时期形成的分封制 B.秦朝建立的郡县制 C.统一货币的制度 D.西汉郡国并行制 5.义和团运动期间,一篇文章说:“夫中国外交之起,处于不得已而成互市(对外通商),其间丧师辱国,赔款割地,盖无约(条约)不损,无战不败,故其时通国君臣上下,以复仇为雪耻,以积愤思报怨,以下令逐客(驱逐外国人)为最快意,以闭关绝市为复见太平。其处势应变,虽曰非宜,其抗志负气,殆非无取(可取)。”下列最能说明该材料中作者对义和团运动的态度的是 ( ▲ ) A.列强侵略是义和团运动的原因 B.义和团的斗争方式不当 C.义和团反抗侵略的精神值得赞扬 D.材料作者有盲目排外的倾向 6.冯子超在《中国抗战史》中这样评价某战役的胜利:“顶多不过是使日本占领徐州作为征服中国的初步计划受到一个重大的打击、延缓一些时候罢了。”作者的观点是 ( ▲ ) A.中国人的抵抗毫无作用 B.台儿庄战役不能改变会战全局 C.平型关大捷的意义有限 D.作者是亲日的汉奸 7.费正清《伟大的中国革命》中认为:“从1860年开始的40年是中国革命明显的孕育时期”这说明这一时期对革命有着重要正面推动的因素已经出现,这些因素是: ( ▲ ) ①民族资本主义产生并逐步发展 ②社会思想上受到了一次启蒙 ③清政府腐败统治下阶级矛盾的加深 ④外国侵略不断加重下民族矛盾的激化 A.②③ B.②③④ C.①② D.①②③④ 8.有人这样评价近代史上的列强侵华:“一半是残忍的破坏和掠夺,一半却是客观上的建设和推动。”最能体现这一特点的一项是 ( ▲ ) A.割占中国大片领土 B.从中国掠走大量贵金属 C.进行惨无人道的大屠杀 D.在通商口岸投资设厂 9.梁启超评价辛亥革命具有“空前绝后”的历史意义,“第一,觉得凡不是中国人都没有权来管中国人的事;第二,觉得凡是中国人都有权管中国人的事”。该观点的依据是 ( ▲ ) A.辛亥革命使民主共和观念深入人心 B.革命使国民的民族民主意识增强 C.革命打击了帝国主义侵略势力 D.革命促进了民众的觉醒 10.二百年来,天安门直接见证了:①古代专制帝王的倒台;②新民主主义革命的开端; ③中华民国政府的倒台;④中华人民共和国的诞生 ( ▲ ) A.①②③ B.①③④ C.②③④ D.①②④ 11.为庆祝中华人民共和国成立六十周年,大型音乐舞蹈史诗《复兴之路》在9月23日至10月5日在北京人民大会堂隆重上演。将1840年到1921年中国共产党成立前80多年的历史,通过《惊梦》《山河祭》《辛亥童谣》《曙色》4个节目生动地表现了出来,反映了民族觉醒的痛苦与艰难。下列能反映“惊梦”“山河祭”“曙色”的历史事件是 ( ▲ ) A.鸦片战争、太平天国、洋务运动 B.鸦片战争、甲午战争、五四运动 C.《南京条约》、辛亥革命、新文化运动 D.甲午战争,辛丑条约、中共成立 12.2010年上海举办世界博览会,显示了21世纪初中国经济发展的强大,也大大提高了中国的国际地位。一百多年前,中英两国谈判,英国选择了上海为通商口岸,在以后的若干年中,英国可以在上海获得的特殊条款有 ( ▲ ) ①关税协商 ②割让土地 ③自由贸易 ④开设工厂 A.①③ B.③④ C.①②④ D.①③④ 13.1949年,前美国驻北平总领事柯乐柏曾以“总领事”身份写信给中华人民共和国外交部,信件被原封不动地退回。这表明 ( ▲ ) A.美国承认新中国为合法政府 B.新中国要清除帝国主义残余势力 C.新中国不承认旧中国建立的外交关系 D.中华人民共和国的合法性不需要美国承认 14.2009年10月1日,为庆祝新中国成立六十周年,首都各界在天安门广场举行了盛大的阅兵式和联合晚会。60年前的10月1日标志着中国 ( ▲ ) A.进入新民主主义社会 B.进入社会主义社会 C.得到了世界各国的认同与支持 D.取得了近百年来第一次反侵略战争的全面胜利 15.胡锦涛总书记在2008年底纪念改革开放30周年大会上,说了一句北方方言“不折腾”,引来与会官员会心一笑,但如何将这三个字翻译成英文却让海内外媒体伤透了脑筋。下列在中国现代史上出现过的违背生产力与生产关系规律的“大折腾”的事件是 ( ▲ ) A.三大改造 B.“大跃进” C.人民公社 D.“文化大革命” 16.实现祖国的完全统一是海内外中华儿女的共同心愿,是维护国家主权和领土完整的要求。为早日解决台湾问题,实现祖国统一大业,1979年元旦,全国人大常委会发表《告台湾同胞书》,全国人大常委会此举的背景主要是 ( ▲ ) A. 工作中心转移到经济建设上的必然结果 B. “一个中国”的原则获得两岸认可 C. 中国原则的坚定性和策略的灵活性 D. 运用“一国两制”构想推进祖国统一 17.下图是一张拍摄于1977年北京、后被中国革命历史博物馆收藏的珍贵图片《上访者》。该照片反映的历史信息包括 ( ▲ ) ①计划经济体制下人们群众的物质生活贫困 ②“文革”结束后农民民主法制意识大大增强 ③农民依然保有传统“告御状”的行为 ④改革开放以来城市流动人口增多 A.①②④ B.①③ C.①② D.②④ 18.一份美国文件记载:“在很机密的基础上,我想请你让你的助理人员起草一份研究材料,对我们在联合国接纳中国问题上采取什么方针提出建议。我认为,我们没有足够的票数去阻挡。……我们确实需要解决的问题是,我们怎样才能逐步造成一种形势,使我们既能保持对台湾的义务,而又不致遭到联合国接纳中国人的抨击。”这一记载反映的是 ( ▲ ) A.在恢复中国在联合国合法席位问题上,美国进退两难 B.“二战”结束时期,美国在联合国常任理事国席位安排上的考虑 C.中国坚持和平共处的外交原则,得到了发展中国家的支持 D.在联合国接纳中国的问题上,美国希望“双代表”制能实现 19.2009年11月16日,“侬好”,美国总统奥巴马一句美国版“上海话”,作为开场白与数百名上海大学生开始了对话。美国总统奥巴马的这句美国版“上海话”在一定程度上也反映了上海在中美关系中的开创性地位,下列事件中最能体现这一特点的是 ( ▲ ) A.中美关系开始正式建交 B.亚太经合组织会议的召开 C.中美关系开始正常化 D.上海浦东的积极开发、开放 20. 新中国民主政治建设中最早建立的制度是 ( ▲ ) A.人民代表大会制度 B. 民族区域自治制度 C. 共产党领导的多党合作和政治协商制度 D.村民民主自治制度 2l、中国古代一位大臣向皇帝进言:“臣闻殷周之王千余岁,封子弟功臣,自为枝辅。今陛下有海内,而子弟为匹夫,卒有田常、六卿之臣,无辅拂,何以相救哉?事不师古而能长久者, 非所闻也。”这位大臣实际上主张 ( ▲ ) A、反对郡县制 B、反对分封制 C、改革中央官制 D、建立中央集权制22、《资治通鉴》载:“国家本置中书、门下以相监察,中书诏敕或有差失,则门下当行驳正。” 材料涉及的政治制度 ( ▲ ) (A)确立于秦朝,汉武帝时期完善 (B)标志着君主专制制度达到顶峰 (C)极大地提高了政府工作效率 (D)削弱了君权,突出了臣下的作用 23、孟德斯鸠说:“中国是一个专制的国家。它的原则是恐怖。在最初的那些朝代,政府的专制精神也许稍微差些;但是,今天的情况却正好相反。”下列最能够反映引文中“今天的情况却正好相反”含义的史实是 ( ▲ ) (A)明朝废除宰相制度 (B)唐朝确立并完善了三省六部制 (C)清朝设置军机处 (D)清朝延续明朝的内阁制度 24、据说明太祖曾经写诗一首描述自己的辛劳:“百僚未起朕先起,百僚已睡朕未睡。不如江南富足翁,日高丈五犹拥被。”为解决上述问题,明太祖 ( ▲ ) (A)设置殿阁大学士以备顾问 (B)选拔翰林院官员人值文渊阁 (C)授予内阁大学士以票拟权 (D)设六部分理全国政务 25、《上海县竹枝词》有诗云:“卅年求富更求强,造炮成船法仿洋。海面未收功一战,总归虚牝掷金黄”与上述内容有关的历史事件是 ( ▲ ) (A)第二次鸦片战争 (B)中法马尾海战 (C)中日甲午战争 (D)八国联军侵华 26、当甲午中日战争正在进行时,恩格斯就预言:“中日战争意味着古老中国的终结,意味着它的整个经济基础全盘的却是逐渐地革命化。”其中的“革命化”是指 ( ▲ ) (A)将导致资产阶级革命 (B)将发生推翻清朝封建统治的革命 (C)民族资本主义将成为中国经济的主体 (D)列强将加强资本输出,客观上刺激中国资本主义的初步发展 27、陕北民歌《移民歌》唱道:“山川秀,天地平,毛主席领导陕甘宁。迎接移民开山林,咱们边区遍地红。”该民歌所反映的内容最早可能发生于 ( ▲ ) (A)北伐战争时期 (B)抗日战争时期 (C)解放战争时期 (D)三大改造时期 28、李大钊说:“太平天国禁了鸦片,却采用了宗教:不建设民国,而建设天国,这是他们失败的一个重要原因。”这段话主要是指太平天国 ( ▲ ) (A)没有现实的革命目标 (B)对西方列强侵略缺乏警觉 (C)缺乏科学理论指导 (D)革命精神不彻底
