第03讲 规律探究性问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)
第10讲 折叠翻转性问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)

12019年中考数学总复习巅峰冲刺专题10折叠翻转性问题【难点突破】着眼思路,方法点拨, 疑难突破;有关图形折叠的相关计算,首先要熟知折叠是一种轴对称变换,即位于折痕两侧的图形关于折痕成轴对称;然后根据图形折叠的性质,即折叠前、后图形的对应边和对应角相等,对应点的连线被折痕垂直平分进行相关计算,折叠问题常常伴随着勾股定理,这是解决问题的关键所在.图形的折叠通常和动点问题结合在一起进行考查,常见的问题类型有以下3种:(1)求线段的取值范围;(2)求最值问题;(3)分类讨论线段长度. 其中第(3)种类型在河南中招考试中为常考类型,解决此类型题,一般运用等量代换,并结合勾股定理或相似三角形的性质来构造方程,进而求解线段的长度.【名师原创】原创检测,关注素养,提炼主题;【原创1】如图,把一张长方形纸片ABCD 进行折叠之后,恰好使其对角顶点A 与C 能够重合,且使的折痕与BC 的交点恰好在其三等分点处,则下列图形长度能够满足题意的是( )A .AB=10,BC=20B . AB=10,BC=30C . 3,BC=20D . 3,BC=30【原创2】如图,D 是等边△ABC 边AB 上的一点,且AD :DB=1:3,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE :CF=___.2 【原创3】如图1,矩形OABC 的对角线OB 、AC 相交于点D,,OC =6,sin ∠BOC=45.反比例函数y =k x(x >0)的图像经过点D ,(1)求反比例函数的关系式;(2)如图2,将ΔA OC 沿过C 点的直线折叠,使点A 落在x 轴上的点E 处,折痕所在直线交y 轴正半轴于点F ,求直线CF 的解析式.(3)如图3,将图2中的直线CF 向上平移m 个单位,与反比例函数y =k x(x >0)的图像相交,当直线与反比例函数的图像只有一个交点时,求m 的值.3 【典题精练】典例精讲,运筹帷幄,举一反三;【例题1】求线段的取值范围:如图,有一矩形纸片ABCD ,AB=8,AD=17,将此矩形纸片折叠,使顶点A 落在BC 边的A′处,折痕所在直线同时经过边AB 、AD (包括端点),设BA′=x ,则x 的取值范围是 .【例题2】求最值问题:如图,现有一张边长为4的正方形纸片ABCD ,点P 为正方形AD 边上的一点(不与点A ,D 重合),将正方形纸片折叠,使点B 落在P 处,点C 落在G 处,PG 交DC 于点H ,折痕为EF ,连结BP ,BH.(1)求证:∠APB =∠BPH.(2)当点P 在边AD 上移动时,△PDH 的周长是否发生变化?并证明你的结论.(3)设AP 为x ,四边形EFGP 的面积为S ,求出S 关于x 的函数表达式,试问S 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.4【例题3】分类讨论线段长度.对一张矩形纸片ABCD 进行折叠,具体操作如下:第一步:先对折,使AD 与BC 重合,得到折痕MN ,展开.第二步:再一次折叠,使点A 落在MN 上的点A′处,并使折痕经过点B ,得到折痕BE ,同时,得到线段BA′,EA′,展开,如图①.第三步:再沿EA′所在的直线折叠,使点B 落在AD 上的点B′处,得到折痕EF ,同时得到线段B′F ,展开,如图②.(1)求证:∠ABE =30°.(2)求证:四边形BFB′E 为菱形.5 【例题4】涉及折叠的函数与几何图形综合问题:已知抛物线y =x 2-2x +a(a<0)与y 轴相交于点A ,顶点为M.直线y =12x -a 分别与x 轴,y 轴相交于B ,C 两点,并且与直线AM 相交于点N.(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则点M ()1,a -1,N ⎝⎛⎭⎫43a ,-13a . (2)如图,将△NAC 沿y 轴翻折,若点N 的对应点N′恰好落在抛物线上,AN′与x 轴交于点D ,连结CD ,求a 的值和四边形ADCN 的面积.(3)在抛物线y =x 2-2x +a(a<0)上是否存在一点P ,使得以P ,A ,C ,N 为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.6【最新试题】名校直考,巅峰冲刺,一步到位。
第06讲 分类讨论性问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)

【难点突破】着眼思路,方法点拨, 疑难突破;1.分类讨论是重要的数学思想,也是一种重要的解题策略,很多数学问题很难从整体上去解决,若将其划分为所包含的各个局部问题,就可以逐个予以解决.分类讨论在解题策略上就是分而治之各个击破.2.一般分类讨论的几种情况:(1)由分类定义的概念必须引起的讨论;(2)计算化简法则或定理、原理的限制,必须引起的讨论;(3)相对位置不确定,必须分类讨论;(4)含有多种不定因素,且直接影响完整结论的取得,必须分类讨论.3.分类讨论要根据引发讨论的原因,确定讨论的对象及分类的方法,分类时要做到不遗漏、不重复,善于观察,善于根据事物的特性与规律,把握分类标准,正确分类.应用分类讨论思想解决问题,必须保证分类科学、统一、不重复、不遗漏,并力求最简.运用分类的思想,通过正确的分类,可以使复杂的问题得到清晰、完整、严密的解答.分类讨论应当遵循的原则是:分类的对象是确定的,标准是统一的,不遗漏、不重复,科学地划分,分清层次应逐级进行,不越级讨论,其中最重要的一条是“不漏不重”.分类讨论的基本方法是:首先要确定讨论对象以及所讨论对象的全体的范围;其次确定分类标准,正确进行合理分类,即标准统一、不漏不重、分类互斥(没有重复);再对各个分类逐步进行讨论,分层进行,获取阶段性结果;最后进行归纳小结,综合得出结论.【名师原创】原创检测,关注素养,提炼主题;【原创1】阅读下列解方程的过程,并完成(1)、(2)小题的解答.解方程:|x﹣2|=3解:当x﹣2<0,即x<2时,原方程可化为:﹣(x﹣2)=3,解得x=﹣1;当x﹣2≥0,即x≥2时,原方程可化为:x﹣2=3,解得x=5;综上所述,方程|x﹣2|=3的解为x=﹣1或x=5.(1)解方程:|2x+1|=5.(2)解方程:|2x+3|﹣|x﹣1|=1.【原创2】已知点P为线段CB上方一点,CA⊥CB,PA⊥PB,且PA=PB,PM⊥BC于M,若CA=1,PM=4.求CB的长是.【原创3】如图,在▱ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2,下列图象中大致反映y与x之间的函数关系的是()A. B. C. D.【原创4】如图所示,在平面直角坐标系中,一次函数 y=kx+b的图像和正比例函数y=3x相交于点A(1,m),且与y轴的交点为C为(0,5),在一次函数y=kx+b图像上存在点B,点B到x轴的的距离为6. (1)求A点的坐标和一次函数的解析式;(2)求△AOB的面积.【原创5】如图所示,平面直角坐标中一边长为4的等边△AOB,抛物线L经过点A、O、B三点。
第10讲 折叠翻转性问题-2019年中考数学总复习巅峰冲刺28讲(解析版)

2019年中考数学总复习巅峰冲刺专题10折叠翻转性问题【难点突破】着眼思路,方法点拨, 疑难突破;有关图形折叠的相关计算,首先要熟知折叠是一种轴对称变换,即位于折痕两侧的图形关于折痕成轴对称;然后根据图形折叠的性质,即折叠前、后图形的对应边和对应角相等,对应点的连线被折痕垂直平分进行相关计算,折叠问题常常伴随着勾股定理,这是解决问题的关键所在.图形的折叠通常和动点问题结合在一起进行考查,常见的问题类型有以下3种:(1)求线段的取值范围;(2)求最值问题;(3)分类讨论线段长度. 其中第(3)种类型在河南中招考试中为常考类型,解决此类型题,一般运用等量代换,并结合勾股定理或相似三角形的性质来构造方程,进而求解线段的长度. 【名师原创】原创检测,关注素养,提炼主题;【原创1】如图,把一张长方形纸片ABCD进行折叠之后,恰好使其对角顶点A与C能够重合,且使的折痕与BC的交点恰好在其三等分点处,则下列图形长度能够满足题意的是()A.AB=10,BC=20 B.AB=10,BC=30C.,BC=20 D.BC=30【解析】:根据折叠图形的性质,利用勾股定理求出AF=2BF,,由此即可判定D正确.解:选项D正确.理由是根据题意可知AF=2BF,利用勾股定理或者30°的直角三角形判断计算AB=,根据线段之间的关系可选得答案。
故选D.【原创2】如图,D是等边△ABC边AB上的一点,且AD:DB=1:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=___.【解析】设AD=k,则DB=3k,∵△ABC为等边三角形,∴AB=AC=4k,∠A=∠B=∠C=∠EDF=60°,∴∠EDA+∠FDB=120°,又∵∠EDA+∠AED=120°,∴∠FDB=∠AED,∴△AED∽△BDF,由折叠,得CE=DE,CF=DF∴△AED的周长为5k,△BDF的周长为7k,∴△AED与△BDF的相似比为5:7∴CE:CF=DE:DF=5:7.故答案为5:7.【原创3】如图1,矩形OA BC的对角线OB、AC相交于点D,,OC=6,sin∠BOC=45.反比例函数y=kx(x>0)的图像经过点D,(1)求反比例函数的关系式;(2)如图2,将ΔAOC沿过C点的直线折叠,使点A落在x轴上的点E处,折痕所在直线交y轴正半轴。
2019年河南中考数学总复习 29_专题一 规律探究

专题突破
栏目索引
2.与图形坐标有关的规律探究 例2-2 (2018河南许昌二模)如图,弹性小球从点P(0,1)出发,沿图 中所示方向运动,当小球碰到正方形OABC的边时反弹,反弹时反 射角等于入射角,小球第1次碰到正方形的边时的点为P1(2,0),第2 次碰到正方形的边时的点为P2(4,1),……,第n次碰到正方形的边
,
1 4
,故选B.
专题训练
栏目索引
精准学,只练你不会的中考必考点
专题训练
栏目索引
4.(2017四川达州)如图,将矩形ABCD绕其右下角的顶点按顺时针 方向旋转90°至①的位置,继续绕右下角的顶点按顺时针方向旋 转90°至②的位置,……,以此类推,这样连续旋转2 017次.若AB=4,
AD=3,则顶点A在整个旋转过程中所经过的路径总长为 (D )
A.2 017π B.2 034π C.3 024π D.3 026π
精准学,只练你不会的中考必考点
专题训练
栏目索引
答案 D 连接AC,BD,∵AB=4,BC=3,
∴AC=BD=5.
由题意可知转动第一次顶点A经过的路径长是 90 4 =2π,
180
转动第二次顶点A经过的路径长是 90 5= 5 π,
精准学,只练你不会的中考必考点
专题突破
栏目索引
专题突破
河南中考数学中规律探究型问题涉及的知识广泛,所以解答 这类题目,不仅要掌握扎实的数学基础知识,还需要有敏锐的观察 能力、严密的逻辑推理能力和一定的计算能力. 其解题过程一般是:从特殊情况入手→探究发现规律→综合归纳 →猜想、得出结论→验证结论.
2 017秒时,点P的坐标为 ( B )
A.
第19讲 线段的最值问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)
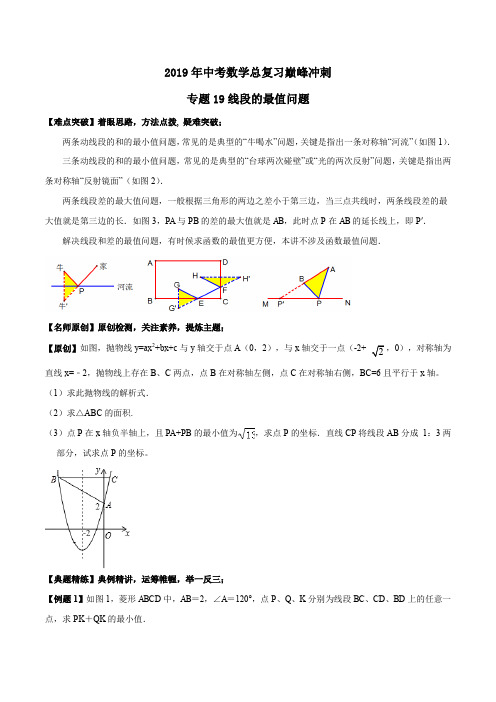
2019年中考数学总复习巅峰冲刺专题19线段的最值问题【难点突破】着眼思路,方法点拨, 疑难突破;两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.【名师原创】原创检测,关注素养,提炼主题;,0),对称轴为【原创】如图,抛物线y=ax2+bx+c与y轴交于点A(0,2),与x轴交于一点(-2+直线x=﹣2,抛物线上存在B、C两点,点B在对称轴左侧,点C在对称轴右侧,BC=6且平行于x轴。
(1)求此抛物线的解析式.(2)求△ABC的面积.(3)点P在x轴负半轴上,且PA+PB的最小值为,求点P的坐标.直线CP将线段AB分成1:3两部分,试求点P的坐标。
【典题精练】典例精讲,运筹帷幄,举一反三;【例题1】如图1,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.图1【例题2】如图1,已知A(0, 2)、B(6, 4)、E(a, 0)、F(a+1, 0),求a为何值时,四边形ABEF周长最小?请说明理由.图1【例题3】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).【最新试题】名校直考,巅峰冲刺,一步到位。
第22讲 函数中四边形存在问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)

2019年中考数学总复习巅峰冲刺专题22函数中四边形存在问题【难点突破】着眼思路,方法点拨, 疑难突破;四边形的存在性问题是一类考查是否存在点,使其能构成某种特殊四边形的问题,如:平行四边形、菱形、梯形的存在性等,往往结合动点、函数与几何,考查分类讨论、画图及建等式计算等.解平行四边形的存在性问题一般分三步:第一步寻找分类标准,第二步画图,第三步计算.难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便.具体的解题思路:①寻找定量,结合特殊四边形判定确定分类;②转化四边形的存在性为点的存在性或三角形的存在性;③借助几何特征建等式.难点拆解:①平行四边形存在性,由定线分别作边、对角线分类,通过平移或旋转画图,借助坐标间关系及中点坐标公式建等式求解.②菱形存在性可转化为等腰三角形存在性处理.③等腰梯形存在性通常直接表达两腰长,利用两腰相等建等式;两腰不易表达,借助对称性和中点坐标公式联立求解.④直角梯形存在性关键是利用好直角.【名师原创】原创检测,关注素养,提炼主题;【原创1】如图,二次函数y=ax2+bx+c(a≠O)与x轴交于点A、B两点,其中点A在点B的左侧,其坐标为(-1,0),与y轴交于点C(0,4),抛物线的对称轴为x=1,连接BC.(1)直接写出a、b、c的值。
(2)对称轴上是否存在两点,并与A、B两点为顶点组成正方形,若存在求出这两点的坐标,若不存在,请说出理由。
(3)若点G为直线BC上方的抛物线上的一动点,试判断以A、B、G、C为顶点的四边形面积有最大值还是有最小值,其数值是多少?(4)若点H为对称轴上的一个动点,点P为抛物线上的一动点,当H、P、B、C四点为顶点的四边形为平行四边形时,求出点H的坐标。
第09讲 方案设计性问题-2019年中考数学总复习巅峰冲刺28讲(解析版)
解得:
x
=
2
y = 3
答:一支圆珠笔需要 2 元,一本笔记本需要 3 元。
(2)设购买圆珠笔 m 支,则购买笔记本(900-m)本,由题意可得:
900 − m m
解得: 445 m 450
2m + 3(900 − m) 1355
2019 年中考数学总复习巅峰冲刺
专题 09 方案设计性问题
【难点突破】着眼思路,方法点拨, 疑难突破; 方案设计与决策型问题对于考查学生的数学创新应用能力非常重要.如让学生设计图形、设计测量方
案、设计最佳方案等都是近年考查的热点,题目多以解答题为主. 方案设计与决策型问题是近几年的热点试题,主要利用图案设计或经济决策来解决实际问题.题型主
,
40 x + 15 y = 2000
20 x + 30 y = 1900
解得:
.
x = 35
y = 40
答:冰糖橙每箱的进价为 35 元,睡美人西瓜每箱的进价为 40 元,……4 分
(2)根据题意要求可设购进的冰糖橙箱数为 a 箱,从而得到睡美人西瓜的箱数为(200-a),根据题意得:
种水果的箱数为(200-a),可根据总利润=单箱利润×购进数量列得 W 关于 a 的函数关系式。
(3)根据条件可得到 A 取值范围,从而根据关系式的增减性判断取得最大利润时 a 的值,可以计算得到最
大利润。
【 解 答 】 解 :( 1 ) 设 冰糖 橙 每 箱 的 进 价 为 x 元 , 睡 美 人 西 瓜 每 箱 的 进 价 为 y 元 , 根 据 题 意 得:
第09讲 方案设计性问题-2019年中考数学总复习巅峰冲刺28讲(解析版)
2019年中考数学总复习巅峰冲刺专题09方案设计性问题【难点突破】着眼思路,方法点拨, 疑难突破;方案设计与决策型问题对于考查学生的数学创新应用能力非常重要.如让学生设计图形、设计测量方案、设计最佳方案等都是近年考查的热点,题目多以解答题为主.方案设计与决策型问题是近几年的热点试题,主要利用图案设计或经济决策来解决实际问题.题型主要包括:1.根据实际问题拼接或分割图形;2.利用方程(组)、不等式(组)、函数等知识对实际问题中的方案进行比较等.方案设计与决策问题就是给解题者提供一个问题情境,要求解题者利用所学的数学知识解决问题,这类问题既考查动手操作的实践能力,又培养创新品质,应该引起高度重视.解答决策型问题的一般思路,是通过对题设信息进行全面分析、综合比较、判断优劣,从中寻找到适合题意的最佳方案.解题策略:建立数学模型,如方程模型、不等式模型、函数模型、几何模型、统计模型等,依据所建的数学模型求解,从而设计方案,科学决策.【名师原创】原创检测,关注素养,提炼主题;【原创1】为了迎接全市的“传统文化体验教育现场会”,我校需要购进一批圆珠笔和笔记本,通过调查发现购买3支圆珠笔和4本笔记本需要18元;购买2支圆珠笔和1本笔记本需要7元。
(1) 求圆珠笔和笔记本的单价各是多少元?学校计划购进圆珠笔和笔记本共900件,其中笔记本的件数不少于圆珠笔的件数,并且计划消费不超过1355元,请问共有几种购买方案?【解析】:1)可根据“购买3支圆珠笔和4本笔记本需要18元;购买2支圆珠笔和1本笔记本需要7元”,列出方程组求出答案;(2)要根据“购进圆珠笔和笔记本共900件,其中笔记本的件数不少于圆珠笔的件数,并且计划消费不超过1355元”来列出不等式组,判断出不同的改造方案【解答】解:(1)设购买一支圆珠笔需要x 元,一本笔记本需要y 元,由题意得:341827x y x y +=⎧⎨+=⎩解得:23x y =⎧⎨=⎩答:一支圆珠笔需要2元,一本笔记本需要3元。
第04讲 新情景设计问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)
【难点突破】着眼思路,方法点拨, 疑难突破;实物情景中的数学,是指有实际背景或现实意义的数学问题,其特点是:(1)创设新情境,赋予新内涵;(2)试题呈现形式活泼新颖;(3)一般取材于学生熟悉的生活实际,具有时代气息和教育价值.这种问题一般都是先提供一种情景,或者一个解题思路,或介绍一种解题方法,或展示一个数学结论的推导过程等文字或图表材料,然后要求大家自主探索,理解其内容、思想方法,把握本质,解答试题中提出的问题.对于这类题求解步骤是“阅读→分析→理解→创新应用”,其中最关键的是理解材料的作用和用意,一般是启发你如何解决问题或为了解决问题为你提供工具及素材.因此这种试题是考查大家随机应变能力和知识的迁移能力.1.涉及到定义知识的新情景问题:它要求学生在新定义的条件下,对提出的说法作出判断,主要考查学生阅读理解能力,分析问题和解决问题的能力.解此类型题的步骤有三:(1)认真阅读,正确理解新定义的含义;(2)运用新定义解决问题;(3)得出结论.2.涉及到数学理论应用探究问题:学习此类型题目,要解决后面提出的新问题,必须仔细研究前面的问题解法.即前面解决问题过程中用到的知识在后面问题中很可能还会用到,因此在解决新问题时,认真阅读,理解阅读材料中所告知的相关问题和内容,并注意这些新知识运用的方法步骤.3.涉及到日常生活中的实际问题:处理此类问题需要结合生活实际将图形转化为数学图形,利用数学知识进行解答。
【名师原创】原创检测,关注素养,提炼主题;【原创】问题情境:情境A:两条直线相交,有一个交点,三条直线相交,最多有3个交点,四条直线呢?情境A图情境B图情境B:在一条直线上任意作两个端点(不重合的两点),可得到一条线段,作三个端点,最多得到3条线段,四个端点呢?情境C:两条有公共端点的射线可组成一个角,从端点出发增加一条射线,可得到3个角,增加两条射线呢?情境C图解决问题:(1)从上面的问题情境中任选一个作答。
第25讲 数学文化性问题-2019年中考数学总复习巅峰冲刺28讲(原卷版)
2019年中考数学总复习巅峰冲刺 专题25 数学文化性问题 【难点突破】着眼思路,方法点拨, 疑难突破; 数学文化指数学的思想、精神、方法、观点、语言,以及它们的形成和发展。数学作为一种文化现象,早已是人们的常识。在近几年的中考中,以数学文化为载体的数学题越来越多,只要我们平时注意积累和了解这方面的常识,解题时注意审题,实现载体与考点的有效转化,透过现象看本质,问题便可迎刃而解. 此类问题涉及到古代数学名著中关于数学计算的典例事例分析,或者典型问题展示,也会涉及到古代著名数学家提出的相关问题,首先理解问题内容,再转化为数学语言进行解答即可,难度一般不大。 主要类型有以科技或数学时事为题材、以数学名著为题材、以数学名人为题材. 【名师原创】原创检测,关注素养,提炼主题; 【原创】《河妇荡杯》是《孙子算经》中著名的趣题之一。原题是:妇女河上荡杯,津吏问“杯何以多?” 妇人曰:“有客。”津吏曰:“客几何?” 妇人曰:“两人共饭,三人共羹,四人共肉,凡用杯六十五。不知客几何?” 大意为:一个妇女在河边洗碗,河官问:“洗多少碗?有多少客 ?”妇女答:“洗 65 只碗,客人二人共用一只饭碗,三人共用一只汤碗,四人共用一只肉碗。你说有多少客人用餐?”
【典题精练】典例精讲,运筹帷幄,举一反三; 【例题1】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=﹣6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?” 译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱; 如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少?” 设有x个人共同买鸡,根据题意列一元一次方程,正确的是( ) A.9x+11=6x﹣16 B.9x﹣11=6x+16 C. D.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【难点突破】着眼思路,方法点拨, 疑难突破;
1、解数式规律型问题的一般方法:
(1)当所给的一组数是整数时,先观察这组数字是自然数列、正数列、奇数列、偶数列还是正整数列经过平方、平方加1或减1等运算后的数列,然后再看这组数字的符号,判断数字符号的正负是交替出现还是只出现一种符号,最后把数字规律和符号规律结合起来从而得到结果;(2)当数字是分数和整数结合时,先把这组数据的所有整数写成分数,然后分别推断出分子和分母的规律,最后得到该组第n项的规律;(3)当所给的代数式含有系数时,先观察其每一项的系数之间是否有自然数列、正整数列、奇数列、偶数列或交替存在一定的对称性,然后观察其指数是否存在相似的规律,最后将系数和指数的规律结合起来求得结果.
数字循环类规律题就是几个数循环出现,解决此类问题时,一般是先求出前几个数,再观察其中隐含的规律,若和序号有关,则第n个数用含n的式子表示,用n除以循环出现的数的个数,找出余数即可找到对应的结果.
2、探索等式规律的一般步骤:
(1)标序数;(2)对比式子与序号,即分别比较等式中各部分与序数(1,2,3,4,…,n)之间的关系,把其隐含的规律用含序数的式子表示出来,通常方法是将式子进行拆分,观察式子中数字与序号是否存在倍数或者次方的关系;(3)根据找出的规律得出第n个等式,并进行检验.
3、根据图形寻找点的坐标的变换特点,这类题目一般有两种考查形式:一类是点的坐标变换在直角坐标系中递推变化;另一类是点的坐标变换在坐标轴上或象限内循环递推变化.解决这类问题可按如下步骤进行:(1)根据图形点坐标的变换特点确定属于哪一类;(2)根据图形的变换规律分别求出第1个点,第2个点,第3个点的坐标,找出点的坐标与序号之间的关系,归纳得出第M个点的坐标与变换次数之间的关系;(3)确定第一类点的坐标的方法:根据(2)中得到的倍分关系,得到第M个点的坐标;确定第二类点坐标的方法:先找出循环一周的变换次数,记为n,用M÷n=ω……q(0≤q<n),则第M次变换与每个循环中第q次变换相同,再根据(2)中得到的第M个点的坐标与变换次数的关系,得到第M个点的坐标.
4、对于求面积规律探索问题的一般步骤:(1)根据题意可得出第一次变换前图形的面积S;(2)通过计算得到第一次变换后图形的面积,第二次变换后图形的面积,第三次变换后图形的面积,归纳出后一个图形的面积与前一个图形的面积之间存在的倍分关系;(3)根据找出的规律,即可求出第M次变换后图形的面积.
5、找图形累加型变化规律的一般步骤:
(1)写序号,记每组图形的序数为“1,2,3,…n”;(2)数图形个数,在图形数量变化时,要数出每组图形表示的个数;(3)寻找图形数量与序数n的关系,若当图形变化规律不明显时,可利用图示法,即针对寻找第n个图形表示的数量时,先将后一个图形的个数与前一个图形的个数进行比对,通常作差(商)来
观察是否有恒等量的变化,然后按照定量变化推导出第n 个图形的个数.
【名师原创】原创检测,关注素养,提炼主题;
【原创1】如图所示,在这个数据运算程序中,若开始输入的x 值为2,那么我们要进行的第一次计算是进行偶数程序,结果输出的是1,返回进行第二次运算则按照奇数程序进行运算,输出的是6,…第2019次输出的结果为 .
【原创2】发现 任意一个偶数减去其
12,再减去余下的13
,一直减去到余下的此偶数的倒数,结果为1. 验证 (1)10减去其12,再减去余下的13,一直减去到余下的14,一直减到最后余下的110
其结果等于几?. (2)设一个偶数2n ,依次减去其12,再减去余下的14,一直减下去,一直减到最后余下的12n ,结果等于几?并验证发现的结论是否正确。
【原创3】如图,在平面直角坐标系中,点A (0,1)和点B (1,0),连接AB,以AB 为边作等边三角形,顶点为C ,过点C 作A 1B 1//AB ,分别交y 轴、x 轴于点A1,B1,再以A 1B 1为边作等边三角形,……,逐次作等边三角形,则第2 017个等边三角形的顶点C 2019坐标是 .
【原创4】如图所示,最外面的正方形的边长为1,在其中作最大的圆,则之间阴影的面积为14π-
;再在
圆内第二次作最大正方形,正方形中再作最大圆,取之间部分为阴影面积,依次逐渐作下去,则第三次作
圆与其外面正方形之间的阴影面积为 ,第2019次作圆与其外面正方形之间的阴影面积是 。
【典题精练】典例精讲,运筹帷幄,举一反三;
【例题1】(2018·湖北随州·3分)我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,
6
,
1
…
)
和
“
正
方
形数”
(
如1
A .33
B .301
C .386
D .571
【例题2】(2018·东营中考)如图,在平面直角坐标系中,点A 1,A 2,A 3,…和点B 1,B 2,B 3,…分别在直线y =15x +b 和x 轴上.△OA 1B 1,△B 1A 2B 2,△B 2A 3B 3,…都是等腰直角三角形,如果点A 1(1,1),那么点A 2 018的纵坐标是 .
【例题3】(2018•贵州黔西南州•12分)“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10.图n 有 多少个点? 我
们
将
每个图
形
分
成
完
全
相
同
的
6
块,每
(1)第5个点阵中有61个圆圈;第n 个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.。
