抽屉原理(修改)
抽屉原理全解

抽屉原理抽屉原理原理1 、2 、3都是第一抽屉原理的表述。
例1:同年出生的400人中至少有2个人的生日相同。
原理3 :把无穷多件物体放入n个抽屉,则至少有一个抽屉里有无穷个物体。
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体。
原理2 :把多于mn(m乘以n)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于m+1的物体。
证明(反证法):若每个抽屉至多放进m个物体,那么n个抽屉至多放进mn个物体,与题设不符,故不可能。
原理1:把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
证明(反证法):如果每个抽屉至多只能放进一个物体,那么物体的总数至多是n,而不是题设的n+k(k≥1),故不可能。
证明(反证法):若每个抽屉都有不少于m个物体,则总共至少有mn个物体,与题设矛盾,故不可能。
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放两个苹果。
这一现象就是我们所说的“抽屉原理”。
抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一个集合里有两个元素。
” 抽屉原理有时也被称为鸽巢原理(“如果有五个鸽子笼,养鸽人养了6只鸽子,那么当鸽子飞回笼中后,至少有一个笼子中装有2只鸽子”)。
它是组合数学中一个重要的原理。
抽屉原理的内容简明朴素,易于接受,它在数学问题中有重要的作用。
许多有关存在性的证明都可用它来解解:将一年中的365天视为365个抽屉,400个人看作400个物体,由抽屉原理1可以得知:至少有2人的生日相同. 400/365=1…35,1+1=2上面数例论证的似乎都是“存在”、“总有”、“至少有”的问题,不错,这正是抽屉原则的主要作用.(需要说明的是,运用抽屉原则只是肯定了“存在”、“总有”、“至少有”,却不能确切地指出哪个抽屉里存在多少.们的差是12。
抽屉原理-抽取游戏

抽屉原理的应用
在计算机科学中,抽屉原理也被用于设计和分析算法 。例如,在解决图论问题时,抽屉原理可以帮助确定 最短路径或最小生成树等问题的解的存在性和唯一性 。
在组合数学中,抽屉原理被广泛应用于解决各种计数 和排列组合问题。例如,在计算不同方式将n个不同 元素放入m个不同容器中的方法数时,抽屉原理可以 提供有效的解决方案。
WENKU
REPORTING
https://
PART 01
引言
游戏介绍
抽屉原理是一种组合数学原理,也被 称为鸽巢原理,它描述了在有限个物 体和无限个容器的情况下,至少有一 个容器包含超过一个物体的情况。
抽屉原理在数学、计算机科学和其他 领域中有广泛的应用,特别是在解决 一些组合优化问题时。
游戏规则
• 游戏目标:玩家需要将一定数量的物品放入有限 数量的抽屉中,使得至少有一个抽屉包含两个或 更多的物品。
除了制定具体的抽取策略外,玩家还可以运用心理战术来影响对手的判断和行动。例如, 故意制造假象,让对手误以为某个抽屉中的物品数量较多,从而影响其抽取决策。
PART 05
抽屉原理与游戏设计
抽屉原理在游戏设计中的应用
资源分配
在游戏中,玩家可能需要分配有限的资源(如金钱、时间等)以获得最佳效果。抽屉原理可以帮助设计者确定在资源 有限的情况下,如何合理分配资源以达到最佳效果。
微积分是研究函数、极限和变 化的数学分支,对于游戏设计 中的优化和动态系统分析非常 有用。例如,在设计角色属性 成长系统时,可以使用微积分 来调整属性成长曲线。
PART 06
结论与展望
游戏的意义与价值
提升逻辑思维能力
抽屉原理游戏需要玩家运用逻辑 推理,通过尝试和排除来找到正 确的答案,有助于提升逻辑思维
人教版数学六年级下册《讲堂点睛》第5单元-抽屉原理2
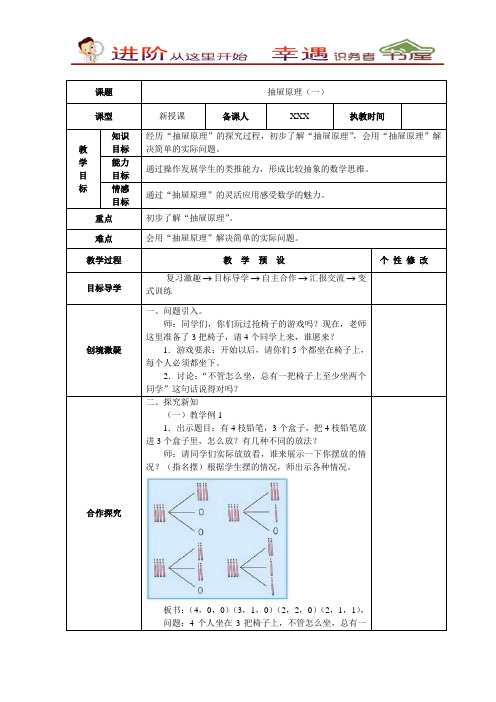
课题抽屉原理(一)课型新授课备课人XXX 执教时间教学目标知识目标经历“抽屉原理”的探究过程,初步了解“抽屉原理”,会用“抽屉原理”解决简单的实际问题。
能力目标通过操作发展学生的类推能力,形成比较抽象的数学思维。
情感目标通过“抽屉原理”的灵活应用感受数学的魅力。
重点初步了解“抽屉原理”。
难点会用“抽屉原理”解决简单的实际问题。
教学过程教学预设个性修改目标导学复习激趣→目标导学→自主合作→汇报交流→变式训练创境激疑一、问题引入。
师:同学们,你们玩过抢椅子的游戏吗?现在,老师这里准备了3把椅子,请4个同学上来,谁愿来?1.游戏要求:开始以后,请你们5个都坐在椅子上,每个人必须都坐下。
2.讨论:“不管怎么坐,总有一把椅子上至少坐两个同学”这句话说得对吗?合作探究二、探究新知(一)教学例11.出示题目:有4枝铅笔,3个盒子,把4枝铅笔放进3个盒子里,怎么放?有几种不同的放法?师:请同学们实际放放看,谁来展示一下你摆放的情况?(指名摆)根据学生摆的情况,师出示各种情况。
板书:(4,0,0)(3,1,0)(2,2,0)(2,1,1),问题:4个人坐在3把椅子上,不管怎么坐,总有一把椅子上至少坐两个同学。
4支笔放进3个盒子里呢?引导学生得出:不管怎么放,总有一个盒子里至少有2枝笔。
问题:(1)“总有”是什么意思?(一定有)(2)“至少”有2枝什么意思?(不少于两只,可能是2枝,也可能是多于2枝?)教师引导学生总结规律:我们把4枝笔放进3个盒子里,不管怎么放,总有一个盒子里至少有2枝铅笔。
这是我们通过实际操作现了这个结论。
那么,你们能不能找到一种更为直接的方法得到这个结论呢?学生思考并进行组内交流。
问题:把6枝笔放进5个盒子里呢?还用摆吗?把7枝笔放进6个盒子里呢?把8枝笔放进7个盒子里呢?把9枝笔放进8个盒子里呢?……你发现什么?(笔的枝数比盒子数多1,不管怎么放,总有一个盒子里至少有2枝铅笔。
)总结:只要放的铅笔数盒数多1,总有一个盒里至少放进2支。
小学奥数—抽屉原理讲解精编版

小学奥数—抽屉原理讲解精编版抽屉原理是数学中一种常用的思想工具,它可以帮助我们解决一些问题。
其中,抽屉原理1指的是将多于n件物品任意放到n个抽屉中,那么至少有一个抽屉中的物品不少于2件;抽屉原理2指的是将多于m×n件物品任意放到n个抽屉中,那么至少有一个抽屉中的物品不少于(m+1)件。
举个例子,假设五年级有47名学生参加一次数学竞赛,成绩都是整数,满分是100分。
已知3名学生的成绩在60分以下,其余学生的成绩均在75~95分之间。
问:至少有几名学生的成绩相同?我们可以以成绩为抽屉,学生为物品。
除3名成绩在60分以下的学生外,其余成绩均在75~95分之间,75~95共有21个不同分数,将这21个分数作为21个抽屉,把47-3=44(个)学生作为物品。
根据抽屉原理2,至少有1个抽屉至少有3件物品,即这47名学生中至少有3名学生的成绩是相同的。
再举个例子,假设夏令营组织2000名营员活动,其中有爬山、参观博物馆和到海滩游玩三个项目。
规定每人必须参加一项或两项活动。
那么至少有几名营员参加的活动项目完全相同?我们可以把活动项目当成抽屉,营员当成物品。
因为“每人必须参加一项或两项活动”,共有3项活动,所以共有6个抽屉。
根据抽屉原理2,至少有一个抽屉中有334件物品,即至少有334名营员参加的活动项目是相同的。
最后再看一个例子,假设要把125本书分给五(2)班学生,如果其中至少有1人分到至少4本书,那么,这个班最多有多少人?我们可以将这道题变形为:125件物品放入若干个抽屉中,如果至少有一个抽屉中有至少4件物品,那么最多有多少个抽屉?因为每个抽屉代表一个学生,所以最多有31个学生。
例1:从1,3,5,7,…,47,49这25个奇数中至少任意取出多少个数,才能保证有两个数的和是52?分析与解答】首先需要构造合适的抽屉。
在这25个奇数中,两两之和是52的有12种组合:{3,49},{5,47},{7,45},{9,43},{11,41},{13,39},{15,37},{17,35},{19,33},{21,31},{23,29},{25,27}。
抽屉原理第1课时

书
设
计
抽屉原理
铅笔数量(枝)文具盒数量(个)结果
54
65
76
109总有一个文具盒里至少放进2枝铅笔。
10099
教
学
后
记
(二)讨论:
1,把4枝铅笔放进3个文具盒中,共有几种不同的分发。
2,把5枝铅笔放进4个文具盒中,那么总有一个文具盒里总是放进几枝铅笔,为什么?
(三)只要放的铅笔数比文具盒的数量多,就总有一个文具盒里至少放进2枝铅笔。
六当堂训练:课本第70页的练习十二第要放的铅笔数比文具盒的数量多,就总有一个文具盒里至少放进2枝铅笔。
课题
抽屉原理
课时
1
撰写人
杨贵群
教学内容
教科书第70页的例1
学习目标
1初步了解抽屉原理。
2通过实物操作,培养学生的动手能力和推理能力。
3通过用抽屉原理解决简单的问题,感受数字的魅力。
学习重难点
1经历抽屉原理探究过程,初步了解抽屉原理。
2理解抽屉原理的内涵。
教法学法
先学后教。动手操作法,小组探究法。
教具准备
每组都有相应数量的文具盒,铅笔
教学过程
教学修改建议
一导入新课,板书课题。
同学们,今天我们来学习一个新的数学问题-----抽屉原理
二出示学习目标:(生齐读一遍)
三出示自学指导:(生齐读一遍)
认真看课本第70页的内容,重点看黄色部分。
1枚举法:即把每一种可能出现的分法都一一例举出来,然后得出结论。
2分解法:实际上和分解法一样,只是把具体的分铅笔抽象成分解书数,每一种结果中总有一个数十不少于2的。
3假设法:比前两种方法抽象,更具一般性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
至少数= 商+1
4.把20枝笔放进4个笔筒里,不管怎 么放,总有一个笔筒里至少放进几枝笔? 20÷4=5(枝) 至少数:5(枝)
铅笔枝数大于笔筒数且两者不能整除
• 至少数= 商+1
物体个数大于抽屉数且两者不能整除
• 至少数= 商+1
抽屉原理简介
“抽屉原理”最先是由19世纪的德国数学 家狄里克雷(Dirichlet)运用于解决数学 问题的,所以又称“狄里克雷原理”。 抽屉原理的应用是千变万化的,用它可 以解决许多有趣的问题,并且常常能得 到一些令人惊异的结果。
2、 你所在的班中,至少有多少人的生日在同一个月?
3、 32只鸽子飞回7个鸽舍,至少有几只鸽子要飞进同个鸽舍?
4、 在街上任意找来50个人,可以确定,这50人中至少有 多少个人的属相相同?
5、 冀英学校五、六年级共有学生370人,在这些学生中, 至少两个人在同一天过生日,为什么?
举一反三:
• 把一些苹果放进5个篮子,要想保 证有个篮子的苹果至少有7个,那 么最少得准备多少个苹果?
一副扑克,拿走大、小王后还有 52张牌,请你任意抽出其中的5张 牌,我不看牌,我敢肯定地说: 这5张牌中至少有两张是同花色, 大家相信吗?
一副扑克,拿走大、小王后还有 52张牌,请你任意抽出其中的5张 牌,我不看牌,我敢肯定地说: 这5张牌中至少有两张是同花色, 大家相信吗?
活动一、
• 把4枝笔放进3个笔筒里,可以怎么 放?
少有2枝。
至少的意思: 是表示“最小的限度”,如至少有10元表示: • 5本书放4个抽屉:“总有一个抽屉里至 少有2本书”,就是说不少于2本,有可能 是3本、4本、5本。至少就是:总有一个抽 屉不少于的意思。
把4枝笔放进3个笔筒里,不管怎么放, 总有一个笔筒里至少放进2枝笔, 这是为什么?
至少数怎么求?
把4枝笔放进3个笔筒里, 不管怎么放, 总有一个笔筒里放的铅笔是 最多的,有2枝、3枝、4枝。
活动一、
• 把5枝笔放,0) 把5枝铅笔放进4个笔筒里, (4,1,0) 不管怎么放,总是有一个笔筒 (3,2,0) 的笔是最多的,有5枝、4枝、3 (3,1,1) 枝、2枝。 (2,2,1)
活动一、
• 把5枝笔放进4个笔筒里,可以怎么放?你能记录 下来吗?
(5,0,0) 把5枝铅笔放进4个笔筒里, (4,1,0) 不管怎么放,总是有一个笔筒 (3,2,0) 的笔是最多的,有5枝、4枝、3 (3,1,1) 枝、2枝。 (2,2,1)
活动一、
• 把5枝笔放进4个笔筒里,可以怎么放?你能记录 下来吗?
(5,0,0) 把5枝铅笔放进4个笔筒里, (4,1,0) 不管怎么放,总是有一个笔筒 (3,2,0) 的笔至少有2枝铅笔。 (3,1,1) (2,2,1)
把4枝笔放进3个笔筒里, 不管怎么放, 总有一个笔筒里放的铅笔是 最多的,有2枝、3枝、4枝。
把4枝笔放进3个笔筒里, 不管怎么放, 总有一个笔筒里放的铅笔至
1.把5枝笔放进4个笔筒里,不管怎 么放,总有一个笔筒里至少放进几枝笔?
5÷4=1(枝)… … 1(枝) 至少数:1 + 1 = 2(枝) 2.把7枝笔放进3个笔筒里,不管怎 么放,总有一个笔筒里至少放进几枝笔? 7÷3=2(枝)… … 1(枝) 至少数:2 + 1 = 3(枝) 3.把23枝笔放进4个笔筒里,不管怎 么放,总有一个笔筒里至少放进几枝笔? 23÷4=5(枝)… … 3(枝) 至少数:5 + 1 = 6(枝)
(7-1)×5+1=31(个)
