东南大学田玉平自动控制原理参考答案4
东南大学控制原理参考答案7

α1 α2 1 1 0 −5 11 −6 1 6 −6 1
P = B AB A2B α2 1
= 0 2 9
−6
1
= −3 2
0
1
1 5 19 1
0 −1 1
P−1 =−−123
−5 3
−2
2
3
1
−1
−2
2
9
自控原理第七章参考答案
0 1 0
0
=A P−= 1AP 0 0 1= , B P= −1B 0
vi=2 λi + a1
所以可得 vi3
=λi 2
+
a1λi
+
a2 )
vin=
λ n−1 i
+
a1λi n−2
+
+
an−1
1
1
λ1 + a1
λn + a1
即=P
λ12 + a1λ1 + a2
λn2 + a1λn + a2
λ1n−1 + a1λ1n−2 + + an−1
λ n−1 n
−4 17 0
3 ,所以完全能观
−4 9 4
= xx12
0
0
7.9
考虑系统
x 3
−6
y
=
[c1
c2
1 0 x1 0
0
1
x2
+
1 u
−11 −6 x3 0
x1
c3
]
x2
x3
试问:除 c=1 c=2 c=3 0 外, c1,c2,c3 取何值时系统是不能观的。
东大22春《自动控制原理Ⅰ》在线平时作业3【参考答案】

《自动控制原理Ⅰ》在线平时作业3【参考答案】试卷总分:100 得分:100一、单选题 (共 25 道试题,共 100 分)1.给定量和扰动量都是自动控制系统的控制量。
A.是B.否标准答案:B2.调节时间的长短反映了系统的A.稳定性B.快速性C.平稳性D.准确性标准答案:B3.稳态误差越小,系统的稳态精度越低。
A.是B.否标准答案:B4.由系统的动态方程推导出传递函数的过程中,主要利用了拉氏变换的()。
A.位移性质B.微分性质C.积分性质D.终值定理标准答案:B5.在自动控制系统中,常用的数学模型有微分方程、传递函数、状态方程、传递矩阵、结构框图和信号流图等。
A.是B.否标准答案:A6.最大超调量反映了系统的平稳性。
A.是B.否标准答案:A7.对于最小相位系统,相位裕度小于零的时候表示闭环系统是稳定的。
()A.是B.否标准答案:B8.调节时间的长短反映了系统过渡过程时间的长短,它反映了系统的快速性。
A.是B.否标准答案:A9.自动控制系统按其主要元件的特性方程式的输入输出特性,可以分为线性系统和非线性系统。
A.是B.否标准答案:A10.最大超调量越大,说明系统过渡过程越不平稳。
A.是B.否标准答案:A11.非线性系统的暂态特性与其初始条件无关。
A.是B.否标准答案:B12.连续系统是指系统的各部分的信号都是模拟的连续函数。
A.是B.否标准答案:A13.系统(或环节)的频率特性是正弦函数作用下,在稳态状态下,系统(或环节)的输出量与输入量之比。
()A.是B.否标准答案:A14.对于最小相位系统,相频特性和幅值特性有唯一的对应关系。
()A.是B.否标准答案:A15.稳态误差越大,系统的稳态精度越高。
A.是B.否标准答案:B16.最大超调量越小,说明系统过渡过程越平稳。
A.是B.否标准答案:A17.{图}A.是B.否标准答案:B18.在自动控制系统中,被控制的设备或过程称为被控对象或对象。
A.是B.否标准答案:A19.按照控制系统中信号的传递方式,可将自动控制系统分为连续系统和离散系统。
《自动控制原理》5章课后习题参考答案.

+
1(
10000(6
.311
2e +=
S S S G
1001.0(11.0(1(1.0(d +++=
S S S S S G 61
.054
.0154.0,
11(2
2
=+==+=
K K
A ω
ωω010
s
900.257.3180 2.16rad
tg ωωω----∙︒=-=,(
(
5
.1,
(5
(6 (7
5.12
K增大和T减少
((1(1(1m K
K s s Ts Ts K
s T s K
Φ=
≈
+++++
K
T m 21=
ζ ,不变(稳定裕度不变
2
22
(12(121b n ωωξξ=-+
-+
5.13
11=+=
p
ssr K e 35
.01
12
416==
=
v
ssr K e %
8.4%100%2
1=⨯=--ξ
πξ
σe 05
.006.13
==≈
ቤተ መጻሕፍቲ ባይዱεξ
ω,S t n s s
rad n n c 8.2707.0707.02=∙=ωωω=0
63
=γdB K g s rad g ∞=∞=ω0,1==r r M ωs
rad n b 4==ωω0
1
1
11006
.787.53.841001.01001.0180180=-=∙-=-+-=----tg
自动控制原理课后习题答案.docx
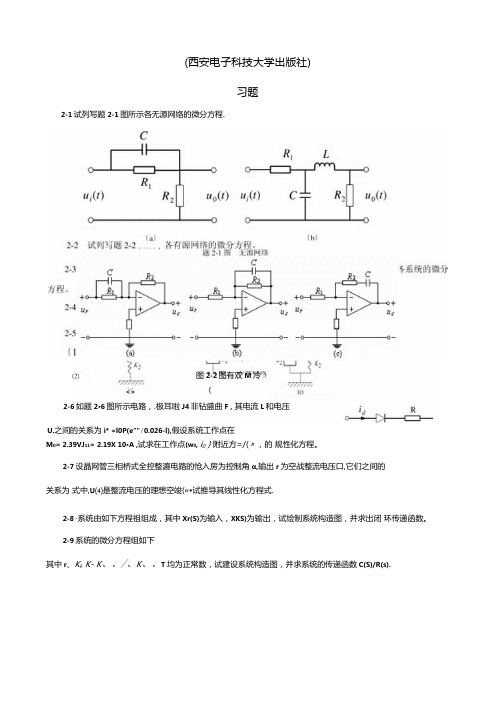
(西安电子科技大学出版社)习题2-1试列写题2-1图所示各无源网络的微分方程.M 0= 2.39VJ 11= 2.19X 10∙A ,试求在工作点(w 0, i 0}附近方=/(〃,的 规性化方程。
2-7设晶网管三相桥式全控整漉电路的怆入房为控制角α,输出r 为空战整流电压口,它们之间的 关系为 式中,U ⑷是整流电压的理想空竣(«•试推导其线性化方程式.2-8 ∙系统由如下方程祖组成,其中Xr(S)为输入,XKS)为输出,试绘制系统构造图,并求出闭 环传递函数。
2-9系统的微分方程组如下其中r 、K l . K- K 、、/、K 、、T 均为正常数,试建设系统构造图,并求系统的传递函数C(S)/R(s).图2-2图有双M 冷 ⑵(W <»U.之间的关系为i* =l0P(e""∕0.026-l),假设系统工作点在 2-6如题2∙6图所示电路,.极耳啦J4非钻盛曲F ,其电流L 和电压2-10试化简即2-10图所示的系统构造图.并求传递函数C(S)11R(S), K(S) C(S)/ C(S) R(S) 筑书规图所材 Gl C(S) G,卡G 5佛与函数 国S) C(S) G) 5 “七; Hl 弟统 £(S) M(S)2-16零初 设某 2-17 g (t) = 7-5e 6f . 咫2∙ 15图求系统 的传速函数, 始条件下的输出响试求该系统的传递 2-18系统的 W'> I 控制系统构造t f 1*1 2-16 W 系统构造图 R(S) ΛU) 2-15 E(S) C (Λ I I - L_rτ∏J ∙13图 系统G:" r ,(5) E(S)凤 F) R ⑸M ⑸松) ⅛4和脉冲响应函数, 单位脉冲响应为。
自动控制原理课后答案

第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。
u rR 1u cR 2CCR 2R 1u ru c(a) (b)图5-75 R-C 网络解 (a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图:⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c)(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如题5-76图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s (1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性:2244221)(ωωωωω+-++=+=Φj j j幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-= 系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时,2=ω,r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω)452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ )4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ(2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应)0(8.08.11)(94≥+-=--t e e t h t t试求系统频率特性。
东大15秋学期《自动控制原理Ⅰ》在线作业2满分答案

东大15秋学期《自动控制原理Ⅰ》在线作业2满分答案一,单选题1. 调节时间越短,系统的快速性越好。
A. 是B. 否正确答案:A2. 系统(或环节)的频率特性是正弦函数作用下,在稳态状态下,系统(或环节)的输出量与输入量之比。
()A. 是自动控制原理课后答案B. 否正确答案:A3. 调节时间中误差带一般取稳态输出值的A. ±2%或±4%B. ±1%或±4%C. ±1%或±5%D. ±2%或±5%正确答案:D4. 对于最小相位系统,增益裕度的分贝数为正表示闭环系统是不稳定的。
()A. 是B. 否正确答案:B5. 典型二阶系统,()时为二阶工程最佳参数。
A.AB.BC.CD.D正确答案:B6. 对于最小相位系统,相位裕度等于零的时候表示闭环系统处于临界稳定状态。
()A. 是B. 否正确答案:A7. 幅相频率特性可以表示成代数形式或指数形式。
()A. 是B. 否正确答案:A8. 典型二阶系统,阻尼比越大,振荡越()。
A. 弱B. 强正确答案:A9. 稳态误差为无穷时,闭环系统()A. 稳定B. 不稳定C. 不一定D.正确答案:A10. 对于一般的控制系统,输出量的暂态过程中,下列哪种情况是稳定的A. 持续振荡过程B. 衰减振荡过程C. 发散振荡过程D. 等幅振荡过程正确答案:B11. 开环对数频率特性的中频段反映了系统的稳定性和暂态性能。
()A. 是B. 否正确答案:A12. 在典型二阶系统中,()时,系统是不稳定的。
A. 过阻尼状态B. 欠阻尼状态C. 临界阻尼状态D. 无阻尼状态正确答案:D13. 在典型二阶系统中,()时为过阻尼状态。
A.AB.BC.CD.D正确答案:A14. 按偏差原则和按补偿原则结合起来构成的系统,称为复合控制系统。
A. 是B. 否正确答案:A15. 最大超调量反映了系统的平稳性。
A. 是B. 否正确答案:A16. 绘制根轨迹的依据是()A. 幅值条件B. 辐角条件C. 幅值条件和辐角条件D.正确答案:B17. 最大超调量越小,说明系统过渡过程越平稳。
自动控制原理第4章
p 26.6
3
自动控制理论
14
4-2 根轨迹绘制的基本法则
八、根之和 若 n-m2 ,闭环极点之和 = 开环极点之和 = 常数
p ,
i 1 i i 1 i
n
n
nm2
表明:在某些根轨迹分支(闭环极点)向左移动,而 另一些根轨迹分支(闭环极点)必须向右移动,才能 维持闭环极点之和为常数。
1 G ( s) H ( s) 0 Q( s) AP( s), P( s) 1 A 0 1 G1 ( s) H1 ( s) Q( s ) P( s ) 等效开环传递函数 G1 ( s ) H1 ( s ) A Q( s)
注意:此等效意义是在特征方程相同,或者是闭环极点相 同的前提下成立;而此时闭环零点是不同的。
180o根轨迹
( s z ) ( s p ) (2k 1)
j 1 i 1
(2k 1)180, (k 0,1,2,)
一、根轨迹的起点和终点 根轨迹起始于开环极点,终止于开环零点。
简要证明如下:
由模值条件
1 * K
(s z
j 1 n i 1
解:开环传递函数有二个极点,一个零点,此类有零点的二 阶系统的根轨迹其复数部分为一个圆,圆心在开环零点处, 半径为零点到分离点的距离。
自动控制理论 21
4-4 系统的性能分析
此系统的分离点:
d1 1.17, d1 6.83
K 2
*
j
利用幅值条件可求得两个分离 点处的根轨迹增益
j 1 j i 1 i
(k 0,1,2,)
K*
s p sz
j 1 i 1 m
n
东南大学自动化学院2012年硕士研究生入学考试自控原理大纲
东南大学自动化学院2012年硕士研究生入学考试大纲
《自动控制原理》考试大纲
一、基本要求
了解自动控制系统的基本构成,理解自动控制的基本原理,熟悉并掌握线性定常控制系统的输入-输出描述和状态空间描述、系统稳定性分析的常用方法、瞬态和稳态性能的分析与计算、以及控制系统的校正、综合方法。
二、考试范围
1.自动控制系统的基本构成和基本控制原理分析。
2.线性定常控制系统(含连续时间系统和离散时间系统)的输入输出描述(运动方程、传递函数、频率特性函数)和状态空间描述以及机理建模方法。
3.线性定常系统(含连续时间系统和离散时间系统)稳定性的基本概念和常用分析方法(代数判据、根轨迹法、频率特性法、李雅普诺夫方法)。
4.线性定常控制系统(连续时间系统为主)的瞬态性能分析(二阶系统为主)和稳态性能分析与计算。
5.线性定常单输入单输出系统的常用校正方法(根轨迹法和频率特性法)。
6.线性定常控制系统(含连续时间系统和离散时间系统)的结构分析(对角线和约当规范形、能控性、能观性)。
7.线性定常单输入单输出系统的综合方法(极点配置、状态观测器设计和基于状态观测器的反馈控制)。
三、题型(共150分)
1.简答题
2.计算题
四、主要参考书
1.田玉平主编,自动控制原理(第二版),科学出版社。
2.吴麒主编,自动控制原理,清华大学出版社。
东南大学自动控制原理2012真题
东南大学二零一二年攻读硕士学位研究生入学考试试卷 请考生注意:试题解答务请考生做在随时卷发放的我校专用“答题纸”上!做在其他答题纸上或试卷上的解答将视为无效答题,不予评分。
试题编号:5c5 试题科目:自动控制原理一、简答题(5*10’=50’)1.对于一个线性定常连续系统,若x(0)不可控,则对任意t>0,是否exp(At)*x(0)仍不可控?为什么?请简述理由。
2.判断两个矩阵是否是状态转移矩阵?若是,求出A 。
(具体矩阵不记得了)3.在开环传递函数中增加一个开环零点,对系统根轨迹有何影响?对系统瞬态性能有何影响?4.对于非最小相位系统,为什么说一定存在K 使得系统不稳定?5.输入-输出稳定性与内部稳定性是否等价?两者有何关系?对于单输入单输出系统两者何时等价?二、综合题(4*25’=100’)1.机电系统建模(比较复杂) R L +-u(t)m2m1fk k k k 1234F=*idx *__dt e=ix x 1+-已知:输入为u(t),输出为x(t)对m 1的电磁力为k 4*i(t )反电动势为e=k 3*要求:画出系统框图,并写出传递函数。
2.对于离散系统_+Z OHk s(s-1)_____e -τs Y(s)U(s)(1)求开环和闭环脉冲传递函数(T=1)(2)根据(1)画出系统根轨迹(3)求出使系统稳定的K 的范围(可利用朱利判据)3.关于离散系统已知两个零输入响应,求系统矩阵G (具体数据不记得)再已知x(0),H ,u,求x(5)。
(利用迭代法即可)4.关于离散系统证明:(比较难)对于n 维线性定常离散系统,证明:一定能找到u (kT )使得在不超过nT (包括nT )的时间内使x(t)回到状态原点的充要条件是该离散系统完全能控。
10级创新玉自动控制原理试卷(B卷)参考答案
07级自动控制原理试卷(A 卷)一、填空(41040⨯=)1. 对控制系统性能要求,主要体现在稳定性、快速性、准确性三个方面。
2. 下述RLC 电路的微分方程是()()()c c c LCu t RCu t u t u ++=。
(以u 输入,c u 为输出)ucu3. 惯性环节的时间常数愈大,则调节时间愈__长___。
4. 闭环系统的特征方程为043234=++-s s s , 则系统必不稳定。
5. 设某开环系统的传递函数为)1(/100)(1+=s s s G ,单位负反馈闭环系统的速度误差系数为__100______。
6. 设开环系统的零、极点分布如下图所示,则实轴上的根轨迹区间为(,4][2,0]-∞-⋃-。
7. 某最小相位系统的开环对数幅频曲线如下图所示,则系统的开环传递函数为123(1)(1)sssωωω++。
)1-8. 设系统的开环幅相频率特性如下图所示,则闭环系统位于右半S 平面极点数为_0_。
(图中P 为开环系统位于右半S 平面的极点数目)9. 校正装置的传递函数为1()0.11c Ts G s Ts +=+,则系统校正装置可提供的最大相位补偿为__55。
______。
10. 某非线性系统的描述函数的负倒数特性及线性部分的频率特性如下图所示,则系统发生等幅振荡的工作点为____P____点。
二、判断题(31030⨯=)1. 一阶惯性环节的时间常数愈大,则快速性能愈好。
(⨯)2. 二阶振荡环节的阻尼系数愈小,其超调量也愈小。
(⨯)3. 一型系统的速度误差系数与增益成反比。
(⨯)4. 增加开环零点(具负实部),可使根轨迹左移,从而增加系统的稳定性能。
(√)5.开环剪切频率越大,其闭环系统的快速性越好。
(√)6. 若闭环系统的零频率1M,则系统必为0型系统。
(√))0(<7. 应将滞后校正装置发生最大负相角的频率值设置在系统的剪切频率处。
(⨯)8. 非线性系统必发生自持振荡。
(⨯)9. 零阶保持器对系统的稳定性能没有影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 对于如下系统,求其传递函数。并判别:系统是否由其传递函数完全表征?系统是否渐进稳定?是否输入-输出稳定?
(1)
0100001061161310xxuyx
解:由3261160sIAsss
得极点为:1231,2,3sss
所以系统渐进稳定。
13231()()6116(1)(2)sGsCsIABsssss
所以系统为输入-输出稳定,但不能由G(s)完全表征。
(2)
010000102500550510xxuyx
解:由3252500sIAss得1235,55,55ssisi 所以不是渐进稳定。
G(s)=C(sI-A)1B=C1502501001sssB=)5)(55)(55()5(50sjsjss
.= )55)(55(50jsjs 所以系统是输入-输出稳定,但不能由G(s)完全表征。
(3)
110001010002110xxuyx
解:由3220sIAsss得1230,1,1sss 所以系统不是渐进稳定。 12()()(1)sGsCsIABs
所以系统是输入-输出稳定,但不能由G(s)完全表征。
(4) (a)解:2
5()27sGsss
,1,2122s,有极点在右半平面
所以既不是渐进稳定,又不是输入-输出稳定。系统可由其传递函数完全表征。. (b)解:)54)(1()1)(3()(2sss
ssSG.,有极点在右半平面
所以既不是渐进稳定,又不是输入-输出稳定。系统可由其传递函数完全表征。 (c)解:1()(1)(3)sGsss,有对消的零极点s=1在右半平面,所以系统不能由传递函数完全表征,不是渐进稳定,是输入-输出稳定 4.2 已知系统的特征方程如下,分别用劳斯和霍尔维茨判据判别稳定性。
(1)010092023sss
1000410020910123ssss, D=100200091010020
D1>0, D2=80>0, D3=8000>0 故该系统将近稳定。 (2)322092000sss
解:3210
1920020010200ssss
123
202000190020200200,200,40000DDDD
所以,系统不稳定 (3)025103234ssss 147/5317.411025301234sssss,D=253001100025300110 D1=10>0; D2=47>0, D3=-153<0, D4=-306<0 ; 所以系统不稳定; (4)6543244478100ssssss
解:6543210
147104480551020102.5109010sssssss
辅助多项式423()5510()2010pssspsss
123444800014710000448000147100004480001471040,20,0,320DDDDD
所以不稳定 (5)025.666)256)(4)(2(2ssss
解: 025.8661986912234ssss
25.866025.8665.521981225.86669101234sssss,D=25.86669100198120025.8666910019812 D1=12>0 , D2=630>0 , D3=0 , D4=0; 所以该系统临界稳定; (6)4328181650ssss
解:432
10
11858161652725sss
ss 1234
8160011850081600118580,1280,4480,22400DDDDD
所以系统稳定
4.3 确定使系统稳定的12
KK和
(a)解:132111(1)()(21)KsGssKsKsK 由劳斯判据得1
K
>0
(b)解:32
2
10(1)()2(101)1010sGssKss
由劳斯判据得2K>0.1
4.4 某单位反馈系统的开环传递函数为02
()(717)KGssss
(1)确定使系统稳定的K的临界值。(2)若要求闭环节点的实部均小于-2,求K的取值范围
解:(1)闭环传递函数为:32()717KGssssK
由劳斯判据:3210117711907ssKKssK得0119K 故临界值时 K=119 (2)令2sp,得32140pppK 由劳斯判据:32101111415014ppKpKpK得1415K 4.5 已知系统的开环传递函数为0(1)()(1)(21)KsGssss,试用劳斯判据确定使系统稳定的参数,K的范围。 解:32
(1)()2(2)(1)KsGsssKsK
由劳斯判据:32
10
212(22)02sKsKKKssK
得002K 或 2202K 4.6 已知系统做等幅震荡,确定系统参数,K的值 解:其特征方程为:32(2)10ssKsK
由劳斯判据:32
10
121(2)(1)1sKsKKKssK
若(2)(1)KK=0
则辅助多项式2()1()2pssKpss 判据为:3210
12121sKsKssK
所以系统参数应满足01(2)1KKK 4.9 由零极点确定根轨迹草图。 4.10
(1) (2)
利用劳斯判据,可求的: 01.08.07.1123Ksss 因为该系统极点都在左半平面,所以该系统稳定
10
111231.07.126.11.07.18.01KsKsKss 所以 20K
001.007.126.1111KKK
求得:0(3) (4) 06510854123234Kssss 0)5.01(2.0442KsKs 303132334
65154136065451081265541KsKsKssKs
4041425.012.0KsKsKs
340>K3>0 402K 4.11 证明:
)(131211SPSPSP
所以1s是根轨迹上的一点。
11223312Kpspsps 4.12 (1)1,1,2NPZ,系统不稳定
(2)1,1,0NPZ,系统稳定 (3)0,2,2NPZ,系统不稳定 (4)2,0,2NPZ,系统不稳定 (5)2,2,0NPZ,系统稳定 (6)0,0,0NPZ,系统稳定 (7)1,1,0NPZ,系统稳定
