大学本科课程第5章-梁弯曲时的位移
合集下载
梁弯曲时的位移1梁的位移——挠度和转角2梁的挠曲线
x
a
3
x3
l2
b2
x
左、右两支座处截面的转角分别为
qA
q1
|x0
Fb l 2 b2 6lEI
Fabl b
6lEI
qB
q2
|xl
Fabl
6lEI
a
当a>b时有
qmax qB
Fabl a
6lEI
根据图中所示挠曲线的大致形状可知,最大挠度wmax 所在w 0 处在现在的情况下应在左段梁内。令左段梁的
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2 以x为自变量进行积分得:
EIw
q 2
lx2 2
x3 3
C1
EIw
q 2
lx3 6
x4 12
C1x
C2
该梁的边界条件为 在 x=0 处 w=0, 在 x=l 处 w=0
悬臂梁和简支梁在简单荷载(集中荷载,集中力偶,分 布荷载)作用下,悬臂梁自由端的挠度和转角表达式,以及 简支梁跨中挠度和支座截面转角的表达式已在本教材的附 录Ⅳ中以及一些手册中给出。根据这些资料灵活运用叠加 原理,往往可较方便地计算复杂荷载情况下梁的指定截面 的挠度和转角。
从几何方面来看,平面曲线的曲率可写作
1
w
x 1 w2 3/2
式中,等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量,而w"是q = w' 沿x方
弯曲时的位移.ppt

q (P1P2 Pn ) q1(P1 ) q 2(P2 ) q n (Pn )
w(P1P2 Pn ) w1(P1) w2 (P2 ) wn (Pn )
2、结构形式叠加(逐段刚化法):
目录
弯曲变形
一、载荷叠加:几个荷载共同作用下梁任意横截面上的变形,
2.转角:梁横截面绕中性轴转动的角度q。
三、转角与挠度的关系(小变形下):
q tanq dw w(x)
dx
目录
弯曲变形
§5-2 挠曲线的近似微分方程及其积分
一、挠曲线近似微分方程
M>0
f (x) 0 f
M<0
f
f (x) 0
1 M z (x)
x
EI z
1
弯曲变形
梁变形前后横截面位置的变化称为位移。
梁在横向荷载作用下产生弯曲变形的同时, 使得横截面产生位移。
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)。
目录
§5-1 梁的位移---挠度及转角
弯曲变形
q
x
F
A
q wB
x
w
B1
一、梁的弯曲变形 挠曲线
3、能用积分法计算单跨静定梁在简单荷载 作用下的转角和挠度方程,
4、能熟练使用叠加法计算指定截面的挠 度和转角位移。
目录
重难点:
弯曲变形
1、挠曲线近似微分方程的理解和梁位移边 界条件的应用。
2、积分法求解单跨静定梁在简单荷载作用下 的位移
3、叠加法求梁的位移。
目录
注意:
梁变形前后轴线形状的改变称为变形。
w(P1P2 Pn ) w1(P1) w2 (P2 ) wn (Pn )
2、结构形式叠加(逐段刚化法):
目录
弯曲变形
一、载荷叠加:几个荷载共同作用下梁任意横截面上的变形,
2.转角:梁横截面绕中性轴转动的角度q。
三、转角与挠度的关系(小变形下):
q tanq dw w(x)
dx
目录
弯曲变形
§5-2 挠曲线的近似微分方程及其积分
一、挠曲线近似微分方程
M>0
f (x) 0 f
M<0
f
f (x) 0
1 M z (x)
x
EI z
1
弯曲变形
梁变形前后横截面位置的变化称为位移。
梁在横向荷载作用下产生弯曲变形的同时, 使得横截面产生位移。
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)。
目录
§5-1 梁的位移---挠度及转角
弯曲变形
q
x
F
A
q wB
x
w
B1
一、梁的弯曲变形 挠曲线
3、能用积分法计算单跨静定梁在简单荷载 作用下的转角和挠度方程,
4、能熟练使用叠加法计算指定截面的挠 度和转角位移。
目录
重难点:
弯曲变形
1、挠曲线近似微分方程的理解和梁位移边 界条件的应用。
2、积分法求解单跨静定梁在简单荷载作用下 的位移
3、叠加法求梁的位移。
目录
注意:
梁变形前后轴线形状的改变称为变形。
第五章 弯曲位移

材料的弹性模量
E 200GPa 20 106 N/cm2
因P和q而引起的最大挠度均 位于梁的中点C,由表6-1查得:
Pl 3 55 1000 9203 yCP 1.38cm 6 48EI 48 20 10 32240 5ql 4 5 8.04 9204 yCq 0.116cm 6 384EI 384 20 10 32240
由表 查得,因P2在C处引起的挠度 和在B处引起的转角(d)为:
BP
P2 l 2 1000 402 2.53 105 rad 6 16EI 16 21 10 188 BP2 a 2.53 105 20 5.06 104 cm
2
Me
Me
Me
Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(a)
Me Me Me Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(b)
(C)
Me
Me
A
l 2
B
l 2
C
l 2
D
AB,CD段弯矩为零,所以这两段保持直 线不发生弯曲变形。AB,BC,CD三段变 形曲线在交界处应有共切线。
查表:选16号工字钢
I z 1130cm4 , Wz 141cm3
41qa 4 24 EI Z
2.按刚度选择 q
q
B
max B1 B 2 B3
A
L 2a
弯曲变形位移(PDF)

15
§5-3 叠加法求梁的挠度与转角
一 载荷叠加:多个载荷同时作用于结构而引起的变形 等于每个载荷单独作用于结构而引起的变形的代数和。
θ (P1P2 ⋅⋅⋅⋅⋅⋅Pn ) = θ1(P1) +θ2(P2) + ⋅⋅⋅⋅⋅⋅ +θn (Pn )
ω(P1P2 ⋅⋅⋅⋅⋅⋅Pn ) = ω1(P1) + ω2 (P2 ) + ⋅⋅⋅⋅⋅⋅ +ωn (Pn )
θ max ≤ [θ ]
≤
⎡ω
⎢⎣ l
⎤ ⎥⎦
θ max
≤ [θ ]
p 设计载荷。
(但:对于土建工程,强度常处于主要地位,刚度常处于从 属地位。特殊构件例外)
20
二 提高刚度的途径 提高刚度主要是指减小梁的弹性位移;
弹性位移不仅与载荷有关,而且与杆长和梁的弯曲刚度(EIz) 有关;
对于梁,其长度对弹性位移影响较大.
dx
5
二 挠曲线近似微分方程
纯弯曲 1 = M
ρ EI z
忽略 Fs 对变形的影响
横力弯曲 1 = M (x) ρ(x) EI z
1
ρ
=
±
[1
d +
2ω dx2 ( dω )2 ]3
2
dx
M (x) EI z
=
±
d 2ω dx2 [1+ ( dω )2 ]32
dx
6
d 2ω = ± M (x)
dx 2
11
四 边界条件与连续条件
1 边界条件
铰支座
固定端
x=0 x=L ω=0
x=0 ω=0 θ =0
x x
y y
12
梁弯曲时的位移1梁的位移——挠度和转角2梁的挠曲线

转角方程 w1 等于零,得
x1
l2 b2 3
aa 2b
3
显然,由于现在a>b,故上式
表明x1<a,从而证实wmax确实 在左段梁内。将上列x1的表达 式代入左段梁的挠曲线方程得
wmax w1 |xx1 9
Fb 3lEI
l2 b2 3
Fb
wmax x和最大挠度wmax为
qmax qA qB
Fl 2 16 EI
wm a x
wC
Fl 3 48 EI
思考: 试绘出图示两根简支梁的弯矩图,并描出它们的挠 曲线。并指出:(1) 跨中挠度是否最大?(2)跨中挠度的值 是否接近最大挠度值?
l/2
l/4
§5-3 按叠加原理计算梁的挠度和转角
两段梁的挠曲线近似微分方程亦需分段列出,并分别进行积分:
左段梁0 x a
右段梁 a x l
挠曲线近似微分方程
EIw1
M1x
F
b l
x
积分得
EIw2
M 2
x
F
b l
x
Fx
a
EIw1
F
b l
x2 2
C1
EIw1
F
b l
x3 6
wC w1 |xl 2 48EI
3l 2 4b2
Fbl 2
16 EI
0.0625
Fbl 2 EI
可见在集中荷载作用于右支座附近这种极端情况下,跨中
挠度与最大挠度也只相差不到3%。因此在工程计算中,只要 简支梁的挠曲线上没有拐点都可以跨中挠度代替最大挠度。
梁的位移经典.ppt
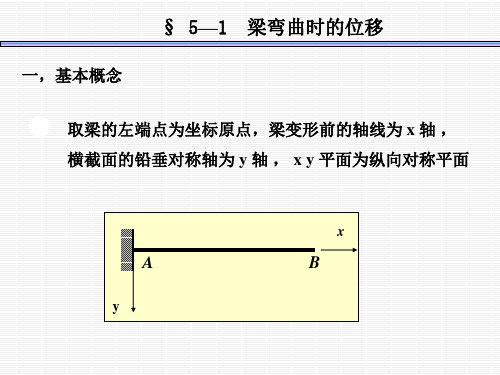
Fx3 FL2 x FL3
6EIz 2EIz 3EIz
例题 5.2
求图所示悬臂梁B端的挠度与转角。
A
x
l
y
边界条件
x0 0 x0 0
xL
B
qL3 6EI z
M x 1 qL x2
B
2
x
EI z
M
x
1 2
q
L
x
2
EI z
EI z
1 6
qL
x3
C1
EI z
1 24
qL
x4
C1x
D2
x a 1Da1 D22a 1aC1C22a
6FEELbI2FIzaZLb32Ca1L3C1aCC2F1Lb2 D6FxL1b26FL2FLb3L12b6FLFa16Lb22Fax3bL122aF162aFa3aFaCba22L6L23LC0bC2 22a D2
EIz2
Fb 6L
叠加法计算位移的条件:
✓1、梁在荷载作用下产生的变形是微小的; ✓2、材料在线弹性范围内工作,梁的位移与荷载呈线性关系; ✓3、梁上每个荷载引起的位移,不受其他荷载的影响。
例题 5.6
试用叠加原理求图示弯曲刚度为EIz的简支梁的跨中
截面挠度ωc和梁端截面的转角θAθB.
F
q
B c qc Fc
EI z
C
B
l2
q2
DA
l2
q
EI z
C
l2
l2
F 1 qL 4
MB
1 16
qL2
B
q2
A
C
l2
l2
q2
M
B
1 16
6EIz 2EIz 3EIz
例题 5.2
求图所示悬臂梁B端的挠度与转角。
A
x
l
y
边界条件
x0 0 x0 0
xL
B
qL3 6EI z
M x 1 qL x2
B
2
x
EI z
M
x
1 2
q
L
x
2
EI z
EI z
1 6
qL
x3
C1
EI z
1 24
qL
x4
C1x
D2
x a 1Da1 D22a 1aC1C22a
6FEELbI2FIzaZLb32Ca1L3C1aCC2F1Lb2 D6FxL1b26FL2FLb3L12b6FLFa16Lb22Fax3bL122aF162aFa3aFaCba22L6L23LC0bC2 22a D2
EIz2
Fb 6L
叠加法计算位移的条件:
✓1、梁在荷载作用下产生的变形是微小的; ✓2、材料在线弹性范围内工作,梁的位移与荷载呈线性关系; ✓3、梁上每个荷载引起的位移,不受其他荷载的影响。
例题 5.6
试用叠加原理求图示弯曲刚度为EIz的简支梁的跨中
截面挠度ωc和梁端截面的转角θAθB.
F
q
B c qc Fc
EI z
C
B
l2
q2
DA
l2
q
EI z
C
l2
l2
F 1 qL 4
MB
1 16
qL2
B
q2
A
C
l2
l2
q2
M
B
1 16
第5章(梁的挠度和转角及挠曲线近似微分方程)
再注意到在图示坐标系中,负弯矩对应于正值w" ,正弯矩对
应于负值的w" ,故从上列两式应有 w M x 2 3/ 2 EI 1 w 由于梁的挠曲线为一平坦的曲线,上式中的w2与1相比可略 去,于是得挠曲线近似微分方程 w M x EI 一般记为 EIw M x
于x轴方向的线位移w称为挠度,横截面对其原来位置的角
位移q 称为横截面的转角。
2
材 料 力 学 Ⅰ 电 子 教 案
在图示坐标系中,挠度w向下为正,向上为负;
顺时针转向的转角q为正,逆时针转向的转角q为负。
3
材 料 力 学 Ⅰ 电 子 教 案
思考题:梁的截面位移与变形有何区别?有何联系?
答:梁的截面位移是指:截面形心的线位移和截面相对其
是挠曲线在该相应点的切线与x轴之间的夹角,从而有转
角方程:
5
q tanq w f x
材 料 力 学 Ⅰ 电 子 教 案
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关,也与支座约束的条件
有关。图a和图b所示两根梁,如果它们的材料和尺寸相同, 所受的外力偶之矩Me也相等,显然它们的变形程度(也就 是挠曲线的曲率大小)相同,但两根梁相应截面的挠度和 转角则明显不同。
10
8
材 料 力 学 Ⅰ 电 子 教 案
从几何方面来看,平面曲线的曲率可写作
1 w x 1 w2
3/ 2
式中,等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量,而w"是q = w' 沿x方 向的变化率,是有正负的。
积分法求梁的位移 积分法求梁的位移
Fb 2 AD段: EIw1 x C1 2l Fb 3 EIw1 x C1 x D1 6l 2 DB段: EIw2 Fb x 2 F x a C2 2l 2 3 Fb 3 F x a EIw2 x C2 x D2 6l 6
位移连续条件: a) x a 时,w1 w2
Fb 3 Fb 3 a C1a a C2 a D2 6l 6l C1a C2 a D2
Fb 2 AD段: EIw1 x C1 2l Fb 3 EIw1 x C1 x 6l 2 DB段: EIw2 Fb x 2 F x a C2 2l 2 3 Fb 3 F x a EIw2 x C2 x D2 6l 6 b) x a 时,w1 ' w2 ' Fb 2 Fb 2 a C1 a C2 2l 2l C1 C2
A
l/2 Ⅰ
F
C D
Ⅱ
B
x
qA
x1 a wC wmax
qB
b
y
当载荷作用在梁的中点,即a=b=l/2时,其最大转 角和挠度为:
q max
Fl 16 EI
2
wmax
Fl wC 48 EI
3
1. 关于分段的确定 原则:挠曲线微分方程发生了变化,均需分段。
2. 位移条件 边界条件:
w’=0,w=0 w=0
x
F D B x b l
A
a
y
解: 1)求弯矩方程
Fb x AD段:M 1 x l Fb x F x a DB段:M 2 x l
2)梁的挠曲线方程
材料力学梁弯曲时的位移演示文稿
例题5-2 试求图示等直梁的挠曲线方程和转角方程,并确定其
最大挠度wmax和最大转角qmax。
22
第二十二页,共55页。
第五章 梁弯曲时的位移
解:该梁的弯矩方程为
M x ql x 1 qx2 q lx x2
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2
以x为自变量进行积分得:
材料力学梁弯曲时的位移演示 文稿
第一页,共55页。
优选材料力学梁弯曲时的位移 Ppt
2
第二页,共55页。
第五章 梁弯曲时的位移
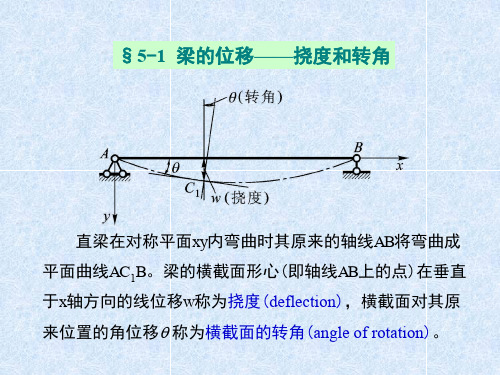
§5-1 梁的位移——挠度和转角
直梁在对称平面xy内弯曲时其原来的轴线AB将弯曲成平面曲 线AC1B。梁的横截面形心(即轴线AB上的点)在垂直于x轴方向的 线位移w称为挠度(deflection),横截面对其原来位置的角位移q 称为横截面的转角(angle of rotation)。
3
第三页,共55页。
第五章 梁弯曲时的位移
弯曲后梁的轴线——挠曲线(deflection curve)为一平坦而 光滑的曲线,它可以表达为w=f(x),此式称为挠曲线方程。由 于梁变形后的横截面仍与挠曲线保持垂直,故横截面的转 角q 也就是挠曲线在该相应点的切线与x轴之间的夹角,从而 有转角方程:
当集中荷载F作用于简支梁的跨中时(b=l/2),最大转角qmax
和最大挠度wmax为
36
q max
qA qB
Fl 2 16EI
Fl 3 wmax wC 48EI
第三十六页,共55页。
第五章 梁弯曲时的位移
思考: 试绘出图示两根简支梁的弯矩图,并描出它们的挠曲线。并
25
第二十五页,共55页。
最大挠度wmax和最大转角qmax。
22
第二十二页,共55页。
第五章 梁弯曲时的位移
解:该梁的弯矩方程为
M x ql x 1 qx2 q lx x2
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2
以x为自变量进行积分得:
材料力学梁弯曲时的位移演示 文稿
第一页,共55页。
优选材料力学梁弯曲时的位移 Ppt
2
第二页,共55页。
第五章 梁弯曲时的位移
§5-1 梁的位移——挠度和转角
直梁在对称平面xy内弯曲时其原来的轴线AB将弯曲成平面曲 线AC1B。梁的横截面形心(即轴线AB上的点)在垂直于x轴方向的 线位移w称为挠度(deflection),横截面对其原来位置的角位移q 称为横截面的转角(angle of rotation)。
3
第三页,共55页。
第五章 梁弯曲时的位移
弯曲后梁的轴线——挠曲线(deflection curve)为一平坦而 光滑的曲线,它可以表达为w=f(x),此式称为挠曲线方程。由 于梁变形后的横截面仍与挠曲线保持垂直,故横截面的转 角q 也就是挠曲线在该相应点的切线与x轴之间的夹角,从而 有转角方程:
当集中荷载F作用于简支梁的跨中时(b=l/2),最大转角qmax
和最大挠度wmax为
36
q max
qA qB
Fl 2 16EI
Fl 3 wmax wC 48EI
第三十六页,共55页。
第五章 梁弯曲时的位移
思考: 试绘出图示两根简支梁的弯矩图,并描出它们的挠曲线。并
25
第二十五页,共55页。
材料力学第五章 梁的变形
连续条件
xa
wB1 wB2
例题 画出挠曲线大致形状。图中C为中间铰。
解: 边界条件
A
C
F
B
wA 0 qA 0
wB 0
两根梁由中间铰连接,挠
曲线在中间铰处,挠度连
续,但转角不连续。
wC左 wC右
qC左 qC右
A
挠曲线的凸向由弯矩的正
负号决定,正弯矩向下凸,
负弯矩向上凸。
例 图示等截面梁,弯曲刚度EI。设梁下有一曲面 y Ax3 ,欲
)
6l
bF l
F
b
C
Bx
x l
aF FRB l
AC段 (0 x a)
EIw1
bF l
x
EIw1
bF 2l
x2
C1
EIw1
bF 6l
x3
C1 x
D1
CB段 (a x l)
EIw2
bF l
x
F(x a)
EIw2
bF 2l
x2
F ( x a)2 2
C2
EIw2
bF 6l
x3
F ( x a)3 6
转角方程,挠度方程
EIw M ( x)
q w m 6lx 3x2 2l 2 6EIl A
m
l
C
w mx 3lx x2 2l 2 6EIl
2 m
y FRA l
l
x B
m FRB l
求 wmax w q 0
3 x0 1 3 l 0.423l
wmax
w
x0
F2 60kN
C
A
F1 200kN
F2
D
