九年级数学上册 18《相似形》平行相似课后作业 (新版)北京课改版
京改版九年级上册数学第十八章 相似形 含答案

京改版九年级上册数学第十八章相似形含答案一、单选题(共15题,共计45分)1、下列四组线段(单位:㎝)中,不能成比例的是()A.a=4,b=4,c=5,d=10B.a=3,b=6,c=2,d=4C.a=1,b= ,c= ,d=D.a=2,b= ,c= ,d=22、如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=3,则线段EF的长度为()A.2B.4C.D.63、如果△ABC∽△DEF,A、B分别对应D、E,且AB∶DE=1∶2,那么下列等式一定成立的是( )A. BC∶DE=1∶2B.△ABC的面积∶△DEF的面积=1∶2C.∠A 的度数∶∠D的度数=1∶2D.△ABC的周长∶△DEF的周长=1∶24、在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判定DE∥BC的是()A. =B. =C. =D. =5、正方形ABCD中,E、F分别为AB、BC的中点,AF与DE相交于点O,则=()A. B. C. D.6、如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当时,DE的长为()A.2B.C.D.47、如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=()cm.A.3B.6C.8D. -18、在△ABC中,DE∥BC,分别交边AB、AC于点D、E,AD:BD=1:2,那么△ADE与△ABC面积的比为()A.1:2B.1:4C.1:3D.1:99、如图,在平面直角坐标系的4×4的正方形方格中,△ABC是格点三角形(三角形的三个顶点是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是()A.(1,4)B.(3,4)C.(3,1)D.(1,4)或(3,4)10、如果把三角形的三边按一定的比例扩大,则下列说法正确的是()A.三角形的形状不变,三边的比变大B.三角形的形状变,三边的比变大 C.三角形的形状变,三边的比不变 D.三角形的形状不变,三边的比不变11、如图,正方形ABCD中,,点E是对角线AC上一点,连接BE,过点E作,交AB于点F,连接DF,交AC于点G,将沿EF翻折,得到,连接DM,交EF于点N,若点F是AB的中点,则的周长是()A. B. C. D.12、如果,则的值是( )A.3B.C.D.13、如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于()A.1∶1B.1∶2C.1∶3D.2∶314、如图,在菱形ABCD中,∠A=60°,AB=2,点M为边AD的中点,连接BD 交CM于点N,则BN的长是()A.1B.C.D.15、已知,则的值为()A. B. C.﹣ D.﹣二、填空题(共10题,共计30分)16、如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为________.17、如图,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF,展开后再折叠-一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,若AD=2,则MN=________。
京改版九年级上册数学第十八章 相似形 含答案

京改版九年级上册数学第十八章相似形含答案一、单选题(共15题,共计45分)1、在一张由复印机放大复印出来的纸上,一个多边形的一条边由原来的1cm变成了4cm,那么这次复印的面积变为原来的()A.不变B.2倍C.3倍D.16倍2、如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若S△BDE :s△CDE=1:3,则S△DOE :S△AOC的值为( )A. B. C. D.3、如图,平行四边形ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于()A.2:5B.3:5C.2:3D.5:74、如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果,AD=9,那么BC的长是()A.4B.6C.2D.35、如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD 的面积为m,△OEB的面积为,则下列结论中正确的是()A.m=5B. m=4C. m=3D. m=106、下列命题中,错误的是()A.所有的正多边形都相似B.有一对锐角相等的两个直角三角形相似 C.全等的三角形一定相似 D.所有的等边三角形都相似7、如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为()A.3B.C.4D.8、如图是一个照相机成像的示意图,如果底片AB宽40mm,焦距是60mm,所拍摄的2m外的景物的宽CD为A.12mB.3mC. mD. m9、如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF ∶S△AOB的值为( )A.1∶3B.1∶5C.1∶6D.1∶1110、将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是,则点C的坐标是()A.(4,2)B.(2,4)C.(,3)D.(3,)11、下列命题中,正确的是()A.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;B.不同向量的单位向量的长度都相等,方向也都相同;C.相似三角形的中线的比等于相似比;D.一般来说,一条线段的黄金分割点有两个.12、如图,在△ABC中,AB=AC=3,BC=4,点D,E分别是边AB,BC上点,连结DE,将△BDE沿DE翻折得到△FDE,点B的对称点F恰好落在边AC上,若以点C,E,F为顶点的三角形与△ABC相似,则BE的长为()A.2B.C. 或2D. 或213、如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,则图中相似三角形有()A.1对B.2对C.3对D.4对14、如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N,给出以下三个结论:①MN∥AB;②= + ;③MN≤AB,其中正确结论的个数是()A.0B.1C.2D.315、如图,在正方形ABCD中,点E是BC延长线上的一点,且AC=EC,连接AE,交CD于点F,若AB=1,则线段DF的长是()A. B. C.2﹣ D. ﹣1二、填空题(共10题,共计30分)16、如图,和是分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=7:2:1,则∠α的度数为________°.17、如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为________.18、如图,∠BAD=∠C,DE⊥AB于E,AF⊥BC于F,若BD=6,AB=8,则DE:AF=________ .19、如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为________.20、如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.4m,请你帮她算一下,树高是________.21、如图,在中,,垂直平分,垂足为,,且,,则的长为________.22、如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD 的延长线于N,则+= ________.23、如图,在△ABC中,∠B的平分线交AC于点D,DE//AB,若AB=9,BC=6,,则等于 ________.24、如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为________ m.25、如图,在矩形ABCD中,AD=2AB=2,E是BC边上的一个动点,连接AE,过点D作DF⊥AE于F,连接CF,当△CDF为等腰三角形时,则BE的长是________.三、解答题(共5题,共计25分)26、已知,,求:代数式的值.27、在△ABC中,M是AB上一点,若过M的直线所截得的三角形与原三角形相似,试说明满足条件的直线有几条,画出相应的图形加以说明.28、如图,△ABC中,点D在BC边上,有下列三个关系式:① BAC=90°,②= ,③AD⊥BC.选择其中两个式子作为已知,余下的一个作为结论,写出已知,求证,并证明.已知:求证:证明:29、如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.(1)求证:AB•AF=CB•CD;(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP 的面积为ycm2.①求y关于x的函数关系式.②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.30、如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE BC.参考答案一、单选题(共15题,共计45分)1、D2、D3、A4、C5、B6、A7、C8、D9、C10、D11、D12、C13、C14、D15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、30、。
九年级数学上册 18.4 相似多边形同步练习 北京课改版(2021年整理)

九年级数学上册18.4 相似多边形同步练习(新版)北京课改版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册18.4 相似多边形同步练习(新版)北京课改版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学上册18.4 相似多边形同步练习(新版)北京课改版的全部内容。
18.4相似多边形一、夯实基础1.两个矩形一定相似.( )2.两个正方形一定相似.( )3.任意两个菱形都相似.( )4.有一个角相等的两个菱形相似. ( )5.边数不同的多边形一定不相似. ( )二、能力提升6.下列四组图形中必相似的是( )A.有一组邻边相等的两个平行四边形B.有一个角相等的两个等腰梯形C.对角线互相垂直的两个矩形D.对角线互相垂直且相等的两个四边形.7.下列说法正确的是( )A.对应边成比例的多边形都相似B.四个角对应相等的梯形都相似C.有一个角相等的两个菱形相似D.有一个锐角相等的两个等腰三角形相似8.四边形ABCD与四边形A1B1C1D1相似,相似比为2:3,四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为5:4,则四边形ABCD与四边形A2B2C2D2相似且相似比为()A. 5:6 B. 6:5 C. 5:6或6:5 D. 8:159.若五边形ABCDE∽五边形MNOPQ,且AB=12,MN=6,AE=7,则MQ= .三、课外拓展10。
如图,将一张长、宽之比为2的矩形纸ABCD依次不断对折,可以得到矩形纸BCFE,AEML,GMFH,LGPN.(1)矩形ABCD、BCFE、AEML、GMFH、LGPN长与宽的比改变了吗?(2)在这些矩形中,有成比例的线段吗?(3)你认为这些大小不同的矩形相似吗?四、中考链接11.(2014 太原)两个正六边形的周长分别为30cm,36cm,则它们的相似比为.12.(2015广州)下列两个图形一定相似的是.A.三角形与四边形B.两个正五边形C.两个六边形D.两个四边形参考答案一、夯实基础1.× 2.√ 3.× 4.√ 5.√二、提升能力6.C ; 7.C ; 8.A ; 9.27; 三、课外扩展 10. 解:(1)矩形ABCD 、BCFE 、AEML 、GMFH 、LGPN 长与宽的比不改变. 设纸的宽为a ,长为2a ,则BC =a ,BE =22aAE =22a ,ME =2aMF =2a,HF =42aLG =42a ,LN =4a∴BE BC=a ∶22a =2ME AE= 22a ∶2a=22aHF MF=∶242=a42=LN LG a ∶4a=2所以五个矩形的长与宽的比不改变.(2)在这些矩形中有成比例的线段.(3)这些大小不同的矩形都相似.四、中考链接11.5:612.B。
京改版九年级上册数学第十八章 相似形 含答案

京改版九年级上册数学第十八章相似形含答案一、单选题(共15题,共计45分)1、已知非负数 x,y,z 满足. .,设,则 W 的最大值与最小值的和为()A.-2B.-4C.-6D.-82、线段AB=10cm,点C是线段AB的黄金分割点,且AC>BC,则AC与AB的关系是()A.AC= ABB.AC= ABC.AC= ABD.AC= AB3、若两个相似三角形的面积之比为1∶4,则它们的周长之比为( )A.1∶2B.1∶4C.1∶5D.1∶164、如图,在▱ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是()A. B. C. D.5、如图,在中,点D、E分别在、边上,,若,,则等于()A.10B.12C.16D.206、已知如图,在中,点、点分别在、边上,且,,,的面积为4,则的面积为( )A.5B.6C.8D.97、点E,F分别在平行四边形ABCD的边BC,AD上,BE=DF,点P在边AB上,AP:PB=1:n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分,将△CDF分成面积为S3、S4的两部分(如图),下列四个等式:①S1:S3=1:n②S1:S4=1:(2n+1)③(S1+S4):(S2+S3)=1:n④(S3﹣S1):(S2﹣S4)=n:(n+1)其中成立的有()A.①②④B.②③C.②③④D.③④8、如图,在4×4正方形网格中画出的三角形中,与图中的三角形相似的是()A. B. C. D.9、在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判定DE∥BC的是()A. =B. =C. =D. =10、如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段 AC 的长为()A.4B.4C.6D.411、如图,AB∥CD,AC、BD相交于点O,过点O的直线分别交AB、CD于点E、F,则下列结论不一定成立的是()A. =B.C.D.12、如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P 分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PM•PH;⑤EF的最小值是.其中正确结论有()A.2个B.3个C.4个D.5个13、两个相似多边形的面积比是9∶16,其中小多边形的周长为36 cm,则较大多边形的周长为()A.48 cmB.54 cmC.56 cmD.64 cm14、把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大;若边长扩大5倍,则面积扩大。
九年级数学上册18.4相似多边形同步练习北京课改版

18.4相似多边形一、夯实基础1.两个矩形一定相似.( )2.两个正方形一定相似.( )3.任意两个菱形都相似.( )4.有一个角相等的两个菱形相似. ( )5.边数不同的多边形一定不相似. ( )二、能力提升6.下列四组图形中必相似的是( )A.有一组邻边相等的两个平行四边形B.有一个角相等的两个等腰梯形C.对角线互相垂直的两个矩形D.对角线互相垂直且相等的两个四边形.7.下列说法正确的是( )A.对应边成比例的多边形都相似B.四个角对应相等的梯形都相似C.有一个角相等的两个菱形相似D.有一个锐角相等的两个等腰三角形相似8.四边形ABCD与四边形A1B1C1D1相似,相似比为2:3,四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为5:4,则四边形ABCD与四边形A2B2C2D2相似且相似比为()A. 5:6 B. 6:5 C. 5:6或6:5 D. 8:159.若五边形ABCDE∽五边形MNOPQ,且AB=12,MN=6,AE=7,则MQ= .三、课外拓展10。
如图,将一张长、宽之比为2的矩形纸ABCD依次不断对折,可以得到矩形纸BCFE,AEML,GMFH,LGPN.(1)矩形ABCD、BCFE、AEML、GMFH、LGPN长与宽的比改变了吗?(2)在这些矩形中,有成比例的线段吗?(3)你认为这些大小不同的矩形相似吗?四、中考链接11.(2014 太原)两个正六边形的周长分别为30cm,36cm,则它们的相似比为.12.(2015广州)下列两个图形一定相似的是.A.三角形与四边形B.两个正五边形C.两个六边形D.两个四边形参考答案一、夯实基础1.× 2.√ 3.× 4.√ 5.√二、提升能力6.C ; 7.C ; 8.A ; 9.27; 三、课外扩展 10. 解:(1)矩形ABCD 、BCFE 、AEML 、GMFH 、LGPN 长与宽的比不改变.设纸的宽为a ,长为2a ,则BC =a ,BE =22a AE =22a ,ME =2a MF =2a ,HF =42a LG =42a ,LN =4a ∴BEBC =a ∶22a =2 ME AE = 22a ∶2a =2 2a HF MF =∶242=a 42=LN LG a ∶4a =2 所以五个矩形的长与宽的比不改变.(2)在这些矩形中有成比例的线段.(3)这些大小不同的矩形都相似.四、中考链接11.5:612.B尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
京改版九年级上册数学第十八章 相似形 含答案
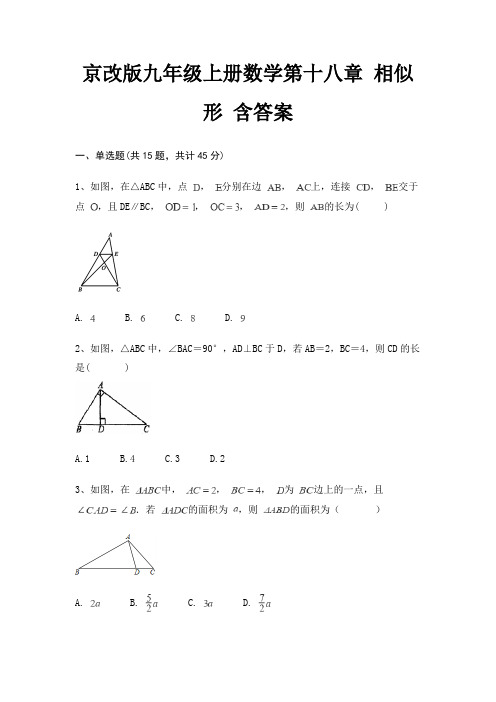
京改版九年级上册数学第十八章相似形含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,点,分别在边,上,连接,交于点,且DE∥BC,,,,则的长为( )A. B. C. D.2、如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=4,则CD的长是( )A.1B.4C.3D.23、如图,在中,,,为边上的一点,且.若的面积为,则的面积为()A. B. C. D.4、如图,点D是BC边上一点且BD:DC=1:2,点F为线段AD上一点且AF:DF=1:2,BF的延长线交AC于E,则AE:AC=()A.1:2B.1:3C.1:4D.1:75、如图所示,图中共有相似三角形( )A.2对B.3对C.4对D.5对6、如图所示,中,,,,,则的值为()A.6B.9C.12D.167、点E,F分别在平行四边形ABCD的边BC,AD上,BE=DF,点P在边AB上,AP:PB=1:n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分,将△CDF分成面积为S3、S4的两部分(如图),下列四个等式:①S1:S3=1:n②S1:S4=1:(2n+1)③(S1+S4):(S2+S3)=1:n④(S3﹣S1):(S2﹣S4)=n:(n+1)其中成立的有()A.①②④B.②③C.②③④D.③④8、如图,在△ABC中,点D、E分别在边AB,AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为()A.4B.6C.8D.99、如图,在正方形ABCD中,E、F分别在CD、AD边上,且CE=DF,连接BE、CF相交于G点。
则下列结论:①BE=CF;②S△BCG = S四边形DFGE;③CG2= BG·GE;④当E为CD中点时,连接DG,则∠FGD=45°。
正确结论的个数是( )A.1B.2C.3D.410、如图,在中,为斜边的中线,过点D作于点E,延长至点F,使,连接,点G在线段上,连接,且.下列结论:①;②四边形是平行四边形;③;④.其中正确结论的个数是()A.1个B.2个C.3个D.4个11、如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对()A.6对B.5对C.4对D.3对12、如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC 相似时,运动的时间是()A.4或4.8B.3或4.8C.2或4D.1或613、如图,在矩形ABCD中,BC=8,对角线AC与BD相交于点O,过点D作AC 的垂线DE,交AC于点E,AE=3CE.则DE的值为()A.4B.2C.4D.214、如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()A.2B.4C.6D.815、已知△ABC∽△DEF,AB:DE=1:2,则△ABC与△DEF的周长比等于()A.1:2B.1:4C.2:1D.4:1二、填空题(共10题,共计30分)16、已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④.其中正确的只有________.(填序号)17、如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC 交BC的延长线于点F.在AF上取点M,使得AM= AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是,则的值是________.18、如图:铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.4m时,长臂端点升高________ m.19、如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为________.20、如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为________.21、下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩笔在黑板上写上三个大字1,2,3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是________ ,错误的是________ (填序号)22、在正方形中,,对角线交于点,点在线段上,且,将射线绕点逆时针转,交于点, 则的长为________.23、如图,△ABC中,∠A的平分线交BC于D,若AB=6cm,AC=4cm,∠A=60°,则AD的长为________cm.24、如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B 到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为________m.25、如图,在△ABC中,高AD与中线CE相交于点F,AD=CE=6,FD=1,则AB=________.三、解答题(共5题,共计25分)26、已知≠0,求的值.27、如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.5米,标杆为3米,且BC=1米,CD=6米,求电视塔的高ED.28、如图,已知E为圆内两弦AB和CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.求证:EF=FG.29、已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,(1)求证:△ABC∽△BCD;(2)若BC=2,求AB的长。
北京课改版九年级数学上册第18章 相似形 18.4 相似多边形 同步练习题
北京课改版九年级上册第18章相似形18. 4相似多边形同步练习一.选择题(共10小题,3*10=30)1. 如图所示,内外两个矩形相似,且对应边平行,则下列结论中正确的是 ( ) A.x y =1 B.x y =a bC.x y =baD .以上答案都不对2. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边为 ( ) A .6 B .8 C .10 D .123. 两个边数相同的多边形相似应具备的条件是( ) A .对应角相等 B .对应边相等C .对应角相等,对应边相等D .对应角相等,对应边成比例4. 下列四组图形中,一定相似的是 ( ) A .正方形与矩形 B .正方形与菱形 C .菱形与菱形 D .正五边形与正五边形5. 下列命题中,是真命题的为 ( ) A .锐角三角形都相似 B .直角三角形都相似C.等腰三角形都相似D.等边三角形都相似6. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她裁剪出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )7. 六边形ABCDEF∽六边形GHIJKL,相似比为2∶1,则下列结论正确的是( ) A.BC=2HIB.∠E=2∠KC.六边形ABCDEF的周长=六边形GHIJKL的周长D.S六边形ABCDEF=2S六边形GHIJKL8. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a,b应满足的条件是()A.a=2b B.a=22bC.a=2b D.a=4b9. 如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推,若各种开本的矩形都相似,那么ABAD等于( )A.22 B. 2C. 0.618D.210. 在梯形ABCD中,AB∥CD,AB=60,CD=15,E,F分别为AD,BC上一点,且EF ∥AB,若梯形DEFC∽梯形EABF,那么EF等于( ).A.15 B.20 C.25 D.30二.填空题(共8小题,3*8=24)11. 如图,在两个相似四边形中,根据已知的数据,图中x=______,y=____,α=______度.12. 如图所示,矩形草坪长20 m,宽10 m,沿草坪四周有1 m宽的环形小路,小路内外边缘所成的矩形__________(填“相似”或“不相似”).13.一张比例尺为1∶250的图纸上,一块多边形区域的周长是54 cm,面积是280 cm2,则该区域的实际周长是________,实际面积是________.14. 在一张由复印机印出来的纸上,一个多边形的一条边长由原来的1 cm变成了4 cm,那么这次复印的放缩比例是________,这个多边形的面积是原来的_______倍.15. 两个五边形相似,一组对应边长分别是3 cm和4.5 cm,若它们的面积之和是78 cm2,则较大的五边形的面积是________.16. 两个相似多边形的最长边分别为35 cm和14 cm,它们的周长的差为60 cm,则这两个多边形的周长分别为____________.17. 已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=______.18. 如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF 的面积为a,则▱ABCD的面积为________.(用含a的代数式表示)三.解答题(共7小题,46分)19. (6分)如图所示的两个相似四边形中,求未知边x,y的长度和角α的大小.20. (6分)已知相似的两个矩形中,一个矩形的长和面积分别为4和12,另一个矩形的宽为6,求这两个矩形面积的比.21. (6分)如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=2,求矩形ABCD的面积.22.(6分) 如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2 m,桌面距离地面为1 m,若灯泡距离地面3 m,求地面上阴影部分的面积.23. (6分)公园里有块草坪,其平面图如图所示,∠A=90°,其比例尺为1∶2 000,根据图中标注的数据(单位:cm),求该草坪的实际周长和面积.24. (8分) 如图,M是四边形ABCD的对角线AC上的点,ME∥CD,MF∥BC,MC∶MA =1∶3.(1)求证:四边形AFME∽四边形ABCD;(2)求四边形AFME与四边形ABCD的面积比.25. (8分) 课本中,把长与宽之比为2的矩形纸片称为标准纸,请思考解决下列问题:(1)将一张标准纸片ABCD(AB<BC)对开,如图①所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上的点F处,折痕为AE(如图②甲);第二步:沿过D点的直线折叠,使C点落在AD边上的点N处,折痕为DG(如图②乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图②丙),此时G点恰好与N点重合.请你探究:矩形纸片ABCD 是否是一张标准纸?请说明理由.(3)不难发现,将一张标准纸如图③一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=2,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2 012次对开后所得标准纸的周长.参考答案1-5 BBDDD 6-10 DACAD 11. 30,125,6512. 不相似 13. 135cm ,1750cm 2 14. 1∶4,16 15. 54cm 216. 100cm ,40cm 17.5+1218. 12a19. 解:∵两个四边形相似,它们的对应边成比例,对应角相等, ∴184=y 6=x7,解得x =31.5,y =27. a =360°-(77°+83°+117°)=83°20. 解: 因为一个矩形的长和面积分别为4和12,则这个矩形的宽为3. 设另一个矩形的长为x ,根据相似多边形对应边的比相等有x 4=63,解得x =8,所以另一个矩形的面积为6×8=48.则它们的面积的比为1248=14.21. 解:∵E ,F 分别为矩形ABCD 的边AD ,BC 的中点,∴AE =12AD ,∵矩形ABCD ∽矩形EABF ,∴EA AB =AB BC, 即AB 2=EA·BC =12BC 2,又∵AB =2,∴BC =22,∴矩形ABCD 的面积=AB·BC =2×22=4 2.22. 解:根据题意和题图可作出如答图所示的图形,DE ,BC 分别是桌面及在地面上形成阴影的直径,根据题意,知DE =1.2 m ,FG =1 m ,AG =3 m. ∴AF =AG -FG =3-1=2 (m). ∵DE ∥BC , ∴△ADE ∽△ABC ,∴DE BC =AF AG ,即1.2BC =23, ∴BC =1.8(m),∴桌面在地面上形成阴影部分的面积为 π·⎝⎛⎭⎫BC 22= π·⎝⎛⎭⎫1.822=0.81 π(m 2)23. 解:连结BD ,由已知条件可得△ABD 和△BDC 是直角三角形,面积之和是0.0036 m 2,四边形ABCD 周长是0.32 m , ∵(12000)2=0.0036S,∴S =1.44×104(m 2). ∵12000=0.32C,∴C =640(m). 故该草坪的实际周长为640 m ,实际面积为1.44×104 m 2. 24. 解:(1)证明:∵ME ∥CD ,∴△AME ∽△ACD , ∴AM AC =ME CD =AE AD,∠AME =∠ACD ,∠AEM =∠D. 同理可证△AMF ∽△ACB ,∴AM AC =MF BC =AFAB ,∠AMF =∠ACB ,∠AFM =∠B ,∴AF AB =MF BC =ME CD =AE AD,∠AFM =∠B ,∠FME =∠BCD ,∠AEM =∠D ,∠FAE =∠BAD ,∴四边形AFME ∽四边形ABCD.25. 解:(1)证明:∵矩形纸片ABCD 是标准纸,∴BCAB = 2.由对开的含义知AF =12BC ,∴AB AF =AB 12BC =2·AB BC =22=2,∴矩形纸片ABEF 也是标准纸.(2)是标准纸.理由如下:设AB =CD =a ,由图形折叠可知DN =CD =DG =a ,DG ⊥EM ,∵由图形折叠可知△ABE ≌△AFE ,∴∠DAE =12∠BAD =45°,∴△ADG 是等腰直角三角形.∴在Rt △ADG 中,AD =AG 2+DG 2=2a , ∴AD AB =2a a=2,∴矩形纸片ABCD 是一张标准纸.(3)第5次对开后所得的标准纸的周长为2+24,第2012次对开后所得的标准纸的周长为1+221005.。
北京课改版九年级数学上册第18章 相似形 18.1.1线段的比和比例的基本性质 同步练
北京课改版九年级上册第18章相似形18.1.1线段的比和比例的基本性质同步练习一.选择题(共10小题,3*10=30)1.如图,线段AB ∶BC =1∶2,则AC ∶BC 等于( )A .1∶3B .2∶3C .3∶1D .3∶22.下列各组线段的长度成比例的是( )A .1 cm ,2 cm ,3 cm ,4 cmB .2 cm ,3 cm ,4 cm ,5 cmC .0.3 m ,0.6 m ,0.5 m ,0.9 mD .30 cm ,20 cm ,90 cm ,60 cm3.下列各组线段(单位:cm)中,是成比例线段的是( )A .1,2,3,4B .1,2,2,4C .3,5,9,13D .1,2,2,34.已知线段AB ,在BA 的延长线上取一点C ,使CA =3AB ,则线段CA 与线段CB 之比为( )A .3∶4B .2∶3C .3∶5D .1∶25.已知a =0.2,b =1.6,c =4,d =12,则下列各式中正确的是( ) A .a ∶b =c ∶d B .a ∶c =d ∶bC .a ∶b =d ∶cD .b ∶a =d ∶c6. 已知2x =3y(y≠0),则下面结论成立的是( )A.x y =32B.x 3=2yC.x y =23D.x 2=y 37.下列说法中正确的有( )①两条线段的比是两条线段的长度之比,比值是一个正数;②两条线段的长度之比是同一单位下的长度之比;③两条线段的比值是一个数量,不带单位;④两条线段的比有顺序,a b 与b a不同,它们互为倒数. A .1个 B .2个C .3个D .4个8.已知x 2=y 3,那么下列式子中一定成立的是( ) A .2x =3y B .3x =2yC .x =2yD .xy =69.等边三角形的一边与这条边上的高的比是( ) A.3∶2 B.3∶1C .2∶ 3D .1∶310.如果a +2b b =52,那么a b的值是( ) A.12B .2 C.15D .5 二.填空题(共8小题,3*8=24)11.已知a =2 cm ,b =30 mm ,则a ∶b =______.12.若3a =5b ,则a b=________. 13. 若线段a ,b ,c ,d 成比例,其中a =3 cm ,b =6 cm ,c =2 cm ,则d =__________.14.已知a ,b ,c ,d 四条线段成比例,其中a =3 cm ,b =(x -1) cm ,c =5 cm ,d =(x +1) cm ,则x =____.15.已知A ,B 两地的实际距离AB =5 km ,画在地图上的距离A′B′=2 cm ,则这张地图的比例尺是_____________.16. 如图,已知AD DB =AE EC,AD =6.4 cm ,DB =4.8 cm ,EC =4.2 cm ,则AC =______cm.17.已知2a +3b a +2b =125,则a b =_____. 18.已知三条线段的长分别为1 cm ,2 cm , 2 cm ,如果另外一条线段与它们是成比例线段,则另外一条线段的长为___________________ cm.三.解答题(共6小题,46分)19. (6分)判断下列线段是否成比例,若是,请写出比例式.(1)a =3 m ,b =5 m ,c =4.5 cm ,d =7.5 cm ;(2)a =7 cm ,b =4 cm ,c =d =27 cm ;20. (6分) 如图,已知AD DB =AE EC ,AE AC =DE BC,AD =10 cm ,DB =8cm ,EC =4cm ,DE=5 cm ,求△ABC 的周长.21. (7分) 已知三条线段的长度分别是4,8,5,试写出另一条线段的长度,使这四条线段为成比例线段.22.(7分) 如图所示,已知矩形ABCD和矩形A′B′C′D′,AB=8 cm,BC=12 cm,A′B′=4 cm,B′C′=6 cm.(1)求A′B′AB和B′C′BC的值;(2)线段A′B′,AB,B′C′,BC是成比例线段吗?23. (10分)如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,已知AC=3,BC =4.(1)线段AD,CD,CD,BD是不是成比例线段?写出你的理由;(2)在这个图形中,能否再找出其他成比例的四条线段?如果能,请至少写出两组.24. (10分)如图,一个矩形剪去一个以宽为边长的正方形后,剩下的矩形长与宽的比与原矩形长与宽的比相等,求原矩形的长与宽的比.参考答案1-5DDBAC 6-10 ADBCA11. 2∶312. 5313. 4 cm14. 415. 1∶25000016. 9.817. -9218. 2 2 cm 或 2 cm 或2219. 解:(1)成比例,a ∶b =c ∶d(2)成比例,a ∶c =d ∶b20. 解:∵AD DB =AE EC ,∴108=AE 4, 解得AE =5 (cm),则AC =AE +EC =5+4=9 (cm) 又∵AE AC =DE BC ,∴59=5BC解得BC =9 (cm),∴△ABC 的周长=AB+BC+AC=18+9+9=36 (cm)21. 解:设所求的线段长度为x.当x ∶4=8∶5时,可求得x =325; 当x ∶4=5∶8时,可求得x =208=52; 当4∶8=5∶x 时,可求得x =404=10. 所以所求的线段长度可能为325或52或10. 22. 解:(1)∵AB =8 cm ,BC =12 cm ,A′B′=4 cm ,B′C′=6 cm , ∴A′B′AB =48=12,B′C′BC =612=12. (2)由(1)知A′B′AB =12,B′C′BC =12,∴A′B′AB =B′C′BC, ∴线段A′B′,AB ,B′C′,BC 是成比例线段.23. 解:(1)由勾股定理得AB =32+42=5,∴12×5·CD =12×3×4, ∴CD =125, 由勾股定理得AD =95,BD =165,AD CD =CD BD, 即AD ,CD ,CD ,BD 是成比例线段(2)能,如AC BC =AD CD ,AC BC =CD BD ,AB AC =AC AD等 24. 解:设原矩形的长是a ,宽是b ,则DE =CF =a -b ,已知BC AB =CD CF, 即a b =b a -b, 整理,得a 2-ab -b 2=0,两边同除以b 2,得(a b )2-a b-1=0, 解得a b =5+12或1-52(舍去). ∴长与宽的比为5+12。
北京课改版九年级数学上册第18章 相似形 18.4 相似多边形 同步练习
北京课改版九年级上册第18章相似形18. 4相似多边形同步练习一.选择题(共10小题,3*10=30)1.下列各组图形中相似的是( )A .①②③B .②③④C .①③④D .①②④2.一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最短边的长为6,则这个多边形的最长边的长为( )A .12B .18C .24D .303.下列说法正确的是( )A .所有的等腰三角形都相似B .四个角都是直角的两个四边形一定相似C .所有的正方形都相似D .四条边对应成比例的两个四边形相似4.若四边形ABCD ∽四边形A′B′C′D′,AB =6,A′B′=8,∠A =45°,B′C′=8,CD =4,则下列说法错误的是( )A .∠A′=45°B .四边形A′B′C′D′与四边形ABCD 的相似比为23C .BC =6D .C′D′=1635.若五边形ABCDE 与五边形A 1B 1C 1D 1E 1相似,且相似比为k 1=5,则五边形A 1B 1C 1D 1E 1与五边形ABCDE的相似比k2为( )A.5 B. 0.2C.6 D.16.如图,在长为8 cm,宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )A.2 cm2 B.4 cm2C.8 cm2 D.16 cm27.在下面的三个矩形中,相似的是( )A.甲和乙B.甲和丙C.乙和丙D.甲、乙和丙8. 如图所示,有两个形状相同的星星图案,则x的值为( )A.15 B.12C.10 D.89. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形和矩形花边,其中每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不相似的是( )10.如图,小明将一张报纸对折后,发现对折后的半张报纸与整张报纸相似,那么整张报纸的长与宽的比是( )A.2∶1 B.3∶1C.3∶1 D.4∶1二.填空题(共8小题,3*8=24)11.若图4-3-1所示的两个四边形相似,则∠α的度数是____.12.如图,已知四边形ABCD∽四边形A′B′C′D′,则∠A=_____,x=____.13.如图,在四边形ABCD中,AD∥BC,AD=12 cm,BC=27 cm,点E,F分别在两边AB,CD上,且EF∥AD,若四边形AEFD∽四边形EBCF,那么EF=____ cm.14.已知四边形A′B′C′D′∽四边形ABCD,其相似比k=23,若A′B′=24,则AB=____. 15.如图,点E,F分别在矩形ABCD的边BC,AD上,EF∥AB,AB=6,AD=8,当AF=____时,矩形ABEF与矩形ADCB相似.16.如图,在▱ABCD中,AB=6,AD=4,EF∥AD,若▱ABCD∽▱ADFE,则AE=____.17.如图,矩形ABCD中,AB=4,M,N分别是AD,BC的中点,MN∥AB,若矩形DMNC 与矩形ABCD相似,则AD的长为________.18.如图,已知梯形ABCD与梯形A′B′C′D′相似,则x=______,∠α=_________.三.解答题(共7小题,46分)19. 在一矩形花坛ABCD的四周修筑小路,使得相对两条小路的宽均相等.花坛的宽AB=20米,长AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似?请说明理由.20.在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,若AB∶A′B′=1∶3,试求BD∶A′C′的值.21.如图,在梯形ABCD中,EF∥AB∥CD,AB=9,CD=4,若EF把原梯形分成两个相似的小梯形,求EF的长.22.如图,矩形A′B′C′D′在矩形ABCD内部.AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.23.如图,G是正方形ABCD的对角线AC上一点,过点G作GE⊥AD,GF⊥AB,垂足分别为E,F.求证:四边形AFGE与四边形ABCD相似.24.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比k.25.一个矩形ABCD的较短边长为2.(1)如图①,将矩形ABCD沿它的长边对折(MN为折痕),得到的矩形与原矩形相似,求它的另一边长;(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC 与原矩形相似,求余下矩形EFDC的面积.参考答案1-5BBCBB 6-10 CBDDA11. 87°12. 107°,8513. 1814. 3615. 9216. 8317. 4 218. 6,118°19. 解:由题意得2020+2y =3030+2x,从而有20(30+2x)=30(20+2y). 解得x y =32. ∴小路的宽x 与y 的比值为32时,能使矩形A′B′C′D′与矩形ABCD 相似 20. 解:AB ∶A′B′=1∶3,可以设AB =a ,则A′B′=3a , ∵∠A =60°,∴△ABD 是等边三角形,∴BD =AB =a ,同理△A′B′D′是等边三角形,则A′C′=3a ,因此BD ∶A′C′=1∶321. 解:∵梯形DCFE ∽梯形EFBA ,∴DC EF =EF AB, ∴EF 2=DC·AB ,又∵DC =4,AB =9,∴EF 2=36,∴EF =622. 解:a +c =2b +2d ,理由如下:设AB =x ,则AD =2x ,那么A′D′=2x -a -c ,A′B′=x -b -d. ∵矩形A′B′C′D′∽矩形ABCD ,∴AD ∶AB =A′D′∶A′B′=2∶1.∴A′D′=2A′B′.∴2x -a -c =2(x -b -d).∴a +c =2b +2d23.证明:∵∠GEA =∠EAF =∠GFA =90°,∴四边形EAFG 为矩形.∵四边形ABCD 为正方形,∴AC 平分∠DAB.又∵GE ⊥AD ,GF ⊥AB ,∴GE =GF ,∴四边形AFGE 为正方形.∴四边形AFGE 与四边形ABCD 相似.24. 解:(1)∵矩形DMNC 与矩形ABCD 相似,∴DM AB =DC AD, 设AD =x ,则DM =12x , ∴12x 4=4x, ∴x 2=32,∴x 1=42或x 2=-42(负值舍去),∴AD =42(2)k =DM AB =224=2225.解:(1)由已知得MN =AB =2,DM =12AD =12BC. ∵将矩形ABCD 沿MN 对折后得到的矩形与原矩形相似,∴矩形DMNC 与矩形ABCD 相似,DM AB =MN BC, ∴DM·BC =AB·MN ,即12BC 2=4, ∴BC =2 2,即它的另一边长为2 2.(2)∵矩形EFDC 与原矩形ABCD 相似,∴DF AB =CD BC. ∵AB =CD =2,BC =4, ∴DF =AB·CD BC=1, ∴矩形EFDC 的面积=CD·DF =2×1=2.。
九年级数学上册 18.5.2 相似三角形的判定同步练习 北京课改版(2021学年)
九年级数学上册18.5.2 相似三角形的判定同步练习(新版)北京课改版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册18.5.2 相似三角形的判定同步练习(新版)北京课改版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学上册18.5.2 相似三角形的判定同步练习(新版)北京课改版的全部内容。
18.5。
2相似三角形的判定一、夯实基础1.下列四个三角形中,与左图中的三角形相似的是( )2.已知△ABC的三边长分别为1、3、2,△A′B′C′的两边长分别为2和6.如果△A BC∽△A′B′C′,那么△A′B′C′的第三边为()A.2B.22C.62D.23.下列说法中,不正确的是( )A.两角对应相等的两个三角形相似B.两边对应成比例的两个三角形相似C.两边对应成比例且夹角相等的两个三角形相似D.三边对应成比例的两个三角形相似4.如图,在△ABC中,点P为AB上一点,给出下列四个条件:①∠ACP=∠B; ②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件是( )A.①②④B.①③④C.②③④ D.①②③5.如图,A、B、C、P、Q、甲、乙、丙、丁都是方格纸的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁4点中的( )A.甲B.乙C.丙D.丁二、能力提升=________时,△AEF∽△BCE.6.如图,在正方形ABCD中,E为AB的中点,当AFAD7.如图,BC平分∠ABD,AB=9,BD=25,当BC=________时,△ABC∽△CBD.8.如图,在△ABC中,D、E分别是AB、AC的中点,若DE=2cm,则BC=_________cm.9.如图,零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10 mm.则零件的厚度x=_______mm.三、课外拓展10.在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,需添加的一个条件是____________(写出一种情况即可).11.一个三角形钢架的三边长分别为20 cm、30 cm和40cm.现在要做一个与其相似的三角形钢架,而只有长为12 cm和30 cm的两根钢管,要求以其中一根钢管为一边,将另一根钢管截成两段作为另两边组成三角形(可剩余).请你写出符合要求的一种截法___________.12.如图,AB BC CA==,试说明:∠ABD=∠EBC.BD BE ED四、中考链接1、(2014,济南)如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P做直线截ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有( )A、1条B、2条C、3条D、4条2、(2015,聊城)如图,锐角ABC∆的高CD和BE相交于点O,图中与ODB∆相似的三角形有( )ﻬ参考答案一、夯实基础1.B 2.D 3.B4.D 5.C二、提升能力6.147.158.49.2.5三、课外扩展10.答案不唯一,如BC=10,EF=511.答案不唯一,如以12 cm长的钢管为一边,从30cm长的钢管上分别截取6 cm、9cm的两段12.因为AB BC CA==,所以△ABC∽△DBE.所以∠ABC=∠DBE.所以∠ABC-∠DBCBD BE ED=∠DBE-∠DBC,即∠ABD=∠EBC四、中考链接1、C2、B以上就是本文的全部内容,可以编辑修改。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行相似课后作业
1、如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF
∥AB,且AD:DB=3:5,那么CF:CB等于( )
A. 5:8 B. 3:8 C. 3:5 D. 2:5
2、如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、
F,AC=4,CE=6,BD=3,则BF=( )
A. 7
B. 7.5
C. 8
D. 8.5
3、如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,
AF=2cm,DF=4cm,AG=3cm,则AC的长为( )
A. 9cm B. 14cm C. 15cm D. 18cm
4、AD是△ABC的高,E为AB的中点,EF⊥BC,如果DC=31BD,那么FC:BF等于( )
A. 35B. 34C. 23D. 32
5、如图,AB∥DE,BC∥EF,则①OA:OD=OB:OE;②OC:OF=OB:OE;③AC∥DF,上述
结论正确的是( )
A. ①
B. ②
C. ①②
D. ①②③
6、如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=2,则DG+EH+FI的长
是( )
A.25 B.3 C.23 D.4
7、如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,
CD=3,则GH的长为
8、如图,已知点D为△ABC中AC边的中点,AE∥BC,ED交AB于点G,交BC的延
长线于点F,若BG:GA=3,BC=8,则AE的长为
9、如图,点A1,A2,A3,…,点B1,B2,B3,…,分别在射线OM,ON上.OA1=1,A1B1=2OA1,
A1A2=2OA1,A2A3=3OA1,A3A4=4OA1,….A1B1∥A2B2∥A3B3∥A4B4∥….则A2B2= ,AnBn=
(n为正整数)
10、已知:AB∥EG∥CD,EG分别交AC于E,BC于F,AD于G,若AE=2EC,AB=9,CD=12.求:
EF与FG的长.
11、如图,四边形ABCD中,点E、F、G分别在边AB、AC、AD上,连接EF,FG.如
果EF∥BC,且AE•AD=AG•AB.求证:FG∥CD.
12、如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求:
(1)求BF和BD的长度.
(2)四边形BDEF的周长.
平行相似课后作业
参考答案
1、解析:先由AD:DB=3:5,求得BD:AB的比,再由DE∥BC,根据平行线分线段成
比例定理,可得CE:AC=BD:AB,然后由EF∥AB,根据平行线分线段成比例定理,可得
CF:CB=CE:AC,则可求得答案.
解:∵AD:DB=3:5,
∴BD:AB=5:8,
∵DE∥BC,
∴CE:AC=BD:AB=5:8,
∵EF∥AB,
∴CF:CB=CE:AC=5:8.
故选A
2、解析:由直线a∥b∥c,根据平行线分线段成比例定理,即可得AC:CE=BD:DF,又
由AC=4,CE=6,BD=3,即可求得DF的长,则可求得答案.
解:∵a∥b∥c,
∴AC:CE=BD:DF,
∵AC=4,CE=6,BD=3,
∴4:6=3:DF,
解得:DF=29,
∴BF=BD+DF=3+29=7.5.
故选B.
3、解析:延长FG交CB的延长线于点H.根据平行四边形的性质,得BC=AD=6cm,
BC∥AD.根据AAS可以证明△AFE≌△BHE,则BH=AF=2cm,再根据BC∥AD,得AG:CG=AF:CH,
求得CG的长,从而求得AC的长.
解:∵四边形ABCD是平行四边形,
∴BC=AD=6cm,BC∥AD.
∴∠EAF=∠EBH,∠AFE=∠BHE,
又AE=BE,
∴△AFE≌△BHE,
∴BH=AF=2cm.
∵BC∥AD,
∴AG:CG=AF:CH,即3:CG=2:8,
则CG=12,
则AC=AG+CG=15(cm).
故选C
4、解析:由AD是△ABC的高,EF⊥BC,即可证得AD∥EF,又由E为AB的中点,根
据平行线分线段成比例定理,可得BF=DF=21BD,又由DC=31BD,即可求得FC:BF的值.
解:∵AD是△ABC的高,EF⊥BC,
∴EF∥AD,
∵E为AB的中点,
∴BF=DF=21BD,
∵DC=31BD,
∴FC=FD+CD=65BD,
∴FC:BF=65BD:21BD=35.
故选A.
5、解析:由AB∥DE,BC∥EF,根据平行线分线段成比例定理,即可证得①OA:OD=OB:OE;
②OC:OF=OB:OE;正确,则可得②OA:OD=OC:OF;,继而证得AC∥DF正确.
解:∵AB∥DE,BC∥EF,
∴OA:OD=OB:OE,故①正确;OC:OF=OB:OE,故②正确;
∴OA:OD=OC:OF,∴AC∥DF,故③正确.
故选D
6、解析:由于D、E、F和G、H、I分别是AB、AC的四等分点,则DG∥EH∥FI,根
据平行线分线段成比例定理,即可求出DG、EH、FI和BC的比例关系,由此可求出DG+EH+FI
的长.解:∵AD=DE=EF=FB,AG=GH=HI=IC,
∴DG∥EH∥FI;
∴AD:AB=DG:BC=1:4,即DG=41BC;
同理可得:EH=21BC,FI=43BC;
∴DG+EH+FI=41BC+21BC+43BC=23BC=3;
故选B
7、解析: 根据平行线分线段成比例定理,由AB∥GH,得出GH:AB=CH:BC,由GH∥
CD,得出GH:CD=BH:BC,将两个式子相加,即可求出GH的长.
解:∵AB∥GH,
∴GH:AB=CH:BC,即GH:2=CH:BC①,
∵GH∥CD,
∴GH:CD=BH:BC,即GH:3=BH:BC②,
①+②,得BCBCBCBHBCCHGHGH32=1
∴132GHGH
解得GH=56.
故答案为56
8、解析:由AE∥BC,可得△AEG∽△BFG,△AED∽△CFD推出AE:BF=AG:BG=1:3,又
有BC的值,再由AE:CF=AD:CD=1,得出AE=CF,代入即可求解AE的长.
解:∵AE∥BC,
∴△AEG∽△BFG,△AED∽△CFD,
∴AE:BF=AG:BG=1:3,AE:CF=AD:CD=1
即AE=CF,
又BC=8,
∴AE8+AE)=1:3
AE=4.
故答案为:4.
9、解析:根据OA1=1,求出A1A2、A2A3、A3A4的值,推出AnAn-1的值,根据平行线分线
段成比例定理得出OA1: OA2=A1B1:A2B2,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),
A4B4=20=4(4+1),推出AnBn=n(n+1)即可.
解:∵OA1=1,
∴A1A2=2×1=2,
A2A3=3×1=3,
A3A4=4,
…
An-2An-1=n-1,
An-1An=n,
∵A1B1∥A2B2∥A3B3∥A4B4∥…,
∴OA1: OA2=A1B1:A2B2,
∴1:(1+2) =2: A2B2,,
∴A2B2=6=2×(2+1),
A3B3=12=3×(3+1),
A4B4=20=4(4+1),
…
∴AnBn=n(n+1),
故答案为:6,n(n+1).
10、解析:根据平行线分线段成比例得,EF:AB=CE:AC,EG:CD=AE:AC,又由AE=2EC得,
CE:AC=1:3,AE:AC=2:3,代入即可求出.解:∵AB∥EG∥CD,
∴EF:AB=CE:AC, EG:CD=AE:AC,
∵AE=2EC,
∴CE:AC=1:3,AE:AC=2:3,
又∵AB=9,CD=12,
∴EF:9=1:3,EG:12=2:3,
解得,EF=3,EG=8,、
∴FG=EG-EF=8-3=5
11、解析: 根据平行线分线段成比例定理由EF∥BC得到AE:AB=AF:AC,而
AE•AD=AG•AB,即AE:AB=AG:AD,则AF:AC=AG:AD,然后根据平行线分线段成比例的
逆定理即可得到结论.
证明:∵EF∥BC,
∴AE:AB=AF:AC,
又∵AE•AD=AG•AB,
∴AE:AB=AG:AD,
∴AF:AC=AG:AD,
∴FG∥AB.
12、解析:(1)由平行线分线段成比例得出比例式,即可得出结果;
(2)先证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
解:(1)∵AE=2CE,
∴CE:AE=1:2,
∵EF∥AB
∴AE:AC=BF:BC=2:3,
∵BC=9,
∴BF=6,
∵DE∥BC
∴BC:AB=CE:AC=1:3,
∵AB=6,
∴BD=2;
(2)∵EF∥AB,DE∥BC
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长2(2+6)=16.
