例题
会计分录大全-会计分录例题大全

会计分录大全例题一1、*企业从银行提取现金4,000元借:现金4000贷:银行存款40002、采购员王强从财务科预借差旅费2000元,现金付讫借:其他应收款-王强2000贷:现金20003、5天后王强到财务科报销差旅费1800元,余款退回企业借:管理费用-差旅费1800现金200贷:其他应收款-王强20004、从*企业采购材料一批,价税款合计数为23400元,该企业适用的增值税税率为17%货款及税款未付,材料当日未运达企业借:在途物资20000应交税金-应交增值税(进项)3400贷;应付账款234005、3天后上述材料运抵企业,验收入库借:原材料20000贷:在途物资200006、以银行存款如数支付上述购买材料的货款及税款借:应付账款23400贷:银行存款234007、从车间领用材料一批,总价值8,000元,其中生产产品直接耗用7,000元,车间一般耗用1,000元借:生产成本7000制造费用1000贷:原材料80008、分配本月工资费用20,000元,其中生产工人工资12,000元,车间管理人员工资5,000元,厂部管理人员工资3,000元借:生产成本12000制造费用5000管理费用3000贷:应付职工薪酬200009、以现金支付本月应付工资借:应付职工薪酬20000贷:现金2000010、按工资总额的14%计提福利费借:生产成本1680制造费用700管理费用420贷:应付福利费280011、对外销售产品一批,不含税售价总额30,000元,增值税适用税率为17%,货款及税款未收到借:应收账款35100贷:主营业务收入30000应交税金-应交增值税(销项)510012、结转上述已销产品的实际成本25,000元借:主营业务成本25000贷:库存商品2500013、收到上述已销产品的货款及税款,存入银行借:银行存款35100贷:应收账款3510014、摊销应由本月负担的保险费等4,000元借:管理费用-保险费4000贷:待摊费用400015、计提固定资产折旧8,000元,其中生产用固定资产折旧6,000元,厂部管理用固定资产折旧2,000元借:制造费用6000管理费用2000贷:累计折旧800016、从银行取得5年期借款20万元,存入银行借:银行存款20万元贷:长期借款20万元17、收到投资者投入企业一项专利权,评估确认价值8万元借:无形资产-专利权8万元贷:实收资本8万元18、按规定交纳本月应交税金5,000元,银行存款付讫借:应交税金5000贷:银行存款500019、按规定支付本月借款的利息费用等4,000元,银行存款付讫借:财务费用4000贷:银行存款400020、以现金800元购买厂部办公用品借:管理费用-办公费800贷:现金80021、从甲公司购入原材料800公斤,单价600元,增值税率17%,价税合计561600元,款项已付,原材料已验收入库借:原材料480000应交税金-应交增值税(进项)81600贷:银行存款额56160022、以银行存款偿还长期借款90000元借:长期借款90000贷:银行存款9000023、向B公司销售商品1000件,单价460元,增值税率17%,价税合计538200元,款项尚未收到借:应收账款-B公司538200贷:主营业务收入460000应交税金-应负增值税(销项)7820024、购入设备一台,价款120000元,以银行存款支付借:固定资产120000借:银行存款12000025、月末提取固定资产折旧:其中生产车间2500元;行政管理部门1860元借:制造费用2500管理费用1860贷:累计折旧436026、结转销售给B公司商品的销售成本320000元借:主营业务成本320000贷:库存商品320000例题二1.月初购进原材料一批并验收入库,至本月末,有关结算账单仍未到材料估计成本为60万元借:原材料60万贷:应付帐款60万2.以银行存款支付本季短期借款利息135000元经查,前2个月已预提100000元借:预提费用100000借:财务费用35000贷:银行存款1350003.月初,企业将所持有的一*面值50万元、不带息的商业承兑汇票向银行申请贴现;贴现利息为1250元,贴现净额已存入A企业的存款账户该项应收票据尚差1个月到期借:银行存款498750借:财务费用1250贷:应收票据5000004.销售不适用的原材料一批,价款30000元,增值税5100元;货款已收妥并存入银行该批材料成本为19000元借:银行存款35100贷:其他业务收入30000贷:应交税金--增值税(销项税额)5100同时:借:其他业务支出19000贷:原材料190005.将本年净利润80万元全部结转至"利润分配"账户借:本年利润80万贷:利润分配--未分配利润80万6.按面值2000万元发行债券一批,期限3年,年利率5%,到期一次还本付息(发行费用略),发行债券款已收妥并存入企业的存款账户借:银行存款2000万贷:应付债券2000万7.存出投资款200万元借:长期债权投资-其他债权投资(本金)200万元贷:银行存款200万元8.计提存货跌价准备35000元借:管理费用35000贷:存货跌价准备350009.从外地购进一批商品,增值税发票上列示价款10000元,增值税1700元双方商定货款采用商业汇票结算,企业已开出、承兑面值11700元、3个月到期的商业汇票交销货方商品未到借:物资采购10000借:应交税金-应交增值税(进项税额)1700贷:应付票据1170010.上项商品到达并验收入库借:库存商品10000贷:物资采购1000011.收入*公司支付的违约金15000元存入银行借:银行存款15000贷:营业外收入1500012.收回去年已作为坏账(采用备抵法核算)核销的应收账款30000元借:银行存款30000贷:应收账款30000同时,借:应收账款30000贷:坏账准备3000013.销售产品一批,价款30万元,增值税51000元,经查,该笔销售业务已于前月预收货款10万元,余款尚未结清该批产品的制造成本为20万元借:应收账款251000借:预收账款100000贷:主营业务收入300000贷:应交税费-应交增值税51000同时:借:主营业务成本200000贷:库存商品20000014.本月应付职工薪酬15000元,其中生产工人的薪酬7000元,车间管理人员薪酬3000元,厂部人员薪酬5000元借:生产成本7000借:制造费用3000借:管理费用5000贷:应付职工薪酬1500015.企业计提固定资产减值准备6000元借:资产减值损失6000贷:固定资产减值准备600016.开出并承兑商业汇票一*,金额50万元、期限3个月,用于抵付前欠购料款借:应付帐款50万贷:应付票据50万17.出售一项专利,收入25万元已存入银行该项专利的账面摊余价值10万元;营业税率5%借:银行存款250000贷:无形资产100000贷:应交税费-应交营业税12500贷:营业外收入13750018.董事会决议,本年度向投资者分配现金利润30万元,下年3月6日支付借:利润分配-应付现金股利300000贷:应付股利300000支付时:借:应付股利300000贷:银行存款(或库存现金)30000019.向*单位销售商品一批,价款100000元,销项增值税17000元,款项尚未收到借:应收帐款117000贷:主营业务收入100000贷:应交税费--增值税(销项税额)17000 20.销售商品一批,价款300000元,增值税51000元,款项已全部收妥并存入银行该批商品成本为200000元借:银行存款351000贷:主营业务收入300000贷:应交税费--增值税(销项税额)51000同时:借:主营业务成本200000贷:库存商品20000021.摊销无形资产2500元借:管理费用2500贷:累计摊销250022.上月末购入材料的应付账款200000元,通过银行转账支付由于在折扣期内付款而享受2%的现金折扣(采用总价法核算)借:应付账款200000贷:银行存款196000贷:财务费用400023.年末,经计算,企业全年应纳所得税94800元借:所得税费用94800贷:应交税费--所得税94800例题三1.*股东一机床一台入股,经股东协商作价2万元2.向银行贷款5万元,作为流动资金,并存入银行3.购入机床一台,价款2万元,增值税率17%,以银行存款支付4.购入钢材5吨,每吨3000元,增值税17%以商业汇票付讫5.将购入的钢材运回,运费2000元,以银行存款支付,装卸力资500元,以现金支付6.钢材入库结转入库钢材的成本7.结算本月应付职工工资20000元,其中生产工人工资15000元,车间管理人员工资2000元,厂部管理人员工资3000元8.计提设备折旧费5000元,全部为车间生产设备9.单位工作人员出差,向会计室借款1000元10.出差人员回单位后报支车旅费1050元1.借:固定资产2万元贷:实收资本2万元2.借:银行存款5万元贷:短期借款5万元3.借:固定资产2.34万元贷:银行存款2.34万元4.借:材料采购1.5万元应交税费-应交增值税(进项)0.255万元贷: 应付票据1.755万元5.借:材料采购0.25万元贷:银行存款0.2万元现金0.05万元6.借:原材料1.75万元贷:材料采购1.75万元7.借:生产成本1.5万元制造费用0.2万元管理费用0.3万元贷:应付工资2万元8.借:制造费用0.5万元贷:累计折旧0.5万元9.借:其他应收款0.1万元贷:现金0.1万元10.借:管理费用0.105万元贷:其他应收款0.1万元现金0.005万元例题四**华丽达公司2006年6月发生以下几项业务:1.销售商品一批,总售价72000元,款已收讫;该商品成本为65000元2.预收货款24000元,款存入银行,商品在下月交付3.以银行存款预付下季度仓库租金10800元4.销售商品一批,总售价84000元,货物已发出,发票已开具,销货合同约定货款将于下月结算;该商品成本为70000元5.以银行存款支付本月水电费3000元6.以银行存款支付本年度第二季度短期借款利息12000元7.当年3月份已预付本年度第二季度的财产保险费6000元如何编制会计分录最佳答案1、借:银行存款72000 贷:主营业务收入61538 贷:应交税金-应交增值税(销项税额)10461 ;借:主营业务成本65000 贷:库存商品650002、借:银行存款24000 贷:预收货款240003、借:待摊费用10800 贷:银行存款10800;(每月)借:销售费用3600 贷:待摊费用36004、借:应收账款84000 贷:销售收入71795 贷:应交税金-应交增值12205 ;借:主营业务成本70000 待:库存商品700005、(管理部门水电费)借:管理费用3000 贷:银行存款3000;(车间生产部门)借:制造费用3000 贷:银行存款30006、(第二季度先预提)借:财务费用12000 贷:应付利息12000;(本月)借:应付利息12000 贷:银行存款120007、借:待摊费用6000 贷:银行存款6000例题五会计分录练习题及答案东方公司为增值税一般纳税人工业企业,2001年月12月份发生下列业务:1、开出现金支票从银行提取现金2000元备用;借:现金2000贷:银行存款20002、用现金支付生产车间办公用品费440元;借:制造费用440贷:现金4403、收到盛达公司前欠货款80000元,存入银行;借:银行存款80000贷:应收账款---盛达公司800004、向前进工厂销售A产品一批,不含增值税的售价为100000元,增值税17000元,款项尚未收到;借:应收账款---前进工厂117000贷:主营业务收入100000应交税金-应交增值税(销项税)170005、接到开户银行的通知,收到光明公司前欠货款150000元;借:银行存款150000贷:应收账款---光明工厂1500006、向大华公司销售B产品一批,不含增值税的售价为200000元,增值税为34000元,合计234000元,当即收到大华公司签发并承兑的面值为234000元,期限为三个月的商业汇票一*;借:应收票据--大华公司234000贷:主营业务收入200000应交税金-应交增值税(销项税额)340007、接到开户银行的通知,胜利工厂签发并承兑的商业汇票已到期,收到胜利工厂支付的票据款120000元;借:银行存款120000贷:应收票据--胜利工厂1200008、向宏达公司购买一批甲材料,按合同规定,东方公司用银行存款预付购货款50000元;借:预付账款--宏达公司50000贷:银行存款500009、收到宏达公司发来的甲材料一批,增值税专用发票上注明的买价为80000元,增值税为13600元,合计93600元扣除预付款50000元,余额43600元东方公司用银行存款支付,甲材料已验收入库;借:原材料-甲材料80000 应交税金-应交增值税(进项税额)13600贷:预付账款--宏达公司50000银行存款4360010、厂部办公室*强因公出差,预借差旅费800元,付以现金;借:其他应收款--*强800贷:现金80011、*强出差回来,向公司报销差旅费700元,余款交回现金;借:管理费用700现金100贷:其他应收款--*强80012、向科达公司购进甲材料一批,增值税专用发票上注明的买价为500000元,增值税85000元,价税合计585000元,材料已验收入库,款项尚未支付;借:原材料-甲材料500000 应交税金-应交增值税(进项税额)85000贷:应付账款-科达公司58500013、向苏达公司购进乙材料一批,增值税专用发票上注明的买价为300000元,增值税51000元,价税合计351000元,款项已通过银行支付,材料尚未到达企业;借:在途物资-乙材料300000应交税金-应交增值税(进项税额)51000贷:银行存款35100014、接上题,向苏达公司购进的乙材料一批,已收到并验收入库;借:原材料-乙材料300000贷:在途物资-乙材料30000015、本月份生产A产品领用甲材料400000元,生产B产品领用甲材料480000元,车间一般消耗甲材料20000元,管理部门耗用乙材料5000元;借:生产成本-A产品400000 --B产品480000制造费用20000管理费用5000贷:原材料-甲材料900000--乙材料500016、用银行存款支付公司下年度的报刊订阅费1200元;借:待摊费用1200贷:银行存款120017、摊销以前已预付应由本月份负担的财产保险费5000元,其中厂部应负担3000元,车间应负担2000元;借:管理费用3000制造费用2000贷:待摊费用500018、从市场上购入一台设备,价值100000元,设备已收到并交付生产使用,款项已通过银行支付;借:固定资产100000贷:银行存款10000019、经计算本月份应提固定资产折旧2000元,其中,厂部使用的固定资产应提折旧8000元,车间使用的固定资产应提折旧12000元;借:管理费用8000制造费用12000贷:累计折旧2000020、用银行存款240000元从其他单位购入一项专利权;借:无形资产-专利权240000贷:银行存款24000021、接上题,专利权分10年平均摊销,本月的摊销额为2000元借:管理费用2000贷:无形资产-专利权2000东方公司为增值税一般纳税人工业企业,2001年月12月份发生下列业务:1、向工商银行签订借款协议,取得借款1000000元,期限六个月,月利率0.4%,借款已转存银行存款账户;借:银行存款1000000贷:短期借款-工商银行10000002、东方公司原借中国银行的一笔短期借款到期,本金500000元,用银行存款归还;借:短期借款-中国银行500000 贷:银行存款5000003、从新华公司购入乙材料一批,增值税发票上注明的买价为70000元,增值税11900元,合计81900元,材料已收到并验收入库,款项尚未支付;借:原材料-乙材料70000 应交税金-应交增值税(进项税额)11900贷:应付账款-新华公司819004、用银行存款支付上述欠新华公司的购料款81900元;借:应付账款-新华公司81900贷:银行存款819005、按合同规定,收到长江公司汇来的购买本企业A产品的购货定金100000元,存入银行存款;借:银行存款100000 贷:预收账款-长江公司1000006、接上题,销售A产品一批给长江公司,不含增值税的售价为150000元,增值税为25500元,合计175500元,扣除预收款100000元,其余款项长江公司尚未支付;借:预收账款-长江公司175500贷:主营业务收入150000应交税金-应交增值税(销项税额)255007、用现金发放本月份职工工资24000元;借:应付工资24000贷:现金240008、分配本月份职工工资24000元,其中生产A产品职工工资为8000元,生产B产品职工工资为10000元,车间管理人员工资为2000元,厂部管理人员工资为4000元;借:生产成本-A产品8000--B产品10000制造费用2000管理费用4000贷:应付工资240009、接上题,按上述工资额的14%计提应付福利费3360元,其中,生产A产品职工应提1120元,生产B产品职工应提1400元,车间管理人员应提280元,厂部管理人员应提560元;借:生产成本-A产品1120--B产品1400制造费用280管理费用560贷:应付福利费336010、职工李明报销医药费300元,经批准后用现金支付;借:应付福利费300贷:现金30011、计提本月份应负担的短期借款利息4000元;借:财务费用4000贷:预提费用400012、用银行存款支付第四季度的银行借款利息10000元,该利息已按月预提借:预提费用10000贷:银行存款10000东方公司为增值税一般纳税人工业企业,2001年月12月份发生下列业务:1、收到国家有关部门投入的货币资金1000000元,已存入银行;借:银行存款1000000 贷:实收资本--国家资本金10000002、收到信达公司投资转来的一台设备,价值为200000元,设备已交付生产使用;借:固定资产200000 贷:实收资本-法人资本金(信达公司)2000003、收到盛华公司捐赠的货币资金500000元,存入银行;借:银行存款500000贷:资本公积5000004、向胜利工厂销售A产品一批,不含增值税的售价为600000元,增值税为102000元,合计702000元,款项已收到并存入银行;借:银行存款702000贷:主营业务收入600000应交税金-应交增值税(销项税额)1020005、销售多余的乙材料一批,不含增值税的售价为50000元,增值税为8500元,合计58500元,款项已存银行;借:银行存款58500贷:其他业务收入50000应交税金-应交增值税(销项税额)85006、结转本月份销售A产品的销售成本390000元,销售B产品的销售成本120000元;借:主营业务成本510000 贷:库存商品-A产品390000--B产品1200007、结转本月份销售乙材料的成本30000元;借:其他业务支出30000贷:原材料-乙材料300008、月末将本月份归集的制造费用36720元分配计入A、B产品的生产成本,按A、B产品生产工人工资比例分配;已知A产品生产工人工资为8000元,B产品生产工人工资为10000元;分配率:36720/(8000+10000)=2.04借:生产成本-A产品16320 (8000*2.04)--B产品20400 (10000*2.04)贷:制造费用367209、本月份生产的A产品已全部完工并验收入库,结转其生产成本已知月初A产品的生产成本为110000元,本月生产A 产品耗用直接材料为400000元,直接人工为9120元,分配的制造费用为16320元B产品月末均未完工;借:库存商品-A产品535440贷:生产成本-A产品53544010、银行存款支付本月份销售A、B产品的运输费、包装费、保险费等计15000元;借:营业费用15000贷:银行存款15000东方公司为增值税一般纳税人工业企业,2001年月12月份发生下列业务:1、因对外投资收到投资单位分来的投资利润220000元,存入银行;借:银行存款220000 贷:投资收益2200002、取得罚款收入3000元,存入银行;借:银行存款3000贷:营业外收入30003、向希望工程捐赠人民币150000元,款项已通过银行支付;借:营业外支出150000贷:银行存款1500004、月末将收入类账户结转本年利润,其中:主营业务收入1050000元,其他业务收入50000元,投资收益220000元,营业外收入30000元;借:主营业务收入1050000 其他业务收入50000投资收益220000营业外收入30000贷:本年利润13500005、月末将费用类账户结转本年利润,其中:主营业务成本510000元,主营业务税金及附加1547元,其他业务支出30238元,管理费用18760元,账务费用4000元,营业费用15000元,营业外支出150000元;借:本年利润729545 贷:主营业务成本510000主营业务税金及附加1547其他业务支出30238管理费用18760财务费用4000营业费用15000营业外支出1500006、计算全年应交的所得税,税额为402750.15元;借:所得税402750.15贷:应交税金-应交所得税402750.157、将上述所得税费用结转本年利润;借:本年利润402750.15贷:所得税402750.158、结转企业全年实现的净利润817704. 85元;借:本年利润817704.85贷:利润分配817704. 859、按净利润的10%提取法定盈余公积81770.49元;借:利润分配81770.49贷:盈余公积81770.4910、经董事会决定向投资者分配股利400000元借:利润分配400000贷:应付股利400000。
工程量计算例题
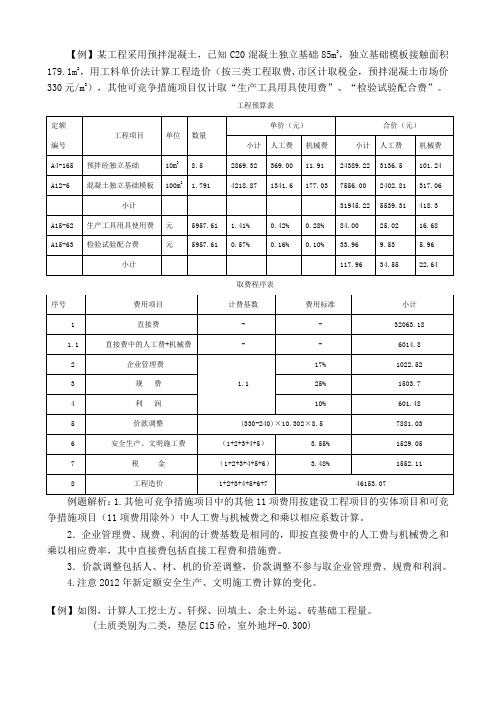
【例】某工程采用预拌混凝土,已知C20混凝土独立基础85m3,独立基础模板接触面积179.1m2,用工料单价法计算工程造价(按三类工程取费,市区计取税金,预拌混凝土市场价330元/m3),其他可竞争措施项目仅计取“生产工具用具使用费”、“检验试验配合费”。
工程预算表取费程序表例题解析:1.其他可竞争措施项目中的其他11项费用按建设工程项目的实体项目和可竞争措施项目(11项费用除外)中人工费与机械费之和乘以相应系数计算。
2.企业管理费、规费、利润的计费基数是相同的,即按直接费中的人工费与机械费之和乘以相应费率,其中直接费包括直接工程费和措施费。
3.价款调整包括人、材、机的价差调整,价款调整不参与取企业管理费、规费和利润。
4.注意2012年新定额安全生产、文明施工费计算的变化。
【例】如图,计算人工挖土方、钎探、回填土、余土外运、砖基础工程量。
(土质类别为二类,垫层C15砼,室外地坪-0.300)【例】如下图所示尺寸,求混凝土带型基础模板和混凝土的工程造价。
备注:按三类工程取费,企业管理费费率为17%,利润费率为10%,规费费率为25%,税金税率为3.48%,安全生产、文明施工费为4.25%。
解:(1)带型基础外侧模板 S1=[(4.5×2+0.5×2)×2+(4.8+0.5×2)×2]×0.3=9.48 m2(2) 带型基础内侧模板 S2=[(4.5-0.5×2)×2+(4.8-0.5×2)×2]×0.3×2=8.76 m2带型基础模板工程量 S= S1+ S2=18.24 m2(模板工程量3分)(3)带形基础混凝土外墙 V=1×0.3×(4.5+4.5+4.8)×2=8.28 m3 (混凝土工程量2分)内墙 V=1×0.3×(4.8-1)=1.14 m3 (混凝土工程量2分)合计:9.42 m3预算表取费:1. 直接费 3329.7元2.其中人+机 1021.36元3.企业管理费 1021.36×17%=173.63元4.规费 1021.36×25%=255.34元5.利润 1021.36×10%=102.14元6安全生产、文明施工费 3860.81×4.25%=164.08元7.税金 4024.89×3.48%=140.07元【例】如图所示内外墙毛石基础、砖基础平面图和剖面图,毛石基础每级高度为350mm,试计算砌体基础工程量。
《椭圆》方程典型例题20例(含标准答案解析]
![《椭圆》方程典型例题20例(含标准答案解析]](https://img.taocdn.com/s3/m/26e3c9fb3186bceb19e8bb56.png)
《椭圆》方程典型例题20例典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程. 分析:题目没有指出焦点的位置,要考虑两种位置. 解:(1)当()02,A 为长轴端点时,2=a ,1=b ,椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a ,椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三 例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112aa x x x M +=+=,2111a x y M M +=-=,4112===a x y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:ac x ca AF =-12, ∴ 11545x ex a AF -=-=. 同理 2545x CF -=. ∵ BF CF AF 2=+,且59=BF , ∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-. 将此式代入①,并利用821=+x x 的结论得 253640-=-x ∴ 4540590=--=x k BT.典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=,112212x ex a MF +=+=.∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x .整理得048325121=++x x .解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122k kk x x +-=+.∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --. 解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-.所求直线方程为0342=-+y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,;(2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y . (2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x . 说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :.过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然MF AM 2+的最小值为AQ ,即M 为所求点,因此3=M y ,且M 在椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九 例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十 例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫ ⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b ,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49s i n 3s i n34222+--=θθb b b 3421s i n 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b ,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,.典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化,120≠∠APB .(2)如果椭圆上存在一个点Q ,使 120=∠AQB ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+ay x ay ,将22222y b a a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2.∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a > ∴2tan -<∠APB故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x∵22222y ba a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b cab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e ∴232≥e 或22-≤e (舍),∴136<≤e .典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k .当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅.∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解.解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α, ∴P 点坐标为)5154,554(.典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=. 分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,ca x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标; (2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQ PF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(. 说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134ea c x -=代入12222=+b y a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12F PF,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα ∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα, ∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+= ∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+b y a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos b a b -=θ,∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-ba b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。
(完整版)高中物理小船渡河模型典型例题(含答案)【经典】..

考点四:小船渡河模型1.(1.(小船渡河问题小船渡河问题小船渡河问题))小船在200 m 宽的河中横渡,水流速度是2 m/s 2 m/s,小船在静水中的航速是,小船在静水中的航速是4 m/s.4 m/s.求:求:求:(1)(1)要使小船渡河耗时最少,应如何航行?最短时间为多少?要使小船渡河耗时最少,应如何航行?最短时间为多少?要使小船渡河耗时最少,应如何航行?最短时间为多少?(2)(2)要使小船航程最短,应如何航行?最短航程为多少?要使小船航程最短,应如何航行?最短航程为多少?要使小船航程最短,应如何航行?最短航程为多少?答案 (1)船头正对河岸航行耗时最少,最短时间为50 s.(2)船头偏向上游,与河岸成60°角,最短航程为200 m.解析 (1)如图甲所示,船头始终正对河岸航行时耗时最少,即最短时间tmin =d v 船=2004s =50 s. (2)如图乙所示,航程最短为河宽d ,即最短航程为200 m ,应使v 合的方向垂直于河岸,故船头应偏向上游,与河岸成α角,有 cos α=v 水v 船=24=12,解得α=60°. 2、一小船渡河,河宽d =180 m 180 m,水流速度,水流速度v1v1==2.5 m/s.2.5 m/s.若船在静水中的速度为若船在静水中的速度为v2v2==5 m/s 5 m/s,求:,求:,求: (1)(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?(2)(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?答案 (1)船头垂直于河岸 36 s 90 5 m (2)船头向上游偏30° 24 3 s 180 m3、已知某船在静水中的速率为v1v1==4 m/s m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d =100 m 100 m,河水的流动速度为,河水的流动速度为v2v2==3 m/s 3 m/s,方向与河岸平行,方向与河岸平行,方向与河岸平行..试分析:试分析:(1)(1)欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移是多大?是多大?(2)(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?解析 (1)根据运动的独立性和等时性,当船在垂直河岸方向上的分速度v⊥最大时,渡河所用时间最短.设船头指向上游且与上游河岸夹角为α,其合速度v 与分运动速度v1、v2的矢量关系如图所示.河水流速v2平行于河岸,不影响渡河快慢,船在垂直河岸方向上的分速度v⊥=v1sin α,则船渡河所用时间为t =d v1sin α. 显然,当sin α=1即α=90°时,v⊥最大,t 最小,此时船身垂直于河岸,船头始终垂直指向对岸,但船实际的航向斜向下游,如图所示.渡河的最短时间tmin =d v1=1004s =25 s 船的位移为l =v 21+v 22tmin =42+32×25 m=125 m 船渡过河时到达正对岸的下游A 处,其顺水漂流的位移为x =v2tmin =3×25 m=75 m.(2)由于v1>v2,故船的合速度与河岸垂直时,船的航行距离最短.设此时船速v1的方向(船头的指向)斜向上游,且与河岸成θ角,如图所示,则cos θ=v2v1=34,θ=arccos 34. 船的实际速度为v 合=v 21-v 22=42-32 m/s =7 m/s 故渡河时间:t′=d v 合=1007 s =10077 s. 答案 (1)t=25s ,x=75m ,l=125m (2)t=10077s 4、河宽60 m 60 m,水流速度,水流速度v1v1==6 m/s 6 m/s,小船在静水中的速度,小船在静水中的速度v2v2==3 m/s 3 m/s,则:,则:,则:(1)(1)它渡河的最短时间是多少?它渡河的最短时间是多少?它渡河的最短时间是多少?(2)(2)最短航程是多少?最短航程是多少?最短航程是多少?答案 (1)20 s (2)120 m5.(单选单选))一小船在静水中的速度为3 m/s 3 m/s,它在一条河宽为,它在一条河宽为150 m 150 m,水流速度为,水流速度为4 m/s 的河流中渡河,则该小船该小船( ( ). 答案答案 CA .能到达正对岸.能到达正对岸B B B.渡河的时间可能少于.渡河的时间可能少于50 s甲 乙 AC .以最短时间渡河时,它沿水流方向的位移大小为200 mD 200 m D.以最短位移渡河时,位移大小为.以最短位移渡河时,位移大小为150 m6. 6.一只小船在静水中的速度为一只小船在静水中的速度为5 m/s 5 m/s,它要渡过一条宽为,它要渡过一条宽为50 m 的河,河水流速为4 m/s 4 m/s,则,则,则( ( ) ) 答案答案 CA.A.这只船过河位移不可能为这只船过河位移不可能为50 mB.B.这只船过河时间不可能为这只船过河时间不可能为10 sC.C.若河水流速改变,船过河的最短时间一定不变若河水流速改变,船过河的最短时间一定不变若河水流速改变,船过河的最短时间一定不变D.D.若河水流速改变,船过河的最短位移一定不变若河水流速改变,船过河的最短位移一定不变若河水流速改变,船过河的最短位移一定不变7.(7.(运动的合成和分解运动的合成和分解运动的合成和分解))某河宽为600 m 600 m,河中某点的水流速度,河中某点的水流速度v 与该点到较近河岸的距离d 的关系如图所示.船在静水中的速度为4 m/s 4 m/s,要想使船渡河的时间最短,下列说法正确的是,要想使船渡河的时间最短,下列说法正确的是,要想使船渡河的时间最短,下列说法正确的是( ( ) ) 答案答案 ADA.A.船在航行过程中,船头应与河岸垂直船在航行过程中,船头应与河岸垂直船在航行过程中,船头应与河岸垂直B.B.船在河水中航行的轨迹是一条直线船在河水中航行的轨迹是一条直线船在河水中航行的轨迹是一条直线C.C.渡河的最短时间为渡河的最短时间为240 sD.D.船离开河岸船离开河岸400 m 时的速度大小为2 5 m/s8. ( (多选多选多选))小船横渡一条两岸平行的河流,船本身提供的速度小船横渡一条两岸平行的河流,船本身提供的速度((即静水速度即静水速度))大小不变、船身方向垂直于河岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则( ( ) ) 答案答案 ACA .越接近河岸水流速度越小.越接近河岸水流速度越小B .越接近河岸水流速度越大.越接近河岸水流速度越大C .无论水流速度是否变化,这种渡河方式耗时最短.无论水流速度是否变化,这种渡河方式耗时最短D .该船渡河的时间会受水流速度变化的影响.该船渡河的时间会受水流速度变化的影响 9. ( (单选单选单选))有一条两岸平直、河水均匀流动、流速恒为v 的大河.小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k ,船在静水中的速度大小相同,则小船在静水中的速度大小为同,则小船在静水中的速度大小为( ( ) ) 答案答案 BA.kv k2k2--1B.v 1-k2C.kv 1-k2D.v k2k2--1解析 设大河宽度为d ,小船在静水中的速度为v0,则去程渡河所用时间t1=d v0,回程渡河所用时间t2=d v 20-v2.由题知t1t2=k ,联立以上各式得v0=v1-k2,选项B 正确,选项A 、C 、D 错误. 10. 10. (单选)如图所示,甲、乙两船在同一条河流边同时开始渡河,河宽为(单选)如图所示,甲、乙两船在同一条河流边同时开始渡河,河宽为H ,河水流速为u ,划船速度为v ,出发时两船相距H 332,甲、乙船头均与岸边成o 60角,且乙船恰好能直达对岸的A 点,则下列判断正确的是点,则下列判断正确的是(( D )A .甲、乙两船到达对岸的时间不同.甲、乙两船到达对岸的时间不同B .两船可能在未到达对岸前相遇.两船可能在未到达对岸前相遇C .甲船在A 点右侧靠岸点右侧靠岸D .甲船也在A 点靠岸点靠岸11.11.如图所示,一艘轮船正在以如图所示,一艘轮船正在以4 m/s 的速度沿垂直于河岸方向匀速渡河,河中各处水流速度都相同,其大小为v1v1==3 m/s 3 m/s,行驶中,轮船发动机的牵引力与船头朝向的方向相同.某时刻发动机突然熄火,轮船,行驶中,轮船发动机的牵引力与船头朝向的方向相同.某时刻发动机突然熄火,轮船牵引力随之消失,轮船相对于水的速度逐渐减小,但船头方向始终未发生变化.求:牵引力随之消失,轮船相对于水的速度逐渐减小,但船头方向始终未发生变化.求:(1)(1)发动机未熄火时,轮船相对于静水行驶的速度大小;发动机未熄火时,轮船相对于静水行驶的速度大小;发动机未熄火时,轮船相对于静水行驶的速度大小;(2)(2)发动机熄火后,轮船相对于河岸速度的最小值.发动机熄火后,轮船相对于河岸速度的最小值.发动机熄火后,轮船相对于河岸速度的最小值.答案 (1)5 m/s (2)2.4 m/s解析 (1)发动机未熄火时,轮船运动速度v 与水流速度v1方向垂直,如图所示,故此时船相对于静水的速度v2的大小:v2=v2+v 21=42+32 m/s =5 m/s ,设v 与v2的夹角为θ,则cos θ=v v2=0.8.(2)熄火前,船的牵引力沿v2的方向,水的阻力与v2的方向相反,熄火后,牵引力消失,在阻力作用下,v2逐渐减小,但其方向不变,当v2与v1的矢量和与v2垂直时,轮船的合速度最小,则vmin =v1cos θ=3×0.8 m/s =2.4 m/s.12.12.如图所示,河宽如图所示,河宽d =120 m 120 m,设小船在静水中的速度为,设小船在静水中的速度为v1v1,河水的流速为,河水的流速为v2.v2.小船从小船从A 点出发,在渡河时,船身保持平行移动若出发时船头指向河对岸上游的B 点,经过10 min 10 min,小船恰好到达河正对岸的,小船恰好到达河正对岸的C 点;若出发时船头指向河正对岸的C 点,经过8 min 8 min,小船到达,小船到达C 点下游的D 点.求:求:(1)(1)小船在静水中的速度小船在静水中的速度v1的大小;的大小;(2)(2)河水的流速河水的流速v2的大小;的大小;(3)(3)在第二次渡河中小船被冲向下游的距离在第二次渡河中小船被冲向下游的距离sCD.答案 (1)0.25 m/s (2)0.15 m/s (3)72 m解析 (1)小船从A 点出发,若船头指向河正对岸的C 点,则此时v1方向的位移为d ,故有v1=d tmin =12060×8m/s =0.25 m/s. (2)设AB 与河岸上游成α角,由题意可知,此时恰好到达河正对岸的C 点,故v1沿河岸方向的分速度大小恰好等于河水的流速v2的大小,即v2=v1cos α,此时渡河时间为t =d v1sin α,所以sin α=d v1t=0.8,故v2=v1cos α=0.15 m/s. (3)在第二次渡河中小船被冲向下游的距离为sCD =v2tmin =72 m.。
数学例题的分类有哪些

数学例题的分类有哪些
数学例题可以根据不同的标准进行分类。
以下是一些常见的分类方式:
1.按题意分类:包括求解题、求证题、求作题等。
2.按所属数学领域分类:包括代数题、平面几何题、三角题等。
3.按题目综合程度分类:包括单一型题与综合型题,综合题目又分横向综合与纵向综合。
4.按评价的客观性分类:包括主观题与客观题。
5.根据题目要素分类:包括标准型题、训练型题、探索型题、问题型题。
6.根据题目条件与答案的确定性分类:包括开放型题与封闭型题。
7.根据应用范畴分类:包括纯数学题与应用题。
需要注意的是,同一个数学例题可能同时属于多个分类,因此在实际使用时需要根据具体情况进行判断。
例题(土管)

市场比较法例题例1:现有甲、乙两宗交易实例,甲的成交总价为83万元人民币,分两期付款,首期支付30万元,余款(53万元)半年后付清,建筑面积250㎡。
乙成交总价19万美元,一次付清,使用面积3000英尺2。
以二者为交易实例,建立价格比较基准。
已知:月利率1%成交时汇率:1$=6. 79元人民币1㎡=10.7639英尺2使用面积=70%建筑面积例2:为评估某写字楼2008年10月1日的正常市场价格,在该写字楼附近地区调查选取了A、B、C三宗类似在上表中,交易情况中,正(负)值表示可比实例的成交价格高(低)于正常价格的幅度;房地产状况中,正(负)值表示可比实例房地产的状况优(劣)于估价对象房地产的状况。
另知:人民币与美元的市场汇价2008年3月1日为1:7.11,2008年10月1日为1:6.83;该类写字楼以人民币为基准的市场价格2008年1月1日至2008年2月1日基本保持不变, 2008年2月1日至2008年5月1日平均每月比上月下降1%,以后平均每月比上月上涨0.5%。
试利用上述资料估算该写字楼2008年10月1日的正常价格。
(如需计算平均值,请采用简单算术平均)。
例3:需要评估某商品住宅在2008年9月初的正常价格,在该住宅附近地区的调查选取了A、B、C已成在表中,交易情况中的负值表示低于正常价格幅度,正值表示高于正常价格幅度;房地产状况比较以估价对象为基准,负值表示劣于估价对象的房地产状况,正值表示优于估价对象的房地产状况。
另外知:2008年1月初人民币与美元的市场汇价为1:7.21;2008年9月初人民币与美元的市场汇价为1:6.83。
该类商品住宅以人民币为基准的价格在2007年6月初至2008年3月初之间平均每月上涨1%,在2008年3月初至2008年9月初之间平均每月下降1.5%。
试利用上述资料估计该商品住宅在2008年9月初的正常价格。
(如需计算平均值,请采用简单算术平均)。
例4:需要评估某商品住宅在2008年8月31日的正常价格,在该住宅附近地区的调查了A、B、C、D、E已成上表中,交易情况、房地产状况中的各正、负值都是按直接比较所得结果。
工程问题10道经典例题
1、一项工程,甲队单独完成需要10天,乙队单独完成需要15天。
若两队合作,完成这项工程需要多少天?A. 5天B. 6天C. 7.5天D. 10天(答案)B2、某工程由甲、乙两队承包,2天可以完成,需支付1800元;由乙、丙两队承包,3天可以完成,需支付1500元;由甲、丙两队承包,2.5天可以完成,需支付1600元。
在保证一星期内完成的前提下,选择哪个队单独承包费用最少?A. 甲队B. 乙队C. 丙队D. 无法确定(答案)B3、一项工程,甲单独做需12小时完成,乙单独做需18小时完成。
若甲先做1小时,然后乙接替甲做1小时,再由甲接替乙做1小时,...两人如此交替工作,问完成任务时共用了多少小时?A. 14小时B. 14.5小时C. 15小时D. 16小时(答案)B4、一项工程,甲、乙两队合作6天可以完成,如果甲队单独做需要15天,那么乙队单独做需要多少天?A. 8天B. 10天C. 12天D. 20天(答案)B5、一项工作,甲单独完成需要12小时,乙单独完成需要15小时,丙单独完成需要20小时。
如果先由甲、乙合做2小时,然后由甲单独做,共需要多少小时完成?A. 10小时B. 12小时C. 14小时D. 16小时(答案)A6、一项工程,甲、乙合作需6天完成,乙、丙合作需9天完成,甲、丙合作需15天完成。
现在甲、乙、丙三人合作需多少天完成?A. 5天B. 6天C. 7天D. 8天(答案)D7、一项工程,甲队单独做20天完成,乙队单独做30天完成。
两队合作多少天可以完成这项工程的一半?A. 5天B. 6天C. 7.5天D. 10天(答案)A8、一个水池有甲、乙两个进水管和丙一个出水管,单开甲管20小时可将水池注满,单开乙管30小时可将水池注满,单开丙管60小时可将满池水放完。
现三管同时打开,多少小时可将水池注满?A. 15小时B. 20小时C. 25小时D. 30小时(答案)A9、一项工程,甲单独做30天可完成,甲、乙两队合作12天可完成,那么乙单独做完成这项工程需要多少天?A. 15天B. 20天C. 24天D. 30天(答案)B10、一项工作,甲、乙两人合作需8天完成,乙、丙两人合作需6天完成,丙、丁两人合作需12天完成。
静力学30个例题
F F
ix
0 0
FAx FBC cos 45 0
FAy FBC sin 45 F1 0
iy
M F A i 0
FBC sin 45
l F1 l 0 2
FBC 2 2 F1 可得 FAx 2 F1 F F 1 Ay ( 2) 三力矩式: M A Fi 0
y F1
A B
F4
y
D C
2
45
A
Fx MB Fy
1
D B Cx
M
F2
x
F3
F
y
A
MC
B
F
解:1 计算力系的主矢 F :
D C
x
F
y
A (-3,0) B
D Cx
Fx Fix F4 cos 45 F2 2 KN F y Fiy F1 F3 F4 sin 45 1KN
有
Fx c xdF
0 L
xc
1 F
q0 x 2 2 0 l dx 3
l
例 11 已知:矩形板的四个顶点上分别作用四个力及一个力偶如图 a 所示。其 中 F1 2 KN , F2 3KN , F3 4 KN , F4 2 KN 力偶矩 M 10 KM m ,转向如图 所示,图中长度单位为 m 。试分别求:1)力系向点 B 简化结果 2)力系向点 C 简化 结果 3)力系简化的最后结果
tg 1 2
FA FB F sin( 90 ) sin 45 sin( 45 )
F sin 45 FA cos
例题
例题一、土方工程1.某建筑物有18个规格相同的独立柱。
室外地坪设计标高为-0.3m,基底设计标高为-2.1m,自垫层上表面四边放坡,边坡坡度1:0.5。
室外地坪以下每个基坑内各部分的尺寸及工程量是:C10混凝土垫层2200×1800×100;每个C25钢筋混凝土基础为1.484m3。
土的最初可松性系数K S=1.14,最终可松性系数K`S=1.05。
试求:(1)土方开挖工程量。
(2)应预留多少回填土(以自然状态土体积计)?(3)如果用斗容量为3 m3的汽车运土,需运多少车?解:2、计算图示方格的挖方与填方工程量,已知方格的边长为30m。
3、某基坑底长80m宽50m,深6m,四面放坡,边坡坡度为1:0.5。
已知土的可松性系数Ks=1.16,K’s=1.07,(1)试求土方开挖工程量。
(2)若混凝土基础和地下室占有体积为1800m3,则应预留多少回填土(以自然状态土体积计)?(3)如果用斗容量为3.0的汽车进行余土外运,需运多少车?4、场地方格网如下图示,方格网的边长为20m ,双向泄水坡度ix =0.2%,iy =0.3%,按挖填平衡原则确定其设计标高。
(提示:设计标高H 0)432(4143210∑∑∑∑+++=H H H H nH 考虑泄水坡度时,y y x x i i l i l H H ±±=0' )二、钢筋混凝土工程1、完成图示各号钢筋的下料长度计算,列出计算式。
2、预应力混凝土屋架,采用机械张拉后张法施工,孔道长度为23.8m,两端张拉,张拉程序为0 103%σcon 采用螺丝端杆锚具,长度为320mm,端杆外露出构件端部长度为120mm,预应力为冷拉Ⅲ级钢筋,直径为25mm,每根长度为8m。
实测钢筋冷拉率γ为4%,弹性回缩率为δ为0.5%,张拉控制应力σcon =0.85f pyk (f pyk =500N /mm 2),计算预应力筋的下料长度和最大张拉力。
公务员行测:图表题例题
公务员⾏测:图表题例题 【例题】根据下列图表,回答1-5题1.该市“⼗五”期间县域经济第⼀产业占三产业⽐重的平均值⽐第三产业的平均值多()。
A.9.48%B.8.48%C.9.88%D.8.88%2.该市“⼗五”期间县域经济第⼆产业⽐上年同期增长最⼤的⼀年是()。
A.2002年B.2003年C.2004年D.2005年3.该市“⼗五”期间县域经济第⼆产业占三产业⽐重超过四分之⼀的⽐重有()A.1B.2C.3D.44.可以⽤来表⽰该市“⼗五”期间县域经济三产业结构变化为折线图的是() 5.下列表述不正确的有()。
Ⅰ.该市“⼗五”期间县域经济中第⼀产业所占⽐重⽐其他两个产业所占的⽐重都⼤Ⅱ.2003年第⼆产业所占⽐重是该市“⼗五”期间第⼆产业所占⽐重最⾼的年份Ⅲ.2005年该市县域经济第⼆产业所占⽐重⽐2004年增加了0.7个百分点A.Ⅰ、ⅡB.Ⅰ、ⅢC.Ⅱ、ⅢD.Ⅰ、Ⅱ、Ⅲ【解析】1.D。
该市“⼗五”期间县城经济第⼀产业占三产业⽐重的平均值为:45.5%+42.9%+39.9%+39.3%+37.8%=41.08%31.7%+33.5%+32.1%+31.9%+31.8%=32.2%两者之差为:41.08%-32.2%=8.88(个百分点)。
2.B。
该市“⼗五”期间县域经济第⼆产业⽐上年同期分别增长了2002年:23.6-22.8=0.8(个百分点),2003年:27.9-23.6=4.3(个百分点),2004年:28.8-27.9=0.9(个百分点),2005年30.5-28.8=1.7(个百分点),故本题正确答案为B。
3.C。
该市“⼗五”期间县域经济第⼆产业占三产业⽐重分别是2001年22.6%,2002年23.6%,2003年27.9%,2004年28.8%,2005年30.5%,其中2003年、2004年、2005年均超过了25%,因此本题正确答案为C。
4.A。
通过给定的柱状图观察该市“⼗五”期间县域经济三产业结构变化的情况,可知A为正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、计算一段整数区间的累加:
1、如图1所示,绘制应用程序界面;
2、编写程序计算一段区间的累加;要求创建一个函数过程来计算累加;
3、开始数字大于或等于结束数字时,弹出一个提示窗口,提示信息如图2所示,
同时将三个文本框全部清空。
4、将编写的程序文件保存在M:盘上。
图1
图2
1、列表框移动几位数据
2、程序启动时,在列表框1显示20个10-100的随机整数;
3、在文本框中输入移动的位数(1-20范围内的整数),然后后点击“向上
移动”按钮,将列表框1中数据移动想要的位数,移动后的数据放入列表框2
中;
4、点击“写入文件”按钮,将列表框2中的数据存入a.txt的文本文件中;
2程序设计要求:
(1)统计字母出现次数
(2)程序运行时,在第一个文本框中输入字符串。点击“统计字母C出现
的次数 ”,将在第二个文本框中显示统计结果(字符C(不区分大小写)出现
的次数);
(3)点击“清除“按钮则清除两个文本框中的内容。
(4)保存
3、列表框判断质数
2、当程序运行时,从文件“text.txt”中读取20个数据并显示在列表框1
中;
3、单击“筛选质数”按钮后,筛选出列表框1里所有的质数,并显示到列
表框2中; (质数为只能整除1和其本身的数字)
4、单击“排序”按钮,完成列表框2数据排序;
5、单击“求总和”按钮后,对列表框2中的数据累加并显示到文本框中;
6、程序保存
60分为例
1、界面设计并正确保存; 15分
2、文件读取并显示在列表框中; 15分
3、筛选质数并在列表框2中正确显示; 15分
4、完成排序并在列表框2中正确显示;10分
5、求总和并显示在文本框中 5分
