解析数学中分段函数
分段函数的极限

分段函数的极限分段函数是指由多个函数按照不同的自变量范围组合而成的一个函数。
在数学中,分段函数的极限是一个非常重要的概念和计算方法。
本文将介绍什么是分段函数的极限,以及如何计算分段函数的极限。
一、分段函数的定义分段函数是由多个函数组合而成的一个函数。
具体地说,它是指在不同的自变量范围内对应的函数是不同的。
例如,在区间(-∞,-1)内,我们定义f(x)=-x;在区间[-1,1]内,我们定义f(x)=x²;在区间(1,∞)内,我们定义f(x)=x+1。
这三个函数组合在一起,就构成了一个分段函数f(x)。
二、分段函数的极限定义在讨论分段函数的极限之前,我们需要先了解什么是函数的极限。
简单地讲,当自变量x无限接近于某个值a时,函数f(x)的值无限接近于某个数L,我们就称函数f(x)在x趋近于a的过程中极限为L,记为lim(x→a)f(x)=L。
例如,当x趋近于1时,f(x)=x²的极限为1。
与一般函数不同,分段函数在每个自变量范围内都有不同的函数式,因此在计算分段函数的极限时,我们需要对每个自变量范围内的函数分别进行讨论。
具体来说,我们需要分别讨论当x趋近于各个自变量范围中的端点时,函数值的趋势,以决定函数是否存在极限。
三、分段函数的极限计算方法对于一个分段函数f(x),我们可以在每个自变量范围内对应的函数上分别计算极限。
然后,我们需要比较每个自变量范围内的函数极限,以确定整个分段函数的极限是否存在。
以下是具体的计算步骤:(1)先找出函数f(x)的定义域和值域。
(2)对于每个自变量范围内的函数,我们需要使用极限的定义来计算它的极限。
例如,当x趋近于-2时,f(x)=x²-2x的极限为6;当x趋近于0时,f(x)=x+3的极限为3。
(3)比较每个自变量范围内的函数极限。
如果存在某个自变量范围,其内部的函数极限不存在或者不唯一,那么我们就认为分段函数的极限不存在。
否则,我们可以得出整个分段函数的极限为各个自变量范围内的函数极限的"局部极限"中的极限值。
八年级数学下册知识点复习专题讲练一次函数中的分段函数含解析202207051160

一次函数中的分段函数分段函数的根本模型1. 分段记费问题〔如收取水费、电费、通信费等类型〕:我国是世界上严重缺水的国家之一。
为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费方法收费,即一月用水10吨以内〔包括10吨〕的用户,每吨收水费a 元;一月用水超过10吨的用户,10吨水仍按每吨元收费,超过10吨的局部,按每吨b 元〔b >a 〕收费。
设一户居民月用水x 吨,应收水费y 元,y 与x 之间的函数关系如下图。
求出a 和b 值。
解析:根据图中的相关数据利用解析式分析求值,解题关键是弄清函数图象的意义。
答案: 1.5a =,b =2。
2. 行程中的分段计算问题:由速度或时间的不同而产生的不同计算。
如图是小明从学校到家里行进的路程s 〔米〕与时间t 〔分〕的函数图象,观察图象,从图中能得到什么信息呢?〔结合背景对图象含义进行理解〕解析:考查函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论。
答案:小明行进总路程为1000米,行进时间为20分钟,前10分钟的行进速度比后10分钟的行进速度慢。
3. 与几何图形有关的分段函数:由图形的运动变化所产生的线段、面积等的不同产生的分段计算。
如图1,在矩形ABCD 中,AB =3,BC =4,动点P 从点A 开始按A →B→C→D 的方向运动到D 。
如图2,设动点P 所经过的路程为x ,△APD 的面积为y 。
〔当点P 与A 或D 重合时,y =0〕,写出y 与x 的函数关系式并画出图象。
解析:利用点运动到不同位置产生对应值解决问题。
图象如图。
203637220710x x y x x x ≤≤⎧⎪=<<⎨⎪-+≤≤⎩。
4. 商品销售中的分段计算:根据数量将商品进行分段销售。
如:某书定价25元,如果一次购置20本以上,超过20本的局部打八折,试写出付款金额y 〔单位:元〕与购书数量x 〔单位:本〕之间的函数关系。
新高一数学分段函数知识点

新高一数学分段函数知识点近年来,高一数学分段函数在教学中越来越受到重视,因为它能够很好地解决现实生活中的实际问题。
分段函数,顾名思义,是由多个线段组成的函数。
在这篇文章中,我将介绍一些新高一数学分段函数的知识点,希望能对学生们的学习有所帮助。
首先,我们需要了解分段函数的定义。
分段函数由若干段曲线组成,每一段曲线都可以用一个公式来表示。
这些公式在不同的区间内有效,并且在连续的区间之间分界。
例如,y = |x| 就是一个分段函数,其中包括两个区间:当x ≥ 0 时,用公式 y = x 表示;当 x < 0 时,用公式 y = -x 表示。
接下来,让我们来看看如何求解分段函数的定义域。
要求解分段函数的定义域,我们需要先求解每个段上的定义域,然后取所有定义域的交集。
举个例子,考虑函数f(x) ={ x+1, x<0{ x^2, x≥0我们需要分别求解 x+1 和 x^2 的定义域。
很显然,x+1 在实数范围内都有定义,而 x^2 的定义域为x ≥ 0 。
因此,函数 f(x) 的定义域为 x≥ 0,即所有段的交集。
另一个需要掌握的重要知识点是分段函数的值域。
求解分段函数的值域时,我们同样需要对每个段上的值域进行求解,然后取所有值域的交集。
举个例子,考虑函数g(x) ={ x+1, x < 0{ √x, x ≥ 0可以看到,x+1 的值域为 (-∞, +∞),而√x 的值域为y ≥ 0。
因此,函数 g(x) 的值域为[0, +∞),即所有段的交集。
除了求解定义域和值域,我们还需要学会如何求解分段函数的零点。
零点是指函数取值为 0 的点。
对于分段函数而言,我们需要分别求解每个段上的零点,并将其进行合并。
举个例子,考虑函数h(x) ={ 2x+1, x<0{ x^2, x≥0我们需要求解 2x+1 = 0 和 x^2 = 0 的零点。
很显然,2x+1 = 0 的零点为 x = -1/2,而 x^2 = 0 的零点为 x = 0。
2019年《·高考总复习》数学:第二章 第3讲 分段函数

f[g(π)]的值为( B )
A.1
B.0
C.-1
D.π
解析:g(π)=0,f[g(π)]=f(0)=0.故选 B.
2019年4月29日
雨衣专享文档
5
3.设函数 f(x)=1x2-+xx2-,2x≤ ,1x>,1, 则 ff12的值为( A )
15 A.16
B.-2176
D.f(2)
解析:由 f(x+1)=-f(x)知 f(x+2)=-f(x+1)=f(x),于是
f(x)是以 2 为周期的周期函数,从而 f(2.5)=f(0.5)=-1,f[f(2.5)]
=f(-1)=f(1)=-1,f[f(1.5)]=f[f(-0.5)]=f(1)=-1,f(2)=f(0)
=1.故选 D.
xx>1
函数,所以-a2≥1, -1-a-5≤a
⇒aa≤≥--23, ⇒-3≤a≤-2.所以
a 的取值范围是-3≤a≤-2.
答案:B
2019年4月29日
雨衣专享文档
28
2019年4月29日
雨衣专享文档
21
解析:因为 f(x)是定义在 R 上的奇函数,当 x>0 时,f(x)= x2-4x,所以当 x<0 时,f(x)=-x2-4x,由xx2>-0,4x>x, 得 x>5. 由-x<x02,-4x>x, 得-5<x<0.故选 A.
答案:A
2019年4月29日
26
【互动探究】
-x2-ax-5x≤1,
3.已知函数 f(x)=a
是 R 上的增函数,
xx>1
则 a 的取值范围是(
)
A.-3≤a<0
人教版初二数学下册《 分段函数》

2x
2
2
2
由题易得直线AB的解析式为
y
3 4
x
3. 2
n 3m3.
42
由此可得
n
3 m 3 42
12m4n12nm21812
解之得
m n
42 11 15 11
点P为42,15. 11 11
易得P直 的 D 线 解析 y2 式 9 x为 4.
(1)在注水过程中,注满A所用时间为 s,再注满B又 用了 s;
(2)求A的高度hA及注水的速度v; (3)求注满容器所需时间及容器的高度.
2.(1)在同一坐标平面内,画出 y1
x
和 y2
1 3
x
4 3
函数的图象;
(2)求出两函数图象的交点坐标;
(3)比较两函数值的大小.
y
2 1━
┃
-1
y1 x
求S与t之间的函数解析式;(3)若直线PD将五边形OABCD分成面积相等
的两部分,求直线PD的函数关系式.
解:(1)由题得
OAOD 6 OAOD 8
解之 O O得 D A 24 或 O O D A 42
M
由题知 3<OD<6, ∴ OA=2, OD=4.
延长CB交x轴于点M.
2t 84<t 6
S与t的函数关系式为85t
486<t
5
11
1211<t 12
2t 3612<t 18
例题 如图1,A、D分别在x轴和y轴上,CD∥x轴,BC∥y轴.点P从D点出 发,以1cm/s的速度,沿五边形OABCD的边匀速运动一周.记顺次连接P、 O、D三点所围成图形的面积为Scm2,点P运动的时间为ts.已知S与t之间的 函数关系如图2中折线段OEFGHI所示.(1)求A、B两点的坐标; (2)
北师大版八年级数学 一次函数中分段函数问题【解析】
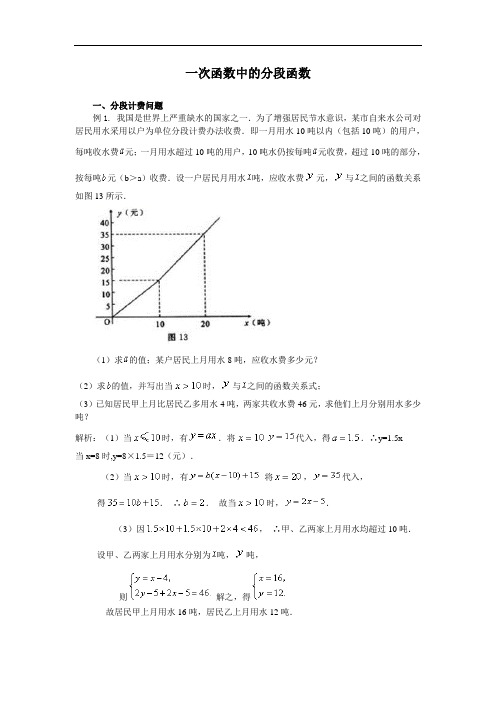
一次函数中的分段函数一、分段计费问题例1.我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费元;一月用水超过10吨的用户,10吨水仍按每吨元收费,超过10吨的部分,按每吨元(b>a)收费.设一户居民月用水吨,应收水费元,与之间的函数关系如图13所示.(1)求的值;某户居民上月用水8吨,应收水费多少元?(2)求的值,并写出当时,与之间的函数关系式;(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?解析:(1)当时,有.将代入,得.∴y=1.5x当x=8时,y=8×1.5=12(元).(2)当时,有将,代入,得.∴.故当时,.(3)因,∴甲、乙两家上月用水均超过10吨.设甲、乙两家上月用水分别为吨,吨,则解之,得故居民甲上月用水16吨,居民乙上月用水12吨.二、行程中的分段函数例2。
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为,两车之间的距离为,图中的折线表示与之间的函数关系.根据图象进行以下探究:信息读取(1)甲、乙两地之间的距离为 km;(2)请解释图中点的实际意义;图象理解(3)求慢车和快车的速度;(4)求线段所表示的与之间的函数关系式,并写出自变量的取值范围;问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?解析:(1)900;(2)图中点的实际意义是:当慢车行驶4h时,慢车和快车相遇.(3)由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为;当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为,所以快车的速度为150km/h.(4)根据题意,快车行驶900km到达乙地,所以快车行驶到达乙地,此时两车之间的距离为,所以点的坐标为.设线段所表示的与之间的函数关系式为,把,代入得解得所以,线段所表示的与之间的函数关系式为.自变量的取值范围是.(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h.把代入,得.此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是,即第二列快车比第一列快车晚出发0.75h.三、与几何图形有关的分段函数例3。
分段函数的类型

分段函数的类型
分段函数是数学中一个重要的概念。
它应用于生产、图形计算等多个领域,引用在很多成功的应用中,例如运筹学与机器学习。
分段函数是一种“离散化”的函数,由一些称为子函数(子分段)的函数组成,子
函数可以是不同类型的函数,它们通常在限定的范围内变化、分开且独立。
分段函数的总函数可以从这些子函数构建出来,从而形成一个可以用于单独计算的函数。
一般来说,分段函数可以分为三种:线性、不等式、多项式函数。
线性函数是在离散点之间连接起来形成的一条折线,而不等式函数则不同,它可以把离散点之间的部分连接起来,形成一条曲线。
多项式函数是在把离散点之间连接起来的所有部分拟合成多项式函数,这样会形成一条更加复杂的折线。
此外,分段函数还可以包含其他复杂的元素,比如曲线,它可以把离散点之间的独立曲线连接起来,形成一个更为复杂的变量函数。
分段函数的相关研究广泛应用于机器学习算法、计算模拟、概率论和经济学中。
借助分段函数,人工智能技术可以解决复杂的优化问题;由于分段函数易于分解,复杂的计算任务也可以很容易地解决。
在经济学中,由于分段函数的稳定性,可以进行安全、有效的金融分析和决策。
总之,分段函数具有广泛的应用价值,它可以有效地帮助我们解决机器学习、计算模拟以及经济分析和决策当中繁杂的问题,必将促进科学技术的更进一步发展。
分段函数的单调性

分段函数的单调性在数学中,分段函数是指由不同的函数段组成的函数。
每个函数段的定义域是不一样的,一般是非连续的。
分段函数在实际应用中比较常见,如渐进函数、分段函数曲线、阶梯函数等,因此理解和掌握分段函数的性质对于我们解决实际问题非常重要。
其中,分段函数的单调性是分析分段函数的一种重要方法,本文将介绍分段函数的单调性及其相关知识。
一、分段函数分段函数可以看做是由多个函数组成的函数。
设函数f(x)在区间[a,b]上的定义域为D,如果D可以被分成n个互不重叠的区间I1,I2,...,In,并且在每个区间Ii上,函数f(x)可以表示为与一些和f(x)有相同定义域的函数ui(x)的和,即f(x)=u1(x),x∈I1u2(x),x∈I2...un(x),x∈In则称f(x)是在区间[a,b]上的分段函数,每个ui(x)被称为f(x)的一个函数段。
二、单调性的定义单调性是指一个函数在其定义域上的单调关系,即函数值的增减关系。
我们说函数f(x)在区间[a,b]上单调递增,就是指对于任意的x1,x2∈[a,b],若x1<x2,则有f(x1)≤f(x2)。
同理,我们说函数f(x)在区间[a,b]上单调递减,就是指对于任意的x1,x2∈[a,b],若x1<x2,则有f(x1)≥f(x2)。
在实际应用中,我们需要掌握如何分析分段函数的单调性,以解决一些与实际问题相关的计算问题。
三、单调性的判断方法我们通常采用以下方法来判断分段函数的单调性。
1.求一阶导数对于分段函数f(x),如果它在每个函数段上都可导,则其导函数f'(x)也是分段函数,且f(x)单调递增/递减,当且仅当f'(x)在对应区间上满足:在x∈(a,b)内,若f'(x)>0,则f(x)在(x1,x2)上单调递增;在x∈(a,b)内,若f'(x)<0,则f(x)在(x1,x2)上单调递减。
2.分类讨论对于分段函数f(x),我们也可以通过分类讨论的方法来判断其单调性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析数学中分段函数
作者:周文国
来源:《数理化学习·高一二版》2012年第11期
分段函数在教材中是以例题的形式出现的,并未作深入说明,学生对此认识往往比较肤浅,本文对分段函数的知识点进行归纳整理,揭开分段函数的面纱.
一、分段函数的含义
所谓“分段函数”,习惯上指在定义域的不同部分,有不同的对应法则的函数,对它应有以下两点基本认识:(1)分段函数是一个函数,不要把它误认为是几个函数;(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
二、求分段函数的函数值
例1 已知函数f(x)=
2x (x
3 (0≤x≤1)
log13x(x>1)
,求
f(f(f(a)))(a
分析:求分段函数的函数值时,首先应该确定自变量在定义域中所在的范围,然后按相应的对应法则求值.
f(x)是分段函数,要求f(f(f(a))),需要确定
f(f(a))的取值范围,为此又需要确定
f(a)的取值范围,然后根据其所在定义域代入相应的解析式,逐步求解.
解:因为
a
f(f(a))=f(2a)=3,因为
3>1,所以
f(f(f(a)))=f(3
)=log13
3
=-12.
规律解答:在解决上述问题时,一定要注意自变量所处的范围,然后再代入进行解决.
三、求分段函数的解析式
例2 已知奇函数f(x)(x∈R),当
x>0时,f(x)=x(5-x)+1,求
f(x)在R上的表达式.
分析:本题可分段进行分析解答,即分为
x
解:因为f(x)是定义在R上的奇函数,所以
f(0)=0;
当x
-x>0,故有f(-x)=-x
[5-(-x)]+1=-x(5+x)+1,
所以f(x)=-f(-x)=x(5-x)-1;所以
x(5-x)+1 (x>0)
0 (x=0)
x(5+x)-1 (x
规律解答:对于分段函数的解析式,尤其要注意在定义域内求出分段函数的解析式.
四、分段函数的图象
例3 已知函数 f(x)=
|x2-2x-3|的图象与直线
y=a有且仅有3个交点,求a的值.
分析:本题可利用数形结合直观地解决.
解:因为f(x)=|(x-1)2-4|=|(x+1)(x-3)|.所以
f(x)=
x2-2x-3 (x≤-1)
-x2+2x+3 (-1
x2-2x-3 (x>3)
通过结合图1,则容易知道a=4.
规律解答:注意要画正确分段函数的图象,可通过数形结合解决.
五、分段函数的最值
例4 求函数[HT5,6]
f(x)=
2x (0≤x≤4)
16-x (8
的最大值、最小值.
分析:可作图比较在各段上的最值,从而确定函数的最大值和最小值.
解:函数
y=f(x)的图象如图2,当
4≤x≤8时,f(x)的最大值为8,当x=0时,
f(x)的最小值为
f(0)=0.。
