Riesz代数上的d-模(英文)
《高等代数》课程教案

《高等代数》课 程 教 案(另有电子多媒体制作的课件教案)(一) 课程概况课程名称: 高等代数I,高等代数II课程学时:两学期,课内周4学时,共计128学时。
课外另有讨论课。
课程性质:必修基础课。
讨论交流:每周安排1次讨论课。
考核方法: 多种形式结合。
平时表现 (课堂讨论、作业、思考题)占10%, 期中考试占20%,期末考试(和小论文小答辩)占70%.开课学期:秋季学期、春季学期。
(二) 使用教材:1.《高等代数学》(第一、二版), 张贤科,许甫华编著,清华大学出版社(主教材)2.《高等代数解题方法》,许甫华、张贤科编著,清华大学出版社(辅导教材)3.《Theory and Problems of Linear Algebra》,S. Lipschutz著, McGraw-Hill出版.4.《Linear Algebra》,S.Berberian著,Oxford Univ. 出版5. 《Advanced Linear Algebra》,S. Roman著,Springer出版社。
(以上3本为参考书)(三) 内容合进度安排 (带星号*的是简单介绍性内容)第一部分 基 础 内 容 (第一学期上课)第1章 数与多项式1.1 数的进化与代数系统 (第1大节上课)*1.2 整数的同余与同余类 (第2大节上课)1.3 多项式形式环 (第3大节上课)1.4 带余除法与整除性1.5 最大公因子与辗转相除法 (第4大节上课)1.6 唯一析因定理1.7 根与重根 (第5大节上课)1.8 与 (第6大节上课)1.9 与1.10 多元多项式 (第7大节上课)1.11 对称多项式习题1 (4 次讨论课)第2章 行列式2.1 排列 (第8大节上课)2.2 行列式的定义2.3 行列式的性质2.4 Laplace 展开 (第9大节上课)2.5 Cramer 法则与矩阵乘法 (第10大节上课)2.6 矩阵的乘积与行列式 (第11大节上课)2.7 行列式的计算习题2 (2次讨论课)第3章 线性方程组3.1 Gauss消元法 (第12大节上课)3.2 方程组与矩阵的秩3.3 行向量空间和列向量空间 (第13大节上课)3.4 矩阵的行秩和列秩3.5 线性方程组解的结构 (第14大节上课)3.6 例题*3.7 结式与消去法习题3 (2次讨论课)第4章 矩阵的运算与相抵4.1 矩阵的运算 (第15大节上课)4.2 矩阵的分块运算4.3 矩阵的相抵 (第16大节上课)4.4 矩阵运算举例 (第17大节上课)4.5 矩阵与映射 (第18大节上课)*4.6 矩阵的广义逆*4.7 最小二乘法习题4 (2 次讨论课)-------------------复习, 期中考试 (第19大节)第5章 线性(向量)空间5.1 线性(向量)空间 (第20大节上课)5.2 线性映射与同构 (21大节上课)5.3 基变换与坐标变换 (第22大节上课)5.4 子空间的和与直和 (第23大节上课)*5.5 商空间习题5 (两次讨论课)第6章 线性变换6.1 线性映射及其矩阵表示 (第24大节上课)6.2 线性映射的运算 (第25大节上课)6.3 线性变换 (第26大节上课)*6.4 线性表示介绍6.5 不变子空间 (第27大节上课)6.6 特征值与特征向量 (第28大节上课)6.7 方阵的相似 (第29大节上课)习题6 (两次讨论课)------------------------复习, 期末考试 (第30-32大节)第二部分 深 入 内 容(第二学期上课)第7章 方阵相似标准形与空间分解7.1 引言: 孙子定理 (第1大节上课)7.2 零化多项式与最小多项式 (第2大节上课)7.3 准素分解与根子空间 (第3大节上课)7.4 循环子空间 (第4大节上课)7.5 循环分解与有理标准形 (第5大节上课)7.6 Jordan 标准形 (第6-7大节上课)7.7 矩阵与空间分解 (第8大节上课)7.8 矩阵的相抵与Smith标准形 (第9大节上课)7.9 三种因子与方阵相似标准形 (第10大节上课) *7.10 方阵函数 (第11大节上课)*7.11 与可交换的方阵*7.12 模分解基本定理7.13 若干例题习题7 (讨论课4次)第8章 双线性型、二次型与方阵相合8.1 二次型与对称方阵 (第12大节上课)8.2 对称方阵的相合 (第13大节上课)8.3 正定实对称方阵 (第14大节上课)8.4 交错方阵的相合及例题 (第15大节上课)8.5 线性函数与对偶空间 (第16大节上课)8.6 双线性函数 (第17大节上课)8.7 对称双线性型与二次型 (第18大节上课)*8.8 二次超曲面的仿射分类*8.9 无限维线性空间习题8 (讨论课 3次)-------------------------复习, 期中考试 (第19大节上课)第9章 欧几里得空间与酉空间9.1 标准正交基 (第20大节上课)9.2 方阵的正交相似 (第21大节上课)9.3 欧几里得空间的线性变换 (第22大节上课)9.4 正定性与极分解 (第23大节上课)*9.5 二次超曲面的正交分类 (第24大节上课)9.6 杂例 (第25大节上课)9.7 Hermite型 (第26大节上课)9.8 酉空间和标准正交基 (第27大节上课)9.9 方阵的酉相似与线性变换 (第28大节上课)*9.10 变换族与群表示9.11 型与线性变换 (第29大节上课)习题9 (讨论课 4次)-------------------------复习, 期末考试 (第30-32大节) 第三部分 选 学 内 容(课外阅读材料, 不在课内讲课, 或稍作介绍)第10章 正交几何与辛几何10.1 根与正交补10.2 正交几何与辛几何的结构10.3 等距变换与反射10.4 Witt定理10.5 极大双曲子空间习题10第11章 Hilbert空间11.1 内积与度量空间11.2 内积空间与完备11.3 逼近与正交直和11.4 Fourier展开11.5 等距同构于11.6 有界函数与Riesz表示习题11第12章 张量积与外积12.1 引言与概述12.2 张量积12.3 线性变换及对偶12.4 张量及其分量12.5 外积12.6 交错张量习题12(四)课程的定位和作用《高等代数》是数学的核心基础课程。
泛函分析重要内容

们同意前人的提法,认为线性泛函与无穷维空间上引进坐标的思想有关,而对偶理论则有如无穷维线性空间上的解析几何学。
距离线性空间SS1. 选择公理,良序定理,佐恩引理有序集的定义:(1)若a在b之先,则b便不在a之先。
(2)若a在b之先,b在c之先,则a在c之先。
这种先后关系记作良序集:A的任何非空子集C都必有一个属于C的最先元素。
良序集的超限归纳法:(1)为真,这里是A中最先的元素。
2)对一切,为真,则亦真那么对一切皆真。
选择公理设N={N}是一个非空集合构成的族,则必存在定义在N上的函数f,使得对一切N都有部分有序称元素族X是部分有序的,如果在其中某些元素对(a,b)上有二元关系,它据有性质:例如X中包换关系在部分有序集下,有上界、极大元和完全有序其中完全有序的C:。
例如在复数域中,按大小关系定义两个复数的关系,则复平面是部分有序的,实轴、虚轴是完全有序的。
佐恩引理设X非空的部分有序集,如果X的任何完全有序子集都有一个上界在X中,则X必含有极大元。
从现代观点来看,泛函分析研究的主要是研究实数域或者复数域上的完备赋范线性空间。
SS2. 线性空间,哈迈尔(Hamel)基线性空间的定义:加法交换、加法结合、有零元,有负元、有单位元等。
线性流形:线性空间中的非空子集,如果它加法封闭、数乘封闭。
线性流形的和M+N:所有形如m+n的元素的集合,其中m∈M, n∈N。
线性流形的直和:如果M∩N={θ},则以代替M+N如果,则称M与N是代数互补的线性流形。
于是有下述定理:定理设M,N是线性空间X的线性流形,则当且仅当对每个x∈X都有唯一的表达式x=m+n, m∈M,n∈N.定理若,则dimX=dimM+dimNHamel基的定义:设X是具有非零元的线性空间,X的子集H称为X的Hamel基,如果(1)H是线性无关的。
(2)H张成的线性流形是整个空间。
则有Hamel基和线性无关子集的关系:定理设X是线性空间,S是X中任意的线性无关子集,则存在X的一个Hamel基使得推论任何非零线性空间必有Hamel基由定理,可有定理设M是线性空间X的线性流形,则必有线性流形使得,即N是M的代数补。
数学专业书籍推荐

1.课程号:课程名:高等代数-1课程英文名:Advanced Algebra-1学时:102 学分:5先修课程:高中数学考试方式:考试基本面向:数学数院各专业教材:《Linear Algebra》彭国华、李德琅,高等教育出版社,2006参考书:1。
《高等代数》北京大学数学系几何代数教研空编高等教育出版社 2.《高等代数》张禾瑞、郝锅新高等教育出版社3.《Linear Slgebra》B。
Jacob W.H.Freeman and Company 1990 课程简介:高等代数以研究线性方程组为出发点来讨论求解和解的结构和分类等问题,进而研究矩阵,行列式,线性空间,线性映射以及二次型的基本理论。
本课程分两个学期讲授。
高等代数-1的主要内容包括线性空间和线性映射,线性变换,欧氏空间,线性和双线性型。
2.课程号:课程名:高等代数-2课程英文名:Advanced Algebra-2学时:102 学分:5先修课程:高等代数-1考试方式:考试基本面向:数学学院各专业教材:《Linear Algebra》彭国华、李德琅,高等教育出版社,2006参考书:1.《高等代数》北京大学数学系几何代数教研空编高等教育出版社 2. L.W. Johnson, R.D. Riess and J.T. Arnold, Introduction to Linear Algebra (5th Edition), Prentice-Hall Inc. and China Machine Press, 2002 3. D.C. Lay, Linear Algebra and Its Applications (3rd Edition), Pearson Addison Wesley Asia Limited and Publishing House of Electronics Industry, 2003课程简介:一元与多元多项式、行列式、线性方程组,矩阵代数,二次型,线性空间,线性变换,矩阵法式,欧氏空间3.课程号:课程名:近世代数课程英文名:Abstract Algebra学时:68 学分:4先修课程:高等代数、数学分析考试方式:考试基本面向:数学学院教材:《近世代数基础》刘绍学编高等教育出版社第一版参考书:1.《近世代数引论》冯克勤、李尚志、查建国中国科学技术大学出版社 19882.《代数学引论》聂灵沼、丁石孙高等教育出版社 19883.《Basic Algebra(I)》N.Jacobso W.H.Freeman and Company 1985 课程简介:代数学是因解多项式方程而发展起来的,而方程解的结构往往是人们感兴趣的的问题,近世代数是研究具有良好代数结构的群,环域,模为主要内容的一门课程。
1汉英力学名词(1993)

BZ反应||Belousov-Zhabotinski reaction, BZ reactionFPU问题||Fermi-Pasta-Ulam problem, FPU problemKBM方法||KBM method, Krylov-Bogoliubov-Mitropolskii method KS[动态]熵||Kolmogorov-Sinai entropy, KS entropyKdV 方程||KdV equationU形管||U-tubeWKB方法||WKB method, Wentzel-Kramers-Brillouin method[彻]体力||body force[单]元||element[第二类]拉格朗日方程||Lagrange equation [of the second kind] [叠栅]云纹||moiré fringe; 物理学称“叠栅条纹”。
[叠栅]云纹法||moiré method[抗]剪切角||angle of shear resistance[可]变形体||deformable body[钱]币状裂纹||penny-shape crack[映]象||image[圆]筒||cylinder[圆]柱壳||cylindrical shell[转]轴||shaft[转动]瞬心||instantaneous center [of rotation][转动]瞬轴||instantaneous axis [of rotation][状]态变量||state variable[状]态空间||state space[自]适应网格||[self-]adaptive meshC0连续问题||C0-continuous problemC1连续问题||C1-continuous problemCFL条件||Courant-Friedrichs-Lewy condition, CFL condition HRR场||Hutchinson-Rice-Rosengren fieldJ积分||J-integralJ阻力曲线||J-resistance curveKAM定理||Kolgomorov-Arnol'd-Moser theorem, KAM theoremKAM环面||KAM torush收敛||h-convergencep收敛||p-convergenceπ定理||Buckingham theorem, pi theorem阿尔曼西应变||Almansis strain阿尔文波||Alfven wave阿基米德原理||Archimedes principle阿诺德舌[头]||Arnol'd tongue阿佩尔方程||Appel equation阿特伍德机||Atwood machine埃克曼边界层||Ekman boundary layer埃克曼流||Ekman flow埃克曼数||Ekman number埃克特数||Eckert number埃农吸引子||Henon attractor艾里应力函数||Airy stress function鞍点||saddle [point]鞍结分岔||saddle-node bifurcation安定[性]理论||shake-down theory安全寿命||safe life安全系数||safety factor安全裕度||safety margin暗条纹||dark fringe奥尔-索末菲方程||Orr-Sommerfeld equation奥辛流||Oseen flow奥伊洛特模型||Oldroyd model八面体剪应变||octohedral shear strain八面体剪应力||octohedral shear stress八面体剪应力理论||octohedral shear stress theory巴塞特力||Basset force白光散斑法||white-light speckle method摆||pendulum摆振||shimmy板||plate板块法||panel method板元||plate element半导体应变计||semiconductor strain gage半峰宽度||half-peak width半解析法||semi-analytical method半逆解法||semi-inverse method半频进动||half frequency precession半向同性张量||hemitropic tensor半隐格式||semi-implicit scheme薄壁杆||thin-walled bar薄壁梁||thin-walled beam薄壁筒||thin-walled cylinder薄膜比拟||membrane analogy薄翼理论||thin-airfoil theory保单调差分格式||monotonicity preserving difference scheme 保守力||conservative force保守系||conservative system爆发||blow up爆高||height of burst爆轰||detonation; 又称“爆震”。
近世代数课后题答案修改版

(2)在乘法表中任取一个 1,在同一列中必有一个 x,在同一行 中必有一个 y,设第四个顶点的元素为 z,见下图,
�
..........a-1.........................c...................
......
...........................................................
k
qk rk
ck dk
5. 举一个偏序集但不是全序集的例子,并画图。 解 考虑到画图的方便,可举有限集的例子,例如:有限集的幂集 对包含关系所构成的偏序集,有限整数集对整除关系所构成的偏 序集。
-1
a=493 1 0
0
b=391 0 1
1
1 102 1 1
2
3 85
34
3(n) 1 17
45
4(n+1) 5 0
5 | 10, 15, 18, 24 2 | 2 3 18 24 3 | 1 3 9 12 1134 得 [10,15,18,24]=5×2×3×3×4=360。 所以需要 360k(k>0) 人。 4. 方程 ax+by=c 在整数范围内有解的充分必要条件是 (a,b)|c 。 证 必要性:由于 (a,b)|a, (a,b)|b,所以 (a,b)|ax+by=c 。 充分性:设 d=(a,b), 于是存在整数 p, q 使 pa+qb=d 。 又由 d|c ,可设 c=dh 。因而有 aph+bqh=dh=c 。 所以 x=ph , y=qh 就是一个解。 5. 分别解同余方程:(1)258x≡131(mod348). (2) 56x=88(mod96). 解 由书中解同余方程的四个步骤求解。 (1)求 (a,m)=(258,348)=6, 6 不能整除 131,所以此同余方程无解。 (2)求 (a,m)=(56,96)=8,由于 8 能整除 88,所以此同余方程有 解。
【国家自然科学基金】_hilbert_基金支持热词逐年推荐_【万方软件创新助手】_20140802
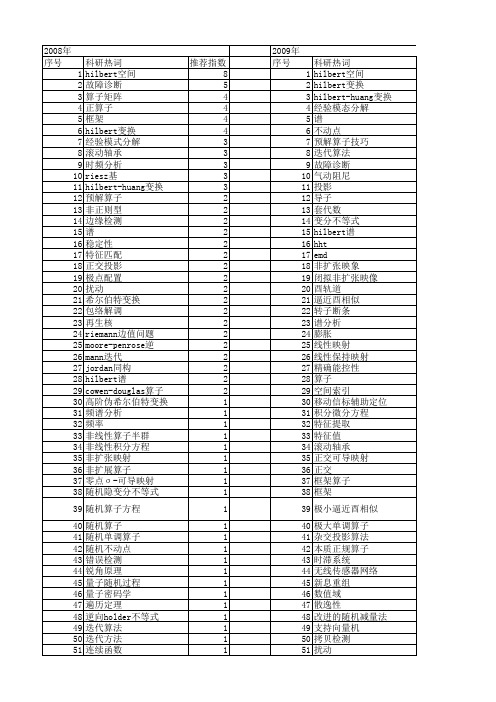
推荐指数 8 5 4 4 4 4 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
油膜振荡. 1 正交经验模态分解 1 正交混合态 1 次连续拟非扩张映像 1 横向反馈系统 1 模算子半群 1 梯度 1 核聚类算法 1 核方法 1 极限环 1 极大单调算子 1 极值点 1 松紧度 1 松弛映象 1 松弛上强制非线性变分不等式 1 本质谱 1 本征模态函数(imf,intrinsic mode 1 function) 有限维hilbert空间 1 最速下降法 1 最优值函数 1 曲线拟合 1 暂态振荡 1 时频分布 1 时延估计 1 日长(lod,length of day) 1 无穷维hamilton算子 1 无条件安全性 1 旋转机械 1 方向导数 1 数字滤波器 1 故障诊断方法 1 收敛性 1 收敛 1 推广的roper-suffridge算子 1 探地雷达 1 振动性 1 拟相似性 1 扩张 1 快速傅立叶变换傅立叶级数频谱细化 1 强收敛 1 强不可约算子 1 强万有的 1 延拓 1 广义预解算子 1 广义逆 1 广义特征值 1 广义混合拟变分包含 1 广义框架 1 广义jordan(α ,β )-导子 1 广义aluthge变换 1 广义(α ,β )-导子 1 平面二次多项式微分系统 1 幂等算子代数 1 带误差的三步投影方法 1
瞎扯数学分析3、泛函分析简介
瞎扯数学分析3、泛函分析简介先声明一下,这篇帖子对数学基础不好或者抽象能力不强的人不友好,建议不要浪费时间。
不过希望工程师们看看,也许有启发,因为泛函分析现在是高水平工程师混饭吃的标配,傅立叶变换,小波分析,最优控制,数学规划,资源最优配置,偏微分方程数值求解,有限元分析,弹性力学数值计算等等等等,基础都是泛函分析。
这是介绍数学思维方式的最后一部分。
主要介绍抽象思维的强大。
由于泛函分析是古典数学和现代数学的桥梁,是古典数学分析,代数和几何以现代观念交叉在一起发展起来的学科,是数学承先启后的门槛,又有广泛的应用,既是所有优化资源配置技术的基础,又是所有控制技术的基础,更是化繁为简的利器。
我在实际工作中体会是几门数学学科在实际应用上的地位是:微积分就像是钢丝钳,粗活细活都能干,凡是能够定义连续因果关系的问题,用微积分试一下没错;线性代数就像是螺丝刀,凡是离散问题,定义线性关系,就能试图找一下构造基(特征根),把问题分解投影到基上,就能分而治之;数理统计就象是扳手,碰到没有明显因果关系的糊涂乱麻问题,先寻找一下趋势外推或线性拟合,找一下统计相关性;实在碰到无法下嘴的问题,只能是数值逼近或数值模拟了。
不过泛函分析是很特殊的工具,类似电钻,可以把困难问题彻底击穿,找到本质。
当然数理方程是工程师的电锯,有招没招锯一下,大卸八块找原理。
作为一个现代工程师,如果工具箱里没钢丝钳,螺丝刀,扳手,榔头,电钻,电锯,可能心中没底,觉得自己全身赤裸,裸奔的工程师,没法见人。
其实现在工程师会不会计算并不重要,因为现在都有现成的计算软件包,关键是在一堆现象中发现问题,定义问题关键因素,并对解决问题知道用什么工具。
泛函分析是把代数(泛函分析有人就称为无穷维空间线性代数),分析(泛函就是把函数当成自变量的广义函数),几何(泛函分析的主要对象之一就是函数组成的赋范空间)整合在一体的学科,是现代数学的门槛,学过泛函分析,基本就算看到现代数学大门了。
数学专业课程详情
wk_ad_begin({pid : 21});wk_ad_after(21, function(){$('.ad-hidden').hide();}, function(){$('.ad-hidden').show();});(1.3) SL2(Z)一模形式,Eisenstein级数丁一函数(1.4)模形式空间的维数(1.5)模形式在"∞"的Fourier展式(1.6) Theta 函数(二)章:Hecke 理论(2.1)点格上的Hecke 对应(2.2)模形式空间上的Hecke算子(2.3) Peterson 内积与Hecke算子的自反性(2.4) Hecke算子的特征形式(2.5)模形式的L-级数(2.6) Hecke算子的迹公式教学方式:讲授教材或教学参考书:(1) N. Koblitz: Introduction to elliptic curves and modular forms (2) J.P.Serre,数论基础,冯克勤译 (3) ng. Elliptic Function. 学生成绩评定方法:考试课程编号:00132610 课程名称:密码学课程类型:研究生和本科生选修课学时学分:54学时,3学分先修要求:高等代数(I)、(II) 基本目的:1.使学生了解传统的密码体制:分组密码和序列密码。
2.使学生了解几种公钥密码体制。
3.使学生了解数字签名,识别和认证的基本方法。
内容提要:1.一些古典密码:移位密码,单表代替密码,多代表替密码,转轮密码。
2.信息论:完全保密,熵,唯一解距离,互信息。
3.序列密码:线性反馈移位寄存器,线性复杂度,非线性组合发生器,组合函数及其相关免疫性。
4.分组密码和数据加密标准:分组密码的工作方式,乘积密码和Feistel密码,DES的算法,DES的特性和强度,对DES的差分攻击。
5.公钥密码体制:计算复杂度,单向函数和陷门函数,RSA密码体制,素性的概率测试,对RSA的攻击,ELGamal密码体制和离散对数,Merkle-Hellman背包体制,椭圆曲线密码体制。
弱集值Amart的Riesz分解
l [  ̄. i E MP ] a r F
即 R =G , +
∈P k ) w 且
∈X , E , G ) ( E I k( , 一 , f x 如
则对 V ∈X’ >f. , z , o>礼 有
一0 ,
m — o. 。
维普资讯
应用 概率 统计 第 _期 Ⅲ
第 十 八 卷
Chi e e J r lo p id Pr ba l y n s ou na fA ple o bit i
2 0 年 5月 02
a d S a it sVo 1 a 0 2 n t t i l 8 No 2 M y 2 0 sc
证明: “ 必要性 ”. { 瓣 : 1 可R e 分解为: 设 R. n n ) i z s
=
Gm+ Z m l
a
本 文 2 0 年 6月2 日收 到, 0 0 9 1 00 2 2 0 年 月 2日收到修 改 穑
・
l
・
维普资讯
得 对 V ∈X 有 x ,
A =
, ) 盯 , ) 则称 R = ( F,
定义12 设 { , 1 为随机集列, | R n ) F为一 随机集, V ∈X , x 有
; 值适应列 . F是弱集值 A at 若存在 A∈P/ )使 称 mr , b( ,
§. 1
主 要 符 号 及 定 义
设 为可分的B nc 空间, 为其对偶空阃,n 瓣 P 为完备的概率空间, ( 为 的所有非空闭子 aah ( , ) 耳 ) 集构成的集族 . 称集值映射 F: n一 耳 ( 为随机集或集值 随机变量, ) 若对于任 意闭集 CCX, F ( ) 有 C= : nC≠ )∈虢 若对于V ∈T( C R , 为集值随机变量, F() . t t ) 则称 { , ∈T 为集值 随机过程 . t ) 若 吼 C (∈T 是 子口 代数, , 关 于 可测, t ) 一 且瓣 T 则称 { , : ∈T 为适应的集值随机过程 . 吼 t ) 本文中 记 只 k x) 』£X, ( ={ 4 A为非空弱紧 凸子集 ) ; 【; 表示 n B nc 空间X 的所有可积有界的, n Xl 到 aah 几乎处 处取值为闭凸集 的随机集的集合; k ; 表示n到B nc 空间 的所有可积 有界 的, l aah 几乎处处取值为
【国家自然科学基金】_同余关系_基金支持热词逐年推荐_【万方软件创新助手】_20140729
科研热词 同余 半环 r0代数 毕竟正则半群 同余格 boole型理论 boole代数 纯整密群 粗糙集代数 粗糙集 粗理想 理想 正则纯整群 正则纯整密群 模糊等价关系 模糊同余 模糊rees同余 标准分解式 指数 子空间 因子 同余类 同余格上的同余关系 同余对 同余关系 双半环 剩余格 ■(■)等价关系 ρ w-下近似 ρ w-上近似 β 粗糙集 skew-环 q-逆断面 mv代数 l*系统 fuzzy等价关系 fuzzy理想 fuzzy同余关系 fibonacci数 (δ )*系统 (~γ )(~r)等价关系
推荐指数 7 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
科研热词 同余 滤子 模糊滤子 格 同余关系 素理想 素因数 粗素理想 粗糙集 粗糙模糊子格 等价关系 积分型余项 理想 泰勒定理 模糊子格 模糊同余关系 模糊关系同态 标准分解式 柯西型余项 极大理想 效应代数 指数 完备格 同构 同态 右侧元 半格分解 剩余格 分布约简 依赖空间 tl-滤子 tl-同余关系 quantale quantaic格 peano型余项 lagrange型余项 heyting代数 fi代数 fibonacci数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Vo1.32(2012) No.5
d—MoDULE 0VER A
数学杂志 : :( 2
RIESZ ALGEBRA FENG Ying (School of Mathem。tics,Southwest Jiaot。ng University,Chengdu 610031,Chinn1
Abstract:In this paperj we introduce the concept of d—module over a Riesz algebra.Bv
the theorems of positive operators,we mainly discuss the d-module structure of the order bidual
of a d-module over a commutative Riesz algebra.Moreover,we study the d-modules over an ideal
generated by a lattice homomorphism or an interval preserving operator. Keywords: Riesz algebra;d-module;order bidual;lattice homomorphism;interval preserv— ing operator 2010 MR Subject Classification:46A40;47B65 Document code: A Article ID:0255.7797(2012)05.0766.07
1 Introduction Accompanied with the study of Riesz algebra,i.e.,lattice algebra,other interesting algebraic structures in Riesz space were also researched,especially for f—module in recent years.It plays a key role in some studies about the theory of positive operator….Motivated by it,a new algebraic concept will be given in this paper,named d-module which is similar to d—algebra.And like the classical discussion of order dual of a lattice algebra『2],the questions whether the order dua1 or second order dua1 of a d—module are also d—modules will be mainly discussed.Furthermore,we study the d—modules over an ideal generated by some special positive operators. First of all,the definition of f—module paper are assumed to be Archimedean. is shown as follows.And all Riesz spaces in this
Definition 1.1 Riesz space L is called an left f—module over an f—algebra A if: (1)L is a left—module over A with respect to a multiplication(a,f).-÷a.f from A× into L,i.e.,(a+b)・f=a・f+b・f,a・(f+g)=a・f+a・g,a・(b・f)=(ab).f,and a・(Af)=(Aa)・f= (0・f)for all a,b∈A,f,g∈L and A∈R; (2)a・f 0 whenever 0 a∈A and 0 f∈ ; (3)f上9 in L implies that a・f上g in L for all a∈A. Based on the Arens multiplication[3】,if L is an f—module over A,we can consider the following multiDlications:
Received date:2010—12—08 Accepted date:2011—06—23 Foundation item:Supported by the Fundamental Research Funds for the Central Universi— ties(SWJTU09BR199;SWJTU09ZT36). Biography:Feng Ying(1979一),female,born at Leshanj Sichuan,lecturer,Ph.D.,major in Banach lattice and positive operator theory. No.5 d-module over a Riesz algebra 767 (1)A×L 一L :(a,f)一a・f:a・f(x)=f(a・x)for x∈ ; (2)A×L L :(a,G)一a・G:a・G(f)=a(a・f)for f∈L ; (3)L×L 一A :(x,f)— ,,: ,,(n)=f(a・ )for a∈ ; (4)L× 一A :(f,G)— ,,G: ,,G(a)=G(a・f)for a∈ ; (5)(A ) × — :(F),)— F・.厂:F・f(x)=F( ,)for x∈ ; (6)(A ) × :(F)G)一F・G:F・o(f)=F( ,,G)for f∈L
2 The Definition of(f_Module Compared with the f—module,we can define a new concept d—module as foilows: Definition 2.1 Let A be a lattice algebra and L be a Riesz space.Then L is called a
left d-module over A when there exists a mapping(a,f)__÷a.f of A×L into L such that the following properties hold: (1)L is a left—module over the Riesz algebra : (2)a・f 0 whenever 0 a∈A and 0 f∈ ; (3)If a∈A十,then a‘(f V g)=a・f V a・g and a・(f A 9)=a・f A a.g hold for all f,g∈L. Right d—module is defined in a similar way. If L is a left d-module over a lattice algebra A,for each a∈ +,the multiplication
mapping丌。0f L into L defined by 7r。(,)=a-f(Vf∈L)is a lattice homomorphism of L. Especially for arbitrary 0∈A,丌。is a disjoint preserving operator and l 0.,l=l 0.I f l l holds for all f∈L.
3 The Order Bidual of a d-Module It was shown that if L is an f-module over A,its order dual L is also an f-module over A(or(A ) )[3]I However these results fail to hold for the order dual of a d_modu1e. Example 3・1 let A be the plane R with the coordinatewise ordering.We can define
multiplication between two elements of R as(Xl,x2)・(y1,y2)=(xly1,xly2).A straight— forward calculation shows that A is an Archimedean d-algebra.So A is a d-module over
itself.
For each order bounded linear functional f∈A and any a=(a1,a2)∈A+,b∈A it is easy to see that a‘Ifl:Ia・fl,and a・(b・f)=(ab)・f.In other words,A is also a d-module over A under the multiplication of(1). Example 3.2 Consider A=R with the coordinatewise vector space operations. partial ordering and the following multiplication for
x’Y=(Xl,x2,x3,x4)(yl,Y2,Y3,Y4)=(XlYl,Xly2,x3y1,x3y2) It is immediate that A is a d-algebra.However for any f∈A and a∈ +.the
multiplication a‘Jf J and Jn・f J may not be equa1.For example,if f(x)=2x1一x3 for each
