一元一次方程
解一元一次方程的四种技巧

解一元一次方程的四种技巧孙昌晋(江苏省连云港新海实验中学ꎬ江苏连云港222000)摘㊀要:一般来说ꎬ解答一元一次方程的大概步骤主要包括:去分母㊁去括号㊁移项㊁合并同类项ꎬ再把未知数的系数化为1.然而ꎬ这个适用于大部分一元一次方程的方法ꎬ也有它不能解决的问题.对形式特殊的一元一次方程ꎬ就要先找到方程的特殊结构ꎬ再选取合适的方法进行求解.解题过程简单ꎬ不仅可以提高解题速度ꎬ还能拓宽思维ꎬ使学习效果显著提升.下面举例来帮助同学更好地解决特殊的一元一次方程.关键词:一元一次方程ꎻ解题技巧ꎻ解题方法中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)14-0020-02收稿日期:2023-02-15作者简介:孙昌晋(1984.2-)ꎬ男ꎬ江苏省连云港人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.1去括号的技巧例1㊀解方程:32[23(14x-1)-2]-2=x.解析㊀通过仔细观察这个方程式我们可以发现ꎬ题目中括号里面的23和括号最外面的32是一组互为倒数的数ꎬ又因为32乘以-2等于-3ꎬ因此ꎬ我们去括号就需要从外向内进行比较好.解㊀先去中括号ꎬ可得(14x-1)-3-2=xꎬ化简得到14x-1-5=xꎬ解得x=-8.例2㊀解方程12{12[12(12x-2)-2]-2}-2=4.解析㊀先观察方程式ꎬ常数4在方程的右边ꎬ方程的左边有一个-2ꎬ我们可以利用合并同类项的方法将右边的常数4和左边的-2合并相加减以后ꎬ方程的左边化成积的式子ꎬ再去掉大括号的系数ꎬ要去大括号就需要用去分母的方式ꎬ经过整理以后得到的式子的形式与原方程是相同的.解㊀先从常数项着手ꎬ移项ꎬ合并同类项后有:12{12[12(12x-2)-2]-2}=6.将分母去掉ꎬ可以得到12[12(12x-2)-2]-2=12.重复上述操作ꎬ经过多次移项㊁合并同类项ꎬ去分母就可以解出:x=124.2将部分看成一个整体求解例3㊀解方程:3x+1()-13x-1()=2x-1()-12x+1().解析㊀首先观察题目所给的方程式ꎬ发现方程的左右两边都有(x+1)与x-1()ꎬ因此我们便把他们看成两个整体分别合并ꎬ最后使用解一般一元一次方程的方法ꎬ经过移项㊁合并同类项ꎬ化简ꎬ求出方程的解.解㊀利用部分当做整体的思想ꎬ把(x+1)与x-1()分别看成两个整体ꎬ再移项ꎬ得:3(x+1)+12(x+1)=2(x-1)+13(x-1)ꎬ合并同类项得72(x+1)=73(x-1).去分母得3(x+1)=2(x-1)ꎬ所以x=-5.例4㊀解方程:3{2x-1-[3(2x-1)+3]}=5.02解㊀观察方程式ꎬ可以将2x-1.看做是一个整体ꎬ然后再按顺序去掉括号ꎬ由此得到3(2x-1)-3[3(2x-1)+3]=5ꎬ再去中括号得到:3(2x-1)-9(2x-1)-9=5ꎬ移项再合并同类项得-6(2x-1)=14.解得x=-23.3合理拆项例5㊀解方程:2x-13-10x+16=2x+14-1.解析㊀我们从拆项这方面考虑ꎬ先把方程式中的每一个分式拆分ꎬ再合并同类项ꎬ这样方程式求解就会简便很多.解㊀23x-13-53x-16=12x+14-1ꎬ将这个方程左右两边合并同类项得到:-x-12=12x-34ꎬ所以-32x=-14ꎬ解得x=16.例6㊀解方程:12(y+1)+13(y+2)=3-14(y+3).解析㊀这道题不能用将部分看成整体的方法求解ꎬ用拆项的办法刚好适用ꎬ方程式中有一个 3 ꎬ再根据题目中各个括号内的常数项和括号前的系数ꎬ所以可以将 3 拆分成为1㊁1㊁1ꎬ然后分别转化成22㊁33㊁44ꎮ解㊀将原方程化为:12y+1()-22[]+13y+2()-33[]+14y+3()-44[]=0ꎬ去小括号㊁合并同类项得:12(y-1)+13(y-1)+14(y-1)=0ꎬ提出(y-1)ꎬ得:(12+13+14)(y-1)=0ꎬ解得y=1.4合理利用分式的基本性质例7㊀解方程:4x-3212-5x-4515=65-x110.解析㊀因为题目中所给方程有分母:12ꎬ15ꎬ110ꎬ而12ˑ2=1ꎬ15ˑ5=1ꎬ110ˑ10=1ꎬ这里可以考虑用分数的性质ꎬ要想去掉分母可以将分母转化成1再去掉ꎬ这样就可以很简便又很迅速地去掉分母.解㊀根据分式的性质ꎬ第一个分式的分子分母同时乘以2ꎬ第二个分式的分子分母同时乘以5ꎬ等式右边分子分母同时乘以10ꎬ得出:(4x-32)ˑ212ˑ2-(5x-45)ˑ515ˑ5=(65-x)ˑ10110ˑ10.化简得:(8x-3)-(25x-4)=12-10xꎬ解出x=-117.例8㊀解方程:4-6x1100-132=150-2x150-152.解㊀化简得到:4-6x1100=1100-x1100-1ꎬ将上述方程式进一步化简得:4-6x1100=1-x1100-1.即4-6x1100=-x1100ꎬ也就是-x=-6x+4ꎬ解得x=45.一般来说对于结构特殊的一元一次方程ꎬ只要抓住了它的结构特征ꎬ就意味着成功了一半ꎬ希望本文能提高同学们解一元一次方程的能力.参考文献:[1]王日.初一学生解一元一次方程应用题的错误类型及教学对策研究[D].兰州:西北师范大学ꎬ2016.[2]郑晓颖.一元一次方程错误类型与错因分析[D].福州:福建师范大学ꎬ2018.[3]白娟.数学史融入一元一次方程教学的实践研究[D].太原:山西师范大学ꎬ2017.[责任编辑:李㊀璟]12。
一元一次方程(含答案)

8.一元一次方程知识纵横早在300多年前法国数学家笛卡尔有一个伟大的设想:首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为解方程.••虽然笛卡尔“伟大设想”没有实现,但是充分说明了方程(equation)的重要性. 一元一次方程(linear equation with one unknown)是代数方程中最基础的部分,是后续学习的基础,其基本内容包括:解方程、方程的解及其讨论.解一元一次方程有一般程序化的步骤,我们在解一元一次方程时,既要学会按部就班(严格按步骤)地解方程,又要能随机应变(灵活打乱步骤)解方程.当方程中的系数是用字母表示时,这样的方程叫含字母系数的方程,含字母系数的一元一次方程总可以化为ax=b 的形式,继续求解时,一般要对字母系数a 、b 进行讨论:1.当a ≠0时,方程有惟一解x=b a2.当a=0且b ≠0时,方程无解;3.当a=0且b=0时,方程有无数个解.例题求解【例1】(1)已知关于x 的方程3[x-2(x-3a )]=4x 和312x a +-158x -=1•有相同的解,•那么这个解是___________. (北京市“迎春杯”竞赛题)(2)如果12+16+112+…+1(1)n n +=20032004,那么n=________.(第18届江苏省竞赛题) 思路点拨 (1)设法建立关于a 的等式,再解关于a 的方程求出a 的值;(2)•恰当地解关于n 的一元一次方程.解:(1) 2728 提示:两方程的解分别为27a 、27221a - ;(2)n=2003 【例2】 当b=1时,关于x 的方程a(3x-2)+b(2x-3)=8x-7有无数多个解,则a 等于(• ). A.2 B.-2 C.-23 D.不存在 (“希望杯”邀请赛试题) 思路点拨 将b=1代入原方程,整理所得方程,就方程解的个数情况建立a 的等式. 解:选A. 提示:原方程化为(3a-6)x=2a-4,则3a-6=0且2a-4=0.【例3】 是否存在整数k,使关于x 的方程(k-5)x+6=1-5x 在整数范围内有解?并求出各个解.思路点拨 把方程的解x 用k 的代数式表示,利用整除的知识求出k.解: 存在整数k,k=±1或k=±5,原方程解分别为x=5 或x=1.【例4】解下列关于x 的方程.(1)4x+b=ax-8;(a ≠4)(2)mx-1=nx;(3)13m(x-n)=14(x+2m).思路点拨首先将方程化为ax=b的形式,•然后注意每个方程中字母系数可能取值的情况进行讨论.解:(1)x=84 ba+-;(2)当m≠n时,方程有惟一解x=1m n -;当m=n时,原方程无解;(3)原方程化为(4m-3)x=4mn+6m,当m≠34时,原方程有惟一解x=4643mn mm+-;当m=34,n=-32(由4mn+6m=0,即n=-64mm=-32得到)时,原方程有无数个解;当m=34,n≠-32时,原方程无解.【例5】已知p、q都是质数,并且以x为未知数的一元一次方程px+5q=97•的解是1,求代数式40p+101q+4的值. (第14届“希望杯”邀请赛试题) 思路点拨用代解法可得到p、q的关系式,进而综合运用整数相关知识分析.解:提示:把x=1代入方程px+5q=97,得p+5q=97,故p与5q中必有一个数是偶数.(1)若p=2,则5q=95,q=19,40p+101q+4=40×2+101×19+4=2003.(2)5q为偶数,则q=2,p=87,而87不是质数,与题设矛盾,舍去,因此原式值为2003.学力训练一、基础夯实1.已知x=-1是关于x的方程7x3-3x2+kx+5=0的解,则k3+2k2-11k-85=______.2.计算器上有一个倒数键1/x,能求出输入的不为零的数的倒数(注:有时需先按shift 或2nd键,再按1/x键,才能实现此功能,下面不再说明).例如,输入2,按下键1/x,则得0.5,现在计算器上输入某数,再依下列顺序按键:1/x-1=1/x-1= ,在显示屏上的结果为-0.75,则原来输入的某数是_______. (第17届江苏省竞赛题)3.方程16(20x+50)+23(5+2x)-12(4x+10)=0的解为______;解方程12{12[12(12x-3)-3]-3}-3=0,得x=_______.4.已知关于x的方程2a(x-1)=(5-a)x+3b有无数多个解,那么a=_____,b=_____.(“希望杯”邀请赛试题)5.和方程x-3=3x+4不同解的方程是( ). A.7x-4=5x-11 B.13x +2=0 C.(a 2+1)(x-3)=(3x+4)(a 2+1) D.(7x-4)(x-1)=(5x-11)(x-1)6.已知a 是任意有理数,在下面各题中(1)方程ax=0的解是x=1 (2)方程ax=a 的解是x=1(3)方程ax=1的解是x=1a(4)方程│a │x=a 的解是x=±1 结论正确的个数是( ).A.0B.1C.2D.3 (江苏省竞赛题)7.方程x-16[36-12(35x+1)]=13x-2的解是( ). A. 1514 B.-1514 C. 4514 D.- 4514 8.已知关于x 的一次方程(3a+8b)x+7=0无解,则ab 是( ).A.正数B.非正数C.负数D.非负数9.解下列关于x 的方程:(1)ax-1=bx; (2)4x+b=ax-8; (3)k(kx-1)=3(kx-1).10.a 为何值时,方程3x +a=2x -16(x-12)有无数多个解?无解?二、能力拓展11.已知方程2(x+1)=3(x-1)的解为a+2,那么方程2[2(x+3)-3(x-a)]=3a•的解为_______.12.•已知关于x•的方程9x-•3=•kx+•14•有整数解,•那么满足条件的所有整数k=_______. (“五羊杯”竞赛题)13.已知14+4(11999+1x )=134,那么代数式1872+48·(19991999x x +)的值为_________. 14.若(3a+2b)x 2+ax+b=0是关于x 的一元一次方程,且有惟一解,则x=_____.15.有4个关于x 的方程:(1)x-2=-1 (2)(x-2)+(x-1)=-1+(x-1) (3)x=0 (4)x-2+11x -=-1+11x - 其中同解的两个方程是( ).A.(1)与(2)B.(1)与(3)C.(1)与(4)D.(2)与(4)16.方程12x ⨯+23x ⨯+…+19951996x ⨯=1995的解是( ). A.1995 B.1996 C.1997 D.199817.已知a+2=b-2=2c =2001,且a+b+c=2001k,那么k 的值为( ). A.14 B.4 C.-14 D.-4 (第15届江苏省竞赛题) 18.若k 为整数,则使得方程(k-1999)x=2001-2000x 的解也是整数的k 值有( ).A.4个B.8个C.12个D.16个 (第12•届“希望杯”邀请赛试题)19.若干本书分给小朋友,每人m 本,则余14本;每人9本,则最后一人只得6本,•问小朋友共几个?有多少本书?20.下边横排有12个方格,每个方格都有一个数字,•已知任何相邻三个数字的和都是20,求x 的值. (上海市竞赛题)X 10E H G F E D C B A 5三、综合创新21.如果a 、b 为定值,关于x 的方程23kx a +=2+6x bk -,无论k 为何值,它的根总是1,求a 、b 的值. (山东省竞赛题)22.将连续的自然数1~1001按如图的方式排列成一个长方形阵列,•用一个正方形框出16个数,要使这个正方形框出的16个数之和分别等于:(1)1988;(2)1991;(•3)2000;(4)2080.这是否可能?若不可能,试说明理由;若可能,请写出该方框16个数中的最小数与最大数. (2002年河北省竞赛题)1 2 3 4 5 6 78 9 10 11 12 13 1415 16 17 18 19 20 2122 23 24 25 26 27 28…………995 996 997 998 999 1000 1001答案:1.-105.2.设原来输入的数为x,则111x-1=-0.75,解得x=0.23.-52;904. 53、-1095.•D •6.A7.A8.B9.(1)当a≠b时,方程有惟一解x=1a b-;当a=b时,方程无解;(2)当a≠4时,•方程有惟一解x=84 ba+-;当a=4且b=-8时,方程有无数个解; 当a=4且b≠-8时,方程无解;(3)当k≠0且k≠3时,x=1k;当k=0且k≠3时,方程无解;当k=3时,方程有无数个解.10.提示:原方程化为0x=6a-12.(1)当a=2时,方程有无数个解;当a≠2时,方程无解.11.10.5 12.10、26、8、-8 提示:x=179k-,9-k│17,则9-k=±1或9-k=±17.13.2000 提示:把(11999+1x)看作一个整体. 14.1.5 15.A 16.B 17.B18.D 提示:x=20011k+为整数,又2001=1×3×23×29,k+1可取±1、±3、±23、•±29、±(3×23)、±(3×29)、±(23×29)、±2001共16个值,其对应的k值也有16个.19.有小朋友17人,书150本. 20.x=521.提示:将x=1代入原方程并整理得(b+4)k=13-2a,此式对任意的k值均成立,即关于k的方程有无数个解.故b+4=0且13-2a=0,解得a=132,b=-4.22.提示:设框中左上角数字为x,则框中其它各数可表示为:x+1,x+2,x+3,x+•7,x+8,x+9,x+10,x+14,x+15,x+16,x+17,x+21,x+22,x+23,x+24, 由题意得:x+(x+1)+(x+2)+(x+3)+…x+24=1998或1999或2000或2001,即16x+192=•2000•或2080解得x=113或118时,16x+192=2000或2080又113÷7=16 (1)即113是第17排1个数,该框内的最大数为113+24=137;118÷7=16 (6)即118是第17排第6个数,故方框不可框得各数之和为2080.。
一元一次方程的概念与解法(复习)
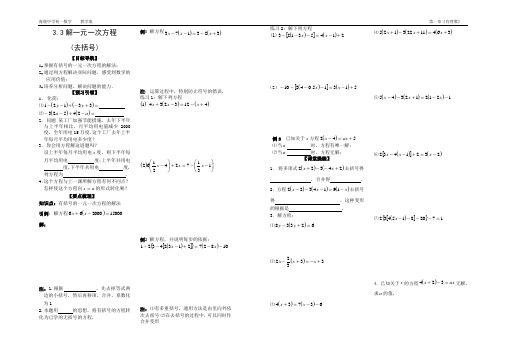
3.3解一元一次方程(去括号)【目标导航】1.掌握有括号的一元一次方程的解法;2.通过列方程解决实际问题,感受到数学的应用价值;3.培养分析问题、解决问题的能力.【预习引领】1. 化简:⑴()()=+-+--33121y y ⑵()()=-+--a a 24523 2.问题 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度.这个工厂去年上半年每月平均用电多少度? 3.你会用方程解这道题吗?设上半年每月平均用电x 度,则下半年每月平均用电 度;上半年共用电 度,下半年共用电 度. 列方程为 . 4.这个方程与上一课所解方程有何不同点?怎样使这个方程向a x =的形式转化呢?【要点梳理】知识点: 有括号的一元一次方程的解法引例:解方程()15000200066=-+x x 解:注:1.根据 ,先去掉等式两边的小括号,然后再移项、合并、系数化为12.本题用 的思想,将有括号的方程转化为已学的无括号的方程.例1 解方程()()323173+-=--x x x注:运算过程中,特别防止符号的错误. 练习1:解下列方程()()()41232341+-=-+x x x()⎪⎭⎫ ⎝⎛--=+⎪⎭⎫ ⎝⎛-1317242162x x x例2 解方程,并说明每步的依据:()[]{}()1082721324321--=+---x x注:⑴有多重括号,通用方法是由里向外依次去括号.⑵在去括号的过程中,可以同时作合并变形.练习2:解下列方程(1)()[]()21453123+-=---x x(2)()[]()51315.04210+-=----x x例3 已知关于x 方程()542+=-ax x ⑴当a 时,方程有唯一解; ⑵当a 时,方程无解;【课堂操练】 1. 将多项式()()24322+--+x x 去括号得 ,合并得 . 2.方程()()()x x x -=---1914322去括号得 ,这种变形的根据是 . 3.解方程: ⑴()62338=+-y y ⑵()33322+-=+-x x x⑶()()63734--=+x x⑷()()()36411223125+=+-+x x x⑸()()()121212345--=+--x x x⑹()[]()2321432-=+--x x x⑺()[]{}1720815432=----x4.已知关于x 的方程()ax x =-+324无解,求a 的值.【课后盘点】1.若关于x 的方程b x x a 3746-=+的解是1=x ,则a 和b 满足的关系式是 . 2.当=x 时,式子()23-x 和()434-+x 的值相等.3.比方程()472=+x 的解的3倍小5的数是 . 4.已知公式()h b a S +=21中,60=S ,6=a ,6=h ,则=b .5.化简下列各式⑴()()223248y xy y xy +-+---⑵()[]a b a b a +----22⑶()[]()y x y x +----25⑷()[]152322+---x x x x6.方程()113=--x x 的根是( ) A .2=x B .1=x C .0=x D .1-=x 7.下列去括号正确的是( )A .()1123=--x x 得4123=--x xB .()x x =++-314得x x =++-344C .()59172+-=-+x x x 得59772+-=--x x x D .()[]21423=+--x x 得24423=++-x x8.解下列方程 ⑴()212-=--t⑵()()32523-=+x x⑶()()23341+=+-x x⑷()()x x x 3234248--+=+⑸()()()x x x -=---1914322 ⑹()x x 415126556=-⎥⎦⎤⎢⎣⎡++9.已知关于x 的方程()3245-=-x ax 无解,求a 的值.10.若x A 34-=,x B 45+=,且B A 3202+=.求x 的值.【课外拓展】1.已知关于x 的方程()251-=-x x m 有唯一解,求m 的值.2.已知关于x 的方程()()b x a x a 3512+-=-有无数多个解,求a 、b 的值.3.三年前父亲的年龄是儿子年龄的4倍,三年后父亲的年龄是儿子年龄的3倍,求父子两人现在的年龄各是多少岁?(设计人:江云桂)No .4一元一次方程的概念与解法(复习)【目标导航】1.复习一元一次方程的概念、等式的性质、一元一次方程的解法;2.能根据题意列一元一次方程解决实际问题;【预习引领】1. 方程,一元一次方程,方程的解; 2. 等式性质;3. 解一元一次方程的步骤及每一步的依据。
一元一次方程

移项:12x-3x+2x=8-4+3
合并同类项:11x=7
7 系数化成1:x= 11 。
1 例题10: 1 1 x 2 4 6 8 1 9 7 5 3
解法1:从外向里逐渐去括号,展开求解:
去大括号得:1 1 x 2 4 6 8 9 7 5 3
意括号前是负号时,去掉负号和括号,括号
里的各项都要变号。括号前有数字因数时要
注意使用分配律。 (3)移项:把含有未知数的项都移到 方程的一边,其他项都移到方程的另一边。 注意移项要变号。
(4)合并同类项:把方程化成最
简形式ax=b (a≠0)。
(5)把未知数的系数化成1:在方 程两边都除以未知数的系数a,得到方 程的解x= 。
去中括号得:1 x 2 4 6 56 63
整理得: 去小括号得:
5 3 1 x2 4 1 5 3 x2 45 3
去分母得:x+2+12=15 移项,合并同类项得:x=1。
解法2:从内向外逐渐去括号,展开求解:
1 4 去小括号得:1 x152 5 6 8 1 9 7
5 x 20 5 5
于是 x=-4
解:(3)两边加5,得 化简得
1 x 55 45 3
1 x9 3
两边同乘-3,得
x=-27
例题8:解方程
1 3
(x-5)=3- (x-5)
2 3
分析:按常规此方程应先去分母,去括号,但
发现方程左右两边都含有x-5项,所以可以把它
们看作一个整体,移项,合并同类项,使运算
一元一次方程应用题8种类型例题

一元一次方程应用题8种类型例题
类型一:物品价格
1.某商店连续3天在降价促销,第一天一种水果的价格为x元,第二
天降价10%,第三天再降价20%,最终第三天的价格为16元,求第一天水
果的原价。
类型二:工作效率
2.甲工人单独工作需要5小时完成某项工作,乙工人单独工作需要7
小时完成同样的工作,如果两人一起工作,需要2.5小时完成,请问他们一起
工作的效率是单独工作的几倍?
类型三:平均分配
3.分别有甲、乙两个人一起捕鱼,如果甲一个人用4小时捕到12条鱼,乙一个人用3小时捕到9条鱼,现在如果两人分配捕到的鱼,每个人平均分
得多少条鱼?
类型四:钱币问题
4.小明有一些1元、2元、5元三种面值的硬币共30枚,共计80元,且5元硬币的数量是1元硬币数量的两倍,求1元硬币的数量。
类型五:行程问题
5.一辆自行车骑行4小时可以到达甲地,同样的路程乘汽车只需要1
小时,如果自行车的速度是每小时10公里,汽车的速度是每小时40公里,
问这段路程的长度是多少?
类型六:温度问题
6.有一加热器每小时的加热量是50瓦,现在将加热时间缩短为原来的
2/3,加热器每小时的加热量增加到了75瓦,求原来的加热器每小时的加热
时间。
类型七:混合物问题
7.有两桶水,一桶水中含有60升的纯净水,另一桶水中含有40升的
纯净水,现从第一桶水中取出x升加入到第二桶水中,使得第二桶水中纯净
水的含量降低为50%,求x值。
类型八:年龄问题
8.某家庭中父亲现在年龄是儿子的7/5倍,2年前父亲的年龄是儿子
的5/3倍,求现在儿子的年龄。
以上是一元一次方程应用题8种类型例题,希望对您有所帮助。
一元一次方程的计算公式

一元一次方程的计算公式一元一次方程,这可是初中数学里的重要角色呀!先来说说一元一次方程的基本形式,它通常长这样:ax + b = 0 (其中 a 不为 0 )。
那怎么求解呢?其实就是把 x 单独“拎”出来,算出它的值。
比如说有个方程 3x + 5 = 14 ,咱们来解解看。
第一步,先把 5 移到等号右边去,变成 3x = 14 - 5 ,也就是 3x = 9 。
接下来,两边同时除以 3 ,得出 x = 3 。
是不是还挺简单的?还记得我之前教过的一个学生小李,他刚开始接触一元一次方程的时候,总是被那些数字和符号绕得晕头转向。
有一次做作业,遇到一个方程 2x - 7 = 11 ,他抓耳挠腮半天也没解出来。
我就走过去问他:“小李,哪里不会啦?”他苦着脸说:“老师,我一看到这些式子就头疼,不知道从哪里下手。
”我笑着跟他说:“别着急,咱们一步步来。
先把 -7 移到等号右边,变成 2x = 11 + 7 ,你算算右边等于多少?”他想了想,回答道:“18 。
”“那接下来呢?”我继续引导他。
他恍然大悟:“两边同时除以 2 ,x 就等于 9 !”从那以后,小李逐渐掌握了解一元一次方程的窍门,做题也越来越顺手了。
再说说一元一次方程在实际生活中的应用。
比如说,你去商店买东西,一个笔记本 5 元,你买了 x 个,一共花了 20 元,那这就可以列出方程 5x = 20 ,从而算出 x = 4 ,也就是说你买了 4 个笔记本。
又比如,从 A 地到 B 地,汽车以每小时 60 千米的速度行驶,x 小时后到达,两地相距 300 千米,那可以列出 60x = 300 ,算出 x = 5 ,也就是 5 小时能到达。
咱们继续深入讲讲。
解一元一次方程还有一些需要注意的地方。
比如移项的时候要变号,乘除的时候要小心别算错。
还有,有时候方程看起来很复杂,但只要按照步骤来,都能迎刃而解。
我还碰到过一个有趣的情况。
有一次课堂小测验,有道题是 4(x - 2) + 3 = 11 ,不少同学都做错了。
完整版一元一次方程及其解法
3.1元一次方程及其解法1. 一元一次方程 (1) 一元一次方程的概念 只含有一个未知数(元),未知数的次数都是 1,且等式两边都是整式的方程叫做一元一 次方程.如:7 — 5x = 3,3(x + 2) = 4— x 等都是一兀一次方程. 解技巧正确判断一元一次方程 判断一元一次方程的四个条件是: ①只含有一个未知数(元);②未知数的次数都是一次; ③未知数的系数不能为 0;④分母中不含未知数,这四个条件缺一不可. 元' (2)方程的解①概念:使方程两边相等的未知数的值叫做方程的解. ②方法:要检验某个数值是不是方程的解,只需看两点: 元方程的解,也叫做方程的根. 一看,它是不是方程中未知数 的值;二看,将它分别代入方程的左边和右边,若方程左、右两边的值相等,则它是方程的 解. 如x = 3是方程2x — 4= 2的解,而y = 3就不是方程2x — 4= 2的解. (3)解方程 求方程的解的过程叫做解方程. 方程的解和解方程是不同的概念,方程的解是求得的结果,它是一个数值(或几个数值), 而解方程是指求出方程的解的过程. 【例1 — 11下列各式哪些是一元一次方程 ( 1 1 , A . S=7ab ; B.x — y = 0; C.x = 0; D. _~ = 1; 2x + 3 =0 ; H.x + 2.解析:E 中不含未知数,所以不是一元一次方程; E.3 — 1 = 2; F.4y — 5= 1; G.2x 2+ 2x + 1 G 中未知数的次数是 2,所以不是 H 虽然形式上字母 元一次方程;A 与B 中含有的未知数不是一个,也不是一元一次方程; 的个数是一个,但它不是等式,所以也不是一元一次方程; D 中分母中含有未知数,不是 元一次方程;只有 C , F 符合一元一次方程的概念,所以它们是一元一次方程.答案:CF【例1 — 21 x = — 3是下列方程(A . — 5(x — 1) = — 4(x — 2) C .尹+ 5= 5解析:对于选项A ,把x =— 3代入所给方程的左右两边,左边=—5 X (— 3— 1) = 20,右边=—4X (— 3 — 2) = 20,因为左边=右边,所以x =— 3是方程一 5(x — 1) = — 4(x — 2)的解; 对于选项B ,把x = — 3代入所给方程的左右两边,左边=4X (— 3) + 2=— 10,右边=1,因为左边工右边,所以x =— 3不是方程4X + 2= 1的解,选项C , D 按以上方法加以判断,都 不能使方程左右两边相等,只有A 的左右两边相等,故应选 A.答案:A2. 等式的基本性质(1) 等式的基本性质① 性质1:等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式.用式子形式表示为:如果 a = b ,那么 a + c = b + c , a — c = b — c.② 性质2 :等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式. 用式子形式表示为:如果 a = b ,那么 ac = bc , |= C(c 工 0).③ 性质3:如果a = b ,那么b = a.(对称性) 如由一8 = y ,得 y =— 8.④ 性质4 :如果a = b , b = c ,那么a = c.(传递性) 女口:若/ 1 = 60° / 2=/ 1,则/ 2= 60°(2) 等量代换 在解题过程中,根据等式的传递性,一个量用与它相等的量代替, 谈重点应用不等式的性质的注意事项(1) 应用等式的基本性质 1时,一定要注意等式两边同时加上整式,才能保证所得结果仍是等式. 这里特别要注意:“同时”坏相等关系.(2) 等式的基本性质 2中乘以(或除以)的仅仅是同一个数而不包括整式,要注意与性质1的区别.⑶等式两边不能都除以 0,因为0不能作除数或分母. 【例2— 11下列运用等式的性质对等式进行的变形中,正确的是( ).5B .若 7a = 5,贝U a = yC .若x= 0,贝U x = 2D .若x— 1 = 1,贝U x — 6= 12 6 解析:首先观察等式的左边是如何由上一步变形得到的, 右边进行相应的变形,得出结论. A 根据等式的基本性质 1,等式U 的两边都减去3y +2,左边是y ,右边是一 3,不是1; C 根据等式的基本性质 2,两边都乘以2,右边应为0,不是2; D 根据等式的基本性质 2, 左边乘以6,而右边漏乘6,故不正确;只有 B 根据等式的基本性质 2,两边都除以 7得 到 a = 7.答案:B)的解.B . 4x + 2= 1 D3x — 1 = 0简称等量代换.(或减去)同一个数或同一个和“同一个”,否则就会破A .若 4y + 2= 3y — 1,贝U y = 1 确定变形的依据,再对等式的【例2— 21利用等式的基本性质解方程:(1)5x — 8 = 12; (2)4x — 2= 2x ; (3)x + 1 = 6; (4)3 — x = 7.分析:利用等式的基本性质求解.先利用等式的基本性质1将方程变形为左边只含有未知数的项,右边含有常数项,再利用等式的基本性质2将未知数的系数化为1.解:(1)方程的两边同时加上8,得5x = 20.方程的两边同时除以 5,得x = 4.⑵方程的两边同时减去2x ,得2x — 2 = 0. 方程的两边同时加上 2, 方程的两边同时除以2, (3) 方程两边都同时「减去 得 x + 1— 1 = 6 — 1,• - x = 6 — 1.”(4) 方程两边都加上x ,得 3 — x + x = 7 + x,3= 7+ x , 方程两边都减去7, 得 3 — 7= 7 + x — 7, •• — 4= x , 即卩 x = — 4.3. 解一元一次方程 (1)移项① 移项的概念及依据: 把方程中的某一项改变符号后, 从方程的一边移到另一边,这种变形叫做移项.因为方程是特殊的等式,所以移项的依据是等式的基本性质 1.② 移项的目的:把所有含有未知数的项移到方程的一边,常数项移到方程的另一边. ③ 移项的过程:移项的过程是项的位置改变和符号变化的过程.即对移动的项进行变号的过程,^口,一 2 — 3x = 7,把一2从方程的左边移到右边,一 2在原方程中前面带有性质符号“-”,移到右边后需变成“ + ”, 在移动的过程中同时变号, 没有移动的项则不变号. 所 以由移项,得一3x = 7+ 2.④ 要注意移项和加法交换律的区别:移项是把某一项从等式的一边移到另一边,变号;而加法交换律中交换加数位置只是改变排列的顺序,符号随着移动而不改变.如, + 5x= 1,把 11x = 11变成 号. 辨误区 在移项时注意 “两变”:一变性质符号,即 “ + ”号变为“—”号,而“—”号变为 “+”号;二变位置,把某项由等号的一边移到另一边.(2)解一元一次方程的步骤解一元一次方程的一般步骤有:去分母、去括号、移项、合并同类项、系数化为得 2x = 2. 得 x = 1.1,移项要35x — 15x + 3从方程的左边移到右边要变号,得 5x = 1 — 3,是属于移项;而把 5x + 11x — 15x = 11,是利用加法交换律,不是移项而是位置的移动,所以不变移项时应注意的问题1具体儿一次方程 (1)这些步骤「在解方程时不一定全部都用到,也不一定按照顺序进行, 可将解出的结果代入原方程进行检解技巧巧解 值得注意的是: 可根据方程的形式,灵活安排步骤; (2)为了避免错误, 验. 【例3— 11下列各选项中的变形属于移项的是 ( A .由 B .由 C .由 D .由 解析: )• 2x = 4,得 x = 27x + 3 = x + 5,得 7x + 3= 5+rX8 — x = x — 5,得一x — x = — 5— 8 x + 9= 3x — 1,得 3x — 1 = x + 9选项A 是把x 的系数化成1的变形;选项 B 中x + 5变成5+ x 是应用加法交换 律,只是把位置变换了一下;选项 C 是作的移项变形;选项 D 是应用等式的对称性 “a = b , 则b = a ”所作的变形.所以变形属于移项的是选项 C. 答案:C 【例3-21解方程宁-5 =亍.分析:方程有分母,将方程两边每一项都要乘以各分母的最小公倍数 12,去掉分母得4(2 — x) — 60= 3(x — 1),再按照步骤求解,特别注意— 5不能漏乘分母的最小公倍数 12. 解:「去分母,方程两边都乘以 12, 得 4(2 — X)— 60= 3(x — 1). 去括号,得 8 — 4x — 60= 3x — 3. 移项,得—4x — 3x =— 3 — 8+ 60. 合并同类项,得—7x = 49. 两边同除以一7,得x = — 7.4.解复杂的一元一次方程解方程是代数中的主要内容之一,一元一次方程化成标准方程后,就成为未知数系数不是0的最简方程.一元一次方程不仅有很多直接应用,而且解一元一次方程是学习解其他方程和方程组的基础. 解方程的过程,实际上就是把方程式不断化简的过程,一直把方程化为x= a(a是一个已知数).(1)复杂的一元一次方程的解法与简单方程的解法其思路是一样的.方程中若含有相同的代数式,可以把此代数式看作一个整体来运算;方程中若含有小数或百分数,就要根据分数的基本性质,把小数或百分数化为整数再去分母运算.(2)要注意把分母整数化和去分母的区别:分母整数化是在某一项的分子、分母上同乘以一个不等于零的数,而去分母是在方程两边同乘以分母的最小公倍数.▼ I .■ "F亠E 0.4x—9 X —5 0.03 + 0.02x 【例4】解万程 C U — =0.50.030.4x—9 0.03 + 0.02X分析:由于0 5和—0~03—的分子、分母中含有小数,可利用分数的基本性质把小数化为整数,在式子瓷^9的分子、分母中都乘以10,变为^^—聖,在式子驾三严的3 + 2x分子、分母中都乘以100,变为然后去分母,再按解一元一次方程的步骤求解.解:分母整数化,得4x—90 X—5 3+ 2x5 — 2 = 3去分母,得6(4x —90)—15(x—5) = 10(3 + 2x).去括号,得24X—540 —15X + 75= 30 + 20x.移项,得24X—15X—20x = 540 —75 + 30.合并同类项,得—11x= 495.两边同除以一11,得x=—45.5.与一元一次方程的解相关的问题方程的解不仅是方程的重要概念,也是考查方程知识时的主要命题点. 解题的关键是理解方程的解的概念.(1)已知方程的解求字母系数:若已知方程的解,将方程的解代入方程,一定使其成立,则得到一个关于另一个未知数的方程,解这个方程,即可求出这个字母系数的值.(2)同解方程:因为两方程的解相同,可直接解第一个方程,求出未知数的值,再把未知数的值代入第二个方程,求出相关字母的值.【例5—1]关于x的方程3x+ 5= 0与3x+ 3k = 1的解相同,贝U k=( ).B 4B . 35解析:解方程3x+ 5= 0,得x=—3.5 将x = —3代入方程3x+ 3k = 1,得一5+ 3k= 1,解得k= 2,故应选C.答案:C【例5—2]若关于x的方程(m —6)x= m —4的解为x= 2,贝U m =解析:把x= 2代入方程(m —6)x = m—4,得(m—6) X 2 = m—4,解得m= 8.答案:86.一元一次方程的常用解题策略我们已经知道,解一元一次方程一般有五个步骤,去分母,去括号,移项,合并同类项,化未知数的系数为1,可有些一元一次方程,若能根据其结构特征,灵活运用运算性质与解题技巧,则不但可以提高解题速度与准确性,而且还可以使解题过程简捷明快,下面介绍解一元一次方程常用的几种技巧.(1)有括号的一元一次方程一般是先去括号,去括号的顺序一般是由小到大去,但有些题目是从外向里去括号,计算反而简单,这就要求仔细观察方程的特点,灵活运用使计算简便的方法.(2)对于一些含有分母的一元一次方程,若硬套解题的一般步骤,先去分母则复杂繁琐,若根据方程的结构特点,先移项、合并同类项,则使运算显得简捷明快.有些特殊的方程却要打破常规,灵活运用一些解题技巧,使运算快捷、简便.巧解可激活思维,使我们克服思维定式,培养创新能力,从而增强学习数学的兴趣.【例6—1]解方程3 3 ^x —1—4 = |x+ 1.3 4 3 3 4 1 1分析:注意到4X 4= 1,把3乘r以中括号的每一项,则可先去中括号,-X 4 * —43 11 3=|x + 1,再去小括号为^x—4—3 = |x + 1,再按步骤解方程就非常简捷了.1 1 3解:去括号,得|x —1—3=討1.移项,合并同类项,得一x= 17.17两边同除以一1,得x=——.x+ 3 x+ 2 = x+ 1 x+ 4【例6-2]解方程7 -5 = 6分析:此题可按照解方程的一般步骤求解, 4 -但本题若直接去分母,则两边乘以最小公倍数420,运算量大容易出错,我们可两边分别通分, 5 x+ 3 —7 x+ 2 2 x+ 1 —3 x+ 435 12把分子整理后再按照解一元一次方程的步骤求解.—x — 10.去分母,得「12( — 2x + 1) = 35( — x — 10). 去括号,得—24x + 12=— 35x — 350. 移项、合并同类项,得11x = — 362.362两边同除以11,得x =—36j 2.题目中,由此可发掘隐含的条件,列一元一次方程解题, 理解掌握数学基础知识.【例7— 11 (1)当a = ___________ 时,式子2a + 1与2— a 互为相反数. ⑵若6的倒数等于X + 2,则x 的值为 __________________ .解析:(1)根据互为相反数的两数和为 0,可得一元一次方程 2a +c 1+ (2 — a) = 0,解得a =—3;(2)由倒数的概念:乘积为 1的两个数互为倒数,可得一元一次方程 6(x + 2) = 1,解 /曰 11得 x=— 6 .11答案:⑴―3 (2)-—解:方程两边分别通分,得 5x + 3 — 7x + 2 2x + 1 — 3x + 4.化简, 3512—2x + 1得—3^ =7.列一元一次方程解题(1) 利用方程的解求未知系数的值 当已知方程的解求方程中字母系数或有关的代数式时,代入原方程,得到关于字母系数的等式 (2) 利用概念列方程「求字母的值利用某些概念的定义,可以列方程求出相关的字母的取值, 如根据同类项的定义或一元一次方程的定义求字母的值.列方程求值的关键是根据所学的知识找出相等关系. 的取值. 谈重点列一元一次方程注意挖掘隐含条件许多数学概念、性质的运用范围、限制条件或使用前提有的是以隐含条件的形式出现在即将方程的解 (或者可以看作关于字母系数的方程),再求解即可.常常采用代入法,再列出方程,解方程从而求出字母发掘隐含条件时需要全面、深刻地【例7-2】已知x=- 2是方程号+誉- 分析:把x=- 2代入原方程,原方程就变成了以k的方程,可以求出k的值.解:把x=-2代入原方程,得-2-k 3k+ 2 - 2+ k+ - (-2)=去分母,得2(- 2-k)+3k+ 2-(- 2) X 6 = 3(-2+ k).去括号,得—4-2k+3k+ 2 + 12=- 6 + 3k.移项、合并同类项,得-2k=- 16.方程两边同除以一2,得k= 8.黑体小四课后作业【题01】下列变形中,不正确的是(【题02】【题03】【题04】A 若x2 5x,则x 5 .C若盘1 x,则r下列各式不是方程的是(A y2c. p2解为xA 2xC 3(xB.D.B.若7x 7,则x 1 .2nax ay .C 22pq q2的方程是(2) (x 3) 5xD.B.D.若关于x的方程2x n23(n 4)0是一儿5x次方程,求n的值.x =爭的解,求k的值.k为未知数的新方程,解含有未知数【题05】 已知(2 m 3)x (2 3m) x 1是关于x 的2儿一次方程,则 m【题06】 若关于 x 的方程 (2 |m|)x 2(m 2)x (52 m) 0 是 儿一次方程,求 m 的解.【题07】 若关于 x 的方程 (k 2)x k 15k 0是一儿' 次方程,则【题08】 若关于 x 的方程 (k 2)x k 15k儿一次方程,则.若关于x 的方程 (k 22)x 4kx5k 0是,儿一次方程, 则方程的解 x =【题09】 (3a 28b )x 5bx 7a 0是关于x 的儿一次方程,且该方程有惟一解,则21 40 B.空4056 1515【题10】解方程:5(3 |x)3(2【题11】解方程: |(4y)1(y【题12】解方程:【题13】解方程:2x 5x65才)363)【题14】解方程:【题15】解方程:【题16】解方程:【题17】解方程:【题18】解方程:1——X0.70.50.2X丄(0.17 0.2X) 10.033(x 4)------ 5x 190.1250.45 0.015 0.01X0.5X 2.50.250.1X 0.9 0.2X0.03 0.70.0152[4X32 1才2)]【题19】解方程:-[丄(丄X 1) 6] 2 03 4 3。
一元一次方程应用题(50道)
一元一次方程应用题(50道)一元一次方程应用题(50道)1. 池塘问题:有一个池塘,里面有一些鱼和青蛙。
已知鱼和青蛙的总数为36,头数为100,请问池塘里有多少只鱼和青蛙?2. 苹果贩卖问题:小明每天贩卖一些苹果和橙子。
已知他卖出的苹果数目是橙子的2倍,他总共卖出了15个水果。
请问他每天贩卖多少个苹果和橙子?3. 铁路站台问题:火车站上有一辆高铁和一辆普速列车,一共有30个车厢。
已知高铁的车厢数是普速列车的2倍,问高铁和普速列车各有多少个车厢?4. 小明和小红问题:小明比小红大2岁,两人年龄之和是28岁。
请问小明和小红分别多少岁?5. 汽车和自行车问题:青松和小明一起从A城到B城,青松骑自行车,每小时的速度是12km/h;小明开汽车,每小时速度是60km/h。
已知他们离开A城和到达B城的时间差2个小时,求A城到B城的距离。
6. 水果和蔬菜问题:在一次农贸市场活动中,小王和小李带来各自的水果和蔬菜卖。
已知小王卖出了10个水果和5个蔬菜,而小李卖出了8个水果和7个蔬菜。
小王的水果每个价格是3元,蔬菜每个价格是2元;小李的水果每个价格是4元,蔬菜每个价格是1元。
请分别计算小王和小李卖出水果和蔬菜的总金额。
7. 儿童和成人门票问题:某游乐园门票分为儿童票和成人票。
已知一天销售的门票总数为48张,总金额为240元。
儿童票的价格是每张15元,成人票的价格是每张20元。
请问儿童票和成人票分别售出了多少张?8. 书包和铅笔盒问题:小明的书包和铅笔盒总共有9个,书包比铅笔盒的数量多3。
请问书包和铅笔盒各有多少个?9. 电脑和手机问题:小王带着电脑和手机出门,电脑的重量是手机的2倍,他们的总重量是6kg。
请问电脑和手机各有多重?10. 停车费问题:某停车场停车费为每小时8元。
小明停车了4小时,停车费用为多少元?11. 毛巾和浴巾问题:某商店有毛巾和浴巾两种商品,已知毛巾的价格是浴巾的三分之一。
小张花了27元买了3个毛巾和2个浴巾,请问每个毛巾和浴巾的价格分别是多少元?12. 配菜问题:在一次聚餐中,小明带来了甲菜和乙菜两种配菜。
初中数学一元一次方程知识点
初中数学一元一次方程知识点初中数学一元一次方程知识点引导语:一元一次方程是初中数学学习的一个重点、难点,需要同学们好好掌握。
以下是初中数学一元一次方程相关知识点,希望能帮助到同学们!一元一次方程定义通过化简,只含有一个未知数,且含有未知数的最高次项的次数是一的等式,叫一元一次方程。
通常形式是ax+b=0(a,b为常数,且a≠0)。
一元一次方程属于整式方程,即方程两边都是整式。
一元指方程仅含有一个未知数,一次指未知数的次数为1,且未知数的系数不为0。
我们将ax+b=0(其中x是未知数,a、b是已知数,并且a≠0)叫一元一次方程的标准形式。
这里a是未知数的系数,b是常数,x的次数必须是1。
即一元一次方程必须同时满足4个条件:⑴它是等式;⑵分母中不含有未知数;⑶未知数最高次项为1; ⑷含未知数的项的系数不为0。
一元一次方程的五个核心问题一、什么是等式?1+1=1是等式吗?表示相等关系的式子叫做等式,等式可分三类:第一类是恒等式,就是用任何允许的数值代替等式中的字母, 等式的两边总是相等, 由数字组成的等式也是恒等式, 如2+4=6, a+b=b+a等都是恒等式;第二类是条件等式, 也就是方程, 这类等式只能取某些数值代替等式中的字母时, 等式才成立, 如x+y=-5, x+4=7等都是条件等式;第三类是矛盾等式, 就是无论用任何值代替等式中的字母, 等式总不成立, 如x2=-2, |a|+5=0等。
一个等式中, 如果等号多于一个, 叫做连等式,连等式可以化为一组只含有一个等号的等式。
等式与代数式不同, 等式中含有等号, 代数式中不含等号。
等式有两个重要性质1)等式的两边都加上或减去同一个数或同一个整式, 所得结果仍然是一个等式;(2)等式的两边都乘以或除以同一个数除数不为零, 所得结果仍然是一个等式。
二、什么是方程, 什么是一元一次方程?含有未知数的等式叫做方程,如2x-3=8,x+y=7 等。
判断一个式子是否是方程, 只需看两点:一是不是等式;二是否含有未知数,两者缺一不可。
一元一次方程的解法
一元一次方程的解法在初中数学中,一元一次方程是我们学习的重要内容之一。
解一元一次方程是我们解决实际问题、进行数学推理的基础。
本文将介绍一元一次方程的解法,帮助中学生和他们的父母更好地理解和应用这一知识。
一元一次方程是指只含有一个未知数,并且未知数的最高次数为1的方程。
它的一般形式可以表示为:ax + b = 0,其中a和b为已知数,x为未知数。
解一元一次方程的关键是找到使等式成立的未知数的值。
一元一次方程的解法有多种,下面将介绍其中的两种常见方法。
方法一:等式两边同时加减同一个数当我们遇到一个一元一次方程时,可以通过等式两边同时加减同一个数,来逐步消去未知数的系数和常数项,最终得到未知数的值。
例如,我们考虑方程2x - 3 = 7。
为了消去常数项-3,我们可以在等式两边同时加上3,得到2x = 10。
接下来,我们再将方程两边同时除以系数2,即可得到x的值,即x = 5。
这种方法简单直观,适用于一些较为简单的方程。
但需要注意的是,当方程中含有分数或小数时,我们需要进行适当的化简和计算,确保结果的准确性。
方法二:倒数法倒数法是一种更加高效的解一元一次方程的方法。
它的基本思想是通过倒数的方式,将未知数的系数化为1,从而简化计算过程。
例如,我们考虑方程3x + 4 = 13。
为了将系数3化为1,我们可以将方程两边同时除以3,得到x + 4/3 = 13/3。
接下来,我们再将方程两边同时减去4/3,即可得到x的值,即x = 13/3 - 4/3 = 9/3 = 3。
倒数法的优势在于可以减少计算的步骤和复杂度,特别适用于系数较大或方程较复杂的情况。
除了以上两种常见的解法,还有一些特殊情况下的解法,如利用代数性质进行变形、利用图像法进行求解等。
这些方法在一些特殊问题中有着重要的应用,可以进一步提高解题的灵活性和准确性。
总结起来,解一元一次方程的关键是找到未知数的值,从而使等式成立。
通过等式两边同时加减同一个数或者利用倒数法,我们可以逐步消去未知数的系数和常数项,最终求得未知数的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
慧通文府(百日学通)教育科技有限公司教研部 第 1 页 共 15 页 一元一次方程
一、本章的学习目标 1、经历“把实际问题抽象为数学的方程”的过程,体会方程是刻画现实世界的一种有效的数学模型,了解一元一次方程及其相关概念,认识从算式到方程是数学的进步。 2、通过观察、归纳得出等式的性质,能利用它们探究一元一次方程的解法。 3、了解解方程的基本目标(使方程逐步转化为x=a的形式),熟悉解一元一次方程的地一般步骤,掌握一元一次方程的解法,体会解法中蕴涵折化归思想。 4、能够“找出实际问题中的已知数和求知数,分析它们之间的关系,高级求知数,列出方程表示问题中的相等立关系”,体会建立数学模型的思想。 5、通过探究实际问题与一元一次方程的关系,进一步体会利用一元一次方程解决问题的基本过程(见下图),感受数学的应用价值,提高分析问题、解决问题的能力。
二、本章知识结构图
基本概念 1、等式:用等号“=”来表示相等关系的式子。可以用a=b来表示. 2、等式的性质: 性质1 等式两边同时加上(或减)同一个数(或式子),所得结果仍相等。 如果a=b,那么ac=bc 性质2 等式两边乘同一个数或除以同一个不为0的数,结果仍相等。 如果a=b,那么ac=bc
如果a=b(c≠0),那么ca=cb 3、方程:含有求知数的等式,叫方程。 4、方程的解:使方程左右两边相等的求知数的值,叫方程的解
方程
等式 概念 性质
方程 概念
方程的解 解方程
一元一次方程 概念 标准形式 解一元一次方程的一般步骤
应用 慧通文府(百日学通)教育科技有限公司教研部
第 2 页 共 15 页 5、解方程:求方程解的过程,叫解方程。 6、一元一次方程:只含有一个求知数,并且求知数的次数是1,系数不等于0的方程,叫一元一次方程。 ax+b=0(其中x是求知数,a、b为已知数且a≠0)是一元一次方程的标准形式。 7、移项:方程中的任何一项,都有可以改变符号后,从方程的一边移到另一边,这种变形叫做移项,这个法则叫移项法则。 8、解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1
三、本章重点难点 1、知道什么是方程、一元一次方程、找相等关系列方程。 2、用移项、合并同类项、去分母等解一元一次方程。 3、会用一元一次方程解决实际问题。
四、本章中考考试内容和考试要求 1、了解方程解的概念,能够根据具体问题中的数量关系,列出方程。 2、了解一元一次方程的有关概念,理解一元一次方程的解法中各个步骤的依据,会列一无一次方程解决实际问题。
五、教学计划 课时 讲课内容 约授课时间/分钟 约练习时间/分钟
一个课时 方程及有关概念 识别方程和等式 等式的性质 等式的性质1、2、3、4 一元一次方程的一般形式及解法
一元一次方程的定义 一元一次方程的解法1 一元一次方程的解法2 一元一次方程的解法3 一元一次方程的解法4 综合解题的思路及步骤 一元一次方程阶段测试
一个课时 一元一次方程的应用
数字和数量分配问题 行程问题 工程问题 利润、折扣及利息问题 浓度问题 几何问题 一元一次方程综合测试 慧通文府(百日学通)教育科技有限公司教研部
第 3 页 共 15 页 六、教学过程 1、方程及有关概念 (1)等式的概念:用“=”表示相等关系的式子,叫做等式。 (2)方程的概念 含有未知数的等式叫做方程。 例:下列各式中,哪个是等式,哪个是方程是方程的请指出未知数。 ① 2x-6 ; ② x-12; ③ 3x-7 = 4x; ④ 8 > 5; ⑤ 1+2 = 3;
⑥ 0114xxx; ⑦ 2x-y = 6–9y; 解:①②④不是等式,其余都是等式 ③⑥⑦是方程。③⑥中未知数是x。⑦中未知数是X和Y。 练习题一: 下列各式中,哪个是等式,哪个是方程。
① x+5 = 0; ②451.01xx; ③123xx; ④ x > 3;⑤ x < y =5;
⑥ 20% + 1 = 56; ⑦ 0.5x = 0.7y + z; ⑧ 100x = 0; ⑨ 4t = 4; ⑩ k = k; 2、等式的基本性质 (1)等式的基本性质1:如果a = b, c表示任意的数或整式,那么a+c = b+c (2)等式的基本性质2:如果a = b, c表示任意的数,那么ac = bc; 例:如果5x = 4 – x ,那么5x +_______ = 4; 解:因为5x = 4 – x 根据等式的基本性质1,等式两边同时加上x得 5x + x = 4 – x + x 所以空中应填x.
如果-31x = 7,那么x = _________;
解:根据等式的基本性质2,等式两边同除以-31得 X = -21 所以空中应填-21. 练习题二: 如果 m + 2n = 0,那么 m = _________; 如果 xy = 6,那么y = _________;
如果 yx = 6,(y0)那么 x = ________;
如果 yx = 6,(y0)那么 y = _________; 如果 m + 2n = 0,那么 n = ________; 如果 3m + 5n = 0, 那么 m = _______;
如果 2m + 4n = 2, 那么 m = _______;
3、一元一次方程的一般形式及解法 (1)定义:只含有一个未知数,并且未知数的最好次数是1的方程叫做一元一次方程。 使方程左右两边相等的求知数的值,叫方程的解 (2)一般形式:ax + b = 0 (a 0) (3)对定义的理解:①等式 慧通文府(百日学通)教育科技有限公司教研部 第 4 页 共 15 页 ②隐含条件 a0 ③未知数只有一个 ④未知数的最高次数是一次 ⑤方程左右两边都是整式 例1:下列各式中是方程的有哪些?一元一次方程有哪些?用序号表示
①312xx;②21x;③133222;④3x;⑤65x;⑥3yx 解:方程是①②⑥;一元一次方程是② 例2:检验下列各数是不是方程151222xxx的解
(1)31x;(2)0x;(3)2x 分析:根据方程解的定义,将2031,,x一一代入计算,使等式成立的x的值是方程的解 答案:(1)把31x分别代入方程的左边和右边,得:
左边9713122,右边971313152 因此,左边=右边,∴31x是方程151222xxx的解 (2)把0x分别代入方程的左边和右边,得: 左边11022,右边110052
因此,左边≠右边,∴0x是方程151222xxx的解 (3)把2x分别代入方程的左边和右边,得: 左边71222,右边712252
因此,左边=右边,∴2x是方程151222xxx的解 例3:若关于x的方程0211xxmm是一元一次方程,求m的值 分析:由于方程中在未知数x的系数和指数的位置出现了待定字母,所以根据一元一次方程的定义进行分情况研究 解:显然方程中0x. 当01m,即1m时,原方程02x是一元一次方程;
当01m时,即1m,∴1m,1m时,原方程为0x是一元一次方程;
当11m,即2m,2m,又011m,∴2m. 因此2m时,原方程为024x是一元一次方程 综合上知,当211或,m时,原方程为一元一次方程. 练习题三: 1、下列方程中属于一元一次方程的是( )
A、011x B、yx16 C、23m D、01322xx 慧通文府(百日学通)教育科技有限公司教研部 第 5 页 共 15 页 2、下列各式中:012x,23x,27102xx,235,15yx,122xx,
001aax中方程个数记为m,一元一次方程个数记为n,则____________nm
3、检验下列未知数的值,哪个是所给方程的解. (1)在531xxx,,中,方程0562xx的解有哪些? (2)在210xxx,,中,方程11xx的解有哪些? 4、已知01374nx是关于x的一元一次方程,则n为多少? 5、若0432mxm是一元一次方程,求m的值
(4)解方程1:移项 例: x – 5 = 2 解: 根据等式性质1得 X = 2+5 X = 7 练习题四:指出下列各式哪些是一元一次方程,如果是一元一次方程求出方程的解。
(1)y + 15 = 6; (2) x1 = 2 (3) m + n = 5; (4) 3x +6 = 2x (5) m – 3 = 2 1 (6) 22x = 1 (7) 3m + 2n = 20(其中n = 4) (8)xy = 5(其中y 是有理数) (9)12x = 5 (9)m = 0
(5)解方程2:化1 例:23x = -4 - x
解: 移项得 25x = -4 X = -58 练习题五: (1) 42x (2)54x+31x = 5 (3) 5y - 5 = 3y (4)10x + 6 = -14 (5) 12x = 14x – 5 (6)3x – 6x = 15
(6)解方程3:去括号 例:15(x-1)-3(x-1) = 6 解:15x –15–3x +3 = 6 12x = 18
x = 23 练习题六:
