1.3.1 二项式定理与二项展开式
合集下载
(vip免费)【数学】1.3.1《二项式定理(一)》课件(新人教A版选修2-3)
2.求（3b+2a）6的展开式的第3项.
3.写出
(3
x
1 )n 23 x
的展开式的第r+1项.
4.用二项式定理展开：
（1） (a 3 b )9 ；
（5.2化）简(：2x
2 )7 x
.
（1）(1 x )5 (1
x)5 ；
1
（2）(2x 2
3x
1 2
)
4
1
(2x 2
3x
1 2
)
4
Thank you！
2)．各项前的系数代表着什么？ 各项前的系数 代表着这些项在展开式 中出现的次数
3)．你能分析说明各项前的系数吗？
3)．你能分析说明各项前的系数吗？
a4 a3b a2b2 ab3 b4 每个都不取b的情况有1种，即C40 ,则a4前的 系数为C40
恰有1个取b的情况有C41种，则a3b前的系数为C41 恰有2个取b的情况有C42 种，则a2b2前的系数为C42 恰有3个取b的情况有C43 种，则ab3前的系数为C43 恰有4个取b的情况有C44种，则b4前的系数为C44
青 春 风 采
高考总分：
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校：北京二中 报考高校：
北京大学光华管理学 院
北京市文科状元 阳光女孩--何旋
来自北京二中，高考成绩672分，还有20 分加分。“何旋给人最深的印象就是她 的笑声，远远的就能听见她的笑声。” 班主任吴京梅说，何旋是个阳光女孩。 “她是学校的摄影记者，非常外向，如 果加上20分的加分，她的成绩应该是 692。”吴老师说，何旋考出好成绩的秘 诀是心态好。“她很自信，也很有爱心。 考试结束后，她还问我怎么给边远地区 的学校捐书”。
1.3.1二项式定理
Liangxiangzhongxue
C03a3 C13 a2b C23 ab2 C33 b3
Bqr6401@
共有四项
三、概念形成
普 概念1.二项式定理
通
高 探索
(a＋b)3＝a3＋3a2b＋3ab2＋b3
中 课 程
＝C03 a3＋ C13a2b＋ C23ab2＋C33b3 (a＋b)4＝(a＋b) (a＋b) (a＋b) (a＋b)
(1-x)n＝C 0-C 1x＋C 2x2-…＋(-1)rC rxr＋…＋(-1)nC nxn
nn
n
n
n
Liangxiangzhongxue
Bqr6401@
四、应用举例
普 例1.(1)求(2a+3b)6展开式中的第3项
通 高
(2)求(3b+2a)6展开式中的第3项
中 课
解: (1) T21 C62 (2a)62 (3b)2 2160a4b2
系数：
Liangxiangzhongxue
2.二项式系数与项的系数不同，二项式系数是组合数，而 项的系数是该项的数字因数。
3.通项公式可用求展开式中任意一项，求时必需明确r=？， 一般地，比所说的第几项少1。
Bqr6401@
三、概念形成
普 概念1.二项式定理
通 例子1：展开(a+b)5
3360
Liangxiangzhongxue
Bqr6401@
四、应用举例
普 通 高 中 课 程 标 准
例4.化简
(1) Cn0 Cn1 Cn2 L Cnr L Cnn
(2) Cn0 Cn1 Cn2 L (1)r Cnr L (1)n Cnn
(3) Cn0 2Cn1 4Cn2 L 2r Cnr L 2n Cnn
二项式定理
思考：1.二项展开式的系数、指数、项数的特点？
2.二项展开式的结构特征？哪一项具有代表性？
知识运用：
1.展开_ = 1 \* GB3 \* MERGEFORMAT _?__ EMBED Equation.KSEE3 \* MERGEFORMAT ___ _ = 2 \* GB3 \* MERGEFORMAT _?__ EMBED Equation.KSEE3 \* MERGEFORMAT ___
总结：二项展开式的通项公式求指定项的方法
变式：1.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___展开式的有理项
2.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___
3.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___
求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___得展开式的第4项的二项式系数和系数________________
变式：_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的展开式中第4项的二项式系数是（）
A _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ B _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ C _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ D _ EMBED Equation.KSEE3 \* MERGEFORMAT ___
2.已知_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的展开式中_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的系数是_ EMBED Equation.KSEE3 \* MERGEFORMAT ___，求常数a的值.
2.二项展开式的结构特征？哪一项具有代表性？
知识运用：
1.展开_ = 1 \* GB3 \* MERGEFORMAT _?__ EMBED Equation.KSEE3 \* MERGEFORMAT ___ _ = 2 \* GB3 \* MERGEFORMAT _?__ EMBED Equation.KSEE3 \* MERGEFORMAT ___
总结：二项展开式的通项公式求指定项的方法
变式：1.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___展开式的有理项
2.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___
3.求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___
求_ EMBED Equation.KSEE3 \* MERGEFORMAT ___得展开式的第4项的二项式系数和系数________________
变式：_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的展开式中第4项的二项式系数是（）
A _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ B _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ C _ EMBED Equation.KSEE3 \* MERGEFORMAT ___ D _ EMBED Equation.KSEE3 \* MERGEFORMAT ___
2.已知_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的展开式中_ EMBED Equation.KSEE3 \* MERGEFORMAT ___的系数是_ EMBED Equation.KSEE3 \* MERGEFORMAT ___，求常数a的值.
浙江省丽水中学高二数学教师教学设计2-3计数原理1.3.1二项式定理(一)
2.（1+2x）7展开式中的第 项的系数-----，二项式系数------.
3.求 展开式中的x4项的系数及其二项式系数和常数项。
（六）课堂小节：1.本节课学习了二项式定理及二项式展开式的通项公式.2.区别二项式系数，项的系数.3.掌握用通项公式求二项式系数，项的系数及项
作业：讲义
教学
反思
个性化设计与改进
（四）举例：
例1.展开 ．（目的：让学生识记二项式定理）
解一： ．
解二： ．
例2．展开 ．（目的：让学生不仅要识记公式而且要能灵活应用公式）
解：
问题的解决：再过810天的那一天是星期几？
3、二项式展开式共有 项，各项的系数 叫二项式系数，
4、 叫二项展开式的通项，用 表示，即通项公式 （r=0,1,2,…,n）
（二）复习
（a+b）2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3
对(a+b)2展开式的分析:
展开后其项的形式为：a2，ab，b2.考虑b:每个都不取b的情况有1种，即 ,则a2前的系数为 .恰有1个取b的情况有种 ，则ab前的系数为 .恰有2个取b的情况有 种，则b2前的
系数为 .
浙江省丽水中学教师教学设计
年级高二科目____数学__主备教师__备课组长审核
课题内容
选修2-3 1.3二项式定理（一）
时间
09.10
教学
资源
分析
课程标准
考试说明
课程标准，考试说明
1.能用计数原理证明二项式定理。
2.会用二项式定理解决与二项展开式有关的简单问题。
教材分析
重点：掌握二项式定理及二项式展开式的通项公式
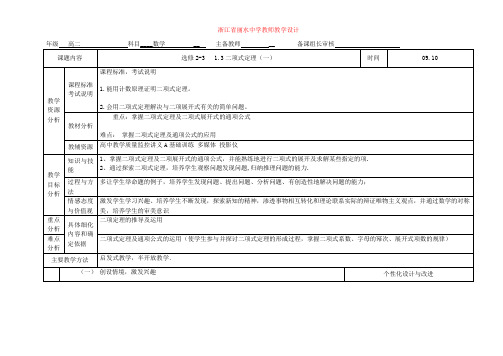
3.求 展开式中的x4项的系数及其二项式系数和常数项。
（六）课堂小节：1.本节课学习了二项式定理及二项式展开式的通项公式.2.区别二项式系数，项的系数.3.掌握用通项公式求二项式系数，项的系数及项
作业：讲义
教学
反思
个性化设计与改进
（四）举例：
例1.展开 ．（目的：让学生识记二项式定理）
解一： ．
解二： ．
例2．展开 ．（目的：让学生不仅要识记公式而且要能灵活应用公式）
解：
问题的解决：再过810天的那一天是星期几？
3、二项式展开式共有 项，各项的系数 叫二项式系数，
4、 叫二项展开式的通项，用 表示，即通项公式 （r=0,1,2,…,n）
（二）复习
（a+b）2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3
对(a+b)2展开式的分析:
展开后其项的形式为：a2，ab，b2.考虑b:每个都不取b的情况有1种，即 ,则a2前的系数为 .恰有1个取b的情况有种 ，则ab前的系数为 .恰有2个取b的情况有 种，则b2前的
系数为 .
浙江省丽水中学教师教学设计
年级高二科目____数学__主备教师__备课组长审核
课题内容
选修2-3 1.3二项式定理（一）
时间
09.10
教学
资源
分析
课程标准
考试说明
课程标准，考试说明
1.能用计数原理证明二项式定理。
2.会用二项式定理解决与二项展开式有关的简单问题。
教材分析
重点：掌握二项式定理及二项式展开式的通项公式
选修2-3第一章1-3-1二项式定理
课前探究学习
课堂讲练互动
活页规范训练
1 4 x＋ 解 (1)法一 x 1 2 1 4 3 2 0 1 2 ＝ C43 x ＋ C43 x · ＋ C43 x · ＋ x x 1 3 1 4 3 4 ＋ C4· C43 x · x x 12 1 2 ＝ 81x ＋ 108x＋ 54＋ ＋ 2. x x 1 4 （ 3x＋ 1） 4 法二 3 x＋ ＝ x2 x 1 ＝ 2(81x4＋ 108x3＋ 54x2＋ 12x＋ 1) x 12 1 2 ＝ 81x ＋ 108x＋ 54＋ ＋ 2. x x 5 1 4 2 3 3 2 4 (2)原式＝ C0 5(x－ 1) ＋ C5(x－ 1) ＋ C5(x－ 1) ＋ C5(x－1) ＋ C5(x 5 5 － 1)＋ C5 － 1 ＝ [( x － 1) ＋ 1] － 1 ＝ x － 1. 5
课前探究学习 课堂讲练互动 活页规范训练
3
规律方法
运用二项式定理展开二项式，要记准展开式公
式，对于较复杂的二项式，有时先化简再展开更简捷；要 搞清楚二项展开式中的项以及该项的系数与二项式系数的
区别．逆用二项式定理可将多项式化简，对于这类问题的
求解，要熟悉公式的特点、项数、各项幂指数的规律以及 各项的系数．
课前探究学习
课堂讲练互动
活页规范训练
2．对通项公式的理解 n－ r r n (1)通项 Tr＋1＝ Cr a b 是 ( a ＋ b ) 的展开式的第 r＋ 1 项，这里 r n ＝ 0， 1，…， n. n－ r r n (2)二项式(a＋ b)n 的第 r＋ 1 项 Cr a b 和 ( b ＋ a ) 的展开式的第 r n n－ r r ＋ 1 项 Cr b a 是有区别的，应用二项式定理时，其中的 a 和 b n 是不能随便交换的． (3)注意二项式系数 Cr 二 n与展开式中对应项的系数不一定相等， 项式系数一定为正，而项的系数有时可为负． (4)通项公式是在 (a＋ b)n 这个标准形式下而言的， 如 (a－ b)n 的二 n－ r r 项展开式的通项公式是 Tr＋1＝ (－ 1)rCr b (只需把－ b 看成 b na n－ r r 代入二项式定理 )，这与 Tr＋ 1＝ Cr a b 是不同的，在这里对应 n 项的二项式系数是相等的都是 Cr 但项的系数一个是 (－ 1)rCr n， n， 一个是 Cr n，可看出二项式系数与项的系数是不同的概念．
二项式定理课件
3 0 3 3 1 2 3 2 3
C
1 3
2 3 3 3
(a b) C a C a b C Байду номын сангаасb C b ③ 展开式：
探究3 仿照上述过程,推导 (a b) 的展开式.
4
1 ab (a b) C a C 2 2
2
0 2 2
3
C b
2 3
2 2 2
2
(a b) C a C a b C ab C b
4
4
分析：为了 方便，可以 先化简后展 开
1 4 2 x 1 ) 2 ( x
1 轾0 4 3 2 1 1 2 3 = 2犏 C4 (2x) - C4 (2x) + C4 (2x) - C4 (2x) + C44 x 臌 1轾 4 3 2 1 = 2犏 16 x 32 x + 24 x 8 x +1 臌 x
k ③二项式系数: C n ( k {0,1,2,, n})
④二项展开式的通项: Tk 1
C a b
k n k k n
二项式定理
(a b) C a C a b C a
n 0 n n k n 1 n 1 n n k k
b C b (n N )
n n n *
*
2．思想方法
(1) 从特殊到一般的数学思维方式.
(2) 用计数原理分析二项式的展开过程.
(3) 类比、等价转换的思想.
1、巩固型作业： 课本28页 联系B组 1、2、3
2、思维拓展型作业：
0 1 探究二项式系数 Cn ，Cn，
C ， ，C 有何性质.
2 n n n
聪 明 在 于 勤 奋 ，
C
1 3
2 3 3 3
(a b) C a C a b C Байду номын сангаасb C b ③ 展开式：
探究3 仿照上述过程,推导 (a b) 的展开式.
4
1 ab (a b) C a C 2 2
2
0 2 2
3
C b
2 3
2 2 2
2
(a b) C a C a b C ab C b
4
4
分析：为了 方便，可以 先化简后展 开
1 4 2 x 1 ) 2 ( x
1 轾0 4 3 2 1 1 2 3 = 2犏 C4 (2x) - C4 (2x) + C4 (2x) - C4 (2x) + C44 x 臌 1轾 4 3 2 1 = 2犏 16 x 32 x + 24 x 8 x +1 臌 x
k ③二项式系数: C n ( k {0,1,2,, n})
④二项展开式的通项: Tk 1
C a b
k n k k n
二项式定理
(a b) C a C a b C a
n 0 n n k n 1 n 1 n n k k
b C b (n N )
n n n *
*
2．思想方法
(1) 从特殊到一般的数学思维方式.
(2) 用计数原理分析二项式的展开过程.
(3) 类比、等价转换的思想.
1、巩固型作业： 课本28页 联系B组 1、2、3
2、思维拓展型作业：
0 1 探究二项式系数 Cn ，Cn，
C ， ，C 有何性质.
2 n n n
聪 明 在 于 勤 奋 ，
人教版高中数学选修2-3教案：1.3.1二项式定理
§1.3.1 二项式定理【教学目标】1.理解二项式定理及推导方法，识记二项展开式的有关特征，能对二项式定理进行简单应用；2.通过对二项式定理内容的研究，体验特殊到一般的发现规律，一般到特殊指导实践的认识事物过程。
【教学重难点】教学重点：二项式定理的内容及归纳过程；教学难点：在二项式展开的过程中，发现各项及各项系数的规律。
【教学过程】一、设置情景，引入课题引入：二项式定理研究的是（a+b）n的展开式。
如（a+b）2=a2+2ab+b2, （a+b）3=？，（a+b）4=？，那么（a+b）n的展开式是什么呢？二、引导探究，发现规律1、多项式乘法的再认识问题1：（a1+ b1）(a2+b2) (a3+ b3)展开式中每一项是怎样构成的？展开式有几项？2、（a+b）3展开式的再认识问题2：将上式中，若令a1=a2=a3=a, b1=b2= b3=b,则展开式又是什么？合作探究1：合并同类项后，为什么a2b的系数是3？教师引导：可以发现a2b是从（a+b）（a+b）（a+b）这三个括号中的任意两个中选a，剩下的一个括号中选b；利用组合知识可以得到a2b应该出现了C23· C11=3次，所以a2b的系数是3。
问题3：（a+b）4的展开式又是什么呢？可以对（a+b）4按a或按b进行分类：（1）四个括号中全都取a，得：C44a4（2）四个括号中有3个取a，剩下的1个取b，得：C34a3· C11b（3）四个括号中有2个取a，剩下的2个取b，得：C24a2· C22b2（4）四个括号中有1个取a，剩下的3个取b，得：C14a· C33b3（5）四个括号中全都取b，得：C44b4小结：对于展开式，只要按一个字母分类就可以了，可以按a分类，也可以按b分类，再如：（1）不取b：C04a4；（2）取1个b：C14a3b；（3）取2个b：C24a2b2；（4）取3个b：C34a b3；（5）取4个b：C44b4，然后将上面各式相加得到展开式。
二项式定理
栏目 导引
第一章 计数原理
探究点 1 二项式定理的正用与逆用 (1)用二项式定理展开1＋1x4；
(2)化简：(x－1)5＋5(x－1)4＋10(x－1)3＋10(x－1)2＋5(x－1)． 【解】 (1)法一：1＋1x4＝1＋C141x＋C241x2＋C341x3＋1x4＝1 ＋4x＋x62＋x43＋x14.
第一章 计数原理
1．3 二项式定理 1．3.1 二项式定理
第一章 计数原理
1.能用计数原理证明二项式定理． 2.掌握二项式定理 及其展开式的通项公式． 3．会用二项式定理解决与二项展开式有关的简单问题．
第一章 计数原理
二项式定理
二项式 (a＋b)n＝ Can＋Can－1b＋…
定理
＋Can－kbk＋…＋Cbn (n∈N*)
二项展开式 公式 右边的式子
二项式系数 C(k∈{0，1，2，…，n})
二项展开式
的通项
Tk＋1＝
Cknan－kbk
栏目 导引
第一章 计数原理
通项公式中的注意点 (1)Tk＋1 是展开式中的第 k＋1 项，而不是第 k 项； (2)公式中 a，b 的指数和为 n，且 a，b 不能随便颠倒位置； (3)要将通项中的系数和字母分离开，以便于解决问题； (4)对二项式(a－b)n 展开式的通项公式要特别注意符号问题．
栏目 导引
第一章 计数原理
2．(x2－1x)n 的展开式中，常数项为 15，则 n 的值为(
)
A．3
B．4
C．5
D．6
解析：选 D.展开式的通项为 Tr＋1＝Crn·(x2)n－r·(－1)r·(x－1)r ＝(－1)r·Cnr ·x2n－3r.
令 2n－3r＝0，得 n＝32r(n，r∈N*)，
1.3.1-2二项式定理
解(1): (1－x2)20的展开式的通项为:
2 r ( x ) Tr 1 C
r 20
4 r 1 4 r 1 8 r 2 x T4r C20 ( x 2 )4r 1 (1)4r 1 C20 r 1 r 1 x 2r 2 Tr 2 C20 ( x 2 )r 1 ( 1)r 1 C20 r 1 4 r 1 C20 C20
r Tr 1 Cn ( xlog2 x )nr ,
展开式的倒数第二项为:
T14 C ( x
13 14
log2 x
) C x
1 14
log2 x
14 x log2 x =112
2
log2 x log2 x log2 8 23
(log2 x) 3
log2 x 3
解得, n 14, k 5,
4r－1=r＋1 或(4r－1)＋(r＋1)=20
2 r , (舍) 或r=4. 3
例2.在(1－x2)20展开式中, 如果第4r项和第r＋2项的二项 式系数相等. (1)求r的值; (2)写出展开式中的第4r项，第r＋2项.
解(2): (1－x2)20的展开式的通项为:
4 r 1 4 r 1 8 r 2 x T4r C20 ( x 2 )4r 1 (1)4r 1 C20 r 1 r 1 x 2r 2 Tr 2 C20 ( x 2 )r 1 ( 1)r 1 C20
二项式定理 （二）
复习回顾
1. 定理 (a+b)n= Cn0an+Cn1an-1b+…+ Cnran-rbr …+Cnnbn (1).项数规律: 二项展开式共有n+1个项 (2).指数规律: 各项的次数均为二项式的次数n (3).字母指数规律: a的次数由n降到0,b的次数由0升到n.
2 r ( x ) Tr 1 C
r 20
4 r 1 4 r 1 8 r 2 x T4r C20 ( x 2 )4r 1 (1)4r 1 C20 r 1 r 1 x 2r 2 Tr 2 C20 ( x 2 )r 1 ( 1)r 1 C20 r 1 4 r 1 C20 C20
r Tr 1 Cn ( xlog2 x )nr ,
展开式的倒数第二项为:
T14 C ( x
13 14
log2 x
) C x
1 14
log2 x
14 x log2 x =112
2
log2 x log2 x log2 8 23
(log2 x) 3
log2 x 3
解得, n 14, k 5,
4r－1=r＋1 或(4r－1)＋(r＋1)=20
2 r , (舍) 或r=4. 3
例2.在(1－x2)20展开式中, 如果第4r项和第r＋2项的二项 式系数相等. (1)求r的值; (2)写出展开式中的第4r项，第r＋2项.
解(2): (1－x2)20的展开式的通项为:
4 r 1 4 r 1 8 r 2 x T4r C20 ( x 2 )4r 1 (1)4r 1 C20 r 1 r 1 x 2r 2 Tr 2 C20 ( x 2 )r 1 ( 1)r 1 C20
二项式定理 （二）
复习回顾
1. 定理 (a+b)n= Cn0an+Cn1an-1b+…+ Cnran-rbr …+Cnnbn (1).项数规律: 二项展开式共有n+1个项 (2).指数规律: 各项的次数均为二项式的次数n (3).字母指数规律: a的次数由n降到0,b的次数由0升到n.
高中数学教学课例《1.3.1二项式定理》课程思政核心素养教学设计及总结反思
在本节课排列的教学中，准备使用多媒体。因为使
用多媒体，有利于提高教学容量。
一．新授
问题 1：如何利用计数原理得到
的展开式？你能由此猜测一下的展开式是什么？
设计意图:掌握二项式的定理
例 1、展开．
解一：
．
解二：
教学过程
．
变式训练：展开
解：
． 师生活动：（1）在初中，由多项式乘法法则得到
的展开式，展开式中各项的系数分别是什么？ （2）由的展开式，写出的展开式 问题 2：由二项式定理，推导二项式定理的通项公
式？ 设计意图：掌握二项式定理的通项公式 例 1、求的展开式中的倒数第项 解：的展开式中共项，它的倒数第项是第项， ． 变式训练：求（1），（2）的展开式中的第项． 解：（1）， （2）． 师生活动：（1）的各项系数各为多少？ （2）自主分析的各项系数，得出二项式的通项公
式？ 二、课堂小结 1、项式定理的探索思路:观察——归纳——猜想
学生学习能
通过复习、推理、分析、归纳的过程总结记忆二项
力分析 式定理
在本节课的教学中，学生可能遇到的问题是对二项
教学策略选 式的展开，产生这一问题的原因是与计数问题连在一起
择与设计 是不容易的。要解决这一问题，就要采用合情推理的方
法，在探究中提出利用两个计数原理得出
⑴
⑵
⑶的各项都是次式的展开问题。
教材分析 的应用有着非常重要的作用，所以在本学科多项式的运
算中有重要的地位，是本学科的核心内容。教学的重点
是二项式定理及通项公式的掌握及运用，解决重点的关
键是要引导分析二项式的展开过程，从而发现二项式展
开成单项式之和是各项系数的规律。
教学目标
1、掌握二项式定理和二项展开式的通项公式 2、能解决二项展开式有关的简单问题