matlab第六讲
第六讲线性规划与非线性规划

(2)若有非线性约束条件:c1 x 0 或c2 x 0, 则建立M
文件c.m定义函数c1 x,c2 x, 一般形式为
function [c1,c2]=c(x)
c1=…
c2=… (3)建立主程序。求解非线性规划的函数是fmincon,
调用格式为 x=fmincon(‘fun’,x0,A1,b1);
故它属于一个整数线性规划问题,这里当成一个线 性规划求解,求得最优解刚好是整数x1=9,x2=0, 故它就是该整数规划的最优解.若用线性规划解法求 得的最优解不是整数,将其取整后不一定是相应整 数规划的最优解,这样的整数规划应用专门的方法 求解.
二、非线性规划
1、二次规划
❖
标准形式:min
z
1
xT
x1 4x2 5
•
x1, x2 0
❖
改写成标准形式:min z
x1 2x2
1 2
x12
1 2
x22
s.t.
2x1 3x2 x1 4x2
6 5
0 0
0 0
x1 x2
❖ 建立M文件fun1.m
❖ 建立主程序(见MATLAB程序(feixianxingguihua1))
工费用如下表.问怎样分配车床的加工任务,才能既满足加
工工件的要求,又使加工费用最低?
车床 类型
甲
乙
单位工件所需加工台时数 工件 1 工件 2 工件 3
0.4
1.1
1.0
0.5
1.2
1.3
单位工件的加工费用 工件 1 工件 2 工件 3
13
9
10
11
12
8
可用台 时数
800
科学计算与Matlab语言 教学大纲

科学计算与Matlab语言一、课程说明课程编号:010631Z10课程名称:科学计算与Matlab语言/ Scientific computing with Matlab language 课程类别:专业教育课程学时/学分:32/2先修课程:程序设计设计基础、高等数学、线性代数适用专业:生物医学工程教材、教学参考书:1.(美)穆尔著,高会生等译. MATLAB实用教程(第二版),电子工业出版社,2010.2.孙蓬主编,曾雷杰等编著. MATLAB基础教程,清华大学出版社,20113.薛山. MATLAB基础教程,清华大学出版社,2011.4.占海明.基于MATLAB的高等数学问题求解,清华大学出版社,2013.5.薛定宇,陈阳泉.高等应用数学问题的MATLAB求解(第三版),清华大学出版社,2013.二、课程设置的目的意义该课程是生物医学工程专业的计算机应用技术课程。
目的是使学生掌握Matlab的基本使用方法,具备利用matlab程序解决工程技术问题的基本能力。
为后续《数字信号处理》、《数字图像处理》、《医学信号处理》、《医学图像处理》等课程,以及编程实践和毕业设计等提供程序设计知识与能力。
三、课程的基本要求知识:掌握MATLAB的数据类型、矩阵输入和操作方法、语法结构、函数的使用以及二维、三维绘图功能,符号代数基本方法,并能够熟练地将MATLAB 应用于学习中,解决相关课程中较为复杂的数学计算问题;能力:注重提高学生解决问题的能力、软件应用能力,尤其是工程技术问题的Matlab解决能力;培养较强的自主学习能力、科技创新能力、工程实践能力;素质:培养学生严谨、规范、理论联系实际的科学态度。
积培养坚持不懈,细心谨慎,实事求是的科研精神。
四、教学内容、重点难点及教学设计五、实践教学内容和基本要求注:要求学生每次实验前完成初步的设计,实验期间进行调试与共性问题讲解。
六、考核方式及成绩评定教学过程中采取讲授、讨论、分析、作业、实验、课前导学的方式进行,注重过程考核,考核方式包括:笔试、作业、讨论、课内互动、实验等;过程考核占总评成绩的50%,期末考试点50%。
《数值分析》教学大纲

《数值分析》教学大纲
一、课程名称:数值分析
二、课程性质:专业选修课
三、授课学时:48学时(实验室32学时)
四、授课对象:计算机专业本科课程学生
五、课程目前:
1.数值分析的定义、内容及其在科学计算中的重要性;
2.数值积分的原理及其应用,包括高斯积分、拉格朗日积分、Lagrange插值法、梯形法等;
3.常微分方程的数值解法,包括隐式Euler方法、欧拉法、Runge-Kutta方法、Adams方法、Lorenz方法等;
4.最优化的原理和算法,包括一阶最优化方法、梯度方法、拟牛顿法、二阶最优化方法及其应用;
5.系统辨识的原理及其应用;
6.数值计算实践,使用MATLAB编程实现数值计算;
六、教学进度安排
第1讲:数值分析的定义、内容及其在科学计算中的重要性
第2讲:数值积分的原理及其应用:高斯积分、拉格朗日积分、Lagrange插值法
第3讲:隐式Euler方法
第4讲:欧拉法
第5讲:Runge-Kutta方法
第6讲:Adams方法
第7讲:Lorenz方法
第8讲:一阶最优化方法、梯度方法和拟牛顿法
第9讲:二阶最优化方法及其应用
第10讲:系统辨识原理及其应用
第11讲:MATLAB编程实现数值计算
七、教学要求
1.熟悉数值分析的定义、内容及其在科学计算中的重要性;。
第6章(形函数)

公式号 6.1 图6-1第六章 单元形函数的讨论在有限单元法的基本理论中,形函数是一个十分重要的概念,它不仅可以用作单元的内插函数,把单元内任一点的位移用结点位移表示,而且可作为加权余量法中的加权函数,可以处理外载荷,将分布力等效为结点上的集中力和力矩,此外,它可用于后续的等参数单元的坐标变换等。
根据形函数的思想,首先将单元的位移场函数表示为多项式的形式,然后利用结点条件将多项式中的待定参数表示成场函数的结点值和单元几何参数的函数,从而将场函数表示成结点值插值形式的表达式。
在本节中,重点讨论几种典型单元的形函数插值函数的构造方式,它们具有一定的规律。
然后以平面三角形单元为例,讨论了形函数的性质,在此基础上分析了有限元的收敛准则。
6.1形函数构造的一般原理单元的类型和形状决定于结构总体求解域的几何特点、问题类型和求解精度。
根据单元形状,可分为一维、二维、三维单元。
单元插值形函数主要取决于单元的形状、结点类型和单元的结点数目。
结点的类型可以是只包含场函数的结点值,也可能还包含场函数导数的结点值。
是否需要场函数导数的结点值作为结点变量一般取决于单元边界上的连续性要求,如果边界上只要求函数值保持连续,称为C0型单元,若要求函数值及其一阶导数值都保持连续,则是C1型单元。
在有限元中,单元插值形函数均采用不同阶次的幂函数多项式形式。
对于C0型单元,单元内的未知场函数的线性变化仅用角(端)结点的参数来表示。
结点参数只包含场函数的结点值。
而对于C1型单元,结点参数中包含场函数及其一阶导数的结点值。
与此相对应,形函数可分为Lagrange 型(不需要函数在结点上的斜率或曲率)和Hermite 型(需要形函数在结点上的斜率或曲率)两大类,而形函数的幂次则是指所采用的多项式的幂次,可能具有一次、二次、三次、或更高次等。
另外,有限元形函数[N ]是坐标x 、y 、z 的函数,而结点位移不是x 、y 、z 的函数,因此静力学中的位移对坐标微分时,只对形函数[N ]作用,而在动力学中位移对时间t 微分时,只对结点位移向量作用。
MATLAB空间面板数据模型操作简介
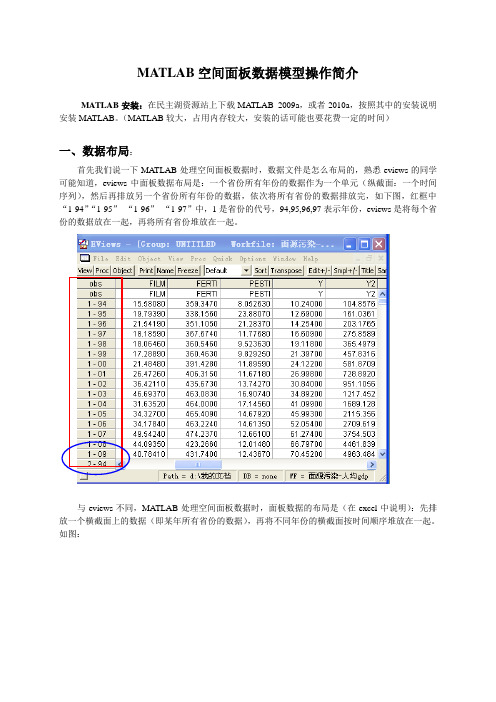
MATLAB空间面板数据模型操作简介MATLAB安装:在民主湖资源站上下载MA TLAB 2009a,或者2010a,按照其中的安装说明安装MATLAB。
(MATLAB较大,占用内存较大,安装的话可能也要花费一定的时间)一、数据布局:首先我们说一下MA TLAB处理空间面板数据时,数据文件是怎么布局的,熟悉eviews的同学可能知道,eviews中面板数据布局是:一个省份所有年份的数据作为一个单元(纵截面:一个时间序列),然后再排放另一个省份所有年份的数据,依次将所有省份的数据排放完,如下图,红框中“1-94”“1-95”“1-96”“1-97”中,1是省份的代号,94,95,96,97表示年份,eviews是将每个省份的数据放在一起,再将所有省份堆放在一起。
与eviews不同,MATLAB处理空间面板数据时,面板数据的布局是(在excel中说明):先排放一个横截面上的数据(即某年所有省份的数据),再将不同年份的横截面按时间顺序堆放在一起。
如图:这里需要说明的是,MA TLAB中省份的序号需要与空间权重矩阵中省份一一对应,我们一般就采用《中国统计年鉴》分地区数据中省份的排列顺序。
(二阶空间权重矩阵我会在附件中给出)。
二、数据的输入:MATLAB与excel链接:在excel中点击“工具→加载宏→浏览”,找到MA TLAB的安装目录,一般来说,如果安装时没有修改安装路径,此安装目录为:C:\Programfiles\MATLAB\R2009a\toolbox\exlink,点击excllink.xla即可完成excel与MATLAB的链接。
这样的话excel中的数据就可以直接导入MATLAB中形成MATLAB的数据文件。
操作完成后excel 的加载宏界面如图:选中“Spreadsheet Link EX3.0.3 for use with MATLAB”即表示我们希望excel 与MATLAB实现链接。
用adams进行仿真第六讲

压缩机设计
洗衣机振动模拟 动力传动装置模拟
工程机械
履带式或轮式车辆动力学分析 车辆稳定性分析 重型工程机械的动态性能预测 工作效率预测 振动载荷谱分析 发动机尺寸确定、载荷预测
耐久性研究
挖掘功率预测 萤石碰撞效应
软件安装/卸载
操作界面简介
工作环境设置 ADAMS软件使用简介 利用adams对机械系统进 行仿真过程 建模方式 应用此软件对简单机械系 统进行仿真
而且,在虚拟样机商业软件方面也发展迅速,成熟的如 MDI公司的ADAMS。
美国B777的应用效果
开发周期:8年->4年
成本降低:25%
100%整机数字化设计 世界垄断与霸主地位
通用公司应用状况
开发周期(48月->24月-> 12月)
碰撞试验(100次 -> 50次) 个性化定单 -> 3小时
通过在线采购降低成本10%
Commanche 时 , 大 规 模 使 用 了 虚 拟 样 机 技 术 。 使 Commanche的开销大幅度降低。
芬兰VTT电子公司正在从事消费类电子产品的 VP研究, 己开发了手机的虚拟样机。
美国波音公司的波音 777型飞机在设计开发过程中全面采 用了虚拟原型样机技术,在没有建造一架物理原型样机的情况 下,节省了大量开发经费,开发周期由八年缩短到四年。
操作界面简介 ADAMS/View启动之后会出现Welcome欢迎窗口。
操作界面简介 ADAMS/View的界面介绍 启动ADAMS/View后,ADAMS/View关闭 Welcome对话 窗口,并进入ADAMS/View的主窗口界面。如图所示。
操作界面简介
点线绘制
实体绘 制
用adams进行仿真第六讲
增加发动机、车身后 整车多体动力学模型
用adams进行仿真第六讲
铁路车辆及装备
悬挂系统设计 磨耗预测 轨道载荷预测 货物加固效果仿真 物料运输设备设计 事故再现 车辆稳定性分析 临界车速预测 乘员舒适性研究
用adams进行仿真第六讲
结构噪声 仿真
双层车 模态仿真
温度场 仿真
D38轻量 化设计
强度 分析
ADAMS软件包括3个最基本的解题程序模块:A/View(基本环 境)、A/Solver(求解器)和A/PostProcessor(后处理)。 另外还有一些特殊场合应用的附加程序模块,A/Rail(机车模 块 ) 、 A/Driver( 驾 驶 员 模 块 ) 、 A/Tire( 轮 胎 模 块 ) 、 A/Linear(线性模块)、A/Flex(柔性模块)、A/Controls(控制模 块 ) 、 A/Car( 轿 车 模 块 ) 、 A/FEA ( 有 限 元 模 块 ) 、 A/Hydraulics ( 液 压 模 块 ) 、 A/Vibrations( 振 动 模 块 ) A/Exchange(接口模块)、A/Animation(高速动画模块)等。
产品概念设计
产品详细设计
用adams进行仿真第六讲
美国GM公司虚拟样机技术 戴维·陈是GM R&D虚拟样机(VP)的首席科学家,他的观点
值得考虑: ➢虚拟样机是一个方向,同时也是一个渐进过程; ➢产品设计的所有要求,用数学模型创建后,一定要验证,
用试验验证; ➢关键是建模(Creating Model),且应在专家指导下进行;
用adams进行仿真第六讲
m=5,k=2,c=1
用adams进行仿真第六讲
已知条件:假设系统处于零平衡位置,外力函数为幅 值为1 的阶跃函数。
一Matlab的简要介绍
在欧美大学里,诸如应用代数、数理统计、自 动控制、数字信号处理等等课程都把MATLAB作为 教学内容之一。
在国外发达国家MATLAB是攻读学位的大学生、 硕士生、博士生必须掌握的基本工具,这几乎成了 20世纪90年代新版教科书与旧版书籍的标志性区别。
在国际学术界,MATLAB已经被确认为准确的、 可靠的科学计算标准软件。
二、学习Matlab的意义
在设计研究单位和工业部门,MATLAB是公认 的进行高效研究、开发的首选软件工具。
学习MATLAB对于大学生将来毕业后开展工作 或进行进一步的学习,以及运用计算机解决工作、 生活中的实际问题都有着重要的意义。
三、Matlab的窗口和菜单
一、MATLAB的窗口组成 (1) Workspace(工作空间窗口):显示工作空间里 保存的所有变量。 (2) Current Directory(当前目录窗口):显示和管 理当前工作路径下文件夹的文件。 (3) Launch Pad(工具启动平台):此窗口显示 MATLAB工具目录,我们可以通过此窗口使用MATLAB 工具。
四、命令窗口的使用及基本命令
一、命令窗口的使用 在MATLAB的命令窗口直接输入命令、函数、 表达式,再按Enter键运行显示相应的结果。
命令窗口会在输入一条语句之后解释执行一条语 句,所以命令窗口非常适合运行比较简单或者单个的 命令、表达式、函数。
在命令窗口中按↑(↓)键可以查看前一条(后一条) 语句。
例15
求
A
2 0
5 6
4 3
5
1
的转置矩阵。
1
6 5
2
说明:矩阵转置运算的命令为’。
七、矩阵的介绍
判例断16A已是知否矩是阵对称矩阵。
第六章 线性规划及其解的实现
第六章 线性规划及其解的实现线性规划是目前应用最广泛的一种系统优化方法,它的理论和方法已十分成熟,可以应用于生产计划、物质调运、资源优化配置、地区经济规划等许多实际问题.线性规划最早由前苏联学者L V Kantorovich 于1939年提出,但他的工作当时并未为人所熟知.直到1947年,美国学者G B Danzing 提出求解线性规划最有效的算法-----单纯性算法后,才引起数学家、经济学家和计算机工作者的重视,并迅速发展成为一门完整的学科而得到广泛的应用.利用线性规划建立数学模型也是中国大学生数学建模竞赛中最常用的方法之一.优化模型的一般形式为T n Xx x x X X f z ),,,(),(min 21 == (1)m i X g t s i ,,2,1,0)(.. =≤ (2)其中)(x f 称为目标函数,)(X g i 称为约束条件.只满足式(2)的X 称为可行解;同时满足式(1)、式(2)两式的解*X X =称为最优解.由式(1)、式(2)组成的模型属于约束优化,若只有式(1)就是无约束优化.一般情况下,优化问题都是有约束的,但是如果最优解不是在可行域的边界上,而是在可行域的内部,那么就可以用无约束优化作比较简单的处理.若f ,i g 均为线性函数,优化模型式(1)、式(2)称为线性规划,否则称为非线性规划. 本章主要对线性规划问题及其解的实现作简要介绍.§6.1 线性规划模型形式及其性质线性规划是运筹学的一个重要分支,应用很广.线性规划问题可以描述为求一组非负变量,这些非负变量在一定线性约束的条件下,使一个线性目标函数取得极小(或极大)值的问题.1、线性规划的标准形式目标函数 n n x c x c x c z +++= 2211m in约束条件 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥=+++=+++=+++0,,,2122112222212111212111n mn mn m m n n n n x x x bx a x a x a b x a x a x a b x a x a x a这里n x x x ,,,21 是变量,i ij i b a c ,,都是已知常数,且0≥i b ,约束条件常用..t s 表示.线性规划用矩阵表示就是T n x x x X cX z ),,,(,min 21 ==T n n m ij b b b b n m a A x b AX t s ),,,(),()(,0,..21 =≤=≥=⨯.2、线性规划的一般形式 目标函数 n n x c x c x c z +++= 2211m in约束条件 ⎪⎪⎩⎪⎪⎨⎧+++++++++mn mn m m n n n n b x a x a x a b x a x a x a b x a x a x a )()()(22112222212*********式中的( )可以是关系符号:≤≥=<>,,,,中的任意一个.3、线性规划化为标准形的方法 把线性规划化为标准形:(1)目标函数一律化为求极小(如果是求极大,则利用)m in(m ax z z -⇔化为求极小).(2)对约束条件中b Ax ≤的不等式,利用加入松弛变量的方法化为等式.如果原约束条件中有""b ≥形式的约束,可以在不等式两边同时加负号化为""b -≤的形式.(3)标准形中一般要求0≥i x .如果某个i x 无此约束,可以引入两个新变量''',i i x x ,令'''i i i x x x -=,0,'''≥i i x x ;如果原来的约束为i i l x ≥,可以令i i i l x x -=',0'≥i x .4、线性规划的基本性质 线性规划有以下基本性质:1)若存在可行域,可行域必为凸集; 2)基可行解对应于可行域的顶点;3)若有最优解,必在可行域的顶点取得.§6.2 线性规划问题的数学模型及其解的基本概念1、线性规划问题的数学模型例1 (生产计划问题)某工厂生产甲、乙两种产品,甲产品每生产一件需耗黄铜2kg 、3个工作日、两个外协件,每件可获利润60元;乙产品每生产一件需耗黄铜4kg 、1个工作日、不需外协件,每件可获利润30元,该厂每月可供生产用的黄铜320kg ,总工作日180个,外协件100个.问应怎样安排生产才能使工厂的利润最高?分析问题,建立数学模型.问题:怎样安排生产,即甲、乙两种产品各生产多少才能使工厂的利润最高?用1x ,2x 分别表示甲、乙两种产品生产的件数,该厂追求的目标是获取最高利润,用数学表达式表示为:213060m axx x f +=.由于生产甲、乙产品的件数要受到生产能力的约束,即 黄铜约束:3204221≤+x x ,工作日约束:180321≤+x x , 外协件约束:10021≤x , 非负约束:0,21≥x x .这样,该厂生产计划问题就归结为如下数学模型:⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤++=.0,,1002,1803,32042..,3060max 211212121x x x x x x x t s x x f例2 (运输问题)计划由三个粮站1A ,2A ,3A 运输某种粮食至三个加工厂1B ,2B ,3B ,三个粮站的供应量和三个加工厂的需求量以及各供应地至需求地的单位运输价(元/t)如表1所示,试作出运费最省的调运计划方案.表 1问题:如何调运,才能使运费最省?设ij x 表示第i 个粮站到第j 个加工厂的粮食数量(单位:3,2,1,,=j i t ),则总运费3332312322211312112050603040709080120x x x x x x x x x f ++++++++=.从各粮站运出的粮食数量不能超过供应量,20131211=++x x x ,30232221=++x x x ,50333231=++x x x ,同时还要保证各加工厂的需要,25312111=++x x x ,50322212=++x x x ,25332313=++x x x ,而运输量应满足0≥ij x .则上述运输问题的数学模型为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=++=++=++=++=++=++++++++++=.0255025503020..2050603040709080120min 332313322212312111333231232221131211333231232221131211ij x x x x x x x x x x x x x x x x x x x t s x x x x x x x x x f从上述两个例子可以看出,虽然两个问题的具体内容和性质不同,但它们都属于优化问题,它们的数学模型都有相同的数学形式,即在一定的线性等式或不等式的条件下,使某一线性函数达到最大(或最小).所谓线性规划问题的数学模型是将实际问题转化为一组线性不等式获等式约束下求线性目标函数的最小(大)值问题.2、解的基本概念对于线性规划问题的标准形式..min ≥==x b Ax t s cx z 其中系数矩阵A 是行满秩的,即)()(n m m A R ≤=,并引入列向量),,2,1(n j P j =表示系数矩阵的列向量.满秩约束条件的解称为线性规划问题的可行解,可行解的全体}0,|{≥==x b Ax x D 称为线性规划问题的可行域.满足目标函数的可行解称为线性规划问题的最优解.系数矩阵A 的任意一个m 阶的可逆方阵B 称为线性规划问题的一个基.显然,A 最多有mn C 个基.基B 中的任意一列向量j P 称为基向量.系数矩阵A 中除基B 外的其余m n -个列向量称为非基向量.显然,选择的基不同,与基对应的非基向量也不尽相同.与基向量j P 对应的变量j x 称为基变量.与非基向量j P 对应的变量j x 称为非基变量.为叙述方便,不妨假设基B 是阵A 的前m 列构成的,即),,,(21m P P P B =,如若不然,则可通过调整变量顺序达到此目的.按上述定义,),,2,1(m j x j =为基变量,),,2,1(n m m j x j ++=为非基变量,记T m B x x x X ),,,(21 =,T n m m N x x x X ),,,(21 ++=,),,,(21n m m P P P N ++=那么约束条件可用分块矩阵表示为b X X N B N B =⎪⎪⎭⎫ ⎝⎛),(令0=N X ,由b BX B =得b B X B 1-= (3) 称⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=-01b B X X X N B为对应于基B 的基解.很显然,由于m B R =)(,即0||≠B ,所以式(3)的解是惟一的.即对应于某个基的基解是惟一的,从而一个线性规划问题最多有mn C 个基解.若基解满足0≥x ,则称基解为基可行解。
第六章控制系统参数优化及仿真
数学中的变分法,拉格朗日乘子法和最大值原理,动态规划等都是解析法,所以也都是间接寻优法。由于在大部分控制系统中目标函数J一般很难写出解析式,而只能在计算动态相应过程中计算出来,所以仿真中一般较少采用间接寻优方法。 (2) 直接寻优法 直接寻优法就是直接在变量空间搜索一组最佳控制变量(又称决策变量,设计变量)。这是一种数值方法,具体办法是,利用目标函数在一局部区域初始状态的性质和已知数值,来确定下一步计算的点,这样一步步搜索逼近,最后接近最优点。
6.1 参数优化与函数优化
优化技术是系统设计中带有普遍意义的一项技术,本节首先讨论优化技术中的一些基本定义和问题. 一、优化问题数学模型的建立 用优化方法解决实际问题一般分三步进行: (1) 提出优化问题,建立问题的数学模型。 (2)分析模型,选择合适的求解方法。 (3)用计算机求解,并对算法,误差,结果进行 评价。 显然,提出问题,确定目标函数的数学表达式是优化问题的第一步,在某种意义上讲也是最困难的一步。以下分别说明变量,约束和目标函数的确定。
第六章 控制系统参数优化及仿真
仿真是将已知系统在计算机上进行复现,它是分析,设计系统的一种重要实验手段。怎样才能使设计出来的系统在满足一定的约束条件下,使某个指标函数达到极值,这就需要优化的仿真实验。所以仿真技术与优化技术两者关系十分密切。
第六章 控制系统参数优化及仿真
优化技术包括内容很多,本章主要介绍与系统最优化技术有关的参数优化技术方法。 第一节首先对控制系统常用的优化技术做一概括性的叙述。 第二节介绍单变量技术的分割法和插值法。 第三节为多变量寻优技术,介绍工程中常用的最速下降法,共轭梯法和单纯形法。 第四节为随机寻优法。 第五节简单介绍具有约束条件的寻优方法。 第六节介绍含函数寻优的基本方法。 最后向读者介绍了Matlab优化工具箱的使用方法。
