武胜县2017初三数学适应题及答案
(完整word版)2017武汉元调数学试卷及答案(Word精校版)

第1页 / 共10页2016-2017学年度武汉市九年级元月调考数学试卷一、选择题(共10小题,每小题3分,共30分)1. 在数1,2,3和4中,是方程2120x x +-=的根的为 A .1 B .2 C .3 D .42. 桌上倒扣着背面图案相同的15张扑克牌,其中9张黑桃、6张红桃,则 A .从中随机抽取1张,抽到黑桃的可能性更大 B .从中随机抽取1张,抽到黑桃和红桃的可能性一样大 C .从中随机抽取5张,必有2张红桃 D .从中随机抽取7张,可能都是红桃3. 抛物线()2235y x =++的顶点坐标是A .(3,5)B .(-3,5)C .(3,-5)D .(-3,-5) 4. 在O 中,弦AB 的长为6,圆心O 到AB 的距离为4,则O 的半径为A .10B .6C .5D .45. 在平面直角坐标系中,有A (2,-1),B (-1,-2),C (2,1),D (-2,1)四点,其中,关于原点对称的两点为 A .点A 和点B B .点B 和点C C .点C 和点D D .点D 和点A6.方程28170x x -+=的根的情况是( )A . 两实数根的和为8-B . 两实数根的积为17C . 有两个相等的实数根D . 没有实数根7.抛物线2(2)y x =--向右平移2个单位得到的抛物线的解析式为( )A . 2y x =- B . 2(4)y x =-- C . 2(2)2y x =--+ D . 2(2)2y x =---8.由所有到已知点O 的距离大于或等于3,并且小于等于5的点组成的图形的面积为( ) A .4π B .9π C .16π D .25π 9.在50包型号为L 的衬衫的包裹中混入了型号为M 的衬衫,每包20件衬衫.每包中混入的M 号衬衫数如下表:A. M 号衬衫一共有47件B. 从中随机取一包,包中L 号的衬衫数不低于9是随机事件C. 从中随机取一包,包中L 号衬衫不超过4的概率为0.26D. 将50包衬衫混合在一起,从中随机拿出一件衬衫,恰好是M 号的概率是0.252第2页 / 共10页10.在抛物线223y ax ax a =--上有A (-0.5,1y ),B (2,2y )和C (3,3y )三点,若抛物线与y 轴的交点在正半轴上,则1y ,2y ,3y 的大小关系为( )A .312y y y <<B .321y y y <<C .213y y y <<D .123y y y <<二.填空题(共6小题,每小题3分,共18分) 11.掷一枚质地不均匀的骰子,做了大量的重复试验,发现“朝上一面为6点”出现的频率越来越稳定于0.4,那么,掷一次该骰子,“朝上一面为6点”的概率为12.如图,四边形ABCD 内接于○O ,E 为CD 延长线上一点,若∠B =110°,则∠ADE 的度数为 13.两年前生产1t 药品成本是6000元,现在生产1t 药品的成本是4860元,则药品成本的年平均下降率是第12题图第15题图14.圆心角为75°的扇形弧长是2.5π,则扇形的半径为15.如图,正三角形的边长为12cm ,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为 cm .16.在平面直角坐标系中,点C 沿着某条路径运动,以点C 为旋转中心,将点A (0,4)逆时针旋转90°到点B (m ,1),若-5≤m ≤5,则点C 运动的路径长为三.解答题(共8小题,共72分) 17.(本题8分)解方程2530x x -+=第3页 / 共10页18.(本题8分)如图,OA ,OB ,OC 都是☉O 的半径,∠AOB =2∠BO C . (1)求证:∠ACB =2∠BAC (2)若AC 平分∠OAB ,求∠AOC 的度数.19.(本题8分)如图,要设计一幅宽20cm ,长30cm 的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3,如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm ?第19题图20.(本题8分)阅读材料,回答问题.材料题1:经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性的大小相同,求三辆汽车经过这个十字路口时,至少有两辆车向左转的概率.题2:有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁(一把钥匙只能开一把锁),第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?我们可以用“袋中摸球”的试验来模拟题1:在口袋中放三个不同颜色的小球,红球表示直行,绿球表示向左转,黑球表示向右转;三辆汽车经过路口,相当于从三个这样的口袋中各随机摸一个球. 问题(1)事件“至少有两辆车向左转”相当于”袋中摸球”的试验中的什么事件? (2)设计一个“袋中摸球”的试验模拟题2,请简要说明你的方案; (3)请直接写出题2的结果.第18题图第4页 / 共10页21.(本题8分) 如图,在Rt △ABC 中,∠BAC =90°,BD 是角平分线,以点D 为圆心,DA 为半径的圆D 与AC 相交于点E .(1)求证:BC 是圆D 的切线; (2)若AB =5,BC =13,求CE 的长.22.(本题10分)某公司产销一种商品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C 是商品件数x商品的销售价格(单位:元)为P =35—x 101.(每个周期的产销利润=P x C ⋅-) (1)直接写出产销成本C 与商品件数x 的函数关系式(不要求写出自变量的取值范围); (2)该公司每个周期产销多少件商品时,利润达到220元? (3)求该公司每个周期的产销利润的最大值.23.(本题10分)如图,在平面直角坐标系中,点A和点B的坐标分别为A(4,0),B(0,2),将△ABO绕点P(2,2)顺时针旋转得到△OCD,点A,B和O的对应点分别为O,C和D.(1)画出△OCD,并写出点C和点D的坐标;(2)连接AC,在直线AC的右侧取点M,使∠AMC=45°.①若点M在x轴上,则点M的坐标为___________;②若△ACM为直角三角形,求点M的坐标;(3)若点N满足∠ANC>45°,请确定点N的位置(不要求说明理由).第5页 / 共10页第6页 / 共10页24. (本题12分)已知抛物线y =221x +mx -2m -2(m ≥0)与x 轴交于A ,B 两点,点A 在点B 的左边,与y 轴交于点C . (1)当m =1时,求点A 和点B 的坐标; (2)抛物线上有一点D (—1,n ),若△ACD 的面积为5,求m 的值;(3)P 为抛物线上A ,B 之间一点(不包括A ,B ),PM ⊥x 轴于M ,求PMBMAM ·的值.第7页 / 共10页2016-2017学年度武汉市部分学校九年级元月调考数学试卷参考答案10. 又∵∴二.16.C 点的轨迹是点(-1,0)和点(4,5)之间的一条线段.所以C 点运动的路径长为三.解答题(共8小题,共72分) 17.解:a =1,b =﹣5,c =3, ∴b 2-4ac =13∴x =5±132∴x 1=5-132 ,x 2=5+13218.(1)证明:在⊙O 中,∵∠AOB =2∠ACB ,∠BOC =2∠BAC , ∵∠AOB =2∠BO C . ∴∠ACB =2∠BA C . (2)解:设∠BAC =x °.∵AC 平分∠OAB ,∴∠OAB =2∠BAC =2x °; ∵∠AOB =2∠ACB ,∠ACB =2∠BAC , ∴∠AOB =2∠ACB =4∠BAC =4x °; 在△OAB 中,∠AOB +∠OAB +∠OBA =180°, 所以,4x +2x +2x =180; x =22.5第18题图第8页 / 共10页所以∠AOC =6x =135°19.解:设横彩条的宽为2xcm ,竖彩条的宽为3xcm .依题意,得(20-2x )(30-3x )=81%×20×30. 解之,得x 1=1,x 2=19,当x =19时,2x =38>20,不符题意,舍去. 所以x =1.答:横彩条的宽为2 cm ,竖彩条的宽为3 cm .20.解:(1)至少摸出两个绿球; (2)一口袋中放红色和黑色的小球各一个,分别表示不同的锁;另一口袋中放红色、黑色和绿色的小球各一个,分别表示不同的钥匙;其中同颜色的球表示一套锁和钥匙.“随机取出一把钥匙开任意一把锁,一次打开锁的概率” ,相当于,“从两个口袋中各随机摸出一个球,两球颜色一样的概率”;(3)1321.(1)证明:过点D 作DF ⊥BC 于点F . ∵∠BAD =90°,BD 平分∠ABC , ∴AD =DF . ∵AD 是⊙D 的半径,DF ⊥BC , ∴BC 是⊙D 的切线(2) 解:∵∠BAC =90°.∴AB 与⊙D 相切, ∵BC 是⊙D 的切线,∴AB =F B .∵AB =5,BC =13, ∴CF =8,AC =12. 在Rt △DFC 中, 设DF =DE =r ,则 r 2+64=(12-r )2,r =103 .∴CE =16322.解:(1)2138010C x x =++(2) 依题意,得(35-110x )·x -(110x 2+3x +80)=220;解之,得x 1=10,x 2=150, 因为每个周期产销商品件数控制在100以内, 所以x =10. 答:该公司每个周期产销10件商品时,利润达到220元 (3) 设每个周期的产销利润为y 元.则y =(35-110x )·x -(110 x 2+3x +80)=﹣15 x 2+32x -80=﹣15 (x -80)2+1200,C第9页 / 共10页因为﹣15<0,所以,当x =80时,函数有最大值1200.答:当每个周期产销80件商品时,产销利润最大,最大值为1200 元23. (1)C (2,4),D (0,4) (2)①M (6,0)②第1种情况:当∠CAM =90°,C (2,4),A (4,0) ∴△CAM 为等腰直角三角形过C 作CH ⊥x 轴于H ,过M 作MG ⊥x 轴于G , ∴△CHA ≌△AGM (AAS )、 ∴AG =CH =4,MG =AH =4-2=2 ∴M (8,2)第二种情况:当∠ACM =90°时,同理可得,M (6,6)(3)N 点在以(5,3)(1,1).(阴影部分)24. 解:(1)当1m =时,2142y x x =+-令0y =,21402x x +-= ∴124,2x x =-= ∴()4,0,(2,0)A B -(2)令212202x mx m +--=即222244x mx m m m ++=++()()()2212222,2022x m m x m x C m OA OC+=+∴=--=-∴=,-∴直线:22AC y x m =---第10页 / 共10页点()1,D n -在抛物线上,∴31,32D m ⎛⎫--- ⎪⎝⎭过点D 作DM ⊥x 轴于点M ,交AC 于点E过点C 作CN ⊥DE 点M .则点()1,21E m ---()()()2123121322112212112252223903;32ACD DE m m m S DE AM DE CNDE AOm m m x m m ⎛⎫∴=-----=+⎪⎝⎭=⋅+⋅=⋅⎛⎫=++= ⎪⎝⎭∴+-=∴==-舍 所以,满足题意m 的值为32(3)设P 点坐标21,222a a am m ⎛⎫+-- ⎪⎝⎭则AM =a +2m +2BM =2-aPM =21222a am m --++()()22222222122224242=122224412222a m a AM BM PM a am m a a m am a a am m a am m a am m ++-⋅=--++-+-+---++--++=--++=(。
2017年安徽中考数学试题(word版-含答案)
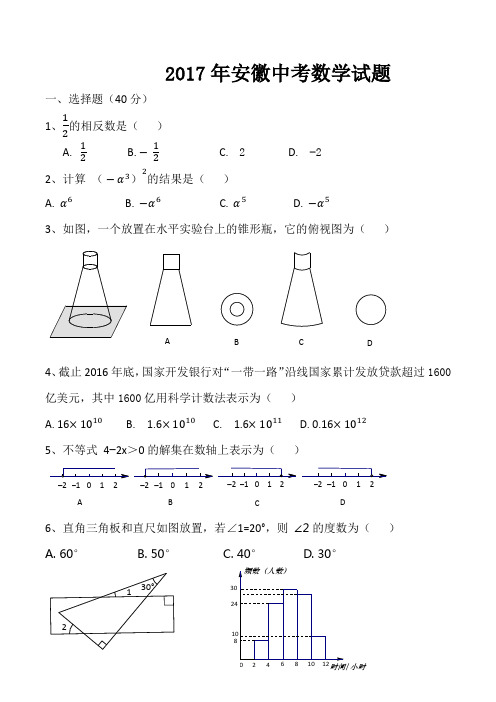
2017年安徽中考数学试题一、选择题(40分) 1、12的相反数是( )A. 12B. −12C. 2D. −22、计算 (−α3)2的结果是( )A. α6B. −α6C. α5D. −α53、如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )4、截止2016年底,国家开发银行对“一带一路”沿线国家累计发放贷款超过1600亿美元,其中1600亿用科学计数法表示为( )A. 16×1010B. 1.6×1010C. 1.6×1011D. 0.16×1012 5、不等式 4−2x >0的解集在数轴上表示为( )6、直角三角板和直尺如图放置,若∠1=20°,则 ∠2的度数为( ) A. 60° B. 50° C. 40° D. 30°DC B A DCBA12–1–2012–1–2012–1–2012–1–2030°21小时7、为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数直方图.已知该校共有1000名学生,据此估计,该校五一期间参加社团时间在8~10 小时之间的学生数大约是( )A. 280B. 240C. 300D. 2608、一种药品原价每盒25元,经过两次降价后每盒16元,设两次降价的百分比都为x ,则x 满足( )A. 16(1+2x )=25B. 25(1−2x )=16C. 16(1+x )2=25 D. 25(1−x )2=169、已知抛物线 y =αx 2+bx +c 与反比例函数y =b x的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac 的图象可能是( )10、如图,在矩形ABCD 中,AB=5,AD=3.动点P 满足S △PAB =13S 矩形ABCD .则点P 到A 、B 两点距离之和PA+PB 的最小值是( ) A. √29 B. √34 C. 5√2 D. √41二、填空题(20分)DCBAPD CBA11、27的立方根是 .12、因式分解:α2b −4αb+4b= .13、如图,已知等边△ABC 的边长为6,AB 为直径的⊙O 与边AC ,BC 分别交于D 、E 两点,则劣弧DE 长为 .14、在三角形纸片ABC 中,∠A =90°,∠C =30°,AC=30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1)剪去△CDE 后得到双层△BDE (如图2)再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个平行四边形,则所得平行四边形的周长为 cm.三、解答题(共90分:其中15~18每题8分共32分;19,20每题10分共20分;21,22每题12分共24分;23题14分) 15、计算 │−2│×cos60° −(13)−116、《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三,人出七,不足四。
2017年武胜县适应性考试

2017年适应性考试化学试卷(时间:60分钟满分:50分)可能用到的相对原子质量:H-1 C-12 O-16 N-14 Cl-35.5 Ag-108第Ⅰ卷(选择题共18分)一、选择题(下面各题给出的四个选项中,只有一个符合题意,请将正确选项填在相应的位置,每小题1.5分,共12小题,满分18分)1.下列物质中属于纯净物的是()A.不锈钢钉 B.稀盐酸 C.纯净的氧气 D.矿泉水2.下列洗涤方法主要利用物质化学性质的是()A.工业上分离液态空气制取氧气、氮气 B.食醋洗去水壶内的水垢C.清水洗涤衣服上的食盐 D.汽油洗涤衣服上的油迹3.推理是一种重要的学习方法,下列推理正确的是()A.在化合物里,正负化合价的代数和为零,所以在同一化合物中金属元素显正价,则非金属元素一定都显负价B.碳酸盐与稀盐酸反应生成气体,所以与稀盐酸反应生成气体的物质一定是碳酸盐C.碱能使酚酞溶液变红,所以使酚酞溶液变红的物质一定是碱D.在化学反应中,一氧化碳和氢气都能夺取氧化铜中的氧,所以一氧化碳和氢气都具有还原性4.下列实验操作正确的是()A.用过氧化氢制取氧气B.过滤C.称量固体D.倾倒二氧化碳5.今年在我县发生了多起人感染H7N9禽流感病例,临床试验数据证明,抗流感新药帕拉米韦氯化钠注射液对H7N9禽流感患者具有显著的治疗作用,下列关于帕拉米韦(C15H28N4O4)的说法正确的是()A.属于无机化合物 B.一个分子中含2个氧分子C.C、H、N、O元素的质量比为15:28:4:4 D.组成元素中,碳元素的质量分数最大6.在一个密闭容器中放入甲、乙、丙、丁四种物质,在一定条件下发生化学反应,一段时间后,测定部分数据如下表:物质甲乙丙丁反应前质量/g 18 1 2 32反应后质量/g X 26 2 12下列说法中,不正确的是()A.反应后物质甲的质量为13g B.乙是生应物C.参加反应的甲和乙的质量比为1:4 D.物质丙可能是该反应的催化剂7.甲、乙两种固体的溶解度曲线如下图所示,下列说法中正确的是()A.20℃时,甲溶液中溶质的质量分数一定大于乙溶液B.40℃时,分别在100g水中加入50g甲、乙,所得溶液中溶质的质量分数相等C.40℃时,分别在100g水中加入30g甲、乙,同时降温至20℃,甲、乙溶液均为饱和溶液D.20℃时,分别在100g水中加入40g甲、乙,加热到40℃时,甲溶液为饱和溶液8.化学与生活密切相关,下列说法不正确的是()A.人体缺铁会导致甲状腺肿大 B.食用牛奶可为人体补充蛋白质C.电器起火时应立即切断电源 D.蒸馏可以将硬水转化为软水9. 除去下列物质中混有少量杂质(括号内为杂质),所选用试剂及操作方法均正确的是()选择物质选用试剂操作方法A CO2(CO) 过量O2点燃B CaO(CaCO3) 足量蒸馏水过滤、蒸发C MnO2(KCl) 适量AgNO3溶液过滤D FeCl2溶液(CuCl2溶液) 足量铁粉过滤10.“低碳生活”简言之就是降低二氧化碳的排放,就是低能量、低消耗、低开支的生活方式。
江西省2017年中考数学试卷(图片版,含答案)

王老师编辑整理 王ห้องสมุดไป่ตู้师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
王老师编辑整理 王老师编辑整理
2017年浙江省绍兴市中考数学适应性试题含答案

D.当∠ ABC=90°时,它是矩形
7.已知关于 x 的一元二次方程 x2 5x p 0( p 是常数 )的一个实数根是 1 ,则二次函数
y x2 5x p 的图像与 x 轴的交点坐标为 (
)
A. (1,0) 、 (- 1,0)
B.(1,0) 、 (- 6,0)
C.(1,0) 、 (5,0)
D.(1,0) 、 (4,0)
图所示的频数分布直方图,则参加书法兴趣小组的频率是
(
)
A . 0.15
B . 0.2
C. 0.1
D. 0.3
第 5 题图
第 8 题图
第 9 题图
6.已知四边形 ABCD 是平行四边形,下列结论中不正.确..的是 (
)
A .当 AB=BC 时,它是菱形
B.当 AC=BD 时,它是正方形
C.当 AC⊥ BD 时,它是菱形
的长是 __▲ ____.
第 12 题图
第 13 题图 1
第 13 题图 2
13.如图 1 所示的晾衣架, 支架主视图的基本图形是菱形, 其示意图如图 2,晾衣架伸缩时,
点 G 在射线 DP 上滑动,∠ CED 的大小也随之发生变化,已知每个菱形边长均等于
30cm,
且 AH=DE=EG=30cm.当∠ CED 由 90°变为 120°时, 点 A 向左移动了 ▲ cm(结果保留根
k y= x (x>0)
16. ABCD 中,已知 AB 2 3 ,∠B=30°,将△ ABC 沿 AC 翻折至△ AB′C,连结 B′D.若
△AB′D是直角三角形,则 BC 长为 _____▲ ___. 三、解答题:
17.( 1)计算: 3tan 300 (
2017年安徽中考数学试题(word版-含答案)

2017年安徽中考数学试题(word 版-含答案)2017年安徽中考数学试题一、选择题(40分) 1、12的相反数是( )A. 12B. −12C. 2D. −2 2、计算 (−α3)2的结果是( )A. α6B. −α6C. α5D. −α53、如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )4、截止2016年底,国家开发银行对“一带一路”沿线国家累计发放贷款超过1600亿美元,其中1600亿用科学计数法表示为( )A. 16×1010B. 1.6×1010C. 1.6×1011D. 0.16×1012 5、不等式 4−2x >0的解集在数轴上表示为( )6、直角三角板和直尺如图放置,若∠1=20°,则 ∠2的度数为( ) A. 60° B. 50° C. 40° D. 30°DC B A DCBA12–1–2012–1–2012–1–2012–1–2030°21频数(人数)小时107、为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数直方图.已知该校共有1000名学生,据此估计,该校五一期间参加社团时间在8~10 小时之间的学生数大约是( )A. 280B. 240C. 300D. 2608、一种药品原价每盒25元,经过两次降价后每盒16元,设两次降价的百分比都为x ,则x 满足( )A. 16(1+2x )=25B. 25(1−2x )=16C. 16(1+x )2=25 D. 25(1−x )2=169、已知抛物线 y =αx 2+bx +c 与反比例函数y =b x的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac 的图象可能是( )10、如图,在矩形ABCD 中,AB=5,AD=3.动点P 满足S △PAB =13S 矩形ABCD .则点P 到A 、B 两点距离之和PA+PB 的最小值是( ) A. √29 B. √34 C. 5√ D. √二、填空题(20分)yxyxyx yx DCBAOO O OPD CBA11、27的立方根是 .12、因式分解:α2b −4αb+4b= .13、如图,已知等边△ABC 的边长为6,AB 为直径的⊙O 与边AC ,BC 分别交于D 、E 两点,则劣弧DE 长为 .14、在三角形纸片ABC 中,∠A =90°,∠C =30°,AC=30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1)剪去△CDE 后得到双层△BDE (如图2)再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个平行四边形,则所得平行四边形的周长为 cm.三、解答题(共90分:其中15~18每题8分共32分;19,20每题10分共20分;21,22每题12分共24分;23题14分) 15、计算 │−2│×cos60° −(13)−116、《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三,人出七,不足四。
江西省2017年中考数学真题试题(含扫描答案)
江西省2017年中等学校招生考试数学试题卷一、选择题(本大题共6个小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.-6的相反数是( ) A.16 B.16- C. 6 D.-6 2. 在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km ,将13000用科学记数法表示应为( ) A.50.1310⨯ B. 41.310⨯ C.51.310⨯ D.31310⨯ 3.下列图形中,是轴对称图形的是( )A. B. C. D.4. 下列运算正确的是( ) A.()2510a a -= B.22236a a a = C. 23a a a -+=- D.623623a a a -÷=-5.已知一元二次方程22510x x -+=的两个根为12,x x ,下列结论正确的是( ) A. 1252x x +=-B.121x x = C. 12,x x 都是有理数 D.12,x x 都是正数 6. 如图,任意四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 上的点,对于四边形EFGH 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )A.当,,,E F G H 是各边中点,且AC BD =时,四边形EFGH 为菱形 B.当,,,E F G H 是各边中点,且AC BD ⊥时,四边形EFGH 为矩形 C. 当,,,E F G H 不是各边中点时,四边形EFGH 可以为平行四边形 D.当,,,E F G H 不是各边中点时,四边形EFGH 不可能为菱形二、填空题(本大题共6小题,每小题3分,满分18分,将答案填在答题纸上)7. 函数y =x 的取值范围是___________.8. 如图1是一把园林剪刀,把它抽象为图2,其中OA OB =,若剪刀张开的角为30°,则A ∠=_________度.9. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为___________.10.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是_____________.11.已知一组从小到大排列的数据:2,5,x ,y ,2x ,11的平均数与中位数都是7,则这组数据的众数是______________.12.已知点()()()0,4,7,0,7,4A B C ,连接,AC BC 得到矩形AOBC ,点D 的边AC 上,将边OA 沿OD 折叠,点A 的对应边为A ',若点A '到矩形较长两对边的距离之比为1:3,则点A '的坐标为____________. 三、解答题 (本大题共5小题,每小题6分,共30分.解答应写出文字说明、证明过程或演算步骤.) 13.(1)计算:21211x x x +÷--; (2)如图,正方形ABCD 中,点,,E F G 分别在,,AB BC CD 上,且090EFG ∠=. 求证:EBF FCG ∆∆ .14.解不等式组:()26324x x x -<⎧⎨-≤-⎩,并把解集在数轴上表示出来.15.端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出的两个都是蜜枣粽的概率.16.如图,已知正七边形ABCDEFG ,请仅用无刻度的直尺,分别按下列要求画图. (1)在图1中,画出一个以AB 为边的平行四边形; (2)在图2中,画出一个以AF 为边的菱形.17. 如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB 水平,且与屏幕BC 垂直.(1)若屏幕上下宽20BC cm =,科学使用电脑时,求眼睛与屏幕的最短距离AB 的长;(2)若肩膀到水平地面的距离100DG cm =,上臂30DE cm =,下臂EF 水平放置在键盘上,其到地面的距离72FH cm =.请判断此时β是否符合科学要求的100°? (参考数据:00001414414sin 69,cos 21,tan 20,tan 4315151115≈≈≈≈,所有结果精确到个位)四、(本大题共3小题,每小题8分,共24分).18. 为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.种类 A B C D E出行方式 共享单车 步行 公交车 的士 私家车根据以上信息,回答下列问题:(1)参与本次问卷调查的市民共有___________人,其中选择B类的人数有_____________人;(2)在扇形统计图中,求A类对应扇形圆心角 的度数,并补全条形统计图;A B C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出(3)该市约有12万人出行,若将,,行”方式的人数.19.如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:单层部分的长度x(... 4 6 8 10 (150)cm )y cm… 73 72 71 …双层部分的长度()(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;(2)根据小敏的身高和习惯,挎带的长度为120cm 时,背起来正合适,请求出此时单层部分的长度; (3)设挎带的长度为lcm ,求l的取值范围.20. 如图,直线()10y k x x =≥与双曲线()20k y x x=>相交于点()2,4P .已知点()()4,0,0,3A B ,连接AB ,将Rt AOB ∆沿OP 方向平移,使点O 移动到点P ,得到A PB ''∆.过点A '作//A C y '轴交双曲线于点C.(1)求k 与k 的值;12(2)求直线PC 的表达式;(3)直接写出线段AB 扫过的面积.五、(本大题共2小题,每小题9分,共18分).21.如图1,O 的直径12,AB P =是弦BC 上一动点(与点,B C 不重合),030ABC ∠=,过点P 作PD OP ⊥交O 于点D .(1)如图2,当//PD AB 时,求PD 的长;(2)如图3,当 DCAC =时,延长AB 至点E ,使12BE AB =,连接DE . ①求证:DE 是O 的切线; ②求PC 的长.22.已知抛物线()21:450C y ax ax a =-->.(1)当1a =时,求抛物线与x 轴的交点坐标及对称轴;(2)①试说明无论a 为何值,抛物线1C 一定经过两个定点,并求出这两个定点的坐标; ②将抛物线1C 沿这两个定点所在直线翻折,得到抛物线2C ,直接写出2C 的表达式; (3)若(2)中抛物线2C 的顶点到x 轴的距离为2,求a 的值. 六、(本大题共12分)23. 我们定义:如图1,在ABC ∆看,把AB 点A 顺时针旋转()000180αα<<得到AB ',把AC 绕点A逆时针旋转β得到AC ',连接B C ''.当0180αβ+=时,我们称A B C '''∆是ABC ∆的“旋补三角形”,∆AB C ''边B C ''上的中线AD 叫做∆ABC 的“旋补中线”,点A 叫做“旋补中心”.特例感知:(1)在图2,图3中,∆AB C ''是∆ABC 的“旋补三角形”,AD 是∆ABC 的“旋补中心”.①如图2,当∆ABC 为等边三角形时,AD 与BC 的数量关系为AD =BC ;_____________②如图3,当∠BAC =900,BC =8时,则AD 长为_________________.猜想论证:(2)在图1中,当ABC ∆为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.拓展应用(3)如图4,在四边形ABCD ,0090,150,12C D BC ∠=∠==,6CD DA ==.在四边形内部是否存在点P ,使PDC ∆是PAB ∆的“旋补三角形”?若存在,给予证明,并求PAB ∆的“旋补中线”长;若不存在,说明理由.。
2017—2018学年人教版九年级上数学9月测试卷含答案
2017—2018学年第一学期 九 年级 数学 科9月测试考试时间 60分钟 满分 100分2017. 10第Ⅰ卷 A 卷 (选择题)一、选择题(每题3分,共39分)1.抛物线()223y x =++的顶点坐标是 ( )A.(-2,3)B.(2,3)C.(-2,-3)D.(2,-3)2、抛物线23x y -=经过平移得到抛物线2)1(32-+-=x y ,平移的方法是( ) A .向左平移1个,再向下平移2个单位 B .向右平移1个,再向下平移2个单位 C .向左平移1个,再向上平移2个单位 D .向右平移1个,再向上平移2个单位 3.二次函数2(0)y ax bx c a =++≠的图象如右图,当0y <时,x 的取值范围是( ) A .13x -<< B .3x > C .1x <- D .3x >或1x <- 4、下列关于抛物线221y x x =--+的描述不正确的是( )A 、对称轴是直线x=14-B 、函数y 的最大值是78C 、与y 轴交点是(0,1)D 、当x=1-时,y=05.二次函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )A .3<kB .03≠<k k 且C .3≤kD .03≠≤k k 且6.若点(2,5),(4,5)是抛物线c bx ax y ++=2上的两个点,则抛物线的对称轴是( ) A .直线1=x B .直线2=x C .直线3=x D .直线4=x 7、如果二次函数c bx ax y ++=2(a>0)的顶点在x 轴的上方,那么( )A 、240b ac -≥ B 、240b ac -< C 、240b ac -> D 、240b ac -= 8. 用配方法将2611y x x =-+化成2()y a x h k =-+的形式为( ).A .2(3)2y x =++错误!未找到引用源。
