加州大学伯克莱分校(UCB)核工系相关课程习题9
麻省理工学院(MIT)相关课程习题7

22.312核反应堆工程2004年秋2004年12月14日,星期二,下午1:30 –下午4:30,24-121房间开卷期末试卷3小时问题#1(55%)-一个压水堆稳压器的结构和热工水力分析a)薄圆柱容器的总薄膜应力可以根据如下式子得到:因此总薄膜应力P m为,ASME规范要求b)以稳压器为一个控制体,根据质量守恒方程可以得到最终稳压器内的冷却剂质量M2:其中,,M1可以根据初始液体和蒸汽的体积和密度(见问题的表1)很容易得到。
能量平衡方程(忽略重力项和动能项)为:其中,h f(=1631kJ/kg)是离开稳压器的水的比焓,Q是稳压器的总加热量,可以根据初始条件得到。
最终内能U2是:其中,x2是稳压器内最终的含汽率(未知)。
另外,稳压器的体积Vp在瞬态过程中保持不变,因此有方程1,2,3,4构成了4个未知数(即M2,U2,Q和x2)的方程组,可联立求解得到Q。
c)1.b的答案与过程的持续时间无关。
只与系统地初始状态和最终状态有关。
d)总释热功率Q(=3MW)与热流密度的关系为:,因此加热器的最小长度为:其中d=1cm,根据沸腾曲线,a)临界热流密度随着压力的降低而增大,随着压力的增大而减小(见核系统,第一卷,527页图12-3),因此如果稳压器内电加热器满功率的情况下压力突然降低,判断不发生沸腾临界的条件还能满足,需要看压力降低的幅度,例如压力降低到10MPa,不会发生沸腾临界,因为10MPa下的临界热流密度比15.5MPa下的值要高。
问题#2(35%)——隔离冷凝器内的空泡分额和压降计算a)(5%)计算冷凝器的排热功率。
(280o C下饱和水参数见表2)b)(5%)用后面给出的简化Chato关系式计算传热管内表面的温度。
(假设传热管内轴向热流密度均匀分布)c)(10%)画出传热管内轴向空泡分额分布图。
(假设管内含气率线性变化,用平衡态均匀流HEM模型计算空泡分额)d)(10%)计算传热管内加速压降,摩擦压降,提升压降和总压降。
原子核物理(卢希庭)课后习题答案全

原子核物理(卢希庭)课后习题答案全<i>答案第一二章很全,后面章节也较多</i>第一章习题1-1 A 利用课本上的公式AZ BA, B已知(书上第四页) E h (其中h是常数为 .63 1034 ) 6B 上课讲的公式<i>答案第一二章很全,后面章节也较多</i>2-2质谱仪工作原理1 2 M qV (1) 2 M 2 q B ( 2) R q 2V qB 2 R 22 2 即M M B R 2V 由,1 2可以解出M A 1.66 10 27<i>答案第一二章很全,后面章节也较多</i>1-31 2 M qV 2 2 M q B R 2VM R 2 qB 2V1M 1 2 q1 B1 2V2 M 2 2 q2 B2<i>答案第一二章很全,后面章节也较多</i>4 1-4, 计算下列各核的半径:He, 2107 47Ag,238 92U, 设r0 1.45 fm.解:由R r0 A 3知,对于He,R 1.45 44 2 1 31fm 2.33 fm1 3对于对于107 47 238 92Ag,R 1.45 107 U,R 1.45 2381fm 6.88 fm fm 8.99 fm31-5, 实验测得241 Am和243 Am的原子光谱的超精细结构由六条谱线., 解:由已知条件知原子的总角动量量子数可以取6个值又电子总角动量j核的自旋I 5 2 5 2已知相应原子能级的电子角动量大于核的自旋,试求241 Am和243 Am核的自旋。
2I 1 6 I即241 Am和243 Am核的自旋为<i>答案第一二章很全,后面章节也较多</i>原子209 Bi的谱线2 D3 分裂成四条子能级,相邻能级的间距比为:4,求核的自旋值6 5: I2以及谱线2 S 1 和2 D3 分裂的能级总数。
大学精品课件:chapter 9(Heat Transfer.J.P.Holman )

9-1 introduction
• The heat transfer convection we discussed before is considered homogeneous singlephase systems. For convection associated with a change of phase of fluid .usually we deal with two conditions.
Dropwise condensation: the liquid can’t wet the surface, droplets formed on the surface , the surface is not completely covered by the liquid , and when droplets goes down ,they can take many droplets in their way with them , so dropwise condensation has no film barrier for heat flow , and its heat transfer rates may be as much as 10 times higher than film condensation.
viscous shear of the vapor on the film is negligible at the edge with vapor; pure vapor , constant property . Only convection in the film , the temperature distribution inside the film between the wall and vapor is linear; The state of the film is still . and the thickness of film is very small , the velocity of the fluid is very slow.
麻省理工学院(MIT)相关课程习题6
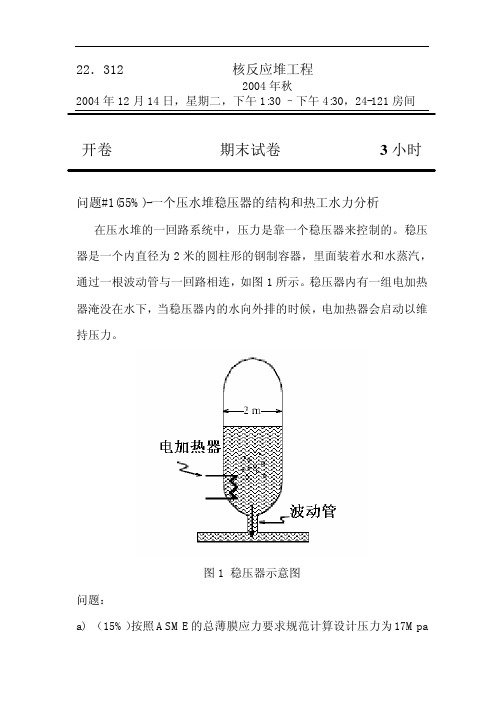
22.312核反应堆工程2004年秋2004年12月14日,星期二,下午1:30 –下午4:30,24-121房间开卷期末试卷3小时问题#1(55%)-一个压水堆稳压器的结构和热工水力分析在压水堆的一回路系统中,压力是靠一个稳压器来控制的。
稳压器是一个内直径为2米的圆柱形的钢制容器,里面装着水和水蒸汽,通过一根波动管与一回路相连,如图1所示。
稳压器内有一组电加热器淹没在水下,当稳压器内的水向外排的时候,电加热器会启动以维持压力。
图1 稳压器示意图问题:a)(15%)按照ASME的总薄膜应力要求规范计算设计压力为17Mpa的稳压器圆柱部分的最小壁面厚度。
(在本题的温度范围内,最大许用应力强度为Sm=184MPa,可用薄壳近似计算应力)b)(20%)假设有3500kg水流出稳压器,为了维持15.5MPa的额定压力,写出计算总加热量的完整方程组。
(假设此过程中保持热力平衡,稳压器的初始条件和相关15.5MPa下的热力参数见表1,解释所有假设均蕴含在你的计算中)c)(5%) 1.b的答案与过程的持续时间有关吗?做必要的解释。
d)(10%) 电加热器包含30个1cm粗的圆柱形热阻,总释热功率为3MW。
在电加热器表面CHF的限制不能超过,试计算满足要求的加热器最小长度。
(15.5MPa的池式沸腾曲线见图2)e)(5%) 如果在电加热器满功率的情况下,稳压器突然降压到10MPa,请问问题“d”中不发生沸腾临界的条件还能满足吗?解释之。
问题#2(35%)——隔离冷凝器内的空泡分额和压降计算一个现代沸水堆采用一个隔离冷凝器来移出一台给水泵失效触发停堆情况下堆内的停堆衰变余热,隔离冷凝器接收50kg/s的280o C 蒸汽并完全把它冷凝。
隔离冷凝器包括200根内直径为3cm,长度为12m的水平圆管,蒸汽在管内流动(图3所示),管子泡在一个大气压的水中。
问题:a)(5%)计算冷凝器的排热功率。
(280o C下饱和水参数见表2)b)(5%)用后面给出的简化Chato关系式计算传热管内表面的温度。
核技术利用辐射安全与防护考核题库全考点

核技术利用辐射安全与防护考核题库全考点一、单选题1、()年,威廉•康拉德•伦琴发现了X射线。
A.1901B.1896C.1898D.1895【答案】D【解析】1895年,德国物理学家威廉•康拉德•伦琴在做电子管实验时,发现了X射线。
2、1895年,()发现了X射线。
A・亨利•贝克勒尔B.玛丽•思克多夫斯卡•居里C.威廉•康拉德•伦琴D.卢瑟福【答案】C【解析】1895年,德国物理学家威廉•康拉德•伦琴在做电子管实验时,发现了X射线。
3、1896年,O发现了天然放射性现象。
A・亨利•贝克勒尔B.玛丽•思克多夫斯卡•居里C.威廉•康拉德•伦琴D.卢瑟福【答案】A【解析】1896年,法国科学家亨利・贝克勒尔在研究铀矿荧光现象的过程中,铀矿物能发射出穿透力很强并能使照相底片感光的不可见的射线。
这种现象被称为放射性,放射性活度单位用贝克(Bq)表示。
4、1898年,O第一个提出了放射性术语。
A.亨利・贝克勒尔B.玛丽•思克多夫斯卡•居里C.威廉•康拉德•伦琴D.卢瑟福【答案】B【解析】1898年,居里夫妇发现镭元素,玛丽•思克多夫斯卡•居里做了进一步研究,第一个提出了放射性术语。
5、()于1902年分离出高纯度的金属镭。
A・亨利•贝克勒尔B.居里夫妇C.威廉・康拉德・伦琴D.卢瑟福【答案】B【解析】居里夫妇于1902年分离出高纯度的金属镭。
6、X射线最早应用在()。
A.农业应用B.地质调查C.医学应用D.科学研究【答案】C【解析】1895年,威廉•康拉德•伦琴发现了X射线。
伦琴为其夫人拍摄了一张手部的X光照片,这个发现预示了辐射的医学应用,从此开启了人类应用辐射的序幕,医学应用有了不断的发展。
□电离辐射与非电离辐射一、单选题1、辐射是以()的形式向周围空间传播能量的统称。
A.波B.粒子C.波或粒子D.热【答案】C【解析】辐射是以波或粒子的形式向周围空间传播能量的统称,也就是携带能量的波或者粒子。
2、按照辐射作用于物质时所产生的效应不同,分为()与()两类。
原子核物理习题答案 卢希庭版全

ln 2 T1/ 2
m M
NA
则235U的半衰期为:
T1/ 2
ln 2 N A M
1 A/m
0.693 6.0221023mol1
1
235g
80.0Bq
2.221016 s 7.0108 a
mg
即235U的半衰期为7.0 108 a
2.7
解:当该核素β放射性强度Iβ随时间的变化是 a 衰变与β衰变共同作用的结果
29328U的半径
r0 1.45 fm
R 2.3 fm R 6.88 fm R 8.99 fm
1.5 解:
当原子能级的电子的总角动量j大于核自旋I时 , 能级分裂为2I+1条。 所以有 2I+1=6 即 I=5/2
故241Am 和 243Am 核的自旋均为5/2
1.6
解:由原子核半径
1
R r0 A 3
第二章 放射性和核的稳定性 习题答案
2.1
解:t 时间内未衰变的份额为 et
所以,t 时间内衰变的份额为 1 et
衰变常量
和半衰期
的关系为: T1 2
ln
2 T1
2
一天衰变的份额: ln2t
1 e
T1
2
17.25 0 0
十天衰变的份额: ln210d 1 e 3.66d 84.95 0 0
6.501012 g
10Bq的质量 3
m2
103 Bq
222g / mol 3.824 2436000s ln 2 6.0221023mol
1.761013 g
2.3
解:
放射性活度为A N
m N M NA
A
m M
第一套(计算机)
《核辐射探测学》研究生课程习题与思考题第一套1. 当电子的速度为2.5×108m/s 时,它的动能和总能量各为多少MeV ?2. 已知32P ,14C ,238U 的半衰期分别为14.26d,5370a,4.468×109a ,试求它们的衰变常数(以s -1为单位)。
3.238Pu 的重要用途之一为制造核电池。
假定238Pu (1/2T 87.75, 5.4992a E MeV α==)的α衰变能的5%转变为电能,当电池的输出 功率为20W 时,此电池应装多少克238Pu ?4. 确定下列核反应中的未知粒子x :(a) 188(,)O d p x , (b) 8739(,)x p Y α , (c) 1231245253(,)Te x d I 。
5. 试计算234U 和241m A 的裂变阈能。
第二套1. 已知: △(92,238)= 47.307MeV ; △(92,239) = 50.572MeV ; △ ( 92, 235) = 40.916MeV ; △(92,236)= 42.442MeV ; 试计算239U,236U 最后一个中子的结合能。
2. 计算下面1.0Ci 的放射源的原子核数?(a )18F ; (b)14C ; (c)222Rn ; (d)235U 。
3. 设Bb (A,Z ),Bb (4He ),Bb (A-4,Z-2)分别为母核、α粒子、子核的结合能,试证明 4Bb(A-4,Z-2)+Bb(He)-Bb(A,Z)Q α=。
4. 能量为6MeV 的质子投射到静态的12C 核上,试求质心的运动速度,取质子的质量为1u 。
5. 设一个聚变堆的功率为100万kW ,以d+T 为燃料,试计算一年要消耗多少氘?这么大功率的电站,若改用煤作燃料,则每年要消耗多少煤(煤的燃料热约为3.3×710 J/kg )?第三套1. 当质子在球形核里均匀均匀分布时,原子核的库仑能为:203(1)54C e Z Z E Rπ-=ε Z 为核电荷数,R 为核半径,r 0 取1.5×10-15m 。
《魅力科学》2020章节测试题与答案
《魅力科学》2020章节测试题与答案1、化学概论——原子结构1.1原子的基本构成1.【单选题】20世纪初,谁对氢原子光谱进行深入研究并找到了对应公式?()A、卢瑟福B、里德堡C、巴尔麦D、普朗克答案:B2.【单选题】19世纪末,()是物理学上三大发现之一。
A、X射线B、放射性C、电子D、以上均是答案:D3【多选题】卢瑟福著名的α粒子穿透金属箔试验中,α粒子穿透金属箔后的运动轨迹包括()。
A、立刻停止B、反射回来C、发生旋转D、直线运动答案:A4【判断题】现状光谱在每个化学元素中都有不同特征。
()答案:正确5【判断题】原子中的基本粒子包括电子核和占主要质量的是电子。
()答案:错误1.2核外电子运动理论模型1.【单选题】光的衍射实验,光电效应说明了光具有()。
A、反射性B、波动性C、粒子性D、折射性答案:C2【填空题】1924年,德布罗意在光的二象性的启发下,提出了()也具有二象性的特征。
答案:电子3【填空题】从距核最近的一条轨道算起,当n=1时,轨道半径约为()pm。
答案:534【判断题】不确定原理对微观,宏观粒子都有用()。
答案:错误5【判断题】玻尔计算出的电子在原子核外运动的轨道半径与后来人们用科学的方法计算出的半径一致()。
答案:正确6【简答题】简单介绍“不确定原理”的由来。
答案:原子核外电子体积小,运动速度快,所有不可能同时得到电子的准确位置和准备动量。
1.3原子核外电子的运动状态及薛定谔方程1.【单选题】()建立迄今最为成功的原子结构模型-波动力学模型。
A、薛定谔B、爱因斯坦C、海森堡D、德布罗意答案:A2.【单选题】波函数ψ有什么变量?()A、rB、θC、ФD、以上均是答案:D2的性3【多选题】根据不同的目的和角度考察波函数ψ和概率密度׀ψ׀质,包括()。
A、径向分布图B、时间分布图C、角度分布图D、空间分布图答案:ACD4【判断题】电子在半径r=53pm球壳上出现的最大概率值就是波尔半径。
大学物理 习题课(质点力学)
列方程
G
N F cos 30 0
0
F sin 30 f G 0
0
y
f N
F sin 30 G 得出: 0 F cos30
0
x
由于 F G
则
选B
F sin 30 1 0 F cos30 3
0
2.设有水平力F作用于斜面上的质点 .为了使 m 物体不滑动,对 的大小有何限制? F
t
解出
3 ln 1 30 t 3
(2) d 3 2 d d d d dt d dt
d 3d
d 0 0 3d
0 e
3
4. 在湖面上以3m/s的速度向东行驶的A船上 看到 B船以4m/s的速率从北面驶近A船。 (1)在湖岸上看,B船的速度如何? (2)如果A船的速度变为6m/s(方向不变), 在A船上看B船的速度又为多少? 解 (1)
6 5 2 6 5 cos53.1 5 m
2 2 0
36.90
5 已知某物体作直线运动,其加速度 a=-kvt,式中k为常量;当t=0时,初速度为v0。
则任一时刻t物体的速度v(t)=
。
t dv ktdt 0 v
dv a kvt dt
将一重为G的木块压靠在竖直壁面 上,如果不论 用怎样大的力 都不能使木块向上滑动 F ,则说明 木块与壁面间的静摩擦 系数的大小为:
A
1 2
1 B 3
C
2 3
D
3
解:受力分析如图:
F
300
300
G
unit 9 period 2
eg: Li Jingjing’s favorite subject is music because it’s fun. Her music teacher is Ms. Xie. …
subject ? ___1____.
My favorite subject is P.E. _2__
Why do you like
P.E.? __3__
Li Ming
Jack
2b Listen and match the subjects you hear with the descriptions.
My favorite subject is science.
Section A 2a-3c Grammar Focus
2a Listen and put the conversation in order. P 72
Because it’s
fun. __4__
What’s your favorite
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Department of Nuclear Engineering
University of California
Berkeley, California
NE 255/J.Vujic Due Sep 16, 2008
Homework Set 1
1. Suppose that the neutron number density is given by
n(z,E)=exp(−z)/E
,
and suppose that the absorption cross section is
Σ
a
(E)=1/E
.
(a) Specify the units for
n(z,E) and
Σ
a
(E)
.
(b) How many neutrons are there with energies between 1 and 2 MeV in the cube
with sides of 1 cm centered at the origin?
(c) What is the rate at which these neutrons are being absorbed?
2. Consider a one-dimensional, monoenergetic, time-independent neutron transport
equation in purely absorbing medium:
µ∂ψ(z,µ)∂z+Σa(z)ψ(z,µ)=Qext(z,µ
), z∈[0,H], and
µ
∈[−1,1].
(d)
Assume the vacuum boundary conditions. List all assumptions that were made in
order to derive this equation, starting from the general neutron transport equation with
7 independent variables.
Solve this equation analytically for angular neutron flux if Qext(z,µ) is isotropic plane
source located at z = 0. Determine thr scalar neutron flux for z∈[0,H].
3. Consider the same problem as defined in Problem 1. Assume that
Q
ext
(z,µ) is
uniformly distributed constant isotropic source. Solve this equation for the angular
and scalar neutron flux:
(a) Using the result from Problem 1 and presenting the uniformly distributed
source as a sum of plane sources.
(b) Using any other method.
4. For the given angular neutron number density
n(r ,E,Ω )=
n
0
4
π
1
E
(1−cosθ)
where r ∈A, and A is a unit area perpendicular to the z-axis, find at r :
(a) The angular neutron flux density,
(b) the energy dependent scalar flux,
(c) the energy independent scalar flux,
(d) the rate at which neutrons exit through the area A,
(e) the rate at which neutrons enter through the area A,
(f) the net current through the area A.
For each quantity specify the corresponding units.
