秋苏科版数学八上2.4《线段、角的轴对称性》学案1
新苏科版八年级数学上册:2.4线段、角的轴对称性(3)导学案
一、我的困惑及解决的方法:
1、2、
二、我明白了:
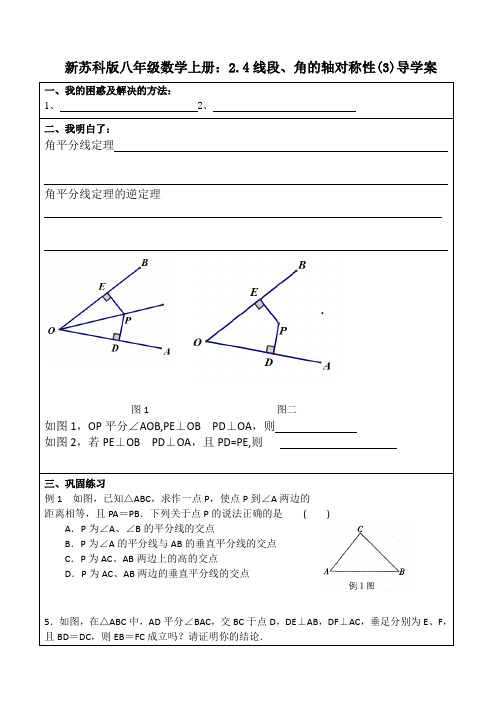
角平分线定理
角平分线定理的逆定理
图1图二
如图1,OP平分∠AOB,PE⊥OB PD⊥OA,则
如图2,若PE⊥OB PD⊥OA,且PD=PE,则
3、巩固练习
例1如图,已知△ABC,求作一点P,使点P到∠A两边的
检查情况反馈:
距离相等,且PA=PB.下列关于点P的说法正确的是( )
A.P为∠A、∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC、AB两边上的高的5.如图,在△ABC中,AD平分∠BAC,交BC于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=DC,则EB=FC成立吗?请证明你的结论.
6. 如图,AD是∠BAC的平分线,DB⊥AB,DC⊥AC,B、C是垂足,那BE与CE有怎样的数量关系?请证明你的结论.
四、拓展延伸
例2如图,在△ABC中,AB>AC,DF垂直平分BC,交△ABC的外
角平分线AD于点D,F为垂足,DE⊥AB于E,连接BD、CD.求证:
∠DBE=∠DCA.
年级检查人:检查日期:年月日周次:周
【最新苏科版精选】苏科初中数学八上《2.4 线段、角的轴对称性》word教案 (9).doc

精品【初中语文试题】2.4线段、角的轴对称性教学目标1.经历探索线段的轴对称性的过程,进一步体验轴对称的性质,发展空间观念.2.探索并掌握线段的垂直平分线的性质.教学重点:线段的垂直平分线的性质.教学难点:线段的垂直平分线的性质.教学过程一、探索研究:线段是轴对称图形吗?为什么?线段 (填“是”或“不是”)轴对称图形,对称轴有 条,分别是 .在线段AB 的垂直平分线l 上任意取一点P ,连接PA 、PB ,PA 和PB 相等吗?证明你的结论. 对于上面的问题我们下面来动手验证一下:1.在一张薄纸上任意画一条线段AB ,折纸,使得两个端点重合,你发现折痕l 与线段AB 的关系是 .2.在折痕l 上任取一点P ,点P 到线段两端点的距离PA,PB 的关系是 .用文字归纳你的结论是 .用符号表达:∵直线l 是AB 的垂直平分线, 点P 在l 上∴ .二、典例研究:例1.如图,在△ABC 中,边AB 的垂直平分线交CB 于点D ,连接AD.若△ADC 的周长为10,AB=7,则△ABC 的周长为( )A .7B .14C .17D .20例2.如图,在四边形ABCD 中,AD ∥BC ,对角线AC 的中点为O ,过点O 作AC 的垂直平分线分别与AD 、BC 相交于点E 、F ,连接AF.求证:AE=A F.三、课堂反馈:1.如图,直线MN 是线段AB 的垂直平分线,垂足为D ,点P 是MN 上一点.若AB=10cm ,则BD= cm ;若PA=10cm ,则PB= cm.2.如图,在△A BC 中,AD ⊥BC 于D.请你再添加一个条件,使得△ABC 是等腰三角形.你添加的条件是 .3.如图,在△ABC 中,AC 的垂直平分线交AC 于E ,交BC 于D ,△ABD 的周长是12cm ,AC=5cm ,则AB+BD+AD= cm ,AB+BD+DC= cm ,△ABC 的周长是 cm.4.如图,P 是线段AB 的垂直平分线上的一点,M 为线段AB 上异于A 、B 的点,则PA 、PB 、PM 的大小关系是PA PB PM (填“>”、“<”或“=”).第3题第2题第1题 第4题精品【初中语文试题】5.在直线l 处找一点P ,使PA=PB.6.如图,在△ABC 中,DE 是AC 的垂直平分线,AE=6cm ,△ABD 的周长为20cm ,求△AB C 的周长.AC 、BC五、课堂小结:我学到的知识:我感悟的方法:。
苏科版八上数学课件:2.4线段、角的轴对称性(1)

M
N
B
E
F
C
例3.如图,已知一个锐角⊿ABC, (1)画出边AB、AC的垂直平分线m,n; (2)直线m,n交于点O,试说明点O到 ⊿ABC三个顶点的距离相等.
随堂练习
1、如图,△ABC中,AD垂直平分BC,AB=5,
BD=2,那么AC=,△ABC的周长=;
A
BD C (1)
2、如随图堂,练在习△ABC中,∠ACB=900,DE 垂直平分AB,垂足为 D,∠CAE:∠EAB=5:2. 问:(1)图中有哪些相等的线段? (2)有哪些相等的角? (3)∠B=___. A
AB的垂直平分线分别交AC、AB
于D、E,△ABD的周长等于28
cm,求DC的长.
A
E D
B
C
变式2:已知:如图,AB=AC=12cm,
AB的垂直平分线分别交AC、AB于
D、E,△BDC的周长等于21cm,求△ABC
的周长.
A
E D
B
C
例2、如图,已知在ΔABC中,BC=7,AB 的垂直平分线分别交AB、BC于点M、E, AC的垂直平分线分别交AC、BC于点N、F, 求ΔAEF的周长.
初中数学课件
金戈铁骑整理制作
2.4线段、角的轴对称性 (1)
想一想
线段的垂直平分线外的点到线段两端
的距离相等吗?
l
P
Q
A
B
例1.已知:如图,AB=AC=12cm, BC=7cm,AB的垂直平分线分别交 AC、AB于D、E,求△BCD的周长.
A
E D
BБайду номын сангаас
C
变式1.已知:如图,AB=AC=12cm,
D
C E B
最新苏科版初中数学八年级上册2.4线段、角的轴对称性(1)优质课教案

课题
24线段、角的轴对称性(1)
第1课时
总第19课时
主备人
审核人
签发人
使用人
学习目标
1.探索并掌握线段的垂直平分线的性质;
2.在“操作--探究---归纳---说理”的过程中学会有条 理地思考和表达,提高演绎推理能力。
3.经历探索线段的轴对称性的过程,进一步体验轴对称的特征,发展空间观念;
(2)同上题图,△AB中AB的垂直平分线交A与点 D,已知AB=7△BD的周长等于11,则△AB的周长=______ _____
(3)同上题图,△AB中AB的垂直平分线交A与点D已知∠A=35°则∠BD=___________°
活动三:试判断:线段的垂直平分线外的点到这条线段两端的距离相等吗?
画图 理由
活动四:利用网格线分别画线段 AB、B、A的垂直平分线
三、当堂检测
1已知点O是△AB的两边AB和A垂直平分线的交点,若OA=5则下列关系式成立的是()
AOB=O=5 BO>5OB>5 DO<5
2已 知点P在线段AB的垂直平分 线上,点Q在线段AB的垂直平分线外,则下列不等式关系成立的是()
AP A+PB>QA+QBBPA+PB<QA+QB
二、课堂助学
活动一:如图,线段AB的垂直平分线l交AB于点O,点P是l上任意 一点,PA与PB相等吗?为什么?通过证明,你发现了什么? 用语言描述你得到的结论.
归纳:_________________________ _____________________________ ________活动二:(1)如图,已知△AB中,B=4AB的垂直平分线交A于点D,若A=6则△BD的周长=_____________
苏科初中数学八上《2.4 线段、角的轴对称性》word教案 (9)

2.4线段、角的轴对称性教学目标1.经历探索线段的轴对称性的过程,进一步体验轴对称的性质,发展空间观念.2.探索并掌握线段的垂直平分线的性质.教学重点:线段的垂直平分线的性质.教学难点:线段的垂直平分线的性质.教学过程一、探索研究:线段是轴对称图形吗?为什么?线段(填“是”或“不是”)轴对称图形,对称轴有条,分别是 .在线段AB的垂直平分线l上任意取一点P,连接PA、PB,PA和PB相等吗?证明你的结论.对于上面的问题我们下面来动手验证一下:1.在一张薄纸上任意画一条线段AB,折纸,使得两个端点重合,你发现折痕l与线段AB的关系是 .2.在折痕l上任取一点P,点P到线段两端点的距离PA,PB的关系是 .用文字归纳你的结论是 .用符号表达:∵直线l是AB的垂直平分线, 点P在l上∴ .二、典例研究:例1.如图,在△ABC中,边AB的垂直平分线交CB于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A.7 B.14 C.17 D.20例2.如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂直平分线分别与AD、BC相交于点E、F,连接AF.求证:AE=A F.三、课堂反馈:1.如图,直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点.若AB=10cm,则BD= cm;若PA=10cm,则PB= cm.2.如图,在△A BC中,AD⊥BC于D.请你再添加一个条件,使得△ABC是等腰三角形.你添加的条件是 .3.如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12cm,AC=5cm,则AB+BD+AD= cm,AB+BD+DC= cm,△ABC的周长是 cm.4.如图,P是线段AB的垂直平分线上的一点,M为线段AB上异于A、B的点,则PA、PB、PM的大小关系是PA PB PM(填“>”、“<”或“=”).5.在直线l处找一点P,使PA=PB.6.如图,在△ABC中,DE是AC的垂直平分线,AE=6cm,△ABD的周长为20cm,求△AB C的周长.四、拓展提高:第3题第2题第1题第4题如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC 于点F、G,△AEG的周长为7,你能求出BC的长吗?五、课堂小结:我学到的知识:我感悟的方法:。
苏科版数学八年级上册 2.4 线段、角的轴对称性(2)导学案

初二数学 第二章轴对称图形 导学案 课题 2.4线段的轴对称性(1)学习目标: 1. 探索并证明线段垂直平分线的性质定理,能利用所学知识提出问题并解决生活中的实际问题; 2. 能利用基本事实有条理的进行证明,做到每一步有根有据,渗透反证法的思想;教师复备及学生学习笔记重难点:利用线段的轴对称性探索线段垂直平分线的性质.利用线段垂直平分线的性质解决生活中的实际问题;教学法:自主学习,讨论,讲练结合导 学 过 程一.自主学习1.线段是_______图形,对称轴是________________________2..线段垂直平分线的定理:_______________________________________二.合作探究实践探索一在一张薄纸上画一条线段AB ,操作并思考:线段是轴对称图形吗?如果是,对称轴在哪里?为什么?实践探索二如图2-17直线l 是线段AB 的垂直平分线,如果沿直线l 翻折,你有什么发现?说说你的看法.实践探索三如图,线段AB 的垂直平分线l 交AB 于点O ,点P 是l上任意一点,PA 与PB 相等吗?为什么?通过证明,你发现了什么?用语言描述你得到的结论.思考: 线段垂直平分线上的点有什么特点?________________________________________________ 例题1:如图在△ABC 中,AB=5cm,AC=3cm,BC 的垂直平分线分别交AB,BC 于点D,E,求△ACD 的周长。
实践探索四_ l _ B _2 _1 _ O _ A 2-17 2-18试判断:线段的垂直平分线外的点到这条线段两端的距离相等吗?1.你能读懂题目吗?题中已知哪些条件?要说明怎样一个结论?2.请你利用题中的已知条件和要说明的结论画出图形.3.根据图形你能证明吗?试一试,让学生自己作图,讨论研究,并给出结论和证明.三.当堂检测1.p52T12..如图要在公路旁设一个公共汽车站,车站应设在什么地方,才能使A,B 两村到车站的距离相等?3.已知:如图在△ABC中,边AB,BC的垂直平分线m,n相交于点O. 求证:点O到△ABC三个顶点的距离相等。
苏科版数学八年级上册2.4 线段、角的对称性(3) 教案 (1)
课题 2.4线段、角的轴对称性(3)课型新授个备人:授课班级:授课时间:教学目标1、经历角的折叠过程探索角的对称性,并发现角平分线的性质和判定点在一个角的平分线上的方法;2、会运用角平分线的性质定理解决生活中的相关问题.重点会运用角平分线的性质定理解决相关问题.难点会运用角平分线的性质定理解决相关问题.教学准备教学设计与过程教学反馈一、【自主预学】初步运用、生成问题1、角是轴对称图形吗?若是,对称轴是什么?2、有下列图形:(1)两个点;(2)一条线段;(3)一个角;(4)一个长方形;(5)两条相交直线;(6)两条平行线。
其中轴对称图形共有()A、3个B、4个C、5个D、6个二【合作互学】师生互动、揭示通法活动一、1、(1)画∠AOB,折纸使OA、OB重合,折痕与∠AOB有什么关系(2)在∠AOB的内部任意取折痕上的一点P,作PD⊥OA,PE⊥OB,垂足为D、E,再沿原折痕重新折叠,你发现了什么?2.像这样的点P还有吗?结论:。
2、在上面第二个结论中,有两个条件(1)OC是∠AOB的平分线,点P在OC上;(2)PD⊥OA,PE⊥OB,才能得出PD=PE,两者缺一不可.下图中PD=PE吗?各缺少了什么条件?做一做1如图,OP是∠AOB的平分线,C是OP上一点,CE⊥OA于点E,CF⊥OB于点F,CE=6㎝,则CF= ㎝教学设计与过程教学反馈2.如图,在△ABC中,∠B=90°,BC=10,∠BAC的角平分线AD交BC于点D,BD:DC=2:3,则点D到AC的距离是________.3.在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB的垂直平分线过点D,交AB于E点.且DE=1cm,BD=2cm.则AC的长为_________cm.活动二、角内部一点到角两边的距离相等,那么这个点在这个角的角平分线上吗?结论:。
四、【点拨导学】生生互动、突出重点画一画:已知∠AOB和C、D两点,请在图中标出一点E,使得点E到OA、OB的距离相等,而且E点到C、D的距离也相等。
苏科版-数学-八年级上册-2.4线段、角的轴对称性教案
教学目标: 知识与技能:经历线段的折叠过程探索线段的对称性,掌握线段垂直平分线的性质定理,过程与方法:经历探索线段的轴对称的过程,在“操作——探究——归纳——证明”的过程中培养思考的严谨性和表达的条理性.情感态度与价值观:会运用所学知识解决生活中实际问题。
教学重点:利用线段的轴对称性探索线段垂直平分线的性质定理.教学难点:灵活运用线段垂直平分线的性质解决实际问题教学过程:一、 学前准备 在一张薄纸上画一条线段AB ,操作并思考:线段是轴对称图形吗?如果是,对称轴在哪里?为什么?二、自学、合作探究 (一)自学、相信自己活动一:如图2-17直线l 是线段AB 的垂直平分线, 如果沿直线l 翻折,你有什么发现?说说你的看法. 结论:线段是轴对称图形,线段的垂直平分线是它的对称轴。
活动二:如图,线段AB 的垂直平分线l 交AB 于点O ,点P 是l 上任意一点,PA 与PB 相等吗?为什么?通过证明,你发现了什么?用语言描述你得到的结论. 线段垂直平分线上的点有什么特点? 总结:线段垂直平分线上的点到线段两端的距离相等.活动三:试判断:线段的垂直平分线外的点到这条线段两端的距离相等吗?引导学生展开讨论:1.你能读懂题目吗?题中已知哪些条件?要说明怎样一个结论?2.请你利用题中的已知条件和要说明的结论画出图形.3.根据图形你能证明吗?试一试,让学生自己作图,讨论研究,并给出结论和证明.教师点评,用幻灯片给出解答过程:解:线段的垂直平分线外的点,到这条线段两端的距离不会相等. 如图,在线段AB 的垂直平分线l 外任取一点P ,连接PA 、PB ,设PA 交l 于点Q ,连接QB . 根据“线段的垂直平分线上的点到线段两端的距离相等”,因为点Q 在AB 的垂直平分线上,所以QA =QB . 于是PA =PQ +QA =PQ +QB .因为三角形的两边之和大于第三边,所以PQ +QB >PB ,即PA >PB .(二)思索、交流例1.如图,△ABC 中,BC =8,边BC 的垂直平分线分别交AB 、AC 于点E 、D ,二次备课BA C _l _ B _2 _1 _ O _ A 2-1721l P O B A 2-18 Q l PB ACB A ED C B ABE =5,求△BCE 的周长.例2.如右图所示,直线MN 和DE 分别是线段 AB 、BC 的垂直平分线,它们交于P 点.PA 和 PC 相等吗?为什么?拓展题:如图,有三家公司,A 、B 、C ,设想共建一个污水处理站M ,使得该站到B 、C 两公司的距离相等,且使A 公司到污水处理站M 的管线最短,试确定污水处理站M 的位置.归纳:三角形的三边垂直平分线的交点到三顶点的距离相等。
苏科版八上数学课件2.4线段、角的轴对称性(1)
A
B
N
M P
Q
A
O
B
C
练习:
1. 如图,如果△ACD的周长为17 cm, △ABC的周长为25 cm,根据这些条
件,你可以求出哪条线段的长?
2. 已知:如图,AB=AC=12 cm,AB的 垂直平分线分别交AC、AB 于D、E, △ABD的周长等于29 cm,求DC的长.
随堂练习
如图,△ABC中,AB的垂直平分线分别 交AB、BC于点D、E,AC的垂直平分线 分别交AC、BC于点F、G,要求△AEG 的周长,还需添加什么条件?
侧,有两个工厂A、B,为了便于两
厂的工人看病,市政府计划在公路
边上修建一所医院,使得两个工厂
的工人都没意见,问医院的院址应选在Fra bibliotek处?B
L
312 国 道
实际问题
2. 如图,在直线L上求作 一点P,使PA=PB.
数学化
实
际
问
A
题
2
数学问题源于生活实践,反过来数学
B
又为生活实践服务
L
p
PA=PB
如图,DA、CB是平面镜前同一发光 点S发出的经平面镜反射后的反射光线, 请通过画图确定发光点S的位置,并将 光路图补充完整.
实际问题1
某市政府为了方便居民的生活,计划
A
在三个住宅小区A、B、C之间修建一个购
物中心,试问,该购物中心应建于何处,
才能使得它到三个小区的距离相等.
B
C
实际问题
1. 求作一点P,使 它和已△ABC的三 个顶点距离相等.
数学化
A
实
际
问
题
1
B
p
2.4线段、角的轴对称性(1)说课稿-苏科版八年级数学上册
2.4 线段、角的轴对称性(1)说课稿-苏科版八年级数学上册一、教材分析本节课是苏科版八年级数学上册中的第2.4节,主要介绍线段和角的轴对称性。
通过本节课的学习,学生将掌握线段和角的轴对称定义、判断和绘制轴对称图形的方法。
在前面的学习中,学生已经学习了线段和角的基本概念和性质,理解了线段和角的度量和运算方法。
通过本节课的学习,可以进一步加深对线段和角的理解,并通过绘制轴对称图形的练习,提高学生的问题解决能力和几何思维能力。
二、教学目标知识与技能目标:1.理解线段的轴对称定义及其性质;2.理解角的轴对称定义及其性质;3.掌握判断线段和角是否具有轴对称的方法;4.能够根据已知条件绘制具有轴对称性的图形。
过程与方法目标:1.注重观察和思考,培养学生的几何思维和推理能力;2.引导学生通过实例分析和讨论,理解轴对称性的概念和特点;3.鼓励学生进行合作学习和探究,培养团队合作意识和解决问题的能力。
情感态度与价值观目标:1.培养学生的观察力和细致心思,培养学生对几何学习的兴趣和热情;2.培养学生的合作精神和团队意识,鼓励学生互帮互助,共同进步。
三、教学重点与难点教学重点:1.线段的轴对称性及其判断方法;2.角的轴对称性及其判断方法;3.绘制具有轴对称性的图形。
教学难点:1.引导学生理解轴对称的概念和特点;2.培养学生观察和分析问题的能力。
四、教学过程与方法引入新知:1.利用实例引入轴对称的概念,例如一把剪刀、一个图形等,让学生观察并发现其中的特点;2.引导学生分析并总结轴对称的特点,例如镜面对称;3.引入线段和角的轴对称性的概念,让学生讨论并理解。
讲解与练习:1.通过示例和图形,讲解线段的轴对称性,并引导学生掌握判断线段是否具有轴对称性的方法;2.通过示例和图形,讲解角的轴对称性,并引导学生掌握判断角是否具有轴对称性的方法;3.组织学生进行练习,巩固判断线段和角是否具有轴对称性的能力。
拓展与应用:1.引导学生思考如何绘制具有轴对称性的图形;2.组织学生进行绘制图形的练习,培养他们的几何思维和创造力;3.引导学生分析和讨论绘制图形的方法和策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.4线段、角的轴对称性(1)
班级:___________ 姓名:___________ 评价:___________
一、【学习目标】
1.经历探索线段的轴对称性的过程,进一步体验轴对称的特征,发展空间观念;
2.探索并掌握线段的垂直平分线的性质;
3.了解线段的垂直平分线是具有特殊性质的点的集合;
4.在“操作--探究--归纳--说理”的过程中学会有条理地思考和表达,提高演绎
推理能力。
二、【学习重难点】
探索并掌握线段的垂直平分线的性质
三、【自主学习】
1、线段是轴对称图形吗?
2、线段的对称轴是什么?
3、线段是轴对称图形, 是它的对称轴。
4、线段垂直平分线上的点到 相等。
四、【合作、探究】
问题1:按要求对折线段后,你发现折痕与线段有什么关系?(折痕就是对称
轴)
问题2:在折痕上任取一点P,连接PA、PB,那么PA与PB的大小有什么关
系?(全等)说说理由。再找一点试一试。 l
P
A O B
结论:
(1)、线段是轴对称图形, 是它的对称轴。
(2)、线段垂直平分线上的点到 相等。
五、【达标巩固】
1、已知ABC中BC=14㎝,AB、AC的垂直平分线分别交BC于E、
F,求出⊿EAF周长
2、如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°, ∠
BAD=60°,则△ABC是__________三角形.
3.利用网格线画图:
(1)在图①中,画线段PQ的垂直平分线
(2)在图②中,找一点O,使OA=OB=OC
4.如图,A、B是高沟至涟水公路l边上两个新建的居民小区,某镇需在公路边增加
一个公共汽车站,这个公共汽车站建在什么位置,才能使两个小区到车站的距离相
等?找出汽车站的位置P,并说明理由。
DEBC
A
l
A
B
Q
P
图①
B
A
C
图②
