基于小波分析的数字滤波器设计
三种信号处理方法的对比分析

三种信号处理方法的对比分析信号处理是一种针对模拟或数字信号的处理和分析技术,旨在提取信号中的有用信息、滤除噪声、增强信号质量和进行数据压缩等。
随着科学技术的不断发展,信号处理方法也在不断创新和提升。
本文将对三种常见的信号处理方法进行对比分析,分别是数字滤波、小波变换和时频分析。
一、数字滤波数字滤波是信号处理中最常见的方法之一,它通过改变信号的频率特性来实现信号的处理和分析。
数字滤波可以分为低通滤波、高通滤波、带通滤波和带阻滤波等不同类型。
数字滤波广泛应用于通信、控制、生物医学等领域,具有计算方便、实时性好、适用范围广等优点。
数字滤波的原理是通过在时域上对信号进行运算,例如求和、加权平均等方式来改变信号波形和频谱特性。
数字滤波器的设计有许多经典的方法,包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等,它们分别适用于不同的滤波需求和设计目标。
二、小波变换小波变换是一种基于尺度函数的信号分析技术,通过分解信号的时间频率特性来实现信号的分析和处理。
小波变换具有多分辨率分析、局部化特征、适应性分析等优点,对非平稳信号特别有效。
小波变换广泛应用于图像处理、音频分析、生物信息处理等领域。
小波变换的原理是通过将信号与不同尺度和位移的小波基函数进行卷积运算,得到信号在不同尺度上的时频表示。
小波变换有许多种不同的小波基函数可供选择,如Haar小波、Daubechies小波、Symlet小波等,它们分别具有不同的频率特性和时间-频率局部化特性。
三、时频分析时频分析的方法有许多种,常见的有短时傅立叶变换(STFT)、时频分布图(Wigner-Ville分布)、Weyl-Heisenberg变换(WHT)等。
这些方法在时域和频域上的分辨率和灵敏度不同,适用于不同类型的信号分析需求。
对比分析从应用领域来看,数字滤波广泛应用于信号去噪、信号增强等领域,小波变换适用于非平稳信号的分析,时频分析适用于瞬时频率和能量分布等特性的分析。
matlab t1小波滤波算法

matlab t1小波滤波算法Matlab T1小波滤波算法是一种用于信号处理的有效工具。
它可以帮助我们去除噪音、平滑信号、提取特征等。
本文将从介绍小波滤波算法的基本概念开始,然后详细说明如何在Matlab中实现T1小波滤波算法。
小波变换是一种数学变换方法,可以将信号分解为不同尺度的子信号。
通过将信号分解为多个频率段,我们可以更好地理解信号的频谱特征。
利用小波变换的特性,我们可以将信号分解为低频和高频成分。
低频成分包含信号的主要特征,而高频成分包含信号的细节信息。
T1小波滤波算法是一种基于小波变换的滤波方法。
它利用了小波分解和重构的原理,从而实现对信号的滤波处理。
该算法主要包含以下几个步骤:1. 读取信号数据:首先,我们需要在Matlab中读取待处理的信号数据。
这可以通过使用Matlab的读取文件函数来实现。
读取的数据可以是一个矩阵,每一列表示一个时刻的采样。
2. 小波分解:接下来,在Matlab中进行小波分解。
这可以通过调用Matlab 中的小波变换函数来实现。
小波变换函数中的参数包括信号数据和小波基。
小波基决定了小波分解的性质,常用的小波基包括haar小波、db小波等。
3. 提取低频成分:在小波分解后,我们可以得到具有不同尺度的低频和高频子信号。
低频子信号包含了主要特征,而高频子信号包含了信号的细节信息。
在T1小波滤波算法中,我们选择保留低频成分,并将高频成分设为零。
4. 小波重构:接下来,在Matlab中进行小波重构。
这可以通过调用Matlab 中的小波重构函数来实现。
小波重构函数中的参数包括低频成分和高频成分。
在T1小波滤波算法中,我们将高频成分设为零,只保留低频成分。
5. 过滤后的信号:最后,我们可以得到滤波后的信号。
通过比较滤波前后的信号,我们可以发现滤波算法的效果。
滤波后的信号能够减少噪音、平滑信号、提取特征等。
在使用Matlab T1小波滤波算法时,需要注意以下几个问题:1. 选择合适的小波基:不同的小波基具有不同的频谱特性。
数字下变频的抽取滤波器组的ASIC设计

谢谢观看
2、可扩展性:数字下变频技术可以通过软件编程实现不同的频率转换,便于 系统的升级和扩展。
3、低功耗:数字下变频技术使用数字电路实现,相对于模拟电路,具有较低 的功耗。
4、高可靠性:数字下变频技术具有较高的稳定性和可靠性,不受环境因素的 影响。
参考内容
引言
数字下变频(DDC)和匹配滤波器是数字信号处理领域的两个重要概念。数字 下变频是将高频信号转换为低频信号的过程,而匹配滤波器则是一种用于信号 检测和识别的滤波器。本次演示旨在探讨基于FPGA的数字下变频及匹配滤波器 的研究,旨在实现高效、实时的信号处理,提高系统性能。
数字滤波器的基本概念
数字滤波器是一种通过数字计算方法对输入信号进行滤波处理的装置。与模拟 滤波器不同,数字滤波器具有更高的稳定性和精度,可以实现对输入信号的任 意处理,并且不会受到环境温度和噪声的干扰。数字滤波器可以根据不同的应 用场景进行分类,如低通滤波器、高通滤波器、带通滤波器和陷波滤波器等。
匹配滤波器
匹配滤波器是一种特殊的滤波器,其作用是最大化输出信号的信噪比。匹配滤 波器的输出与输入信号具有相同的幅度和相位响应,因此它可以有效地提高信 号的能量,降低噪声的干扰。在实际应用中,匹配滤波器的设计通常采用恒定 幅度和恒定相位响应的滤波器,其实现方法包括时域和频域两种方法。在数字 下变频中,匹配滤波器可以有效地提高信号的质量和分辨率。
结论
本次演示对数字滤波器的设计技术进行了详细的介绍,包括其基本概念、分类、 设计原理以及多种设计方法。通过这些内容的介绍,可以了解到数字滤波器设 计技术在信号处理领域中的重要性和广泛应用。随着科技的不断发展和进步, 相信数字滤波器的未来发展将会更加广阔,其在新型滤波器、高速滤波器和多 维滤波器等方面的研究与应用将会得到更深入的拓展。
小波变换滤波算法

小波变换滤波算法一、引言小波变换滤波算法是一种常用的信号处理方法,它可以将原始信号分解为不同频率的子信号,然后通过滤波处理得到所需的信号特征。
在信号处理领域,小波变换滤波算法被广泛应用于信号去噪、数据压缩、边缘检测等方面。
二、小波变换的基本原理小波变换是一种时频分析方法,它将信号分解为时域和频域两个方向上的信息,具有局部性和多分辨性的特点。
小波变换利用一组母小波函数进行信号的分解和重构,其中包括连续小波变换和离散小波变换两种方法。
连续小波变换是将信号与连续小波函数进行卷积,然后通过尺度参数和平移参数对信号进行分解和重构。
离散小波变换是将信号与离散小波函数进行卷积,然后通过下采样和上采样操作对信号进行分解和重构。
三、小波变换滤波算法的实现步骤1. 选择合适的小波基函数,常用的小波基函数有Haar小波、Daubechies小波、Symlet小波等。
不同的小波基函数适用于不同类型的信号处理任务。
2. 对原始信号进行小波变换,得到信号的小波系数。
小波系数包含了信号的不同频率成分和时域信息。
3. 根据需要选择合适的滤波器,常用的滤波器有低通滤波器和高通滤波器。
低通滤波器用于去除高频噪声,高通滤波器用于去除低频噪声。
4. 对小波系数进行滤波处理,去除不需要的频率成分。
可以通过滤波器的卷积操作实现。
5. 对滤波后的小波系数进行逆变换,得到滤波后的信号。
四、小波变换滤波算法的应用1. 信号去噪小波变换滤波算法可以去除信号中的噪声,提高信号的质量。
通过选择合适的小波基函数和滤波器,可以将噪声滤除,保留信号的有效信息。
2. 数据压缩小波变换滤波算法可以将信号分解为不同频率的子信号,然后根据需要选择保留的频率成分,对信号进行压缩。
这样可以减少数据的存储空间和传输带宽。
3. 边缘检测小波变换滤波算法可以提取信号的边缘信息,对于图像处理和边缘检测任务有很好的效果。
通过对小波系数的处理,可以将信号的边缘特征突出出来。
五、小波变换滤波算法的优缺点小波变换滤波算法具有以下优点:1. 可以提取信号的时频信息,具有局部性和多分辨性的特点。
数字滤波 最小相位数字滚降

数字滤波最小相位数字滚降
最小相位数字滤波是一种常用的信号处理技术,可以用于去除信号中的噪声和干扰,使得信号更清晰、更易于分析。
在数字滤波中,最小相位滤波器被广泛应用于音频处理、图像处理和通信系统等领域。
最小相位数字滤波器是一种特殊的数字滤波器,它具有最小的群延迟和最小的相位畸变。
通过优化滤波器的相位响应,最小相位滤波器能够使信号在频域上更加紧凑,减少信号在时域上的延迟。
这种滤波器在许多实际应用中都能取得很好的效果。
最小相位数字滤波的设计方法有很多种,其中一种常用的方法是基于极点和零点的分解。
通过将滤波器的传递函数分解为极点和零点的乘积形式,可以得到最小相位滤波器的频率响应。
然后,通过调整极点和零点的位置,可以进一步优化滤波器的相位响应。
最小相位数字滤波器不仅可以用于去除信号中的噪声和干扰,还可以用于信号的重构和增强。
通过对信号进行最小相位滤波处理,可以使得信号的频谱更加集中,提高信号的信噪比和分辨率。
同时,最小相位滤波器还可以用于信号的时频分析和谐波检测等应用。
最小相位数字滤波是一种非常重要的信号处理技术,它在许多领域都有广泛的应用。
通过优化滤波器的相位响应,最小相位滤波器能够提高信号的质量和可分析性,为后续的信号处理任务提供了良好
的基础。
数字信号处理第七章 FIR数字滤波器设计

窗函数的几个参数:
旁瓣瓣的峰最值大值n相—对窗主函瓣数最的大幅值频的函衰数减W(g (dB))的;最大旁
过渡带宽度B—用该窗函数设计的FIRDF的过渡带宽
度;
阻带最小衰减s—用该窗函数设计的FIRDF的阻带
返回
回到本节
④ h(n)奇对称,N为偶数
• 相位特性:
• 频率特性:
N 3 2
Hg () 2hnsin n n0
• Hg()在=0,2 处为零,即H(z)在 z=1处有零点; • Hg() 在=0,2 奇对称,在=处偶对称。
返回
回到本节
(3)线性相位FIRDF的零点分布特点
N 1
将 h(n) h(N 1 n) 代入式 H (z) h(n)zn 得到:
①窗谱主瓣宽度要窄,以获得较陡的过渡带; ②相对于主瓣幅度,旁瓣要尽可能小,使能量尽量 集中在主瓣中,这样就 可以减小肩峰和余振,以提 高阻带衰减和通带平稳性。 但实际上这两点不能兼得,一般总是通过增加主瓣 宽度来换取对旁瓣的抑制。
返回
回到本节 7.2.3 典型窗函数介绍
1.矩形窗(Rectangle Window)
N 1
H e j Hg e j h(n)e jn n0
N 1 2
[h(n)e jn h(N n 1)e j(N n1) ] n0
j N 1 N / 21
j (n N 1)
j (n N 1)
e 2 [h(n)e
2 h(n)e 2 ]
n0
N / 21
e j 2h(n) cos(n ) n0
1
e
j
] N 1 2
基于Matlab的信号分析与数字滤波器设计
基于Matlab的信号分析与数字滤波器设计作者:赵子曦来源:《电脑知识与技术》2021年第29期摘要:对于信号的时域分析只能获取部分信息,因此在频域作出信号频谱以辅助分析显得十分重要。
在进行频谱分析后,会发现信号包含复杂噪声,因此使用软件设计滤波器去噪。
在Matlab的基础上,本文首先采用经典的傅里叶变换对各类信号进行频谱分析,然后用窗函数法设计FIR数字滤波器。
在声音信号上的实验证明,本文设计的FIR数字滤波器可以有效压制噪声,提取良好声音信号。
关键词:信号频谱分析; Matlab;滤波器;信号去噪中图分类号:TP311 文献标识码:A文章编号:1009-3044(2021)29-0114-02进入21世纪以来,计算机技术飞速发展,大数据、物联网、人工智能(AI:Artificial Intelligence)成为学界、工业界的研究热点,随之对信号分析技术提出了更高的要求,也带来了新的机遇。
在摩尔定律的基础上,计算机有限的算力在复杂数据的处理上显得吃力,而现代数据处理又十分追求更高的效率、更快的速度和更准确的结果。
Matlab是工程领域应用广泛的一款成熟软件,它拥有强大的矩阵运算能力和科学数据处理能力,可以处理十分微小的电路信号,因此使用Matlab进行信号分析与处理、数字滤波器设计等对于电路分析、小信号分析、波形重整具有十分重要的意义。
1信号频域分析1.1离散傅里叶变换与窗函数实际上,计算机存储的所有数据都是离散的,它们需要运用时域和频域都是离散的离散傅里叶变换(Discrete Fourier Transform,DFT)进行处理。
TD(Time-Domain)连续信号经采样后,通过快速傅里叶变换成为FD(Frequency-Domain)采样。
通过数学表达式绘图,不难看出输入DFT进行变换的时域信号和变换后输出的频域信号均为有限长序列,即主值序列。
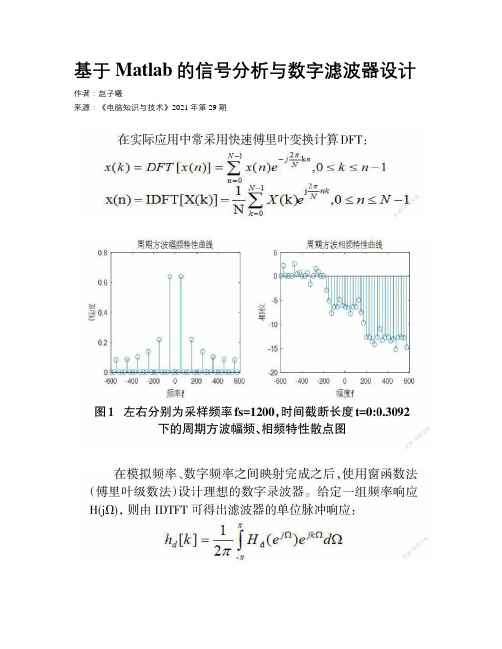
在实际应用中常采用快速傅里叶变换计算DFT:连续周期、连续非周期、离散周期、离散非周期信号的频谱与 DFT之间的关系:时域上的信号是非周期的,则频域上的信号是连续的;时域上的信号是周期的,则频域上的信号是离散的;反之亦然。
模拟信号处理中的数字滤波器设计思路

模拟信号处理中的数字滤波器设计思路数字滤波器在模拟信号处理中起着至关重要的作用,可以有效地去除信号中的噪声和干扰,提高信号的质量和准确性。
设计一个高效可靠的数字滤波器需要综合考虑信号的特性、滤波器的类型和参数设置等多个因素。
首先,确定信号的特性是设计数字滤波器的关键。
需要分析信号的频率范围、幅度范围以及所含的噪声类型,这些信息可以帮助选择合适的滤波器类型和参数。
常见的数字滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器,每种类型有不同的特性适用于不同的信号。
其次,根据信号的特性选择合适的数字滤波器类型。
如果信号包含高频噪声,可以选择低通滤波器;如果信号包含低频噪声,可以选择高通滤波器;如果信号需要保留一定频率范围,可以选择带通滤波器;如果信号需要去除某个频率范围,可以选择带阻滤波器。
合理选择滤波器类型可以有效地去除信号中的噪声和干扰。
在选择滤波器类型的基础上,需要确定滤波器的参数设置。
包括截止频率、通带波动和阻带衰减等参数。
截止频率是指滤波器开始起作用的频率,通带波动是指在通带范围内信号的波动情况,阻带衰减是指在阻带范围内信号的减弱情况。
合理设置这些参数可以使滤波器在有效去除噪声的同时尽可能保留原始信号的特性。
另外,数字滤波器的设计还需要考虑实现方式和计算复杂度。
常见的数字滤波器实现方式包括FIR滤波器和IIR滤波器,它们各有优劣。
FIR滤波器具有线性相位和稳定性优点,适用于需要保持信号相位信息的场合;IIR滤波器具有较高的滤波效率和计算速度,适用于计算资源有限的场合。
根据实际需求选择合适的实现方式。
最后,在设计数字滤波器时需要进行系统性能评估和优化。
可以通过频率响应、时域响应、幅频响应和群延迟等指标对滤波器性能进行评估,根据评估结果对滤波器进行优化。
一般来说,希望滤波器具有较窄的过渡带宽、较高的阻带衰减和较小的相位失真。
通过不断调整参数和算法,可以使滤波器达到最佳性能。
综上所述,设计数字滤波器是模拟信号处理中的重要任务,需要综合考虑信号特性、滤波器类型、参数设置、实现方式和系统性能等多个因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于小波分析的数字滤波器设计
本文介绍了利用小波分析技术设计数字滤波器的方法。
首先,介绍了小波分析技术和数字滤波器的概念,并用例子来证明小波分析技术能够很好地实现数字滤波器的设计。
其次,介绍了小波变换和小波基函数,并对它们在数字滤波器设计中的应用进行了详细说明。
最后,介绍了小波多尺度分析方法,分析了它在数字滤波器设计中的应用和优势,并提出了一些测试结果来验证它的有效性。
【Introduction】
数字滤波器是一种有效的数据处理技术,它利用数字信号处理理论来滤除噪声,提取信号,改善信号质量。
它在许多科学领域都有重要的应用,如生物信号处理、运动控制、图像处理、声纳测量以及电信信号的处理等等。
本文的研究重点将放在利用小波分析技术来设计数字滤波器上。
【小波分析技术】
小波分析技术是一种数字信号处理技术,它被广泛应用在对信号的分解和降噪等方面。
小波分析技术具有分析时可以达到快速、精确、分数阶等优点,它使用了一种特殊的矩阵作为基本结构,可以实现将一幅图像或者一个信号从低频到高频的分解过程,它还可以用来实现数字滤波器的设计和实现。
下面以一个例子来说明小波分析技术在数字滤波器设计中的应用。
假定有一个信号,其中含有一些噪声,利用小波分析技术,只要选择合适的小波分析算子,可以将信号分解为有效的模式和噪声成分,
然后采用数字滤波器来去除噪声,最后恢复信号的原有特征。
【小波变换】
小波变换(Wavelet Transform)是一种用来分解数据的技术,它可以将信号分解成多个小时间尺度和多个小频率尺度的模式,这些模式可以表示信号中的特征信息。
小波变换相比于其他信号分析技术更加全面,能够实现更高的分解精度,为信号的分析和处理提供便利。
小波变换最重要的特性就是它利用了小波基函数(Wavelet Basis Function)来进行变换,小波基函数形状可以根据应用场景自由调整,能够更加精确地分解出信号中的特征信息,使得它在数字滤波器设计中,具有很好地波形匹配能力,能够更加准确地框定信号模式。
【小波多尺度分析】
小波多尺度分析(Wavelet Multiscale Analysis)是一种基于小波分析技术的新技术,它可以用来进行时间尺度和频率尺度的层次性分解。
它的分解能力比小波变换要强,它不仅能够分解出信号的局部特征,而且还可以分解出信号的全局特征。
小波多尺度分析在数字滤波器设计过程中,能够更加有效地抽取出信号的特征信息,从而可以更加精确地构建滤波器,它具有更高的降噪性能,且降噪效果更加稳定。
【Conclusion】
本文介绍了小波分析技术在数字滤波器设计中的应用,以及小波变换和小波多尺度分析技术在数字滤波器设计中的应用和优势。
小波
分析技术在数字滤波器设计过程中具有很好的波形匹配能力,能够更加精确地框定信号模式,而小波多尺度分析在能够抽取信号特征信息的基础上,还可以有效地去除噪声,改善信号质量,提高滤波器的性能。
