09函数y=Asin(ωx+ψ)的图象与应用(第二课时)
高二数学函数y=asin(ωx+φ)的图象2

0
2
2
7 2
3 2
2
13 2
2
5
0
2
0
2
0
(1)列表 :
X x y
0
2
2
7 2
3 2
2
13 2
y
2
5
0
2
0
2
0
2
(2)描点 :
O -2
2
2
7 13 ( ,0), (2 ,2), ( ,0), (5 ,2), ( ,0) 2 2 2
2)当 a < 0 时,将 y = f(x)图象向下平移 a 个单位;
二、对称变换
y = f(x)
1、y = f( x )
将 y = f(x)的图象在 x 轴正半轴上的图象保留,
并将这部分图象对称地翻折到 x 轴的负半轴上,
这两部分图象共同构成了 y = f( x )的图象;
2、y = f(x)
即得函数 y = f(ax)的图象;
三、伸缩变换 y = f(x) (a > 0 且 a ≠1)
→
2、y = af(x)
1 )当 a >1 时,将 y = f(x)图象上每一个点的 横坐标不变,纵坐标伸长到原来的 a倍,
2 )当 0 < a <1 时,将 y = f(x)图象上每一个点的 横坐标不变,纵坐标缩短到原来的 a倍,
1 π y = 2sin( x ) 作出函数 3 6 的图象, 并指出它的周期、频率、相位、初相、最值 及单调区间.
例题2
1 π 画出函数y = 2sin( x - )的简图. 3 6
函数y=Asin(ωx+φ)的图象及应用
单位长度.
1 2 3 4 5 6 7
解析
答案
π 6.将函数y=cos 2x+1的图象向右平移 个单位长度,再向下平移1个单位 4 长度后得到的函数图象对应的表达式为
A.y=sin 2x √ C.y=cos 2x B.y=sin 2x+2 D.y=cos
π 2 x - 4
1 π x - y=2sin2 3的振幅、频率和初相分别为
1 π B.2,4π,3 π D.2,4π,-3
√
1 π C.2,4π,-3
解析
1 ω 1 π 由题意知 A=2,f=T=2π=4π,初相为-3.
1
2
3
4
5
6
7
解析
答案
4.[P62 例 4] 如图,某地一天从 6 ~ 14 时的温度变化曲 线近似满足函数y=Asin(ωx+φ)+b,则这段曲线的 π 3π x + y=10sin +20,x∈[6,14] 8 4 函数解析式为______________________________.
π π 解析 将函数 y=cos 2x+1 的图象向右平移4个单位长度得到 y=cos 2x-4
+1=sin 2x+1,再向下平移 1 个单位长度得到 y=sin 2x,故选 A.
1
2
3
4
5
6
7
解析
答案
7.设函数
π π ω >0 ,- < φ < f(x)=3sin(ωx+φ) 的图象关于直线 2 2
2π x= 3 对称,
①③ 它的周期是 π,则下列说法正确的是________.( 填序号)
3 ①f(x)的图象过点0,2 ; π 2π ②f(x)在12, 3 上是减函数; 5π , 0 ③f(x)的一个对称中心是 ; 12
人教版数学必修第一册综合复习:函数y=Asin(ωx+φ)的图象及应用课件

,
2
4
2
B.0, , ,
3
4
6
3
2
,π
D.0, , , ,
2
3
2.用五点法作函数y=sin(x- )在一个周期内的图象时,
6
7
2
,0
,1
,
0
6
主要确定的五个点是________,________,________,
3
6
,
0
,
−1
________,________.
2
,π)上
[-2,1)
有实数根,则m的取值范围是_______________.
方法点拨:方程根的个数可转化为两个函数图象的交点个数.
考向3
三角函数模型的应用
[例8] 如图,某大风车的半径为2米,每12秒旋转一周,它的
最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点
M从最低点O开始,逆时针方向旋转40秒后到达点P,则点P到
长度,得到函数y=g(x)的图象.若函数y=g(x)图象的一个
5
对称中心为点(
12
,0),求θ的最小值.
(3)作出函数f(x)在长度为一个周期的闭区间上的图象.
方法总结
五点法作图,即用“五点法”作y=Asin(ωx+φ)的
简图,主要是通过变量代换,设z=ωx+φ,由z取0,
2
,π,
2
,2π来求出相应的x. 通过列表,计算得出
φ对函数图象变化的影响.
问题,体会三角函数是描述周期变
化现象的重要函数模型.
核心
函数y=Asin(ωx+ψ)的图象

(2) y=sin(x+ )的图像可以看作是把正弦曲线y=sinx
图像经过相位变换得到。
(3) y=Asinx的图像可以看作是把正弦曲线y=sinx图 像经过振幅变换得到。 (4)作图时,要注意坐标轴刻度,x轴是实数轴,角一 律用弧度制。
作业
画出函数 y 2 sin( x ) 的图象,并说明 3 他与函数 y sin x 的的闭区间上的 简图并判断与y=sinx的关系:
(1)
3 y sin x 2
(2)
y sin( x ) 2
解 ( 2) y sin x 图象上各点向右
平移
y sin( x
2
)
2
个单位
y 1
3 2
O 1
2
2
5 2
x
y sin( x
y sin x
(3).画出函数 y 2sin( x ) 的图象. 3.思考题:函数y 5 sin 2 x 的图象经过怎样的变换后能得到y 5 sin( 2 x ) 8 的图象?
小结
(1)用“五点法”作y=Asinx与y=sin(x+ )的简图 时,先要确定周期,找出五个关键点,然后再列表、描 点、用光滑曲线连接五点,作出一个周期内的图象,最后 通过平移得到完整的图象.
自学检测
函数 y 4 sin( 2 x ) 的振幅,周期,初相 5 各是多少?
反馈评价
函数y=Asin(ωx+φ) (其中A,ω,φ是常 数)广泛应用于物理和工程技术中物体,例 如:作简谐振动时,位移s与时间t的关系; 交流电中,电流强度i与时间t的关系,都可 用这类函数来表示,
【公开课课件】函数y=Asin(ωx φ)的图象变换课件-高一下学期北师大版(2019)必修第二册

− 的图象向左平移 个单位
4
3
把所得曲线向右平移 个单位长度,得
3
长度,可得 = + − =
到函数 =
−
4
的图象,则
() = ( )
A.
2
−
7
12
C. 2 −
7
12
B.
2
+
12
D. 2
+
12
+
来的2倍,得到图象的解析式为
纵坐标不变,
= ,则 的值为
横坐标变为原来的2倍
__________.
1
函数 = 的图
2
象,所以 =
1
.
2
4
与x轴的两个相邻交点间的距
为 ,要得到函数() = 的图象,
1 2
3
离为 ⋅ = ,
2
3
只需将()的图象( )
∴ = 3,∴ () =
A.向左平移 个单位长度
12
B.向右平移 个单位长度
4
C.向左平移 个单位长度
4
3π
D.向右平移 个单位长度
4
3 +
图象
y=2sin x的图象向右
平移 个单位得到y=
6
2sin −
6
Байду номын сангаас
的图象
y=2sin − 的图象所
6
有点的横坐标缩短到原
1
来的 倍得到y=
函数y=Asin(ωx+φ)的性质及应用 课件

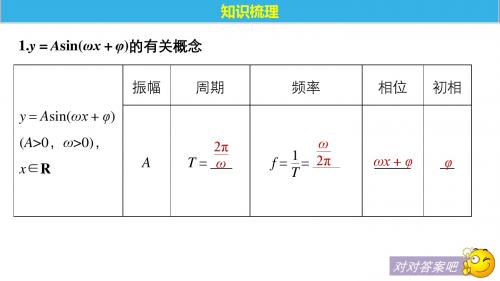
1.函数y=Asin(ωx+φ),x∈[0,+∞)(其中A>0,ω>0)中各量的物理意义 物理中,描述简谐运动的物理量, 如振幅、周期和频率等都与函数y=Asin(ωx+φ)中的常数有关: (1)A:它表示做简谐运动的物体离开平衡位置的最大距离,称为振幅(amplitude of vibration);
(3)由 y=sin(2x-34π)知,
x
0
π
3π
5π
7π
8
8
8
8
π
2x-34π
-34π
-π2
0
π 2
π
5π 4
y
-
2 2
-1
0
1
0
-
2 2
故函数y=f(x)在区间[0,π]上的图象是
相位、初相概念理解错误
典例 4 函数 y=2sin(-2x+π3)的相位和初相分别是( )
A.-2x+π3,π3
[解析] (1)由 2x+φ=kπ+π2,k∈Z 得 x=k2π+π4-φ2, 令k2π+π4-φ2=π8,解得 φ=kπ+π4,k∈Z. ∵-π<φ<0,∴φ=-34π. (2)由(1)知,f(x)=sin(2x-34π). 由 2kπ-π2≤2x-34π≤2kπ+π2(k∈Z)
解得 kπ+π8≤x≤kπ+58π(k∈Z) 故函数的单调递增区间是[kπ+π8,kπ+58π](k∈Z). 同理可得函数的单调递减区间是[kπ+58π,kπ+98π](k∈Z). 当 2x-34π=2kπ+π2(k∈Z),即 x=kπ+58π(k∈Z)时函数有最大值 1; 当 2x-34π=2kπ-π2(k∈Z),即 x=kπ+π8(k∈Z)时函数有最小值-1.
函数y=Asin(ωx+φ)的性质与图象及其简单应用课件-2025届高三数学一轮复习
3.(2024 · 舒城模拟)将函数的图象向左平移 个单位长度,得到函数的图象,若在,上为增函数,则 的最大值为( ) .
A
A.2 B.3 C.4 D.
解析 依题意,,由, ,得,即的一个单调递增区间是,,因为在 ,上为增函数,所以,,,故,即 的最大值为2.故选A.
三角函数的实际应用
典例4 (双空题)如图,这是矩形与半圆 的组合图形,其中,为半圆弧上一点,,垂足为 ,点在线段上,且,设 ,则的面积与 的关系式为 _______________________________, 的最大值为_ _____.
1.(多选题)(2024 · 沧州模拟)已知函数为常数, 的图象关于直线对称,函数 ,则下列说法正确的是( ) .
ABC
A.将的图象向左平移个单位长度可以得到 的图象B.的图象关于点, 对称C.在, 上单调递减D. 的最大值为1
解析 由题意, ,, , 将的图象向左平移 个单位长度,所得图象的解析式为 ,A正确; ,B正确; 当,时,,,,此时 是减函数,C正确;的最大值为,D错误.故选 .
D
A.向左平移个单位长度 B.向右平移 个单位长度C.向左平移个单位长度 D.向右平移 个单位长度
解析 因为,所以把函数 图象上的所有点向右平移个单位长度可得到函数 的图象.故选D.
2.(2024 · 梅州模拟)为了得到函数 的图象,只需将函数 的图象( ) .
A
A.向左平移个单位长度 B.向左平移 个单位长度C.向右平移个单位长度 D.向右平移 个单位长度
题组3 走向高考
5.(2023 · 新高考Ⅰ卷)已知函数在 上有且仅有3个零点,则 的取值范围是______.
北师大高中数学必修第一册学案:第5章 5.6 第2课时 函数y=Asin(ωx+φ)的图象及变换
第2课时 函数y =A sin(ωx +φ)图象及性质的应用类型1 “五点法”作函数y =A sin(ωx +φ)的图象 【例1】 已知函数y =12sin ⎝ ⎛⎭⎪⎫2x +π6,x ∈R.(1)用“五点法”作出它在一个周期内的简图;(2)该函数的图象可由y =sin x (x ∈R )的图象经过怎样的平移和伸缩变换得到? [解] (1)列表:(2)函数y =sin x 的图象向左平移π6个单位长度,得到函数y =sin ⎝ ⎛⎭⎪⎫x +π6的图象,再保持纵坐标不变,把横坐标缩短为原来的12倍,得到函数y =sin ⎝ ⎛⎭⎪⎫2x +π6的图象,再保持横坐标不变,把纵坐标缩短为原来的12倍,得到函数y =12sin ⎝ ⎛⎭⎪⎫2x +π6的图象.1.“五点法”作图的实质利用“五点法”作函数f (x )=A sin(ωx +φ)的图象,实质是利用函数的三个零点,两个最值点画出函数在一个周期内的图象.2.用“五点法”作函数f (x )=A sin(ωx +φ)图象的步骤 第一步:列表.第三步:用光滑曲线连接这些点,形成图象.[跟进训练]1.已知函数f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3,在给定坐标系中作出函数f (x )在[0,π]上的图象.[解] f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3,列表如下.图象如图.类型2 求三角函数的解析式【例2】 如图是函数y =A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的图象的一部分,求此函数的解析式.借助函数图象你能发现哪些信息?参数A 、ω、φ的求解分别与哪些信息相关?[解] 法一:(逐一定参法) 由图象知A =3, T =5π6-⎝ ⎛⎭⎪⎫-π6=π,∴ω=2πT =2, ∴y =3sin(2x +φ).∵点⎝ ⎛⎭⎪⎫-π6,0在函数图象上,∴-π6×2+φ=0+2k π,k ∈Z ,又|φ|<π2,∴φ=π3, ∴y =3sin ⎝ ⎛⎭⎪⎫2x +π3.法二:(五点对应法)由图象知A =3. ∵图象过点⎝ ⎛⎭⎪⎫π3,0和⎝ ⎛⎭⎪⎫5π6,0,∴⎩⎪⎨⎪⎧πω3+φ=π,5πω6+φ=2π,解得⎩⎪⎨⎪⎧ω=2,φ=π3.∴y =3sin ⎝ ⎛⎭⎪⎫2x +π3.法三:(图象变换法)由A =3,T =π,点⎝ ⎛⎭⎪⎫-π6,0在图象上,可知函数图象由y =3sin 2x 向左平移π6个单位长度而得, ∴y =3sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π6,即y =3sin ⎝ ⎛⎭⎪⎫2x +π3.给出y =A sin(ωx +φ)的图象的一部分,确定A ,ω,φ的方法(1)逐一定参法:如果从图象可直接确定A 和ω,则选取“五点法”中的“第一零点”的数据代入“ωx +φ=0”(要注意正确判断哪一点是“第一零点”)求得φ或选取最大值点时代入公式ωx +φ=π2+2k π,k ∈Z ,选取最小值点时代入公式ωx +φ=3π2+2k π,k ∈Z .(2) 五点对应法:将若干特殊点代入函数式,可以求得相关待定系数A ,ω,φ.这里需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入列式.(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y =A sin ωx ,再根据图象平移、伸缩规律确定相关的参数.[跟进训练]|φ|<π22.(1)已知函数f (x )=A cos(ωx +φ)+BA >0,ω>0,的部分图象如图所示,则函数f (x )的解析式为( )A .y =2cos ⎝ ⎛⎭⎪⎫x 2-π4+4B .y =2cos ⎝ ⎛⎭⎪⎫x 2+π4+4C .y =4cos ⎝ ⎛⎭⎪⎫x 2-π4+2D .y =4cos ⎝ ⎛⎭⎪⎫x 2+π4+2 (2)已知函数f (x )=A sin(ωx +φ),x ∈R ⎝ ⎛⎭⎪⎫其中A >0,ω>0,0<φ<π2的图象与x 轴的交点中,相邻两个交点的距离为π2,且图象上一个最低点为M ⎝ ⎛⎭⎪⎫2π3,-2,求f (x )的解析式.(1)A [由函数f (x )的最大值和最小值得A +B =6,-A +B =2,所以A =2,B =4, 函数f (x )的周期为⎣⎢⎡⎦⎥⎤π2-⎝⎛⎭⎪⎫-π2×4=4π,又ω>0, 所以ω=12,又因为点⎝ ⎛⎭⎪⎫π2,6在函数f (x )的图象上.所以6=2cos ⎝ ⎛⎭⎪⎫12×π2+φ+4,所以cos ⎝ ⎛⎭⎪⎫π4+φ=1,所以π4+φ=2k π,k ∈Z ,所以φ=2k π-π4,k ∈Z ,又|φ|<π2, 所以φ=-π4,所以f (x )=2cos ⎝ ⎛⎭⎪⎫12x -π4+4.](2)[解] 由最低点M ⎝ ⎛⎭⎪⎫2π3,-2,得A =2.在x 轴上两相邻交点之间的距离为π2,故T 2=π2, 即T =π,ω=2πT =2ππ=2.由点M ⎝ ⎛⎭⎪⎫2π3,-2在图象上得2sin ⎝ ⎛⎭⎪⎫2×2π3+φ=-2,即sin ⎝ ⎛⎭⎪⎫4π3+φ=-1, 故4π3+φ=2k π-π2(k ∈Z ), ∴φ=2k π-11π6(k ∈Z ).又φ∈⎝ ⎛⎭⎪⎫0,π2,∴φ=π6.故f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6.类型3 函数y =A sin(ωx +φ)性质的综合应用【例3】 已知函数f (x )=sin(ωx +φ)(ω>0,0≤φ<π)是R 上的偶函数,其图象关于点M ⎝ ⎛⎭⎪⎫3π4,0对称,且在区间⎣⎢⎡⎦⎥⎤0,π2上是单调函数,求φ和ω的值.[解] ∵f (x )在R 上是偶函数,∴当x =0时,f (x )取得最大值或最小值, 即sin φ=±1,得φ=k π+π2,k ∈Z . 又0≤φ<π,∴φ=π2.由f (x )的图象关于点M ⎝ ⎛⎭⎪⎫3π4,0对称,可知sin ⎝ ⎛⎭⎪⎫3π4ω+π2=0,解得ω=43k -23,k ∈Z .又f (x )在⎣⎢⎡⎦⎥⎤0,π2上是单调函数,∴T ≥π,即2πω≥π,∴0<ω≤2,∴当k =1时,ω=23;当k =2时,ω=2. 综上,φ=π2,ω=23或2.将本例中“偶”改为“奇”,“其图象关于点M 3π4,0对称,且在区间⎣⎢⎡⎦⎥⎤0,π2上是单调函数”改为“在区间⎣⎢⎡⎦⎥⎤-3π2,π2上为增函数”,试求ω的最大值.[解] 因为f (x )是奇函数,所以f (0)=sin φ=0,又0≤φ<π,所以φ=0. 因为f (x )=sin ωx 在⎣⎢⎡⎦⎥⎤-π2ω,π2ω上是增函数.所以⎣⎢⎡⎦⎥⎤-3π2,π2⊆⎣⎢⎡⎦⎥⎤-π2ω,π2ω,于是⎩⎪⎨⎪⎧ω>0,-3π2≥-π2ωπ2≤π2ω,,解得0<ω≤13,所以ω的最大值为13.研究函数y =A sin(ωx +φ)性质的基本策略(1)首先将所给函数的解析式转化为y =A sin(ωx +φ)的形式. (2)熟记正弦函数y =sin x 的图象与基本性质. (3)充分利用整体代换思想解决问题.(4)熟记有关函数y =A sin(ωx +φ)的奇偶性、对称性、单调性的重要结论.[跟进训练]3.(多选)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3,以下命题中为真命题的是( )A .函数f (x )的图象关于直线x =π12对称 B .x =-π6是函数f (x )的一个零点C .函数f (x )的图象可由g (x )=sin 2x 的图象向左平移π3个单位长度得到D .函数f (x )在⎣⎢⎡⎦⎥⎤0,π12上是增函数ABD [令2x +π3=k π+π2(k ∈Z ),当k =0时,x =π12,即函数f (x )的图象关于直线x =π12对称,选项A 正确;令2x +π3=k π(k ∈Z ),当k =0时,x =-π6,即x =-π6是函数f (x )的一个零点,选项B 正确;2x +π3=2⎝ ⎛⎭⎪⎫x +π6,故函数f (x )的图象可由g (x )=sin 2x 的图象向左平移π6个单位长度得到,选项C 错误;若x ∈⎣⎢⎡⎦⎥⎤0,π12,则2x +π3∈⎣⎢⎡⎦⎥⎤π3,π2,故f (x )在⎣⎢⎡⎦⎥⎤0,π12上是增函数,选项D 正确.故选ABD.]1.已知函数f (x )=A sin ⎝ ⎛⎭⎪⎫π3x +π6(A >0)在它的一个最小正周期内的图象上,最高点与最低点的距离是5,则A 等于( )A .1B .2C .4D .82.已知函数y =A sin(ωx +φ)+B 的一部分图象如图所示,如果A >0,ω>0,|φ|<π2,则( )A .A =4B .ω=1C .φ=π6 D .B =43.同时具有性质“(1)最小正周期是π;(2)图象关于直线x =π3对称;(3)在⎣⎢⎡⎦⎥⎤-π6,π3上单调递增”的一个函数是( ) A .y =sin ⎝ ⎛⎭⎪⎫x 2+π6B .y =cos ⎝ ⎛⎭⎪⎫2x +π3C .y =sin ⎝ ⎛⎭⎪⎫2x -π6D .y =cos ⎝ ⎛⎭⎪⎫2x -π64.某同学用“五点法”画函数y=A sin(ωx+φ)(A>0,ω>0,|φ|<π2)在一个周期内的简图时,列表如下:5.已知函数f(x)=sin(2x+φ)(-π<φ<0)图象的一条对称轴是直线x=π6,则φ的值为__________.1.求函数y=A sin(ωx+φ)的解析式中的“φ”的方法有哪些?[提示](1)把图象上的一个已知点的坐标代入来求.(2)寻找“五点作图法”中的某一个点来求,具体如下:利用“第一点”时,令ωx+φ=0;利用“第二点”(即图象的“峰点”)时,令ωx+φ=π2;利用“第三点”(即图象下降时与x轴的交点)时,令ωx+φ=π;利用“第四点”(即图象的“谷点”)时,令ωx+φ=3π2;利用“第五点”时,令ωx+φ=2π.注意:要观察题目所给图象是否适合用“五点作图法”.2.在研究函数y=A sin(ωx+φ)(A>0,ω>0)性质时,常采用什么方法?[提示]采用“换元”法整体代换,将(ωx+φ)看作一个整体,可令“z=ωx+φ”,借助y=A sin z的性质求解.。
5.6 函数y=Asin(ωx+ψ)(教材完美复刻)课件 人教A版2019版必修一 原创精品
如图, 以O为原点,以与水平面平行的直线为x轴建立直角坐标系. 设t 0
时, 盛水筒M位于点P0 , 以Ox为始边,OP0为终边的角为, 经过t s后运动到 点P( x, y), 于是, 以Ox为始边,OP为终边的角为 x , 并且有
y r sin(t )
①
所以, 盛水筒M距离水面的高度H与时间t的关系是
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人 距离地的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确 到0.1)
(3) 如图,甲、乙两人的位置分别用点A, B表示, 则AOB 2 . 经过
48 24
t
min 后甲距离地面的高度为H1
55
sin
15
分析:摩天轮上的座舱运近似地看作是质点在圆周 上做匀速旋转.在旋转过程中,游客距离地面的高 度呈现周而复始的变化,因此可以考虑用三角函数 来刻画.
设座舱距离地面最近的位置为点P, 以轴心O为原点,与地面平行的直线
为x轴建立直角坐标系.
(1) 设t 0 min时, 游客甲位于点P(0, 55), 以OP为终边的角为 ,
步骤1 步骤2 步骤3 步骤4
y
1
o
-1
2
y
1
o
-1
2
1y
2
3 2
x
(沿x轴平行移动)
3
2 2
x
(横坐标伸长或缩短)
o 2
3 2
2
x
-1
(纵坐标伸长或缩短)
y
1
2
o
3 2
x
-1
2
例1
画出函数y
2
sin
3
高中数学 函数y=Asin(ωx+φ)的图像课件 新人教A版必修4
课堂小节:
1.Y=Asin(ωx+φ) (A>0,ω>0)中,A叫振幅,φ叫 伸缩 初相.A,ω的变化引起______变换,φ的变化引 平移 起______变换.
(横向变换可简记为:左加右减,小 伸大缩.)
再见!
函数y=Asin(ωx+φ) 的图象
引入:
函数y=Asin(ωx+φ)的图象有什么特征?
周期2π/ω Φ 初相 A 振幅 相位ωx+φ
本节课我们来探索A,ω,φ对y=Asin(ωx+φ)图象 的影响
探究一:对 y sin( x ) 的图象的影响
π Y=sin(x+ ) 和 Y=sin(x- π ) 的简图 例1.画出 3 4 Y=sinx的图象 向左平移π/3个单位长度 Y=sin(x+π ) 的图象 3 Y=sin(x- π ) 的图象 Y=sinx的图象 向右平移π/4个单位长度 4 y Y=sin(x+π ) Y=sinx y sin( x 3 1
例4.用“五点法”画出函数y=3sin(2x+π/3)的简 图. 7 解: x
2x
36012 Nhomakorabea3
sin(2 x / 3) 0
3sin(2x+π/3) y 3
5 6
2
3 2
12
5 6
2
1
0
-1
0
0
3
0
-3
0
2
1
3
oπ 6 12 -1
2
3 2
2
步骤4
得到y A sin( x )在某周期内的简图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
恩城中学2019-2020第一学期高一数学学科导学稿(学生版)
编号B4-12
编写人:吴志章 审稿:高一级备课组 定稿日: 2019.12.12
高一( )班 第 小组 姓名: 评价:
一、课题 §1.5 函数y = Asin(ωx+)图象(第二课时)(必修4,P49~ P55)
二、数学核心素养目标:
1、课程目标:
(1)
会用“五点法”作函数)sin(xAy的图象;
(2)会根据条件求函数的解析式。
2、通过对函数y=sinx到y=Asin(ωx+φ)的图象变换规律的探索过程的体验,培养
学生的观察能力和探索问题的能力,数形结合的思想。
一、复习
1、作出y=2sin(2x-4)的图象. (作法:五点作图法. )
列表:
2
x
-4
x
y=2 sin(2x-4)
2. 讨论上述两个函数如何由y=sinx变换得到?如何变换得到y=sinx?
2
的物理意义:其中,二、函数)0,0)(,0[)sin(AAxxy
1、定义:函数y=Asin(ωx+φ)中 (A>0,ω>0),A叫振幅,T=2叫周期,f=1T=2叫
频率,ωx+φ叫相位,φ叫初相.
2、练习:
函数y=2sin(2x-4) 周期 、频率 、相位 、初相 .
最大(小)值及x为何值 单调性
三、应用
例1、教材P54页的例2。
2.例由右图所示函数图象,求
sin()(||).yAx的表达式
sin()(0,0,)2 .yAxA练习:右图所示的曲线是的图象的一部分,
求这个函数的解析式
37
2
1
2
y
o
x
8
88
5
2
2
y
o
x
12
6
3
结合图形观察有关性质(周期、振幅),依次求各量.小结:由图得几何性质,转化为
相应数量关系. 注意求初相.
【反思归纳】 确定y=Asin(ωx+φ)+B(A>0,ω>0)的解析式的步骤
(1)求A,B,确定函数的最大值M和最小值m,则A=M-m2,B=M+m2.
(2)求ω,确定函数的周期T,则ω=2πT.
(3)求φ,常用方法有:
①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)
或把图象的最高点或最低点代入.
②五点法:确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.
四、 练习:
1、已知函数y=3sin(2x+6)+1.
① 定义域为 ,值域为 ,周期为 ,
相位为 、初相为 .
② 当x= 时,y有最小值,ymin= .
当x= 时,y有最大值,ymax= .
③ 当x∈ 时,y单调递增,
当x∈ 时,y单调递减.
五、课时小结:
1、会用“五点法”作函数)sin(xAy的图象
2、对于给定条件求函数
)sin(xAy
的解析式一般先确定振幅A,周期T,
解得,最后用点(最高或最低点)代入求。
4
六、课后作业:
1、
1.为了得到函数y=sin3x+π4的图象,可以将函数y=cos 3x的图象
( )
A.向右平移π12个单位 B.向右平移π4个单位
C.向左平移π12个单位 D.向左平移π4个单位
2、(2015高考新课标全国卷Ⅰ)
函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )
(A)kπ-14,kπ+34,k∈Z
(B)2kπ-14,2kπ+34,k∈Z
(C)k-14,k+34,k∈Z
(D)2k-14,2k+34,k∈Z
