人《圆锥的体积》课件PPT
合集下载
北师大版六年级下册数学《圆锥的体积》 (共19张PPT)

出圆锥体积的计算公式:v= sh
在公式运用方面:采取逐步深入的模式,让 学生讨论在:①已知圆锥的高与底面半径;②已 知圆锥的高与底面直径;③已知圆锥的高与底面 周长三种情况下,如何使用公式计算。
三、说学法
新课改要求:让学生有充足的时间和广阔的 空间学习,教师只是学生学习的指导者和参与者。
针对本节课,在学法上主要采取: 1、学生通过自己动手进行操作实验、观察比较、 讨论小结,最终推导出圆锥的计算公式,从而初 步学会运用实验的方法来探索新知识。 2、学生能做的、能想的、能说的,让学生自己 做、自己想、自己说。 3、教师提出恰当合理的问题,让学生在分析、 讨论、探索的前提下争取自己解决,对于有一定 困难的问题,老师再从中提醒、点拨,从而挖掘 学生的潜能,让他们体验学习成功的乐趣。
北师大版 六年级下册 第一单元 圆柱与圆锥
一、说教材
1、教材分析 “圆锥的体积”教学是在学生学习了立体
图形——长方体、正方体、圆柱体的基础上, 认识了圆柱和圆锥的特征,会计算圆柱的表面 积、体积的基础上进行教学的。教材突出了探 索体积计算公式的过程,引导学生在实验基础 上进行公式推导。通过观察、比较、分析、推 理、概括和抽象,自主发现圆锥的体积计算公 式,积累数学活动经验,经历数学化的过程,获 得解决问题的方法。
北师大版 六年级下册 第一单元 圆柱与圆锥
汽车产业开发区第七小学 执教者:齐 毅
一、自主学习
1.圆柱的体积公式:( V = Sh )
2.圆柱与圆锥有哪些相同的特征: (底面都是圆形,侧面都是曲面,都有高 )。
3.在推导圆柱体积计算公式的过程中,我 们把(圆柱体)转化成(长方体) 。
4.猜想:等底等高的圆柱和圆锥的体积 (不相等 )。(填“相等”或“不相等”)
在公式运用方面:采取逐步深入的模式,让 学生讨论在:①已知圆锥的高与底面半径;②已 知圆锥的高与底面直径;③已知圆锥的高与底面 周长三种情况下,如何使用公式计算。
三、说学法
新课改要求:让学生有充足的时间和广阔的 空间学习,教师只是学生学习的指导者和参与者。
针对本节课,在学法上主要采取: 1、学生通过自己动手进行操作实验、观察比较、 讨论小结,最终推导出圆锥的计算公式,从而初 步学会运用实验的方法来探索新知识。 2、学生能做的、能想的、能说的,让学生自己 做、自己想、自己说。 3、教师提出恰当合理的问题,让学生在分析、 讨论、探索的前提下争取自己解决,对于有一定 困难的问题,老师再从中提醒、点拨,从而挖掘 学生的潜能,让他们体验学习成功的乐趣。
北师大版 六年级下册 第一单元 圆柱与圆锥
一、说教材
1、教材分析 “圆锥的体积”教学是在学生学习了立体
图形——长方体、正方体、圆柱体的基础上, 认识了圆柱和圆锥的特征,会计算圆柱的表面 积、体积的基础上进行教学的。教材突出了探 索体积计算公式的过程,引导学生在实验基础 上进行公式推导。通过观察、比较、分析、推 理、概括和抽象,自主发现圆锥的体积计算公 式,积累数学活动经验,经历数学化的过程,获 得解决问题的方法。
北师大版 六年级下册 第一单元 圆柱与圆锥
汽车产业开发区第七小学 执教者:齐 毅
一、自主学习
1.圆柱的体积公式:( V = Sh )
2.圆柱与圆锥有哪些相同的特征: (底面都是圆形,侧面都是曲面,都有高 )。
3.在推导圆柱体积计算公式的过程中,我 们把(圆柱体)转化成(长方体) 。
4.猜想:等底等高的圆柱和圆锥的体积 (不相等 )。(填“相等”或“不相等”)
《圆锥体积》公式(动画版)PPT课件

圆锥的特性
圆锥的侧面是一个曲 面,展开后呈扇形。
圆锥的高是从圆锥的 顶点到底面的垂直距 离。
圆锥的底面是一个圆, 其半径为圆锥的底面 半径。
圆锥的应用
在工程、建筑和制造业等领域,圆锥 经常被用作基础几何形状来设计和制 造各种结构和机械部件。
在日常生活和科学实验中,圆锥也经 常被用来描述和解决各种实际问题, 如沙堆、冰淇淋蛋筒等。
推导过程中的关键点
利用微积分的知识,将圆锥体切割成无数个小的圆柱体, 每个圆柱体的体积为πr²h/3,再将这些圆柱体的体积相加 即可得到圆锥体的体积公式。
回顾圆锥体积公式的应用
圆锥体积公式的应用
注意事项
圆锥体积公式在日常生活和工程中有 着广泛的应用,如计算圆锥形物体的 容积、计算圆锥形物体的表面积等。
详细描述:将圆锥体积与其他几何形状的体积进行对比 分析,加深学生对圆锥体积的理解。
05
总结与回顾
总结圆锥体积公式的推导过程
圆锥体积公式的推导过程
通过将圆锥体切割成无数个小的圆柱体,再将这些圆柱体 的体积相加,最终得到圆锥体的体积公式。
圆锥体积公式
V=1/3πr²h,其中V表示体积,r表示底面半径,h表示高。
谢谢观看
圆锥体积的计算公式
圆锥体积计算公式
V = (1/3) × π × r^2 × h,其中r为 底面半径,h为高。
圆锥体积公式的推导
利用圆柱体积公式,将圆柱的底面半 径替换为圆锥的底面半径,高替换为 圆锥的高,得到圆锥体积的计算公式 。
03
圆锥体积公式的应用
计算圆锥的体积
总结词
通过圆锥体积公式,我们可以计算出圆锥体的体积。
圆锥与圆柱的关系
总结词
圆锥的体积课件ppt

表面积由底面和侧面组成, 底面的面积是πr²,侧面的面积 是πrl,其中r为底面半径,l为母
线长。
圆锥的体积是底面面积与高的乘 积的三分之一,即V = (1/3)πr²h。
因此,圆锥的体积与表面积之间 没有直接的关系,但可以通过底
面半径和高来间接计算。
02
圆锥的体积计算
圆锥的体积课件
• 圆锥的体积公式 • 圆锥的体积计算 • 圆锥的体积与现实生活 • 圆锥的体积与其他几何体的关系
01
圆锥的体积公式
圆锥的体积公式推导
圆锥的体积公式为:V = (1/3)πr²h,其中r为底面半径,
h为高。
该公式是通过将圆锥切割成若干 个小的圆柱体,然后求和圆柱体 的体积,最后得到圆锥的体积。
01
03
在自然现象描述方面,圆锥的体积可用于描述如沙漏、 火山喷发等现象的过程和规律,帮助人们更好地理解
和预测这些自然现象。
04
在手工艺品制作方面,圆锥的体积可用于计算手工艺 品如陶器、花瓶等材料的用量,从而制作出精美的艺 术品。
04
圆锥的体积与其他几何体的关系
圆锥的体积与圆柱体的关系
总结词
圆锥的体积是其底面积与高的乘积的 三分之一,这与圆柱体的体积公式存 在关联。
圆锥的体积计算方法
01
圆锥的体积计算公式
V = (1/3)πr²h,其中r是底面半径,h是高。
02 03
圆锥体积公式的推导
通过微积分的知识,将圆锥的底面分割成无数个小的扇形,再将这些扇 形旋转并叠加成一个近似于圆柱体的形状,通过求这个圆柱体的体积来 近似得到圆锥的体积。
圆锥体积公式的应用
在几何、物理、工程等领域中,圆锥的体积公式被广泛应用于计算各种 实际问题,如求圆锥形物体的容积、液体容量等。
线长。
圆锥的体积是底面面积与高的乘 积的三分之一,即V = (1/3)πr²h。
因此,圆锥的体积与表面积之间 没有直接的关系,但可以通过底
面半径和高来间接计算。
02
圆锥的体积计算
圆锥的体积课件
• 圆锥的体积公式 • 圆锥的体积计算 • 圆锥的体积与现实生活 • 圆锥的体积与其他几何体的关系
01
圆锥的体积公式
圆锥的体积公式推导
圆锥的体积公式为:V = (1/3)πr²h,其中r为底面半径,
h为高。
该公式是通过将圆锥切割成若干 个小的圆柱体,然后求和圆柱体 的体积,最后得到圆锥的体积。
01
03
在自然现象描述方面,圆锥的体积可用于描述如沙漏、 火山喷发等现象的过程和规律,帮助人们更好地理解
和预测这些自然现象。
04
在手工艺品制作方面,圆锥的体积可用于计算手工艺 品如陶器、花瓶等材料的用量,从而制作出精美的艺 术品。
04
圆锥的体积与其他几何体的关系
圆锥的体积与圆柱体的关系
总结词
圆锥的体积是其底面积与高的乘积的 三分之一,这与圆柱体的体积公式存 在关联。
圆锥的体积计算方法
01
圆锥的体积计算公式
V = (1/3)πr²h,其中r是底面半径,h是高。
02 03
圆锥体积公式的推导
通过微积分的知识,将圆锥的底面分割成无数个小的扇形,再将这些扇 形旋转并叠加成一个近似于圆柱体的形状,通过求这个圆柱体的体积来 近似得到圆锥的体积。
圆锥体积公式的应用
在几何、物理、工程等领域中,圆锥的体积公式被广泛应用于计算各种 实际问题,如求圆锥形物体的容积、液体容量等。
《圆锥的体积公式》课件

圆锥的数学计算公式
圆锥的体积公式
圆锥的体积公式为:V = (1/3)πr²h,其中V表示体积,r表 示底部半径,h表示高度。
推导圆锥的体积公式
通过对圆锥的分析和推理,可 以得出其体积公式的推导过程。 这个过程充满了数学的美妙。
圆锥的侧面积公式
圆锥的侧面积公式为:S = πrl, 其中S表示侧面积,r表示底部 半径,l表示斜边长度。
《圆锥的体积公式》PPT 课件
本PPT将详细介绍圆锥的体积公式以及相关内容。通过本课件,您将全面了解 圆锥的数学计算公式、实际应用及其优缺点。让我们一起探索吧!
简介
什么是圆锥
圆锥是由一个圆锥面和一个尖顶构成的几何体。它具有特殊形状和独特的属性。
圆锥的特点
圆锥具有一个尖角和一个底部圆形面。它可以分为直角圆锥、斜角圆锥等不同类型。
通过数学的推导和几何形状的 分析,我们可以得到圆锥的体 积公式。这是一种深奥而重要 的数学成果。
圆锥的应用范围
圆锥的应用范围广泛,涵盖建 筑、工程、制造业等许多行业。 它在现实生活中扮演着重要的 角色。
圆锥的优缺点
圆锥具有形状独特和结构稳定 等优点,但也存在制造成本较 高和加工难度较大等不足之处。
参考文献
本PPT没有涉及特定的参考文献,但参考了诸多数学和几何学的相关资料。
实际应用
1
圆锥的应用领域
圆锥广泛应用于建筑、工程、制造业等
ห้องสมุดไป่ตู้圆锥的计算方法
2
领域。它们在各个行业中发挥着重要的 作用。
根据圆锥的不同应用场景,我们可以采
用不同的计算方法来求解其体积和侧面
积。
3
圆锥的优点和不足
圆锥的优点包括形状独特、结构稳定等; 不足之处可能包括制造成本较高、难以 加工等。
人教版《圆锥的体积》(完美版)PPT课件3
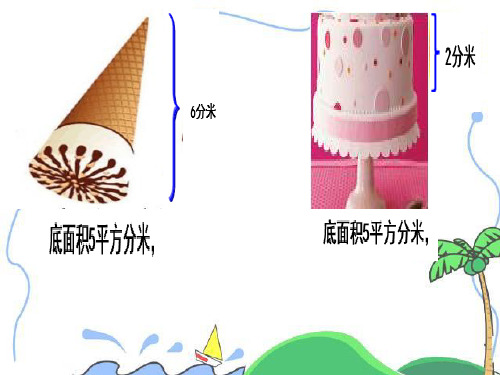
答:这个零件的体积是200立方厘米。
你发现了什么?
圆柱的体积是与它等底 等高圆锥体积的3倍.
例3、工地上有一堆沙子,近似于 一个圆锥(如下图)。这堆沙子的 体积大约是多少?如果每立方米沙 子重1.5t,这堆沙子大约重多少吨 ?(得数保留两位小数)
1.2m
4m
(√ )
选择题:
1、一个圆柱的体积是30立方厘米,与它等 底等高的圆锥体积是( )1立方厘米
(1)10 (2)30
(3)90
2、 有一圆锥的体积是30立方厘米,与 它等底等高的圆柱体积是( )3立方厘 米
(1)10
(2)30
(3)90
3、如图把圆柱形铅笔削成圆锥形,削 去部分的体积是圆柱体积的(2 )
你认为 ( )的列式是正确的。
3、正方体、长方体、圆锥体的体积都等于底面积×高。
(2 ) d =6厘米
h =2厘米
圆柱的体积是圆锥体积的9倍
2、 有一圆锥的体积是30立方厘米,与它等底等高的圆柱体积是( )立方厘米
4、高相等,圆锥底面半径是圆柱底面半径的3倍
我们总习惯把成功当成一种结果,事实上,成功在本质上是一种自强不息的状态,有了这种状态,我们才会成为一名真正的强者!
(1)三分之一 (2)三分之二 (3)无法确定
考考你:
有一根底面直径是6厘米,长是15厘米的圆 柱形钢材,要把它削成与它等底等高的圆锥形 零件。要削去钢材多少立方厘米?
15厘米
6厘米
塑料瓶中的水有(
)毫升?
塑料瓶底的面积与锥形杯口的面积相等,塑料
瓶子中的饮料倒入锥形杯子中,能倒满( )杯
我们总习惯把成 功当成一种结果,事 实上,成功在本质上 是一种自强不息的 状态,有了这种状态, 我们才会成为一名 真正的强者!
你发现了什么?
圆柱的体积是与它等底 等高圆锥体积的3倍.
例3、工地上有一堆沙子,近似于 一个圆锥(如下图)。这堆沙子的 体积大约是多少?如果每立方米沙 子重1.5t,这堆沙子大约重多少吨 ?(得数保留两位小数)
1.2m
4m
(√ )
选择题:
1、一个圆柱的体积是30立方厘米,与它等 底等高的圆锥体积是( )1立方厘米
(1)10 (2)30
(3)90
2、 有一圆锥的体积是30立方厘米,与 它等底等高的圆柱体积是( )3立方厘 米
(1)10
(2)30
(3)90
3、如图把圆柱形铅笔削成圆锥形,削 去部分的体积是圆柱体积的(2 )
你认为 ( )的列式是正确的。
3、正方体、长方体、圆锥体的体积都等于底面积×高。
(2 ) d =6厘米
h =2厘米
圆柱的体积是圆锥体积的9倍
2、 有一圆锥的体积是30立方厘米,与它等底等高的圆柱体积是( )立方厘米
4、高相等,圆锥底面半径是圆柱底面半径的3倍
我们总习惯把成功当成一种结果,事实上,成功在本质上是一种自强不息的状态,有了这种状态,我们才会成为一名真正的强者!
(1)三分之一 (2)三分之二 (3)无法确定
考考你:
有一根底面直径是6厘米,长是15厘米的圆 柱形钢材,要把它削成与它等底等高的圆锥形 零件。要削去钢材多少立方厘米?
15厘米
6厘米
塑料瓶中的水有(
)毫升?
塑料瓶底的面积与锥形杯口的面积相等,塑料
瓶子中的饮料倒入锥形杯子中,能倒满( )杯
我们总习惯把成 功当成一种结果,事 实上,成功在本质上 是一种自强不息的 状态,有了这种状态, 我们才会成为一名 真正的强者!
《圆锥的体积》1PPT课件

•
• •
•
•
D.
圆锥的体积比圆柱体积——。
2
1、一个圆柱体体积是27立方分 米,与它等底等高的圆锥的体积是 ( )立方分米。
2、一个圆锥体积是15立方厘 米,与它等底等高的圆柱的体积是 ( )立方厘米.
思考
要求圆锥的体积,必须知道
1 哪两个条件?为什么要乘 ? 3
主页
例1、一个圆锥形的零件,底面 积是170平方厘米,高是12厘米。 这个零件的体积是多少?
1 × 170 × 12=680 (立方厘米) 3
答:这个零件的体积是680立方 厘米。
求圆锥的体积,还可能出现哪些 情况?在这些情况下,分别怎样求圆锥的体积?想一想主页必要条件
V =
1 3
sh
计算圆锥的体积所必须的条件可以是:
底面积和高 底面半径和高 底面直径和高 底面周长和高
圆锥体积
选择笔练:求出下列各圆锥的体积
苏科版六年级数学下册
圆锥的体积
复习:
口算下列圆柱的体积。 ①底面积是7平方厘米,高 8厘米, 体积 = ? ②底面半径是 3分米, 高10分米, 体积 = ? ③底面直径是 6分米, 高10分米, 体积 = ?
1、说一说圆锥有哪些特征?
(1)顶部:是一个顶点; 圆锥特征 (2)底面:是一个圆; (3)侧面:是一个曲面(展开是一个扇形); (4)高只有一条。
S=3.14平方米 r=1米
h=3米 h=3米
d=2米
C=6.28米
h=3米
h=3米
努 力 吧 !
一、填空: 用字母表示是(V= 3 s h )。 1 2. 圆柱体积的 3与和它( 等底等高 )的圆 锥的体积相等。 3. 一个圆柱和一个圆锥等底等高,圆柱的 体积是3立方分米,圆锥的体积是( 1 ) 立方分米。 4. 一个圆锥的底面积是12平方厘米,高是 6厘米,体积是( 24 )立方厘米。
圆锥的认识和体积PPT课件
圆锥的底面展开图是 一个圆。
圆锥的表面积计算
圆锥的表面积=圆锥的侧面积+圆锥的底面积。 圆锥的侧面积=πrl(其中r为底面半径,l为母线长)。
圆锥的底面积=πr^2。
圆锥的特殊性质和定理
圆锥的轴截面是等腰三角形。
圆锥的侧面展开图扇形的圆心角等于360度减去底 面圆心角。
圆锥的母线长等于底面圆的直径时,圆锥侧面展 开图是一个半圆。
圆锥是正方体的一种特殊形式,当正方 体的边长等于其高时,正方体就变成了
圆锥。
圆锥的体积是正方体体积的1/3,这是 圆锥和正方体在几何学中经常一起出现,
由于它们的几何形状和尺寸决定的。
特别是在析几何和微积分中。
05
圆锥的拓展知识
圆锥的展开图
圆锥的侧面展开图是 一个扇形。
圆锥的侧面展开图扇 形的弧长等于圆锥底 面的周长。
圆锥的认识和体积ppt课 件
• 圆锥的初步认识 • 圆锥的体积计算 • 圆锥的实际应用 • 圆锥与其他几何体的关系 • 圆锥的拓展知识
01
圆锥的初步认识
圆锥的定义和特点
总结词
圆锥是由一个圆形底面和与之相对的顶点构成的几何体,其特点是侧面展开后 为一个扇形。
详细描述
圆锥是一种常见的几何体,其底面是一个固定的圆,而顶点则位于圆的正上方。 侧面由无数个等腰三角形组成,当这些三角形展开时,形成一个扇形。圆锥的 侧面高与底面半径之间的比例关系决定了圆锥的形状。
圆锥和圆柱在几何学中经常一起出现,特别是在解析几何和微积分中。
圆锥与球体的关系
圆锥的体积是球体体积的1/3,这是由于它们的几何形 状和尺寸决定的。
圆锥是球体的一种特殊形式,当球体的半径等于其高 时,球体就变成了圆锥。
