大学物理刚体力学总结
(完整版)大学物理力学总结

大学物理力学公式总结➢第一章(质点运动学)1.r=r(t)=x(t)i+y(t)j+z(t)kΔr=r(t+Δt)- r(t)一般地|Δr|≠Δr2.v=drdt a=dvdx=d r2dt23.匀加速运动:a=常矢v0=v x+v y+v z r=r0+v0t+12at24.匀加速直线运动:v= v0+at x=v0t+12at2 v2-v02=2ax5.抛体运动:a x=0 a y=-gv x=v0cos v y=v0sinθ-gtx=v0cosθ•t y=v0sinθ•t-12gt26.圆周运动:角速度ω=dθdt =v R角加速度α=dωdt加速度a=a n+a t法相加速度a n=v2R=Rω2,指向圆心切向加速度a t=dvdt=Rα,沿切线方向7.伽利略速度变换:v=v’+u➢第二章(牛顿运动定律)1.牛顿运动定律:第一定律:惯性和力的概念,惯性系的定义, p=m v第二定律:F=dpdt当m为常量时,F=m a第三定律:F12=-F21力的叠加原理:F=F1+F2+……2.常见的几种力:重力:G=m g弹簧弹力:f=-kx3.用牛顿定律解题的基本思路:1)认物体2)看运动3)查受力(画示力图)4)列方程(一般用分量式)➢第三章(动量与角动量)1.动量定理:合外力的冲量等于质点(或质点系)动量的增量,即F dt=d p2.动量守恒定律:系统所受合外力为零时,p=∑p i i =常矢量 3. 质心的概念:质心的位矢 r c =∑m i i r im(离散分布) 或 r c =∫rdmm(连续分布)4. 质心运动定理:质点系所受的合外力等于其总质量乘以质心的加速度,即 F=m a c5. 质心参考系:质心在其中静止的平动参考系,即零动量参考系。
6. 质点的角动量:对于某一点, L=r ×p=m r ×v7. 角动量定理: M =dLdt其中M 为合外力距,M=r ×F ,他和L 都是对同一定点说的。
大学物理第三章刚体力学

薄板的正交轴定理:
Jz Jx J y
o x
y
X,Y 轴在薄板面上,Z轴与薄板垂直。
例3、质量m,长为l 的四根均匀细棒, O 组成一正方形框架,绕过其一顶点O 并与框架垂直的轴转动,求转动惯量。 解:由平行轴定理,先求出一根棒 对框架质心C的转动惯量:
C
m, l
1 l 2 1 2 2 J ml m( ) ml 12 2 3
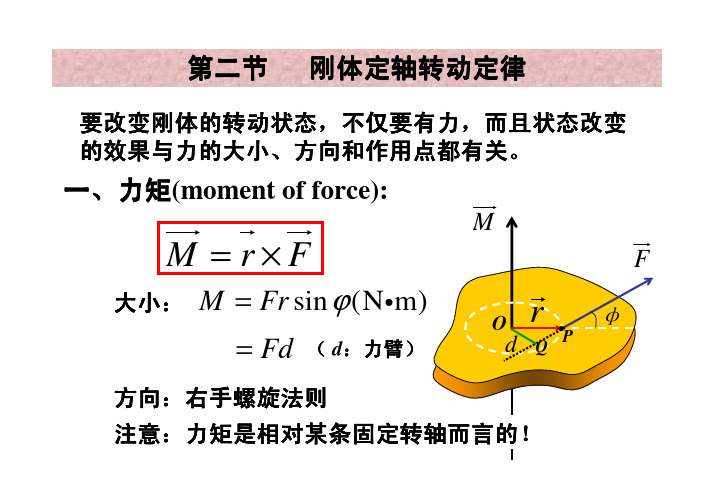
M F2 d F2 r sin
若F位于转动平面内,则上式简化为
M Fd Fr sin
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
例9 行星运动的开普勒第二运动定律:行星对太阳 的位矢在相等的时间内扫过相等的面积。 解:行星在太阳引力(有心 力)作用下沿椭圆轨道运动, 因而行星在运行过程中,它 对太阳的角动量守恒不变。
L rmvsin 常量
因而掠面速度:
dS dt
r dr sin 2dt
1 rv sin 常量 2
Fi fi Δmi ai
切向的分量式为
Fi sin i f i sin i mi ri
Fi sin i f i sin i mi ri
两边同乘ri,得
Fi ri sin i fi ri sin i mi ri2
上式左边第一项为外力Fi对转轴的力矩,而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程,求和得
质点的角动量一质量为m的质点以速度v运动相对于坐标原点o的位置矢量为r定义质点对坐标原点o的角动量为sinrmv282质点的角动量定理质点所受的合外力对某一参考点的力矩等于质点对该点的角动量对时间的变化率角动量定理
大学物理_第06章 刚体力学

接触点相同线速度时: 1r1 2r2
联立解得:
1
J1
J1 ( r1 r2
)2
J2
0
2
r1 r2
J1
J1
(
r1 r2
)2
J
2
0
书上177页
解: dm
2 rdr
m2 rdr R2
2mrdr R2
df
2mrdr R2
g
dM
r
2mrdr R2
g et
2mr 2dr R2
g
M
R
dM
0
R 0
2mr 2 dr R2
dm dV
其中、、分别为质量线密度、面密度和体密度。
转动惯量
2). 转动惯量的计算:
质点、圆环、圆筒绕中心轴转动
z
z
Rm
oR m
R
m
o
质点的转动惯量为
Jo mR2
对于匀质圆环和薄圆筒,因各质元到轴的垂直距
离都相同,则有
Jo mR2
圆盘、圆柱绕中心轴转动
对于质量为m、半径为R、厚为l 的均匀圆盘取半径为 r宽
需要一个动力学方程 — 角动量定理
角动量定理: M dL
dt
转轴转动角动量表达式:
Mz
dLz dt
转轴分量角动量定理表达式:
n
Lz z mi (xi2 yi2 ) z J i1
转动定律:
Mz
dLz dt
d (J)
dt
J
d
dt
J
z v
r
P
当刚体绕固定轴转动时,刚体对该轴的转动惯量与角加速 度的乘积等于外力对此轴的合力距。 — 定轴转动定律
大学物理力学部分归纳总结

运动学部分解题指导
1、已知运动方程,求速度,加速度,用微分法。
两 大 类
? v
?
? dr
,
? a
?
? dv
dt
dt
型 2、已知加速度和初始条件,求速度、位移、路
程和运动方程(或已知速度和初始条件,求位移、
路程和运动方程),用积分法。
? ? t?
? v ? v0 ?
a ?dt
t0
? ? t?
? r ? r0 ?
3、功率
P
?
dW
?
? F
?dr?
?
? F
?v?
?
Fv cos?
dt dt
6
4、保守力作功与势能概念: dW ? ? dEp
? WA?
B
?
B
? f
?dr?
?
Ep ( A) ?
EP (B)
?
?[Ep (B) ?
Ep ( A)]
A
万有引力势能
重力势能
? E p
?
? r
?
G
mM r2
dr
?
?G
mM r
0
? Ep ? (? mg)dz ? mgz
? (3)判断过程中对某点(或某轴)合外力矩是否为零,或者 角动量守恒条件是否成立。
? (4)若守恒条件成立,确定正方向,列方程,求解
? 分解综合法:对于较为复杂问题,不是只用一个定理、定律
就能解决,要将整个过程分解成几个子过程,对每一子过程
应用上述方法。
18
典型习题分析
? 例题(1) 如图所示,木块 A的质量为 1.0kg ,木块B的
9、功率
大学物理 第四章 刚体的转动小结

1 2
1 2
• 8、(本题4分) v 从某点开始 • 一物体在某瞬时,以初速度 运动,在 t时间内,经一长度为S的曲线 路径后,又回到出发点,此时速度为 , -v 则在这段时间内: S • 物体的平均速率是 ; t 2v • 物体的平均加速度是 t .0 Nhomakorabea0
0
• 9、(本题3分) • 一圆锥摆摆长为l、摆锤质量为m,在 水平面上作匀速圆周运动,摆线与铅直 线夹角θ,则 • (1) 摆线的张力T= mg / cos _____________________; • (2) 摆锤的速率v= _____________________.
t
a
v v0 a t
2 2 2 v v0 2 a( x x0 )
x x0 v0t
1
at
2
t
a-t曲线下面积为Δ t 时间内的Δv
二、曲线运动
1、位置矢量,运动方程,参数方程,轨道方程
2、位移、速度、加速度;
直角坐标系
v dr dt
dx dy dz i j k dt dt dt
0 2 0
• 13、(本题10分) • 一质量为m的物体悬于一条轻绳的一 端,绳另一端绕在一轮轴的轴上,如图 所示.轴水平且垂直于轮轴面,其半径 为r,整个装置架在光滑的固定轴承之 上.当物体从静止释放后,在时间t内下 降了一段距离S.试求整个轮轴的转动惯 量(用m、r、t和S表示).
x
d dx
v
2
a
S r
v r
(5)切向加速度和法向加速度
dv v 2 a e e n R e R e n dt R
1.3大学物理(上)刚体力学基础解析

四、转动定律的应用
[例3.3]: 质量为m的二物体A、B。A放在倾角为α的光滑 斜面上,经定滑轮由不可伸长的轻绳与B相连。定滑轮半 径R,质量为m。物体运动m时,绳与滑轮无相对滑动。 求绳中张力T1和T2及物体的加速度。 [分析]: 要采用隔离体法
T1 mg NA a T1 A mg β T2 T2 B a
1、刚体的平动 若刚体中所有点的运动轨迹都保持完全相同,或者说 刚体内任意两点间的连线总是平行于它们的初始位置 间的连线. 刚体平动
2、刚体的转动 刚体中所有的点都绕同一直线做圆周运动 . 分定轴转动和非定轴转动 . 转动又
质点运动
三、刚体定轴转动的描述
1、角位移、角速度和角加速度
刚体在一段时间内转过的角 度Δθ=θ2-θ1称为角位移
平均角速度
角速度
t
t 0
转动平面
lim
d t dt
角加速度
d lim t 0 t dt
2、角量与线量的关系
当刚体绕固定轴转动时,若刚体上某质元 i 到转轴的 距离为ri ,则该质元的线速度为
vi ri
切向加速度和法向加速度分别为
则 k 2 J k 2 即 J (2)求时间t d d 2 由M J J , 则 k J dt dt 1 0 1 t k 3 即 d dt 2 0 0 J
3-3
刚体定轴转动的动能定律
一、转动动能 n 1 1 n 1 2 2 2 2 2 Ek mi ri ( mi ri ) J 2 i 1 2 i 1 2
dm ds dm dV
面密度和体密度。
线分布
面分布
体分布
注 意
只有对于几何形状规则、质量连续且均匀分布
大学物理CH.-刚体力学(PDF)
β
ri Fi
sinϕi
+
ri
fi
sinθi
=
∆mi
r2 i
β
质点∆mi的外力矩
质点∆mi的内力矩
对所有质点求和,可以得到:
∑ ∑ ∑ riFi sinϕi +
ri fi sinθi =
∆mi
r2 i
β
i=1
i=1
i=1
合内力矩∑ri fi sinθi 为零,则:
∑ ∑ riFi sinϕi =
∆mi
F = 0 p = 常量
Ek
=
1 2
mv2
A = ∫ F ⋅ dr =∆Ek
刚体定轴转动规律
M = r × F = dL = J β
dt
L = r × p = Jω
∫t2 Mdt = ∆L t1
M = 0 L = 常量
Ek
=
1 2
Jω2
A = ∫ M ⋅ dθ = ∆Ek
第五节 进 动 一、 进动(precession)现象:
= ∫ r 2λdl l
质量体分布,例如立方体、球体 质量面分布,例如薄片、薄球壳 质量线分布,例如细棒、细环
例2 计算质量为 m ,长为 L 的匀质细棒绕通过其 端点的垂直轴的转动惯量。
解:J = ∫ r 2dm
z
dm = λdl = m dl o
L
∫ J = L l2 ⋅ m dl 0L = 1 mL2 3
o ω
o’
ω
oG
二、杠杆回转仪的分析
设右图中的刚体回转仪处于平
o
衡状态,现将重物左移并将飞
ω 轮作如图方向旋转。则飞轮进
动的方向如何?
大学物理第五章刚体力学

d π 2 t dt 150
1 2 π 2 ct t 2 150 π t 2 t dt 积分 0 d 150 0
π 3 t rad 450
在 300 s 内转子转过的转数
π 3 4 N ( 300 ) 3 10 2 π 2 π 450
矩为零,故 F 对转轴的 力矩
其中 Fz 对转轴的力
F Fz F
z
k
O
F
M z k r F
r
Fz
F
M z rF sin
(2)刚体内作用力和反作用力的力矩互相抵消.
M ij
rj
j
Fji
ij
O
M ji
y
y
x
O Q
h
O
x
L
y 解 设水深h,坝长L,在坝面上取面积 元 dA Ldy ,作用在此面积元上的力
dF pdA pLdy
y
y
dA dA
x
O Q
h
h
y
dy dy
x
y dF O
pdA pLdy
Lx L
O
令大气压为 p0 ,则
p p0 g (h y)
dF PdA [ p0 g( h y )] Ldy
2
外力矩 Ft
内力矩
2
M ij 0
Fit Fit Ft
Ft
M ej ∑mi ri
定义转动惯量
J m r
j
2 j j
J r dm
2
o r
转动定律
M ej J
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理刚体力学总结 大学物理刚体力学总结 大学物理刚体力学总结 篇一: 大学物理力学总结 大学物理力学公式总结 ? 第一章(质点运动学) 1. r=r(t)=x(t)i+y(t)j+z(t)k Δr=r(t+Δt)- r(t) 一般地 |Δr |?Δr 2. v= a= dt dx d??d?? d2??dt 3. 匀加速运动: a=常矢 v0=vx+vy+vz r=r0+v0t+at2 ???? 4. 匀加速直线运动: v= v0+at x= v02 v2-v02=2ax 21 5. 抛体运动: ax=0 ay=-g vx=v0cs vy=v0sinθ-gt x=v0csθ?t y=v0sinθ?tgt2 21 6. 圆周运动: 角速度 = dt Rdθ v 角加速度 dt dω 加速度 a=an+at 法相加速度 an==Rω2 ,指向圆心 Rv2 切向加速度 at=Rα ,沿切线方向 dt d?? 7. 伽利略速度变换: v=v’+u ? 第二章(牛顿运动定律) 1. 牛顿运动定律: 第一定律: 惯性和力的概念,惯性系的定义 第二定律: F=, p=mv dtd?? 当m为常量时,F=ma 第三定律: F12=-F21 力的叠加原理: F=F1+F2+„„ 2. 常见的几种力: 重力: G=mg 弹簧弹力: f=-kx 3. 用牛顿定律解题的基本思路: 1) 认物体 2) 看运动 3) 查受力(画示力图) 4) 列方程(一般用分量式) ? 第三章(动量与角动量) 1. 动量定理: 合外力的冲量等于质点(或质点系)动量的增量,即 Fdt=dp 2. 动量守恒定律: 系统所受合外力为零时, p= ??????=常矢量 3. 质心的概念: 质心的位矢 rc= ???????? 离散分布) m 或 rc = ??dmm (连续分布) 4. 质心运动定理: 质点系所受的合外力等于其总质量乘以质心的加速度,即 F=mac 5. 质心参考系: 质心在其中静止的平动参考系,即零动量参考系。 6. 质点的角动量: 对于某一点, L=r×p=mr×v 7. 角动量定理: M= dtd?? 其中M 为合外力距,M=r×F,他和L 都是对同一定点说的。(质点系的角动量定理具有同一形式。) 8. 角动量守恒定律: 对某定点,质点(或质点系)受到的合外力矩为零时,则对于同一定点的L= 常矢量 ? 第四章(功和能) 1. 功: dA=F?dr , AAB=L ??????? A 2. 动能定理: 对于一个质点: Amvb- a2 2 2 1 2 B 1 对于一个质点系: Aext+Aint = EkB – EkA 3. 一对力的功: 两个质点间一对内力的功之和为 AAB= ??????????? ??它只决定于两质点的相对路径 4. 保守力: 做功与相对路径形状无关的一对力,或者说,沿相对的闭合路径移动一周做功为零的一对力。 5. 势能: 对保守内力可引进势能的概念。一个系统的势能Ep决定于系统的位形,定义为 –ΔEp=EpA – EpB = AAB 取B点为势能零点,即EpB=0,则 EpA = AAB 引力势能: EpGm1m2 r ?? 重力势能: Ep=mgh,以物体在地面为势能零点。 弹簧的弹性势能: Ep2,以弹簧的自然伸长为势能零点。 (来自:.smhaida.Cm 海达 范文 网:大学物理刚体力学总结)21 6. 由势能函数求保守力: Ft=- dEpdl 7. 机械能守恒定律: 在只有保守内力做功的情况下,系统的机械能保持不变。它是普遍的能量守恒定律的特例。 8. 守恒定律的意义: 不究过程的细节而对系统的初、末状态下结论;相应于自然界的每一种对称性,都存在着一个守恒定律。 9. 碰撞: 完全非弹性碰撞: 碰后合在一起; 弹性碰撞: 碰撞时无动能损失。 ? 第五章(刚体的定轴转动) 1. 刚体的定轴转动: 匀加速转动: ω=ω0+at ,θ=ω0t+at2 , ω2-ω02 =2αθ 21 2. 刚体定轴转动定律: MzdLzdt 以转动轴为z轴,为外力对转轴的力矩之和;Lz=Jω,J为刚体对转轴的转动惯量,则 M=Jα 3. 刚体的转动惯量: J= ????????2 (离散分布) , J= r2 dm(连续分布) 平行轴定理: J=Jc+md2 4. 刚体转动的功和能: 力矩的功: A= Mdθ θ1转动动能: Ek=Jω2 21θ2 刚体的重力势能: Ep=mghc 机械能守恒定律: 只有保守力做功时, Ek+ Ep =常量 5. 对定轴的角动量守恒: 系统(包括刚体)所受的对某一固定轴的合外力距为零时,系统对此轴的总角动量保持不变。 ※一些均匀刚体的转动惯量 篇二: 大学物理力学总结 大学物理力学公式总结 ? 第一章(质点运动学) 1. r=r(t)=x(t)i+y(t)j+z(t)k Δr=r(t+Δt)- r(t) 一般地 |Δr |?Δr 2. v= a== 3. 匀加速运动: a=常矢 v0=vx+vy+vz r=r0+v0t+at2 4. 匀加速直线运动: v= v0+at x= v0t+at2 v2-v02=2ax 5. 抛体运动: ax=0 ay=-g vx=v0cs vy=v0sinθ-gt x=v0csθ?t y=v0sinθ?t-gt2 6. 圆周运动: 角速度 ω== 角加速度 α= 加速度 a=an+at 法相加速度 an==R ,指向圆心 切向加速度 at==Rα ,沿切线方向 7. 伽利略速度变换: v=v’+u ? 第二章(牛顿运动定律) 1. 牛顿运动定律: 第一定律: 惯性和力的概念,惯性系的定义 第二定律: F= , p=mv 当m为常量时,F=ma 第三定律: F12=-F21 力的叠加原理: F=F1+F2+„„ 2. 常见的几种力: 重力: G=mg 弹簧弹力: f=-kx 3. 用牛顿定律解题的基本思路: 1) 认物体 2) 看运动 3) 查受力(画示力图) 4) 列方程(一般用分量式) ? 第三章(动量与角动量) 1. 动量定理: 合外力的冲量等于质点(或质点系)动量的增量,即 Fdt=dp 2. 动量守恒定律: 系统所受合外力为零时, p=常矢量 3. 质心的概念: 质心的位矢 rc=(离散分布) 或 rc = (连续分布) 4. 质心运动定理: 质点系所受的合外力等于其总质量乘以质心的加速度,即 F=mac 5. 质心参考系: 质心在其中静止的平动参考系,即零动量参考系。 6. 质点的角动量: 对于某一点, L=r×p=mr×v 7. 角动量定理: M= 其中M 为合外力距,M=r×F,他和L 都是对同一定点说的。(质点系的角动量定理具有同一形式。) 8. 角动量守恒定律: 对某定点,质点(或质点系)受到的合外力矩为零时,则对于同一定点的L= 常矢量 ? 第四章(功和能) 1. 功: dA=F?dr , AAB=L 2. 动能定理: 对于一个质点: AAB =mvb2 -mva2 对于一个质点系: Aext+Aint = EkB – EkA 3. 一对力的功: 两个质点间一对内力的功之和为 AAB= 它只决定于两质点的相对路径 4. 保守力: 做功与相对路径形状无关的一对力,或者说,沿相对的闭合路径移动一周做功为零的一对力。 5. 势能: 对保守内力可引进势能的概念。一个系统的势能Ep决定于系统的位形,定义为 –ΔEp=EpA – EpB = AAB 取B点为势能零点,即EpB=0,则 EpA = AAB 引力势能: Ep=-,以两质点无穷远分离时为势能零点。 重力势能: Ep=mgh,以物体在地面为势能零点。 弹簧的弹性势能: Ep=kx2,以弹簧的自然伸长为势能零点。 6. 由势能函数求保守力: Ft=- 7. 机械能守恒定律: 在只有保守内力做功的情况下,系统的机械能保持不变。它是普遍的能量守恒定律的特例。 8. 守恒定律的意义: 不究过程的细节而对系统的初、末状态下结论;相应于自然界的每一种对称性,都存在着一个守恒定律。 9. 碰撞: 完全非弹性碰撞: 碰后合在一起; 弹性碰撞: 碰撞时无动能损失。 ? 第五章(刚体的定轴转动) 1. 刚体的定轴转动: 匀加速转动: ω=ω0+at ,θ=ω0t+at2 , ω2-ω02 =2αθ 2. 刚体定轴转动定律: Mz= 以转动轴为z轴,为外力对转轴的力矩之和;Lz=Jω,J为刚体对转轴的转动惯量,则 M=Jα 3. 刚体的转动惯量: J=2 (离散分布) , J=dm(连续分布) 平行轴定理: J=Jc+md2 4. 刚体转动的功和能: 力矩的功: A= 转动动能: Ek=Jω2 刚体的重力势能: Ep=mghc 机械能守恒定律: 只有保守力做功时, Ek+ Ep =常量
