第06章 梁的复杂问题(作业解答)
第6章梁的位移

梁 的 位 移
§6-1 概
I. 梁的位移
述
直梁ACB; 形心主惯性平面xy; 平面弯曲; 挠曲线AC1B;
F
A C B
x
C1
挠曲线
y
F
A C B
x
w(挠度)
C1
挠曲线
y
挠度:横截面的形心(即轴线上的点)在y方 向的线位移w。在图示坐标系中,方向向下的w为 正。工程中常用梁,w<<l,横截面的形心在x方向 的线位移可略去。
qCF
wCF
qCF×a
由位移关系可得B截面的挠度和转角分别为
wBF
q BF
2 Fa Fa 5Fa wCF qCF a a 3EI EI 3EI 2 Fa q CF EI
3 2 3
qBMe
A B
wBMe
Me= Fa
由图b可得B截面的挠度和转角分别为
wBM e
EI w x M x d x C1
当梁的弯矩方程需要分段列出时,挠曲线的微 分方程也应分段建立。若梁可分为n段,每段分别积 分两次之后,共有2n个积分常数。确定这些积分常 数,除了要应用位移边界条件之外,还要利用分段 处的位移连续条件(挠曲线的连续、光滑条件), 即在分段点xi处,wi(xi)= wi+1(xi) ,wi (xi)= wi+1(xi) 。
ql 3 ql 3 7 ql 3 48 EI 384 EI 384 EI
q B q B1 q B 2
ql 3 ql 3 9ql 3 48 EI 384 EI 384 EI
例 用叠加法求图示弯曲刚度为EI的外伸梁C截面的 挠度以及D截面的挠度和转角。
第6章-梁的内力PPT课件

(3)计算截面C稍右处的剪力FsR、弯矩MCR。
M C
MCR
A
l/2
FA
Fy 0
FsR
ql FsRFA2 0
MCF0
解之得:
FsR
ql 4
M CR MFA2 lq 2 l4 l0
精选PPT课M件CR 0
14
建筑力学
❖ 计算剪力和弯矩的规律
(1) 梁内任一截面上的剪力,其大小等于该截面左侧(或右侧) 梁上所有外力的代数和;梁内任一截面的弯矩,其大小等 于该截面左侧(或右侧)梁上所有外力对于该截面形心之矩的
★ 由平衡方程 F得y ,0
F s x F s x d s x F q x d 0 x
dFsx qx
dx
(9-1)
几何意义:剪力图上某点处的切线斜率等于该点处荷载
集度的大小。
精选PPT课件
23
建筑力学
★ 由平衡方程 MC 得,0
M x dx M M x F sx d q x x d d 2 x 0 x
(3)列出各段的剪力方程和弯矩方程:各段列剪力方程和弯矩方程时, 所取的坐标原点与坐标轴x的正向可视计算方便而定,不必一 致。
(4) 画剪力图和弯矩图:先根据剪力方程(或弯矩方程)判断剪力图(或 弯矩图)的形状,确定其控制截面,再根据剪力方程(或弯矩方 程)计算其相应截面的剪力值(或弯矩值),然后描点并画出整个 全梁的剪力图(或弯矩图)
解之得: Fs 4kN 精选PPTM 课件144 kNm
12
[例]
简支梁受均布荷载q和集中力偶M=ql2/4的作用,如图所示。求截面C 的剪力和弯矩。
M
q
结构力学课后解答:第6章 力法
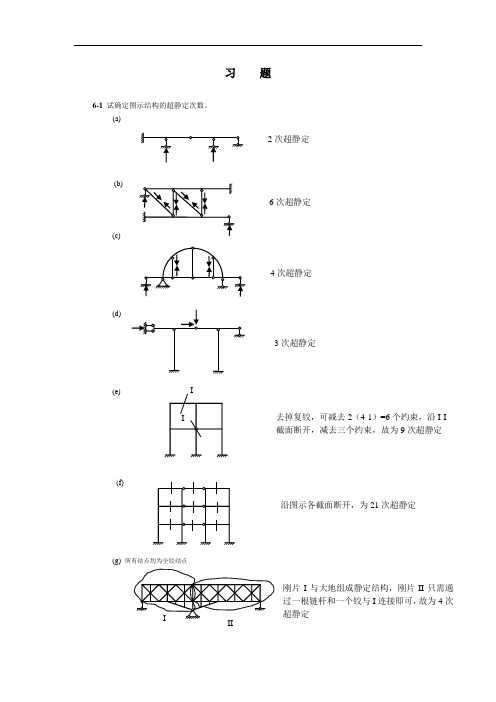
习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定6- 38(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ p lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图126- 40解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m 6m810810计算1M,由对称性知,可考虑半结构。
材料力学第06章作业刘06
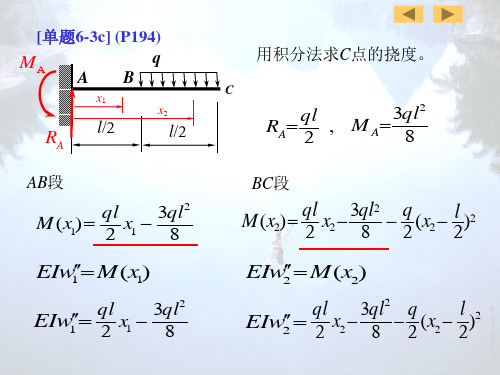
5.05mm
[单题6-10b] 求悬臂梁C点的挠度和B点的转角。 (P195)
F
A
B
C
l/2
l/2
F
F
A
B
l/2
C
θB1
f1
A
B
l/2
f2 C
l/2
F
F
A
B
l/2
C
θB1
f1
f1
fB
B
l 2
fB
F
(
l 2
)3
3EI
B
F(2l )2 2EI
f1
F
(
l 2
)3
3EI
F
(
l 2
)2
2EI
l 2
5Fl3 48EI
)2
2EI
F l2 8EI
C
F
B2
q 2
(x2
2l )2
EIw2
ql 4
x22
3ql2 8
x2
q 6
(x2
x10 , 1 w1
C10 ,
2l )3 C2
0 ,
ql EIw2 12
x22
3ql2 16
x22
q 24
(x2
l 2
)4
C2x2 D2
[孙题5-4] (P117)
Pql 2
RB
q
B
A
D
x1
l/2
x2
l
RC 用积分法求A、B截面的转 角和A、D点的挠度。
[单题6-3c] (P194)
MA
A
q B
x1
l/2 RA
x2
l/2
材料力学第6章2-例2
2.06%
超过的值小于 5% ,这在工程上还是允许的。
综合上述,梁的正应力、切应力及主应力的强度均满足。
5
小结
进行梁的强度计算时,在弯矩最大截面上距中性轴最远的 点和剪力最大截面上位于中性轴的点,有可能成为梁的危险点。
但如果在梁的弯矩和剪力都比较大的截面上,某些点由于 正应力和切应力都比较大,由它们组成的主应力相当大时也可 能成为梁的危险点。
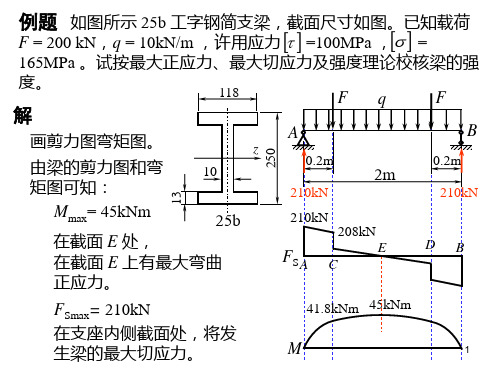
例题 如图所示 25b 工字钢简支梁,截面尺寸如图。已知载荷
F = 200 kN,q = 10kN/m ,许用应力 =100MPa , =
165MPa 。试按最大正应力、最大切应力及强度理论校核梁的强
度。
解
118
Fq
F
画剪力图弯矩图。
A
z
B
由梁的剪力图和弯
10
0.2m
0.2m
2m
矩图可知:
210kN
210 103 10 212.7
98.7 MPa
100 MPa
max
(3) 梁的主应力强度校核
梁的危险点也可能出现在 C(D) 截面翼缘和腹板的交界处,
危险点的应力状态,如图所示。
3
13 250
My Iz
(41.8106 ) ( 250 13) 2
5284 104
88.6 MPa
梁的弯曲正应力发生在中间截面 E 上的上、下边缘处,
危险点的应力状态,如图所示。
max
max
M max Wz
45 106 423103
106.4 MPa
165MPa
(2) 梁的弯曲切应力校核
梁的弯曲切应力发生在支座内侧截面的中性轴上,
危险点的应力状态,如图所示。
材力第6章习题解

(b-1)
(b) f max
习题 6-5 图
6-6 度。
简支梁承受间断性分布载荷,如图所示。试用奇导函数写出其小挠度微分方程,并确定其中点挠
—30—
q q
w
x
习题 6-6 图
A
B
C
D
E
q
l
l
(a)
l
l
解:采用左手系: M A 0 , FRE 定初参数 E ,∵ w A w | x 4l 0F Nhomakorabea l 2 6
—31—
1 FP l 2 FP 3 x x (0 xl ) EI 6 2 3 2 F l F l F F 1 P BD 段挠曲线方程(原点在点 B) : w1 ( x) P x P x3 P x l 3 EI 6 6 3 3
建筑力学 第六章答案
6-1 求图示桁架AB 、AC 的相对转角,各杆EA 为常量。
解:(1)实状态桁架各杆的轴力如图(b )所示。
(b)(a)N(d )(c)题6-1(2)建立虚设单位力状态如(c )所示,求AB 杆的转角。
1113(2)82i P iAB i i P a P a P a N N l P a a a E A EA EA EA EAϕ⋅⋅⋅⋅-⋅-⋅⋅⋅==++⨯=∑(↺)(3)建立虚设单位力状态如(d )所示,求AC 杆的转角。
113(2)()(72i P i AC i iP a P a N N lPa a E A EA EA EAϕ⋅⋅⋅-⋅-⋅⋅==+⨯=∑(↺)故,AB 、AC 的相对转角为两杆转角之差:8(7(10.414AB AC P P P PEA EA EA EAϕϕϕ+-=-=-==-(夹角减小)6-2 求半圆曲梁中点K 的竖向位移。
只计弯曲变形。
EI 为常数。
方法一 解:(1)荷载作用下的实状态的约束反力如图(a )所示。
以任意半径与水平坐标轴的顺时针夹角为自变量,其弯矩方程为:sin (0)P M θθπ=-≤≤Pr(2)建立虚设单位力状态如(b )所示,其弯矩方程为:[]1cos )(0)2211cos()cos )()222i M πθθππθθθπ⎧≤≤⎪⎪=⎨⎪-=≤≤⎪⎩(r -r r -r (r +r(a)题6-2(3)积分法求半圆曲梁中点K 的竖向位移。
20233220022311cos )(sin )cos )(sin )2211cos )sin cos )sin sin sin 2)sin sin 2)2222cos 2i V Pk Pr Pr M M ds rd rd EIEI EI Pr Pr d d d d EI EI Pr EI πππππππππθθθθθθθθθθθθθθθθθθθ⋅-⋅-⋅∆==+⎡⎤⎡⎤=-⋅+⋅=-+⋅⎢⎥⎢⎥⎣⎦⎣⎦=-∑⎰⎰⎰⎰⎰⎰⎰(r -r (r +r (-(+(-(+(-11320211cos 2)cos cos 2)442Pr EI πππθθθ⎡⎤⎢⎥+-+=-↑⎢⎥⎣⎦()( 方法二:本题也可以只算纵向对称轴左边,再乘2。
建筑力学第六章梁的弯曲内力
M1
2--2 截面
qL
q
Fs 2
x2
q( x2 a) qL Fs 2 0 1 2 qLx M q ( x a ) 0 mC 0 , 2 2 2 2 M2 Fs 2 q( x2 a L)
y
F
0,
1 M 2 q( x2 a)2 qLx2 2
MA
FAY
[例] 列出梁内力方程并画出内力图。
A
L
F B
解:①求支反力
FAY F ; M A FL
x
F(x) F
②写出内力方程
Fs ( x) FAY F
M ( x) FAY x M A F ( x L)
(0 x l )
FL
x
(0 x l )
③根据方程画内力图
第 6章
梁的弯曲内力
一、弯曲实例
工厂厂房的天车大梁
1
火车的轮轴:
F
F
F
F
楼房的横梁:
阳台的挑梁:
2. 平面弯曲
工程中常见的梁,其横截面大多为矩形、工字形、 T形、十字形、槽形等
它们都有对称轴,梁横截面的对称轴和梁的轴线所 组成的平面通常称为纵向对称平面 。
平面弯曲
纵向对称面
•具有纵向对称面 •外力都作用在此面内 •弯曲变形后轴线变成对称面内的平面曲线
二、弯曲的概念:
受力特点——作用于杆件上的外力都垂直于杆的轴线。 变形特点——杆轴线由直线变为一条曲线。
P
主要产生弯曲变形的杆--- 梁。 三、平面弯曲的概念:
RA
q
M
NB
F1
q
F2
M
6章习题解材料力学课后习题题解解析
s 1,max = s 2,max =
M 1,max Wz M 2,max Wz
3F / 2 = = 1.3[s ] Wz F (6 - a ) / 4 = = [s ] Wz
A
C a/2 3m a/2
D
B
3m
F
A 3m 3m B
3F / 2 F (6 - a ) / 4 / = 1.3 Wz Wz a = 1.39m
A 2000 10kN.m
B 3000 15kN
C 1000
D
40.6
5kN
M B yB ,max M C yC ,max
5kN.m
t,max
MC 5 103 ymax 109.4 74.42MPa [ t ] 4 Iz 735 10
150
z
[σc]=160MPa Iz=735×104mm4 B截面下部受压, C截面上部受压
20kN·m
300
a b d c y z
75
I z = 4.05? 108 mm4
M -25 10-6 a = ya = -150 =9.26MPa; 8 Iz 4.05 10 M b = yb =0; Iz M -25 10-6 c = yC = 75=-4.63MPa; 8 Iz 4.05 10 M -25 10-6 d = yd = 150=-9.26MPa 8 Iz 4.05 10
120
6.9 试求图示梁固定端截面上腹板与翼缘交界处k点的切应力 τk,以及全梁横截面上的最大弯曲切应力τmax。
解:梁各个 截面剪力相 等,都等于 20kN
* FS Sz k = d Iz
20kN A 2000 B
材料力学06梁的应力
σ max
M = Wz
抗弯截面模量。 抗弯截面模量。
Iz Wz = y max
矩形截面的W 矩形截面的Wz
z
圆形截面的W 圆形截面的Wz
z
纯弯曲正应力公式的推广
梁发生横力弯曲时,横截面上一般既有弯矩也有剪力,所以 梁发生横力弯曲时,横截面上一般既有弯矩也有剪力, 梁变形以后其横截面不再保持为平面, 梁变形以后其横截面不再保持为平面,且纵向纤维层之间也 存在相互的挤压,即平面假设、 存在相互的挤压,即平面假设、纵向纤维间无挤压假设均不 成立。严格的说, 成立。严格的说,纯弯曲模型推导出的正应力计算公式不适 用于梁在横力弯曲时横截面上的正应力计算 对于工程中常见的细长梁(跨长与横截面高度之比大于5) 对于工程中常见的细长梁(跨长与横截面高度之比大于 ) 梁在横力弯曲时横截面上的正应力仍然按公式( ) 梁在横力弯曲时横截面上的正应力仍然按公式(6.2)计算
(三)静力学关系: 静力学关系: 横截面上的微内力 σdA 组成的 空间平行力系, 空间平行力系,仅能简化为三个内力 分量。 分量。 y z y
z x σdA
FN = ∫ σ dA = 0
A
∫
→
A
ydA = 0 , S z = 0 ∴ z (中性)轴过形心
My =
∫
A
(σ d A ) z = 0,
M → = ρ EI z
1
弯曲变形的基本公式(中性层曲率) 弯曲变形的基本公式(中性层曲率)
三、平面弯曲杆横截面上的正应力 1.计算公式 计算公式
2.分布规律 分布规律 横截面上任一点处的正应力大小, 横截面上任一点处的正应力大小,与该点至中性轴的距 离成正比,即正应力沿截面宽度均匀分布, 离成正比,即正应力沿截面宽度均匀分布,沿高度呈线性分 中性轴的一侧为拉应力,另一侧为压应力。 布。中性轴的一侧为拉应力,另一侧为压应力。 3.正应力公式讨论 正应力公式讨论: 3.正应力公式讨论: 1)适用于均匀连续、各向同性材料,在线弹性范围小变 )适用于均匀连续、各向同性材料, 形时的等截面直杆。 形时的等截面直杆。 2)在纯弯曲时,横截面在弯曲变形后保持平面,公式为精 )在纯弯曲时,横截面在弯曲变形后保持平面, 确解;横力弯曲时,横截面不再保持平面, 确解;横力弯曲时,横截面不再保持平面,公式为近似 误差< 。 解,当梁的跨高比 l/h>5 时,误差<2%。 + − 3) 若中性轴为截面对称轴,则 σ max = σ max ) 若中性轴为截面对称轴, ;
