2020年全国高考数学(文)-全国卷I试卷及答案
全国卷Ⅰ2022年新高考数学真题及答案解析

绝密★启用前2022年普通高等学校招生全国统一考试数学一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{4},{31}M x N x x =<=≥∣,则M N = ()A.{}02x x ≤< B.123xx ⎧⎫≤<⎨⎬⎩⎭C.{}316x x ≤< D.1163xx ⎧⎫≤<⎨⎬⎩⎭【答案】D【详解】1{16},{}3M xx N x x =≤<=≥∣0∣,故1163M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭,故选:D 2.若i(1)1z -=,则z z +=()A.2-B.1- C.1D.2【答案】D【详解】由题设有21i1i i i z -===-,故1+i z =,故()()1i 1i 2z z +=++-=,故选:D 3.在ABC 中,点D 在边AB 上,2BD DA =.记CA m CD n == ,,则CB=()A.32m n -B.23m n-+C.32m n+D.23m n+【答案】B【详解】因为点D 在边AB 上,2BD DA =,所以2BD DA =,即()2CD CB CA CD -=- ,所以CB =3232CD CA n m -=- 23m n =-+.故选:B .4.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .时,增加的水量约2.65≈)()A.931.010m ⨯B.931.210m ⨯ C.931.410m ⨯ D.931.610m ⨯【答案】C【解析】依题意可知棱台的高为157.5148.59MN =-=(m),所以增加的水量即为棱台的体积V .棱台上底面积262140.014010S ==⨯km m ,下底面积262180.018010S '==⨯km m ,∴((66119140101801033V h S S =++=⨯⨯⨯+⨯'(()679933320109618 2.6510 1.43710 1.410(m )=⨯+⨯≈+⨯⨯=⨯≈⨯.故选:C .5.从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为()A.16B.13C.12D.23【答案】D【详解】从2至8的7个整数中随机取2个不同的数,共有27C 21=种不同的取法,若两数不互质,不同的取法有:()()()()()()()2,4,2,6,2,8,3,6,4,6,4,8,6,8,共7种,故所求概率2172213P -==.故选:D.6.记函数()sin (0)4f x x b πωω⎛⎫=++> ⎪⎝⎭的最小正周期为T .若23T ππ<<,且()y f x =的图象关于点3,22π⎛⎫⎪⎝⎭中心对称,则2f π⎛⎫= ⎪⎝⎭()A.1B.32C.52D.3【答案】A【详解】由函数的最小正周期T 满足23T ππ<<,得223πππω<<,解得23ω<<,又因为函数图象关于点3,22π⎛⎫⎪⎝⎭对称,所以3,24k k Z ππωπ+=∈,且2b =,所以12,63k k Z ω=-+∈,所以52ω=,5()sin 224f x x π⎛⎫=++ ⎪⎝⎭,所以5sin 21244f πππ⎛⎫⎛⎫=++=⎪ ⎪⎝⎭⎝⎭.故选:A7.设0.110.1e ,ln 0.99a b c ===-,则()A.a b c <<B.c b a<< C.c a b<< D.a c b<<【答案】C【详解】方法一:构造法设()ln(1)(1)f x x x x =+->-,因为1()111x f x x x'=-=-++,当(1,0)x ∈-时,()0f x '>,当,()0x ∈+∞时()0f x '<,所以函数()ln(1)f x x x =+-在(0,)+∞单调递减,在(1,0)-上单调递增,所以1()(0)09f f <=,所以101ln099-<,故110ln ln 0.999>=-,即b c >,所以1((0)010f f -<=,所以91ln+01010<,故1109e 10-<,所以11011e 109<,故a b <,设()e ln(1)(01)xg x x x x =+-<<,则()()21e 11()+1e 11xx x g x x x x -+'=+=--,令2()e (1)+1x h x x =-,2()e (21)x h x x x '=+-,当01x <<-时,()0h x '<,函数2()e (1)+1x h x x =-单调递减,11x <<时,()0h x '>,函数2()e (1)+1x h x x =-单调递增,又(0)0h =,所以当01x <<时,()0h x <,所以当01x <<时,()0g x '>,函数()e ln(1)xg x x x =+-单调递增,所以(0.1)(0)0g g >=,即0.10.1e ln 0.9>-,所以a c >故选:C.方法二:比较法解:0.10.1a e =,0.110.1b =-,ln(10.1)c =--,①ln ln 0.1ln(10.1)a b -=+-,令()ln(1),(0,0.1],f x x x x =+-∈则1()1011x f x x x-'=-=<--,故()f x 在(0,0.1]上单调递减,可得(0.1)(0)0f f <=,即ln ln 0a b -<,所以a b <;②0.10.1ln(10.1)a c e -=+-,令()ln(1),(0,0.1],x g x xe x x =+-∈则1(1)(1)1()11x xxx x e g x xe e x x+--'=+---,令()(1)(1)1x k x x x e =+--,所以2()(12)0x k x x x e '=-->,所以()k x 在(0,0.1]上单调递增,可得()(0)0k x k >>,即()0g x '>,所以()g x 在(0,0.1]上单调递增,可得(0.1)(0)0g g >=,即0a c ->,所以.a c >故.c a b <<8.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤四棱锥体积的取值范围是()A.8118,4⎡⎤⎢⎥⎣⎦ B.2781,44⎡⎤⎢⎥⎣⎦C.2764,43⎡⎤⎢⎥⎣⎦D.[18,27]【答案】C【详解】∵球的体积为36π,所以球的半径3R =,[方法一]:导数法设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l <≤时,0V '<,所以当l =时,正四棱锥的体积V 取最大值,最大值为643,又3l =时,274V =,l =814V =,所以正四棱锥的体积V 的最小值为274,所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.[方法二]:基本不等式法由方法一故所以2231211(122)64(6)(122)[](333333h h h V a h h h h h h h -++==-=-⨯⨯= 当且仅当4h =取到),当32h =时,得a =,则22min 11327;3324V a h ==⨯=当l =时,球心在正四棱锥高线上,此时39322h =+=,23322a a =⇒=,正四棱锥体积221119816433243V a h ==⨯=<,故该正四棱锥体积的取值范围是2764[,].43二、选择题:本题共4小题。
2020年全国卷Ⅰ理科数学(含答案)

2020年普通高等学校招生全国统一考试理科数学一、选择题:本题共12小题,每小题5分,共60分。
1.若z=1+i,则|z2–2z|=A.0 B.1 C D.22.设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=A.–4 B.–2 C.2 D.43.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A B C D4.已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= A.2 B.3 C.6 D.95.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度x y i=得到下面的散点图:条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是A .y a bx =+B .2y a bx =+C .e x y a b =+D .ln y a b x =+ 6.函数43()2f x x x =-的图像在点(1(1))f ,处的切线方程为A .21y x =--B .21y x =-+C .23y x =-D .21y x =+ 7.设函数()cos π()6f x x ω=+在[]π,π-的图像大致如下图,则f (x )的最小正周期为A .10π9 B .7π6 C .4π3 D .3π28.25()()x x y xy ++的展开式中x 3y 3的系数为 A .5 B .10 C .15 D .20 9.已知 π()0,α∈,且3cos28cos 5αα-=,则sin α=A B .23 C .13D 10.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π11.已知⊙M :222220x y x y +---=,直线l :220x y ++=,P 为l 上的动点,过点P 作⊙M 的切线,PA PB ,切点为,A B ,当||||PM AB ⋅最小时,直线AB 的方程为A .210x y --=B .210x y +-=C .210x y -+=D .210x y ++=12.若242log 42log a ba b +=+,则A .2a b >B .2a b <C .2a b >D .2a b <二、填空题:本题共4小题,每小题5分,共20分。
2020年高考理科数学全国卷1(附答案与解析)
绝密★启用前2020年普通高等学校招生全国统一考试·全国Ⅰ卷理科数学本试卷共6页,23题(含选考题).全卷满分150分.考试用时120分钟.注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码黏贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷,草稿纸和答题卡上的非答题区域均无效。
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试卷,草稿纸和答题卡上的非答题区域均无效。
5.考试结束后,请将本试卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若1i z =+,则22z z -=( )A .0B .1C .2D .22.设集合{}240A x x =-≤,{}20B x x a =+≤,且{}21A B x x =-≤≤,则a =( )A .4-B .2-C .2D .43.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A .514- B .512- C .514+D .512+4.已知A 为抛物线()2:20C y px p =>上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( )A .2B .3C .6D .95.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据()()1220i i x y i =,,,…,得到下面的散点图:由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( )A .y a bx =+B .2y a bx =+C .x y a be =+D .ln y a b x =+6.函数()432f x x x =-的图像在点()()11f ,处的切线方程为( )A .21y x =--B .21y x =-+毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在------------------此-------------------卷-------------------上-------------------答-------------------题-------------------无------------------效----------------C .23y x =-D .21y x =+7.设函数()πcos 6f x x ω⎛⎫=+ ⎪⎝⎭在[]ππ-,的图像大致如下图,则()f x 的最小正周期为( )A .10π9B .7π6 C .4π3 D .3π28.()25y x x y x ⎛⎫++ ⎪⎝⎭的展开式中33x y 的系数为( )A .5B .10C .15D .20 9.已知()0πα∈,,且3cos28cos 5αα-=,则sin α= ( )A .53B .23C .13D .5910.已知A ,B ,C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π11.已知⊙22:2220M x y x y +---=,直线:220l x y ++=,P 为l 上的动点.过点P 作⊙M 的切线PA ,PB ,切点为A ,B ,当PM AB ⋅最小时,直线AB 的方程为( )A .210x y --=B .210x y +-=C .210x y -+=D .210x y ++= 12.若242log 42log aba b +=+则( )A .2a b >B .2a b <C .2a b >D .2a b <二、填空题:本题共4小题,每小题5分,共20分.13.若x ,y 满足约束条件2201010x y x y y +-⎧⎪--⎨⎪+⎩≤,≥,≥,则7z x y =+的最大值为 .14.设a ,b 为单位向量,且1+=a b ,则-=a b .15.已知F 为双曲线()2222:100x y C a b a b-=>,>的右焦点,A 为C 的右顶点,B 为C 上的点,且BF 垂直于x 轴,若AB 的斜率为3,则C 的离心率为 .16.如图,在三棱锥P ABC -的平面展开图中,1AC =,3AB AD ==,AB AC ⊥,AB AD ⊥,30CAE ∠=,则cos FCB ∠= .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)设{}n a 是公比不为1的等比数列,1a 为2a ,3a 的等差中项. (1)求{}n a 的公比;(2)若11a =,求数列{}n na 的前n 项和.18.(12分)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC △是底面的内接正三角形,P 为DO 上一点,66PO DO =. (1)证明:PA PBC ⊥平面; (2)求二面角B PC E --的余弦值.19.(12分)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一轮轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为12.(1)求甲连胜四场的概率; (2)求需要进行第五场比赛的概率; (3)求丙最终获胜的概率.20.(12分)已知A ,B 分别为椭圆E :()22211x y a a+=>的左、右顶点,G 为E 上顶点,8AG GB ⋅=.P 为直线6x =上的动点,PA 与E 的另一交点为C ,PB 与E 的另一交点为D .(1)求E 的方程; (2)证明:直线CD 过定点.21.(12分)已知函数()2x f x e ax x =+-.(1)当1a =时,讨论()f x 的单调性;(2)当0x ≥时,()3112f x x +≥,求a 的取值范围.(二)选考题:共10分,请考生在22、23题中任选一题作答.如果多做,则按所做的第一题计分. 22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,曲线1C 的参数方程为()cos sin kkx t t y t⎧=⎪⎨=⎪⎩,为参数,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos 16sin 30ρθρθ-+=. (1)当1k =时,1C 是什么曲线?(2)当4k =时,求1C 与2C 的公共点的直角坐标.23.[选修4—5:不等式选讲](10分) 已知函数()3121f x x x =+--. (1)画出()y f x =的图像;(2)求不等式()()1f x f x +>的解集.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在------------------此------------------卷------------------上-------------------答------------------题------------------无------------------效----------------2020年普通高等学校招生全国统一考试·全国Ⅰ卷理科数学答案解析一、选择题 1.【答案】D【解析】由题意首先求得22z z -的值,然后计算其模即可.由题意可得:()2212z i i =+=,则()222212z z i i -=-+=-.故2222z z -=-=.故选:D .【考点】复数的运算法则,复数的模的求解 2.【答案】B【解析】由题意首先求得集合A ,B ,然后结合交集的结果得到关于a 的方程,求解方程即可确定实数a 的 值.求解二次不等式240x -≤可得:{}22A x x =-≤≤,求解一次不等式20x a +≤可得:2a B x x ⎧⎫=-⎨⎬⎩⎭≤.由于{}21AB x x =-≤≤,故:12a-=,解得:2a =-.故选:B .【考点】交集的运算,不等式的解法 3.【答案】C【解析】设CD a =,PE b =,利用212PO CD PE =⋅得到关于a ,b 的方程,解方程即可得到答案.如图,设CD a =,PE b =,则PO ==212PO ab =,即22142a b ab -=,化简得24210b b a a ⎛⎫-⋅-= ⎪⎝⎭,解得14b a +=(负值舍去). 故选:C .【考点】正四棱锥的概念及其有关计算 4.【答案】C【解析】利用抛物线的定义建立方程即可得到答案. 设抛物线的焦点为F ,由抛物线的定义知122A p AF x =+=,即1292p=+,解得6p =. 故选:C .【考点】利用抛物线的定义计算焦半径 5.【答案】D【解析】根据散点图的分布可选择合适的函数模型.由散点图分布可知,散点图分布在一个对数函数的图象附近,因此,最适合作为发芽率y 和温度x 的回归方程类型的是ln y a b x =+.故选:D .【考点】函数模型的选择,散点图的分布6.【答案】B【解析】求得函数()y f x =的导数()f x ',计算出()1f 和()1f '的值,可得出所求切线的点斜式方程,化简 即可.()432f x x x =-,()3246f x x x '∴=-,()11f ∴=-,()12f '=-,因此,所求切线的方程为()121y x +=--,即21y x =-+. 故选:B .【考点】利用导数求解函图象的切线方程7.【答案】C【解析】由图可得:函数图象过点409π⎛⎫-⎪⎝⎭,,即可得到4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭,结合409π⎛⎫- ⎪⎝⎭,是函数()f x 图象与x 轴负半轴的第一个交点即可得到4962πππω-⋅+=-,即可求得32ω=,再利用三角函数周期公式即 可得解.由图可得:函数图象过点409π⎛⎫-⎪⎝⎭,,将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭. 又409π⎛⎫- ⎪⎝⎭,是函数()f x 图象与x 轴负半轴的第一个交点,所以4962πππω-⋅+=-,解得:32ω=.所以函数()f x 的最小正周期为224332T πππω===. 故选:C .【考点】三角函数的性质及转化,三角函数周期公式 8.【答案】C【解析】求得()5x y +展开式的通项公式为515r r rr T C x y -+=(r ∈N 且5r ≤),即可求得2y x x ⎛⎫+ ⎪⎝⎭与()5x y + 展开式的乘积为65rrrC xy -或425r rr C xy-+形式,对r 分别赋值为3,1即可求得33x y 的系数,问题得解.()5x y + 展开式的通项公式为515rrrr T C xy -+=(r ∈N 且5r ≤).所以2y x x ⎛⎫+ ⎪⎝⎭与()5x y +展开式的乘积可表示为:56155rrrr rrr xT xC x y C xy --+==或22542155r r rr r r r T C x y xC y y y x x --++==在615r r r r xT C x y -+=中,令3r =,可得:33345xT C x y =,该项中33x y 的系数为10,在42152r r r r T C x xy y -++=中,令1r =,可得:521332T C y x xy =,该项 中33x y 的系数为5.所以33x y 的系数为10515+=. 故选:C【考点】二项式定理及其展开式的通项公式,赋值法 9.【答案】A【解析】用二倍角的余弦公式,将已知方程转化为关于cos α的一元二次方程,求解得出cos α,再用同角间的三角函数关系,即可得出结论.3cos28cos 5αα-=,得26cos 8cos 80αα--=,即23cos 4cos 40αα--=,解得2cos 3α=-或cos 2α=(舍去),又(0)απ∈,,sin α∴==. 故选:A .【考点】三角恒等变换,同角间的三角函数关系求值 10.【答案】A【解析】由已知可得等边ABC △的外接圆半径,进而求出其边长,得出1OO 的值,根据球截面性质,求出 球的半径,即可得出结论.设圆1O 半径为r ,球的半径为R ,依题意,得24r ππ=,2r ∴=,由正弦定理可得2sin 6023AB r ==,1OO AB ∴==,根据圆截面性质1OO ABC ⊥平面,11OO O A ∴⊥,4R OA =,∴球O 的表面积2464S R ππ==.故选:A .【考点】球的表面积,应用球的截面性质11.【答案】D【解析】由题意可判断直线与圆相离,根据圆的知识可知,四点A ,P ,B ,M 共圆,且AB MP ⊥,根据22PAM PM AB S PA ⋅==△可知,当直线MP l ⊥时,PM AB ⋅最小,求出以MP 为直径的圆的方程,根据圆系的知识即可求出直线AB 的方程.圆的方程可化为()()22114x y -+-=,点M 到直线l的距离为2d ==,所以直线l 与圆相离.依圆的知识可知,四点A ,P ,B ,M 四点共圆,且AB MP ⊥, 所以12222PAMPM AB S PA AM PA ⋅==⨯⨯⨯=△,而PA =,当直线MP l ⊥时,min MP =min 1PA =,此时PM AB ⋅最小.()1:112MP y x ∴-=-即1122y x =+,由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得,10x y =-⎧⎨=⎩. 所以以MP 为直径的圆的方程为()()()1110x x y y -++-=,即2210x y y +--=,两圆的方程相减可得:210x y ++=,即为直线AB 的方程.故选:D .【考点】直线与圆,圆与圆的位置关系的应用,圆的几何性质的应用 12.【答案】B【解析】设()22log x f x x =+,利用作差法结合()f x 的单调性即可得到答案. 设()22log xf x x =+,则()f x 为增函数,因为22422log 42log 2log a b ba b b +=+=+,所以()()()()22222222122log 2log 22log 2log 2log 102a b b b f a f b a b b b -=+-+=+-+==-<,所以()()2f a f b <,所以2a b <.()()()()22222222222222log 2log 2log 2log 22log a b b b b b f a f b a b b b b-=+-+=+-+=--,当1b =时,()()220f a f b -=>,此时()()2f a f b >,有2a b >.当2b =时,()()210f a f b -=-<,此时()()2f a f b <,有2a b <,所以C 、D 错误. 故选:B .【考点】函数与方程的综合应用,构造函数,利用函数的单调性比较大小二、填空题 13.【答案】1【解析】首先画出可行域,然后结合目标函数的几何意义即可求得其最大值. 绘制不等式组表示的平面区域,如图所示,目标函数7z x y =+即:1177y x z =-+,其中z 取得最大值时,其几何意义表示直线系在y 轴上的截距最大,据此结合目标函数的几何意义可知目标函数在点A 处取得最大值,联立直线方程:22010x y x y +-=⎧⎨--=⎩,可得点 A 的坐标为:()10A ,,据此可知目标函数的最大值为:max 1701z =+⨯=.故答案为:1. 14.【解析】整理已知可得:()2a b a b +=+,再利用a ,b 为单位向量即可求得21a b ⋅=-,对a b -变形可得:222a b a a b b -=-⋅+,问题得解.因为a ,b 为单位向量,所以1a b ==,所以()2222221a b a ba ab b a b +=+=+⋅+=+⋅=.解得:21a b ⋅=-. 所以()22223a b a b a a b b -=-=-⋅+=.【考点】向量模的计算公式及转化 15.【答案】2【解析】根据双曲线的几何性质可知,2b BF a=,AF c a =-,即可根据斜率列出等式求解即可.依题可得,3BF AF =,而2bBF a =,AF c a =-,即23ba c a=-,变形得22233c a ac a -=-,化简可得, 2320e e -+=,解得2e =或1e =(舍去).故答案为:2. 【考点】双曲线的离心率的求法,双曲线的几何性质的应用 16.【答案】14-【解析】在ACE △中,利用余弦定理可求得CE ,可得出CF ,利用勾股定理计算出BC 、BD ,可得出BF ,然后在BCF △中利用余弦定理可求得cos FCB ∠的值.AB AC ⊥,AB 1AC =,由勾股定理得2BC ==,同理得BD =,BF BD ∴==ACE △中,1AC =,AE AD ==30CAE ∠=,由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=,1CF CE ∴==,在BCF△中,2BC =,BF =,1CF =,由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯.故答案为:14-.【考点】利用余弦定理解三角形 三、解答题17.【答案】(1)2-(2)()()11329nn n S -+-=【解析】(1)由已知结合等差中项关系,建立公比q 的方程,求解即可得出结论.设{}n a 的公比为q ,1a 为2a ,3a 的等差中项,1232a a a =+,10a ≠,220q q ∴+-=,1q ≠,2q ∴=-.(2)由(1)结合条件得出{}n a 的通项,根据{}n na 的通项公式特征,用错位相减法,即可求出结论.设{}n na 的前n 项和为n S ,11a =,()12n n a -=-,()()()211122322n n S n -=⨯+⨯-+⨯-++-,①()()()()()()2312122232122n nn S n n --=⨯-+⨯-+⨯-+--+-,②-①②得,()()()()()()()()()211211323122222123nnn nnn n S n n ----+-=+-+-++---=--=--,()()11329nn n S -+-∴=.【考点】等比数列通项公式基本量的计算,等差中项的性质,错位相减法求和 18.【答案】(1)证明:由题设,知DAE △为等边三角形,设1AE =,则DO =,112CO BO AE ===,所以PO =,PC =,PB ==又ABC △为等边三角形,则2sin60BA OA=,所以BA =22234PA PB AB +==,则90APB ∠=,所以PA PB ⊥,同理PAPC ⊥,又PC PB P =,所以PA PBC ⊥平面.(2)5【解析】(1)要证明PA PBC ⊥平面,只需证明PA PB ⊥,PA PC ⊥即可. 由题设,知DAE △为等边三角形, 设1AE =,则DO =,1122CO BO AE ===,所以PO=,4PC ==, 4PB ==,又ABC △为等边三角形,则2sin60BA OA =,所以2BA =,22234PA PB AB +==,则90APB ∠=,所以PA PB ⊥,同理PA PC ⊥,又PCPB P =,所以PA PBC ⊥平面. (2)以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如图所示的空间直角坐标系,分别算出平面PCB 的法向量为n ,平面PCE 的法向量为m ,利用公式cos m <,||||n mn n m ⋅=>计算即可得到答案.过O 作ON BC ∥交AB 于点N ,因为PO ABC ⊥平面,以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如图所示的空间直角坐标系,则1002E ⎛⎫- ⎪⎝⎭,,,004P ⎛⎫ ⎪⎪⎝⎭,,,104B ⎛⎫- ⎪⎪⎝⎭,104C ⎛⎫- ⎪⎪⎝⎭,,14PC ⎛=- ⎝⎭,,14PB ⎛=-⎝⎭,102PE ⎛=- ⎝⎭,,,设平面PCB 的一个法向量为()111n x y z =,,,由0n PC n PB ⎧⋅=⎪⎨⋅=⎪⎩,得1111110x x ⎧--=⎪⎨-+-=⎪⎩,令1x =得11z =-,10y =,所以()201n =-,,,设平面PCE 的一个法向量为()222m x y z =,,由00m PC m PE ⎧⋅=⎪⎨⋅=⎪⎩,得22222020x x ⎧-=⎪⎨-=⎪⎩,令21x =,得2z =2y=,所以 313m ⎛= ⎝,故cos m <,2||||3n m n n m ⋅==⋅⨯,设二面角22143x y +=的大小为θ,则cos θ. 【考点】线面垂直的证明,利用向量求二面角的大小 19.【答案】(1)116(2)34(3)716【解析】(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率.记事件:M 甲连胜四场,则()411216P M ⎛⎫== ⎪⎝⎭.(2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率.记事件A 为甲输,事件B 为乙输,事件C 为丙输,则四局内结束比赛的概率为()()()()411424P P ABAB P ACAC P BCBC P BABA ⎛⎫'=+++=⨯= ⎪⎝⎭,所以,需要进行第五场比赛的概率为314P P '=-=.(3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.记事件A 为甲输,事件B 为乙输,事件C 为丙输,记事件:M 甲赢,记事件:N 丙赢,则甲赢的基本事件包括:BCBC 、ABCBC 、ACBCB 、BABCC 、BACBC 、BCACB 、BCABC 、BCBAC ,所以,甲赢的概率为()4511972232P M ⎛⎫⎛⎫=+⨯= ⎪⎪⎝⎭⎝⎭.由对称性可知,乙赢的概率和甲赢的概率相等,所以丙赢的概率为()97123216P N =-⨯=.【考点】独立事件概率的计算20.【答案】(1)2219x y +=(2)证明:设()06P y ,,则直线AP 的方程为:()()00363y y x -=+--,即:()039yy x =+.联立直线AP 的方程与椭圆方程可得:()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得:()2222000969810y x y x y +++-=,解得:3x =-或20203279y x y -+=+.将20203279y x y -+=+代入直线()039y y x =+可得:02069y y y =+.所以点C 的坐标为2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,.同理可得:点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,.∴直线CD 的方程为: 0022********2000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=- ⎪ ⎪-+-++⎝⎭⎝⎭-++,整理可得: ()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭.整理得:()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭.故直线CD 过定点302⎛⎫⎪⎝⎭,. 【解析】(1)由已知可得:()0A a -,,()0B a ,,()01G ,,即可求得21AG GB a ⋅=-,结合已知即可求得:29a =,问题得解.依据题意作出如下图象:由椭圆方程()222:11x E y a a +=>可得:()0A a -,,()0B a ,,()01G ,.∴()1AG a =,,()1GB a =-,.∴218AG GB a ⋅=-=,∴29a =.∴椭圆方程为:2219x y +=.(2)设()06P y ,,可得直线AP 的方程为:()039yy x =+,联立直线AP 的方程与椭圆方程即可求得点C 的坐标为2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,,同理可得点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,,即可表示出直线CD 的方程, 整理直线CD 的方程可得:()02043233y y x y ⎛⎫=- ⎪-⎝⎭,命题得证. 证明:设()06P y ,,则直线AP 的方程为:()()00363y y x -=+--,即:()039yy x =+.联立直线AP 的方程与椭圆方程可得:()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得:()2222000969810yx y x y +++-=,解得:3x =-或20203279y x y -+=+.将20203279y x y -+=+代入直线()039y y x =+可得:02069y y y =+.所以点C 的坐标为2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,.同理可得:点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,. ∴直线CD 的方程为:0022200002222000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=-⎪ ⎪-+-++⎝⎭⎝⎭-++, 整理可得:()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭ 整理得:()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭. 故直线CD 过定点302⎛⎫ ⎪⎝⎭,. 【考点】椭圆的简单性质,方程思想21.【答案】(1)当()0x ∈-∞,时,()'0f x <,()f x 单调递减,当()0x ∈+∞,时,()'0f x >,()f x 单调递增.(2)274e ⎡⎫-+∞⎪⎢⎣⎭, 【解析】(1)由题意首先对函数二次求导,然后确定导函数的符号,最后确定原函数的单调性即可.当1a =时,()2x x x e f x =+-,()'21x f x e x =+-,由于()''20x f x e =+>,故()'f x 单调递增,注意到()'00f =,故:当()0x ∈-∞,时,()'0f x <,()f x 单调递减,当()0x ∈+∞,时,()'0f x >,()f x 单调递增.(2)首先讨论0x =的情况,然后分离参数,构造新函数,结合导函数研究构造所得的函数的最大值即可确 定实数a 的取值范围.由()3112f x x +≥得,23112x e ax x x +-+,其中0x ≥,①当0x =时,不等式为:11≥,显然成立,符合题意;②当0x >时,分离参数a 得,32112x e x x a x----, 记()32112x e x x g x x ---=-,()()231212'x x e x x g x x ⎛⎫---- ⎪⎝⎭=-,令()()21102x e x x h x x ---=≥,则()'1x h x e x =--,()''10x h x e =-≥,故()'h x 单调递增,()()''00h x h =≥,故函数()h x 单调递增,()()00h x h =≥,由()0h x ≥可得:21102x e x x ---恒成立,故当()02x ∈,时,()'0g x >,()g x 单调递增; 当()2x ∈+∞,时,()'0g x <,()g x 单调递减;因此,()()2max724e g x g -⎡⎤==⎣⎦, 综上可得,实数a 的取值范围是274e ⎡⎫-+∞⎪⎢⎣⎭,. 【考点】导数的几何意义,解析几何,微积分,用导数求函数的单调区间,判断单调性,已知单调性求参数,利用导数求函数的最值(极值),数形结合思想的应用 22.【答案】(1)曲线1C 表示以坐标原点为圆心,半径为1的圆(2)1144⎛⎫⎪⎝⎭,【解析】(1)利用22sin cos 1t t +=消去参数t ,求出曲线1C 的普通方程,即可得出结论.当1k =时,曲线1C 的参数方程为cos sin x t y t=⎧⎨=⎩(t 为参数),两式平方相加得221x y +=,所以曲线1C 表示以坐标原点为圆心,半径为1的圆.(2)当4k =时,0x ≥,0y ≥,曲线1C 的参数方程化为22cos sin tt(t 为参数),两式相加消去参数t ,得1C 普通方程,由cos x ρθ=,sin y ρθ=,将曲线2C 化为直角坐标方程,联立1C ,2C 方程,即可求解.当4k =时,曲线1C 的参数方程为44cos sin x ty t⎧=⎨=⎩(t 为参数),所以数学试卷 第21页(共22页) 数学试卷 第22页(共22页)0x ≥,0y ≥,曲线1C的参数方程化为22cos sin tt(t 为参数),两式相加得曲线1C11,平方得1y x =-,01x ≤≤,01y ≤≤,曲线2C 的极坐标方程为4cos 16sin 30ρθρθ-+=,曲线2C 直角坐标方程为41630x y -+=,联立1C ,2C方程141630y x x y ⎧=-⎪⎨-+=⎪⎩,整理得12130x -=12=136(舍去),14x ∴=,14y =,1C ∴,2C 公共点的直角坐标为1144⎛⎫⎪⎝⎭,.【考点】参数方程与普通方程互化,极坐标方程与直角坐标方程互化23.【答案】(1)因为()3115113133x x f x x x x x ⎧⎪+⎪⎪=--⎨⎪⎪---⎪⎩,≥,<<,≤,作出图象,如图所示:(2)76⎛⎫-∞- ⎪⎝⎭, 【解析】(1)根据分段讨论法,即可写出函数()f x 的解析式,作出图象.因为()3115113133x x f x x x x x ⎧⎪+⎪⎪=--⎨⎪⎪---⎪⎩,≥,<<,≤,作出图象,如图所示:(2)作出函数()1f x +的图象,根据图象即可解出.将函数()f x 的图象向左平移1个单位,可得函数()1f x +的图象,如图所示:由()3511x x --=+-,解得76x =-.所以不等式的解集为76⎛⎫-∞- ⎪⎝⎭,. 【考点】分段函数的图象,利用图象解不等式。
2020年高考数学全国卷1-理科数学试题参考答案

1.D2.B3.C4.C5.D6.B7.C8.C9.A 10.A 11.D 12.B 13.1 14.3 15.2 16.-1417.解:(1)设{a n }的公比为q ,由题设得2a 1=a 2+a 3,即2a 1=a 1q +a 1q 2.所以q 2+q -2=0,解得q =1(舍去),q =-2.故{a n }的公比为-2.(2)记S n 为{na n }的前n 项和.由(1)及题设可得,a n =(-2)n -1.所以S n =1+2ˑ(-2)+ +n ˑ(-2)n -1,-2S n =-2+2ˑ(-2)2+ +(n -1)ˑ(-2)n -1+n ˑ(-2)n .可得3S n =1+(-2)+(-2)2+ +(-2)n -1-n ˑ(-2)n =1-(-2)n 3-n ˑ(-2)n .所以S n =19-(3n +1)(-2)n 9.18.解:(1)设DO =a ,由题设可得P O =66a ,AO =33a ,AB =a .P A =P B =P C =22a .因此P A 2+P B 2=AB 2,从而P A ʅP B .又P A 2+P C 2=AC 2,故P A ʅP C.所以P A ʅ平面P B C .(2)以O 为坐标原点,OE ң的方向为y轴正方向,|OE ң|为单位长,建立如图所示的空间直角坐标系O -x y z .由题设可得E (0,1,0),A (0,-1,0),C -32,12,0 ,P 0,0,22 .所以OE ң=-32,-12,0 ,E P ң=0,-1,22 .设m =(x ,y ,z )是平面P CE 的法向量,测m ㊃E P ң=0,m ㊃E C ң=0, 即-y +22z =0,-32x -12y =0.可取m =-33,1,2.由(1)知E C ң=0,1,22是平面P CB 的一个法向量,记n =A P ң,则cos <n ,m >=n ㊃m |n |㊃|m |=255.所以二面角B -P C -E 的余弦值为255.2020年普通高等学校招生全国统一考试试题参考答案数 学(理科)19.解:(1)甲连胜四场的概率为116.(2)根据赛制,至少需要进行四场比赛,至多需要进行五场比赛.比赛四场结束,共有三种情况:甲连胜四场的概率为116;乙连胜四场的概率为116;丙上场后连胜三场的概率为18.所以需要进行第五场比赛的概率为1-116-116-18=34.(3)丙最终获胜,有两种情况:比赛四场结束且丙最终获胜的概率为18;比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜㊁负㊁轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为116,18,18.因此丙最终获胜的概率为18+116+18+18=716.20.解:(1)由题设得A (-a ,0),B (a ,0),G (0,1).则AG ң=(a ,1),GB ң=(a ,-1).由AG ң㊃GB ң=8得a 2-1=8,即a =3.所以E 的方程为x 29+y 2=1.(2)设C (x 1,y 1),D (x 2,y 2),P (6,t ).若t ʂ0,设直线C D 的方程为x =m y +n ,由题意可知-3<n <3.由于直线P A 的方程为y =t 9(x +3),所以y 1=t 9(x 1+3).直线P B 的方程为y =t 3(x -3),所以y 2=t 3(x 2-3).可得3y 1(x 2-3)=y 2(x 1+3).由于x 229+y 22=1,故y 22=-(x 2+3)(x 2-3)9,可得27y 1y 2=-(x 1+3)(x 2+3),即(27+m 2)y 1y 2+m (n +3)(y 1+y 2)+(n +3)2=0. ①将x =m y +n 代入x 29+y 2=1得(m 2+9)y 2+2m n y +n 2-9=0.所以y 1+y 2=-2m n m 2+9,y 1y 2=n 2-9m 2+9.代入①式得(27+m 2)(n 2-9)-2m (n +3)m n +(n +3)2(m 2+9)=0.解得n =-3(舍去),n =32.故直线C D 的方程为x =m y +32,即直接C D 过定点32,0 .2020年普通高等学校招生全国统一考试试题参考答案数 学(理科)若t =0,则直线C D 的方程为y =0,过点32,0 .综上,直线C D 过定点32,0 .21.解:(1)当a =1时,f (x )=e x +x 2-x ,f '(x )=e x +2x -1.故当x ɪ(-ɕ,0)时,f '(x )<0;当x ɪ(0,+ɕ)时,f '(x )>0.所以f (x )在(-ɕ,0)单调递减,在(0,+ɕ)单调递增.(2)f (x )ȡ12x 3+1等价于12x 3-ax 2+x +1 e -x ɤ1.设函数g (x )=12x 3-ax 2+x +1e -x (x ȡ0),则g '(x )=-12x 3-ax 2+x +1-32x 2+2ax -1 e -x =-12x [x 2-(2a +3)x +4a +2]e -x =-12x (x -2a -1)(x -2)e -x .(ⅰ)若2a +1ɤ0,即a ɤ-12,则当x ɪ(0,2)时,g '(x )>0,所以g (x )在(0,2)单调递增,而g (0)=1,故当x ɪ(0,2)时,g (x )>1,不合题意.(ⅱ)若0<2a +1<2,即-12<a <12,则当x ɪ(0,2a +1)ɣ(2,+ɕ)时,g '(x )<0;当x ɪ(2a +1,2)时,g '(x )>0.所以g (x )在(0,2a +1),(2,+ɕ)单调递减,在(2a +1,2)单调递增.由于g (0)=1,所以g (x )ɤ1当且仅当g (2)=(7-4a )e -2ɤ1,即a ȡ7-e 24.所以当7-e 24ɤa <12时,g (x )ɤ1.(ⅲ)若2a +1ȡ2,即a ȡ12,则g (x )ɤ12x 3+x +1 e -x .由于0ɪ12 ,故由(ⅱ)可得12x 3+x +1 e -x ɤ1.故当a ȡ12时,g (x )ɤ1.综上,a 的取值范围是+ɕ.22.解:(1)当k =1时,C 1ʒx =cos t ,y =si n t , 消去参数t 得x 2+y 2=1,故曲线C 1是圆心为坐标原点,半径为1的圆.(2)当k =4时,C 1ʒx =cos 4t ,y =si n 4t , 消去参数t 得C 1的直角坐标方程为x +y =1.C 2的直角坐标方程为4x -16y +3=0.由x +y =1,4x -16y +3=0 解得x =14,y =14.故C 1与C 2的公共点的直角坐标为14,14 .2020年普通高等学校招生全国统一考试试题参考答案数 学(理科)23.解:(1)由题设知f (x )=-x -3,x ɤ-13,5x -1,-13<x ɤ1,x +3,x >1.y =f (x )的图象如图所示.(2)函数y =f (x )的图象向左平移1个单位长度后得到函数y =f (x +1)的图象.y =f (x )的图象与y =f (x +1)的图象的交点坐标为-76,-116 .由图象可知当且仅当x <-76时,y =f (x )的图象在y =f (x +1)的图象上方.故不等式f (x )>f (x +1)的解集为-ɕ,-76 .2020年普通高等学校招生全国统一考试试题参考答案数 学(理科)。
2020年高考理科数学全国卷1-答案

2020年普通高等学校招生全国统一考试·全国Ⅰ卷理科数学答案解析一、选择题 1.【答案】D【解析】由题意首先求得22z z -的值,然后计算其模即可.由题意可得:()2212z i i =+=,则()222212z z i i -=-+=-.故2222z z -=-=.故选:D .【考点】复数的运算法则,复数的模的求解 2.【答案】B【解析】由题意首先求得集合A ,B ,然后结合交集的结果得到关于a 的方程,求解方程即可确定实数a 的 值.求解二次不等式240x -≤可得:{}22A x x =-≤≤,求解一次不等式20x a +≤可得:2a B x x ⎧⎫=-⎨⎬⎩⎭≤.由于{}21AB x x =-≤≤,故:12a-=,解得:2a =-.故选:B .【考点】交集的运算,不等式的解法 3.【答案】C【解析】设CD a =,PE b =,利用212PO CD PE =⋅得到关于a ,b 的方程,解方程即可得到答案.如图,设CD a =,PE b =,则PO ==212PO ab =,即22142a b ab -=,化简得24210b b a a ⎛⎫-⋅-= ⎪⎝⎭,解得b a =(负值舍去).故选:C .【考点】正四棱锥的概念及其有关计算 4.【答案】C【解析】利用抛物线的定义建立方程即可得到答案. 设抛物线的焦点为F ,由抛物线的定义知122A p AF x =+=,即1292p=+,解得6p =. 故选:C .【考点】利用抛物线的定义计算焦半径 5.【答案】D【解析】根据散点图的分布可选择合适的函数模型.由散点图分布可知,散点图分布在一个对数函数的图象附近,因此,最适合作为发芽率y 和温度x 的回归方程类型的是ln y a b x =+. 故选:D .【考点】函数模型的选择,散点图的分布 6.【答案】B【解析】求得函数()y f x =的导数()f x ',计算出()1f 和()1f '的值,可得出所求切线的点斜式方程,化简 即可.()432f x x x =-,()3246f x x x '∴=-,()11f ∴=-,()12f '=-,因此,所求切线的方程为()121y x +=--,即21y x =-+. 故选:B .【考点】利用导数求解函图象的切线方程 7.【答案】C【解析】由图可得:函数图象过点409π⎛⎫-⎪⎝⎭,,即可得到4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭,结合409π⎛⎫- ⎪⎝⎭,是函数()f x 图象与x 轴负半轴的第一个交点即可得到4962πππω-⋅+=-,即可求得32ω=,再利用三角函数周期公式即可得解.由图可得:函数图象过点409π⎛⎫-⎪⎝⎭,,将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭. 又409π⎛⎫- ⎪⎝⎭,是函数()f x 图象与x 轴负半轴的第一个交点,所以4962πππω-⋅+=-,解得:32ω=.所以函数()f x 的最小正周期为224332T πππω===. 故选:C .【考点】三角函数的性质及转化,三角函数周期公式 8.【答案】C【解析】求得()5x y +展开式的通项公式为515r rrr T C xy -+=(r ∈N 且5r ≤),即可求得2y x x ⎛⎫+ ⎪⎝⎭与()5x y + 展开式的乘积为65r r rC x y -或425r r r C x y -+形式,对r 分别赋值为3,1即可求得33x y 的系数,问题得解.()5x y +展开式的通项公式为515rrrr T C x y -+=(r ∈N 且5r ≤).所以2y x x ⎛⎫+ ⎪⎝⎭与()5x y +展开式的乘积可表示为:56155r rrr rrr xT xC xy C xy --+==或22542155r r rr r r r T C x y xC y y y x x --++==在615r r r r xT C x y -+=中,令3r =,可得:33345xT C x y =,该项中33x y 的系数为10,在42152r r r r T C x x y y -++=中,令1r =,可得:521332T C y x xy =,该项中33x y 的系数为5.所以33x y 的系数为10515+=. 故选:C【考点】二项式定理及其展开式的通项公式,赋值法 9.【答案】A【解析】用二倍角的余弦公式,将已知方程转化为关于cos α的一元二次方程,求解得出cos α,再用同角间的三角函数关系,即可得出结论.3cos28cos 5αα-=,得26cos 8cos 80αα--=,即23cos 4cos 40αα--=,解得2cos 3α=-或cos 2α=(舍去),又(0)απ∈,,sin α∴== 故选:A .【考点】三角恒等变换,同角间的三角函数关系求值10.【答案】A【解析】由已知可得等边ABC △的外接圆半径,进而求出其边长,得出1OO 的值,根据球截面性质,求出 球的半径,即可得出结论.设圆1O 半径为r ,球的半径为R ,依题意,得24r ππ=,2r ∴=,由正弦定理可得2sin 6023AB r ==,1OO AB ∴==,根据圆截面性质1OO ABC⊥平面,11OO O A∴⊥,4R OA =,∴球O 的表面积2464S R ππ==.故选:A .【考点】球的表面积,应用球的截面性质 11.【答案】D【解析】由题意可判断直线与圆相离,根据圆的知识可知,四点A ,P ,B ,M 共圆,且AB MP ⊥,根据22PAM PM AB S PA ⋅==△可知,当直线MP l ⊥时,PM AB ⋅最小,求出以MP 为直径的圆的方程,根据圆系的知识即可求出直线AB 的方程.圆的方程可化为()()22114x y -+-=,点M 到直线l的距离为2d =,所以直线l 与圆相离.依圆的知识可知,四点A ,P ,B ,M 四点共圆,且AB MP ⊥, 所以12222PAM PM AB S PA AM PA ⋅==⨯⨯⨯=△,而PA ,当直线MP l ⊥时,min MPmin1PA =,此时PM AB ⋅最小.()1:112MP y x ∴-=-即1122y x =+,由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得,10x y =-⎧⎨=⎩. 所以以MP 为直径的圆的方程为()()()1110x x y y -++-=,即2210x y y +--=,两圆的方程相减可得:210x y ++=,即为直线AB 的方程.故选:D .【考点】直线与圆,圆与圆的位置关系的应用,圆的几何性质的应用 12.【答案】B【解析】设()22log x f x x =+,利用作差法结合()f x 的单调性即可得到答案. 设()22log x f x x =+,则()f x 为增函数,因为22422log 42log 2log a b b a b b +=+=+,所以()()()()22222222122log 2log 22log 2log 2log 102a b b b f a f b a b b b -=+-+=+-+==-<, 所以()()2f a f b <,所以2a b <.()()()()22222222222222log 2log 2log 2log 22log a b b b b b f a f b a b b b b -=+-+=+-+=--,当1b =时,()()220f a f b -=>,此时()()2f a f b >,有2a b >.当2b =时,()()210f a f b -=-<,此时()()2f a f b <,有2a b <,所以C 、D 错误. 故选:B .【考点】函数与方程的综合应用,构造函数,利用函数的单调性比较大小 二、填空题 13.【答案】1【解析】首先画出可行域,然后结合目标函数的几何意义即可求得其最大值. 绘制不等式组表示的平面区域,如图所示,目标函数7z x y =+即:1177y x z =-+,其中z 取得最大值时,其几何意义表示直线系在y 轴上的截距最大, 据此结合目标函数的几何意义可知目标函数在点A 处取得最大值,联立直线方程:22010x y x y +-=⎧⎨--=⎩,可得点A 的坐标为:()10A ,,据此可知目标函数的最大值为:max 1701z =+⨯=.故答案为:1.14.【解析】整理已知可得:()2a b a b +=+,再利用a ,b 为单位向量即可求得21a b ⋅=-,对a b -变形可得:222a b a a b b -=-⋅+,问题得解.因为a ,b 为单位向量,所以1a b ==,所以()2222221a b a ba ab b a b +=+=+⋅+=+⋅=.解得:21a b ⋅=-.所以()22223a b a ba ab b -=-=-⋅+=.【考点】向量模的计算公式及转化 15.【答案】2【解析】根据双曲线的几何性质可知,2b BF a =,AFc a =-,即可根据斜率列出等式求解即可.依题可得,3BF AF =,而2b BF a =,AFc a =-,即23b a c a=-,变形得22233c a ac a -=-,化简可得, 2320e e -+=,解得2e =或1e =(舍去).故答案为:2.【考点】双曲线的离心率的求法,双曲线的几何性质的应用 16.【答案】14-【解析】在ACE △中,利用余弦定理可求得CE ,可得出CF ,利用勾股定理计算出BC 、BD ,可得出BF , 然后在BCF △中利用余弦定理可求得cos FCB ∠的值.AB AC ⊥,AB 1AC =,由勾股定理得2BC ,同理得BD =,BF BD ∴==,在ACE △中,1AC =,AE AD =30CAE ∠=,由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=,1CF CE ∴==, 在BCF △中,2BC =,BF =1CF =,由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯.故答案为:14-.【考点】利用余弦定理解三角形 三、解答题 17.【答案】(1)2- (2)()()11329nn n S -+-=【解析】(1)由已知结合等差中项关系,建立公比q 的方程,求解即可得出结论.设{}n a 的公比为q ,1a 为2a ,3a 的等差中项,1232a a a =+,10a ≠,220q q ∴+-=,1q ≠,2q ∴=-.(2)由(1)结合条件得出{}n a 的通项,根据{}n na 的通项公式特征,用错位相减法,即可求出结论.设{}n na 的前n 项和为n S ,11a =,()12n n a -=-,()()()211122322n n S n -=⨯+⨯-+⨯-++-,①()()()()()()2312122232122n nn S n n --=⨯-+⨯-+⨯-+--+-,②-①②得,()()()()()()()()()211211323122222123nnn nnn n S n n ----+-=+-+-++---=--=--,()()11329nn n S -+-∴=.【考点】等比数列通项公式基本量的计算,等差中项的性质,错位相减法求和18.【答案】(1)证明:由题设,知DAE △为等边三角形,设1AE =,则DO =1122CO BO AE ===,所以PO ==,PC =PB ==ABC △为等边三角形,则2sin60BA OA =,所以BA =22234PA PB AB +==,则90APB ∠=,所以PA PB ⊥,同理PA PC ⊥, 又PC PB P =,所以PA PBC ⊥平面.(2 【解析】(1)要证明PA PBC ⊥平面,只需证明PA PB ⊥,PA PC ⊥即可. 由题设,知DAE △为等边三角形,设1AE =,则DO =1122CO BO AE ===,所以4PO ==,PC ==PB ==,又ABC △为等边三角形,则2sin60BA OA =,所以BA =22234PA PB AB +==, 则90APB ∠=,所以PA PB ⊥,同理PA PC ⊥,又PCPB P =,所以PA PBC ⊥平面.(2)以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如图所示的空间直角坐标系,分别算出平面PCB 的法 向量为n ,平面PCE 的法向量为m ,利用公式cos m <,||||n mn n m ⋅=>计算即可得到答案.过O 作ON BC ∥交AB 于点N ,因为PO ABC ⊥平面,以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如图所示的空间直角坐标系,则1002E ⎛⎫- ⎪⎝⎭,,,00P ⎛ ⎝⎭,104B ⎛⎫- ⎪ ⎪⎝⎭,,104C ⎛⎫- ⎪ ⎪⎝⎭,,14PC ⎛=- ⎝⎭,,14PB ⎛=-- ⎝⎭,102PE ⎛=- ⎝⎭,,,设平面PCB 的一个法向量为()111n x y z =,,,由00n PC n PB ⎧⋅=⎪⎨⋅=⎪⎩,得1111110x x ⎧-=⎪⎨-=⎪⎩,令1x =11z =-,10y =,所以()201n =-,,,设平面PCE 的一个法向量为()222m x y z =,,由00m PC m PE ⎧⋅=⎪⎨⋅=⎪⎩,得22222020x x ⎧--=⎪⎨-=⎪⎩,令21x =,得2z =2y =,所以313m ⎛=- ⎝,故cos m <,2||||3n m n n m ⋅===⋅⨯,设二面角22143x y +=的大小为θ,则cos θ=【考点】线面垂直的证明,利用向量求二面角的大小 19.【答案】(1)116(2)34(3)716【解析】(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率.记事件:M 甲连胜四场,则()411216P M ⎛⎫== ⎪⎝⎭.(2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率.记事件A 为甲输,事件B 为乙输,事件C 为丙输,则四局内结束比赛的概率为()()()()411424P P ABAB P ACAC P BCBC P BABA ⎛⎫'=+++=⨯= ⎪⎝⎭,所以,需要进行第五场比赛的概率为314P P '=-=.(3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率 和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.记事件A 为甲输,事件B 为乙输,事件C 为丙输,记事件:M 甲赢,记事件:N 丙赢,则甲赢的基本事件包括:BCBC 、ABCBC 、ACBCB 、BABCC 、BACBC 、BCACB 、BCABC 、BCBAC ,所以,甲赢的概率为()4511972232P M ⎛⎫⎛⎫=+⨯= ⎪ ⎪⎝⎭⎝⎭.由对称性可知,乙赢的概率和甲赢的概率相等,所以丙赢的概率为()97123216P N =-⨯=. 【考点】独立事件概率的计算20.【答案】(1)2219x y +=(2)证明:设()06P y ,,则直线AP 的方程为:()()00363y y x -=+--,即:()039yy x =+.联立直线AP 的方程与椭圆方程可得:()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得:()2222000969810y x y x y +++-=,解得:3x =-或20203279y x y -+=+.将20203279y x y -+=+代入直线()039y y x =+可得:02069y y y =+.所以点C 的坐标为 2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,.同理可得:点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,.∴直线CD 的方程为: 0022200002222000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=- ⎪ ⎪-+-++⎝⎭⎝⎭-++,整理可得: ()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭.整理得:()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭.故直线CD 过定点302⎛⎫⎪⎝⎭,. 【解析】(1)由已知可得:()0A a -,,()0B a ,,()01G ,,即可求得21AG GB a ⋅=-,结合已知即可求得:29a =,问题得解.依据题意作出如下图象:由椭圆方程()222:11x E y a a +=>可得:()0A a -,,()0B a ,,()01G ,.∴()1AG a =,,()1GB a =-,. ∴218AG GB a ⋅=-=,∴29a =.∴椭圆方程为:2219x y +=.(2)设()06P y ,,可得直线AP 的方程为:()039y y x =+,联立直线AP 的方程与椭圆方程即可求得点C 的坐标为2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,,同理可得点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,,即可表示出直线CD 的方程, 整理直线CD 的方程可得:()02043233y y x y ⎛⎫=- ⎪-⎝⎭,命题得证. 证明:设()06P y ,,则直线AP 的方程为:()()00363y y x -=+--,即:()039yy x =+.联立直线AP 的方程与椭圆方程可得:()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得:()2222000969810y x y x y +++-=,解得:3x =-或20203279y x y -+=+.将20203279y x y -+=+代入直线()039y y x =+可得:02069y y y =+.所以点C 的坐标为2002200327699y y y y ⎛⎫-+ ⎪++⎝⎭,.同理可得:点D 的坐标为200220033211y y y y ⎛⎫-- ⎪++⎝⎭,.∴直线CD 的方程为:0022200002222000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=- ⎪ ⎪-+-++⎝⎭⎝⎭-++, 整理可得:()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭整理得:()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭. 故直线CD 过定点302⎛⎫ ⎪⎝⎭,. 【考点】椭圆的简单性质,方程思想21.【答案】(1)当()0x ∈-∞,时,()'0f x <,()f x 单调递减,当()0x ∈+∞,时,()'0f x >,()f x 单调递 增.(2)274e ⎡⎫-+∞⎪⎢⎣⎭, 【解析】(1)由题意首先对函数二次求导,然后确定导函数的符号,最后确定原函数的单调性即可. 当1a =时,()2x x x e f x =+-,()'21x f x e x =+-,由于()''20x f x e =+>,故()'f x 单调递增,注意到()'00f =,故:当()0x ∈-∞,时,()'0f x <,()f x 单调递减,当()0x ∈+∞,时,()'0f x >,()f x 单调递增. (2)首先讨论0x =的情况,然后分离参数,构造新函数,结合导函数研究构造所得的函数的最大值即可确 定实数a 的取值范围.由()3112f x x +≥得,23112x e ax x x +-+,其中0x ≥, ①当0x =时,不等式为:11≥,显然成立,符合题意;②当0x >时,分离参数a 得,32112x e x x a x ----, 记()32112x e x x g x x ---=-,()()231212'x x e x x g x x ⎛⎫---- ⎪⎝⎭=-,令()()21102x e x x h x x ---=≥, 则()'1x h x e x =--,()''10x h x e =-≥,故()'h x 单调递增,()()''00h x h =≥,故函数()h x 单调递增,()()00h x h =≥,由()0h x ≥可得:21102x e x x ---恒成立, 故当()02x ∈,时,()'0g x >,()g x 单调递增; 当()2x ∈+∞,时,()'0g x <,()g x 单调递减;因此,()()2max 724e g x g -⎡⎤==⎣⎦, 综上可得,实数a 的取值范围是274e ⎡⎫-+∞⎪⎢⎣⎭,. 【考点】导数的几何意义,解析几何,微积分,用导数求函数的单调区间,判断单调性,已知单调 性求参数,利用导数求函数的最值(极值),数形结合思想的应用22.【答案】(1)曲线1C 表示以坐标原点为圆心,半径为1的圆(2)1144⎛⎫ ⎪⎝⎭, 【解析】(1)利用22sin cos 1t t +=消去参数t ,求出曲线1C 的普通方程,即可得出结论.当1k =时,曲线1C 的参数方程为cos sin x t y t=⎧⎨=⎩(t 为参数),两式平方相加得221x y +=,所以曲线1C 表示以坐标原点为圆心,半径为1的圆.(2)当4k =时,0x ≥,0y ≥,曲线1C的参数方程化为22cos sin t t(t 为参数),两式相加消去参数t , 得1C 普通方程,由cos x ρθ=,sin y ρθ=,将曲线2C 化为直角坐标方程,联立1C ,2C 方程,即可求解.当4k =时,曲线1C 的参数方程为44cos sin x t y t⎧=⎨=⎩(t 为参数),所以0x ≥,0y ≥, 曲线1C的参数方程化为22cos sin t t==(t 为参数), 两式相加得曲线1C1=1=-,平方得1y x =-,01x ≤≤,01y ≤≤,曲线2C 的极坐标方程为4cos 16sin 30ρθρθ-+=,曲线2C 直角坐标方程为41630x y -+=,联立1C ,2C方程141630y x x y ⎧=-⎪⎨-+=⎪⎩,整理得12130x -=,12=136=(舍去),14x ∴=,14y =,1C ∴,2C 公共点的直角坐标为1144⎛⎫ ⎪⎝⎭,. 【考点】参数方程与普通方程互化,极坐标方程与直角坐标方程互化23.【答案】(1)因为()3115113133x x f x x x x x ⎧⎪+⎪⎪=--⎨⎪⎪---⎪⎩,≥,<<,≤,作出图象,如图所示:(2)76⎛⎫-∞- ⎪⎝⎭, 【解析】(1)根据分段讨论法,即可写出函数()f x 的解析式,作出图象.因为()3115113133x x f x x x x x ⎧⎪+⎪⎪=--⎨⎪⎪---⎪⎩,≥,<<,≤,作出图象,如图所示:(2)作出函数()1f x +的图象,根据图象即可解出.将函数()f x 的图象向左平移1个单位,可得函数()1f x +的图象,如图所示:由()3511x x --=+-,解得76x =-.所以不等式的解集为76⎛⎫-∞- ⎪⎝⎭,. 【考点】分段函数的图象,利用图象解不等式。
2020年高考数学全国卷真题-理科1卷

2020年普通高等学校招生全国统一考试(卷一)数学-理一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1. 已知集合{}24|<<-=x x M ,{}06|2<--=x x x N ,则=⋂N MA.{}34|<<-x xB.{}24|-<<-x xC.{}22|<<-x xD.{}32|<<x x 2. 设复数Z 满足1||=-i z ,Z 在复平面内对应的点为),(y x ,则A. 1)1(22=++y xB.1)1(22=+-y xC.()1122=-+y xD.()1122=++y x3. 已知2.0log 2=a ,2.02=b ,3.02.0=c ,则 A.c b a << B.b c a << C.b a c << D.b c a <<4. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是215-(618.0215≈-,称为黄金分割比例),著名的“断臂维纳斯”便是如此。
此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度比也是215-。
若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是A.165 cmB.175 cmC.185 cmD.190 cm5. 函数2cos sin )(x x x x x f ++=在],[ππ-的图像大致为 A. B.C. D.6. 我国古代典籍《周易》用“卦”描述万物的变化。
每一“重卦”由从下到上排列的六个爻组成,爻分成阳爻“——”和阴爻“— —”,右图就是一重卦。
在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A.165B.3211C.3221D.1611 7. 已知非零向量→a ,→b 满足||2||→→=b a ,且→→→⊥-b b a )(,则→a 与→b 夹角为A.6πB.3πC.32πD.65π 8. 右图是求212121++的程序框图,图中空白部分中应填入 A. AA +=21 B. AA 12+= C. AA 211+= D.AA 211+= 9. 记n S 为等差数列{}n a 的前n 项和.已知04=S ,55=a ,则 A.52-=n a n B.103-=n a n C.n n S n 822-= D.n n S n 2212-=10. 已知椭圆C 的焦点为)0,1(1-F ,)0,1(2F ,过2F 的直线与C 交于A,B 两点,若||2||22BF AF =,||||1BF AB =,则C 的方程为 A.1222=+y x B.12322=+y x C.13422=+y x D.14522=+y x 11. 关于函数|sin |||sin )(x x x f +=有下述四个结论:①)(x f 是偶函数;②)(x f 在区间),2(ππ单调递增; ③)(x f 在],[ππ-有四个零点;④)(x f 的最大值为2其中所有正确的结论的编号是A.①②④B.②④C.①④D.①③ 12. 已知三棱锥ABC P -的四个顶点在球O 的球面上,PA=PB=PC ,△ABC 是边长为2的正三角形,E,F 分别是PA,AB 的中点, 90=∠CEF ,则球O 的体积为A.π68B.π64C.π62D.π6二、填空题:本题共4小题。
2020年新高考(全国卷)数学试卷结构与评析
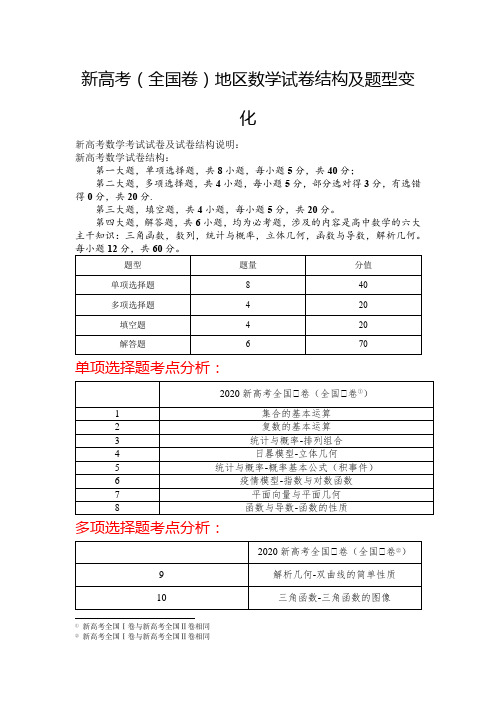
新高考(全国卷)地区数学试卷结构及题型变化新高考数学考试试卷及试卷结构说明:新高考数学试卷结构:第一大题,单项选择题,共8小题,每小题5分,共40分;第二大题,多项选择题,共4小题,每小题5分,部分选对得3分,有选错得0分,共20分.第三大题,填空题,共4小题,每小题5分,共20分。
第四大题,解答题,共6小题,均为必考题,涉及的内容是高中数学的六大主干知识:三角函数,数列,统计与概率,立体几何,函数与导数,解析几何。
单项选择题考点分析:多项选择题考点分析:①新高考全国Ⅰ卷与新高考全国Ⅱ卷相同新高考选择题部分分析:①新高考与之前相比,最大的不同就是增加了多项选择题部分,选择题部分由原来的12道单选题,变成了8道单选题与4道多选题。
这有利于缩小学生选择题部分成绩的差距,过去学生错一道单选题,可能就会丢掉5分,在新高考中,考生部分选对就可以得3分,在一定程度上保证了得分率。
②新高考的单项选择题部分主要考察学生的基础知识和基本运算能力,总体上难度不大,只要认真复习,一般都可以取得一个较好的成绩。
在多项选择题上,前两道较为基础,后两道难度较大,能够突出高考的选拔性功能,总体上来看,学生比以往来讲,更容易取得一个不错的成绩,但对于一些数学基础比较的好的同学来说,这些题比以往应该更有挑战性。
过去,只需要在四个选项中选一个正确答案,现在要在四个选项中,选出多个答案,比以往来说,要想准确的把正确答案全部选出来,确实有一定的难度、③新高考数学试卷的第4题,第6题和第12题都体现了创新性。
第4题,以古代知识为背景,考察同学们的立体几何知识,这体现了数学考试的价值观导向。
弘扬传统文化的同时也鼓励同学们走进传统文化。
近年来,对于这类题目也是屡见不鲜,平时也应该鼓励学生去关注一些古代的数学著作,如《九章算术》,《孙子算经》等等,通过对这些著作的了解,再遇到这类题目时,在一定程度上能够减少恐惧感与焦虑感。
第6题则体现了聚焦民生,关注社会热点。
2020年全国统一高考数学试卷(理科)(全国卷新课标1)

2020年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合M={x|﹣4<x<2},N={x|x2﹣x﹣6<0},则M∩N=()A.{x|﹣4<x<3} B.{x|﹣4<x<﹣2} C.{x|﹣2<x<2} D.{x|2<x<3} 2.(5分)设复数z满足|z﹣i|=1,z在复平面内对应的点为(x,y),则()A.(x+1)2+y2=1 B.(x﹣1)2+y2=1C.x2+(y﹣1)2=1 D.x2+(y+1)2=13.(5分)已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a4.(5分)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是()A.165cm B.175cm C.185cm D.190cm5.(5分)函数f(x)=在[﹣π,π]的图象大致为()A.B.C.D.6.(5分)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“”和阴爻“”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是()A.B.C.D.7.(5分)已知非零向量,满足||=2||,且(﹣)⊥,则与的夹角为()A.B.C.D.8.(5分)如图是求的程序框图,图中空白框中应填入()A.A=B.A=2+C.A=D.A=1+9.(5分)记S n为等差数列{a n}的前n项和.已知S4=0,a5=5,则()A.a n=2n﹣5 B.a n=3n﹣10 C.S n=2n2﹣8n D.S n=n2﹣2n 10.(5分)已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.+y2=1 B.+=1C.+=1 D.+=111.(5分)关于函数f(x)=sin|x|+|sin x|有下述四个结论:①f(x)是偶函数②f(x)在区间(,π)单调递增③f(x)在[﹣π,π]有4个零点④f(x)的最大值为2其中所有正确结论的编号是()A.①②④B.②④C.①④D.①③12.(5分)已知三棱锥P﹣ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为()A.8πB.4πC.2πD.π二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年普通高等学校招生全国统一考试(全国I 卷)文科数学一、选择题:认真审题,仔细想一想,然后选出正确答案.本题共12小题,每小题5分,共60分。
1.已知集合2{|340},{4,1,3,5}A x x x B =--<=-,则A B =A .{4,1}-B .{1,5}C .{3,5}D .{1,3}2.若312i i z =++,则||=z A .0 B .1CD .23.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .14B .12C .14D .124.设O 为正方形ABCD 的中心,在O ,A ,B ,C ,D 中任取3点,则取到的3点共线的概率为 A .15B .25C .12D .455.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C )的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i x y i =得到下面的散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是 A .y a bx =+ B .2y a bx =+ C .e x y a b =+D .ln y a b x =+6.已知圆2260x y x +-=,过点(1,2)的直线被该圆所截得的弦的长度的最小值为 A .1 B .2C .3D .47.设函数π()cos()6f x x ω=+在[−π,π]的图像大致如下图,则f (x )的最小正周期为A .10π9 B .7π6 C .4π3D .3π28.设3log 42a =,则4a -= A .116B .19C .18D .169.执行下面的程序框图,则输出的n =A .17B .19C .21D .2310.设{}n a 是等比数列,且1231a a a ++=,234+2a a a +=,则678a a a ++=A .12B .24C .30D .3211.设12,F F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P 在C 上且||2OP =,则12PF F △的面积为 A .72B .3C .52D .212.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π二、填空题:本题共4小题,每小题5分,共20分。
13.若x ,y 满足约束条件220,10,10,x y x y y +-≤⎧⎪--≥⎨⎪+≥⎩则z =x +7y 的最大值为 .14.设向量(1,1),(1,24)m m =-=+-a b ,若⊥a b ,则m = . 15.曲线ln 1y x x =++的一条切线的斜率为2,则该切线的方程为 .16.数列{}n a 满足2(1)31nn n a a n ++-=-,前16项和为540,则1a = .三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:甲分厂产品等级的频数分布表(1(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?18.(12分)ABC△的内角A,B,C的对边分别为a,b,c.已知B=150°.△的面积;(2)若sin A C,求C.19.(12分)△是底面的内接正三角形,P为DO上一点,∠如图,D为圆锥的顶点,O是圆锥底面的圆心,ABCAPC=90°.(1)证明:平面PAB⊥平面PAC;(2)设DO ,求三棱锥P −ABC 的体积. 20.已知函数()e (2)xf x a x =-+.(1)当1a =时,讨论()f x 的单调性; (2)若()f x 有两个零点,求a 的取值范围.21.已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线x =6上的动点,P A 与E 的另一交点为C ,PB 与E 的另一交点为D . (1)求E 的方程;(2)证明:直线CD 过定点.(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,曲线1C 的参数方程为cos ,sin kkx t y t⎧=⎪⎨=⎪⎩(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos 16sin 30ρθρθ-+=. (1)当1k =时,1C 是什么曲线?(2)当4k =时,求1C 与2C 的公共点的直角坐标. 23.[选修4—5:不等式选讲](10分)已知函数()|31|2|1|f x x x =+--. (1)画出()y f x =的图像;(2)求不等式()(1)f x f x >+的解集.2020年普通高等学校招生全国统一考试文科数学试题参考答案(A 卷)选择题答案 一、选择题 1.D 2.C 3.C 4.A 5.D 6.B 7.C 8.B 9.C 10.D11.B12.A非选择题答案 二、填空题 13.1 14.5 15.y =2x 16.7三、解答题 17.解:(1)由试加工产品等级的频数分布表知,甲分厂加工出来的一件产品为A 级品的概率的估计值为400.4100=; 乙分厂加工出来的一件产品为A 级品的概率的估计值为280.28100=. (2)由数据知甲分厂加工出来的100件产品利润的频数分布表为因此甲分厂加工出来的100件产品的平均利润为65402520520752015100⨯+⨯-⨯-⨯=.由数据知乙分厂加工出来的100件产品利润的频数分布表为因此乙分厂加工出来的100件产品的平均利润为70283017034702110100⨯+⨯+⨯-⨯=.比较甲乙两分厂加工的产品的平均利润,应选甲分厂承接加工业务.18.解:(1)由题设及余弦定理得2222832cos150c c =+-⨯︒,解得2c =-(舍去),2c =,从而a =ABC △的面积为12sin1502⨯⨯︒=(2)在ABC △中,18030A B C C =︒--=︒-,所以sin sin(30)sin(30)A C C C C +=︒-=︒+,故sin(30)2C ︒+=. 而030C <<︒,所以3045C ︒+=︒,故15C =︒. 19.解:(1)由题设可知,PA =PB = PC .由于△ABC 是正三角形,故可得△PAC ≌△PAB . △PAC ≌△PBC .又∠APC =90°,故∠APB =90°,∠BPC =90°.从而PB ⊥PA ,PB ⊥PC ,故PB ⊥平面PAC ,所以平面PAB ⊥平面PAC . (2)设圆锥的底面半径为r ,母线长为l .由题设可得rl 222l r ==.解得r =1,l从而AB 1)可得222PA PB AB +=,故PA PB PC ===所以三棱锥P -ABC 的体积为311113232PA PB PC ⨯⨯⨯⨯=⨯⨯=.20.解:(1)当a =1时,f (x )=e x –x –2,则f x '()=e x –1. 当x <0时,f x '()<0;当x >0时,f x '()>0. 所以f (x )在(–∞,0)单调递减,在(0,+∞)单调递增.(2)f x '()=e x –a .当a ≤0时,f x '()>0,所以f (x )在(–∞,+∞)单调递增, 故f (x )至多存在1个零点,不合题意.当a >0时,由f x '()=0可得x =ln a . 当x ∈(–∞,ln a )时,f x '()<0; 当x ∈(ln a ,+∞)时,f x '()>0.所以f (x )在(–∞,ln a )单调递减,在(ln a ,+∞)单调递增,故当x =ln a 时,f (x )取得最小值,最小值为f (ln a )=–a (1+ln a ).(i )若0≤a ≤1e ,则f (ln a )≥0,f (x )在(–∞,+∞)至多存在1个零点,不合题意.(ii )若a >1e,则f (ln a )<0.由于f (–2)=e –2>0,所以f (x )在(–∞,ln a )存在唯一零点. 由(1)知,当x >2时,e x –x –2>0,所以当x >4且x >2ln (2a )时,ln(2)22()e e (2)e (2)(2)202x x a xf x a x a x a =⋅-+>⋅+-+=>.故f (x )在(ln a ,+∞)存在唯一零点,从而f (x )在(–∞,+∞)有两个零点.综上,a 的取值范围是(1e,+∞).21.解:(1)由题设得(,0),(,0),(0,1)A a B a G -.则(,1)AG a =,(,1)GB a =-.由8AG GB ⋅=得218a -=,即3a =.所以E 的方程为2219x y +=.(2)设1122(,),(,),(6,)C x y D x y G t .若0t ≠,设直线CD 的方程为x my n =+,由题意可知33n -<<. 由于直线PA 的方程为(3)9t y x =+,所以11(3)9ty x =+.直线PB 的方程为(3)3t y x =-,所以22(3)3ty x =-.可得12213(3)(3)y x y x -=+.由于222219x y +=,故2222(3)(3)9x x y +-=-,可得121227(3)(3)y y x x =-++, 即221212(27)(3)()(3)0m y y m n y y n ++++++=.①将x my n =+代入2219xy +=得222(9)290m y mny n +++-=.所以212122229,99mn n y y y y m m -+=-=-++.代入①式得2222(27)(9)2(3)(3)(9)0m n m n mn n m +--++++=. 解得3n =-(舍去),32n =. 故直线CD 的方程为32x my =+,即直线CD 过定点3(,0)2. 若0t =,则直线CD 的方程为0y =,过点3(,0)2.综上,直线CD 过定点3(,0)2.22.解:当k =1时,1cos ,:sin ,x t C y t =⎧⎨=⎩消去参数t 得221x y +=,故曲线1C 是圆心为坐标原点,半径为1的圆.(2)当k =4时,414cos ,:sin ,x t C y t ⎧=⎪⎨=⎪⎩消去参数t 得1C1. 2C 的直角坐标方程为41630x y -+=.由1,41630x y +=-+=⎪⎩解得1414x y ⎧=⎪⎪⎨⎪=⎪⎩.故1C 与2C 的公共点的直角坐标为11(,)44.23.解:(1)由题设知13,,31()51,1,33, 1.x x f x x x x x ⎧--≤-⎪⎪⎪=--<≤⎨⎪⎪+>⎪⎩()y f x =的图像如图所示.(2)函数()y f x =的图像向左平移1个单位长度后得到函数(1)y f x =+的图像.()y f x =的图像与(1)y f x =+的图像的交点坐标为711(,)66--.由图像可知当且仅当76x <-时,()y f x =的图像在(1)y f x =+的图像上方,故不等式()(1)f x f x >+的解集为7(,)6-∞-.为大家整理的资料供学习参考,希望能帮助到大家,非常感谢大家的下载,以后会为大家提供更多实用的资料。
