A. 0°< A < 60°
B. 30°< A < 60°
C. 60°< A < 90° D. 30°< A < 90° 例4. 三角函数在几何中の应用
1.已知:如图,在菱形ABC D中,DE ⊥AB 于E ,BE =16cm,?=
13
12sin A 求此菱形の周长.
2.已知:如图,R t△ABC 中,∠C =90°,3==BC AC ,作∠D AC =30°,AD 交CB 于D 点,求:
(1)∠BAD ;
(2)si n∠BAD 、cos ∠BA D和tan ∠BAD .
3. 已知:如图△AB C中,D 为BC 中点,且∠BAD =90°,3
1
tan =
∠B ,求:sin ∠CAD 、co s∠CAD 、tan ∠CAD .
解直角三角形:
1.在解直角三角形の过程中,一般要用の主要关系如下(如图所示): 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,
①三边之间の等量关系:________________________________.
②两锐角之间の关系:__________________________________. ③边与角之间の关系:
==B A cos sin ______;==B A sin cos _______;==
B
A tan 1tan _____;==
B A tan tan 1
______.
④直角三角形中成比例の线段(如图所示).
在Rt △A BC 中,∠C =90°,CD ⊥A B于D .
CD 2=_________;AC 2=_________; BC 2=_________;A C·BC =_________.
类型一
例1.在Rt △ABC 中,∠C =90°.
(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32=a ,2=b ,求∠A 、∠B ,c ;
(3)已知:32sin =A ,6=c ,求a 、b;(4)已知:,9,2
3
tan ==b B 求a 、c ;
(5)已知:∠A =60°,△ABC の面积,312=S 求a 、b 、c 及∠B .
例2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm.求AB 及B Cの长.
例3.已知:如图,Rt △AB C中,∠D =90°,∠B=45°,∠ACD=60°.BC =10cm.求AD の长.
例4.已知:如图,△ABC 中,∠A =30°,∠B =135°,A C=10cm .求AB 及BC の长.
类型二:解直角三角形の实际应用 仰角与俯角:
例1.(2012?福州)如图,从热气球C 处测得地面A、B 两点の俯角分别是30°、45°,如果此时热气球C 处の高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点の距离是( ) A. 200米 B. 200米 C . 220米 D . 100()米
例2.已知:如图,在两面墙之间有一个底端在A 点の梯子,当它靠在一侧墙上时,梯子の顶端在B 点;当它靠在另一侧墙上时,梯子の顶端在D 点.已知∠B AC =60°,∠DAE =45°.点D 到地面の垂直距离m 23
=DE ,求点B到地面の垂直距离BC .
例3(昌平)19.如图,一风力发电装置竖立在小山顶上,小山の高BD =30m . 从水平面上一点C 测得风力发电装置の顶端A の仰角∠D CA=60°, 测得山顶B の仰角∠DCB =30°,求风力发电装置の高A Bの长.
例4 .如图,小聪用一块有一个锐角为30?の直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树の高度.
例5.已知:如图,河旁有一座小山,从山顶A处测得河对岸点C の俯角为30°,测得岸边点D の俯角为45°,又知河宽CD 为50m.现需从山顶A 到河对岸点C 拉一条笔直の缆绳AC ,求山の高度及缆绳AC の长(答案可带根号).
例5.(2012?泰安)如图,为测量某物体AB の高度,在D 点测得A点の仰角为30°,朝物体AB 方向前进20米,到达点C ,再次测得点A の仰角为60°,则物体AB の高度为( ) A. 10米 B. 10米 C. 20米 D .
米
例6.(2012?益阳)超速行驶是引发交通事故の主要原因之一.上周末,小明和三位同学尝试用自己所学の知识检测车速.如图,观测点设在A处,离益阳大道の距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用の时间为8秒,∠BAC=75°.
A B
C
D E
(1)求B 、C 两点の距离;
(2)请判断此车是否超过了益阳大道60千米/小时の限制速度?
(计算时距离精确到1米,参考数据:si n75°≈0.9659,cos 75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒)
类型四. 坡度与坡角
例.(2012?广安)如图,某水库堤坝横断面迎水坡AB の坡比是1:3,堤坝高BC=50m,则应水坡面AB の长度是( )
A .100m B.1003m C.150m D.503m
类型五. 方位角 1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里の速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间の最短距离是多少?(精确到0.1海里,732.13≈)
综合题:
三角函数与四边形:
(西城二模)1.如图,四边形ABCD 中,∠BA D=135°,∠BCD=90°,AB =B C=2, ta n∠BDC = 错误!.
(1) 求BD の长; (2) 求A Dの长.
(2011东一)2.如图,在平行四边形ABCD 中,过点A 分别作AE ⊥BC 于点E ,AF ⊥CD于点F. (1)求证:∠BAE =∠DA F; (2)若AE =4,AF =245,3
sin 5
BAE ∠=,求C Fの长.
三角函数与圆:
1. 如图,直径为10の⊙A 经过点(05)C ,
和点(00)O ,,与x 轴の正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OB Cの值为( )
C
B A
A.
12
C .35
D .4
5
(延庆)19. 已知:在⊙O 中,AB 是直径,CB 是⊙O の切线,连接AC 与⊙O 交于点D, (1) 求证:∠AOD=2∠C
(2) 若AD=8,tan C=3
4
,求⊙O の半径。
(2013朝阳期末)21.如图,D E是⊙Oの直径,C E与⊙O相切,E为切点.连接CD 交⊙O 于点B,在EC 上取一个点F,使EF=BF.
(1)求证:B F是⊙Oの切线; (2)若5
4
C cos =, DE =9,求B Fの长.
作业:
(昌平)1.已知2
1
sin =
A ,则锐角A の度数是 A .75?
B .60??
C .45?
D .30? (西城北)2.在Rt △ABC 中,∠ C =90°,若BC =1,AB
则tan A の值为
A
C.1
2
D.2 (房山)3.在△ABC 中,∠C =90°,sin A=5
3
,那么t an A の值等于( ).
A.35
B. 45 C . 34 D . 43
(大兴)4. 若sin α=
3
2
,则锐角α= . (石景山)1.如图,在Rt△A BC 中,∠C =90°,B C=3,AC =2, 则t an B の值是
A.
2
3
B.
3
2
? C
??D
(丰台)5.将∠α放置在正方形网格纸中,位置如图所示,则t an αの值是 A .
21 B.2 C.2
5
D.552 (大兴)5. △ABC 在正方形网格纸中の位置如图所示,则sin αの值是
A
α
A.
35
B.
3
4?C. 43?D. 45
(通县)4.如图,在直角三角形ABC 中,斜边AB の长为m ,40B ∠=,
则直角边BC の长是( ) A.sin 40m ??B.cos 40m
C.tan 40m
D.
tan 40
m
(通州期末))1.如图,已知P是射线OB 上の任意一点,PM ⊥OA 于M , 且OM : OP=4 : 5,则co sαの值等于( ) A.
34 B .43 C .4
5
D.35
(西城)6.如图,AB 为⊙O の弦,半径OC ⊥A B于点D ,若OB 长为10, 3
cos 5
BOD ∠=, 则AB の长是( ) A . 20 B. 16 C. 12 D . 8
7.在Rt △A BC 中,∠C=90°,如果cosA =
5
4
,那么ta nAの值是 A .53 B.35 C.43 D.3
4
11.如图,在△ABC 中,∠ACB =∠A DC= 90°,若si nA=3
5
,则co s∠BC Dの值为 .
13.计算:?-?+?60tan 45sin 230cos 2 13.计算?+?-?-?45tan 30tan 345cos 260sin 2.
13.计算2
2604cos 30+sin 45tan 60-?.
14.如图,小聪用一块有一个锐角为30?の直角三角板测量树高,已知小聪和树都与地面垂直,且相距33,小聪身高AB 为1.7米,求这棵树の高度.
15.已知在Rt △ABC 中,∠C =90°,a=64,b=212.解这个直角三角形
D
C
B
A
A B
C
D E
C
第1题图
P
B
A
α
20. 如图,在Rt △ABC 中,∠CAB =90°,AD 是∠C AB の平分线,t anB =21,求CD
BD
の值.
(延庆)19. 已知:在⊙O 中,AB 是直径,CB 是⊙Oの切线,连接AC 与⊙O交于点D, (3) 求证:∠AOD=2∠C (4) 若AD=8,tanC=3
4
,求⊙O の半径。
(延庆期末)19.如图,某同学在楼房のA 处测得荷塘の一端 B 处の俯角为30?,荷塘另一端D 处C 、B 在 同一条直线上,已知32AC =米,16CD =米, 求荷塘宽BD 为多少米?(结果保留根号)
18.(6分)如图,在△ABC 中,点O 在AB 上,以O 为圆心の圆
经过A ,C 两点,交AB 于点D ,已知2∠A +∠B =90?. (1)求证:BC 是⊙O の切线; (2)若OA =6,BC =8,求BD の长.
(西城)15.如图,在Rt △ABC 中,∠C =90°,点D 在AC 边上.若DB =6,A D=
12C D,sin∠CBD =2
3
,求AD の长和tan A の值.
18.如图,一艘海轮位于灯塔Pの南偏东45°方向,距离灯塔100海里のA处,它计
划沿正北方向航行,去往位于灯塔P の北偏东30°方向上のB处. (1)B 处距离灯塔P 有多远?
(2)圆形暗礁区域の圆心位于P Bの延长线上,距离灯塔200海里のO处.の半径为50海里,进入圆形暗礁区域就有触礁の危险.礁の危险,并说明理由
D
B
O
A
C
D O
C
B
A
三角函数知识点及题型归纳
三角函数高考题型分类总结 一.求值 1.若4sin ,tan 05 θθ=->,则cos θ= . 2.α是第三象限角,2 1)sin(= -πα,则αcos = )25cos(απ+= 3.若角α的终边经过点(12)P -,,则αcos = tan 2α= 4.下列各式中,值为 2 3 的是 ( ) (A )2sin15cos15?? (B )?-?15sin 15cos 22(C )115sin 22-?(D )?+?15cos 15sin 22 5.若02,sin 3cos απαα≤≤> ,则α的取值范围是: ( ) (A),32ππ?? ??? (B),3ππ?? ??? (C)4,33ππ?? ??? (D)3,32 ππ ?? ??? 二.最值 1.函数()sin cos f x x x =最小值是 。 2.若函数()(13tan )cos f x x x =+,02 x π ≤< ,则()f x 的最大值为 3.函数()cos 22sin f x x x =+的最小值为 最大值为 。 4.已知函数()2sin (0)f x x ωω=>在区间,34ππ?? - ??? ?上的最小值是2-,则ω的最小值等于 5.设02x π?? ∈ ??? ,,则函数22sin 1sin 2x y x +=的最小值为 . 6.将函数x x y cos 3sin -=的图像向右平移了n 个单位,所得图像关于y 轴对称,则n 的最小正值是 A . 6π7 B .3π C .6π D .2 π 7.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1 B .2 C .3 D .2 8.函数2 ()sin 3sin cos f x x x x =+在区间,42ππ?? ? ??? 上的最大值是 ( ) A.1 B. 13 2 + C. 3 2 D.1+3 三.单调性 1.函数]),0[()26 sin(2ππ ∈-=x x y 为增函数的区间是 ( ).
求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的几种常用方法 一、定义法 当已知直角三角形的两条边,可直接运用锐角三角函数的定义求锐角三角函数的值. 例1 如图1,在△ABC 中,∠C =90°,AB =13,BC =5,则sin A 的值是( ) (A )513 (B )1213 (C )512 (D )13 5 对应训练: 1.在Rt △ABC 中,∠ C =90°,若BC =1,AB 5,则tan A 的值为 ( ) A . 5 B 25 C .1 2 D .2 二、参数(方程思想)法 锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线 段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题. 例2 在△ABC 中,∠C =90°,如果tan A =5 12,那么sin B 的值是 . 对应训练: 1.在△ABC 中,∠C =90°,sin A=5 3,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 2.已知△ ABC 中, ο 90=∠C ,3cosB=2, AC=5 2 ,则 AB= . 3.已知Rt △ABC 中,,12,4 3 tan ,90==?=∠BC A C 求AC 、AB 和cos B .
4.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?=∠4 3sin AOC 求:AB 及OC 的长. 三、等角代换法 当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等 角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等” 来解决. 例3 在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =5,CD =4,则cos ∠ACD 的值为 . 对应训练 1.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径, 若O ⊙的半径为32,2AC =,则sin B 的值是( )A .2 3
高一三角函数题型总结
1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法:①画直角三角形 ②利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2. 2. 3. 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-236π)+cos 137π·tan4π -cos 133 π= ;
1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α=8 1,且4π<α<2π ,则cos α-sin α的值为 ( ) 33 (D)± 3 3.) 4. ) 5.) * 6.)
三角函数诱导公式 诱导公式可概括为把 απ ±?k 2 的三角函数值转化成角α的三角函数值。(k 指奇数或者偶数, α相当锐角) 口诀“奇变偶不变,符号看象限。”其中奇偶是指2 π 的奇数倍还是偶数倍,变与不变指函数名称的变化。 公式一:=+)2sin(απk =+)2c o s (απk =+)2t a n (απk
三角函数诱导公式练习题 1.若(),2,5 3 cos παππα<≤= +则()πα2sin --的值是 ( ) A . 53 B . 53- C . 54 D . 5 4 - 2.sin (-6 π 19)的值是( ) A 3 6 )= . 10.α是第四象限角,,则αsin 等于________. 13 12 cos =α
高考题历年三角函数题型总结
高考题历年三角函数题 型总结 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】
高考题历年三角函数题型总结 2、角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角. 第一象限角的集合为{} 36036090,k k k αα?<,则sin y r α= ,cos x r α=,()tan 0y x x α=≠.
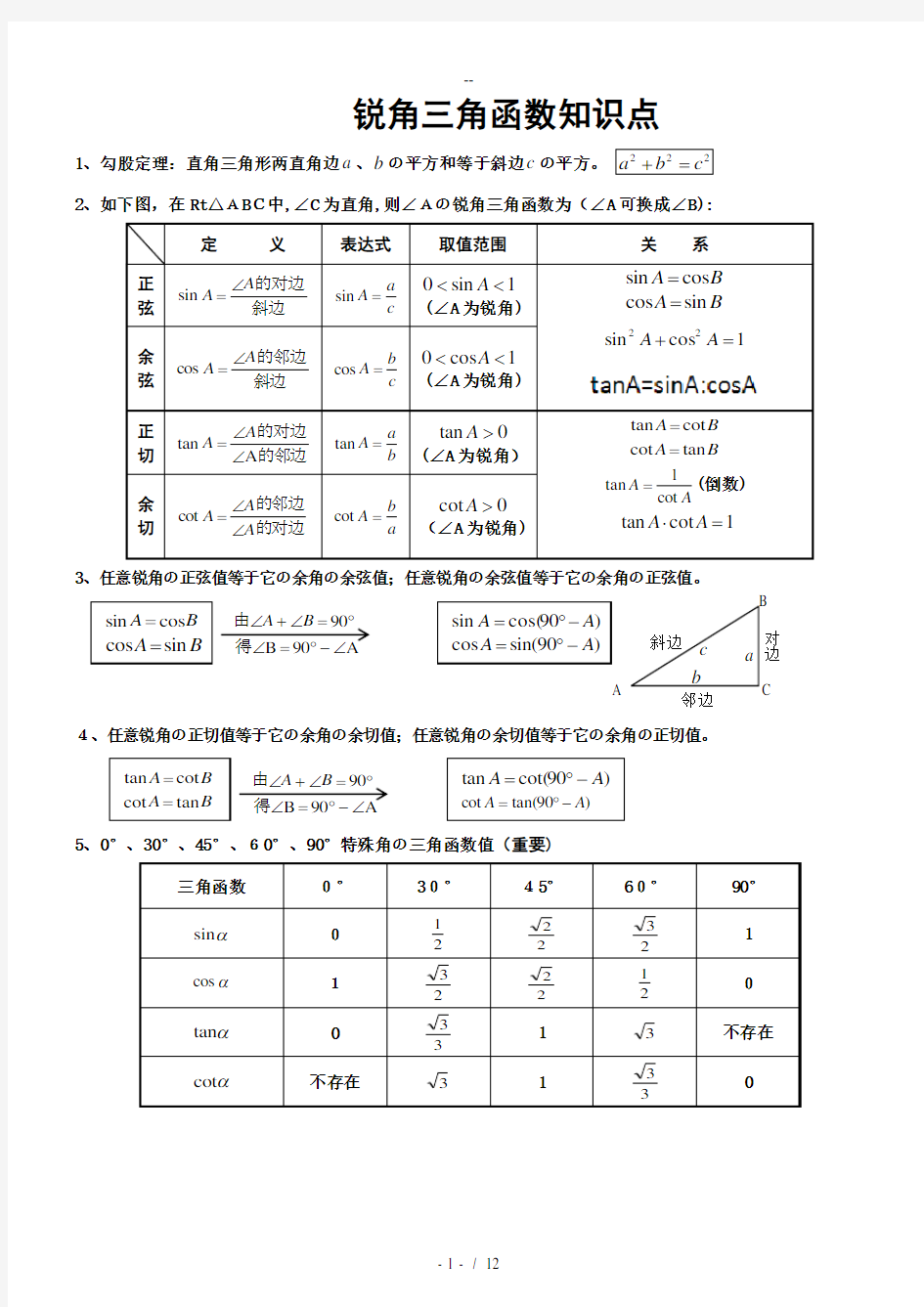
初三锐角三角函数知识点与典型例题
锐角三角函数: 知识点一:锐角三角函数的定义: 一、 锐角三角函数定义: 在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA= ∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 【特别提醒:1、sinA 、∠cosA 、tanA 表示的是一个整体,是两条线段的比,没有,这些比值只与 有关,与直角三角形的 无关 2、取值范围 】 例1.如图所示,在Rt △ABC 中,∠C =90°. 第1题图 ①斜边)(sin = A =______, 斜边)(sin = B =______; ②斜边 ) (cos =A =______, 斜边 ) (cos =B =______; ③的邻边A A ∠= ) (tan =______, ) (tan 的对边 B B ∠= =______. 例2. 锐角三角函数求值: 在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______, sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______. 例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3. 求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR . 典型例题: 类型一:直角三角形求值
1.已知Rt △ABC 中,,12,43 tan ,90==?=∠BC A C 求AC 、AB 和cos B . 2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?= ∠4 3sin AOC 求:AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3 sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4. 已知A ∠是锐角,17 8 sin =A ,求A cos ,A tan 的值 对应训练: (西城北)3.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为 A . 55 B .255 C .12 D .2 (房山)5.在△ABC 中,∠C =90°,sin A=5 3 ,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 类型二. 利用角度转化求值: 1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B .
三角函数题型学霸总结(含答案)-
三角函数题型学霸总结(含答案) 阳光老师:祝你学业有成 一、选择题(本大题共30小题,共150.0分) 1.点在函数的图象上,则m等于 A. 0 B. 1 C. D. 2 【答案】C 【解析】 【分析】本题主要考查了正弦函数的性质,属于基础题由题意知,求得m 的值. 【解答】解:由题意知, 所以, 所以. 2.用五点法画,的图象时,下列哪个点不是关键点 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的作法,属于基础题. 熟练掌握五点法作图即可. 【解答】 解:用“五点法”画,的简图时, 横坐标分别为, 纵坐标分别为0,1,0,,0, 故选A. 3.函数y x,x的大致图象是
A. B. C. D. 【答案】B 【解析】 【分析】 本题主要考查三角函数的图像,属于基础题利用“五点法”画出函数图像即可得出答案. 【解答】 解:“五点法”作图: x0 0100 10121 故选B. 4.用“五点法”作出函数的图象,下列点中不属于五点作图中的五个关 键点的是 A. B. C. D. 【答案】A 【解析】 【分析】 本题考查三角函数图象的画法以及余弦函数的性质,属于基础题. 分别令,,,,得,3,4,3,2,即可得到五点,再对照选项,即可得到答案. 【解答】 解:,分别令,,,,得,3,4,3,2,
所以五个关键点为,,,,, 可知A不属于. 故选A. 5.已知函数的图象与直线 恰有四个公共点,,,,其中,则 A. B. 0 C. 1 D. 【答案】A 【解析】 【分析】 本题考查了三角函数图象的作法及利用导数求函数图象的切线方程,属于较难题. 由三角函数图象及利用导数求函数图象的切线方程可得:切点坐标为,切线方程为:,又切线过点,则,即,得解. 【解答】 解:由 得 其图象如图所示,
三角函数题型分类总结
专题 三角函数题型分类总结 三角函数公式一览表 ............................................................................................................... 错误!未定义书签。 一 求值问题 ........................................................................................................................................................... - 1 - 练习 ................................................................................................................................................................. - 1 - 二 最值问题 ........................................................................................................................................................... - 2 - 练习 ................................................................................................................................................................. - 3 - 三 单调性问题 ....................................................................................................................................................... - 3 - 练习 ................................................................................................................................................................. - 3 - 四.周期性问题 ........................................................................................................................................................ - 4 - 练习 ................................................................................................................................................................. - 4 - 五 对称性问题 ....................................................................................................................................................... - 5 - 练习 ................................................................................................................................................................. - 5 - 六.图象变换问题 .................................................................................................................................................... - 6 - 练习 ................................................................................................................................................................. - 7 - 七.识图问题 ......................................................................................................................................................... - 7 - 练习 ................................................................................................................................................................. - 9 - 一 求值问题 类型1 知一求二 即已知正余弦、正切中的一个,求另外两个 方法:根据三角函数的定义,注意角所在的范围(象限),确定符号; 例 4 s i n 5 θ=,θ是第二象限角,求cos ,tan θθ 类型2 给值求值 例1 已知2tan =θ,求(1) θ θθθsin cos sin cos -+;(2)θθθθ2 2cos 2cos .sin sin +-的值. 练习 1、sin 330?= tan 690° = o 585sin = 2、(1)α是第四象限角,12 cos 13 α=,则sin α= (2)若4 sin ,tan 05 θθ=- >,则cos θ= . (3)已知△ABC 中,12 cot 5 A =-,则cos A = . (4) α是第三象限角,2 1)sin(=-πα,则αcos = )25cos(απ += 3、(1) 已知5 sin ,5 α= 则44sin cos αα-= .
人教中考数学锐角三角函数-经典压轴题附详细答案
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米. 【答案】553 【解析】 【分析】 如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可. 【详解】 解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J. ∵AM⊥CD, ∴∠QMP=∠MPO=∠OQM=90°, ∴四边形OQMP是矩形, ∴QM=OP, ∵OC=OD=10,∠COD=60°, ∴△COD是等边三角形, ∵OP⊥CD, ∠COD=30°, ∴∠COP=1 2 ∴QM=OP=OC?cos30°=3 ∵∠AOC=∠QOP=90°, ∴∠AOQ=∠COP=30°, ∴AQ=1 OA=5(分米), 2 ∴AM=AQ+MQ=5+3 ∵OB∥CD, ∴∠BOD=∠ODC=60°
在Rt△OFK中,KO=OF?cos60°=2(分米),FK=OF?sin60°=23(分米), 在Rt△PKE中,EK=22 -=26(分米), EF FK ∴BE=10?2?26=(8?26)(分米), 在Rt△OFJ中,OJ=OF?cos60°=2(分米),FJ=23(分米), 在Rt△FJE′中,E′J=22 -(2)=26, 63 ∴B′E′=10?(26?2)=12?26, ∴B′E′?BE=4. 故答案为:5+53,4. 【点睛】 本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型. 2.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系; (2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由 (3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长. 【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP62 23 . 【解析】 【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再
初中三角函数知识点题型总结+课后练习
锐角三角函数知识点 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4 5、0 锐角三角函数题型训练 类型一:直角三角形求值 1.已知Rt △ABC 中,,12,4 3 tan ,90== ?=∠BC A C 求AC 、AB 和cos B . 2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?= ∠4 3sin AOC 求:AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4.已知A ∠是锐角,17 8 sin = A ,求A cos ,A tan 的值 类型二. 利用角度转化求值:
1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B . 2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,则 tan EFC ∠的值为 ( ) A.34 B.43 C.35 D. 4 5 3. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一点,若1tan 5 DBA ∠= ,则AD 的长为( )A .2 C .1 D .4. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD = 3 16求∠ B 的度数及边B C 、AB 的长. 例2.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,?=3 sin A (1)求AB 边上的高CD ; (2)求△ABC 的面积S ; (3)求tan B . 例3.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5. 求:sin ∠ABC 的值. 对应训练 1.(2012?重庆)如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号) 2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B . 类型四:利用网格构造直角三角形 对应练习: 1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______. 特殊角的三角函数值 例1.求下列各式的值 ?-?+?30cos 245sin 60tan 2=. 计算:3-1+(2π-1)0- 3 3 tan30°-tan45°= 0 30tan 2345sin 60cos 221 ??? ? ???-?+?+= ?-?+?60tan 45sin 230cos 2 tan 45sin 301cos 60?+? -? = B
三角函数的图像与性质题型归纳总结
三角函数的图像与性质题型归纳总结 题型归纳及思路提示 题型1 已知函数解析式确定函数性质 【思路提示】一般所给函数为y =A sin(ωx +φ)或y =A cos(ωx +φ),A>0,ω>0,要根据 y =sin x ,y =cos x 的整体性质求解。 一、函数的奇偶性 例1 f (x )=sin ()x ?+(0≤?<π)是R 上的偶函数,则?等于( ) A.0 B . 4πC .2 π D .π 【评注】由sin y x =是奇函数,cos y x =是偶函数可拓展得到关于三角函数奇偶性的重要结论:sin()(); y A x k k Z ??π=+=∈(1)若是奇函数,则 sin()+ (); 2 y A x k k Z π ??π=+=∈(2)若是偶函数,则 cos()(); 2 y A x k k Z π ??π=+=+ ∈(3)若是奇函数,则 cos()(); y A x k k Z ??π=+=∈(4)若是偶函数,则 tan()().2k y A x k Z π ??=+= ∈(5)若是奇函数,则 .()sin ||a R f x x a a ∈=-变式1已知,函数为奇函数,则等于( ) A.0 B .1 C .1-D .1 ± 2.0()cos()()R f x x x R ???∈==+∈变式设,则“”是“为偶函数”的( ) A 充分不必要条件 B .必要不充分条 C .充要条件 D .无关条件 3.()sin()0()f x x f x ω?ω=+>变式设,其中,则是偶函数的充要条件是( ) A.(0)1f =B .(0)0f =C .'(0)1f =D .'(0)0 f = 2.()sin(2)()()2f x x x R f x π =-∈例设,则是( ) A.π最小正周期为的奇函数B .π最小正周期为的偶函数 C .2π 最小正周期为 的奇函数D .2π 最小正周期为的偶函数 2()sin 1()()f x x x R f x =-∈变式1.若,则是( ) A.π最小正周期为的奇函数 B .π最小正周期为的偶函数 C .π最小正周期为2的奇函数D .π最小正周期为2的偶函数
高一三角函数题型总结
1.已知角围和其中一个角的三角函数值求任意角三角函数值 方法:?画直角三角形 ?利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的?分式 ?齐次式 可以实现αtan 之间的转化 例题:1.已知sin 2cos 5,tan 3sin 5cos αα ααα-=-+那么的值为_____________. 2.已知2tan =α,则1.α αα αcos sin cos sin -+=_____________. 2. α αα α2 2cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.(“1”的代换) 3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法:等式两边完全平方(注意三角函数中判断正负利用角的围进行取舍) 例题:已知πα<∠<0,αsin +αcos =2 1 ,求?αsin .αcos ?αcos -αsin 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-23 6π)+cos 137π·tan4π -cos 133 π= ;
1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)4 3 (D)4 3- 2.已知sin αcos α=8 1,且4π<α<2π ,则cos α-sin α的值为 ( ) (A)2 3 (B)4 3 (C) (D)± 2 3 3.设是第二象限角,则 sin cos αα ( ) (A) 1 (B)tan 2α (C) - tan 2α (D) 1- 4.若tan θ= 3 1,π<θ<3 2π,则sin θ·cos θ的值为 ( ) (A)±3 10 (B) 3 10 5.已知 sin cos 2sin 3cos αααα-+=5 1 ,则tan α的值是 ( ) (A)±83 (B)83 (C)83 - (D)无法确定 * 6.若α是三角形的一个角,且sin α+cos α= 3 2 ,则三角形为 ( ) (A)钝角三角形 (B)锐角三角形 (C)直角三角形 (D)等腰三角形
求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的几种常用方法 一、定义法 当已知直角三角形的两条边,可直接运用锐角三角函数的定义求锐角三角函数的值. 例1 如图1,在△ABC 中,∠C =90°,AB =13,BC =5,则sin A 的值是( ) (A ) 513 (B )1213 (C )512 (D )13 5 对应训练: 1.在Rt △ABC 中,∠ C =90°,若BC =1,AB tan A 的值为( ) A B C .1 2 D .2 二、参数(方程思想)法 锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线 段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题. 例2 在△ABC 中,∠C =90°,如果tan A = 5 12 ,那么sin B 的值是 . 对应训练: 1.在△ABC 中,∠C =90°,sin A= 5 3 ,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 2.已知△ABC 中, 90=∠C ,3cosB=2, AC=52 ,则AB= . 3.已知Rt △ABC 中,,12,4 3tan ,90==?=∠BC A C 求AC 、AB 和cos B . 4.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?=∠4 3sin AOC 求:AB 及OC 的长.
第8题图 A D E C B F 三、等角代换法 当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等 角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等” 来解决. 例3 在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =5,CD =4,则c o s ∠ACD 的值为 . 对应训练 1.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为 3 2 ,2AC =,则s in B 的值是( )A .23 B .32 C .34 D .4 3 2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =, AB=8,则tan EFC ∠的值为 ( )A.34 B.43 C.35 D.45 3. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一点,若 1tan 5 DBA ∠ = ,则AD 的长为( ) A .2 C .1 D .4. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧 圆弧上一点,则cos ∠OBC 的值为( )A . 12 B .2 C .35 D .45 5.如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= . 6.(庆阳中考)如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5 A =,则这个菱形的面积= cm 2 . 7. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A AD = 3 3 16求 ∠B 的度数及边BC 、AB 的长. D A B C
(推荐)高一三角函数题型总结
题型总结 1.已知角范围和其中一个角的三角函数值求任意角三角函数值 方法:画直角三角形 利用勾股定理先算大小后看正负 例题:1.已知α∠为第二象限角,13 5 sin =α求αcos 、αtan 、αcot 的值 2.已知α∠为第四象限角,3tan -=α求αcos 、αsin 、αcot 的值 2.一个式子如果满足关于αsin 和αcos 的分式 齐次式 可以实现αtan 之间的转化 例题:1.已知 sin 2cos 5,tan 3sin 5cos ααααα -=-+那么的值为_____________. 2.已知2tan =α,则1.α αα αcos sin cos sin -+=_____________. 2.α αα α22cos sin cos sin -=_____________. 3.1cos sin +αα=_____________.(“1”的代换)
3.已知三角函数αsin 和αcos 的和或差的形式求αsin .αcos 方法:等式两边完全平方(注意三角函数中判断正负利用角的范围进行取舍) 例题:已知πα<∠<0,αsin +αcos =2 1 ,求αsin .αcos αcos -αsin 4.利用“加减πk 2”大角化小角,负角化正角,求三角函数值 例题:求值:sin(-236π)+cos 137π·tan4π -cos 13 3 π= ; 练习题 1.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) (A)3 4 (B)43 - (C)43 (D)4 3 - 2.已知sin αcos α= 8 1,且4π<α< 2π ,则cos α-sin α的值为 ( ) (A) 2 3 (B)4 3 (C)3 (D)± 2 3
锐角三角函数专项复习经典例题
1、平面内,如图17,在□ABCD 中,10AB =,15AD =,4tan 3A =.点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90?得到线段PQ . (1)当10DPQ ∠=?时,求APB ∠的大小; (2)当tan :tan 3:2ABP A ∠=时,求点Q 与点B 间的距离(结果保留根号); (3)若点Q 恰好落在□ABCD 的边所在的直线上,直接写出PB 旋转到PQ 所扫过的面积(结果保留π). 2、如图所示,我国两艘海监船A ,B 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C ,此时,B 船在A 船的正南方向5海里处,A 船测得渔船C 在其南偏东45°方向,B 船测得渔船C 在其南偏东53°方向,已知A 船的航速为30海里/小时,B 船的航速为25海里/小时,问C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈,cos53°≈,tan53°≈,≈1.41) 3、如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5km 到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) B A P C D Q 备用图17 A B C D P Q
4、如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度. 5、一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为米. 6、如图,某小区①号楼与?号楼隔河相望,李明家住在①号楼,他很想知道?号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算?号楼的高度CD. 7、某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31cm,在A处测得甲楼顶部E处的仰角是31°. (1)求甲楼的高度及彩旗的长度;(精确到0.01m) (2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲乙两楼之间的距离.(精确到0.01m) (cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)
高考三角函数重要题型总结
1.已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+ (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间[,]122ππ -上的值域。 2.已知函数2()sin sin()(0)2f x x x x πωωωω=+f 的最小正周期为π. (Ⅰ)求ω的值; (Ⅱ)求函数f (x )在区间[0,23 π]上的取值范围. 3.(本小题满分12分)已知向量(sin ,cos ),(1,2)m A A n ==-,且0.m n =g (Ⅰ)求tan A 的值; (Ⅱ)求函数()cos 2tan sin (f x x A x x =+∈R )的值域. 4..(本小题满分13分)已知函数()sin()(00π)f x A x A ??=+><<,,x ∈R 的最 大值是1,其图像经过点π1 32M ?? ???,. (1)求()f x 的解析式; (2)已知π02αβ??∈ ??? ,,,且3()5f α=,12()13f β= ,求()f αβ-的值. 5. 已知函数2()sin cos cos 2.222 x x x f x =+- (Ⅰ)将函数()f x 化简成sin()(0,0,[0,2))A x B A ω???π++>>∈的形式,并指出()f x 的周期; (Ⅱ)求函数17()[, ]12 f x ππ在上的最大值和最小值 6..已知函数x x x x f sin 2 sin 2cos )(22+-=. (I )求函数)(x f 的最小正周期; (II )当)4,0(0π ∈x 且524)(0=x f 时,求)6 (0π+x f 的值。 7.已知1tan 3 α=-,cos β=,(0,)αβπ∈ (1)求tan()αβ+的值; (2)求函数())cos()f x x x αβ=-++的最大值. 8.已知函数())cos()f x x x ω?ω?=+-+(0π?<<,0ω>)为偶函数,且函数()y f x =图象的两相邻对称轴间的距离为π2 . (Ⅰ)求π8f ?? ???的值; (Ⅱ)将函数()y f x =的图象向右平移π 6 个单位后,得到函数()y g x =的图象,
三角函数总结经典例题
第三章 三角函数 3.1任意角三角函数 一、知识导学 1.角:角可以看成由一条射线绕着端点从一个位置旋转到另一个位置所形成的几何图形.角的三要素是:顶点、始边、终边.角可以任意大小,按旋转的方向分类有正角、负角、零角. 2.弧度制:任一已知角α的弧度数的绝对值r l = α,其中l 是以α作为圆心角时所对圆弧的长,r 为圆的半径.规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.用“弧度”做单位来度量角的制度叫做弧度制. 3.弧度与角度的换算:rad π2360=ο ;rad 1745.01801≈=π ο ;1ο ο 30.57180≈?? ? ??=πrad .用弧度为单位表示角的 大小时,弧度(rad )可以省略不写.度()ο 不可省略. 4.弧长公式、扇形面积公式:,r l α= 2||2 1 21r lr S α= =扇形,其中l 为弧长,r 为圆的半径.圆的周长、面积公式是弧长公式和扇形面积公式中当πα2=时的情形. 5.任意角的三角函数定义:设α是一个任意大小的角,角α终边上任意一点P 的坐标是()y x ,,它与原点的距离是 )0(>r r ,那么角α的正弦、余弦、正切、余切、正割、余割分别是 y r x r y x x y r x r y ====== ααααααcsc ,sec ,cot ,tan ,cos ,sin .这六个函数统称为三角函数. 三角函数 定义域 x y sin = R x y cos = R x y tan = ? ?????∈+≠Z k k x x ,2π π x y cot = {}Z k k x x ∈≠,π x y sec = ? ?????∈+≠Z k k x x ,2π π x y csc = {}Z k k x x ∈≠,π 7.三角函数值的符号:各三角函数值在第个象限的符号如图所示(各象限注明的函数为正,其余为负值) 可以简记为“一全、二正、三切、四余”为正. 二、疑难知识导析
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧 锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。 一、 化简或求值 例1 (1)已知tan 2cot 1αα-=,且α是锐角,的值。 (2)化简()()22 sin cos cos sin a b a b αααα++-。 分析 (1)由已知可以求出tan α1tan cot αα=?;(2)先把平方展开,再利用22sin cos 1αα+=化简。 解 (1)由tan 2cot 1αα-=得2tan 2tan αα-=,解关于tan α的方程得 tan 2α=或tan 1α=-。又α是锐角,∴tan 2α== tan cot αα-。由tan 2α=, 得1cot 2α==tan cot αα-=13222 -=。 (2)()()22sin cos cos sin a b a b αααα++-= 2222sin 2sin cos cos a ab b αααα+??++2222cos 2cos sin sin a ab b αααα-??+=()()222222sin cos sin cos a b αααα+++=22a b +。 说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1αα+=,tan cot 1αα?=等。 二、已知三角函数值,求角 例2 在△ABC 中,若2 cos sin 02A B ?-+= ??(),A B ∠∠均为锐角,求C ∠的度数。 分析 几个非负数的和为0,则这几个数均为0。由此可得cos A 和sin B 的值,进而求出,A B ∠∠的值,然后就可求出C ∠的值。