北京市东城区2012届九年级上学期期末考试数学试卷
2024年北京初三九年级上学期数学期末考《新定义》
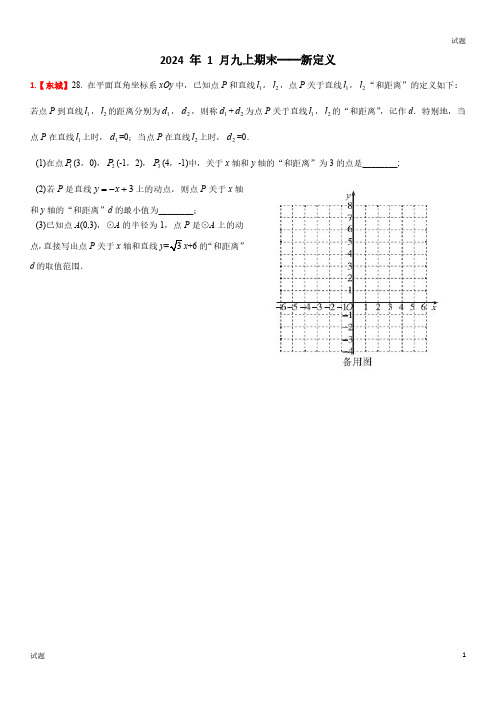
2024年1月九上期末——新定义1.【东城】28.在平面直角坐标系xOy 中,已知点P 和直线1l ,2l ,点P 关于直线1l ,2l “和距离”的定义如下:若点P 到直线1l ,2l 的距离分别为1d ,2d ,则称1d +2d 为点P 关于直线1l ,2l 的“和距离”,记作d .特别地,当点P 在直线1l 上时,1d =0;当点P 在直线2l 上时,2d =0.(1)在点1P (3,0),2P (-1,2),3P (4,-1)中,关于x 轴和y 轴的“和距离”为3的点是________;(2)若P 是直线3y x =-+上的动点,则点P 关于x 轴和y 轴的“和距离”d 的最小值为________;(3)已知点A (0,3),⊙A 的半径为1,点P 是⊙A 上的动点,直接写出点P 关于x 轴和直线y =3x +6的“和距离”d 的取值范围.2.【西城】28.如图,在平面直角坐标系xOy 中,点()1,0S -,()1,0T .对于一个角α(0180α︒<≤︒),将一个图形先绕点S 顺时针旋转α,再绕点T 逆时针旋转α,称为一次“α对称旋转”.备用图(1)点R 在线段ST 上,则在点()1,1A -,()3,2B -,()2,2C -,()0,2D -中,有可能是由点R 经过一次“90°对称旋转”后得到的点是________;(2)x 轴上的一点P 经过一次“α对称旋转”得到点Q .①当60α=︒时,PQ =________;②当30α=︒时,若QT x ⊥轴,求点P 的坐标;(3)以点O 为圆心作半径为1的圆.若在O 上存在点M ,使得点M 经过一次“α对称旋转”后得到的点在x 轴上,直接写出α的取值范围.3.【海淀】28.在平面直角坐标系xOy 中,将中心为T 的正方形记作正方形T ,对于正方形T 和点P (不与O 重合)给出如下定义:若正方形T 的边上存在点Q ,使得直线OP 与以TQ 为半径的T 相切于点P ,则称点P 为正方形T 的“伴随切点”.(1)如图、正方形T 的顶点分别为点O ,()2,2A ,()4,0B ,()2,2C -.①在点()12,1P ,()21,1P ,()31,1P -中,正方形T 的“伴随切点”是________;②若直线y x b =+上存在正方形T 的“伴随切点”,求b 的取值范围;(2)已知点(),1T t t +,正方形T 的边长为2.若存在正方形T 的两个“伴随切点”M ,N ,使得OMN △为等边三角形,直接写出t 的取值范围.4.【朝阳】28.在平面直角坐标系xOy 中,已知A (t -2,0),B (t +2,0).对于点P 给出如下定义:若∠APB=45°,则称P 为线段AB 的“等直点”.(1)当t =0时,①在点),(22201+P ,),(042-P ,)-,(2223-P ,),(524P 中,线段AB 的“等直点”是________;②点Q 在直线y =x 上,若点Q 为线段AB 的“等直点”,直接写出点Q 的横坐标.(2)当直线t x y +=上存在线段AB 的两个“等直点”时,直接写出t 取值范围.5.【石景山】28.在平面直角坐标系xOy 中,⊙O 的半径为1.对于⊙O 的弦AB 和点C 给出如下定义:若点C 在弦AB 的垂直平分线上,且点C 关于直线AB 的对称点在⊙O 上,则称点C 是弦AB 的“关联点”.(1)如图,点13(22A ,,13(22B -,.在点1(00)C ,,2(10)C ,,3(11)C ,,4(20)C ,中,弦AB 的“关联点”是;(2)若点1(0)2C ,是弦AB 的“关联点”,直接写出AB 的长;(3)已知点(02)M ,,(0)15N ,.对于线段MN 上一点S ,存在⊙O 的弦PQ ,使得点S 是弦PQ 的“关联点”.记PQ 的长为t ,当点S 在线段MN 上运动时,直接写出t 的取值范围.6.【丰台】28.在平面直角坐标系xOy中,⊙O的半径为1,对于线段AB和x轴上的点P,给出如下定义:将线段AB绕点P旋转180°可以得到⊙O的弦A'B'(A',B'分别为A,B的对应点),则称线段AB为⊙O以点P 为中心的“关联线段”.(1)如图,已知点A(-2,-1),B(-2,0),C(-2,1),D(-1,1),在线段AC,BD,CD中,⊙O以点P 为中心的“关联线段”是;x的取值范围;(2)已知点E(-4,1),线段EF是⊙O以点P为中心的“关联线段”,求点F的横坐标F (3)已知点E(m,1),若直线y=-x+2m上存在点F,使得线段EF是⊙O以点P为中心的“关联线段”,直接写出m的取值范围.备用图7.【昌平】28.对于在平面直角坐标系xOy 中⊙T 和⊙T 外的点P ,给出如下定义:已知⊙T 的半径为1,若⊙T 上存在点Q ,满足PQ ≤2,则称点P 为⊙T 的关联点.(1)如图1,若点T 的坐标为(0,0),28题图1①在点1P (3,0),2P (3,-2),3P (-2,2)中,是⊙T 的关联点的是____________;②直线2y x b =+分别交x 轴,y 轴于点A ,B ,若线段AB 存在⊙T 的关联点,求b 的取值范围;(2)已知点C (0,D (1,0),T (m ,1),△COD 上的每一个点都是⊙T 的关联点,直接写出m 的取值范围.28题图28.【通州】28.在平面直角坐标系xOy 中,O 的半径为1.给出如下定义:过O 外一点P 做直线与O 交于点M 、N ,若M 为线段PN 的中点,则称线段PN 是O 的“外倍线”。
2022-2023学年北京东城区初三第一学期数学期末试卷及答案

2022-2023学年北京东城区初三第一学期数学期末试卷及答案一、选择题(每题2分,共16分)1. 若关于的一元二次方程有一个根为,则的值为( ) x 220x x m -+=0m A. 2 B. 1C. 0D.1-【答案】C 【解析】【分析】将代入方程,即可求解.0x =220x x m -+=【详解】解:∵关于的一元二次方程有一个根为, x 220x x m -+=0∴, 0m =故选:C .【点睛】本题考查了一元二次方程的解的定义,将代入方程是解题的关键. 0x =2. 下列图形中是中心对称图形的是( ) A. 正方形 B. 等边三角形C. 直角三角形D. 正五边形 【答案】A 【解析】【分析】根据中心对称图形的概念求解即可. 【详解】解:A 、是中心对称图形,本选项正确; B 、不是中心对称图形,本选项错误; C 、不是中心对称图形,本选项错误; D 、不是中心对称图形,本选项错误. 故选A .【点睛】本题考查了中心对称图形的概念.中心对称图形是要寻找对称中心,绕对称中心旋转180度后与原图形重合.3. 关于二次函数的最大值或最小值,下列说法正确的是( ) 22(4)6y x =-+A. 有最大值4 B. 有最小值4C. 有最大值6D. 有最小值6 【答案】D 【解析】【分析】根据二次函数的解析式,得到a 的值为2,图象开口向上,函数22(4)6y x =-+有最小值,根据定点坐标(4,6),即可得出函数的最小值.【详解】解:∵在二次函数中,a=2>0,顶点坐标为(4,6), 22(4)6y x =-+∴函数有最小值为6. 故选:D .【点睛】本题主要考查了二次函数的最值问题,关键是根据二次函数的解析式确定a 的符号和根据顶点坐标求出最值.4. 一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是确定事件的为( ) A. 至少有1个球是黑球 B. 至少有1个球是白球 C. 至少有2个球是黑球 D. 至少有2个球是白球【答案】A 【解析】【分析】列出摸出的三个球的颜色的所有可能情况即可.【详解】根据题意可得,摸出的三个球的颜色可能为:两个白球,一个黑球;一个白球,两个黑球;三个黑球,则可知摸出的三个球中,至少有一个黑球, 故必然事件是至少有一个黑球, 故选:A .【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.5. 某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x ,根据题意可得方程( )A. 180(1﹣x)2=461B. 180(1+x )2=461C. 368(1﹣x)2=442D. 368(1+x )2=442【答案】B 【解析】【分析】本题为增长率问题,一般用增长后的量=增长前的量×(1+增长率),如果设这个增长率为x ,根据“2月份的180万只,4月份的产量将达到461万只”,即可得出方程. 【详解】解:从2月份到4月份,该厂家口罩产量的平均月增长率为x ,根据题意可得方程:180(1+x )2=461, 故选:B .【点睛】本题考查了一元二次方程的实际应用,理解题意是解题关键.6. 如图,在中,是直径,弦的长为5,点D 在圆上,且, 则O AB AC 30ADC ∠=︒O 的半径为( )A. B. 5C. D.2.57.510【答案】B 【解析】【分析】连接,由题意易得,在中解三角形求解. BC 30ABC ADC ∠=∠=︒Rt ACB 【详解】连接,BC30ABC ADC ∴∠=∠=︒在中,是直径, O AB ,90ACB ∴∠=︒在中,Rt ACB ,,90ACB ∠=︒30ABC ∠=︒5AC =210AB AC ==5OA =故选:B .【点睛】本题主要考查圆周角定理及含直角三角形的性质;熟练掌握圆周角定理及含30︒直角三角形的性质是解题的关键.30︒7. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC ,BD 分别与⊙O 切于点C ,D ,延长AC ,BD 交于点P .若,⊙O 的半径为6cm ,则图中的120P ∠=︒ CD长为( )A. π cmB. 2π cmC. 3π cmD. 4π cm【答案】B 【解析】【分析】连接OC 、OD ,利用切线的性质得到,根据四边形的内角和90OCP ODP ∠=∠=︒求得,再利用弧长公式求得答案. 60COD ∠=︒【详解】连接OC 、OD ,分别与相切于点C ,D ,,AC BD Q O ∴,90OCP ODP ∠=∠=︒,120360P OCP ODP P COD ∠=︒∠+∠+∠+∠=︒, ∴,60COD ∠=︒的长, CD∴6062(cm)180ππ⨯==故选:B【点睛】此题考查圆的切线的性质定理,四边形的内角和,弧长的计算公式,熟记圆的切线的性质定理及弧长的计算公式是解题的关键.8. 如图,正方形和的周长之和为,设圆的半径为,正方形的边长为ABCD O 20cm cm x ,阴影部分的面积为.当x 在一定范围内变化时,y 和S 都随x 的变化而变化,cm y 2cm S 则y 与x ,S 与x 满足的函数关系分别是( )A. 一次函数关系,一次函数关系B. 一次函数关系,二次函数关系 C .二次函数关系,二次函数关系D. 二次函数关系,一次函数关系【答案】B 【解析】【分析】根据圆的周长公式和正方形的周长公式先得到,再根据152y x π=-+得到,由此即可得到答案.S S S =-阴影正方形圆2215254S x x πππ⎛⎫=--+ ⎪⎝⎭【详解】解:∵正方形和的周长之和为,圆的半径为,正方形的边ABCD O 20cm cm x 长为, cm y ∴, 4220y x π+=∴, 152y x π=-+∵,S S S =-阴影正方形圆∴,22222211552524S y x x x x x ππππππ⎛⎫⎛⎫=-=-+-=--+ ⎪ ⎪⎝⎭⎝⎭∴y 与x ,S 与x 满足的函数关系分别是一次函数关系,二次函数关系, 故选B .【点睛】本题考查二次函数与一次函数的识别、正方形的周长与面积公式,理清题中的数量关系,熟练掌握二次函数与一次函数的解析式是解答的关键. 二、填空题 (每题2分,共16分)9. 在平面直角坐标系中,抛物线与y 轴交于点C ,则点C 的坐标为xOy 245y x x =-+_________. 【答案】 (0,5)【解析】【分析】令,代入抛物线,得到点C 的纵坐标,即可得解. 0x =245y x x =-+【详解】解:依题意,令,得到,0x =5y =故抛物线与y 轴交于点C 的坐标为, 245y x x =-+(0,5)故答案为 :(0,5)【点睛】本题考查了二次函数与y 轴交点问题,令,即可得到抛物线与y 轴交点的纵0x =坐标. 10. 把抛物线向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线2112y x =+的解析式为_______. 【答案】 21(1)22y x =+-【解析】【分析】直接根据“上加下减,左加右减”进行计算即可. 【详解】解:抛物线, 2112y x =+向左平移1个单位长度,再向下平移3个单位长度, 得到 ()211132y x =++-即 ()21122y x =+-故答案为:. ()21122y x =+-【点睛】本题主要考查函数图像的平移;熟记函数图像的平移方式“上加下减,左加右减”是解题的关键.11. 请写出一个常数c 的值,使得关于x 的方程有两个不相等的实数根,则220x x c ++=c 的值可以是____________.【答案】0,(答案不唯一,即可). 1c <【解析】【分析】利用一元二次方程根的判别式求出c 的取值范围即可得到答案. 【详解】解:因为方程有两个不相等的实数根, 220x x c ++=所以 2Δ240c =->解得1c <故答案为:0,(答案不唯一,即可)1c <【点睛】本题主要考查了一元二次方程根的判别式;熟知一元二次方程根的判别式是解题的关键.12. 2022年3月12日是我国第44个植树节,某林业部门为了考察某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:幼树移植数(棵)100 1000 5000 8000 10000 15000 20000 幼树移植成活数(棵)87 893 4485 7224 8983 13443 18044 幼树移植成活的频率0.870 0.893 0.897 0.903 0.898 0.896 0.902 估计该种幼树在此条件下移植成活的概率是______.(结果精确到0.1)【答案】0.9【解析】【分析】大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.【详解】∵幼树移植数20000时,幼树移植成活的频率是0.902,∴估计该种幼树在此条件下移植成活的概率为0.902,精确到0.1,即为0.9,故答案为:0.9.【点睛】本题考查了用大量试验得到的频率可以估计事件的概率,大量反复试验下频率稳定值即概率.13. 以▱ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为_____.【答案】(2,﹣1)【解析】【分析】根据平行四边形是中心对称图形,再根据▱ABCD对角线的交点O为原点和点A的坐标,即可得到点C的坐标.【详解】解:∵▱ABCD对角线的交点O为原点,A点坐标为(﹣2,1),∴点C的坐标为(2,﹣1),故答案为:(2,﹣1).【点睛】此题考查中心对称图形的顶点在坐标系中的表示.14. 如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作AD∥OB交⊙O于点D ,连接CD .若∠B=50°,则∠OCD 的度数等于___________.【答案】20°##20度 【解析】【分析】连接OA ,如图,根据切线的性质得到∠OAB=90°,则利用互余可计算出∠AOB=40°,再利用圆周角定理得到∠ADC=20°,然后根据平行线的性质得到∠OCD 的度数.【详解】解:连接OA ,如图,∵AB 切⊙O 于点A , ∴OA⊥AB, ∴∠OAB=90°, ∵∠B=50°,∴∠AOB=90°-50°=40°, ∴∠ADC=∠AOB=20°, 12∵AD∥OB,∴∠OCD=∠ADC=20°. 故答案为:20°.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.15. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×失+失²).弧田(图中阴影部分)由圆弧和其所对的弦所12=围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为,半径等于4米的弧田,按照上述公式计算出弧田的面积约为______ 米120︒.)21.73≈【答案】 8.92【解析】【分析】由题意可知于D ,交圆弧于C ,由题意得米,解得OC AB ⊥4AO =120AOB ∠=︒米,再求出,最后由勾股定理得到,由垂径定理求出即可得122OD OA ==CD AD AB 出结果.【详解】解:如图,由题意可知,,,(米),120AOB ∠=︒AB CD ⊥4OA OB ==, 30,90DAO ADO ∴∠=︒∠=︒12AD BD AB ==(米)122OD OA ∴==(米)422CD OC OD ∴=-=-=AD ∴===(米)2AB AD ∴==弧田面积 ∴()212AB CD CD =⨯+()21222=⨯+2=+(平方米)8.92≈故答案为:8.92【点睛】本题考查了勾股定理以及垂径定理的应用;熟练掌握垂径定理是解答本题的关键.16. 我们给出如下定义:在平面内,点到图形的距离是指这个点到图形上所有点的距离的最小值.在平面内有一个矩形,中心为O ,在矩形外有一点P ,,,4,2ABCD AB AD ==3OP =当矩形绕着点O 旋转时,则点P 到矩形的距离d 的取值范围为__________.【答案】 32d ≤≤【解析】【分析】根据题意分别求出当过的中点E 时,此时点P 与矩形上所有点的OP AB ABCD 连线中,;当过顶点A 时,此时点P 与矩形上所有点的连线中,;d PE =OP ABCD d PA =当过顶点边中点F 时,此时点P 与矩形上所有点的连线中,,即OP AD ABCD d PF =可求解.【详解】解:如图,当过的中点E 时,此时点P 与矩形上所有点的连线中,OP AB ABCD ,, d PE =112OE AD ==∴;2d PE OP OE ==-=如图,当过顶点A 时,此时点P 与矩形上所有点的连线中,,OP ABCD d PA =矩形,中心为O ,,4,2ABCD AB AD ==∴,2,90BC AD B ==∠=︒∴, AC ==∴ 12OA AC ==∴;3d AP OP OA ==-=-如图,当过顶点边中点F 时,此时点P 与矩形上所有点的连线中,OP AD ABCD ,, d PF =122OF AB ==∴;1d PF OP OF ==-=综上所述,点P 到矩形的距离d 的取值范围为.32d ≤≤故答案为:32d ≤≤【点睛】本题考查矩形的性质,旋转的性质,根据题意得出临界点时点d 的值是解题的关键.三、解答题(共68分,17-22题,每题5分,23-26题,每题6分,27-28题,每题7分)17. 下面是小美设计的“过圆上一点作圆的切线”的尺规作图过程.已知:点A 在上.O 求作:的切线.O AB作法: ①作射线;OA ②以点A 为圆心,适当长为半径作弧,交射线于点C 和点D ;OA ③分别以点C ,D 为圆心,大于长为半径作弧,两弧交点B ; 12CD ④作直线.AB 则直线即为所求作的的切线.AB O 根据小美设计的尺规作图过程,解决下面的问题:(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:连接,.BC BD 由作图可知,, .AC AD =BC =∴ .BA OA ∵ 点A 在上,O ∴直线是的切线( ) (填写推理依据) .AB O 【答案】(1)见解析;(2);;经过半径的外端并且垂直于这条半径的直线是圆的切线.BD ⊥【解析】【分析】(1)依据题意,按步骤正确尺规作图即可;(2)结合作图,完成证明过程即可.【小问1详解】补全图形如图所示,【小问2详解】证明:连接,.BC BD由作图可知,,.AC AD =BC BD =∴,BA OA ⊥∵ 点A 在上,O ∴直线是的切线(经过半径的外端并且垂直于这条半径的直线是圆的切线,AB O 故答案为:;;经过半径的外端并且垂直于这条半径的直线是圆的切线BD ⊥【点睛】本题考查了尺规作图能力和切线的证明;能够按要求规范作图是解题的关键.18. 如图,是的直径,弦于点E ,,若,求的AB O CD AB ⊥2CD OE =4AB =CD 长.【答案】.CD =【解析】【分析】由垂径定理得到,推出,在中,利用勾股定理即CE DE =CE OE =Rt COE △可求解.【详解】解:如图,连接. OC∵是的直径,弦于点E ,AB O CD AB ⊥∴.CE DE =又∵,2CD OE =∴.CE OE =∵,4AB =∴.2OC =在中,,Rt COE △222CE OE OC +=∴CE =∴.CD =【点睛】本题考查了垂径定理、勾股定理,掌握垂直于弦的直径平分这条弦是解题的关键.19. 下面是小聪同学用配方法解方程:的过程,请仔细阅读后,2240x x p --=()0p >解答下面的问题.2240x x p --=解:移项,得:.①224x x p -=二次项系数化为1,得:.② 222p x x -=配方,得.③ 2212p x x -+=即. 2(1)2p x -=∵,0p >∴ 1x -=∴ 11x =+11x =(1)第②步二次项系数化为1的依据是什么?(2)整个解答过程是否正确?若不正确,说出从第几步开始出现的错误,并直接写出此方程的解.【答案】(1)等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等(2)不正确,解答从第③步开始出错, 1x =2x =【解析】【分析】(1)根据等式的性质2即可写出依据;(2)根据配方法解一元二次方程的步骤即可求解. 【小问1详解】等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等;【小问2详解】不正确,解答从第③步开始出错,正确的步骤为:配方,得.③ 22112p x x -+=+即 22(1)2p x +-=∵,0p >∴.④ 1x -=∴.⑤ 1x =2x =此方程的解为. 1x =2x =【点睛】本题考查等式的性质和解一元二次方程,解题的关键是读懂材料,明确每一步的做题依据.20. 如图,已知抛物线L :y =x 2+bx+c 经过点A(0,﹣5),B(5,0).(1)求b ,c 的值;(2)连结AB ,交抛物线L 的对称轴于点M .求点M 的坐标;【答案】(1),;(2)交点M 的坐标为(2,-3).4b =-5c =-【解析】【分析】(1)将点A 、点B 坐标代入函数解析式,求解方程组即可;(2)设直线AB 的解析式为:,将点A 、点B 坐标代入函数解析式求解确()0y kx b k =+≠定解析式,然后根据(1)中确定二次函数解析式,求出其对称轴,求两条之间交点即可确定点M 的坐标.【详解】解:(1)将点A 、点B 坐标代入函数解析式可得:, 50255c b c -=⎧⎨=++⎩解得:, 45b c =-⎧⎨=-⎩∴,;4b =-5c =-(2)设直线AB 的解析式为:,()0y kx b k =+≠将点A 、点B 坐标代入函数解析式可得:, 505b k b-=⎧⎨=+⎩解得:, 15k b =⎧⎨=-⎩∴一次函数解析式为:,5y x =-由(1)得二次函数解析式为:,245y x x =--对称轴为:, 22b x a=-=直线与的交点为M ,5y x =-2x =∴当时,,2x ==3y -∴交点M 的坐标为(2,-3).【点睛】题目主要考查利用待定系数法确定二次函数与一次函数解析式,两条直线的交点问题,二次函数的基本性质,理解题意,熟练运用待定系数法确定解析式是解题关键.21. 如图,在边长均为1个单位长度的小正方形组成的网格中,点,,均为格点(每A B O 个小正方形的顶点叫做格点).(1)作点关于点的对称点;A O 1A (2)连接,将线段绕点顺时针旋转得到线段,点的对应点为,1AB 1A B 1A 90︒11A B B 1B 画出旋转后的线段;11A B (3)连接,,求出的面积(直接写出结果即可).1AB 1BB 1ABB 【答案】(1)见解析 (2)见解析(3)8【解析】【分析】(1)根据网格的特点作出点关于点的对称点;A O 1A(2)根据题意,画出旋转后的线段,即可求解;11A B (3)根据网格的特点,以及三角形面积公式求得面积即可求解.【小问1详解】解:如图所示,点即为所求;1A 【小问2详解】解:如图所示,线段即为所求;11A B 【小问3详解】解:如图所示,. 118282ABB S =⨯⨯= 【点睛】本题考查了画中心对称图形,画旋转图形,网格中求三角形面积,数形结合是解题的关键.22. 2022年3月23日,“天宫课堂”第二课在中国空间站开讲,神舟十三号飞行乘组航天员翟志刚、王亚平、叶光富讲了又一堂精彩的太空科普课.这场充满奇思妙想的太空授课,让科学的种子在亿万青少年的心里生根发芽.小明和小亮对航天知识产生了极大兴趣,他们在中国载人航天网站了解到,航天知识分为“梦圆天路”、“飞天英雄”、“探秘太空”、“巡天飞船”等模块.他们决定先从“梦圆天路”、“飞天英雄”、“探秘太空”三个模块中随机选择一个进行学习,分别设这三个模块为A ,B ,C ,用画树状图或列表的方法求出小明和小亮选择相同模块的概率. 【答案】 13【解析】【分析】先画出树状图,从而可得所有等可能的结果,再找出小明和小亮选择相同模块的结果,然后利用概率公式计算即可得. 【详解】解:由题意,画树状图如下:由图可知,所有等可能的结果共有9种,其中,小明和小亮选择相同模块的结果有3种. 则小明和小亮选择相同模块的概率为, 3193P ==答:小明和小亮选择相同模块的概率为. 13【点睛】本题考查了利用列举法求概率,正确画出树状图是解题关键.23. 已知关于x 的一元二次方程. ()22120x m x m +++-=(1)求证:无论m 取何值,此方程总有两个不相等的实数根;(2)当该方程的判别式的值最小时,写出m 的值,并求出此时方程的解.【答案】(1)见解析 (2),m =122,1x x =-=【解析】【分析】(1)判断判别式的符号,即可得证;(2)求出判别式的值最小时的m 的值,再解一元二次方程即可.【小问1详解】证明:∵,22(21)4(2)49m m m ∆=+-⨯-=+∵,20m ≥∴.2Δ490m =+>∴无论m 取何值,方程总有两个不相等的实数根.【小问2详解】解:由题意可知,当时,的值最小.0m =249m ∆=+将代入,得0m =2(21)20x m x m +++-=220x x +-=解得:.122,1x x =-=【点睛】本题考查一元二次方程的判别式与根的个数的关系,以及解一元二次方程.熟练掌握判别式与根的个数的关系,以及解一元二次方程的方法,是解题的关键.24. 掷实心球是中考体育考试项目之一,实心球投掷后的运动轨迹可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从投掷到着陆的过程中,实心球的竖直高度(单位:y m)与水平距离(单位:m)近似满足函数关系.某位同学进行了两x 2()y a x h k =-+(0)a <次投掷.(1)第一次投掷时,实心球的水平距离与竖直高度的几组数据如下:x y 水平距离x/m 0 2 4 6 8 10竖直距离y/m 1.67 2.632.95 2.63 1.670.07根据上述数据,直接写出实心球竖直高度的最大值,并求出满足的函数关系;2()y a x h k =-+(0)a <(2)第二次投掷时,实心球的竖直高度y 与水平距离近似满足函数关系x .记实心球第一次着地点到原点的距离为,第二次着地点到原点20.09( 3.8) 2.97y x =--+1d 的距离为,则_____ (填“>”“=”或“<”).2d 1d 2d 【答案】(1),2.9520.08(4) 2.95y x =--+(2)>【解析】【分析】(1)先根据表格中的数据找到顶点坐标,即可得出实心球竖直高度的最大值,并利用待定系数法得到抛物线解析式;(2)设着陆点的纵坐标为0,分别代入第一次和第二次的函数关系式,求出着陆点的横坐标即为 和,然后进行比较即可.1d 2d 【小问1详解】解:由表格数据可知,抛物线的顶点坐标为, (42.95),所以实心球竖直高度的最大值为,2.95设抛物线的解析式为:,2(4) 2.95y a x =-+将点代入,得, (01.67),1.67162.95a =+解得,0.08a =-∴抛物线的解析式为:;20.08(4) 2.95y x =--+【小问2详解】解:第一次抛物线解析式为,20.08(4) 2.95y x =--+令,得到(负值舍去), 0y =4x =+第二次抛物线的解析式为,20.09( 3.8) 2.97y x =--+令,得到(负值舍去)0y = 3.8x =+, 4 3.8+>+ ,12d d ∴>故答案为:>【点睛】本题主要考查了二次函数的应用,待定系数法求函数关系式,解题的关键是读懂题意,列出函数关系式.25. 如图,点在以为直径的上,平分交于点D ,交于点E ,C AB O CD ACB ∠O AB 过点D 作交F .DF AB CO(1)求证:直线是的切线;DF O(2)若°,DF 的长.30A ∠=AC =【答案】(1)见解析 (2) FD =【解析】【分析】(1)连接,证明可得结论;OD DF OD AB OD ⊥⊥,,(2)再中,,,得到,,再在Rt ACB △30A ∠=︒AC =4AB =2OD =Rt ODF △中,由,继而求得;60F ∠=︒FD 【小问1详解】证明:连接. OD∵ 是的直径,平分,AB O CD ACB ∠ AD DB∴=∴ .90AOD BOD ∠=∠=︒又∵ ,FD AB ∥∴ .90ODF BOD ∠=∠=︒即 .OD DF ⊥∴ 直线为的切线.DF O 【小问2详解】解:∵ 是的直径,AB O ∴.90ACB ∠=︒又∵,,30A ∠=︒AC =∴ .4AB =∴ .2OD =∵ ,AO CO =30ACO A ∴∠=∠=︒∴ .60COB A ACO ∠=∠+∠=︒∵ ,DF AB ∴ ,60F ∠=︒,30FOD ∴∠=︒设则,,FD x =22OF FD x ==又,2OD =在中,由勾股定理得:,Rt ODF △22224x x +=解得:, x =故 FD =【点睛】本题属于圆综合题,考查了垂径定理,圆周角定理,平行线的判定,特殊角的直角三角形性质,等知识,解题的关键是学会添加常用辅助线解决问题.26. 已知二次函数. ()2430y ax ax a =-+≠(1)求该二次函数的图象与y 轴交点的坐标及对称轴.(2)已知点都在该二次函数图象上,()()()()12343,1,12,,,,,y y y y --①请判断与的大小关系: (用“”“”“”填空);1y 2y 1y 2y >=<②若,,,四个函数值中有且只有一个小于零,求a 的取值范围.1y 2y 3y 4y 【答案】(1)抛物线与y 轴交点的坐标为,对称轴()0,32x =(2)①; ② =3154a -≤<-【解析】【分析】(1),可得抛物线与y 轴交点的坐标,再根据抛物线对称轴公式解答,即可0x =求解;(2)①根据题意可得点关于直线对称,即可求解;②根据题意可得点()()12,3,1,y y 2x =在对称轴的左侧,点在对称轴的右侧,然后分两种情况:()()()2341,,,1,2,y y y --()13,y 当时,当时,即可求解.0a >a<0【小问1详解】解:令,则,0x =3y =∴抛物线与y 轴交点的坐标为 .()0,3对称轴. 422a x a-=-=【小问2详解】解:① ∵函数图象的对称轴为直线,2x =∴点关于直线对称,()()12,3,1,y y 2x =∴,12y y =故答案为:;=②∵函数图象的对称轴为直线,,2x =3112>>->-∴点在对称轴的左侧,点在对称轴的右侧.()()()2341,,,1,2,y y y --()13,y 当时,在对称轴的左侧,y 随x 的增大而减小,0a >∴,不合题意.1234y y y y =<<当时,在对称轴的左侧,y 随x 的增大而增大,则,a<01234y y y y =>>,,,四个函数值可以满足,1y 2y 3y 4y 12340y y y y >=≥>∴,340,0y y ≥<即当时,,当时,.=1x -3430y a a =++≥2x =-44830y a a =++<解得 . 3154a -≤<-【点睛】本题考查了二次函数图象与性质,掌握二次函数图象与性质是解题的关键.27.如图,是等腰直角三角形,,为延长线上一点,ABC 90ACB AC BC ∠=︒=,D AC 连接,将线段绕点逆时针旋转得到线段,过点作于点,BD BD D 90︒DE E EFAC ⊥F 连接. AE(1)依题意补全图形;(2)比较与的大小,并证明;AF CD (3)连接,为的中点,连接,用等式表示线段之间的数量BE G BE CG CD CG BC ,,关系,并证明.【答案】(1)见解析 (2),见解析AF CD =(3),见解析BC CD =【解析】【分析】(1)根据旋转的性质画图即可;(2)根据旋转的性质以及等腰直角三角形可以得到全等三角形,再根据全等三角形的性质即可求出结论;(3)根据题意画出已知图形,再根据图形得到全等三角形,利用全等三角形的性质和等腰直角三角形的性质即可求出结论.【小问1详解】解:补全图形如图所示【小问2详解】解:,理由如下:AF CD =∵EF AD ⊥∴90EFD ∠=︒∵90ACB ∠=︒∴EFD BCD ∠=∠∵90ACB ∠=︒∴90CBD CDB ∠∠=︒+由题意可知,90BDE ∠=︒∴90EDF BDC ∠∠=︒+∴EDF CBD ∠=∠在和中EFD △DCB △EDF CBD EFD DCB ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴≌EFD △()AAS DCB ∴EF CD DF BC ==,∵BC AC =∴AC DF =∴AF CD =【小问3详解】解: 理由如下:BC CD =连接,DGFG∵ ,为的中点,DE BD =G BE 90BDE ∠=︒∴EG BG DG ==,90DGB ∠=︒∵90EFD DGE ∠=∠=︒∴GEF CDG ∠=∠在和中EFG DCG △EF DC GEF CDG EG DG =⎧⎪∠=∠⎨⎪=⎩∴≌ EFG SAS DCG ()∴,FG CG =EGF DGC ∠=∠∴90EGF EGC DGC EGC ∠+∠=∠+∠=︒即90CGF ∠=︒∴为等腰直角三角形CGF △∴CF =∵ ,BC AC AF CF ==+AF CD =∴BC CD =+【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质等相关知识点,掌握全等三角形的性质和旋转的性质是解题的关键.28. 在平面直角坐标系中,我们给出如下定义:将图形M 绕直线上某一点P 顺时xOy 3x =针旋转,再关于直线对称,得到图形N ,我们称图形N 为图形M 关于点P 的二次90︒3x =关联图形.已知点.()0,1A (1)若点P 的坐标是,直接写出点A 关于点P 的二次关联图形的坐标________;()3,0(2)若点A 关于点P 的二次关联图形与点A 重合,求点P 的坐标(直接写出结果即可);(3)已知的半径为1,点A 关于点P 的二次关联图形在上且不与点A 重合. O O 若线段,其关于点P 的二次关联图形上的任意一点都在及其内部,求此时 P 点1AB =O 坐标及点B 的纵坐标的取值范围.B y 【答案】(1)()2,3(2)()3,2-(3),, ()3,3-12102B y ≤≤【解析】【分析】(1)根据二次关联图形的定义分别找到和,过点作轴于点D ,可A 'A ''A 'A D x '⊥证得,从而得到,即可求解;AOP PDA ' ≌1,3OA PD OP A D '====(2)根据题意得:点P 位于x 轴的下方,设点P 的纵坐标为m ,过点P 作轴于点PE y ⊥E ,过点作轴交延长线于点F ,坐标为m ,表达点的坐标,可得出结论;A 'A F x '⊥EP A '(3)由(2)可知,点的坐标,由A 关于点P 的二次关联图形在上且不与点A 重合A ''O 可得出点的坐标,由线段,其关于点P 的二次关联图形上的任意一点都在及A ''1AB =O 其内部,找到临界点,可得出的坐标,进而可得出点B 的坐标,即可得出的取值B ''B ''B y 范围.【小问1详解】如图1,根据二次关联图形的定义分别找到和,过点作轴于点D ,A 'A ''A 'A D x '⊥∴90A DP AOP '∠=∠=︒由旋转可知,,90,APA AP A P ''∠=︒=∴,90APO A PD A PD PA D '''∠+∠=∠+=︒∴,APO PA D '∠=∠∴,()AAS AOP PDA ' ≌∴,1,3OA PD OP A D '====∴,()4,3A '∵点和关于直线对称,A 'A ''3x =∴点,()2,3A ''即点A 关于点P 的二次关联图形的坐标为;()2,3故答案为:()2,3【小问2详解】解:根据题意得:点P 位于x 轴的下方,设点P 的纵坐标为m ,如图,过点P 作轴于点E ,过点作轴交延长线于点F ,PE y ⊥A 'A F x '⊥EP由(1)得: ,AEP PFA ' ≌∴,1,3AE PF m EP A F '==-==∴,()4,3A m m '-+根据题意得:点A 和点关于直线对称,A '3x =∴,46m -=解得:,2m =-∴点P 的坐标为,()3,2-【小问3详解】解:设点P 的纵坐标为n ,由(2)得:,()4,3A n n '-+∴,()2,3A n n ''++∵在上,A ''O ∴,()()22231n n +++=解得:(舍去)或,2n =-3-∴点P 的坐标为,()3,3-∵,其关于点P 的二次关联图形上的任意一点都在及其内部,1AB =AB O 此时点是一个临界点,连接,如图, B ''OB∵,1OA A B OB ''''''''===∴是等边三角形,OA B '''' 过点作轴于点M ,则, B ''B M x ''⊥12A M OM ''==∴ B M ''=∴, 1,2B ⎛''- ⎝∴, 13,2B ⎛' ⎝∴, 12B ⎫⎪⎭由对称性得:另一个点的坐标为, 12B ⎛⎫ ⎪ ⎪⎝⎭∴的取值范围为. B y 102B y ≤≤【点睛】本题属于新定义类问题,主要考查轴对称最值问题,等边三角形的性质与判定,圆的定义等相关知识,关键是理解给出新定义,画出对应的图形.。
北京市房山区2012届九年级上学期期末考试数学试卷

房山 2011——2012学年度第一学期终结性检测试卷一、(本题共32分,每小题4分)1.若3:4:=b a ,则下列各式中正确的式子是( ).A .b a 34=B .31-=-b b aC .34=a b D .b a 43=2、两个圆的半径分别是2cm 和7cm ,圆心距是8cm ,则这两个圆的位置关系是A .外离B .外切C .相交D .内切3、已知圆锥的母线长和底面圆的直径均是10㎝,则这个圆锥的侧面积是( ). A.50π㎝2 B. 50π㎝2 C. 50π㎝2 D. 50π㎝2.4、如图,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E , 若AD=4,BD=2,则BCDE的值是( )A.32B.21C.43D.535.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 436.将抛物线22y x =向下平移1个单位,得到的抛物线解析式为( ).A .22(1)y x =+ B .22(1)y x =- C .221y x =+ D .221y x =-7. 如图,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=,8PA =,那么弦AB 的长是( )A .4B .8C .43D .838、根据图1所示的程序,得到了y 与x 的函数图象,如图2.若点M 是y 轴正半轴上任意一点,过点M 作PQ ∥x 轴交图象于点P ,Q ,连接OP ,OQ .则以下结论: ①x <0 时,②△OPQ 的面积为定值. ③x >0时,y 随x 的增大而增大.MQ=2PM .⑤∠POQ 可以等于90°.其中正确结论是( )A 、①②④B 、②④⑤C 、③④⑤D 、②③⑤PBAOED CB A二、(本大题共16分,每小题4分)填空题: 9.在△ABC 中,∠C=90° ,1cos 2B =,则B ∠= . 10. 已知反比例函数2k y x-=,其图象在第二、四象限内,则k 的取值范围是 . 11、 把抛物线=y 223x x --化为=y ()2x m k -+的形式,其中,m k 为常数,则m-k =.12. 如图,圆圈内分别标有0,1,2,3,…,11这12个数字,电子跳骚每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳骚从标有数字“0”的圆圈开始,按逆时针方向跳了2010次后,落在一个圆圈中,该圆圈所标的数字是 三、(本大题共30分,每小题5分)解答题:13. 计算:2sin30°+4cos30°·tan60°-cos 245° 解:14. 已知抛物线c bx x y ++=2经过点(1,-4)和(-1,2). 求抛物线解析式. 解:15. 如图:AC ⌒ =CB ⌒ ,D E ,分别是半径OA 和OB 的中点 求证:CD=CE. 证明:16. 已知:如图,四边形ABCD 是平行四边形,F 是AB 上一点,连接DF 并延长交CB 的延长线于E.求证:AD :AF =CE :AB 证明:CBOEDA第3页17. 如图,△ABC 内接于⊙O ,点E 是⊙O 外一点,EO ⊥BC 于点D. 求证:∠1=∠E. 证明:18. 如图,在Rt OAB △中,90OAB ∠=,且点B 的坐标为(4,2). (1)画出OAB △绕点O 逆时针旋转90后的11OA B △; (2)求点A 旋转到点1A 所经过的路线长. 解:四、(本大题共20分,每小题5分)解答题: 19、今年“五一”假期.某数学活动小组组织一次登山活动。
北京市怀柔区2012届九年级上学期期末考试数学试题

7题图6题图5题图4题图怀柔区2011——2012学年度第一学期期末九年级教学质量检测数 学 试 卷 2012.1一、选择题(共8道小题,每小题4分,共32分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.13-的相反数是 ( ) A .3- B .3 C .13-D .132.已知,ABC △中,∠C=90°,sin ∠3,则∠A 的度数是 ( ) A .30° B .45° C .60° D . 90° 3.若反比例函数2k y x+=的图象位于第二、四象限内,则k 的取值范围是 ( ) A .2k >- B .2k <- C .0k > D .0k <4.如图,⊙O 的半径为5,AB 为弦,OC ⊥AB ,垂足为C ,若OC =3,则弦AB 的长为( ). A . 8 B .6C .4D .105.如图,D 是ABC △边AB 上一点,则下列四个条件不.能单独判定.....ABC ACD △∽△的是( ) A .B ACD ∠=∠ B .ADC ACB ∠=∠ C .AC AB CD BC=D .2AC AD AB =⋅6.如图,若将飞镖投中一个被平均分成6份的圆形靶子,则落在阴影部分的概率是 ( ) A .12 B .56 C .13 D .237.如图,BC 是⊙O 的直径,A 、D 是⊙O 上两点,若∠D = 35°,则∠OAC 的度数是 ( )A .35°B .55°C .65°D .70°8.如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,AB =2,D 是AB 边上的一个动点(不与点A 、B 重合),过点D 作CD 的垂线交射线CA 于点E .设AD=x ,CE=y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 ( )二、填空题(共4道小题,每小题4分,共16分)9.如图,在△ABC 中,DE ∥BC ,若DE=1,BC =3,那么△ADE 与△ABC 面积的比为 .10.如图,点A 、B 、C 是半径为3cm 的⊙O 上三个点,且︒=∠30ABC , 则劣弧 »AC 的长是 .11.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上, 则∠AED 的正弦值等于 .12.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填 整数之和都相等,则第99个格子中的数为 ,2012个格子中的数为 .三、解答题(本题共30分,每小题5分) 13.计算:2sin 452cos 60360+18.︒+︒︒ 14.已知抛物线228y x x =--.(1)用配方法把228y x x =--化为2()y x h k =-+形式;(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大.3abc-12…11题图10题图AEOBC DOABCDE9题图BCAE解15.解不等式: 4(x +1)≤5x +8,并把它的解集在数轴上表示出来.解:16.如图:已知,梯形ABCD 中,∠B =90°,AD ∥BC ,AB ⊥BC ,AB=AD =3,BC =7. 求cos ∠C. 解:17. 以直线1x =为对称轴的抛物线过点A (3,0)和点B(0,3),求此抛物线的解析式. 解:18.如图,在ABC △中,90C =o∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,AC=8,BC=6.求DE 的长.解:四、解答题(本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20米, 此时小明正好站在A 处,并测得60CBD ∠=o,牵引底端B 离地面1.5米, 求此时风筝离地面的高度. 解:20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).甲超市.球 两 红 一红一白 两 白 礼金券(元)205020乙超市:球两 红一红一白两 白礼金券(元) 50 20 50(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况; (2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由. 解:21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=o,延长AB 到点C ,使得∠ACD =45°. (1)求证:CD 是⊙O 的切线; (2)若22AB =OC 的长.证明:22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E .(1)求半圆O 的半径; (2)求图中阴影部分的面积.解:五、解答题(本题共22分, 23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y 轴于点()02D -,,若4AOD S =△. (1)求反比例函数和一次函数的解析式;(2)观察图象,请指出在y 轴的右侧,当12y y >时x 的取值范围,当1y <2y 时x 的取值范围.解:24. 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转BC D EDBACOAxyB OCD(第25题)α角,旋转后的矩形记为矩形EDCF .在旋转过程中,(1)如图①,当点E 在射线CB 上时,E 点坐标为 ;(2)当CBD ∆是等边三角形时,旋转角α的度数是 (α为锐角时); (3)如图②,设EF 与BC 交于点G ,当EG =CG 时,求点G 的坐标.(4) 如图③,当旋转角90α=o时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A 的抛物线上.图① 图② 图③解:25.如图,在平面直角坐标系中,顶点为(4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧). 已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积. 解:x yαFE DBO AC xy αF ED BOAC参考答案一、选择题(共8道小题,每小题4分,共32分)下面各题均有四个选项,其中只有一个..是符合题意的.二、填空题(本题共16分,每小题4分) 题号 9 101112 答案91π55 2; -1三、解答题(本题共30分,每小题5分)13.计算:2sin 452cos 6060︒+︒︒解: 原式=12+222⋅⋅分 =………………………………………………5分14.已知抛物线228y x x =--.(1)用配方法把228y x x =--化为2()y x h k =-+形式;(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大.解(1)228y x x =--=x 2-2x+1-1-8=(x -1)2 -9.………………………………………………3分(2)抛物线的顶点坐标是 (1,-9)抛物线的对称轴方程是 x =1 ……………………………4分 抛物线与x 轴交点坐标是(-2,0)(4,0);当x >1 时,y 随x 的增大而增大. ………………………………5分 15.解不等式: 4(x +1)≤5x +8,并把它的解集在数轴上表示出来. 解: 去括号,得 4x +4≤5x +8 ……………………………… 1分 移项、合并同类项,得-x ≤4……………………………… 3分系数化为1,得 x ≥4- ……………………………… 4分不等式的解集在数轴上表示如下:………………… 5分16.如图:已知,梯形ABCD 中,∠B =90°,AD ∥BC ,AB ⊥BC ,AB=AD =3, BC =7.BCAED求cos ∠C.解:方法一、作DE ⊥BC ,如图1所示,…………1分 ∵AD ∥BC ,AB ⊥BC ,AB=AD =3,∴四边形ABED 是正方形.…………………2分 ∴DE=BE=AB =3. 又∵BC =7,∴EC =4,……………………………………3分 由勾股定理得CD =5.…………………………4分 ∴ cos ∠C=45EC CD =.…………………………5分 方法二、作AE ∥CD ,如图2所示,……………1分 ∴∠1=∠C ,∵AD ∥BC ,∴四边形AECD 是平行四边形.………………2分 ∵A B=AD=3,∴EC=AD =3, 又∵BC =7,∴BE=4,……………………………………3分∵ AB ⊥BC ,由勾股定理得AE=5. ………………4分 ∴ cos ∠C= cos ∠1=45BE AE =. …………………………5分 17. 以直线1x =为对称轴的抛物线过点A (3,0)和点B(0,3),求此抛物线的解析式. 解:设抛物线的解析式为2(1)y a x b =-+, ………………………………………1分Q 抛物线过点A (3,0)和B(0,3). ∴40,3.a b a b +=⎧⎨+=⎩ 解得1,4.a b =-⎧⎨=⎩… ………4分∴抛物线的解析式为223y x x =-++. ……………………………………5分18.如图,在ABC △中,90C =o∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB⊥交AC 于E ,86AC BC ==,.求DE 的长. 解:在ABC △中,9086C AC BC ===o,,∠, 2210AB AC BC ∴=+=.…………………2分又6BD BC ==Q ,4AD AB BD ∴=-=. DE AB ⊥Q ,90ADE C ∴==o∠∠.又A A =Q ∠∠, AED ABC ∴△∽△.………………………………4分图1图2DE ADBC AC∴=. .3684=⨯=⋅=BC AC AD DE ………………………5分四、解答题(本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20米,此时小明正好站在A 处,并测得60CBD ∠=o,牵引底端B 离地面1.5米, 求此时风筝离地面的高度.解:依题意得,90CDB BAE ABD AED ∠=∠=∠=∠=︒, ∴四边形ABDE 是矩形 ,…………1分1.5.DE AB ∴== ……………2分在Rt BCD △中,sin ,CDCBD BC∠=……………3分 又∵ 20BC = ,60CBD ∠=o,由BCCD=ο60sin ∴ 3sin 6020103CD BC =⋅︒=⨯= .……………4分 103 1.5CE ∴=+ .………………………………………5分即此时风筝离地面的高度为()103 1.5+米 .20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).甲超市.球 两 红 一红一白 两 白 礼金券(元)205020乙超市:球 两 红 一红一白 两 白 礼金券(元)502050(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况; (2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由. 解:(1)树状图为:…………2分(2)∵去甲超市购物摸一次奖获50元礼金券的概率是P (甲)=64=32,…………3分去乙超市购物摸一次奖获50元礼金券的概率是P (乙)=62=31……………………4分 ∴我选择去甲超市购物……………………………………………………………………5分21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=o,延长AB 到点C ,使得∠ACD =45°. (1)求证:CD 是⊙O 的切线; (2)若AB =OC 的长. (1)证明:连接OD .∵OA OD =,22.5A ∠=o, 22.5ODA A ∴∠=∠=︒,45DOC ∴∠=︒ . ……………………1分∵45ACD ∠=o,90ODC ∴∠=︒ ,OD CD ∴⊥ . ……………………2分又∵点D 在⊙O 上,∴CD 是⊙O 的切线 .……………………3分 (2)∵直径AB =12OD AB ∴==. …………… 4分 在Rt OCD △中,sin ODC OC= ,∴sin 45OC ︒= ,∵sin 452︒=,2OC ∴= .……………………5分22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E .(1)求半圆O 的半径;(2)求图中阴影部分的面积. 解:(1)解:连结OD ,OC ,∵半圆与AC ,BC 分别相切于点D ,E .∴DCO ECO ∠=∠,且OD AC ⊥.…………………1分∵AC BC =, ∴CO AB ⊥且O 是AB 的中点.∴122AO AB ==.AC∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==. 即半圆的半径为1. ……………………………………….3分(2)设CO =x ,则在R t AOC △中,因为30A ∠=︒,所以AC =2x ,由勾股定理得:222AC OC AO -= 即 222(2)2x x -= 解得 23x =23x =舍去)∴ 112343422ABC S AB OC =⋅=⨯=△. …………………….4分 ∵ 半圆的半径为1, ∴ 半圆的面积为2π,∴ 438332S ππ-=-=阴影….…………………………….5分五、解答题(本题共22分,23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y 轴于点()02D -,,若4AOD S =△. (1)求反比例函数和一次函数的解析式;(2)观察图象,请指出在y 轴的右侧,当12y y >时x 的取值范围,当1y <2y 时x 的取值范围.解:作AE y ⊥轴于E ∵42AOD S OD ==△, ∴.421=⋅AE OD ∴4AE =. ………………………………………1分 ∵AB OB C ⊥,为OB 的中点,∴90DOC ABC OC BC OCD BCA ==︒==∠∠,,∠∠. ∴Rt Rt DOC ABC △≌△.…………………………………3分∴2AB OD ==. ∴A (4,2). 将A (4,2)代入1k y x =中,得8k =. 18y x∴=. ……………4分 将()42A ,和()02D ,-代入2y ax b =+,得422a b b +=⎧⎨=-⎩解之得:12a b =⎧⎨=-⎩∴22y x =-.…………………………………………………………………5分 (2)在y 轴的右侧,当12y y >时,04x <<. ………………………6分当1y <2y 时x >4. ……………………………………………………7分24. 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转α角,旋转后的矩形记为矩形EDCF .在旋转过程中,(1)如图①,当点E 在射线CB 上时,E 点坐标为 ;(2)当CBD ∆是等边三角形时,旋转角α的度数是 (α为锐角时); (3)如图②,设EF 与BC 交于点G ,当EG =CG 时,求点G 的坐标.(4) 如图③,当旋转角90α=o时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A 的抛物线上.图① 图② 图③解:(1)E (4,132) ………………………………………………1分(2)︒60 …………………………………………………………………2分 (3)设x CG =,则x EG =,x FG -=6,在Rt △FGC 中,∵222CG FG CF =+,∴222)6(4x x =-+,解得 313=x ,即313=CG . ∴G (4,313). …………………………………………………………4分(4)设以点C 为顶点的抛物线的解析式为2)4(-=x a y .x y αFE DBO A C xy αF ED BOACx(第25题)x把A (0,6)代入得,2)40(6-=a . 解得, 83=a . ∴此抛物线的解析式为2)4(83-=x y .……………………………………6分 ∵矩形EDCF 的对称中心为对角线FD 、CE 的交点H ,∴由题意可知H 的坐标为(7,2). 当7=x 时,2827)47(832≠=-=y , ∴点H 不在此抛物线上. ………………………………………………7分25.如图,在平面直角坐标系中,顶点为(4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧). 已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积.解:(1)设抛物线为2(4)1y a x =--.∵抛物线经过点A (0,3),∴23(04)1a =--.∴14a =. ∴抛物线为2211(4)12344y x x x =--=-+. …………2 (2) 答:l 与⊙C 相交. ……………………………………3证明:当21(4)104x --=时,12x =,26x =.∴B 为(2,0),C 为(6,0). ∴AB ==设⊙C 与BD 相切于点E ,连接CE , 则90BEC AOB ∠=︒=∠.∵90ABD ∠=︒,∴∠ABO +∠CBE =90°. 又∵∠ABO +∠BAO =90°,∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆.∴CE BCOB AB =.∴2CE =.∴2CE =>.…………4分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2. ∴抛物线的对称轴l 与⊙C 相交. …………………5分 (3) 解:如图,过点P 作平行于y 轴的直线交AC 于点Q .由点A (0,3)点C (6,0)可求出直线AC 的解析式为132y x =-+.………………6分 设P 点的坐标为(m ,21234m m -+),则Q 点的坐标为(m ,132m -+).∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.此时,P 点的坐标为(3,34-). …………………8分解答(3)的关键是作PQ ∥y 轴交AC 于Q ,以PQ 为公共底,OC 就是高,用抛物线、直线解析式表示P 、Q 两点的纵坐标,利用三角形的面积推导出面积与P 点横坐标m 的函数关系式, 即:2327(3)44PAC S m ∆=--+.评分说明:部分解答题有多种解法,以上各题只给出了部分解法,学生的其他解法可参照评分标准给分.。
2016-2017学年北京市东城区九年级(上)期末数学试卷含答案解析

2016-2017学年北京市东城区九年级(上)期末数学试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.(3分)(2019•开封一模)关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k 的值为()A.k=4B.k=﹣4C.k≥﹣4D.k≥42.(3分)(2016•南充)抛物线y=x2+2x+3的对称轴是()A.直线x=1B.直线x=﹣1C.直线x=﹣2D.直线x=2 3.(3分)(2016秋•仙桃期末)剪纸是我国的非物质文化遗产之一,下列剪纸作品中是中心对称图形的是()A.B.C.D.4.(3分)(2016•宜昌)在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是()A.甲组B.乙组C.丙组D.丁组5.(3分)(2016秋•东城区期末)在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是()A.y=(x+1)2+1B.y=(x﹣3)2+1C.y=(x﹣3)2﹣5D.y=(x+1)2+2 6.(3分)(2016•苏州)已知点A(2,y1)、B(4,y2)都在反比例函数y(k<0)的图象上,则y1、y2的大小关系为()A.y1>y2B.y1<y2C.y1=y2D.无法确定7.(3分)(2016•河北)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.8.(3分)(2016•宁波)如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为()A.30πcm2B.48πcm2C.60πcm2D.80πcm29.(3分)(2016•湖州)如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是()A.25°B.40°C.50°D.65°10.(3分)(2016秋•东城区期末)城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用.名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置.为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系y=ax2+bx+c(a,b,c是常数,且a≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是()A.4.8B.5C.5.2D.5.5二、填空题(本题共18分,每小题3分)11.(3分)(2016秋•东城区期末)请你写出一个图象分别位于第二、四象限的反比例函数的解析式,这个解析式可以是.12.(3分)(2016•菏泽)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m=.13.(3分)(2016秋•东城区期末)二次函数y=x2﹣4x﹣2的最小值为.14.(3分)(2016秋•东城区期末)天坛是古代帝王祭天的地方,其中最主要的建筑就是祈年殿.老师希望同学们利用所学过的知识测量祈年殿的高度,数学兴趣小组的同学们设计了如图所示的测量图形,并测出竹竿AB长2米,在太阳光下,它的影长BC为1.5米,同一时刻,祈年殿的影长EF约为28.5米.请你根据这些数据计算出祈年殿的高度DE 约为米.15.(3分)(2016秋•东城区期末)如图,在Rt△ABC中,∠ACB=90°,AC=2,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为.16.(3分)(2016秋•东城区期末)如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交点D的坐标为;菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)17.(5分)(2018秋•丹东期末)解方程:2x2﹣4x﹣1=0(用配方法)18.(5分)(2016秋•东城区期末)如图,在△ABC中,AD是中线,∠B=∠DAC,若BC =8,求AC的长.19.(5分)(2016秋•东城区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.20.(5分)(2016秋•东城区期末)如图,在平面直角坐标系中,O为坐标原点,Rt△ABO的边AB垂直于x轴,垂足为点B,反比例函数y1(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.(1)求反比例函数y1(x>0)的解析式;(2)设经过C,D两点的一次函数解析式为y2=k2x+b,求出其解析式,并根据图象直接写出在第一象限内,当y2>y1时,x的取值范围.21.(5分)(2016秋•东城区期末)列方程或方程组解应用题:公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为20m2,求原正方形空地的边长.22.(5分)(2016秋•东城区期末)按照要求画图:(1)如图甲,在平面直角坐标系中,点A,B,C的坐标分别为(﹣1,3),(﹣4,1),(﹣2,1),将△ABC绕原点O顺时针旋转90°得到△A1B1C1,点A,B,C的对应点为点A1,B1,C1.画出旋转后的△A1B1C1;(2)如图乙,下列3×3网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形(画出两种即可).23.(5分)(2018•吉林模拟)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.24.(5分)(2016秋•东城区期末)在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(﹣1,0).(1)求抛物线的解析式;(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.25.(5分)(2019•临清市一模)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O 于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.(1)求证:DE是⊙O的切线;(2)若,AD=4,求CE的长.26.(5分)(2016秋•东城区期末)问题探究:新定义:将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”).解决问题:已知在Rt△ABC中,∠BAC=90°,AB=AC=2.(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,求AD的长;(2)在图2和图3中,分别画出一条等积线段,并求出它们的长度.(要求:使得图1、图2和图3中的等积线段的长度各不相等)27.(7分)(2016秋•东城区期末)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣4(m≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,﹣3).(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使P A+PC的值最小,求点P的坐标;(3)将抛物线在B,C之间的部分记为图象G(包含B,C两点),若直线y=5x+b与图象G有公共点,请直接写出b的取值范围.28.(7分)(2016秋•东城区期末)点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE 之间有怎样的数量关系,直接写出结论不必证明.29.(8分)(2016秋•东城区期末)在平面直角坐标系xOy中,有如下定义:若直线l和图形W相交于两点,且这两点的距离不小于定值k,则称直线l与图形W成“k相关”,此时称直线与图形W的相关系数为k.(1)若图形W是由A(﹣2,﹣1),B(﹣2,1),C(2,1),D(2,﹣1)顺次连线而成的矩形:①l1:y=x+2,l2:y=x+1,l3:y=﹣x﹣3这三条直线中,与图形W成“相关”的直线有;②画出一条经过(0,1)的直线,使得这条直线与W成“相关”;③若存在直线与图形W成“2相关”,且该直线与直线y x平行,与y轴交于点Q,求点Q纵坐标y Q的取值范围;(2)若图形W为一个半径为2的圆,其圆心K位于x轴上.若直线y x与图形W 成“3相关”,请直接写出圆心K的横坐标x K的取值范围.2016-2017学年北京市东城区九年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.(3分)(2019•开封一模)关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k 的值为()A.k=4B.k=﹣4C.k≥﹣4D.k≥4【解答】解:∵关于x的一元二次方程x2+4x+k=0有两个相等的实数根,∴△=42﹣4k=16﹣4k=0,解得:k=4.故选:A.2.(3分)(2016•南充)抛物线y=x2+2x+3的对称轴是()A.直线x=1B.直线x=﹣1C.直线x=﹣2D.直线x=2【解答】解:∵y=x2+2x+3=(x+1)2+2,∴抛物线的对称轴为直线x=﹣1.故选:B.3.(3分)(2016秋•仙桃期末)剪纸是我国的非物质文化遗产之一,下列剪纸作品中是中心对称图形的是()A.B.C.D.【解答】解:A、是中心对称图形,故本选项正确;B、不是中心对称图形,故本选项错误;C、不是中心对称图形,故本选项错误;D、不是中心对称图形,故本选项错误.故选:A.4.(3分)(2016•宜昌)在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是()A.甲组B.乙组C.丙组D.丁组【解答】解:根据模拟实验的定义可知,实验相对科学的是次数最多的丁组.故选:D.5.(3分)(2016秋•东城区期末)在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是()A.y=(x+1)2+1B.y=(x﹣3)2+1C.y=(x﹣3)2﹣5D.y=(x+1)2+2【解答】解:抛物线y=x2﹣2x﹣1可化简为y=(x﹣1)2﹣2,先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式y=(x﹣1+2)2﹣2+3=(x+1)2+1;故选:A.6.(3分)(2016•苏州)已知点A(2,y1)、B(4,y2)都在反比例函数y(k<0)的图象上,则y1、y2的大小关系为()A.y1>y2B.y1<y2C.y1=y2D.无法确定【解答】解:∵点A(2,y1)、B(4,y2)都在反比例函数y(k<0)的图象上,∴每个象限内,y随x的增大而增大,∴y1<y2,故选:B.7.(3分)(2016•河北)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.【解答】解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确;D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误.故选:C.8.(3分)(2016•宁波)如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为()A.30πcm2B.48πcm2C.60πcm2D.80πcm2【解答】解:∵h=8,r=6,可设圆锥母线长为l,由勾股定理,l10,圆锥侧面展开图的面积为:S侧2×6π×10=60π,所以圆锥的侧面积为60πcm2.故选:C.9.(3分)(2016•湖州)如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是()A.25°B.40°C.50°D.65°【解答】解:连接OC,∵圆O是Rt△ABC的外接圆,∠ACB=90°,∴AB是直径,∵∠A=25°,∴∠BOC=2∠A=50°,∵CD是圆O的切线,∴OC⊥CD,∴∠D=90°﹣∠BOC=40°.故选:B.10.(3分)(2016秋•东城区期末)城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用.名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置.为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系y=ax2+bx+c(a,b,c是常数,且a≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是()A.4.8B.5C.5.2D.5.5【解答】解:将(4,0.43)、(5,1.1)、(6,0.87)代入解析式得:,解得:,∴y=﹣0.45x2+4.72x﹣11.25,当x 5.244时,y取得最大值,故选:C.二、填空题(本题共18分,每小题3分)11.(3分)(2016秋•东城区期末)请你写出一个图象分别位于第二、四象限的反比例函数的解析式,这个解析式可以是y(答案不唯一).【解答】解:∵函数图象分别位于第二、四象限,∴k<0,∴符合条件的函数解析式为:y(答案不唯一).故答案为:y(答案不唯一).12.(3分)(2016•菏泽)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m=6.【解答】解:∵m是关于x的方程x2﹣2x﹣3=0的一个根,∴m2﹣2m﹣3=0,∴m2﹣2m=3,∴2m2﹣4m=6,故答案为:6.13.(3分)(2016秋•东城区期末)二次函数y=x2﹣4x﹣2的最小值为﹣6.【解答】解:y=x2﹣4x﹣2=(x﹣2)2﹣6,由于函数开口向上,因此函数有最小值,且最小值为﹣6,故答案为:﹣6.14.(3分)(2016秋•东城区期末)天坛是古代帝王祭天的地方,其中最主要的建筑就是祈年殿.老师希望同学们利用所学过的知识测量祈年殿的高度,数学兴趣小组的同学们设计了如图所示的测量图形,并测出竹竿AB长2米,在太阳光下,它的影长BC为1.5米,同一时刻,祈年殿的影长EF约为28.5米.请你根据这些数据计算出祈年殿的高度DE 约为38米.【解答】解:根据相同时刻的物高与影长成比例,设祈年殿DE的高度为x米,则可列比例为,解得x=38.所以祈年殿DE的高度为38米.故答案为38.15.(3分)(2016秋•东城区期末)如图,在Rt△ABC中,∠ACB=90°,AC=2,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为.【解答】解:由旋转可知AD=BD,∵∠ACB=90°,AC=2,∴CD=BD,∵CB=CD,∴△BCD是等边三角形,∴∠BCD=∠CBD=60°,∴BC AC=2,∴阴影部分的面积22÷2,故答案为:.16.(3分)(2016秋•东城区期末)如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交点D的坐标为(1,1);菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为(﹣1,﹣1).【解答】解:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(,),即(1,1).每秒旋转45°,则第60秒时,得45°×60=2700°,2700°÷360=7.5周,OD旋转了7周半,菱形的对角线交点D的坐标为(﹣1,﹣1),故答案为:(1,1),(﹣1,﹣1).三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)17.(5分)(2018秋•丹东期末)解方程:2x2﹣4x﹣1=0(用配方法)【解答】解:2x2﹣4x﹣1=0x2﹣2x0x2﹣2x+11(x﹣1)2∴x1=1,x2=1.18.(5分)(2016秋•东城区期末)如图,在△ABC中,AD是中线,∠B=∠DAC,若BC =8,求AC的长.【解答】解:∵∠B=∠DAC,∠C=∠C,∴△ABC∽△DAC,∴,∴AC2=CD•BC,∵AD是中线,BC=8,∴CD=4,∴AC=4.19.(5分)(2016秋•东城区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.【解答】解:如图,连接OC.∵弦CD⊥AB于点E,CD=6,∴CE=ED CD=3.∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,∴OE,∴BE=OB﹣OE=4.20.(5分)(2016秋•东城区期末)如图,在平面直角坐标系中,O为坐标原点,Rt△ABO 的边AB垂直于x轴,垂足为点B,反比例函数y1(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.(1)求反比例函数y1(x>0)的解析式;(2)设经过C,D两点的一次函数解析式为y2=k2x+b,求出其解析式,并根据图象直接写出在第一象限内,当y2>y1时,x的取值范围.【解答】解:(1)∵OB=4,AB=3,点A在第一象限,∴点A的坐标为(4,3),∵点C为线段OA的中点,∴点C的坐标为(2,).∵点C在反比例函数y1(x>0)的图象上,∴k1=23.∴反比例函数的解析式为y(x>0).(2)当x=4时,y,∴点D的坐标为(4,).将C(2,)、B(4,)代入y2=k2x+b,,解得:,∴一次函数解析式为y2x.观察函数图象可知:当2<x<4时,一次函数图象在反比例函数图象的上方,∴当y2>y1时,x的取值范围为2<x<4.21.(5分)(2016秋•东城区期末)列方程或方程组解应用题:公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为20m2,求原正方形空地的边长.【解答】解:设原正方形空地的边长为xm,根据题意,得(x﹣1)(x﹣2)=20,解方程,得x1=6,x2=﹣3(舍),答:原正方形空地的边长为6m.22.(5分)(2016秋•东城区期末)按照要求画图:(1)如图甲,在平面直角坐标系中,点A,B,C的坐标分别为(﹣1,3),(﹣4,1),(﹣2,1),将△ABC绕原点O顺时针旋转90°得到△A1B1C1,点A,B,C的对应点为点A1,B1,C1.画出旋转后的△A1B1C1;(2)如图乙,下列3×3网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形(画出两种即可).【解答】解:(1)如图甲所示:旋转后的△A1B1C1即为所求;(2)如图乙所示:答案不唯一.23.(5分)(2018•吉林模拟)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.【解答】解:(1)所有可能出现的结果如图:从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取相同数字的结果有3种,所以两人抽取相同数字的概率为;(2)不公平.从表格可以看出,两人抽取数字和为2的倍数有5种,两人抽取数字和为5的倍数有3种,所以甲获胜的概率为,乙获胜的概率为.∵>,∴甲获胜的概率大,游戏不公平.24.(5分)(2016秋•东城区期末)在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(﹣1,0).(1)求抛物线的解析式;(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.【解答】解:(1)由题意可求点A的坐标为(3,0).将点A(3,0)和点B(﹣1,0)代入y=﹣x2+bx+c,得解得∴抛物线的解析式y=﹣x2+2x+3.(2)如图,∵点C的坐标为(0,3),点D(1,0),∴满足条件的点P的纵坐标为2.∴﹣x2+2x+3=2.解得,.∴点P的坐标为,或,.25.(5分)(2019•临清市一模)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O 于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.(1)求证:DE是⊙O的切线;(2)若,AD=4,求CE的长.【解答】(1)证明:连接OD.∵OA=OD,∴∠BAD=∠ODA.∵AD平分∠BAC,∴∠BAD=∠DAC.∴∠ODA=∠DAC.∴OD∥AE.∵DE⊥AE,∴OD⊥DE.∴DE是⊙O的切线;(2)∵OB是直径,∴∠ADB=90°.∴∠ADB=∠E.又∵∠BAD=∠DAC,∴△ABD∽△ADE.∴.∴AB=10.由勾股定理可知.连接DC,∴.∵A,C,D,B四点共圆.∴∠DCE=∠B.∴△DCE∽△ABD.∴.∴CE=2.26.(5分)(2016秋•东城区期末)问题探究:新定义:将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”).解决问题:已知在Rt△ABC中,∠BAC=90°,AB=AC=2.(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,求AD的长;(2)在图2和图3中,分别画出一条等积线段,并求出它们的长度.(要求:使得图1、图2和图3中的等积线段的长度各不相等)【解答】解:(1)在Rt△ABC中,∵,∠C=45°,AD是△ABC的一条等积线段,∴点D为线段BC的中点,BC=4,∴AD=2;(2)符合题意的图形如右上角图2和图3所示:如图2,当BD是△ABC的一条等积线段时,∵在Rt△ABC中,∠BAC=90°,AB=AC=2,BD是△ABC的一条等积线段,∴点D为AC的中点,∴AD,∴BD;如图3,当DE是△ABC的一条等积线段时,此时DE∥BC,则△ADE的面积等于△ABC面积的一半,∵在Rt△ABC中,∠BAC=90°,AB=AC=2,∴△ABC的面积为:,∴△ADE的面积是2,设AD=a,则,得a2=4,∴DE.27.(7分)(2016秋•东城区期末)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣4(m≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,﹣3).(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使P A+PC的值最小,求点P的坐标;(3)将抛物线在B,C之间的部分记为图象G(包含B,C两点),若直线y=5x+b与图象G有公共点,请直接写出b的取值范围.【解答】解:(1)由题意可得,m﹣4=﹣3.∴m=1.∴抛物线的解析式为:y=x2﹣2x﹣3.(2)如图,点A关于抛物线的对称轴对称的点是B,连接BC交对称轴于点P,则点P就是使得P A+PC的值最小的点.由y=x2﹣2x﹣3,得对称轴是x=1,由B(3,0),C(0,﹣3),得直线BC的解析式为y=x﹣3,当x=1时,y=1﹣3=﹣2,∴点P的坐标为(1,﹣2).(3)当x=0时,直线y=5x+b≤﹣3,解得b≤﹣3;直线y=5x+b与抛物线相切时,得x2﹣7x﹣(3+b)=0,49+4(﹣3﹣b)≥0,解得b,符合题意的b的取值范围是b≤﹣3.28.(7分)(2016秋•东城区期末)点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE 之间有怎样的数量关系,直接写出结论不必证明.【解答】解:(1)OE=OF.理由:如图1,∵四边形ABCD是矩形,∴OA=OC,∵AE⊥BP,CF⊥BP,∴∠AEO=∠CFO=90°,∵在△AOE和△COF中,,∴△AOE≌△COF(AAS),∴OE=OF;(2)补全图形如右图2,OE=OF仍然成立.证明:延长EO交CF于点G,∵AE⊥BP,CF⊥BP,∴AE∥CF,∴∠EAO=∠GCO,又∵点O为AC的中点,∴AO=CO,在△AOE和△COG中,,∴△AOE≌△COG(ASA),∴OG=OE,∴Rt△EFG中,OF EG,∴OE=OF;(3)CF=OE+AE或CF=OE﹣AE.证明:①如图2,当点P在线段OA上时,∵∠OEF=30°,∠EFG=90°,∴∠OGF=60°,由(2)可得,OF=OG,∴△OGF是等边三角形,∴FG=OF=OE,由(2)可得,△AOE≌△COG,∴CG=AE,又∵CF=GF+CG,∴CF=OE+AE;②如图3,当点P在线段OA延长线上时,∵∠OEF=30°,∠EFG=90°,∴∠OGF=60°,同理可得,△OGF是等边三角形,∴FG=OF=OE,同理可得,△AOE≌△COG,∴CG=AE,又∵CF=GF﹣CG,∴CF=OE﹣AE.29.(8分)(2016秋•东城区期末)在平面直角坐标系xOy中,有如下定义:若直线l和图形W相交于两点,且这两点的距离不小于定值k,则称直线l与图形W成“k相关”,此时称直线与图形W的相关系数为k.(1)若图形W是由A(﹣2,﹣1),B(﹣2,1),C(2,1),D(2,﹣1)顺次连线而成的矩形:①l1:y=x+2,l2:y=x+1,l3:y=﹣x﹣3这三条直线中,与图形W成“相关”的直线有l1和l2;②画出一条经过(0,1)的直线,使得这条直线与W成“相关”;③若存在直线与图形W成“2相关”,且该直线与直线y x平行,与y轴交于点Q,求点Q纵坐标y Q的取值范围;(2)若图形W为一个半径为2的圆,其圆心K位于x轴上.若直线y x与图形W 成“3相关”,请直接写出圆心K的横坐标x K的取值范围.【解答】解:(1)①如图1中,直线l1与l2图形W成“相关”的直线.故答案为l1和l2.②符合题意的直线如图2中所示.夹在直线a和b或c和d之间的(含直线a,b,c,d)都是符合题意的.③如图3中,设符合题意的直线的解析式为y x+b,由题意可知符合题意的临界直线分别经过点(﹣1,1),(1,﹣1).分别代入可求出b1=1,b2=﹣1,∴﹣1y Q≤1.(2)如图4中,⊙K与直线交于点A、B,直线与x轴交于点D(﹣3,0),作KC⊥AB 于C.在Rt△AKC中,∵AC=BC,KA=2,∴CO,在Rt△CDK,∵∠CDO=30°,∴DK=2CO,根据对称性可知,当﹣3x K≤﹣3时,若直线y x与图形W成“3相关”.第31页(共31页)。
北京市东城区2023年九年级上学期《数学》期末试卷与参考答案

北京市东城区2023年九年级上学期《数学》期末试卷与参考答案一、选择题每题2分,共16分。
1. 若关于的一元二次方程有一个根为0,则m 的值为( )A. 2 B. 1C. 0 D. 答案;C2. 下列图形中是中心对称图形的是( )A. 正方形 B. 等边三角形C. 直角三角形 D. 正五边形答案;A3. 关于二次函数的最大值或最小值,下列说法正确的是( )A. 有最大值4B. 有最小值4C. 有最大值6D. 有最小值6答案;D4. 一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是确定事件的为( )A. 至少有1个球是黑球B. 至少有1个球是白球C. 至少有2个球是黑球D. 至少有2个球是白球答案;Ax 220x x m -+=1-22(4)6y x =-+5. 某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x ,根据题意可得方程( )A. 180(1﹣x)2=461B. 180(1+x )2=461C. 368(1﹣x)2=442D. 368(1+x )2=442答案;B6. 如图,在中,是直径,弦的长为5,点D 在圆上,且, 则的半径为( )A. B. 5C. D. 答案;B7. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC ,BD 分别与⊙O切于点C ,D ,延长AC ,BD 交于点P .若,⊙O 的半径为6cm ,则图中的长O e AB AC 30ADC ∠=︒O e 2.57.510120P ∠=︒»CDA. π cmB. 2π cmC. 3π cmD. 4π cm 答案;B8. 如图,正方形和的周长之和为,设圆的半径为,正方形的边长为,阴影部分的面积为.当x 在一定范围内变化时,y 和S 都随x 的变化而变化,则y 与x ,S 与x 满足的函数关系分别是( )A. 一次函数关系,一次函数关系B. 一次函数关系,二次函数关系C 二次函数关系,二次函数关系D. 二次函数关系,一次函数关系答案;B.ABCD O e 20cm cm x cm y 2cm S每题2分,共16分。
北京市东城区2010-2011学年九年级(上)期末数学试卷(含答案)
东城区2010-2011学年第一学期期末统一检测初三数学试卷2011.011. 一元二次方程122=-bx x 的常数项为( ) A. 1- B. 1 C. 0 D. 1±2. 下列图形中,是中心对称的图形是( )3. 若DEF ABC ∆∆~,1:2:=DE AD 且ABC ∆的周长为16,则DEF ∆的周长为( ) A. 4 B. 16 C. 8 D. 324. 如图,在⊙O 中,CD 是直径,AB 是弦,CD AB ⊥于M ,8=AB ,5=OC ,则MD 的长为( )A. 4B. 2C.2 D. 15. 若关于x 的方程0222=--ax x 有两个不相等的实数根,则a 的值是( )A. 2B. 4C. 6D. 86. 抛物线2)1(32-+-=x y 经过平移得到抛物线23x y -=,平移的方法是( )A. 向左平移1个单位,再向下平移2个单位B. 向右平移1个单位,再向下平移2个单位C. 向左平移1个单位,再向上平移2个单位D. 向右平移1个单位,再向上平移2个单位 7. 某圆与半径为2的圆相切,若两圆的圆心距为5,则此圆的半径为( )A. 3B. 7C. 3或7D. 5或78. 小明从二次函数c bx ax y ++=2的图象(如图)中观察得到了下面五条信息:①0<c ; ②0>abc ;③0>+-c b a ;④032=-b a ;⑤04>-b c ;你认为正确的信息是( ) A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤ 9. 抛物线152--=x x y 与y 轴的交点坐标是__________ 10. 若将分别写有“生活”、“城市”的2张卡片,随机放入“让生活更美好”中的两个内(每个只放1张卡片),则其中文字恰好组成“城市让生活更美好”的概率______11. 如图,AB ,AC 是⊙O 的两条弦,︒=∠30A ,经过点C 的切线与OB 的延长线交于点D ,则D ∠的度数为_________ 12. 在等腰梯形ABCD 中,BC AD //,AD BC 4=,2=AD ,︒=∠45B 。
北京市怀柔区2012届九年级上学期期末考试数学试题
7题图6题图5题图4题图怀柔区2011——2012学年度第一学期期末九年级教学质量检测数 学 试 卷 2012.1一、选择题(共8道小题,每小题4分,共32分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.13-的相反数是 ( ) A .3- B .3 C .13-D .132.已知,ABC △中,∠C=90°,sin ∠3,则∠A 的度数是 ( ) A .30° B .45° C .60° D . 90° 3.若反比例函数2k y x+=的图象位于第二、四象限内,则k 的取值范围是 ( ) A .2k >- B .2k <- C .0k > D .0k <4.如图,⊙O 的半径为5,AB 为弦,OC ⊥AB ,垂足为C ,若OC =3,则弦AB 的长为( ). A . 8 B .6C .4D .105.如图,D 是ABC △边AB 上一点,则下列四个条件不.能单独判定.....ABC ACD △∽△的是( ) A .B ACD ∠=∠ B .ADC ACB ∠=∠ C .AC AB CD BC=D .2AC AD AB =⋅6.如图,若将飞镖投中一个被平均分成6份的圆形靶子,则落在阴影部分的概率是 ( ) A .12 B .56 C .13 D .237.如图,BC 是⊙O 的直径,A 、D 是⊙O 上两点,若∠D = 35°,则∠OAC 的度数是 ( )A .35°B .55°C .65°D .70°8.如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,AB =2,D 是AB 边上的一个动点(不与点A 、B 重合),过点D 作CD 的垂线交射线CA 于点E .设AD=x ,CE=y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 ( )二、填空题(共4道小题,每小题4分,共16分)9.如图,在△ABC 中,DE ∥BC ,若DE=1,BC =3,那么△ADE 与△ABC 面积的比为 .10.如图,点A 、B 、C 是半径为3cm 的⊙O 上三个点,且︒=∠30ABC , 则劣弧 »AC 的长是 .11.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上, 则∠AED 的正弦值等于 .12.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第99个格子中的数为 ,2012个格子中的数为 .三、解答题(本题共30分,每小题5分) 13.计算:2sin 452cos 60360+18.︒+︒︒ 14.已知抛物线228y x x =--.(1)用配方法把228y x x =--化为2()y x h k =-+形式;(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,3abc-12…11题图10题图AEOBC DOABCDE9题图BCAED抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大. 解15.解不等式: 4(x +1)≤5x +8,并把它的解集在数轴上表示出来. 解:16.如图:已知,梯形ABCD 中,∠B =90°,AD ∥BC ,AB ⊥BC ,AB=AD =3,BC =7. 求cos ∠C. 解:17. 以直线1x =为对称轴的抛物线过点A (3,0)和点B(0,3),求此抛物线的解析式. 解:18.如图,在ABC △中,90C =o∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,AC=8,BC=6.求DE 的长.解:四、解答题(本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20米, 此时小明正好站在A 处,并测得60CBD ∠=o,牵引底端B 离地面1.5米, 求此时风筝离地面的高度. 解:20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).甲超市.球 两 红 一红一白 两 白 礼金券(元)205020乙超市:球 两 红 一红一白 两 白 礼金券(元)502050(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况; (2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由. 解:21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=o,延长AB 到点C ,使得∠ACD =45°. (1)求证:CD 是⊙O 的切线; (2)若22AB =,求OC 的长.证明:22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E .(1)求半圆O 的半径;(2)求图中阴影部分的面积.解:五、解答题(本题共22分,23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y 轴于点()02D -,,若4AOD S =△. (1)求反比例函数和一次函数的解析式;(2)观察图象,请指出在y 轴的右侧,当12y y >时x 的取值范围,当1y <2y 时x 的取值范围.解:BC D E DBACOAxyB OCD24. 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转α角,旋转后的矩形记为矩形EDCF .在旋转过程中,(1)如图①,当点E 在射线CB 上时,E 点坐标为 ;(2)当CBD ∆是等边三角形时,旋转角α的度数是 (α为锐角时); (3)如图②,设EF 与BC 交于点G ,当EG =CG 时,求点G 的坐标.(4) 如图③,当旋转角90α=o时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A 的抛物线上.图① 图② 图③解:25.如图,在平面直角坐标系中,顶点为(4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧). 已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积. 解:x yαFE DBO AC xy αF ED BOAC参考答案一、选择题(共8道小题,每小题4分,共32分)下面各题均有四个选项,其中只有一个..是符合题意的. 题 号 1 2 3 4 5 6 7 8 答 案DCBACABC二、填空题(本题共16分,每小题4分) 题号 9 101112 答案91π55 2; -1三、解答题(本题共30分,每小题5分) 13.计算:2sin 452cos 603tan 60+18.︒+︒-︒解: 原式=212+2-33+3222⋅⋅⋅…………………………4分 =2+1-3+32=42-2………………………………………………5分14.已知抛物线228y x x =--.(1)用配方法把228y x x =--化为2()y x h k =-+形式;(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,抛物线与x 轴交点坐标是 ,当x 时,y 随x 的增大而增大.解(1)228y x x =--=x 2-2x+1-1-8=(x -1)2 -9.………………………………………………3分(2)抛物线的顶点坐标是 (1,-9)抛物线的对称轴方程是 x =1 ……………………………4分 抛物线与x 轴交点坐标是(-2,0)(4,0);当x >1 时,y 随x 的增大而增大. ………………………………5分 15.解不等式: 4(x +1)≤5x +8,并把它的解集在数轴上表示出来. 解: 去括号,得 4x +4≤5x +8 ……………………………… 1分 移项、合并同类项,得-x ≤4……………………………… 3分系数化为1,得 x ≥4- ……………………………… 4分不等式的解集在数轴上表示如下:………………… 5分BCAED16.如图:已知,梯形ABCD 中,∠B =90°,AD ∥BC ,AB ⊥BC ,AB=AD =3,BC =7. 求cos ∠C.解:方法一、作DE ⊥BC ,如图1所示,…………1分 ∵AD ∥BC ,AB ⊥BC ,AB=AD =3,∴四边形ABED 是正方形.…………………2分 ∴DE=BE=AB =3. 又∵BC =7,∴EC =4,……………………………………3分 由勾股定理得CD =5.…………………………4分 ∴ cos ∠C=45EC CD =.…………………………5分 方法二、作AE ∥CD ,如图2所示,……………1分 ∴∠1=∠C ,∵AD ∥BC ,∴四边形AECD 是平行四边形.………………2分 ∵A B=AD=3,∴EC=AD =3, 又∵BC =7,∴BE=4,……………………………………3分∵ AB ⊥BC ,由勾股定理得AE=5. ………………4分 ∴ cos ∠C= cos ∠1=45BE AE =. …………………………5分 17. 以直线1x =为对称轴的抛物线过点A (3,0)和点B(0,3),求此抛物线的解析式. 解:设抛物线的解析式为2(1)y a x b =-+, ………………………………………1分Q 抛物线过点A (3,0)和B(0,3). ∴40,3.a b a b +=⎧⎨+=⎩ 解得1,4.a b =-⎧⎨=⎩… ………4分∴抛物线的解析式为223y x x =-++. ……………………………………5分18.如图,在ABC △中,90C =o∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB⊥交AC 于E ,86AC BC ==,.求DE 的长. 解:在ABC △中,9086C AC BC ===o,,∠, 2210AB AC BC ∴=+=.…………………2分又6BD BC ==Q ,4AD AB BD ∴=-=. DE AB ⊥Q ,90ADE C ∴==o∠∠. 又A A =Q ∠∠,图1 图2AED ABC ∴△∽△.………………………………4分DE ADBC AC∴=. .3684=⨯=⋅=BC AC AD DE ………………………5分四、解答题(本题共20分,每小题5分)19.如图,小明在十月一日到公园放风筝,风筝飞到C 处时的线长为20米,此时小明正好站在A 处,并测得60CBD ∠=o,牵引底端B 离地面1.5米, 求此时风筝离地面的高度.解:依题意得,90CDB BAE ABD AED ∠=∠=∠=∠=︒, ∴四边形ABDE 是矩形 ,…………1分1.5.DE AB ∴== ……………2分在Rt BCD △中,sin ,CDCBD BC∠=……………3分 又∵ 20BC = ,60CBD ∠=o,由BCCD=ο60sin ∴ 3sin 60201032CD BC =⋅︒=⨯= .……………4分 103 1.5CE ∴=+ .………………………………………5分即此时风筝离地面的高度为()103 1.5+米 .20.甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).甲超市.球 两 红 一红一白 两 白 礼金券(元)205020乙超市:球 两 红 一红一白 两 白 礼金券(元)502050(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况; (2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由. 解:(1)树状图为:…………2分(2)∵去甲超市购物摸一次奖获50元礼金券的概率是P (甲)=64=32,…………3分去乙超市购物摸一次奖获50元礼金券的概率是P (乙)=62=31……………………4分 ∴我选择去甲超市购物……………………………………………………………………5分21. 如图,AB 是⊙O 的直径,AD 是弦,22.5A ∠=o,延长AB 到点C ,使得∠ACD =45°. (1)求证:CD 是⊙O 的切线; (2)若22AB =,求OC 的长. (1)证明:连接OD .∵OA OD =,22.5A ∠=o, 22.5ODA A ∴∠=∠=︒,45DOC ∴∠=︒ . ……………………1分∵45ACD ∠=o,90ODC ∴∠=︒ ,OD CD ∴⊥ . ……………………2分又∵点D 在⊙O 上,∴CD 是⊙O 的切线 .……………………3分 (2)∵直径22AB =122OD AB ∴==. …………… 4分 在Rt OCD △中,sin ODC OC= ,∴ 2sin 45OC ︒= ,∵ 2sin 452︒=,2OC ∴= .……………………5分22.在△ABC 中,∠C=120°,AC=BC ,AB=4,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E .(1)求半圆O 的半径;(2)求图中阴影部分的面积. 解:(1)解:连结OD ,OC ,∵半圆与AC ,BC 分别相切于点D ,E .∴DCO ECO ∠=∠,且OD AC ⊥.…………………1分∵AC BC =, ∴CO AB ⊥且O 是AB 的中点.∴122AO AB ==. BCD E DBACO∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==. 即半圆的半径为1. ……………………………………….3分(2)设CO =x ,则在R t AOC △中,因为30A ∠=︒,所以AC =2x ,由勾股定理得:222AC OC AO -= 即 222(2)2x x -= 解得 23x =(23x =-舍去)∴ 112343422ABC S AB OC =⋅=⨯⨯=△. …………………….4分 ∵ 半圆的半径为1, ∴ 半圆的面积为2π,∴ 438332S ππ-=-=阴影. ….…………………………….5分五、解答题(本题共22分,23题7分,24题7分,25题8分) 23.如图所示,在直角坐标系中,点A 是反比例函数1ky x=的图象上一点,AB x ⊥轴的正半轴于B 点,C 是OB 的中点;一次函数2y ax b =+的图象经过A 、C 两点,并交y 轴于点()02D -,,若4AOD S =△. (1)求反比例函数和一次函数的解析式;(2)观察图象,请指出在y 轴的右侧,当12y y >时x 的取值范围,当1y <2y 时x 的取值范围.解:作AE y ⊥轴于E ∵42AOD S OD ==△, ∴.421=⋅AE OD ∴4AE =. ………………………………………1分 ∵AB OB C ⊥,为OB 的中点,∴90DOC ABC OC BC OCD BCA ==︒==∠∠,,∠∠. ∴Rt Rt DOC ABC △≌△.…………………………………3分∴2AB OD ==. ∴A (4,2). 将A (4,2)代入1k y x =中,得8k =. 18y x∴=. ……………4分 将()42A ,和()02D ,-代入2y ax b =+,得422a b b +=⎧⎨=-⎩解之得:12a b =⎧⎨=-⎩∴22y x =-.…………………………………………………………………5分 (2)在y 轴的右侧,当12y y >时,04x <<. ………………………6分当1y <2y 时x >4. ……………………………………………………7分24. 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转α角,旋转后的矩形记为矩形EDCF .在旋转过程中,(1)如图①,当点E 在射线CB 上时,E 点坐标为 ;(2)当CBD ∆是等边三角形时,旋转角α的度数是 (α为锐角时); (3)如图②,设EF 与BC 交于点G ,当EG =CG 时,求点G 的坐标.(4) 如图③,当旋转角90α=o时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A 的抛物线上.图① 图② 图③解:(1)E (4,132) ………………………………………………1分(2)︒60 …………………………………………………………………2分 (3)设x CG =,则x EG =,x FG -=6,在Rt △FGC 中,∵222CG FG CF =+,∴222)6(4x x =-+,解得 313=x ,即313=CG . ∴G (4,313). …………………………………………………………4分(4)设以点C 为顶点的抛物线的解析式为2)4(-=x a y .x y αFE DBO A C xy αF ED BOACAxyBOCD(第25题)EPQ Axy BOCD(第25题)把A (0,6)代入得,2)40(6-=a . 解得, 83=a . ∴此抛物线的解析式为2)4(83-=x y .……………………………………6分 ∵矩形EDCF 的对称中心为对角线FD 、CE 的交点H ,∴由题意可知H 的坐标为(7,2). 当7=x 时,2827)47(832≠=-=y , ∴点H 不在此抛物线上. ………………………………………………7分25.如图,在平面直角坐标系中,顶点为(4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧). 已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积.解:(1)设抛物线为2(4)1y a x =--.∵抛物线经过点A (0,3),∴23(04)1a =--.∴14a =. ∴抛物线为2211(4)12344y x x x =--=-+. …………2分 (2) 答:l 与⊙C 相交. ……………………………………3分 证明:当21(4)104x --=时,12x =,26x =.∴B 为(2,0),C 为(6,0). ∴223213AB =+=.设⊙C 与BD 相切于点E ,连接CE , 则90BEC AOB ∠=︒=∠.∵90ABD ∠=︒,∴∠ABO +∠CBE =90°. 又∵∠ABO +∠BAO =90°,∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆.∴CE BCOB AB =.∴62213CE -=.∴8213CE =>.…………4分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2. ∴抛物线的对称轴l 与⊙C 相交. …………………5分 (3) 解:如图,过点P 作平行于y 轴的直线交AC 于点Q .由点A (0,3)点C (6,0)可求出直线AC 的解析式为132y x =-+.………………6分 设P 点的坐标为(m ,21234m m -+),则Q 点的坐标为(m ,132m -+).∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.此时,P 点的坐标为(3,34-). …………………8分解答(3)的关键是作PQ ∥y 轴交AC 于Q ,以PQ 为公共底,OC 就是高,用抛物线、直线解析式表示P 、Q 两点的纵坐标,利用三角形的面积推导出面积与P 点横坐标m 的函数关系式, 即:2327(3)44PAC S m ∆=--+.评分说明:部分解答题有多种解法,以上各题只给出了部分解法,学生的其他解法可参照评分标准给分.。
精选题库北京市东城区九年级上学期数学期末试卷【答案版】
4.(2 分)点 A(x1, y1), B( x2,y2)都在反比例函数
的图象上,若 x1< x2
< 0,则( ) A.y2> y1>0 B.y1>y2>0 C. y2<y1<0 D.y1<y2< 0 【解答】 解:∵ k=2> 0, ∴此函数图象的两个分支分别位于一、 三象限, 且在每一象限内 y 随 x 的增大而 减小, ∵ x1<x2<0, ∴点 A(x1, y1), B( x2,y2)位于第三象限, ∴ y2<y1<0, 故选: C.
则点 B 的坐标为
.
12.( 2 分)如图, AB 是⊙ O 的弦, C 是 AB 的中点,连接 OC并延长交⊙ O 于点
D.若 CD=1,AB=4,则⊙ O 的半径是
.
13.(2 分)某校九年级的 4 位同学借助三根木棍和皮尺测量校园内旗杆的高度. 为
了方便操作和观察,他们用三根木棍围成直角三角形并放在高 1m 的桌子上,且
(m/n )
(n)
( m/n )
50
47
0.940
1500
ቤተ መጻሕፍቲ ባይዱ
1335
0.890
270
235
0.870
3500
3203
0.915
400
369
0.923
7000
6335
0.905
750
662
0.883
14000
12628
0.902
下面有四个推断:
①当移植的树数是 1 500 时,表格记录成活数是 1 335,所以这种树苗成活的概
27.( 7 分)如图 1,在△ ABC中,∠ ACB=90°,AC=2,BC=2 ,以点 B 为圆心, 为半径作圆.点 P 为⊙ B 上的动点,连接 PC,作 P'C⊥ PC,使点 P'落在直线
2022年北京市东城初三(上)期末数学试卷及答案
2022北京东城初三(上)期末数 学一、选择题(每题2分,共16分)1.(2分)一元二次方程2250x x +−=的二次项系数、一次项系数、常数项分别是( )A .2,1,5B .2,1,5−C .2,0,5−D .2,0,52.(2分)下列四个图形中,是中心对称图形的是( )A .B .C .D .3.(2分)将抛物线2y x =向上平移3个单位后所得的解析式为( )A .23y x =+B .23y x =−C .2(3)y x =+D .2(3)y x =−4.(2分)在平面直角坐标系xOy 中,点(2,3)A 关于原点对称的点的坐标是( )A .(2,3)−B .(2,3)−C .(3,2)D .(2,3)−−5.(2分)用配方法解方程241x x +=,变形后结果正确的是( )A .2(2)5x +=B .2(2)2x +=C .2(2)5x −=D .2(2)2x −=6.(2分)中国象棋文化历史久远,在图中所示的部分棋盘中,“馬”的位置在“⋯””(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“⋅”标记,则“馬”随机移动一次,到达的位置在“⋯”上方的概率是( )A .18B .16C .14D .127.(2分)如图,PA ,PB 是O 的切线,A ,B 为切点,点C 为O 上一点,若70ACB ∠=︒,则P ∠的度数为( )A .70︒B .50︒C .20︒D .40︒8.(2分)如图,线段5AB =,动点P 以每秒1个单位长度的速度从点A 出发,沿线段AB 运动至点B .以点A 为圆心,线段AP 的长为半径作圆.设点P 的运动时间为t ,点P ,B 之间的距离为y ,A 的面积为S .则y 与t ,S 与t 满足的函数关系分别是( )A .正比例函数关系、一次函数关系B .一次函数关系,正比例函数关系C .一次函数关系,二次函数关系D .正比例函数关系,二次函数关系二、填空题(每题2分,共16分)9.(2分)抛物线23(1)2y x =−−+的顶点坐标是 .10.(2分)若关于x 的一元二次方程220x x m ++=的一根为1−,则m 的值是 ” .11.(2分)请写出一个开口向上,并且与y 轴交于点(0,2)的抛物线的表达式: ” .12.(2分)社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里,装有20个除颜色不同外其余均相同的黑、白两种球.将盒子里面的球搅匀后,从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象,如图所示,经分析可以推断“摸出黑球”的概率为” .13.(2分)2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育活动.据了解,某展览中心3月份的参观人数为10万人,5月份的参观人数增加到12.1万人.设参观人数的月平均增长率为x ,则可列方程为” .14.(2分)如图,将ABC ∆绕点A 顺时针旋转得到ADE ∆,若110DAE ∠=︒,40B ∠=︒,则C ∠的度数为” .15.(2分)斛是中国古代的一种量器.据《汉书⋅律历志》记载:“斛底,方而圜(”u án )其外,旁有庣(”i āo )焉.”意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆.”如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的边长为”尺.16.(2分)如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE CF=,AE,DF交于点P,则APD∠的度数为”;连接CP,线段CP的最小值为”.三、解答题(共68分,17-22题,每题5分,23-26题,每题6分,27-28题,每题7分)17.(5分)解方程:2280x x−−=.18.(5分)如图,AB为O的弦,OC AB⊥于点M,交O于点C.若O的半径为10,:3:2OM MC=,求AB的长.19.(5分)下面是小明设计的“作圆的内接等腰直角三角形”的尺规作图过程.已知:O(如图1).求作:O的内接等腰直角三角形ABC.作法:如图2.①作直径AB;②分别以点A,B为圆心,大于12AB的长为半径作弧,两弧交于点M;③作直线MO交O于C,D两点;④连接AC,BC.所以ABC∆就是所求作的等腰直角三角形.根据小明设计的尺规作图过程,解决下面的问题:(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:连接MA ,MB .MA MB =,OA OB =,MO ∴是AB 的垂直平分线. 又直线MO 交O 于点C ,AC ∴= . AB 是直径,ACB ∴∠= ( )(填写推理依据).ABC ∴∆是等腰直角三角形.20.(5分)如图,在平面直角坐标系xOy 中,抛物线22y ax x c =++的部分图象经过点(0,3)A −,(1,0)B .(1)求该抛物线的解析式;(2)结合函数图象,直接写出0y <时,x 的取值范围.21.(5分)如图.在平面直角坐标系xOy 中,OAB ∆的顶点坐标分别为(0,0)O ,(5,0)A ,(4,3)B −.将OAB ∆绕点O 顺时针旋转90︒得到△OA B '',点A 旋转后的对应点为A '.(1)画出旋转后的图形△OA B '',并写出点A '的坐标;(2)求点B 经过的路径BB '的长(结果保留)π.22.(5分)2021年6月17日,神舟十二号成功发射,标志着我国载人航天踏上新征程.某学校举办航天知识讲座,需要两名引导员,决定从A ,B ,C ,D 四名志愿者中通过抽签的方式确定两人.抽签规则:将四名志愿者的名字分别写在四张完全相同且不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字.(1)“A 志愿者被选中”是” 事件(填“随机”、“不可能”或“必然””);(2)用画树状图或列表的方法求出A ,B 两名志愿者同时被选中的概率.23.(6分)已知关于x 的一元二次方程2(4)40x k x k −++=.(1)求证:该方程总有两个实数根;(2)若该方程有一个根小于2,求k 的取值范围.24.(6分)为了改善小区环境,某小区决定在一块一边靠墙(墙长为25)m 的空地上修建一个矩形小花园ABCD .小花园一边靠墙,另三边用总长40m 的栅栏围住,如图所示.设矩形小花园AB 边的长为x m ,面积为y 2m .(1)求y 与x 之间的函数关系式;(2)当x 为何值时,小花园的面积最大?最大面积是多少?25.(6分)如图,AC 是O 的弦,过点O 作OP OC ⊥交AC 于点P ,在OP 的延长线上取点B ,使得BA BP =.(1)求证:AB 是O 的切线;(2)若O 的半径为4,PC =AB 的长.26.(6分)在平面直角坐标系xOy 中,点(1,)m 和(2,)n 在抛物线2y x bx =−+上.(1)若0m =,求该抛物线的对称轴;(2)若0mn <,设抛物线的对称轴为直线x t =.①直接写出t 的取值范围;②已知点1(1,)y −,3(2,2)y ,3(3,)y 在该抛物线上,比较1y ,2y ,3y 的大小,并说明理由. 27.(7分)如图,在等边三角形ABC 中,点P 为ABC ∆内一点,连接AP ,BP ,CP ,将线段AP 绕点A 顺时针旋转60︒得到AP ',连接PP ',BP '.(1)用等式表示BP '与CP 的数量关系,并证明;(2)当120BPC ∠=︒时,①直接写出P BP '∠的度数为” ;②若M 为BC 的中点,连接PM ,用等式表示PM 与AP 的数量关系,并证明.28.(7分)在平面直角坐标系xOy 中.O 的半径为1,对于直线l 和线段AB ,给出如下定义:若将线段AB 关于直线l 对称,可以得到O 的弦(A B A ''',B '分别为A ,B 的对应点),则称线段AB 是O 的关于直线l 对称的“关联线段”.例如:在图1中,线段AB 是O 的关于直线l 对称的“关联线段”.(1)如图2,点1A ,1B ,2A ,2B ,3A ,3B 的横、纵坐标都是整数.①在线段11A B ,22A B ,33A B 中,O 的关于直线2y x =+对称的“关联线段”是” ;②若线段11A B ,22A B ,33A B 中,存在O 的关于直线y x m =−+对称的“关联线段”,则m = ;(2)已知直线(0)y b b =+>交x 轴于点C ,在ABC ∆中,3AC =,1AB =.若线段AB 是O 的关于直线(0)y x b b =+>对称的“关联线段”,直接写出b 的最大值和最小值,以及相应的BC 长.参考答案一、选择题(每题2分,共16分)1.【分析】根据多项式的项和单项式的系数定义得出答案即可.【解答】解:一元二次方程2250x x +−=的二次项系数,一次项系数,常数项分别是2,1,5−, 故选:B .【点评】本题考查了单项式的系数定义,多项式的项的定义和一元二次方程的一般形式,注意:找多项式的各项系数时带着前面的符号.2.【分析】根据中心对称图形的概念对各选项分析判断即可得解.把一个图形绕某一点旋转180︒,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.【解答】解:A .不是中心对称图形,故本选项不合题意;B .不是中心对称图形,故本选项不合题意;C .是中心对称图形,故本选项符合题意;D .不是中心对称图形,故本选项不合题意.故选:C .【点评】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.3.【分析】根据二次函数变化规律:左加右减,上加下减,进而得出变化后解析式. 【解答】解:抛物线2y x =向上平移3个单位,∴平移后的解析式为:23y x =+.故选:A .【点评】此题考查了抛物线的平移以及抛物线解析式的性质,熟练记忆平移规律是解题关键.4.【分析】两个点关于原点对称时,它们的坐标符号相反.由此可求点A 关于原点对称的点的坐标. 【解答】解:点(2,3)A ,A ∴点关于原点对称的点为(2,3)−−,故选:D .【点评】本题考查关于原点对称的点的坐标,熟练掌握关于原点对称的点的坐标特点是解题的关键.5.【分析】两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.【解答】解:241x x +=,则24414x x ++=+,即2(2)5x +=,故选:A .【点评】本题主要考查解一元二次方程的方法−−配方法,掌握配方法是解本题的关键.6.【分析】用“−−−”(图中虚线)的上方的黑点个数除以所有黑点的个数即可求得答案.【解答】解:观察“馬”移动一次能够到达的所有位置,即用“●”标记的有8处,位于“−−−”(图中虚线)的上方的有2处,所以“馬”随机移动一次,到达的位置在“−−−”上方的概率是2184=,故选:C .【点评】本题考查概率的求法与运用,一般方法:如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A 出现m 种结果,那么事件A 的概率P (A )m n=,难度适中. 7.【分析】连接OA 、OB ,根据圆周角定理求出AOB ∠,根据切线的性质得到OA PA ⊥,OB PB ⊥,根据四边形内角和等于360︒计算,得到答案.【解答】解:连接OA 、OB ,70ACB ∠=︒,2140AOB ACB ∴∠=∠=︒, PA ,PB 是O 的切线,OA PA ∴⊥,OB PB ⊥,360909014040P ∴∠=︒−︒−︒−︒=︒,故选:D .【点评】本题考查的是切线的性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.8.【分析】根据题意列出函数关系式,即可判断函数的类型.【解答】解:5y t =−,属于一次函数关系,2S t π=,属于二次函数关系,故选:C .【点评】本题考查了函数关系式,根据题意列出函数关系式是解题的关键.二、填空题(每题2分,共16分)9.【分析】直接根据顶点式的特点求顶点坐标.【解答】解:23(1)2y x =−−+是抛物线的顶点式,∴顶点坐标为(1,2).故答案为(1,2).【点评】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在2()y a x h k =−+中,对称轴为x h =,顶点坐标为(,)h k .10.【分析】先把1x =−代入方程,可得关于m 的一元一次方程,解即可.【解答】解:把1x =−代入方程,得2(1)2(1)0m −+⨯−+=,解得1m =.故答案是:1.【点评】本题考查了一元二次方程的解,解题的关键是代入后正确的计算,难度不大.11.【分析】根据二次函数的性质,所写出的函数解析式a 是正数,2c =即可.【解答】解:开口向上,并且与y 轴交于点(0,2)的抛物线的表达式为22y x =+,故答案为:22y x =+(答案不唯一).【点评】本题主要考查二次函数,解题的关键是熟练掌握二次函数的图象和性质.12.【分析】根据频率估计概率即可得出“摸出黑球”的概率.【解答】解:由图可知,随着“摸球游戏”的次数增多,“摸出黑球”的频率逐渐稳定在0.2左右,所以,“摸出黑球”的概率为0.2,故答案为:0.2.【点评】本题主要考查用频率估计概率,需要注意的是试验次数要足够大,次数太少时不能估计概率.13.【分析】利用5月份的参观人数3=月份的参观人数(1⨯+月平均增长率)2,即可得出关于x 的一元二次方程,此题得解.【解答】解:依题意得:210(1)12.1x +=.故答案为:210(1)12.1x +=.【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.14.【分析】由旋转的性质可得DAE BAC ∠=∠,由三角形的内角和定理即可求解.【解答】解:将ABC ∆绕点A 顺时针旋转得到ADE ∆,110DAE BAC ∴∠=∠=︒,40B ∠=︒,1801804011030C B BAC ∴∠=︒−∠−∠=︒−︒−︒=︒,故答案为:30︒.【点评】本题考查了旋转的性质,三角形内角和定理等知识,灵活运用这些性质解决问题是本题的关键.15.【分析】根据正方形性质确定CDE ∆为等腰直角三角形,CE 为直径,根据题意求出正方形外接圆的直径CE ,求出CD ,问题得解.【解答】解:如图,四边形CDEF 为正方形,90D ∴∠=︒,CD DE =,CE ∴为直径,45ECD ∠=︒,由题意得 2.5AB =,2.50.2522CE ∴=−⨯=,CD ∴==.【点评】本题考查了正方形外接圆的性质,等腰直角三角形性质,解题关键是判断出正方形对角线为其外接圆直径.16.【分析】根据“边角边”证明ADE ∆和DCF ∆全等,根据全等三角形对应角相等可得DAE CDF ∠=∠,然后求出90APD ∠=︒,取AD 的中点O ,连接OP ,根据直角三角形斜边上的中线等于斜边的一半可得点P 到AD 的中点的距离不变,再根据两点之间线段最短可得C 、P 、O 三点共线时线段CP 的值最小,然后根据勾股定理列式求出CO ,再求解即可. 【解答】解:四边形ABCD 是正方形,AD CD ∴=,90ADE DCF ∠=∠=︒,在ADE ∆和DCF ∆中,AD CD ADE BCD DE CF =⎧⎪∠=∠⎨⎪=⎩,()ADE DCF SAS ∴∆≅∆,DAE CDF ∴∠=∠,90CDF ADF ADC ∠+∠=∠=︒,90ADF DAE ∴∠+∠=︒,90APD ∴∠=︒,取AD 的中点O ,连接OP ,则112122OP AD ==⨯=(不变), 根据两点之间线段最短得C 、P 、O 三点共线时线段CP 的值最小,在Rt COD ∆中,根据勾股定理得,CO ==,所以,1CP CO OP =−=−.故答案为:90︒1−.【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,确定出点P 到AD 的中点的距离是定值是解题的关键.三、解答题(共68分,17-22题,每题5分,23-26题,每题6分,27-28题,每题7分)17.【分析】利用因式分解法解方程.【解答】解:(4)(2)0x x −+=,40x −=或20x +=,所以14x =,22x =−.【点评】本题考查了解一元二次方程−因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.18.【分析】先求出OM 的值,再根据垂径定理求出AM BM =,再根据勾股定理求出AM 即可. 【解答】解:设3OM x =,2MC x =,O 的半径为10, 3210x x ∴+=,解得:2x =, 即6OM =, 连接OA ,OC AB ⊥,OC 过圆心O ,AM BM ∴=,90AMO ∠=︒,由勾股定理得:8BM AM ====, 8816AB ∴=+=.【点评】本题考查了勾股定理和垂径定理,能熟记垂直于弦的直径平分这条弦是解此题的关键. 19.【分析】(1)根据题干要求的步骤依次求解即可; (2)根据圆周角定理求解即可. 【解答】解:(1)如图所示:(2)证明:连接MA ,MB .MA MB =,OA OB =,MO ∴是AB 的垂直平分线.又直线MO 交O 于点C , AC BC ∴=.AB 是直径,90ACB ∴∠=︒(直径所对的圆周角是直角), ABC ∴∆是等腰直角三角形.故答案为:BC 、90︒,直径所对的圆周角是直角.【点评】本题主要考查作图—复杂作图,解题的关键是掌握线段垂直平分线的尺规作图和圆周角定理. 20.【分析】(1)通过待定系数法求解.(2)求出抛物线与x 轴交点坐标,通过抛物线开口向上求解.【解答】解:(1)将(0,3)A −,(1,0)B 代入22y ax x c =++得302c a c −=⎧⎨=++⎩,解得13a c =⎧⎨=−⎩,223y x x ∴=+−.(2)令2230x x +−=, 解得3x =−或1x =, ∴抛物线经过(3,0)−,(1,0),抛物线开口向上, 0y ∴<时,31x −<<.【点评】本题考查二次函数的性质,解题关键是掌握待定系数法求函数解析式,掌握二次函数与方程及不等式的关系.21.【分析】(1)将点A 、B 分别绕点O 顺时针旋转90︒得到其对应点,再与点O 首尾顺次连接即可; (2)根据弧长公式求解即可.【解答】解:(1)如图所示,△OA B ''即为所求.点A '的坐标为(0,4)−;(2)由图知,90AOA ∠'=︒,5OB ==, ∴点B 在旋转过程中所走过的路径长90551802BB ππ⨯'==. 【点评】本题主要考查作图—旋转变换,解题的关键是掌握旋转变换的定义与性质及弧长公式. 22.【分析】(1)根据随机事件、不可能事件及必然事件的概念求解即可;(2)画树状图,共有12种等可能的结果,其中A ,B 两名志愿者同时被选中的结果有2种,再由概率公式求解即可.【解答】解:(1)“A 志愿者被选中”是随机事件,故答案为:随机; (2)画树状图如下:共有12种等可能的结果,其中A ,B 两名志愿者同时被选中的结果有2种,A ∴,B 两名志愿者同时被选中的概率为21126=. 【点评】此题考查的是树状图法求概率以及随机事件的概念.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;解题时要注意此题是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.23.【分析】(1)根据根的判别式:△222[(4)]16816(4)0k k k k k =−+−=−+=−,即可得到结论;(2)利用分解因式法解一元二次方程,可得出14x =、2x k =,根据方程有一根小于2,即可得出关于k 的一元一次不等式,解之即可得出k 的取值范围.【解答】(1)证明:△222[(4)]16816(4)0k k k k k =−+−=−+=−, ∴无论k 为任何实数时,此方程总有两个实数根;(2)解:2(4)40x k x k −++=,(4)()0x x k ∴−−=, 14x ∴=,2x k =.方程有一根小于2, 2k ∴<,k ∴的取值范围为2k <.【点评】本题考查了根的判别式、因式分解法解一元二次方程以及解一元一次不等式,解题的关键是:(1)牢记“当△0时,方程有两个实数根”;(2)利用因式分解法解一元二次方程结合方程一根小于2,找出关于k 的一元一次不等式.24.【分析】(1)根据矩形的面积公式写出函数解析即可; (2)根据函数的性质求最值即可.【解答】解:(1)由题意得:2(402)240y x x x x =−=−+, 040225x <−, ∴15202x <, y ∴与x 之间的函数关系式为215240(20)2y x x x =−+<;(2)由(1)知,222402(10)200y x x x =−+=−−+, 20−<,15202x <,∴当10x =时,y 有最大值,最大值为200,答:当10x =时,小花园的面积最大,最大面积是2200m .【点评】本题考查的是二次函数的实际应用.关键是根据函数的性质求最值.25.【分析】(1)根据等腰三角形的性质得到C OAC ∠=∠,BPA BAP ∠=∠,求得CPO BAP ∠=∠,推出90BAO ∠=︒,根据切线判定定理得到AB 是O 的切线;(2)根据勾股定理得到2OP ==,设BA BP x ==,根据勾股定理即可得到结论. 【解答】(1)证明:OA OC =, C OAC ∴∠=∠,PB BA =, BPA BAP ∴∠=∠,CPO BPA ∠=∠, CPO BAP ∴∠=∠, OP OC ⊥,90COP ∴∠=︒, 90C CPO ∴∠+∠=︒,90CAO BAP ∴∠+∠=︒,即90BAO ∠=︒, OA 是O 的半径,AB ∴是O 的切线;(2)解:90COP ∠=︒,4OC =,PC =,2OP ∴===,设BA BP x ==, 90BAO ∠=︒,222AB AO OB ∴+=,2224(2)x x ∴+=+, 3x ∴=,∴线段AB 的长为3.【点评】本题考查了切线的判定和性质,勾股定理,等腰三角形的性质,熟练掌握切线的判定定理是解题的关键. 26.【分析】(1)把点(1,0)代入2y x bx =−+求得b 的值,即可根据对称轴公式求得答案; (2)①分类讨论b 的正负情况,根据0mn <可得对称轴在12x =与直线1x =之间;②根据各点到对称轴的距离判断【解答】解:(1)若0m =,则点(1,0)在抛物线2y x bx =−+上, 01b ∴=−+,解得1b =,∴抛物线的对称轴为直线112(1)22b x =−=−=⨯−−;(2)①2y x bx =−+,∴抛物线开口向下且经过原点,当0b =时,抛物线顶点为原点,0x >时y 随x 增大而减小,0m n >>不满足题意, 当0b <时,抛物线对称轴在y 轴左侧,同理,0n m >>不满足题意, 当0b >时,抛物线对称轴在y 轴右侧,1x =时0m >,2x =时0n <, 即抛物线和x 轴的2个交点,一个为(0,0),另外一个在1和2之间, ∴抛物线对称轴在直线12x =与直线1x =之间, 即112t <<; ②点1(1,)y −与对称轴距离3(1)22t <−−<, 点3(2,2)y 与对称轴距离13122t <−<,点3(3,)y 与对称轴距离5232t <−< 312y y y ∴<<.【点评】本题考查二次函数的性质,二次函数图象上点的坐标特征,解题关键是熟练掌握待定系数法求函数解析式及根据数形结合求解.27.【分析】(1)利用SAS 证明ABP ACP '∆≅∆,即可得出答案;(2)①由三角形内角和定理知8618060BPC ∠+∠=︒−∠=︒,再利用角度之间的转化对P BP '∠进行转化,475608606608P BP '∠=∠+∠=∠+︒−∠=︒−∠+︒−∠,从而解决问题;②延长PM 到N ,使PM MN =,连接BN ,CN ,得出四边形PBNC 为平行四边形,则//BN CP 且BN CP =,再利用SAS 证明△P BP NBP '≅∆,得2PP PN PM '==. 【解答】解:(1)BP CP '=, 证明:ABC ∆是等边三角形, AB AC ∴=,60BAC ∠=︒, 2360∴∠+∠=︒将线段AP 绕点A 顺时针旋转60︒得到AP ',AP AP '∴=,60PAP '∠=︒,1260∴∠+∠=︒, 13∴∠=∠,()ABP ACP SAS '∴∆≅∆,(2)①当120BPC ∠=︒时, 则8618060BPC ∠+∠=︒−∠=︒, ABP ACP '∆≅∆, 45∴∠=∠, 47P BP '∴∠=∠+∠5608=∠+︒−∠ 606608=︒−∠+︒−∠120(68)=︒−∠+∠ 12060=︒−︒ 60=︒,故答案为:60︒;②2AP PM =,理由如下:延长PM 到N ,使PM MN =,连接BN ,CN ,M 为BC 的中点,BM CM ∴=,∴四边形PBNC 为平行四边形, //BN CP ∴且BN CP =, BN BP '∴=,96∠=∠,又8660∠+∠=︒, 8960∴∠+∠=︒, 60PBN P BP '∴∠=︒=∠,又BP BP =,P B BN '=,∴△()P BP NBP SAS '≅∆, 2PP PN PM '∴==,又APP '∆为正三角形,PP AP '∴=, 2AP PM ∴=.【点评】本题是几何变换综合题,主要考查了旋转的性质,等边三角形的判定与性质,全等三角形的判定与性质,平行四边形的判定与性质等知识,利用倍长中线构造平行四边形是解题的关键.28.【分析】(1)①分别画出线段11A B ,22A B ,33A B 关于直线2y x =+对称线段,如图,即可求解;②从图象性质可知,直线y x m =−+与x 轴的夹角为45︒,而线段11A B ⊥直线y x m =−+,线段11A B 关于直线y x m =−+对称线段还在直线11A B 上,显然不可能是O 的弦;线段33A B =O 的最长的弦为2,得线段33A B的对称线段不可能是O 的弦,而线段22//A B 直线y x m =−+,线段22A B =,∴线段22A B 的对称线段线段22A B ''线段22A B ,且线段22A B ''=O 上,有两种可能,画出对应图形即可求解;(2)先表示出OC =,b 最大时就是OC 最大,b 最小时就是CO 长最小,根据线段AB 关于直线3y x b =−+对称线段A B ''在O 上,得3A C AC ''==,再由三角形三边关系得A C OA OC A C OA '−''+',得当A '为(1,0)−时,如图3,OC 最小,此时C 点坐标为(2,0);当A '为(1,0)时,如图3,OC 最大,此时C 点坐标为(4,0),分两种情形分别求解.【解答】解:(1)①分别画出线段11A B ,22A B ,33A B 关于直线2y x =+对称线段,如图, 发现线段11A B 的对称线段是O 的弦,∴线段11A B ,22A B ,33A B 中,O 的关于直线2y x =+对称的“关联线段”是11A B ,故答案为:11A B ;②从图象性质可知,直线y x m =−+与x 轴的夹角为45︒, ∴线段11A B ⊥直线y x m =−+,∴线段11A B 关于直线y x m =−+对称线段还在直线11A B 上,显然不可能是O 的弦,线段33A B =O 的最长的弦为2, ∴线段33A B 的对称线段不可能是O 的弦,线段22A B 是O 的关于直线y x m =−+对称的“关联线段”,而线段22//A B 直线y x m =−+,线段22A B =∴线段22A B 的对称线段线段22A B ''线段22A B ,且线段22A B ''=平移这条线段,使其在O 上,有两种可能, 第一种情况:2A '、2B '的坐标分别为(0,1)、(1,0), 此时3m =;第二种情况:2A '、2B '的坐标分别为(1,0)−、(0,1)−, 此时2m =, 故答案为:3或2;(2)直线(0)y b b =+>交x 轴于点C ,当0y =时,0y b =+=,解得:x =,OC ∴=,b 最大时就是OC 最大,b 最小时就是CO 长最小,线段AB 是O 的关于直线(0)y x b b =+>对称的“关联线段”,∴线段AB 关于直线y x b =+对称线段A B ''在O 上, 3A C AC ∴''==,在△A CO '中,A C OA OC A C OA '−''+',∴当A '为(1,0)−时,如图3,OC 最小,此时C 点坐标为(2,0),将点C 代入直线3y x b =−+中,20b +=,解得:b过点B '作B D A C '⊥'于点D , 1A B A O B O ''='='=, 60B A D ∴∠''=︒,12A D ∴'=,B D '=15322CD ∴=−=,在Rt △B DC '中,B C '==∴当A '为(1,0)时,如图3,OC 最大,此时C 点坐标为(4,0),将点C 代入直线y b =+中,403b ⨯+=,解得:b过点B '作B D A C '⊥'于点D , 1A B A O B O ''='='=, 60B A D ∴∠''=︒,12A D ∴'=,2B D '=,17322CD ∴=+=,在Rt △B DC '中,B C '==b ∴BC =BC =【点评】本题考查了以圆为背景的阅读理解题,勾股定理,三角形三边关系,解决问题的关键是找出不同情境下的“关联线段”和阅读理解能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E DCBA东城区2011—2012学年第一学期期末统一检测初三数学试题 2012.1学校 班级 姓名 考号一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.抛物线221y x =-+()的顶点坐标是A .(2,1)B .(-2,-1)C .(-2,1)D .(2,-1)2.下列图形中,是中心对称图形的是A B C D 3.如图,在△ABC 中,若DE ∥BC ,AD =5,BD =10,DE =4, 则BC 的值为A.8B.9C.10D.12 4.下列事件中,属于必然事件的是A. 随机抛一枚硬币,落地后国徽的一面一定朝上B. 打开电视任选一频道,正在播放北京新闻Q PNMOCBAA OCABC. 一个袋中只装有5个黑球,从中摸出一个球是黑球D. 某种彩票的中奖率是10%,则购买该种彩票100张一定中奖 5. 如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°, 则∠C 的度数为A .116°B .58°C .42°D .32°6.已知x =1是方程x 2+bx +b -3=0的一个根,那么此方程的另一个根为A. -2B. -1C. 1D. 2 7. 如图,直径AB 为6的半圆O ,绕A 点逆时针旋转60°,此时点B到了点B ',则图中阴影部分的面积为A .6πB .5πC .4πD .3π8. 已知二次函数2y ax bx c =++的图象如图所示,那么一次函数24y bx b ac =+-与反比例函数2c by x-=在同一坐标系内的图象大致为二、填空题(本题共16分,每小题4分)9.已知关于x 的一元二次方程有一个根为0.请你写出一个符合条件的一元二次方程是 . 10. 将抛物线2y x =-向左平移2个单位,再向上平移1个单位后,得到的抛物线的解析式为 .11.如图,⊙O 是△ABC 的外接圆,∠BAC=60°,若⊙O 的半径OC 为2,则弦BC 的长为 .12.如图,在Rt △ABC 中,∠ACB =90°,∠ABC =30°,直角∠MON 的顶点O 在AB 上, OM 、ON 分别交CA 、CB 于点P 、Q ,∠MON 绕点O任意旋转.当12OA OB =DCBA 时,OPOQ的值为;当1OAOB n=时,OPOQ的值为 .(用含n的式子表示)三、解答题(本题共30分,每小题5分)13.解方程:.14.已知排水管的截面为如图所示的圆O,半径为10,圆心O到水面的距离是6,求水面宽AB.15D在边AB上,满足且∠ACD =∠ABC,若AC = 2,AD = 1,求DB16.在平面直角坐标系xoy中,已知ABC△三个顶点的坐标分别为()()()1,2,3,4,2,9.A B C---⑴画出ABC△;⑵画出ABC△绕点A顺时针旋转90后得到的11AB C△,并求出1CC的长..22410x x--=17. 2(1) 求该二次函数的解析式;(2) 当x为何值时,y有最小值,最小值是多少?(3) 若A(m,y1),B(m+2, y2)两点都在该函数的图象上,计算当m取何值时,12?y y18.为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给出的数据求树高ED.四、解答题(本题共20分,每小题5分)19.如图,邻边不等..的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,请你计算AB的长度(可利用的围墙长度超过6m).20. 如图,已知直线PA 交⊙O 于A 、B 两点,AE 是⊙O 的直径,点C 为⊙O 上一点,且AC平分∠PAE ,过C 作CD PA ⊥,垂足为D .(1) 求证:CD 为⊙O 的切线;(2) 若CD =2AD ,⊙O 的直径为10,求线段AC 的长.21. 在一个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5 . (1)求口袋中红球的个数;(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球不放回,再摸出一个.请用画树状图的方法求甲摸到两个球且得2分的概率.22.李经理在某地以10元/千克的批发价收购了2 000千克核桃,并借一仓库储存.在存放过程中,平均每天有6千克的核桃损耗掉,而且仓库允许存放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
(1)存放x 天后,将这批核桃一次性出售,如果这批核桃的销售总金额为y 元,试求出y 与x 之间的函数关系式;(2)如果仓库存放这批核桃每天需要支出各种费用合计340元,李经理要想获得利润22 500元,需将这批核桃存放多少天后出售?(利润=销售总金额-收购成本-各种费用)五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.已知:关于x 的方程2(1)(1)20a x a x --++=.(1) 当a 取何值时,方程2(1)(1)20a x a x --++=有两个不相等的实数根; (2) 当整数a 取何值时,方程2(1)(1)20a x a x --++=的根都是正整数. 24.已知△ABC 和△ADE 是等腰直角三角形,∠ACB =∠ADE =90°,点F 为BE 中点,连结DF 、CF .图1FE DCBA图2ABCDE F图3ABCDEF(1)如图1, 当点D 在AB 上,点E 在AC 上,请直接写出此时线段DF 、CF 的数量关系和位置关系(不用证明);(2)如图2,在(1)的条件下将△ADE 绕点A 顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断; (3)如图3,在(1)的条件下将△ADE 绕点A 顺时针旋转90°时,若AD =1,AC=求此时线段CF 的长(直接写出结果).25.在平面直角坐标系xOy 中,抛物线235y mx x m =+++与x 轴交于A 、B 两点(点A在点B 的左侧),与y 轴交于点C (0 , 4),D 为OC 的中点. (1)求m 的值;(2)抛物线的对称轴与 x 轴交于点E ,在直线AD 上是否存在点F ,使得以点A 、B 、F 为顶点的三角形与ADE ∆ 相似?若存在,请求出点F 的坐标,若不存在,请说明理由;(3)在抛物线的对称轴上是否存在点G ,使△GBC 中BC 求出点G 的坐标;若不存在,请说明理由.6.东城区2011-2012学年度第一学期期末统一测试参考答案初三数学一、 选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分)13.2,4,1,a b c ==-=-解:224(4)42(1)24.2b ac ∴∆=-=--⨯⨯-=分3x =则分=. 1222522x x ==分14. 解:过O 点作OC ⊥AB ,连结OB .………1分∴ 2AB BC =.…………2分在Rt △OBC 中,222BC OC OB +=. ∵ 10OB =,6OC =,∴ 可求出8BC =.………4分 ∴ 16AB =.DCBA 答:水面宽AB 为16.…………5分 15.解:在△ACD 和△ABC 中,∵ ∠ACD =∠ABC ,∠A 是公共角,∴ △ACD ∽△ABC . ………2分∴ AD ACAC AB=.……3分 ∵ AC = 2,AD = 1, ∴ 4AB =.………4分∴ DB = AB - AD = 3.………5分16.解:⑴如图所示,ABC △即为所求.…1分⑵如图所示,11AB C △即为所求. …3分分5101 =CC17.解:(1)由表格可知,二次函数图像y =x 2+bx +c 图象经过点(0,3)和点(1 , 0),可求出,b =-4, c =3 .∴ 243y x x =-+. ………2分 (2)当x =2时,y 有最小值,最小值为-1 . ………4分 (3)将A (m ,y 1),B (m +2, y 2)两点分别代入243y x x =-+,则有 ,3421+-=m m y 3)2(4)2(22++-+=m m y ,1,21<>m y y 可得由. ……5分18.解:过点A 作AG ⊥DE 于点G ,交CF 于点H .由题意可得 四边形ABCH 、ABDG 、CDGH 都是矩形,AB ∥CF ∥DE .∴ △AHF ∽△AGE . ………2分∴AH HFAG GE=. 由题意可得16AH BC AG BD ====, , 3.1 1.6 1.5FH FC HC FC AB =-=-=-=. ∴1 1.56GE=. ∴ GE = 9 . …………4分∴ 9 1.610.6ED GE DG GE AB =+=+=+=. 答:树高ED 为10.6米. …………5分四、解答题(本题共20分,每小题5分)19.解:设x AB =m ,则(62)BC x =- m . ………1分 根据题意可得,4)26(=-x x . ………2分 解得 舍)(2,121==x x ………4分答:AB 的长为1 m . …………5分 20.(1)证明:连接OC . ……………………………………1分∵ 点C 在⊙O 上,OA =OC ,∴ .OCA OAC ∠=∠ ∵ CD PA ⊥,∴ 90CDA ∠=,有90CAD DCA ∠+∠=.∵ AC 平分∠PAE ,∴ .DAC CAO ∠=∠∴ .DAC OCA ∠=∠ ……………………………………1分 ∴ 90.DCO DCA ACO DCA DAC ∠=∠+∠=∠+∠=∵ 点C 在⊙O 上,OC 为⊙O 的半径,∴ CD 为⊙O 的切线. ……………………………………2分 (2)解:连结CE .∵ AE 是⊙O 的直径,∴ 90ACE ∠=.∴ ADC ACE ∠=∠. 又∵DAC CAE ∠=∠ ,∴ ADC △∽ACE △. ………………3分 ∴AD CDAC CE=.又∵ CD =2AD ,∴ CE =2AC . ……………………………………4分 设AC =x .在Rt ACE △中,由勾股定理知222.AC CE AE += ∵ AE =10,∴ ()222100.x x +=解得x =∴AC = . ……………………………………5分 21.解:(1)设袋中有红球x 个,则有20.52+1+x= .解得 x =1.所以,袋中的红球有1个. ………1分 (2)画树状图如下:…………3分由上述树状图可知:所有可能出现的结果共有12种.其中摸出两个得2分的有4种. ∴ P (从中摸出两个得2分)=41123=. …………5分 22.解:(1)由题意得y 与x 之间的函数关系式为y =()()x x 620005.010-+=2000094032++-x x (1≤x ≤60,且x 为整数). ………2分(2)由题意得:2000094032++-x x -10×2000-340x =22500 . ………4分2 13 2 1 3 1 1 2 3 3 2 开始白 白 红 黄白 红 黄 第二次 第一次 得分白 白 黄白 红 黄白 白 红解方程 得:1x =50 ,2x =150(不合题意,舍去).答:李经理想获得利润22500元需将这批核桃存放50天后出售. ………5分 23.解:(1)∵ 方程2(1)(1)20a x a x --++=有两个不相等的实数根, ∴ ⎩⎨⎧>∆≠-.0,01a即 []221,(1)4(1)2(3)0.a a a a ≠⎧⎪⎨∆=----⋅=->⎪⎩ ∴ 1≠a 且3≠a . ………2分(2)① 当10a -=时,即1a =时,原方程变为220x -+=.方程的解为 1x =; …………3分② 当10a -≠时,原方程为一元二次方程2(1)(1)20a x a x --++= .[]2224(1)4(1)2(3)0b ac a a a ∆=-=-+--=-≥.(1)(3)2(1)a a x a -±-=-1221,.1x x a ==- ………4分 ∵ 方程2(1)(1)20a x a x --++=都是正整数根. ∴ 只需21a -为正整数. ∴ 当11a -=时,即2a =时,22x =;当12a -=时,即3a =时,21x =; ………6分 ∴ a 取1,2,3时,方程2(1)(1)20a x a x --++=的根都是正整数.………7分24. 解:(1)线段DF 、CF 之间的数量和位置关系分别是相等和垂直.…………1分(2)(1)中的结论仍然成立.证明: 如图,此时点D 落在AC 上,延长DF 交BC 于点G . (2)BFG分………2分∵ 90ADE ACB ∠=∠=︒, ∴ DE ∥BC .∴ ,DEF GBF EDF BGF ∠=∠∠=∠.又∵ F 为BE 中点, ∴ EF=BF .∴ △DEF ≌△GBF . ………3分 ∴ DE =GB ,DF =GF . 又∵ AD =DE ,AC =BC , ∴ DC =GC .∵ 90ACB ∠=︒,∴ DF = CF , DF ⊥CF . …………5分(3) 线段C F …………7分 25.解:(1)抛物线m m mx y +++=532与y 轴交于点C (0 , 4),∴ 5 4.m +=∴ 1.m =- ………1分 (2)抛物线的解析式为 234y x x =-++.可求抛物线与x 轴的交点A (-1,0),B (4,0). 可求点E 的坐标3(,0)2.由图知,点F 在x 轴下方的直线AD 上时,ABF ∆是钝角三角形,不可能与ADE ∆相似,所以点F 一定在x 轴上方.此时ABF ∆与ADE ∆有一个公共角,两个三角形相似存在两种情况: ① 当AB AEAF AD=时,由于E 为AB 的中点,此时D 为AF 的中点, 可求 F 点坐标为(1,4). ………3分② 当AB AD AF AE =时,5,52AF AF =解得过F 点作FH ⊥x 轴,垂足为H .可求 F 的坐标为352(,). ……………4分(3) 在抛物线的对称轴上存在符合题意的点G .由题意,可知△OBC 为等腰直角三角形,直线BC 为 4.y x =-+ 可求与直线BC y =-x +9或y =-x -1. …………………6分∴ 点G 在直线y =-x +9或y =-x -1上. ∵ 抛物线的对称轴是直线23=x , ∴ ⎪⎩⎪⎨⎧+-==.9,23x y x 解得..215,23⎪⎪⎩⎪⎪⎨⎧==y x 或⎪⎩⎪⎨⎧--==.1,23x y x 解得⎪⎪⎩⎪⎪⎨⎧-==.25,23y x ∴ 点G 的坐标为31535(,)-2222或(,). ………8分。
