空间几何体的表面积与体积修改知识课件
合集下载
二、空间几何体的表面积与体积复习课件

考 点 探 究 • 挑 战 高 考
答案: 3
考 向 瞭 望 • 把 脉 高 考
第8章 立体几何
双 基 研 习 • 面 对 高 考
5.(2009年高考上海卷)若等腰直角三角形的直 角边长为2,则以一直角边所在的直线为轴旋 转一周所成的几何体体积是________.
8π 答案: 3
考 点 探 究 • 挑 战 高 考
考 点 探 究 • 挑 战 高 考
考 向 瞭 望 • 把 脉 高 考
第8章 立体几何
双 基 研 习 • 面 对 高 考
2 ∴AP=AB= 2,EG= . 2 1 ∴S△ABC= AB· BC 2 1 = × 2×2= 2, 2 1 ∴VEABC= S△ ABC· EG 3 1 2 1 = × 2× = . 3 2 3
考 向 瞭 望 • 把 脉 高 考
第8章 立体几何
双 基 研 习 • 面 对 高 考
解:如图所示,只有当圆柱的底面圆为直三棱 柱的底面三角形的内切圆时,圆柱的体积最大, 削去部分体积才能最小,设此时圆柱的底面半 径为R,圆柱的高即为直三棱柱的高.
考 点 探 究 • 挑 战 高 考
考 向 瞭 望 • 把 脉 高 考
考 向 瞭 望 • 把 脉 高 考
第8章 立体几何
考点探究•挑战高考
考点突破 几何体的表面积 求解有关多面体表面积的问题,关键是找到其特征 几何图形,如棱柱中的矩形,棱台中的直角梯形, 棱锥中的直角三角形,它们是联系高与斜高、边长 等几何元素间的桥梁,从而架起求侧面积公式中的 未知量与条件中已知几何元素间的联系;求球的表 面积关键是求其半径;旋转体的侧面积就是它们侧 面展开图的面积.
双 基 研 习 • 面 对 高 考
考 点 探 究 • 挑 战 高 考
2023高考数学基础知识综合复习第18讲简单几何体的表面积与体积 课件(共24张PPT)

分叫作棱台
(2)旋转体的形成
几何体
旋转图形
圆柱
矩形
旋转轴
矩形一边所在的直线
圆锥
直角三角形
一直角边所在的直线
圆台
直角梯形或等腰梯形
球
半圆或圆
直角腰所在的直线或等腰梯形
上下底中点连线所在的直线
直径所在的直线
2.空间几何体的直观图
空间几何体的直观图常用斜二测画法来画,其画法步骤为:
①画轴:在平面图形上取互相垂直的x轴和y轴,作出与之对应的x'轴
3
4
3 = .故选 D.
考点一
考点二
考点三
本题考查四面体的体积的最大值的求法,涉及空间中线线、线面、
面面间的位置关系等基础知识,考查运算求解能力,属于难题.处理
此类问题时,往往先去找到不变的量,再根据题中的所给条件的变
化规律找到最值,从而得到体积的最值.
和y'轴,使得它们正方向的夹角为45°(或135°);
②画线(取长度):平面图形中与x轴平行(或重合)的线段画出与x'轴
平行(或重合)的线段,且长度不变,平面图形中与y轴平行(或重合)的
线段画出与y'轴平行(或重合)的线段,且长度为原来长度的一半;
③连线(去辅助线):连接有关线段,擦去作图过程中的辅助线.
径,从而进一步求解.
考点一
考点二
考点三
◆角度3.体积最值问题
例5(1)(2019年1月浙江学考)如图,线段AB是圆的直径,圆内一条动
弦CD与AB交于点M,且MB=2AM=2,现将半圆沿直径AB翻折,则三
棱锥C-ABD体积的最大值是(
)
2
3
1
3
A.
(2)旋转体的形成
几何体
旋转图形
圆柱
矩形
旋转轴
矩形一边所在的直线
圆锥
直角三角形
一直角边所在的直线
圆台
直角梯形或等腰梯形
球
半圆或圆
直角腰所在的直线或等腰梯形
上下底中点连线所在的直线
直径所在的直线
2.空间几何体的直观图
空间几何体的直观图常用斜二测画法来画,其画法步骤为:
①画轴:在平面图形上取互相垂直的x轴和y轴,作出与之对应的x'轴
3
4
3 = .故选 D.
考点一
考点二
考点三
本题考查四面体的体积的最大值的求法,涉及空间中线线、线面、
面面间的位置关系等基础知识,考查运算求解能力,属于难题.处理
此类问题时,往往先去找到不变的量,再根据题中的所给条件的变
化规律找到最值,从而得到体积的最值.
和y'轴,使得它们正方向的夹角为45°(或135°);
②画线(取长度):平面图形中与x轴平行(或重合)的线段画出与x'轴
平行(或重合)的线段,且长度不变,平面图形中与y轴平行(或重合)的
线段画出与y'轴平行(或重合)的线段,且长度为原来长度的一半;
③连线(去辅助线):连接有关线段,擦去作图过程中的辅助线.
径,从而进一步求解.
考点一
考点二
考点三
◆角度3.体积最值问题
例5(1)(2019年1月浙江学考)如图,线段AB是圆的直径,圆内一条动
弦CD与AB交于点M,且MB=2AM=2,现将半圆沿直径AB翻折,则三
棱锥C-ABD体积的最大值是(
)
2
3
1
3
A.
苏教版高三数学复习课件7.2 空间几何体的表面积和体积

S直棱柱侧= ch 直棱柱的侧面展开图是矩形
正棱锥
底面是正多边形, 并且顶点在底面的 正投影是底面中心 的棱锥叫做 正棱锥
S正棱锥侧 正棱锥的侧面展开图是一些全 等的等腰三角形
=
正棱台
正棱锥被平行于底 面的平面所截,截 面和底面之间的部 分叫做 正棱台
S正棱台侧
正n棱台的侧面展开图是n个全 等的等腰梯形.
1.多面体的展开图:(1)直棱柱的侧面展开图是矩形.(2)正棱锥的侧
面展开图是由一些全等的等腰三角形拼成的,底面是正多边形.(3)正
棱台的侧面展开图是由一些全等的等腰梯形拼成的,底面是正多边 形. 2.旋转体的展开图:(1)圆柱的侧面展开图是矩形,矩形的长是底面 圆周长,宽是圆柱的母线长.(2)圆锥的侧面展开图是扇形,扇形的半 径是圆锥的母线长,弧长是圆锥的底面周长.(3)圆台的侧面展开图是 扇环,扇环的上、下弧长分别为圆台的上、下底面周长.
1.(2010·栟茶中学学情分析)正方体中,连接相邻两个面的中心的连 线可以构成一个美丽的几何体.若正方体的边长为1,则这个美丽的 几何体的体积为________.
答案:
2.圆柱的侧面展开图是边长为 6π和4π的矩形,则圆柱的全面积为 ________. 答案:6π(4π+3)或8π(3π+1)
(其中R为球半径).
3.几何体的体积公式 (1)柱体的体积公式V= (2)锥体的体积公式V= (3)台体的体积公式V= 面面积,h为高). (4)球的体积公式V= (其中R为球半径).
Sh
(其中S为底面面积,h为高). (其中S为底面面积,h为高). (其中S′,S为上、下底
探究:对于不规则的几何体应如何求其体积? 提示:对于求一些不规则几何体的体积常用割补的方法,转化成已知 体积 公式的几何体进行解决.虽说在某些情况下,割补法优于整体法,但
简单几何体的表面积和体积(1)课件-高一下学期数学人教A版(2019)必修第二册

因为棱锥1、2的底面积相等,即:SAAB SABB 高也相等,即:点C到平面 所以棱锥1、2的体积相等.
知识点一 棱柱、棱锥、棱台的体积
问题4:由祖暅原理可知,底面面积相等,高相等的两个棱锥,体 积相等.那么如果棱锥的底面积是S,高为h,则棱锥的体积公式 是什么?
因为棱锥2、3的底面积相等,即: SBBC SBCC 高也相等,即:点 到平面B 所以棱锥2、3的体积相等.
分析:正四棱台的上底面和下底面均为正方形,侧面是由四个等腰梯形组成的.
小结与反思
要计算棱台的体积关键是要弄清楚棱台的五个基本量(上、下 底面边长、高、斜高、侧棱),然后将基本量转化到直角三角形中 求解,最后再代入体积公式求出体积.
课堂检测
5-1、(金太阳P1141题)已知高为3的三棱柱ABC-A1B1C1的底面边长为1 的正三角形,如图所示,则三棱锥B1-ABC求它的体积.
多面体的表面积就是围成多面体的各个面的面积之和. 棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
知识点一 棱柱、棱锥、棱台的表面积
问题2:在初中已经学过了正方体和长方体的表面积,你知道正方体 和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
空间问题
平面图形面积 平面问题
知识点一 棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧 面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面 积和底面面积之和.
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯 形的面积问题.
2
PART TWO
例题精讲
例1.(教材P114)四面体P-ABC的各棱长均为a,求它的表面积 .
=
知识点一 棱柱、棱锥、棱台的体积
问题4:由祖暅原理可知,底面面积相等,高相等的两个棱锥,体 积相等.那么如果棱锥的底面积是S,高为h,则棱锥的体积公式 是什么?
因为棱锥2、3的底面积相等,即: SBBC SBCC 高也相等,即:点 到平面B 所以棱锥2、3的体积相等.
分析:正四棱台的上底面和下底面均为正方形,侧面是由四个等腰梯形组成的.
小结与反思
要计算棱台的体积关键是要弄清楚棱台的五个基本量(上、下 底面边长、高、斜高、侧棱),然后将基本量转化到直角三角形中 求解,最后再代入体积公式求出体积.
课堂检测
5-1、(金太阳P1141题)已知高为3的三棱柱ABC-A1B1C1的底面边长为1 的正三角形,如图所示,则三棱锥B1-ABC求它的体积.
多面体的表面积就是围成多面体的各个面的面积之和. 棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
知识点一 棱柱、棱锥、棱台的表面积
问题2:在初中已经学过了正方体和长方体的表面积,你知道正方体 和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
空间问题
平面图形面积 平面问题
知识点一 棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧 面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面 积和底面面积之和.
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯 形的面积问题.
2
PART TWO
例题精讲
例1.(教材P114)四面体P-ABC的各棱长均为a,求它的表面积 .
=
高一数学 空间几何体的表面积与体积 ppt

15 cm
15 cm
例2.如图,一个圆台形花盆盆口直径20cm,盆底直 径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为 了美化花盆的外观,需要涂油漆.已知每平方米用100毫 升油漆,涂100个这样的花盆需要多少油漆(取 3.14, 结果精确到1毫升,可用计算器)? 解:花盆外壁的表面积:
r O
l
O
2 r
圆柱的侧面展开图是矩形
S 2 r 2 rl 2 r ( r l )
2
S r 2 rl r (r l )
2r
l
r
圆锥的侧面展开图是扇形
O
(1)联系圆柱和圆锥的展开图,你能想 象圆台展开图的形状并且画出它吗?
(2)如果圆台的上,下底面半径分别 为 r , r ,母线长为l,你能计算出它 的表面积吗?
S [( 15 2 15 20 1.5 ) 15 15] ( )2 2 2 2 2
20cm
1000(cm 2 ) 0.1( m 2 )
15 cm
15 cm
涂100个花盆需油漆: 0.1 100 100 1000 (毫升) 答:涂100个这样的花盆约需要1000毫升油漆.
圆柱 S 2r 2 rl 柱体、锥体、台体的表面积 圆台S r2 r 2 rl rl 圆锥 S r rl
2
展开图
各面面积之和
作业:
P28. 习题1.3 A组 第1,2题
∵ BC a , SD SB 2 BD 2 a 2 ( )2
S A B D C
SSBC
a 2
3 a 2
1 1 3 3 2 BC SD a a a 2 2 2 4
15 cm
例2.如图,一个圆台形花盆盆口直径20cm,盆底直 径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为 了美化花盆的外观,需要涂油漆.已知每平方米用100毫 升油漆,涂100个这样的花盆需要多少油漆(取 3.14, 结果精确到1毫升,可用计算器)? 解:花盆外壁的表面积:
r O
l
O
2 r
圆柱的侧面展开图是矩形
S 2 r 2 rl 2 r ( r l )
2
S r 2 rl r (r l )
2r
l
r
圆锥的侧面展开图是扇形
O
(1)联系圆柱和圆锥的展开图,你能想 象圆台展开图的形状并且画出它吗?
(2)如果圆台的上,下底面半径分别 为 r , r ,母线长为l,你能计算出它 的表面积吗?
S [( 15 2 15 20 1.5 ) 15 15] ( )2 2 2 2 2
20cm
1000(cm 2 ) 0.1( m 2 )
15 cm
15 cm
涂100个花盆需油漆: 0.1 100 100 1000 (毫升) 答:涂100个这样的花盆约需要1000毫升油漆.
圆柱 S 2r 2 rl 柱体、锥体、台体的表面积 圆台S r2 r 2 rl rl 圆锥 S r rl
2
展开图
各面面积之和
作业:
P28. 习题1.3 A组 第1,2题
∵ BC a , SD SB 2 BD 2 a 2 ( )2
S A B D C
SSBC
a 2
3 a 2
1 1 3 3 2 BC SD a a a 2 2 2 4
空间几何体的表面积与体积的复习课课件
2. 所 有 棱 长 为 1 的 正 三 棱 锥 的 全 面 积 3 为 . 解析 3 2 S=4× × = 3. 1 4
3. 如 图 所 示 , 在 棱 长 为 4 的 正 方 体 ABCD—A1B1C1D1 中,P 是 A1B1 1 上一点,且 PB1= A1B1,则多 4 面 体 为
解析
16 3
a,则长方体的体对角线长为 (2a)2+a2+a2= 6a.又长方体外接球的直径 2R 等于长方体的 体对角线,∴2R= 6a.∴S 球=4πR2=6πa2.
题型剖析
题型一 几何体的展开与折叠 例 1 有一根长为 3π cm, 底面半径为 1 cm 的圆 柱形铁管,用一段铁丝在铁管上缠绕 2 圈, 并使铁丝的两个端点落在圆柱的同一母线 的两端,求铁丝的最短长度为多少? 思维启迪: 把圆柱沿这条母线展开,将问题转
P—BCC1B1 的 体 积 .
∵四棱锥 P—BB1C1C 的底面积为 16,
高 PB1=1, 1 16 ∴VP—BB1C1C= × 1= . 16× 3 3
4. 若正方体的棱长为 2,则以该正方体各个 面的中心为顶点的凸多面体的体积为( B ) 2 2 3 2 A. B. C. D. 6 3 3 3
化为平面上两点间的最短距离.
解
把圆柱侧面及缠绕其上的铁丝展开,在平
面上得到矩形 ABCD(如图所示), 由题意知 BC =3π cm,AB=4π cm, A 点 与点 C 分别是铁丝的起、 止 位置,故线段 AC 的长度即 为铁丝的最短长度. AC= AB2+BC2=5π cm, 故铁丝的最短长度为 5π cm.
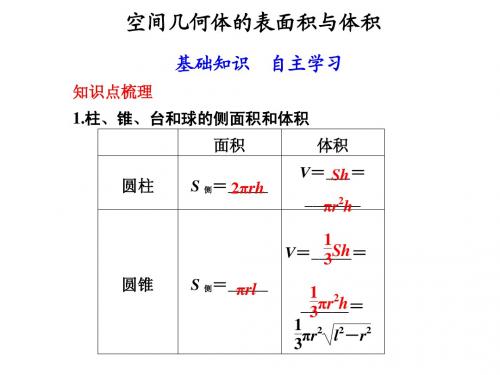
1 V= (S 上+S 下 3 圆台 + S上S下)h= π(r1+r2)l S 侧=________ 1 π(r2+r2+ 3 1 2 r1r2)h 直棱 柱 正棱 锥
