2012年全国中考数学试题分类解析汇编(159套63专题)专题5 分式
2012年全国中考数学试题分类解析汇编专题52:平面几何的综合
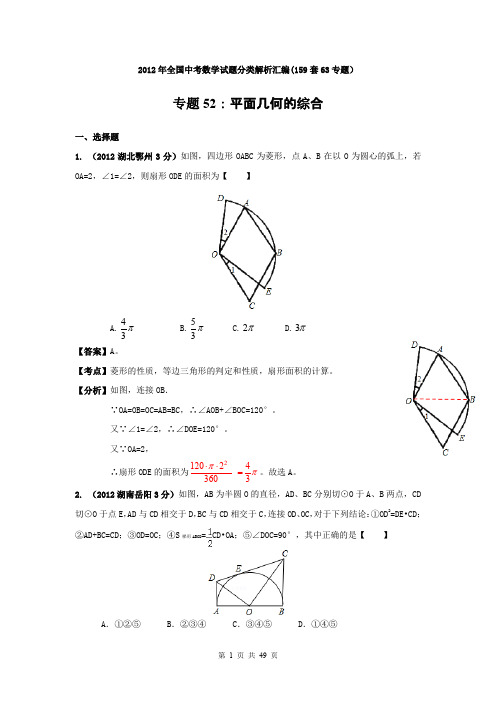
2012年全国中考数学试题分类解析汇编(159套63专题)专题52:平面几何的综合一、选择题1. (2012湖北鄂州3分)如图,四边形OABC 为菱形,点A 、B 在以O 为圆心的弧上,若OA=2,∠1=∠2,则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。
【考点】菱形的性质,等边三角形的判定和性质,扇形面积的计算。
【分析】如图,连接OB .∵OA=OB=OC=AB=BC,∴∠AOB+∠BOC=120°。
又∵∠1=∠2,∴∠DOE=120°。
又∵OA=2,∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。
故选A 。
2. (2012湖南岳阳3分)如图,AB 为半圆O 的直径,AD 、BC 分别切⊙O 于A 、B 两点,CD 切⊙O 于点E ,AD 与CD 相交于D ,BC 与CD 相交于C ,连接OD 、OC ,对于下列结论:①OD 2=DE•CD; ②AD+BC=CD;③OD=OC;④S 梯形ABCD =CD•OA;⑤∠DOC=90°,其中正确的是【 】A .①②⑤ B.②③④ C.③④⑤ D.①④⑤【答案】A 。
【考点】切线的性质,切线长定理,相似三角形的判定与性质。
1052629【分析】如图,连接OE ,∵AD 与圆O 相切,DC 与圆O 相切,BC 与圆O 相切,∴∠DAO=∠DEO=∠OBC=90°,∴DA=DE,CE=CB ,AD∥BC。
∴CD=DE+EC=AD+BC。
结论②正确。
在Rt△ADO 和Rt△EDO 中,OD=OD ,DA=DE ,∴Rt△ADO≌Rt△EDO(HL )∴∠AOD=∠EOD。
同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC。
又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°。
结论⑤正确。
∴∠DOC=∠DEO=90°。
2012年全国中考数学试题分类解析汇编专题50:圆与圆的位置关系

2012年全国中考数学试题分类解析汇编(159套63专题)专题50:圆与圆的位置关系一、选择题1. (2012上海市4分)如果两圆的半径长分别为6和2,圆心距为3,那么这两个圆的位置关系是【】A.外离B.相切C.相交D.内含【答案】D。
【考点】圆与圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
因此,∵两个圆的半径分别为6和2,圆心距为3,6﹣2=4,4>3,即两圆圆心距离小于两圆半径之差,∴这两个圆的位置关系是内含。
故选D。
2. (2012浙江杭州3分)若两圆的半径分别为2cm和6cm,圆心距为4cm,则这两圆的位置关系是【】A.内含B.内切C.外切D.外离【答案】B。
【考点】圆与圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
因此,∵两圆的半径分别为2cm和6cm,圆心距为4cm.则d=6﹣2=4。
∴两圆内切。
故选B。
3. (2012浙江宁波3分)如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a 与b 满足的关系式是【 】A .b= aB .C .D . 【答案】D 。
【考点】圆锥的计算。
【分析】∵半圆的直径为a ,∴半圆的弧长为a2π。
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,∴设小圆的半径为r ,则:2r=a 2ππ,解得:1r=a 4如图小圆的圆心为B ,半圆的圆心为C ,作BA⊥CA 于A 点,则由勾股定理,得:AC 2+AB 2=BC 2,即:2221a a +b =a+a 24224ππππ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,整理得:。
中考数学复习专题折叠问题

2012年全国中考数学试题分类解析汇编159套63专题专题31:折叠问题一、选择题1. 2012广东梅州3分如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2= A.150°B.210°C.105°D.75°答案A;考点翻折变换折叠问题,三角形内角和定理;分析∵△A′DE是△ABC翻折变换而成,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°;∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°,∴∠1+∠2=360°﹣2×105°=150°;故选A;2. 2012江苏南京2分如图,菱形纸片ABCD中,∠A=600,将纸片折叠,点A、D分别落在A’、D’处,且A’D’经过B,EF为折痕,当D’F⊥CD时,CFFD的值为A. 312-B.36C.2316-D.318+答案A;考点翻折变换折叠问题,菱形的性质,平行的性质,折叠的性质,锐角三角函数定义,特殊角的三角函数值;分析延长DC与A′D′,交于点M,∵在菱形纸片ABCD中,∠A=60°,∴∠DCB=∠A=60°,AB∥CD;∴∠D=180°-∠A=120°;根据折叠的性质,可得∠A′D′F=∠D=120°,∴∠FD′M=180°-∠A′D′F=60°;∵D′F⊥CD,∴∠D′FM=90°,∠M=90°-∠FD′M=30°;∵∠BCM=180°-∠BCD=120°,∴∠CBM=180°-∠BCM-∠M=30°;∴∠CBM=∠M;∴BC=CM;设CF=x,D′F=DF=y, 则BC=CM=CD=CF+DF=x+y;∴FM=CM+CF=2x+y,在Rt△D′FM 中,tan∠M=tan30°=D F y FM 2x y '==+x =;∴CF x FD y ==;故选A; 3. 2012江苏连云港3分小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B 的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°角的正切值是A +1B +1C .D 答案B;考点翻折变换折叠问题,折叠的性质,矩形的性质,等腰三角形的性质,三角形内角和定理,锐角三角函数定义,勾股定理;分析∵将如图所示的矩形纸片ABCD 沿过点B 的直线折叠,使点A 落在BC 上的点E 处,∴AB=BE,∠AEB=∠EAB=45°,∵还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处, ∴AE=EF,∠EAF=∠EFA=0452=°;∴∠FAB=°;设AB =x,则AE =EF x,∴°=tan∠FAB=t FB 1AB x==;故选B; 4. 2012广东河源3分如图,在折纸活动中,小明制作了一张△ABC 纸片,点D 、E 分别在边AB 、AC 上,将△ABC 沿着DE 折叠压平,A 与A′重合.若∠A=75o,则∠1+∠2=A .150oB .210oC .105oD .75o答案A;考点折叠的性质,平角的定义,多边形内角和定理;分析根据折叠对称的性质,∠A′=∠A=75o;根据平角的定义和多边形内角和定理,得∠1+∠2=1800-∠ADA′+1800-∠AEA′=3600-∠ADA′+∠AEA′=∠A′+∠A=1500;故选A;5. 2012福建南平4分如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别和AE、AF折叠,点B、D恰好都将在点G处,已知BE=1,则EF的长为A.32B.52C.94D.3答案B;考点翻折变换折叠问题,正方形的性质,折叠的性质,勾股定理;分析∵正方形纸片ABCD的边长为3,∴∠C=90°,BC=CD=3;根据折叠的性质得:EG=BE=1,GF=DF;设DF=x,则EF=EG+GF=1+x,FC=DC-DF=3-x,EC=BC-BE=3-1=2;在Rt△EFC中,EF2=EC2+FC2,即x+12=22+3-x2,解得:3x2 =;∴DF=32,EF=1+35=22;故选B;6. 2012湖北武汉3分如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A 恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是A.7 B.8 C.9 D.10答案C;考点折叠的性质,矩形的性质,勾股定理;分析根据折叠的性质,EF=AE=5;根据矩形的性质,∠B=900;在Rt△BEF中,∠B=900,EF=5,BF=3,∴根据勾股定理,得BE4;∴CD=AB=AE+BE=5+4=9;故选C;7. 2012湖北黄石3分如图所示,矩形纸片ABCD中,AB=6cm,BC=8 cm,现将其沿EF对折,使得点C与点A重合,则AF长为A. 25cm8B.25cm4C.25cm2D. 8cm答案B;考点翻折变换折叠问题,折叠对称的性质,矩形的性质,勾股定理;分析设AF=xcm,则DF=8-xcm,∵矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,∴DF=D′F,在Rt△AD′F 中,∵AF 2=AD′2+D′F 2,即x 2=62+8-x 2,解得:x=()25cm 4;故选B; 8. 2012湖北荆门3分如图,已知正方形ABCD 的对角线长为2,将正方形ABCD 沿直线EF 折叠,则图中阴影部分的周长为A . 8B . 4C . 8D . 6答案C; 考点翻折变换折叠问题,折叠的对称性质,正方形的性质,勾股定理;分析如图,∵正方形ABCD 的对角线长为22,即BD=22,∠A=90°,AB=AD,∠ABD=45°,∴AB=BDcos∠ABD=BDcos45°=222=22⨯; ∴AB=BC=CD=AD=2;由折叠的性质:A′M=AM,D′N=DN,A′D′=AD,∴图中阴影部分的周长为A′M+BM+BC+CN+D′N+A′D′=AM+BM+BC+CN+DN+AD=AB+BC+CD+AD=2+2+2+2=8;故选C;9. 2012四川内江3分如图,在矩形ABCD 中,AB=10,BC=5点E 、F 分别在AB 、CD 上,将矩形ABCD 沿EF 折叠,使点A 、D 分别落在矩形ABCD 外部的点A 1、D 1处,则阴影部分图形的周长为答案D;考点翻折变换折叠问题,矩形和折叠的性质;分析根据矩形和折叠的性质,得A 1E=AE,A 1D 1=AD,D 1F=DF,则阴影部分的周长即为矩形的周长,为210+5=30;故选D;10. 2012四川资阳3分如图,在△ABC 中,∠C=90°,将△ABC 沿直线MN 翻折后,顶点C 恰好落在AB 边上的点D 处,已知MN∥AB,MC=6,NC =23,则四边形MABN 的面积是A .63B .123C .183D .243答案C;考点翻折变换折叠问题,折叠对称的性质,相似三角形的判定和性质,分析连接CD,交MN 于E,∵将△ABC 沿直线MN 翻折后,顶点C 恰好落在AB 边上的点D 处,∴MN⊥CD,且CE=DE;∴CD=2CE;∵MN∥AB,∴CD⊥AB;∴△CMN∽△CAB; ∴2CMN CAB S CE 1S CD 4∆∆⎛⎫== ⎪⎝⎭; ∵在△CMN 中,∠C=90°,MC=6,NC=23 ,∴CMN 11S CM CN 62 3 6 322∆=⋅=⨯⨯= ∴CAB CMN S 4S 46 3 24 3∆∆==⨯=;∴CAB CMN MABN S S S 24 36 318 3∆∆=-=-=四形边;故选C;11. 2012贵州黔东南4分如图,矩形ABCD 边AD 沿拆痕AE 折叠,使点D 落在BC 上的F 处,已知AB=6,△ABF 的面积是24,则FC 等于A .1B .2C .3D .4答案B;考点翻折变换折叠问题,折叠的性质,矩形的性质,勾股定理;分析由四边形ABCD 是矩形与AB=6,△ABF 的面积是24,易求得BF 的长,然后由勾股定理,求得AF 的长,根据折叠的性质,即可求得AD,BC 的长,从而求得答案:∵四边形ABCD 是矩形,∴∠B=90°,AD=BC;∵AB=6,∴S △ABF =12ABBF=12×6×BF=24;∴BF=8; ∴2222AF AB BF 6810=+=+=;由折叠的性质:AD=AF=10,∴BC=AD=10;∴FC=BC﹣BF=10﹣8=2;故选B;12. 2012贵州遵义3分如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE,延长BG 交CD 于F 点,若CF=1,FD=2,则BC 的长为A .32B .26C .25D .23答案B;考点翻折变换折叠问题,矩形的性质和判定,折叠对称的性质,全等三角形的判定和性质,勾股定理;分析过点E 作EM⊥BC 于M,交BF 于N;∵四边形ABCD 是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME 是矩形;∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM;∵∠ENG=∠BNM,∴△ENG≌△BNMAAS;∴NG=NM;∵E 是AD 的中点,CM=DE,∴AE=ED=BM=CM;∵EM∥CD,∴BN:NF=BM :CM;∴BN=NF;∴NM=12CF=12;∴NG=12; ∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣1522=;∴BF=2BN=5∴BC ==故选B;13. 2012山东泰安3分如图,将矩形纸片ABCD 沿EF 折叠,使点B 与CD 的中点重合,若AB=2,BC=3,则△FCB′与△B′DG 的面积之比为A .9:4B .3:2C .4:3D .16:9答案D;考点翻折变换折叠问题,折叠对称的性质,勾股定理,相似三角形的判定和性质;分析设BF=x,则由BC=3得:CF=3﹣x,由折叠对称的性质得:B′F=x;∵点B′为CD 的中点,AB=DC=2,∴B′C=1;在Rt△B′CF 中,B′F 2=B′C 2+CF 2,即22x 1(3x)=+-,解得:5x 3=,即可得CF=54333-=; ∵∠DB′G=∠DGB′=90°,∠DB′G+∠CB′F=90°,∴∠DGB′=∠CB′F;∴Rt△DB′G∽Rt△CFB′;根据面积比等于相似比的平方可得: 22PCB B DG S FC 416()S B D 39∆'∆'⎛⎫=== ⎪'⎝⎭;故选D; 14. 2012山东潍坊3分已知矩形ABCD 中,AB=1,在BC 上取一点E,沿AE 将ΔABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,则AD= .AD .2 答案B;考点翻折变换折叠问题,折叠的性质,矩形的性质,正方形的判定和性质,相似多边形的性质; 分析∵矩形ABCD 中,AF 由AB 折叠而得,∴ABEF 是正方形;又∵AB=1,∴AF= AB=EF=1;设AD=x,则FD=x -1;∵四边形EFDC 与矩形ABCD 相似,∴EF AD FD AB =,即1x x 11=-; 解得115?x =2+,215x =2-负值舍去; 经检验115x 2+=是原方程的解;故选B; 15. 2012广西河池3分如图,在矩形ABCD 中,AD >AB,将矩形ABCD 折叠,使点C 与点A 重合, 折痕为MN,连结CN .若△CDN 的面积与△CMN 的面积比为1︰4,则MN BM 的值为 A .2B .4C .25D .26 答案D;考点翻折变换折叠问题,折叠的性质,矩形、菱形的判定和性质,勾股定理;分析过点N 作NG⊥BC 于G,由四边形ABCD 是矩形,易得四边形CDNG 是矩形,又由折叠的性质,可得四边形AMCN 是菱形,由△CDN 的面积与△CMN 的面积比为1:4,根据等高三角形的面积比等于对应底的比,可得DN :CM=1:4,然后设DN=x,由勾股定理可求得MN 的长,从而求得答案:过点N 作NG⊥BC 于G,∵四边形ABCD 是矩形,∴四边形CDNG 是矩形,AD∥BC;∴CD=NG,CG=DN,∠ANM=∠CMN;由折叠的性质可得:AM=CM,∠AMN=∠CMN,∴∠ANM=∠AMN;∴AM=AN;∴AM=CM,∴四边形AMCN 是平行四边形;∵AM=CM,∴四边形AMCN 是菱形;∵△CDN 的面积与△CMN 的面积比为1:4,∴DN:CM=1:4;设DN=x,则AN=AM=CM=CN=4x,AD=BC=5x,CG=x;∴BM=x,GM=3x;在Rt△CGN 中,()2222NG CN CG 4x x 15x =-=-=, 在Rt△MNG 中,()()2222MN GM NG 3x 15x =26x =+=+, ∴MN 26x ==26BM x;故选D; 16. 2012河北省3分如图,在平行四边形ABCD 中,∠A=70°,将平行四边形折叠,使点D 、C 分别落在点F 、E 处点F 、E 都在AB 所在的直线上,折痕为MN,则∠AMF 等于A .70°B .40° C.30° D.20°答案B;考点翻折变换折叠问题,平行四边形的性质,平行线的性质,平角的定义;分析∵四边形ABCD是平行四边形,∴AB∥CD;∵根据折叠的性质可得:MN∥AE,∠FMN=∠DMN,∴AB∥CD∥MN;∵∠A=70°,∴∠FMN=∠DMN=∠A=70°;∴∠AMF=180°-∠DMN-∠FMN=180°-70°-70°=40°;故选B;17. 2012青海西宁3分折纸是一种传统的手工艺术,也是每一个人从小就经历的事,它是一种培养手指灵活性、协调能力的游戏,更是培养智力的一种手段.在折纸中,蕴涵许多数学知识,我们还可以通过折纸验证数学猜想.把一张直角三角形纸片按照图①~④的过程折叠后展开,请选择所得到的数学结论A.角的平分线上的点到角的两边的距离相等B.在直角三角形中,如果一个锐角等于30o,那么它所对的直角边等于斜边的一半C.直角三角形斜边上的中线等于斜边的一半D.如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形答案C;考点翻折变换折叠问题;分析如图②,∵△CDE由△ADE翻折而成,∴AD=CD;如图③,∵△DCF由△DBF翻折而成,∴BD=CD;∴AD=BD=CD,点D是AB的中点;∴CD=12AB,即直角三角形斜边上的中线等于斜边的一半;故选C;二、填空题1. 2012上海市4分如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,点D在AC上,将△ADB 沿直线BD翻折后,将点A落在点E处,如果AD⊥ED,那么线段DE的长为▲ .1;考点翻折变换折叠问题,折叠对称的性质,锐角三角函数定义,特殊角的三角函数值,三角形内角和定理,等腰三角形的判定和性质;分析∵在Rt△ABC 中,∠C=90°,∠A=30°,BC=1, ∴0BC 1AC 3tan A tan30===∠; ∵将△ADB 沿直线BD 翻折后,将点A 落在点E 处,∴∠ADB=∠EDB,DE=AD;∵AD⊥ED,∴∠CDE=∠ADE=90°,∴∠EDB=∠ADB=00036090=1352-; ∴∠CDB=∠EDB﹣∠CDE=135°-90°=45°;∵∠C=90°,∴∠CBD=∠CDB=45°;∴CD=BC=1;∴DE=AD=AC﹣CD=31-;2. 2012浙江丽水、金华4分如图,在等腰△ABC 中,AB =AC,∠BAC=50°.∠BAC 的平分线与AB 的中垂线交于点O,点C 沿EF 折叠后与点O 重合,则∠CEF 的度数是 ▲ . 答案50°;考点翻折变换折叠问题,等腰三角形的性质,三角形内角和定理,线段垂直平分线的判定和性质;分析利用全等三角形的判定以及垂直平分线的性质得出∠OBC=40°,以及∠OBC=∠OCB=40°,再利用翻折变换的性质得出EO =EC,∠CEF=∠FEO,进而求出即可:连接BO,∵AB=AC,AO 是∠BAC 的平分线,∴AO 是BC 的中垂线;∴BO=CO;∵∠BAC=50°,∠BAC 的平分线与AB 的中垂线交于点O,∴∠OAB=∠OAC=25°;∵等腰△ABC 中, AB =AC,∠BAC=50°,∴∠ABC=∠ACB=65°;∴∠OBC=65°-25°=40°;∴∠OBC=∠OCB=40°;∵点C 沿EF 折叠后与点O 重合,∴EO=EC,∠CEF=∠FEO;∴∠CEF=∠FEO=1800-2×400÷2=50°;3. 2012浙江绍兴5分如图,在矩形ABCD 中,点E,F 分别在BC,CD 上,将△ABE 沿AE 折叠,使点B 落在AC 上的点B′处,又将△CEF 沿EF 折叠,使点C 落在EB′与AD 的交点C′处.则BC :AB 的值为 ▲ ;答案3;考点翻折变换折叠问题,折叠的性质,矩形的性质,平行的性质,等腰三角形的性质,全等三角形的判定和性质,锐角三角函数定义,特殊角的三角函数值;分析连接CC′,∵将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处,∴EC=EC′,∴∠EC′C=∠ECC′,∵∠DC′C=∠ECC′,∴∠EC′C=∠DC′C.∴CC′是∠EC'D的平分线;∵∠CB′C′=∠D=90°,C′C=C′C,∴△CB′C′≌△CDC′AAS;∴CB′=CD;又∵AB′=AB,∴B′是对角线AC中点,即AC=2AB;∴∠ACB=30°;∴tan∠ACB=tan30°=AB1BC3=;∴BC:AB=3;4. 2012浙江台州5分如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=▲ 度.答案;考点折叠问题,折叠的对称性质,正方形的性质,等腰直角三角形的判定和性质,勾股定理,相似三角形的判定和性质,三角形内角和定理,平角定义;分析由折叠的对称和正方形的性质,知△ABE≌△A′BE,∴∠BEA′=,△A′DE是等腰直角三角形;设AE=A′E=A′D =x,则ED=2x;设CD=y,则BD=2y;∴ED2x BD2y==2==2A D x CD y',;∴ED BD=A D CD';又∵∠EDA′=∠A′DC=450,∴△EDA′∽△A′DC;∴∠DA′C=∠DEA′=+450=;∴∠BA′C=1800-=;5. 2012江苏宿迁3分如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C’,D’处,C’E交AF于点G.若∠CEF=70°,则∠GFD’=▲ °.答案40;考点折叠问题矩形的性质,平行的性质;分析根据折叠的性质,得∠DFE=∠D’FE;∵ABCD 是矩形,∴AD∥BC;∴∠GFE=∠CEF=70°,∠DFE=1800-∠CEF=110°;∴∠GFD’=∠D’FE-∠GFE=110°-70°=40°;6. 2012江苏盐城3分如图,在△ABC 中,D,、E 分别是边AB 、AC 的中点,∠B=50°o.现将△ADE 沿DE 折叠,点A 落在三角形所在平面内的点为A 1,则∠BDA 1的度数为 ▲ °. 答案80; 考点翻折变换折叠问题,折叠对称的性质,三角形中位线定理,平行的性质; 分析∵D、E 分别是边AB 、AC 的中点,∴DE∥BC 三角形中位线定理;∴∠ADE=∠B=50°两直线平行,同位角相等;又∵∠ADE=∠A 1DE 折叠对称的性质,∴∠A 1DA=2∠B;∴∠BDA 1=180°-2∠B=80°;7. 2012江苏扬州3分如图,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,如果AB 2BC 3=,那么tan∠DCF 的值是 ▲ .答案52; 考点翻折变换折叠问题,翻折对称的性质,矩形的性质,勾股定理,锐角三角函数定义; 分析∵四边形ABCD 是矩形,∴AB=CD,∠D=90°,∵将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,∴CF=BC,∵AB 2BC 3=,∴CD 2CF 3=;∴设CD =2x,CF =3x, ∴22DF=CF CD 5x -=;∴tan∠DCF=DF 5x 5=CD 2x 2=; 8. 2012湖北荆州3分如图,已知正方形ABCD 的对角线长为2,将正方形ABCD 沿直线EF 折叠,则图中阴影部分的周长为 ▲答案8;考点翻折变换折叠问题,折叠的对称性质,正方形的性质,勾股定理;分析如图,∵正方形ABCD 的对角线长为22,即BD=22,∠A=90°,AB=AD,∠ABD=45°,∴AB=BDcos∠ABD=BDcos45°=222=22⨯; ∴AB=BC=CD=AD=2;由折叠的性质:A′M=AM,D′N=DN,A′D′=AD,∴图中阴影部分的周长为A′M+BM+BC+CN+D′N+A′D′=AM+BM+BC+CN+DN+AD=AB+BC+CD+AD=2+2+2+2=8;9. 2012湖南岳阳3分如图,在Rt△ABC 中,∠B=90°,沿AD 折叠,使点B 落在斜边AC 上,若AB=3,BC=4,则BD= ▲ . 答案32; 考点翻折变换折叠问题;1052629分析如图,点E 是沿AD 折叠,点B 的对应点,连接ED,∴∠AED=∠B=90°,AE=AB=3,∵在Rt△ABC 中,∠B=90°,AB=3,BC=4,∴2222AC=AB +BC 3+45==;∴EC=AC﹣AE=5﹣3=2;设BD=ED=x,则CD=BC ﹣BD=4﹣x,在Rt△CDE 中,CD 2=EC 2+ED 2,即:4﹣x 2=x 2+4,解得:x=32;∴BD=32; 10. 2012四川达州3分将矩形纸片ABCD,按如图所示的方式折叠,点A 、点C 恰好落在对角线BD上,得到菱形BEDF.若BC=6,则AB 的长为 ▲ .答案23;考点翻折变换折叠问题,折叠的性质,菱形和矩形的性质,勾股定理;分析设BD 与EF 交于点O;∵四边形BEDF 是菱形,∴OB=OD=12BD; ∵四边形ABCD 是矩形,∴∠C=90°;设CD=x,根据折叠的性质得:OB=OD= CD=x,即BD=2x,在Rt△BCD 中,BC 2+CD 2=BD 2,即62+x 2=2x 2,解得:x=23;∴AB=CD=23;11. 2012贵州黔西南3分把一张矩形纸片矩形ABCD 按如图方式折叠,使顶点B 和点D 重合,折痕为EF,若AB =3cm,BC =5cm,则重叠部分△DEF 的面积为 ▲ cm 2;答案5110;考点折叠问题,折叠的性质,矩形的性质,勾股定理;分析设ED=x,则根据折叠和矩形的性质,得A′E=AE=5-x,A′D=AB=3;根据勾股定理,得222ED A E A D ='+',即()222x 5x 3=-+,解得17x 5=; ∴DEF 11751S 3=2510∆=⋅⋅cm 2; 12. 2012河南省5分如图,在Rt△ABC 中,∠C=900,∠B=300,BC=3,点D 是BC 边上一动点不与点B 、C 重合,过点D 作DE⊥BC 交AB 边于点E,将∠B 沿直线DE 翻折,点B 落在射线BC 上的点F 处,当△AEF 为直角三角形时,BD 的长为 ▲答案1或2;13. 2012内蒙古包头3分如图,将△ABC 纸片的一角沿DE 向下翻折,使点A 落在BC 边上的A ′点处,且DE ∥BC ,下列结论:① ∠AED =∠C ;② A D A E DB EC''=; ③ BC= 2DE ;④ BD A E A C AD A E S S S ∆'∆''=+四形边;其中正确结论的个数是 ▲ 个;答案4;考点折叠问题,折叠对称的性质,平行线的性质,等腰三角形的判定和性质,直角三角形两锐角的关系,三角形中位线定理,全等、相似三角形的判定和性质;分析①∵DE ∥BC,∴根据两直线平行,同位角相等,得∠AED =∠C;∴①正确;②∵根据折叠对称的性质,A ′D=AD,A ′E=AE;∵DE ∥BC,∴根据两直线分线段成比例定理,得AD AE DB EC =;∴A D A E DB EC ''=;∴②正确;③连接A A ′,∵根据折叠对称的性质,A ,A ′关于DE 对称;∴A A ′⊥DE;∵DE ∥BC,∴A A ′⊥BC;∵A ′D=AD,∴∠DA A ′=∠D A ′A;∴∠DB A ′=∠D A ′B;∴BD= A ′D;∴BD=AD;∴DE 是△ABC 的中位线;∴BC= 2DE;∴③正确;④∵DE ∥BC,∴△ABC ∽△ADE;∵由③BC= 2DE,∴ADE ABC 1S S 4∆∆=;∵根据折叠对称的性质,△ADE ≌△A ′DE;∴ABC AD A E 1S S 2∆'=四形边;∴BD A E A C ABC 1S S =S 2∆'∆'∆+,即BD A E A C AD A E S S S ∆'∆''=+四形边;∴④正确;综上所述,正确结论的个数是4个;14. 2012黑龙江绥化3分长为20,宽为a 的矩形纸片10<a <20,如图那样折一下,剪下一个边长等于矩形宽度的正方形称为第一次操作;再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形称为第二次操作;如此反复操作下去,若在第n 次操作后,剩下的矩形为正方形,则操作停止.当n=3时,a 的值为 ▲ .答案12或15;考点翻折变换折叠问题,正方形和矩形的性质,剪纸问题,分类归纳图形的变化类;分析根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽;当10<a <20时,矩形的长为20,宽为a,所以,第一次操作时,所得正方形的边长为a,剩下的矩形相邻的两边分别为20-a,a;第二次操作时,由20-a<a可知所得正方形的边长为20-a,剩下的矩形相邻的两边分别为20-a,a-20-a=2a-20;∵20-a-2a-20=40-3a,∴20-a与2a-20的大小关系不能确定,需要分情况进行讨论;第三次操作时,①当20-a>2a-20时,所得正方形的边长为2a-20,此时,20-a-2a-20=40-3a,∵此时剩下的矩形为正方形,∴由40-3a=2a-20得a=12;①当2a-20>20-a时,所得正方形的边长为20-a,此时,2a-20-20-a=3a-40,∵此时剩下的矩形为正方形,∴由3a-40=20-a得a=15;故答案为12或15;15. 2012黑龙江黑河、齐齐哈尔、大兴安岭、鸡西3分如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为▲答案2898;考点翻折变换折叠问题,矩形的性质,折叠对称的性质,勾股定理; 分析∵四边形ABCD是矩形,∴∠A=∠B=90°,BC=AD=8,CD=AB;∵△AFD的面积为60,即12ADAF=60,解得:AF=15;∴DF17==;由折叠的性质,得:CD=CF=17;∴AB=17;∴BF=AB-AF=17-15=2; 设CE=x,则EF=CE=x,BE=BC-CE=8-x,在Rt△BEF中,EF2=BF2+BE2,即x2=22+8-x2,解得:x=174,即CE=174,∴△DEC的面积为:12CDCE=12×17×17289=48;三、解答题1. 2012天津市10分已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A11,0,点B0,6,点P为BC边上的动点点P不与点B、C重合,经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.Ⅰ如图①,当∠BOP=300时,求点P的坐标;Ⅱ如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t 的式子表示m ;Ⅲ在Ⅱ的条件下,当点C′恰好落在边OA 上时,求点P 的坐标直接写出结果即可. 答案解:Ⅰ根据题意,∠OBP=90°,OB=6;在Rt△OBP 中,由∠BOP=30°,BP=t,得OP=2t;∵OP 2=OB 2+BP 2,即2t 2=62+t 2,解得:t 1=23,t 2=-23舍去. ∴点P 的坐标为23 ,6;Ⅱ∵△OB′P、△QC′P 分别是由△OBP、△QCP 折叠得到的,∴△OB′P≌△OBP,△QC′P≌△QCP;∴∠OPB′=∠OPB,∠QPC′=∠QPC;∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,∴∠OPB+∠QPC=90°;∵∠BOP+∠OPB=90°,∴∠BOP=∠CPQ;又∵∠OBP=∠C=90°,∴△OBP∽△PCQ;∴OB BP PC CQ=; 由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m .∴6t 11t 6m =--;∴2111m t t 666=-+0<t <11; Ⅲ点P 的坐标为11133-,6或11+133,6; 考点翻折变换折叠问题,坐标与图形性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质;分析Ⅰ根据题意得,∠OBP=90°,OB=6,在Rt△OBP 中,由∠BOP=30°,BP=t,得OP=2t,然后利用勾股定理,即可得方程,解此方程即可求得答案;Ⅱ由△OB′P、△QC′P 分别是由△OBP、△QC P 折叠得到的,可知△OB′P≌△OBP, △QC′P≌△QCP,易证得△OBP∽△PCQ,然后由相似三角形的对应边成比例,即可求得答案;Ⅲ首先过点P 作PE⊥OA 于E,易证得△PC′E∽△C′QA,由勾股定理可求得C′Q 的长,然后利用相似三角形的对应边成比例与2111m t t 666=-+,即可求得t 的值: 过点P 作PE⊥OA 于E,∴∠PEA=∠QAC′=90°;∴∠PC′E+∠EPC′=90°;∵∠PC′E+∠QC′A=90°,∴∠EPC′=∠QC′A ;∴△PC′E∽△C′QA;∴PE PC AC C Q'='';∵PC′=PC=11-t,PE=OB =6,AQ=m,C′Q=CQ=6-m, ∴22AC C Q AQ 3612m '='-=-; ∴611t 6m3612m -=--; ∵6t 11t 6m =--,即611t t 6m -=-,∴66=t3612m -,即23612m=t -; 将2111m t t 666=-+代入,并化简,得23t 22 t 36=0-+;解得:12111311+13t t 33-==,; ∴点P 的坐标为11133-,6或11+133,6; 2. 2012海南省11分如图1,在矩形ABCD 中,把∠B、∠D 分别翻折,使点B 、D 分别落在对角线BC 上的点E 、F 处,折痕分别为CM 、AN.1求证:△AND≌△CBM.2请连接MF 、NE,证明四边形MFNE 是平行四边形,四边形MFNE 是菱形吗请说明理由3P 、Q 是矩形的边CD 、AB 上的两点,连结PQ 、CQ 、MN,如图2所示,若PQ=CQ,PQ∥MN;且AB=4,BC=3,求PC 的长度.答案1证明:∵四边形ABCD 是矩形,∴∠D=∠B,AD=BC,AD∥BC;∴∠DAC=∠BCA;又由翻折的性质,得∠DAN=∠NAF,∠ECM=∠BCM,∴∠DAN=∠BCM;∴△AND≌△CBMASA;2证明:∵△AND≌△CBM,∴DN=BM;又由翻折的性质,得DN=FN,BM=EM,∴FN=EM;又∠NFA=∠ACD+∠CNF=∠BAC+∠EMA=∠MEC,∴FN∥EM;∴四边形MFNE 是平行四边形;四边形MFNE 不是菱形,理由如下:由翻折的性质,得∠CEM=∠B=900,∴在△EMF 中,∠FEM>∠EFM;∴FM>EM;∴四边形MFNE 不是菱形;3解:∵AB=4,BC=3,∴AC=5;设DN=x,则由S△ADC=S△AND+S△NAC得3 x+5 x=12,解得x=32,即DN=BM=32;过点N作NH⊥AB于H,则HM=4-3=1;在△NHM中,NH=3,HM=1,由勾股定理,得∵PQ∥MN,DC∥AB,∴四边形NMQP在△CBQ中由勾股定理,得BQ=1;∴NP=MQ=12;∴PC=4-32-12=2;考点翻折问题,翻折的性质,矩形的性质,平行的性质,全等三角形的判定和性质,平行四边形的判定和性质,菱形的判定,勾股定理;分析1由矩形和翻折对称的性质,用ASA即可得到△AND≌△CBM;2根据一组对边平行且相等的四边形是平行四边形的判定即可证明;3设DN=x,则由S△ADC=S△AND+S△NAC可得DN=BM=32;过点N作NH⊥AB于H,则由勾股定理可得NM=从而根据平行四边形的性质和已知PQ=CQ,即可求得;因此,在△CBQ中,应用勾股定理求得BQ=1;从而求解;3. 2012广东省9分如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE 沿EF折叠,使点D落在D′处,点D′恰好与点A重合.1求证:△ABG≌△C′DG;2求tan∠ABG的值;3求EF的长.答案1证明:∵△BDC′由△BDC翻折而成,∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,∴∠ABG=∠ADE;在△ABG≌△C′DG中,∵∠BAG=∠C,AB= C′D,∠ABG=∠AD C′,∴△ABG≌△C′DGASA;2解:∵由1可知△ABG≌△C′DG,∴GD=GB,∴AG+GB=AD;设AG=x,则GB=8﹣x,在Rt△ABG中,∵AB2+AG2=BG2,即62+x2=8﹣x2,解得x=74;∴7AG74tan ABGAB624∠===;3解:∵△AEF是△DEF翻折而成,∴EF垂直平分AD;∴HD=12AD=4;∵tan∠ABG=tan∠ADE=724;∴EH=HD×724=4×77=246;∵EF垂直平分AD,AB⊥AD,∴HF是△ABD的中位线;∴HF=12AB=12×6=3;∴EF=EH+HF=725 +3=66;考点翻折变换折叠问题,翻折变换的性质,矩形的性质,全等三角形的判定和性质,勾股定理,锐角三角函数定义,三角形中位线定理;分析1根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论;2由1可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,从而得出tan∠ABG的值;3由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=12AD=4,再根据tan∠ABG的值即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结果;4. 2012广东深圳8分如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.1求证:四边形AFCE为菱形;2设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.答案1证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEF=∠EFC;由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,∴∠EFC=∠CEF;∴CF=CE;∴AF=CF=CE=AE;∴四边形AFCE为菱形;2解:a、b、c三者之间的数量关系式为:a2=b2+c2;理由如下:由折叠的性质,得:CE=AE;∵四边形ABCD是矩形,∴∠D=90°;∵AE=a,ED=b,DC=c,∴CE=AE=a;在Rt△DCE中,CE2=CD2+DE2,∴a、b、c三者之间的数量关系式可写为:a2=b2+c2;考点翻折变换折叠问题,矩形的性质,折叠的性质,平等的性质,菱形的判定,勾股定理;分析1由矩形ABCD与折叠的性质,易证得△CEF是等腰三角形,即CE=CF,即可证得AF=CF=CE=AE,即可得四边形AFCE为菱形;2由折叠的性质,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之间的数量关系式为:a2=b2+c2;答案不唯一5. 2012广东珠海9分已知,AB是⊙O的直径,点P在弧AB上不含点A、B,把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.1当P、C都在AB上方时如图1,判断PO与BC的位置关系只回答结果;2当P在AB上方而C在AB下方时如图2,1中结论还成立吗证明你的结论;3当P、C都在AB上方时如图3,过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.答案解:1PO与BC的位置关系是PO∥BC;21中的结论PO∥BC成立;理由为:由折叠可知:△APO≌△CPO,∴∠APO=∠CPO;又∵OA=OP,∴∠A=∠APO;∴∠A=∠CPO;又∵∠A与∠PCB都为PB所对的圆周角,∴∠A=∠PCB;∴∠CPO=∠PCB;∴PO∥BC;3证明:∵CD为圆O的切线,∴OC⊥CD;又∵AD⊥CD,∴OC∥AD;∴∠APO=∠COP;由折叠可得:∠AOP=∠COP,∴∠APO=∠AOP;又∵OA=OP,∴∠A=∠APO;∴∠A=∠APO=∠AOP;∴△APO为等边三角形;∴∠AOP=60°;又∵OP∥BC,∴∠OBC=∠AOP=60°;又∵OC=OB,∴△BC为等边三角形;∴∠COB=60°;∴∠POC=180°﹣∠AOP+∠COB=60°;又∵OP=OC,∴△POC也为等边三角形;∴∠PCO=60°,PC=OP=OC;又∵∠OCD=90°,∴∠PCD=30°;在Rt△PCD中,PD=12 PC,又∵PC=OP=12AB,∴PD=14AB,即AB=4PD;考点折叠的性质,圆心角、弧、弦的关系,圆周角定理,平行的判定和性质,切线的性质,全等三角形的性质,等腰三角形的性质,等边三角形的判定和性质,含30度角的直角三角形的性质;6. 2012福建龙岩12分如图1,过△ABC的顶点A作高AD,将点A折叠到点D如图2,这时EF 为折痕,且△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG 折叠,使B、C两点都与点D重合,得到一个矩形EFGH如图3,我们称矩形EFGH为△ABC的边BC上的折合矩形.1若△ABC的面积为6,则折合矩形EFGH的面积为;2如图4,已知△ABC,在图4中画出△ABC的边BC上的折合矩形EFGH;3如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,BC边上的高AD= ,正方形EFGH的对角线长为.答案解:13;2作出的折合矩形EFGH:32a ;;考点新定义,折叠问题,矩形和正方形的性质,勾股定理;分析1由折叠对称的性质,知折合矩形EFGH的面积为△ABC的面积的一半,2按题意,作出图形即可;3由如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,正方形边长为a,BC边上的高AD为EFGH边长的两倍2a;根据勾股定理可得正方形EFGH;7. 2012福建龙岩13分矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A的对应点A′落在线段BC上,再打开得到折痕EF.1当A′与B重合时如图1,EF= ;当折痕EF过点D时如图2,求线段EF的长; 2观察图3和图4,设BA′=x,①当x的取值范围是时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.答案解:15;由折叠轴对称性质知A′D=AD=5,∠A=∠EA′D=900;在Rt△A′DC中,DC=AB=2,∴ A C4'==;∴A′B=BC-A′C=5-4=1;∵∠EA′B+∠BEA′=∠EA′B+∠FA′C=900,∴∠BEA′=∠FA′C;又∵∠B=∠C=900,∴Rt△EBA′∽Rt△A′CF;∴A E A BA F FC''=',即A E153'=∴5A E3 '=;在Rt△A′EF中,EF;2①3x5≤≤;②证明:由折叠轴对称性质知∠AEF=∠FEA′,AE=A′E,AF=A′F;又∵AD∥BC,∴∠AFE=∠FEA′ ;∴∠AEF=∠AFE ;∴AE=AF;∴AE=A′E=AF=A′F;∴四边形AEA′F 是菱形;考点折叠的性质,矩形的性质,勾股定理,相似三角形的判定和性质,平行的性质,等腰三角形的性质,菱形的判定;分析1根据折叠和矩形的性质,当A′与B 重合时如图1,EF= AD=5;根据折叠和矩形的性质,以及勾股定理求出A′B 、A′F 和FC 的长,由Rt△EBA′∽Rt△A′CF 求得5A E 3'=,在Rt△A′EF 中,由勾股定理求得EF 的长; 2①由图3和图4可得,当3x 5≤≤时,四边形AEA′F 是菱形;②由折叠和矩形的性质,可得AE=A′E,AF=A′F;由平行和等腰三角形的性质可得AE=AF;从而AE=A′E=AF=A′F;根据菱形的判定得四边形AEA′F 是菱形;8. 2012湖北恩施8分如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC 的中点E,再折出线段AE,然后通过折叠使EB 落到线段EA 上,折出点B 的新位置B′,因而EB′=EB.类似地,在AB 上折出点B″使AB″=AB′.这是B″就是AB 的黄金分割点.请你证明这个结论. 答案证明:设正方形ABCD 的边长为2,E 为BC 的中点,∴BE=1;∴AE =;又1;1;∴)AB AB 12"=::;∴点B″是线段AB 的黄金分割点; 考点翻折折叠问题,正方形的性质,勾股定理,折叠对称的性质,黄金分割;分析设正方形ABCD 的边长为2,根据勾股定理求出AE 的长,再根据E 为BC 的中点和翻折不变性,求出AB″的长,二者相比即可得到黄金比;9. 2012湖北天门、仙桃、潜江、江汉油田12分如图,抛物线y=ax 2+bx+2交x 轴于A ﹣1,0,B4,0两点,交y 轴于点C,与过点C 且平行于x 轴的直线交于另一点D,点P 是抛物线上一动点. 1求抛物线解析式及点D 坐标;2点E 在x 轴上,若以A,E,D,P 为顶点的四边形是平行四边形,求此时点P 的坐标;3过点P 作直线CD 的垂线,垂足为Q,若将△CPQ 沿CP 翻折,点Q 的对应点为Q′.是否存在点P,使Q′恰好落在x 轴上若存在,求出此时点P 的坐标;若不存在,说明理由. 答案解:1∵抛物线y=ax 2+bx+2经过A ﹣1,0,B4,0两点,。
2012年中考数学分类解析(159套63专题)专题54_图形的旋转变换

2012年全国中考数学试题分类解析汇编(159套63专题)专题54:图形的旋转变换一、选择题1. (2012天津市3分)将下列图形绕其对角线的交点逆时针旋转900,所得图形一定与原图形重合的是【 】(A )平行四边形 (B )矩形 (C )菱形 (D )正方形 【答案】D 。
【考点】旋转对称图形【分析】根据旋转对称图形的性质,可得出四边形需要满足的条件:此四边形的对角线互相垂直、平分且相等,则这个四边形是正方形。
故选D 。
2. (2012广东佛山3分)如图,把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ,则在旋转过程中这个三角板扫过的图形的面积是【 】A .πB ..3+42π.11124π【答案】D 。
【考点】旋转的性质,勾股定理,等边三角形的性质,扇形面积。
【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD 计算即可:在△ABC 中,∠ACB=90°,∠BAC=30°,AB=2,∴BC=12AB=1,∠B=90°-∠BAC=60°。
∴AC =∴AB C 1S B C A C 22∆=⨯⨯=设点B 扫过的路线与AB 的交点为D ,连接CD , ∵BC=DC,∴△BCD 是等边三角形。
∴BD=CD=1。
∴点D 是AB 的中点。
∴AC D AB C 11S S 2224∆∆==⨯=S 。
∴1AC D AC A BC D ABC S S S ∆∆=++扇形扇形的面扫过积26013113603604464124ππππ⨯⨯=+=++=+故选D 。
3. (2012广东汕头4分)如图,将△ABC 绕着点C 顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是【 】A .110° B.80° C.40° D.30° 【答案】B 。
全国各地2012年中考数学分类解析(159套63专题)专题17 一次函数(正比例函数)的应用剖析
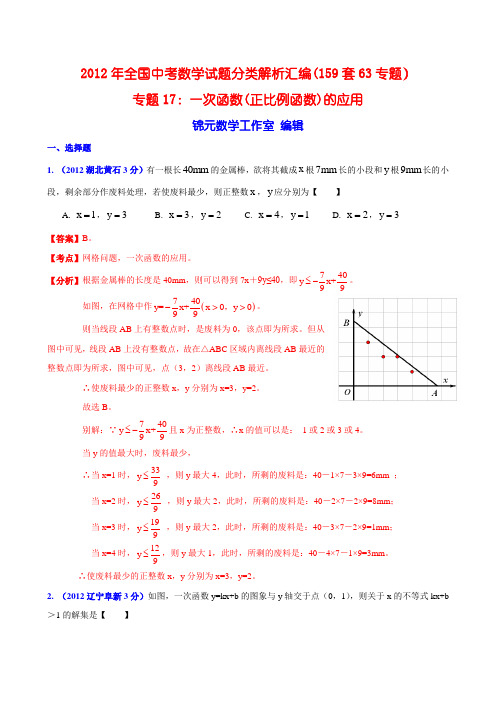
2012年全国中考数学试题分类解析汇编(159套63专题)专题17:一次函数(正比例函数)的应用锦元数学工作室 编辑一、选择题1. (2012湖北黄石3分)有一根长40mm 的金属棒,欲将其截成x 根7mm 长的小段和y 根9mm 长的小 段,剩余部分作废料处理,若使废料最少,则正整数x ,y 应分别为【 】A. x 1=,y 3=B. x 3=,y 2=C. x 4=,y 1=D. x 2=,y 3= 【答案】B 。
【考点】网格问题,一次函数的应用。
【分析】根据金属棒的长度是40mm ,则可以得到7x +9y≤40,即740y x+99≤-。
如图,在网格中作()740y=x+x 0y 099>>-,。
则当线段AB 上有整数点时,是废料为0,该点即为所求。
但从图中可见,线段AB 上没有整数点,故在△ABC 区域内离线段AB 最近的整数点即为所求,图中可见,点(3,2)离线段AB 最近。
∴使废料最少的正整数x ,y 分别为x=3,y=2。
故选B 。
别解:∵740y x+99≤-且x 为正整数,∴x 的值可以是: 1或2或3或4。
当y 的值最大时,废料最少, ∴当x=1时,33y 9≤,则y 最大4,此时,所剩的废料是:40-1×7-3×9=6mm ; 当x=2时,26y 9≤ ,则y 最大2,此时,所剩的废料是:40-2×7-2×9=8mm ;当x=3时,19y 9≤ ,则y 最大2,此时,所剩的废料是:40-3×7-2×9=1mm ;当x=4时,12y 9≤,则y 最大1,此时,所剩的废料是:40-4×7-1×9=3mm 。
∴使废料最少的正整数x ,y 分别为x=3,y=2。
2. (2012辽宁阜新3分)如图,一次函数y=kx+b 的图象与y 轴交于点(0,1),则关于x 的不等式kx+b >1的解集是【 】A.x>0 B.x<0 C.x>1 D.x<1【答案】B。
(最新最全)2012年全国各地中考数学解析汇编(按章节考点整理)分3个考点精选48题)

(最新最全)2012年全国各地中考数学解析汇编(按章节考点整理)第十一章 因式分解(分3个考点精选48题)11.1 提公因式法(2012北京,9,4)分解因式:269mn mn m ++= .【解析】原式=m (n 2+6n +9)=m (n +3)2【答案】m (n +3)2【点评】本题考查了提公因式及完全平方的知识点。
(2012广州市,13, 3分)分解因式a 2-8a 。
【解析】提取公因式即可分解因式。
【答案】:a(a -8).【点评】本题考查了因式分解的方法。
比较简单。
(2012浙江省温州市,5,4分)把24a a -多项式分解因式,结果正确的是( )A. ()4a a -B. (2)(2)a a +-C. (2)(2)a a a +-D. 2(2)4a --【解析】分解因式按“一提二套”原则:有公因式的先提取公因式,再套用平方差公式或完全平方公式,本题可直接提公因式.【答案】A【点评】有公因式的要先提取公因式,然后再考虑运用平方差公式或完全平方公式进行分解.因式分解要分解到每个多项式因式都不能再分解为止,此题较基础.(湖南株洲市3,9)因式分解:22a a -= .【解析】22(2)a a a a -=-【答案】(2)a a -【点评】本题主要考查因式分解的常用方法及步骤:先提取公因式,再运用公式法进行分解. (2012四川成都,1l ,4分)分解因式:25x x -=________.解析:因式分解的基本方法是提取公因式法、公式法、分组分解法。
本题只有两项,所以,只能用提取公因式法和平方差公式法。
观察可知有公因式x ,提取公因式法分解为x(x-5)。
答案:x(x-5)。
点评:公因式的确定方法是:系数是各项系数的最大公约数,字母是各项都有的字母,指数取最小。
(2012湖北随州,11,4分)分解因式:249x -=______________________。
解析:22249(2)3(23)(23)x x x x -=-=+-。
2012年全国各地中考数学试题分类解析汇编--第二章 无理数与实数(4)
2012年全国各地中考数学试题分类解析汇编第二章无理数与实数(4)1、(2012•黄石)计算:(3- 2)0+4sin60°-|2-23|.考点:实数的运算;零指数幂;特殊角的三角函数值.分析:任何不为0的数的0次幂都是1;熟记特殊角的三角函数值;去绝对值符号之前先搞清楚内面的数的性质,然后再去掉符号.解答:(3- 2)0+4sin60°-|2-23|=1+4×3/2 -(23-2)=1+23 -23 +2=3.点评:此题考查实数的有关运算,解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、特殊角的三角函数值、绝对值等考点的运算.2、(2012•湖州)计算:16-(1/2012)0+(-2)2+tan45°.考点:实数的运算;零指数幂;特殊角的三角函数值.专题:计算题.分析:分别进行二次根式的化简、零指数幂,然后代入tan45°=1,进行运算即可.解答:16-(1/2012) 0+(-2)2+tan45°=4-4+4+1=8.点评:此题考查了实数的运算,解答本题关键是掌握零指数幂的运算,二次根式的化简,属于基础题.3、(2012•衡阳)计算:(-1)2012-(-3)+(-1/2)1 + 9考点:实数的运算;负整数指数幂.专题:计算题.分析:分别计算负整数指数幂、二次根式的化简,然后合并即可得出答案.解答:(-1)2012-(-3)+(-1/2) 1-+ 9=1+3-2+3=5.点评:此题考查了实数的运算,关键是掌握各部分的运算法则,属于基础题,注意细心运算.4、(2012•河北)计算:|-5|-(2-3)0+6×(1/3 -1/2)+(-1)2.考点:实数的运算;零指数幂.专题:计算题.分析:分别运算绝对值、零指数幂、及有理数的混合运算,最后合并即可得出答案.解答:|-5|-(2-3)0+6×(1/3 -1/2)+(-1)2=5-1+(2-3)+1=4.点评:此题考查了实数的运算及有理数的混合运算,注意掌握零指数幂的运算及有理数的混合运算法则,一定要细心解答.5、(2012•海南)(1)计算:8+ 2+|-4|-(1/3)1-(2)解不等式组: x-1<33-x>0考点:实数的运算;负整数指数幂;解一元一次不等式组.专题:计算题.分析:(1)根据绝对值、负整数指数幂和二次根式化简得到原式=2 2+ 2+4-3,然后合并即可;(2)解第一个不等式得到x<4,解第二个不等式②得x<3,然后根据同小取小即可得到不等式组的解集.解答:(1)8+ 2+|-4|-(1/3)1-=2 2 +2 +4-3=32 +1;(2) x-1<3①3-x>0②,解不等式①得x<4,解不等式②得x<3,∴x<3.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了绝对值、负整数指数幂以及解一元一次不等式组.6、(2012•桂林)计算:(-1)2012- 18+2cos45°+|-4|.考点:实数的运算;特殊角的三角函数值.专题:计算题.分析:分别进行二次根式的化简,取绝对值,特殊角的三角函数值的代入,然后合并运算即可.解答:(-1)2012- 18+2cos45°+|-4|=1-32 +2×2/2 +2=3-22.点评:此题考查了实数的运算及特殊角的三角函数值,属于基础题,关键是运算法则的掌握,对于特殊角的三角函数值我们一定要熟练记忆.7、(2012•广元)计算:2cos45°-(-1/4)1--8-(π- 3)0.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据45°角的余弦等于2/2,有理数的负整数指数次幂等于正整数指数次幂的倒数,二次根式的化简,任何非0数的0次幂等于1进行计算即可得解.解答:2cos45°-(-1/4)1--8-(π- 3)0,=2×2/2 -(-4)-22 -1,= 2+4-22 -1,=3- 2.点评:本题考查了实数的运算,主要利用了特殊角的三角函数值,负整数指数幂,二次根式的化简,零指数幂,是基础运算题,注意运算符号的处理.8、(2012•广东)计算:2-2sin45°-(1+ 8)0+21-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:本题涉及零指数幂、负指数幂、特殊角的三角函数值3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:2-2sin45°-(1+ 8)0+21-= 2 -2×2/2 -1+1 /2=-1 /2 .点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、特殊角的三角函数值、绝对值等考点的运算.9、(2012•广安)计算:18/2 -(-2 /3)-cos45°+31-.考点:实数的运算;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:先将二次根式化为最简,然后计算负整数指数幂,代入特殊角的三角函数值,最后合并即可.解答:18/2 -(-2 /3)-cos45°+31-=3 2/2 +2/ 3 -2/2 +1/ 3= 2 +1.点评:此题考查了实数的运算,解答本题的关键是掌握负整数指数幂的运算,也要熟练记忆一些特殊角的三角函数值.10、(2012•德阳)计算:(-2)2-+|sin30°-1|+(-1/π) 0+161 考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:根据负整数指数幂、零指数幂、二次根式、绝对值特殊角的三角函数值等分别进行计算,然后根据实数的运算法则求得计算结果.解答:(-2)2-+|sin30°-1|+(-1/π) 0+161 =1/4 +1-1/2 +1+1/4 =2.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值特殊角的三角函数值等考点的运算.11、(2012•达州)计算:(-2012) 0+8-4sin45°+(1/2)1-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值. 专题:计算题.分析:题涉及零指数幂、负指数幂、二次根式化简、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:(-2012) 0+8-4sin45°+(1/2) 1-=1+22 -4×2/2 +2 =1+22 -22 +2 =3点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、负指数幂、二次根式化简、特殊角的三角函数值等概念.12、(2012•赤峰)(1)计算:161-sin30°+(-2)2--(5 - 2)0;(2)求不等式组 x-3(x-2)≥4(1+4x )/3>x-1的整数解.考点:实数的运算;零指数幂;负整数指数幂;一元一次不等式组的整数解;特殊角的三角函数值.专题:计算题.分析:(1)将二次根式化为最简,然后代入sin30°的值,再进行零指数幂及负整数指数幂的运算,从而合并可得出答案;(2)分别解两个不等式,从而得出不等式组的解,继而判断解集中的整数解即可. 解答:(1)161-sin30°+(-2)2 -(5 - 2)0=1/4 -1/2 +1/4 -1 =-1.(2) x-3(x-2)≥4 ①1+4x 3 >x-1 ② 解①得:x ≤1, 解②得:x >-4, 解集为:-4<x ≤1,整数解为:-3,-2,-1,0,1.点评:此题考查了实数的运算、零指数幂、一元一次不等式组的整数解,属于基础题,注意掌握各部分的运算法则.13、(2012•成都)(1)计算:4cos45°-8+(π+ 3) 0+(-1) 2(2)解不等式组: x-2<0(2x+1)/3≥1考点:实数的运算;零指数幂;解一元一次不等式组;特殊角的三角函数值. 专题:计算题.分析:(1)根据45°角的余弦等于2/2,二次根式的化简,任何非0数的0次幂等于1,有理数的乘方进行计算即可得解;(2)先求出两个不等式的解集,再确定这两个解集的公共部分即可.解答:(1)4cos45°-8+(π+ 3) 0+(-1) 2=4×2/2 -22+1+1=22 -22 +2=2;(2) x-2<0①2x+1 3 ≥1②,解不等式①得,x<2,解不等式②得,x≥1,所以不等式组的解集是1≤x<2.点评:(1)本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此题的关键是熟练掌握特殊角的三角函数值、零指数幂、二次根式等考点的运算;(2)主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).14、(2012•郴州)计算:(1/2)1-+(π-3.14)0-2tan45°+(-1)2012.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据a0=1(a≠0)、负整数指数幂、tan45°=1和乘方的定义得到原式=2+1-2×1+1,再进行乘法运算得到原式=2+1-2+1,然后进行加减运算即可.解答:(1/2) 1-+(π-3.14) 0-2tan45°+(-1) 2012=2+1-2×1+1=2+1-2+1=2.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了a0=1(a≠0)、负整数指数幂以及特殊角的三角函数值.15、(2012•常德)计算:|-1|+(3-π)0-(1/2)1-+tan45°.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据绝对值的定义、零指数幂的法则、负整数指数幂的法则、特殊三角函数值计算即可.解答:|-1|+(3-π) 0-(1/2) 1-+tan45°=1+1-2+1=1.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了a0=1(a≠0)、负整数指数幂以及特殊角的三角函数值.16、(2012•长沙)计算:(1/2)1-+2sin30°- 9考点:实数的运算;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:分别计算负整数指数幂及二次根式的化简,然后代入sin30°的值即可.解答:(1/2) 1-+2sin30°- 9=2+2×1/2 -3=0.点评:此题考查了实数的运算,解答本题的关键是熟练负整数指数幂的运算,也要熟练记忆一些特殊角的三角函数值.17、(2012•滨州)计算:|-2|+(-1)2012×(π-3)0-8+(-2)2-.考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.分析:分别运算零指数幂、负整数指数幂,二次根式的化简,然后合并即可得出答案.解答:|-2|+(-1) 2012×(π-3) 0-8+(-2) 2-=2+1×1-22+1/4=13/4 -22.点评:此题考查了实数的运算,解答本题要求我们熟练零指数幂的运算、负整数指数幂的运算及根式的化简,难度一般.18、(2012•毕节地区)计算:27+(-1/2)1--2tan60°-(-1)2012.考点:实数的运算;负整数指数幂;特殊角的三角函数值.分析:根据负指数幂、二次根式化简,整数指数幂、特殊角的三角函数值分别进行计算,然后根据实数的运算法则求得计算结果.解答:27+(-1/2) 1--2tan60°-(-1) 2012=33 +(-2)-23 -1= 3 -3.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、整数指数幂、二次根式、特殊角的三角函数值等考点的运算.19、(2012•北京)计算:(π-3)0+ 18-2sin45°-(1/8)1-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:分别根据零指数幂、二次根式的化简、负整数指数幂的运算,得出各部分的最简值,继而合并可得出答案.解答:(π-3)0+ 18-2sin45°-(1/8)1-=1+32 -2×2/ 2 -8=-7+22.点评:此题考查了实数的运算,掌握零指数幂、负整数幂的运算法则是关键,另外要求我们熟练记忆一些特殊角的三角函数值.20、(2012•北海)计算:4cos45°+(π+3)0- 8+(1/6)1-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据45°角的余弦等于2/ 2,任何非0数的0次幂等于1,二次根式的化简,有理数的负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解.解答:4cos45°+(π+3)0- 8+(1/6) 1-,=4×2/ 2+1-22 +6,=22 -22 +1+6,=7.点评:本题考查了实数的运算,主要有特殊角的三角函数值,零指数幂,二次根式的化简,负整数指数幂,是基础运算题,特殊角的三角函数值容易混淆,需熟练掌握.21、(2012•白银)计算:|-1|-2sin30°+(π-3.14)0+(1/2)2-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据绝对值的性质,30°角的正弦等于1/2,任何非0数的0次幂等于1,有理数的负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解.解答:|-1|-2sin30°+(π-3.14)0+(1/2) 2-,=1-2×1/2 +1+4,=1-1+1+4,=5.点评:本题考查了实数的运算,主要有绝对值的性质,特殊角的三角函数值,零指数幂,负整数指数幂,是基础运算题,特殊角的三角函数值容易混淆,需熟练掌握.22、(2012•巴中)计算:2cos45°+(2-1)0-(1 /2)1-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:根据45°角的余弦等于2/2,任何非0数的0次幂等于1,有理数的负整数指数次幂等于正整数指数次幂的倒数,进行计算即可得解.新世纪教育网 精品资料版权所有@新世纪教育网解答:解:2cos45°+(2-1)0-(1 /2)1=2×2/2 +1-2= 2 -1.点评:本题考查了实数的运算,主要利用了零指数幂,负整数指数幂,以及特殊角的三角函数值,是基础题,熟记性质以及特殊角的三角函数值是解题的关键.新世纪教育网-- 中国最大型、最专业的中小学教育资源门户网站。
2012年全国中考数学试题分类解析汇编专题:38等腰(边)三角形
2012年全国中考数学试题分类解析汇编(159套63专题)专题:38等腰(边)三角形一、选择题1. (2012宁夏区3分)一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是【】A.13 B.17 C.22 D.17或22【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长;题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形:①若4为腰长,9为底边长,由于4+4<9,则三角形不存在;②9为腰长,则符合三角形的两边之和大于第三边。
∴这个三角形的周长为9+9+4=22。
故选C。
2. (2012广东肇庆3分)等腰三角形两边长分别为4和8,则这个等腰三角形的周长为【】A.16 B.18 C.20 D.16或20【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析:①当4为腰时,4+4=8,故此种情况不存在;②当8为腰时,8-4<8<8+4,符合题意。
∴此三角形的周长=8+8+4=20。
故选C。
3. (2012江苏常州2分)已知三角形三边的长分别为4,9,则这个等腰三角形的周长为【】A.13B.17C.22D.17或22【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】由三角形三边的长分别为4,9,知三角形三边的长分别为4,4,9或4,9,9,但由于4,4,9与三角形的构成条件“两边之和大于第三边,两边之差小于第三边”不符,因此,三角形三边的长只能分别为4,9,9 ,周长为22。
故选C。
4. (2012江苏徐州3分)如果等腰三角形的两边长分别为2和5,则它的周长为【】A.9 B.7 C.12D.9或12【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】根据等腰三角形的性质,如果等腰三角形的两边长分别为2和5,则另一边可能是2或5。
2012年全国各地中考数学试题分类解析汇编--第二章 无理数与实数(3)
2012年全国各地中考数学试题分类解析汇编第二章无理数与实数(3)(--|-1|+(2012-π)0-(1/ 2 )1-.1、(2012•珠海)计算:2)2考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.分析:根据二次根式的性质,负数的绝对值等于它的相反数,任何非0数的0次幂等于1,有理数的负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解.(--|-1|+(2012-π)0-(1/ 2 )1-,解答:2)2=2-1+1-2,=0.点评:本题考查了实数的运算,解题的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值的性质等考点的运算.2、(2012•株洲)计算:21-+cos60°-|-3|.考点:实数的运算;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:将2-1转化为12,写出出cos60°的值,求出-|-3|再计算即可.解答:21-+cos60°-|-3|=1/ 2 +1/ 2 -3= -2.点评:本题考查了实数的运算、负整数指数幂、特殊角的三角函数值,目的在于考查实数的综合运算能力.3、(2012•重庆)计算:4+(π-2)0-|-5|+(-1)2012+(1/3)2-.考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.分析:分别计算零指数幂、负整数指数幂、绝对值,然后将各部分的最简值合并即可得出答案.解答:4+(π-2) 0-|-5|+(-1) 2012+(1/3) 2-=2+1-5+1+9=8.点评:此题考查了实数的运算,属于基础题,解答本题的关键是熟练各部分的运算法则,难度一般.4、(2012•肇庆)计算:|-32|-6sin45°+41-.考点:实数的运算;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:本题涉及绝对值、负整数指数幂、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|-32|-6sin45°+41=32-6×22+1 /4=32-32+1/ 4=1/ 4 .点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、负整数指数幂、特殊角的三角函数值等知识.5、(2012•漳州)计算:4-(π-3) 0+|-5|.考点:实数的运算;零指数幂.专题:计算题.分析:根据a0=1(a≠0)、绝对值和算术平方根的定义得到原式=2-1+5,然后进行加减运算即可.解答:4-(π-3) 0+|-5|=2-1+5=6.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了a0=1(a≠0)、绝对值以及算术平方根的定义6、(2012张家界)阅读材料:对于任何实数,我们规定符号的意义是=ad﹣bc.例如:=1×4﹣2×3=﹣2,=(﹣2)×5﹣4×3=﹣22.(1)按照这个规定,请你计算的值;(2)按照这个规定,请你计算:当x2﹣4x+4=0时,的值.考点:实数的运算;解一元二次方程-配方法.专题:新定义.分析:(1)根据符号的意义得到=5×8-7×6,然后进行实数的乘法运算,再进行实数的减法运算即可;(2)利用配方法解方程x2﹣4x+4=0得x=2,则. =,然后根据符号.的意义得到3×1-4×1,再进行实数的运算.解答:(1)=5×8﹣7×6=﹣2;(2)由x 2﹣4x+4=0得(x ﹣2)2=4,∴x=2,∴==3×1﹣4×1=﹣1.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了配方法解一元二次方程以及阅读理解能力.7、(2012•张家界)计算: 考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:利用零指数幂、负指数幂、绝对值以及特殊角的三角函数值的知识,即可求得答案. 解答:=1﹣3+2﹣+3×=﹣+=0. 点评:此题考查实数的混合运算.此题难度不大,注意解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、特殊角的三角函数值、绝对值等考点的运算.8、(2012•湛江)计算:|-3|- 4+(-2012)0.考点:实数的运算;零指数幂.专题:计算题.分析:根据绝对值、平方根、0指数幂的定义解答.解答:|-3|- 4+(-2012)0=3-2+1=2.点评:本题考查了实数的运算,解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.9、(2012•岳阳)计算:3- +(31)1--(2012-π)0+2cos30°. 考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:本题涉及零指数幂、负指数幂、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:3- +(31)1--(2012-π)0+2cos30°=3- 3+3-1+2×23 =3- 3 +3-1+3=5.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、负指数幂、特殊角的三角函数值等考点.10、(2012•义乌市)计算:|-2|+(-1)2012-(π-4)0. 考点:实数的运算;零指数幂.分析:由零指数幂,绝对值与幂的乘方的性质,即可得将原式化简为2+1-1,继而求得答案.解答:|-2|+(-1)2012-(π-4)0=2+1-1=2.点评:此题考查了实数的混合运算.此类题目是各地中考题中常见的计算题型,注意解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.11、(2012•湘潭)计算:(21)1--3tan45°-(π+2012) 0. 考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:分别根据负整数指数幂、特殊角的三角函数值及0指数幂计算出各数,再根据实数混合运算的法则进行解答即可. 解答:(21)1--3tan45°-(π+2012) 0=2-3-1=-2.点评:本题考查的是实数的运算,熟知负整数指数幂、特殊角的三角函数值及0指数幂的计算法则是解答此题的关键.12、(2012•咸宁)计算:|22-3|-((-21)2-+ 18考点:实数的运算;负整数指数幂.专题:探究型.分析:先根据绝对值的性质、负整数指数幂及算术平方根计算岀各数,再根据实数混合运算的法则进行计算即可.解答:|22-3|-((-21)2-+ 18 =3-22 -4+32= 2-1.点评:本题考查的是实数的运算,熟知绝对值的性质、负整数指数幂及算术平方根的计算是解答此题的关键.13、(2012•天门)计算:(-2)×(-5)-(-2000)+ 4.考点:实数的运算.专题:计算题.分析:先进行乘法运算和开方运算得到原式=10+2000+2,然后进行实数的加法运算即可.解答:(-2)×(-5)-(-2000)+ 4=10+2000+2=2012.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.14、(2012•台州)计算:|-1/2 |+21-- 8考点:实数的运算;负整数指数幂.专题:计算题.分析:本题涉及绝对值、负整数指数幂、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|-1/2 |+21-- 8=1/ 2 +1/ 2 -22=1-22点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、负整数指数幂、二次根式化简等考点的运算.15、(2012•随州)计算:(-1)3+| 3-2|+2sin60°-4考点:实数的运算;特殊角的三角函数值.专题:计算题.分析:先根据有理数的乘方、绝对值的性质及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可.解答:(-1)3+| 3-2|+2sin60°-4=-1+2- 3+2×3/2 -2=-1.点评:本题考查的是实数的混合运算,熟记有理数的乘方、绝对值的性质及特殊角的三角函数值是解答此题的关键.16、(2012•宿迁)计算:|2- 3|+(-1)0+2cos30°.考点:实数的运算;零指数幂;特殊角的三角函数值.专题:计算题.分析:根据a0=1(a≠0)、绝对值的意义和cos30°= 3/2得到原式=2-3+1+2×3/2,再进行乘法运算得到原式=2- 3+1+ 3,然后合并即可.解答:|2- 3|+(-1)0+2cos30°=2- 3+1+2×3/2=2- 3+1+ 3=3.点评:本题考查了实数的运算:先进行乘方或开方运算,再进行乘除运算,然后进行加减运算.也考查了a0=1(a≠0)、绝对值以及特殊角的三角函数值.17、(2012•苏州)计算:(3-1)0+|-2|- 4考点:实数的运算;零指数幂.专题:计算题.分析:分别计算零指数幂、绝对值及二次根式的化简,然后合并即可得出答案.解答:(3-1)0+|-2|- 4=1+2-2=1.点评:此题考查了实数的运算及零指数幂的知识,属于基础运算题,解答此题的关键是熟练掌握各部分的运算法则.18、(2012•沈阳)计算:(-1)0+| 4-1|+2sin45°.考点:实数的运算;特殊角的三角函数值.分析:本题涉及正整数指数幂、绝对值、二次根式、特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:(-1)0+| 4-1|+2sin45°=1+ 2 -1+2×2/2=22.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握正整数指数幂、特殊角的三角函数值、二次根式、绝对值等考点的运算.19、(2012•深圳)计算:|-4|+(1/2)1--( 3-1)0- 8cos45°.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:本题涉及绝对值、负整数指数幂、0指数幂、二次根式化简、特殊角的三角函数值等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|-4|+(1/2) 1--( 3-1) 0- 8cos45°=4+2-1-22×2/2=5-2=3.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、负整数指数幂、0指数幂、二次根式化简、特殊角的三角函数值等考点的运算.20、(2012•衢州)计算:|-2|+21--cos60°-(1- 2)0.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:根据零指数幂、负整数指数幂以及特殊角的三角函数值的运算规律计算即可.解答:|-2|+21--cos60°-(1- 2)0=2+1/ 2 -1/ 2 -1=2-1=1.点评:此题考查了实数的运算、零指数幂、特殊角的三角函数值,属于基础题,解答本题的关键是熟练每部分的运算法则.21、(2012•黔东南州)计算:(-1/2)1-- 12+(1-2)0-|3-2|考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.分析:根据负整数指数幂、二次根式的化简、零指数幂及绝对值的知识,分别得出各部分的最简值,继而合并可得出答案.解答:(-1/2) 1-- 12+(1-2)0-|3-2|=-2-23+1-(2-3)=-1-23-2+3=-3- 3.点评:此题考查了实数的运算、零指数幂及负整数指数幂的知识,属于基础题,掌握各部分的运算法则是解答本题的关键.22、(2012•莆田)计算:|-2|+ 4-(-1)2.考点:实数的运算.专题:计算题.分析:本题涉及绝对值、乘方、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|-2|+ 4-(-1) 2=2+2-1=3.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、乘方、二次根式化简等考点的运算.23、(2012•攀枝花)计算:|1-2|-2sin45°+(π-3.14)0+22-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:本题涉及零指数幂、负指数幂、绝对值、特殊角的三角函数值.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|1-2|-2sin45°+(π-3.14) 0+22-= 2-1-2×2/2 +1+1/ 4= 2 -1- 2 +1+1/ 4=1 /4 .点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.24、(2012•宁夏)计算:22•sin45°-(-2012)0-|1- 2|+(-1/2)2-.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:根据零指数幂、负整数指数幂、特殊三角函数值和绝对值的运算法则求出各项的值,然后根据四则运算求出结果即可.解答:22•sin45°-(-2012) 0-|1- 2|+(-1/2) 2-=22•2/ 2 -1-(2-1)+4=6-2点评:本题主要考查实数的运算的知识点,解答本题的关键是掌握零值数幂、负整数指数幂的运算法则,此题比较简单.25、(2012•南平)(1)计算:(-3)3×(1/3)2-+|π-4|-20120.(2)解不等式组:2x-1<7 ①3x<2x+8 ②考点:实数的运算;零指数幂;负整数指数幂;解一元一次不等式组.专题:探究型.分析:(1)分别根据有理数的乘方、负整数指数幂、绝对值的性质及0指数幂计算出各数,再根据有理数混合运算的法则进行解答即可;(2)分别求出各不等式的解集,再求出其公共解集即可.解答:解:(1)(-3)3×(1/3)2-+|π-4|-20120=-27×9+4-π-1=-240-π;(2)由①得,x<4;由②得,x<8,故此不等式组的解集为:x<4.点评:本题考查的是实数的运算及解一元一次不等式组,熟知有理数的乘方、负整数指数幂、绝对值的性质及0指数幂的计算法则是解答此题的关键.26、(2012•内江)计算:|1- 12|+(-1)2012+(8-π/8)0-364+(1/3)1-.考点:实数的运算;零指数幂;负整数指数幂.专题:计算题.分析:本题涉及零指数幂、负指数幂、乘方、绝对值、立方根等考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:|1- 12|+(-1) 2012+(8-π/8) 0-364+(1/3) 1-=23-1+1+1-4+3=23.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、负指数幂、乘方、绝对值、立方根等考点的运算.27、(2012•梅州)计算:|- 3|- 12+2sin60°+(1/3)1-.考点:实数的运算;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:分别根据绝对值的性质、特殊角的三角函数值及负整数指数幂计算出各数,再根据实数混合运算的法则进行计算即可.解答:|- 3|- 12+2sin60°+(1/3)1-= 3-23+2×3/2 +3=3.点评:本题考查的是实数的混合运算,熟知绝对值的性质、特殊角的三角函数值及负整数指数幂的计算法则是解答此题的关键.28、(2012•凉山州)计算:-12012-|1- 2cos45°|+ (-2)2×(1/2)2-+(π-1.4)0.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.专题:计算题.分析:分别根据有理数的乘方、绝对值的性质、特殊角的三角函数值及负整数指数幂、0指数幂计算出各数,再根据实数混合运算的法则进行计算即可.解答:-12012-|1- 2cos45°|+ (-2) 2×(1/2) 2-+(π-1.4) 0=-1-0+2×4+1=8.点评:本题考查的是实数的运算,熟知有理数的乘方、绝对值的性质、特殊角的三角函数值及负整数指数幂、0指数幂的运算是解答此题的关键.29、(2012•连云港)计算:9-(-1/5)0+(-1)2012.考点:实数的运算;零指数幂.专题:计算题.分析:分别进行二次根式的化简、零指数幂,然后将各部分的最简值进行合并即可得出答案.解答:9-(-1/5)0+(-1)2012=3-1+1=3.点评:此题考查了实数的运算,解答本题的关键是熟练零指数幂的运算及二次根式的化简,属于基础题.30、(2012•丽水)计算:2sin60°+|-3|- 12-(1/3)1-.考点:实数的运算;负整数指数幂;特殊角的三角函数值.分析:本题涉及特殊角的三角函数值、绝对值、二次根式化简、负指数四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:2sin60°+|-3|- 12-(1/3) 1-=2×3/2 +3-23-3=3+3-23-3新世纪教育网 精品资料版权所有@新世纪教育网=-3.点评:本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.新世纪教育网-- 中国最大型、最专业的中小学教育资源门户网站。
2012年全国中考数学试题分类解析汇编(159套63专题)专题16_一次函数(正比例函数)的图像和性质(附答案)
2012年全国中考数学试题分类解析汇编(159套63专题)专题16:一次函数(正比例函数)的图像和性质一、选择题1. (2012山西省2分)如图,一次函数y=(m ﹣1)x ﹣3的图象分别与x 轴、y 轴的负半轴相交于A .B ,则m 的取值范围是【 】A . m >1B . m <1C . m <0D . m >02. (2012陕西省3分)下列四组点中,可以在同一个正比例函数图象上的一组点是【 】 A .(2.-3),(-4,6) B .(-2,3),(4,6)C .(-2,-3),(4,-6)D .(2,3),(-4,6)3. (2012陕西省3分)在同一平面直角坐标系中,若一次函数y x 3=-+与y 3x 5=-图象交于点M ,则点M 的坐标为【 】A .(-1,4)B .(-1,2)C .(2,-1)D .(2,1)4. (2012浙江温州4分)一次函数y=-2x+4图象与y 轴的交点坐标是【 】 A. (0, 4) B. (4, 0) C. (2, 0) D. (0, 2 )5. (2012江苏苏州3分)若点(m ,n )在函数y=2x+1的图象上,则2m-n 的值是【 】 A.2 B.-2 C.1 D. -16. (2012江苏徐州3分)一次函数y=x -2的图象不经过【 】 A .第一象限 B .第二象限 C .第三象限D .第一象限7. (2012福建宁德4分)一次函数y 1=x +4的图象如图所示,则一次函数y 2=-x +b 的图象与y 1=x +4的图象的交点不可能...在【 】A .第一象限B .第二象限C .第三象限D .第四象限8. (2012福建泉州3分)若y kx 4=-的函数值y 随着x 的增大而增大,则k 的值可能是下列的【 】.A .4- B.21-C.0D.3 9. (2012湖南娄底3分)对于一次函数y=﹣2x+4,下列结论错误的是【 】 A . 函数值随自变量的增大而减小 B . 函数的图象不经过第三象限C . 函数的图象向下平移4个单位长度得y=﹣2x 的图象D . 函数的图象与x 轴的交点坐标是(0,4)10. (2012四川乐山3分)若实数a 、b 、c 满足a+b+c=0,且a <b <c ,则函数y=ax+c 的图象可能是【 】A .B .C .D .11. (2012四川南充3分)下列函数中是正比例函数的是【 】( A )y=-8x(B )y=8x-( C )y=5x 2+6 (D )y= -0.5x-112. (2012辽宁沈阳3分)一次函数y=-x+2的图象经过【 】A.一、二、三象限B.一、二、四象限C.一、三、四象限D.二、三、四象限 13. (2012山东滨州3分)直线1y x =-不经过【 】A .第一象限B .第二象限C .第三象限D .第四象限14. (2012江西南昌3分)已知一次函数y=kx+b (k≠0)经过(2,﹣1)、(﹣3,4)两点,则它的图象不经过【 】 A . 第一象限 B . 第二象限C . 第三象限D .第四象限15. (2012吉林长春3分)有一道题目:已知一次函数y=2x+b ,其中b <0,…,与这段描述相符的函数图像可能是【 】二、填空题1. (2012上海市4分)已知正比例函数y=kx (k≠0),点(2,﹣3)在函数上,则y 随x 的增大而 ▲ (增大或减小).2. (2012浙江湖州4分)一次函数y=kx+b (k ,b 为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为 ▲3. (2012江苏南京2分)已知一次函数y kx k 3=+-的图像经过点(2,3),则k 的值为 ▲4. (2012湖南长沙3分)如果一次函数y=mx+3的图象经过第一、二、四象限,则m 的取值范围是 ▲ .5. (2012湖南永州3分)一次函数y=﹣x+1的图象不经过第 ▲ 象限.6. (2012湖南怀化3分)如果点()()1122P 3,y ,P 2,y 在一次函数y 2x 1=-的图像上,则1y ▲ 2y .(填“>”,“<”或“=”)7. (2012湖南衡阳3分)如图,一次函数y=kx+b 的图象与正比例函数y=2x 的图象平行且经过点A (1,﹣2),则kb= ▲ .8. (2012湖南株洲3分)一次函数y=x+2的图象不经过第▲ 象限.9. (2012贵州贵阳4分)在正比例函数y=﹣3mx中,函数y的值随x值的增大而增大,则P(m,5)在第▲ 象限.10. (2012江西省3分)已知一次函数y=kx+b(k≠0)经过(2,﹣1)、(﹣3,4)两点,则其图像不经过...第▲ 象限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 37 页 2012年全国中考数学试题分类解析汇编(159套63专题) 专题5:分式 一、选择题
1. (2012安徽省4分)化简xxxx112的结果是【 】 A.x+1 B. x-1 C.—x D. x 【答案】D。 【考点】分式的加法运算 【分析】分式的加减,首先看分母是否相同,同分母的分式加减,分母不变,分子相加减,如果分母不同,先通分,后加减,本题分母互为相反数,可以化成同分母的分式加减: 222(1)111111xxxxxxxxxxxxxxx
。故选D。
2. (2012浙江湖州3分)要使分式1x有意义,x的取值范围满足【 】 A.x=0 B.x≠0 C.x>0 D.x<0 【答案】B。 【考点】分式有意义的条件。 【分析】根据分式分母不为0的条件,要使1x在实数范围内有意义,必须x≠0。故选B。 3.(2012浙江嘉兴、舟山4分)若分式x1x+2的值为0,则【 】 A. x=﹣2 B. x=0 C. x=1或2 D. x=1 【答案】D。 【考点】分式的值为零的条件。
【分析】∵分式x1x+2的值为0,∴x1=0x+2x+20,解得x=1。故选D。 4. (2012浙江绍兴4分)化简111xx可得【 】 A.21xx B. 21xx C.2
21xxx
D.221xxx
【答案】B。 第 2 页 共 37 页
【考点】分式的加减法。 【分析】原式=211(1)xxxxxx。故选B。 5. (2012浙江义乌3分)下列计算错误的是【 】 A.0.2ab2ab0.7ab7ab B.3223xyxyxy C.ab1ba D.123ccc 【答案】A。 【考点】分式的混合运算。 【分析】根据分式的运算法则逐一作出判断: A、0.2ab2a10b0.7ab7a10b,故本选项错误;
B、3223xyxyxy,故本选项正确; C、abba1baba,故本选项正确; D、123ccc,故本选项正确。 故选A。 6. (2012湖北武汉3分)一列数a1,a2,a3,„,其中a1= 1 2,an= 1 1+an-1 (n为不小于2的整数),则 a4=【 】 A. 5 8 B. 8 5 C. 13 8 D. 8 13 【答案】 A。 【考点】求代数式的值。
【分析】由 a1=12,an=n11+a,
得234123112113115a===a===a===1231+a31+a51+a81+1+1+235,,。故选A。
7. (2012湖北天门、仙桃、潜江、江汉油田3分)化简2211x+1x1的结果是【 】 第 3 页 共 37 页
A.21x+1 B.21x1 C.(x+1)2 D.(x﹣1)2 【答案】D。 【考点】分式的混合运算。 【分析】将原式括号中的两项通分并利用同分母分式的减法法则计算,分子合并,同时将除式的分母利用平方差公式分解因式,然后利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分后即可得到最简结果:
2
2
x+1x121x+121x11===x1x+1x1x+1x+1x1x+11
。故
选D。 8. (2012湖北宜昌3分)若分式2a+1有意义,则a的取值范围是【 】 A.a=0 B.a=1 C.a≠﹣1 D.a≠0 【答案】C。 【考点】分式有意义的条件。 【分析】根据分式分母不为0的条件,要使2a+1在实数范围内有意义,必须a+10a1。故选C。 9. (2012四川凉山4分)已知b5a13,则abab的值是【 】 A.23 B.32 C.94 D.49 【答案】D。 【考点】比例的性质。 【分析】∵b5a13,∴设出b=5k,得出a=13k,把a,b的值代入abab,得, ab13k5k8k4===ab13k5k18k9。故选D。
10. (2012山东临沂3分)化简4122aaa的结果是【 】 A. 2aa B. 2aa C. 2aa D. 2aa 【答案】A。 【考点】分式的混合运算。 第 4 页 共 37 页
【分析】4+22+21==222aaaaaaaaa。故选A。 11. (2012山东威海3分)化简22x1+x93x的结果是【 】 A. 1x3 B. 1x+3 C. 13x D. 23x+3x9 【答案】B。 【考点】分式运算法则,平方差公式。 【分析】通分后约分化简即可: 22
2xx+32x1x31+x93xx9x+3x3x+3
。故选B。
12. (2012山东淄博4分)化简222a1a1aaa2a1的结果是【 】 (A)1a (B)a (C)11aa (D)11aa 【答案】A。 【考点】分式的除法。
【分析】2222a1a1a1a11==aaa2a1aa1a1a1a。故选A。
13. (2012广西钦州3分)如果把5xx+y的x与y都扩大10倍,那么这个代数式的值【 】 A.不变 B.扩大50倍 C.扩大10倍 D.缩小到原来的110 【答案】A。 【考点】分式的基本性质。 【分析】依题意分别用10x和10y去代换原分式中的x和y,利用分式的基本性质化简即可:
∵510x105x5x10x+10y10xyx+y,∴新分式与原分式的值相等。故选A。 14. (2012河北省3分)化简 221x1x1的结果是【 】 A.2x1 B.32x1 C.2x+1 D.2(x+1) 【答案】C。 【考点】分式的乘除法。 第 5 页 共 37 页
【分析】将分式22x1的分母 因式分解,再将除法转化为乘法进行计算: 22122(x1)x1x1(x1)(x1)x1
。故选C。
15. (2012新疆区5分)若分式23x有意义,则x的取值范围是【 】 A.x≠3 B.x=3 C.x<3 D.x>3 【答案】A。 【考点】分式有意义的条件。 【分析】根据分式分母不为0的条件,要使23x在实数范围内有意义,必须3﹣x≠0,即x≠3。故选A。二、填空题 1. (2012天津市3分)化简22x1x1x1-的结果是 ▲ .
【答案】1x1。 【考点】分式的加减法。 【分析】根据同分母分式相加减,分母不变,只把分子相加减计算,然后约分即可得解:
222x1x11==x1x1x1x1
。
2. (2012山西省3分)化简222x1x12+xx2x+1x+x的结果是 ▲ . 【答案】3x。 【考点】分式的混合运算。 【分析】2222x+1x1x1x12x12123+=+=+=xxx+1xxxxx2x+1x+xx1。
3. (2012宁夏区3分)当a ▲ 时,分式1a2有意义. 【答案】2。 【考点】分式有意义的条件。 【分析】根据分式分母不为0的条件,要使1a2在实数范围内有意义,必须a20a2。 第 6 页 共 37 页
4. (2012浙江杭州4分)化简2m163m12得 ▲ ;当m=﹣1时,原式的值为 ▲ . 【答案】m+43,1。 【考点】分式的化简和求值。 【分析】先把分式的分子和分母分解因式并得出约分后即可,把m=﹣1代入上式即可求出当m=﹣1时原式的值: 2m+4m4m16m+4==3m123m43
;
当m=﹣1时,原式=1+4=13。 5. (2012浙江台州5分)计算yxyx的结果是 ▲ . 【答案】2x 【考点】分式的乘法和除法。
【分析】根据分式的乘法和除法运算法则计算即可:2yxxy=xy=xx=xxy。
6. (2012浙江温州5分)若代数式21x1的值为零,则x= ▲ . 【答案】3。 【考点】分式的值为零的条件,解分式方程。 【分析】由题意得,21x1=0,解得:x=3,经检验的x=3是原方程的根。 7. (2012江苏镇江2分)若117+mnm+n,则nm+mn的值为 ▲ 。 【答案】5。 【考点】求分式的值,完全平方公式的应用。 【分析】∵22222117m+n7+m+n7mnm+2mn+n7mnm+n5mnmnm+nmnm+n, ∴22nmn+m5mn+===5mnmnmn。
8. (2012福建莆田4分)当1a2时,代数式22a22a1的值为 ▲ . 【答案】1。
