专题四 第2讲
【步步高 通用(理)】2014届高三二轮专题突破 专题四 第2讲

热点分类突破
专题四 第2讲
(1)立体几何中,要证线垂直于线,常常先证线垂 直于面,再用线垂直于面的性质易得线垂直于线.要证线平
∴平面EMC∥平面PAB. ∵EC⊂平面EMC, ∴EC∥平面PAB.
本 讲 栏 目 开 关
专题四 第2讲
方法二
如图,延长DC、AB,
设它们交于点N,连接PN. ∵∠NAC=∠DAC=60° , AC⊥CD,∴C为ND的中点. ∵E为PD的中点,∴EC∥PN. ∵EC⊄平面PAB,PN⊂平面PAB, ∴EC∥平面PAB.
答案 (1)D
(2)D
热点分类突破
考点二 线线、线面的位置关系
专题四 第2讲
例2 如图,在四棱锥P—ABCD中,∠ABC =∠ACD=90° ,∠BAC=∠CAD=60° , PA⊥平面ABCD,E为PD的中点,PA=
本 讲 栏 目 开 关
2AB. (1)若F为PC的中点,求证:PC⊥平面AEF; (2)求证:EC∥平面PAB.
本 连接EM,CM. 讲 栏 目 则EM∥PA. 开 ∵EM⊄平面PAB,PA⊂平面PAB, 关
∴EM∥平面PAB. 在Rt△ACD中,∠CAD=60° ,MC=AM, ∴∠ACM=60° .而∠BAC=60° ,∴MC∥AB. ∵MC⊄平面PAB,AB⊂平面PAB,
热点分类突破
∴MC∥平面PAB.∵EM∩MC=M,
热点分类突破
确的是 C.若l∥α,m⊂α,则l∥m
本 讲 栏 目 开 关
专题四 第2讲
( D.若l∥α,m∥α,则l∥m )
(2)设l,m是两条不同的直线,α是一个平面,则下列命题正 A.若l⊥m,m⊂α,则l⊥α B.若l⊥α,l∥m,则m⊥α
解析 (1)对于A,直线l1与l3可能异面、相交; 对于C,直线l1、l2、l3可能构成三棱柱的三条棱而不共面;
第2讲 非谓语动词 讲义

知识运用篇专题四语法填空有提示词填空第2讲非谓语动词•技法1:知晓句法功能•高考语法填空对非谓语动词的考查多为基本句法功能的考查,因此掌握非谓语动词的句法功能对解题非常重要。
•(2016·全国卷Ⅲ)People probably cooked their food in large pots,______________(use) twigs(树枝)to remove it.•[解题思路]•①首先分析句子结构→句子缺少非谓语•②然后分析非谓语句法功能→非谓语作状语•③最后判断主被动关系→people和use存在主动关系•尝试解答:_using_•[技法解读]•1.非谓语动词作定语•(1)非谓语动词作定语时,表示将来时要想到用不定式。
I have many letters to write tomorrow afternoon.我明天下午有许多信要写。
•(2)非谓语动词作定语时,表正在进行或主动进行时要想到用现在分词。
•The boy playing in the playground is my brother.正在操场上玩耍的那个小男孩是我弟弟。
•(3)非谓语动词作定语时,表示已经完成或被动完成时要想到用过去分词。
•The trees blown down in the storm have been moved off the road.•在风暴中被刮倒的树木已被移出道路。
•2.非谓语动词作状语•(1)非谓语动词作目的状语、出乎意料的结果状语或某些形容词(表喜、怒、哀、乐)表语后的原因状语时,要想到用不定式。
•Firemen had to break in to reach the people trapped inside.•为了抢救困在屋里的人,消防人员不得不破门而入。
•(2)非谓语动词作时间状语、伴随状语、原因状语、条件状语或意料之中的结果状语时,如果动词和逻辑主语存在主动关系,要想到用现在分词。
专题四-对数运算与对数函数-讲义教学-2
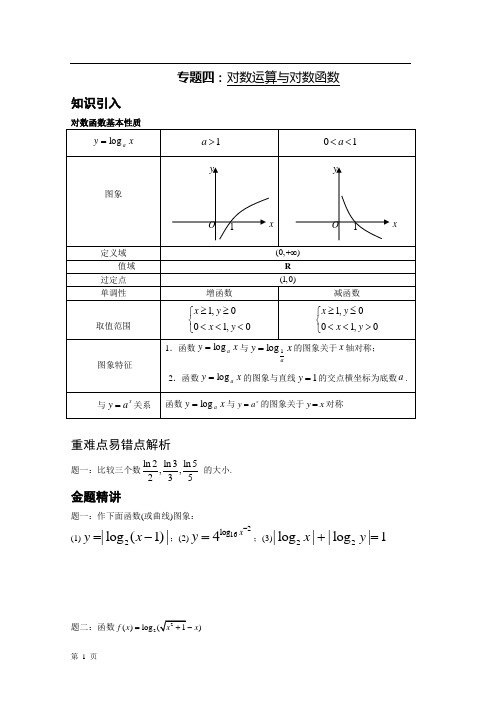
专题四:对数运算与对数函数 知识引入
对数函数基本性质
重难点易错点解析
题一:比较三个数ln 2ln 3ln 5,,235
的大小. 金题精讲
题一:作下面函数(或曲线)图象:
(1)2|log (1)|y
x =-;(2)216log 4x y -=;(3)22|log ||log |1x y +=
题二:函数2()log )f x x =
(1)判断函数的奇偶性,并证明; (2)求函数的单调递减区间.
题三:下面说法对吗?
(1)“函数)(x f 有反函数”的充要条件是“函数)(x f 是单调函数”
(2)函数与反函数如果有交点,则交点一定在直线x y =上;
(3)增函数与反函数如果有交点,则交点一定在直线x y =上;
(4)偶函数没有反函数
满分冲刺
题一:已知:当0x >时,2ln(1)2x x x +>
+ 证明:19291(
)10e
<
题二:已知1x 是方程lg 3x x +=的根,2x 是方程103x x +=的根,则12x x +的值是
讲义参考答案
重难点易错点解析
题一
答案:ln5ln2ln3 523
<<
金题精讲
题一
答案:略
题二
答案:(1)奇函数(2)(,)
-∞+∞
题三
答案:(1) 错(2)错(3)对(4)对
满分冲刺
题一
答案:略
题二
答案:3
思维拓展
题一
答案:③④。
专题四 二 美苏之间的冷战(详细备课资料)

专题四二美苏之间的冷战(详细备课资料)雅尔塔体系事实上划分美苏的势力范围,这样,在雅尔塔体系中,美苏逐渐成为处于支配地位的两极,形成两极格局。
所谓两极格局,是指二战后出现的美苏对抗的格局。
这种对抗不是直接的武力对抗,而是采取除此之外的一切方式。
相互遏制,却又不诉诸武力。
我们把这种除战争以外的一切敌对行动总称为冷战。
简单来讲,冷战是非战争的对抗,落脚点是对抗。
美苏在二战期间是盟友,二战结束以后,美苏之间为什么会出现冷战呢?即两国为什么会对抗呢?一、冷战局面的形成原因二战之后,美苏为什么展开对抗?将这一问题分为两层:(1)美苏两国为什么不继续合作了?(2)在不继续合作的同时,美苏两国为什么走向了对抗?首先思考二战以后,美苏两国为什么不继续保持以前的盟友关系,继续合作呢?①二战结束,失去了战时同盟的基础。
二战期间,美国与苏联结成反法西斯同盟,合作的基础是抗击共同的敌人法西斯。
随着二战结束,共同的敌人法西斯被彻底打败,美国与苏联失去了战争时期结成的那种同盟关系的基础。
这只能解释在二战以后,美苏两国为什么不继续合作呢。
美苏在不继续合作的同时,为什么走向了对抗?②社会制度和意识形态的差异。
两国对抗的原因之一是两国社会制度和意识形态的巨大差异。
③国家利益的冲突:美国认为苏联是其称霸世界的最大障碍(根本原因)根据政治学原理,外交政策制定的出发点是国家利益。
美苏对抗的根本原因在于两国国家利益的根本对立。
二战结束后,美国经济、军事实力急剧膨胀,成为资本主义世界头号经济和军事强国。
美国实力的上升使其政治野心膨胀起来,美国力图称霸世界。
与此同时,苏联的军事力量空前壮大,国际地位空前提高,成为唯一能够与美国相抗衡的政治军事大国,并且积极扩大自己的势力。
美国统治集团认为强大的苏联已经成为它称霸世界的最大障碍。
于是美国采取种种措施遏制苏联,苏联针锋相对,采取反击措施,导致出现美苏两国对抗的局面。
所以美苏走向对抗的根本原因是两国国家利益的冲突。
《创新设计》2022高考数学(浙江专用理科)二轮专题精练:专题四 立体几何4-2 Word版含解析

第2讲空间中的平行与垂直(建议用时:60分钟)一、选择题1.在下列命题中,不是公理的是().A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.假如一条直线上的两点在一个平面内,那么这条直线上全部的点都在此平面内D.假如两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线解析选项A是面面平行的性质定理.答案 A2.(2022·辽宁卷)已知m,n表示两条不同直线,α表示平面.下列说法正确的是().A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α解析法一若m∥α,n∥α,则m,n可能平行、相交或异面,A错;若m⊥α,n⊂α,则m⊥n,由于直线与平面垂直时,它垂直于平面内任始终线,B正确;若m⊥α,m⊥n,则n∥α或n⊂α,C错;若m∥α,m⊥n,则n与α可能相交,可能平行,也可能n⊂α,D错;法二如图,在正方体ABCD-A′B′C′D′中,用平面ABCD表示α.A项中,若m为A′B′,n为B′C′,满足m∥α,n∥α,但m与n是相交直线,故A错.B项中,m⊥α,n⊂α,∴m⊥n,这是线面垂直的性质,故B正确.C项中,若m为AA′,n为AB,满足m⊥α,m⊥n,但n⊂α,故C错.D项中,若m为A′B′,n为B′C′,满足m∥α,m⊥n,但n∥α,故D错.答案 B3.(2021·丽水模拟)已知两条直线a,b与两个平面α,β,b⊥α,则下列命题中正确的是().①若a∥α,则a⊥b;②若a⊥b,则a∥α;③若b⊥β,则α∥β;④若α⊥β,则b∥β.A.①③B.②④C.①④D.②③解析过直线a作平面γ使α∩γ=c,则a∥c,再依据b⊥α可得b⊥c,从而b⊥a,命题①是真命题;下面考虑命题③,由b⊥α,b⊥β,可得α∥β,命题③为真命题.故正确选项为A.答案 A4.已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中确定能推出m⊥β的是().A.α⊥β,且m⊂αB.m∥n,且n⊥βC.α⊥β,且m∥αD.m⊥n,且n∥β解析依据定理、性质、结论逐个推断.由于α⊥β,m⊂α⇒可能平行、相交、m在β面内,故A错误;由线面垂直的性质定理可知B正确;若α⊥β,m∥α,则m,β的位置关系也不确定,故C错误;若m⊥n,n∥β,则m,β的位置关系也不确定,故D错误.答案 B5.已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有().A.1 B.2 C.3 D.4解析①中m,n可能异面或相交,故不正确;②由于m∥α,n⊥β且α⊥β成立时,m,n 两直线的关系可能是相交、平行、异面,故不正确;③由于m⊥α,α∥β可得出m⊥β,再由n∥β可得出m⊥n,故正确;④分别垂直于两个垂直平面的两条直线确定垂直,正确.故选B.答案 B6.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则().A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l解析假设α∥β,由m⊥平面α,n⊥平面β,则m∥n,这与已知m,n为异面直线冲突,那么α与β相交,设交线为l1,则l1⊥m,l1⊥n,在直线m上任取一点作n1平行于n,那么l1和l都垂直于直线m与n1所确定的平面,所以l1∥l.答案 D7.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H 必在().A.直线AB上B.直线BC上C.直线AC上D.△ABC的内部解析∵AC⊥AB,AC⊥BC1,AB∩BC1=B,∴AC⊥平面ABC1.又AC⊂平面ABC,∴平面ABC1⊥平面ABC,∴C1在面ABC上的射影H必在两平面交线AB上,故选A.答案 A二、填空题8.设α和β为两个不重合的平面,给出下列四个命题:①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;②若α外一条直线l与α内的一条直线平行,则l和α平行;③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.其中为真命题的是________(写出全部真命题的序号).解析由①知α内两条相交直线分别平行于平面β,则两条相交直线确定的平面α平行于平面β,故①为真命题;由线面平行的判定定理知,②为真命题;对于③,如图,α∩β=l,a ⊂α,a⊥l,但不愿定有α⊥β,故③为假命题;对于④,直线l与平面α垂直的充分必要条件是l与α内的两条相交直线垂直,故④为假命题.综上所述,真命题的序号为①②.答案①②9.(2021·金华调研)下列四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出直线AB∥平面MNP的图形的序号是________(写出全部符合要求的图形序号).。
高考数学二轮复习 第一部分 专题篇 专题四 立体几何 第二讲 空间点、线、面位置关系的判断课时作业

2017届高考数学二轮复习第一部分专题篇专题四立体几何第二讲空间点、线、面位置关系的判断课时作业理1.(2016·正定摸底)已知直线a与平面α,β,α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线解析:设直线a和点B所确定的平面为γ,则α∩γ=a,记β∩γ=b,∵α∥β,∴a ∥b,故存在唯一一条直线b与a平行.答案:D2.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,且m⊥α,则l⊥α;②若m∥l,且m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.其中正确命题的个数是( )A.1 B.2C.3 D.4解析:易知①正确;②错误,l与α的具体关系不能确定;③错误,以墙角为例即可说明;④正确,可以以三棱柱为例证明,故选B.答案:B3.如图所示,O为正方体ABCDA1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是( )A.A1D B.AA1C.A1D1D.A1C1解析:由题意知,A1C1⊥平面DD1B1B,又OB1⊂面DD1B1B,所以A1C1⊥OB1,故选D.答案:D4.(2016·某某模拟)设m、n为两条不同的直线,α、β为两个不同的平面,给出下列命题:①若m⊥α,m⊥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥α,则m∥n;④若m⊥α,n⊥α,则m∥n.上述命题中,所有真命题的序号是( )A.①④B.②③C.①③D.②④解析:由线面垂直的性质定理知①④正确;平行于同一条直线的两个平面可能相交,也可能平行,故②错;平行于同一平面的两条直线可能平行,也可能相交或异面,故③错.选A. 答案:A5.如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )A.AP⊥PB,AP⊥PCB.AP⊥PB,BC⊥PBC.平面BPC⊥平面APC,BC⊥PCD.AP⊥平面PBC解析:A中,因为AP⊥PB,AP⊥PC,PB∩PC=P,所以AP⊥平面PBC,又BC⊂平面PBC,所以AP⊥BC,故A正确;C中,因为平面BPC⊥平面APC,BC⊥PC,所以BC⊥平面APC,AP⊂平面APC,所以AP⊥BC,故C正确;D中,由A知D正确;B中条件不能判断出AP⊥BC,故选B.答案:B6.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是( ) A.垂直B.相交不垂直C .平行D .重合 解析:如图,分别取另三条棱的中点A ,B ,C 将平面LMN 延展为平面正六边形AMBNCL ,因为PQ ∥AL ,PR ∥AM ,且PQ 与PR 相交,AL与AM 相交,所以平面PQR ∥平面AMBNCL ,即平面LMN ∥平面PQR .答案:C7.一个面截空间四边形的四边得到四个交点,如果该空间四边形的两条对角线与这个截面平行,那么此四个交点围成的四边形是________.解析:如图,由题意得AC ∥平面EFGH ,BD ∥平面EFGH .∵AC ⊂平面ABC ,平面ABC ∩平面EFGH =EF ,∴AC ∥EF ,同理AC ∥GH ,所以EF ∥GH .同理,EH ∥FG ,所以四边形EFGH 为平行四边形.答案:平行四边形8.(2016·某某模拟)如图,在正方体ABCD A 1B 1C 1D 1中,P 为棱DC 的中点,则D 1P 与BC 1所在直线所成角的余弦值等于________.解析:连接AD 1,AP (图略),则∠AD 1P 就是所求角,设AB =2,则AP =D 1P =5,AD 1=22,∴cos ∠AD 1P =12AD 1D 1P =105. 答案:1059.如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,点E ,F 分别是棱BC ,CC 1的中点,P 是侧面BCC 1B 1内一点,若A 1P ∥平面AEF ,则线段A 1P 长度的取值X 围是________.解析:取B 1C 1中点M ,则A 1M ∥AE ;取BB 1中点N ,则MN ∥EF (图略),∴平面A 1MN ∥平面AEF .若A 1P ∥平面AEF ,只需P ∈MN ,则P 位于MN 中点时,A 1P 最短;当P 位于M 或N 时,A 1P 最长.不难求得A 1P 的取值X 围为⎣⎢⎡⎦⎥⎤324,52. 答案:⎣⎢⎡⎦⎥⎤324,52 10.(2016·某某模拟)如图,在四面体ABCD 中,平面BAD ⊥平面CAD ,∠BAD =90°.M ,N ,Q 分别为棱AD ,BD ,AC 的中点.(1)求证:CD ∥平面MNQ ;(2)求证:平面MNQ ⊥平面CAD .证明:(1)因为M ,Q 分别为棱AD ,AC 的中点,所以MQ ∥CD ,又CD ⊄平面MNQ ,MQ ⊂平面MNQ ,故CD ∥平面MNQ .(2)因为M ,N 分别为棱AD ,BD 的中点,所以MN ∥AB ,又∠BAD =90°,故MN ⊥AD .因为平面BAD ⊥平面CAD ,平面BAD ∩平面CAD =AD ,且MN ⊂平面ABD ,所以MN ⊥平面CAD ,又MN ⊂平面MNQ ,所以平面MNQ ⊥平面CAD .11.(2016·某某五校联考)如图,四棱锥P ABCD 中,底面ABCD 是菱形,PA =PD ,∠BAD =60°,E 是AD 的中点,点Q 在侧棱PC 上.(1)求证:AD ⊥平面PBE ;(2)若Q 是PC 的中点,求证:PA ∥平面BDQ ;(3)若V P BCDE =2V Q ABCD ,试求CP CQ的值.解析:(1)证明:由E 是AD 的中点,PA =PD 可得AD ⊥PE .又底面ABCD 是菱形,∠BAD =60°,所以AB =BD ,又因为E 是AD 的中点,所以AD ⊥BE ,又PE ∩BE =E ,所以AD ⊥平面PBE .(2)证明:连接AC (图略),交BD 于点O ,连接OQ .因为O 是AC 的中点, Q 是PC 的中点,所以OQ ∥PA ,又PA ⊄平面BDQ ,OQ ⊂平面BDQ ,(3)设四棱锥P BCDE ,Q ABCD 的高分别为h 1,h 2.所以V P BCDE =13S 四边形BCDE h 1, V Q ABCD =13S 四边形ABCD h 2.又因为V P BCDE =2V Q ABCD ,且S 四边形BCDE =34S 四边形ABCD ,所以CP CQ =h 1h 2=83. 12.(2016·某某模拟)一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC 的中点为M ,GH 的中点为N .(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由);(2)证明:直线MN ∥平面BDH ;(3)过点M ,N ,H 的平面将正方体分割为两部分,求这两部分的体积比.解析:(1)点F ,G ,H 的位置如图所示.(2)证明:连接BD ,设O 为BD 的中点,连接OM ,OH ,AC ,BH ,MN .∵M ,N 分别是BC ,GH 的中点,∴OM ∥CD ,且OM =12CD ,NH ∥CD ,且NH =12CD , ∴OM ∥NH ,OM =NH ,则四边形MNHO 是平行四边形,∴MN ∥OH ,又∵MN ⊄平面BDH ,OH ⊂平面BDH ,(3)由(2)知,OM∥NH,OM=NH,连接GM,MH,过点M,N,H的平面就是平面GMH,它将正方体分割为两个同高的棱柱,高都是GH,底面分别是四边形BMGF和三角形MGC,体积比等于底面积之比,即3∶1.。
2020浙江高考政治二轮专题强化训练:专题四第二讲 新发展理念和中国特色社会主义新时代的经济建设
专题强化训练一、判断题(正确的在括号内写T,错误的写F)1.当前我国经济保持高速增长。
(F)2.必须把科技创新摆在国家发展全局的核心位置。
(T)3.坚持共享发展,必须坚持发展朝着同步富裕方向不断迈进。
(F)4.推动我国经济结构的战略性调整,就是要大力发展第三产业,减少第一、第二产业的数量。
(F)5.绿色发展注重的是解决发展内外联动问题。
(F)二、选择题(每小题给出的四个选项中,只有一项是符合题目要求的)6.我国当前的社会主要矛盾已由人民群众日益增长的物质文化需要同落后的社会生产之间的矛盾,转变为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾。
这()①意味着我国社会主义现代化建设目标已经实现②表明我国居民的生活水平不断提高③意味着我国居民消费己经由生存型消费转变为发展型和享受型消费④源于我国改革开放以来经济的发展和居民收入的增加A.①②B.②③C.②④D.③④解析:选C。
我国社会主要矛盾的转化,源于我国改革开放以来经济的发展和居民收入的增加,表明我国居民的生活水平不断提高,②④符合题意;我国社会主义现代化建设目标还没有实现,①错误;③不符合实际,排除。
7.某市提出下列发展经济思路:统筹外向型经济和内源型经济,外资内资一齐引;统筹先进制造业和现代服务业,二、三产业一块抓;统筹城镇化和新农村建设,促进城乡一体化。
下列说法中能够概括这一思路的是()A.统筹兼顾,增强发展的协调性B.以人为本,注重发展的目的性C.创新发展,提高对外开放水平D.转型提升,注重发展的科学性解析:选A。
题中内外统筹、制造业与服务业统筹、城镇化和新农村统筹,各方面协调发展,体现的是统筹兼顾,增强发展的协调性,故选A项。
B、C、D三项与题意不符。
8.党的十八大以来,我国经济建设取得重大成就,人民生活不断改善,生态文明建设成效显著。
下面属于经济方面的成就的是()①经济保持中高速增长,对世界经济增长的贡献率不断提高②合理有序的收入分配格局基本形成,高收入者占人口多数③覆盖城乡居民的社会保障体系基本建立,人民健康大幅提高④创新驱动发展战略大力实施,创新型国家建设成果丰硕A.①②B.①③C.①④D.②④解析:选C。
2019届高考数学二轮复习 第二部分专项二 专题四 2 第2讲 空间点、线、面的位置关系 学案 Word版含解析
第2讲 空间点、线、面的位置关系年份卷别考查内容及考题位置命题分析卷Ⅰ面面垂直的证明·T 18(1)卷Ⅱ异面直线所成的角·T 9 线面垂直的证明·T 20(1)2018卷Ⅲ面面垂直的证明·T 19(1)卷Ⅰ面面垂直的证明·T 18(1)空间异面直线所成角的余弦值的计算·T 10卷Ⅱ线面平行的证明·T 19(1)2017卷Ⅲ圆锥、空间线线角的求解·T 16 面面垂直的证明·T 19(1)卷Ⅰ求异面直线所成的角·T 11 面面垂直的证明·T 18(1)空间中线、面位置关系的判定与性质·T 14卷Ⅱ线面垂直的证明·T 19(1)2016卷Ⅲ线面平行的证明·T 19(1)1.高考对此部分的命题较为稳定,一般为“一小一大”或“一大”,即一道选择或填空题和一道解答题或仅一道解答题.2.选择题一般在第10~11题的位置,填空题一般在第14题的位置,多考查线面位置关系的判断,难度较小.3.解答题多出现在第18或19题的第一问的位置,考查空间中平行或垂直关系的证明,难度中等. 空间线面位置关系的判定(基础型)判断与空间位置关系有关命题真假的3种方法(1)借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断.(2)借助于反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.(3)借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.[考法全练]1.在正方体ABCD A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A .A 1E ⊥DC 1 B .A 1E ⊥BD C .A 1E ⊥BC 1D .A 1E ⊥AC解析:选C.A1B1⊥平面BCC1B1,BC1⊂平面BCC1B1,所以A1B1⊥BC1,又BC1⊥B1C,且B1C∩A1B1=B1,所以BC1⊥平面A1B1CD,又A1E⊂平面A1B1CD,所以BC1⊥A1E.故选C.2.已知直线l和两个不同的平面α,β,则下列命题是真命题的是( )A.若l∥α,且l∥β,则α∥βB.若l⊥α,且l⊥β,则α∥βC.若l⊂α,且α⊥β,则l⊥βD.若l∥α,且α∥β,则l∥β解析:选B.对于A,若l∥α,且l∥β,则α∥β或α与β相交,所以A错;因为垂直于同一条直线的两个平面平行,所以B正确;对于C,若l⊂α,且α⊥β,则l与β相交或l∥β或l⊂β,所以C错;对于D,若l∥α,且α∥β,则l∥β或l⊂β,所以D错.故选B.3.(2018·惠州第二次调研)设l,m,n为三条不同的直线,α为一个平面,则下列命题中正确的个数是( )①若l⊥α,则l与α相交;②若m⊂α,n⊂α,l⊥m,l⊥n,则l⊥α;③若l∥m,m∥n,l⊥α,则n⊥α;④若l∥m,m⊥α,n⊥α,则l∥n.A.1 B.2C.3 D.4解析:选C.对于①,若l⊥α,则l与α不可能平行,l也不可能在α内,所以l与α相交,①正确;对于②,若m⊂α,n⊂α,l⊥m,l⊥n,则有可能是l⊂α,故②错误;对于③,若l∥m,m∥n,则l∥n,又l⊥α,所以n⊥α,故③正确;对于④,因为m⊥α,n⊥α,所以m∥n,又l∥m,所以l∥n,故④正确.选C.4.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β;②如果m⊥α,n∥α,那么m⊥n;③如果α∥β,m⊂α,那么m∥β;④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号)解析:对于命题①,可运用长方体举反例证明其错误:如图,不妨设AA′为直线m,CD 为直线n,ABCD所在的平面为α,ABC′D′所在的平面为β,显然这些直线和平面满足题目条件,但α⊥β不成立.命题②正确,证明如下:设过直线n的某平面与平面α相交于直线l,则l∥n,由m⊥α知m⊥l,从而m⊥n,结论正确.由平面与平面平行的定义知命题③正确.由平行的传递性及线面角的定义知命题④正确.答案:②③④ 空间中平行、垂直关系的证明(综合型)直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.[典型例题]由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得四边形ABCD为正方形,O为AC与BD的交到的几何体如图所示.点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.【证明】 (1)取B1D1的中点O1,连接CO1,A1O1,由于ABCDA1B1C1D1为四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C.又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD.又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD.因为B1D1∥BD,所以EM ⊥B 1D 1,A 1E ⊥B 1D 1.又A 1E ,EM ⊂平面A 1EM ,A 1E ∩EM =E ,所以B 1D 1⊥平面A 1EM .又B 1D 1⊂平面B 1CD 1,所以平面A 1EM ⊥平面B 1CD 1.平行关系及垂直关系的转化空间平行、垂直关系证明的主要思想是转化,即通过判定、性质定理将线线、线面、面面之间的平行、垂直关系相互转化.[对点训练]1.如图,在四棱锥P ABCD 中,平面PAB ⊥平面ABCD ,AD ∥BC ,PA ⊥AB ,CD ⊥AD ,BC =CD =AD ,E 为AD 的中点.12(1)求证:PA ⊥CD .(2)求证:平面PBD ⊥平面PAB .证明:(1)因为平面PAB ⊥平面ABCD ,平面PAB ∩平面ABCD =AB ,又因为PA ⊥AB ,所以PA ⊥平面ABCD .则PA ⊥CD .(2)由已知,BC ∥ED ,且BC =ED ,所以四边形BCDE 是平行四边形,又CD ⊥AD ,BC =CD ,所以四边形BCDE 是正方形,连接CE (图略),所以BD ⊥CE ,又因为BC ∥AE ,BC =AE ,所以四边形ABCE 是平行四边形,所以CE ∥AB ,则BD ⊥AB .由(1)知PA ⊥平面ABCD ,所以PA ⊥BD ,又因为PA ∩AB =A ,则BD ⊥平面PAB ,且BD ⊂平面PBD ,所以平面PBD ⊥平面PAB .2.如图,已知斜三棱柱ABC A 1B 1C 1中,点D ,D 1分别为AC ,A 1C 1上的点.(1)当等于何值时,BC 1∥平面AB 1D 1?A 1D 1D 1C1(2)若平面BC 1D ∥平面AB 1D 1,求的值.ADDC解:(1)如图,取D 1为线段A 1C 1的中点,此时=1,A 1D 1D 1C1连接A 1B 交AB 1于点O ,连接OD 1.由棱柱的性质,知四边形A 1ABB 1为平行四边形,所以点O 为A 1B 的中点.在△A 1BC 1中,点O ,D 1分别为A 1B ,A 1C 1的中点,所以OD 1∥BC 1.又因为OD 1⊂平面AB 1D 1,BC 1⊄平面AB 1D 1,所以BC 1∥平面AB 1D 1.所以当=1时,BC 1∥平面AB 1D 1.A 1D 1D 1C1(2)由已知,平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O .因此BC 1∥D 1O ,同理AD 1∥DC 1.因为=,=.A 1D 1D 1C 1A 1O OB A 1D 1D 1C 1DC AD又因为=1,所以=1,即=1.A 1O OB DC AD AD DC 平面图形的折叠问题(综合型)[典型例题]如图①,在直角梯形ABCD 中,AD ∥BC ,∠ADC =90°,AB =BC .把△BAC 沿AC折起到△PAC 的位置,使得P 点在平面ADC 上的正投影O 恰好落在线段AC 上,如图②所示,点E ,F 分别为棱PC ,CD 的中点.(1)求证:平面OEF ∥平面PAD ;(2)求证:CD ⊥平面POF ;(3)若AD =3,CD =4,AB =5,求三棱锥E CFO 的体积.【解】 (1)证明:因为点P 在平面ADC 上的正投影O 恰好落在线段AC 上,所以PO ⊥平面ADC ,所以PO ⊥AC .由题意知O 是AC 的中点,又点E 是PC 的中点,所以OE ∥PA ,又OE ⊄平面PAD ,PA ⊂平面PAD ,所以OE ∥平面PAD .同理,OF ∥平面PAD .又OE ∩OF =O ,OE ,OF ⊂平面OEF ,所以平面OEF ∥平面PAD .(2)证明:因为OF ∥AD ,AD ⊥CD ,所以OF ⊥CD .又PO ⊥平面ADC ,CD ⊂平面ADC ,所以PO ⊥CD .又OF ∩PO =O ,所以CD ⊥平面POF .(3)因为∠ADC =90°,AD =3,CD =4,所以S △ACD =×3×4=6,12而点O ,F 分别是AC ,CD 的中点,所以S △CFO =S △ACD =,1432由题意可知△ACP 是边长为5的等边三角形,所以OP =,523即点P 到平面ACD 的距离为,523又E 为PC 的中点,所以E 到平面CFO 的距离为,543故V E CFO =××=.1332543583平面图形折叠问题的求解方法(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量,一般情况下,线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.(2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形. [对点训练]如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =,AB =BC =AD =a ,E 是AD 的π212中点,O 是AC 与BE 的交点,将△ABE 沿BE 折起到图2中△A 1BE 的位置,得到四棱锥A 1BCDE .(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为36,求a 的值.2解:(1)证明:在图1中,因为AB =BC =AD =a ,E 是AD 的中点,12∠BAD =,所以BE ⊥AC .π2即在图2中,BE ⊥A 1O ,BE ⊥OC ,从而BE ⊥平面A 1OC ,又CD ∥BE ,所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE ,且平面A 1BE ∩平面BCDE =BE ,又由(1)知,A 1O ⊥BE ,所以A 1O ⊥平面BCDE ,即A 1O 是四棱锥A 1BCDE 的高.由图1知,A 1O =AB =a ,平行四边形BCDE 的面积S =BE ·OC =a 2.2222从而四棱锥A 1BCDE 的体积为V =×S ×A 1O =×a 2×a =a 3,13132226由a 3=36,得a =6.262一、选择题1.设α为平面,a 、b 为两条不同的直线,则下列叙述正确的是( )A .若a ∥α,b ∥α,则a ∥b B .若a ⊥α,a ∥b ,则b ⊥αC .若a ⊥α,a ⊥b ,则b ∥αD .若a ∥α,a ⊥b ,则b ⊥α解析:选B.若a ∥α,b ∥α,则a 与b 相交、平行或异面,故A 错误;易知B 正确;若a⊥α,a⊥b,则b∥α或b⊂α,故C错误;若a∥α,a⊥b,则b∥α或b⊂α或b与α相交,故D错误.故选B.2.设l是直线,α,β是两个不同的平面,则下列说法正确的是( )A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若α⊥β,l⊥α,则l∥βD.若α⊥β,l∥α,则l⊥β解析:选B.对于A,若l∥α,l∥β,则α∥β或α与β相交,故A错;易知B正确;对于C,若α⊥β,l⊥α,则l∥β或l⊂β,故C错;对于D,若α⊥β,l∥α,则l与β的位置关系不确定,故D错.故选B.3.如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的是( )A.平面ABC⊥平面ABDB.平面ABD⊥平面BCDC.平面ABC⊥平面BDE,且平面ACD⊥平面BDED.平面ABC⊥平面ACD,且平面ACD⊥平面BDE解析:选C.因为AB=CB,且E是AC的中点,所以BE⊥AC,同理,DE⊥AC,由于DE∩BE =E,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE.故选C.4.已知m,n是两条不同的直线,α,β是两个不同的平面,给出四个命题:①若α∩β=m,n⊂α,n⊥m,则α⊥β;②若m⊥α,m⊥β,则α∥β;③若m⊥α,n⊥β,m⊥n,则α⊥β;④若m∥α,n∥β,m∥n,则α∥β.其中正确的命题是( )A.①②B.②③C.①④D.②④解析:选B.两个平面斜交时也会出现一个平面内的直线垂直于两个平面的交线的情况,①不正确;垂直于同一条直线的两个平面平行,②正确;当两个平面与两条互相垂直的直线分别垂直时,它们所成的二面角为直二面角,故③正确;当两个平面相交时,分别与两个平面平行的直线也平行,故④不正确.3 5.(2018·高考全国卷Ⅱ)在长方体ABCDA1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为( )A. B.1556C.D.5522解析:选C.如图,连接BD 1,交DB 1于O ,取AB 的中点M ,连接DM ,OM ,易知O 为BD 1的中点,所以AD 1∥OM ,则∠MOD 为异面直线AD 1与DB 1所成角.因为在长方体ABCD A 1B 1C 1D 1中,AB =BC =1,AA 1=,AD 13==2,DM ==,DB 1==,所以OMAD 2+DD AD 2+(12AB )252AB 2+AD 2+DD 5=AD 1=1,OD =DB 1=,于是在△DMO 中,由余弦定理,得cos ∠MOD =121252=,即异面直线AD 1与DB 1所成角的余弦值为,故选C.12+(52)2-(52)22×1×5255556.如图,在矩形ABCD 中,AB =,BC =1,将△ACD 沿AC 折3起,使得D 折起后的位置为D 1,且D 1在平面ABC 上的射影恰好落在AB 上,在四面体D 1ABC 的四个面中,有n 对平面相互垂直,则n 等于( )A .2B .3C .4D .5解析:选B.如图,设D 1在平面ABC 上的射影为E ,连接D 1E ,则D 1E ⊥平面ABC ,因为D 1E ⊂平面ABD 1,所以平面ABD 1⊥平面ABC .因为D 1E ⊥平面ABC ,BC ⊂平面ABC ,所以D 1E ⊥BC ,又AB ⊥BC ,D 1E ∩AB =E ,所以BC ⊥平面ABD 1,又BC ⊂平面BCD 1,所以平面BCD 1⊥平面ABD 1,因为BC ⊥平面ABD 1,AD 1⊂平面ABD 1,所以BC ⊥AD 1,又CD 1⊥AD 1,BC ∩CD 1=C ,所以AD 1⊥平面BCD1,又AD 1⊂平面ACD 1,所以平面ACD 1⊥平面BCD 1.所以共有3对平面互相垂直.故选B.二、填空题7.(2018·广州调研)正方体ABCD A 1B 1C 1D 1的棱长为2,点M 为CC 1的中点,点N 为线段DD 1上靠近D 1的三等分点,平面BMN 交AA 1于点Q ,则线段AQ 的长为________.解析:如图所示,在线段DD 1上靠近点D 处取一点T ,使得DT =,因为N 是线段DD 1上靠近D 1的三等分点,故D 1N =,故NT =2-1323-=1,因为M 为CC 1的中点,故CM =1,连接TC ,由NT ∥CM ,1323且CM =NT =1,知四边形CMNT 为平行四边形,故CT ∥MN ,同理在AA 1上靠近A 处取一点Q ′,使得AQ ′=,连接BQ ′,TQ ′,则有BQ ′∥CT ∥MN ,故13BQ ′与MN 共面,即Q ′与Q 重合,故AQ =.13答案:138.如图,∠ACB =90°,DA ⊥平面ABC ,AE ⊥DB 交DB 于点E ,AF ⊥DC 交DC 于点F ,且AD =AB =2,则三棱锥D AEF 体积的最大值为________.解析:因为DA ⊥平面ABC ,所以DA ⊥BC ,又BC ⊥AC ,DA ∩AC =A ,所以BC ⊥平面ADC ,所以BC ⊥AF .又AF ⊥CD ,BC ∩CD =C ,所以AF ⊥平面DCB ,所以AF ⊥EF ,AF ⊥DB .又DB ⊥AE ,AE ∩AF =A ,所以DB ⊥平面AEF ,所以DE 为三棱锥D AEF 的高.因为AE 为等腰直角三角形ABD 斜边上的高,所以AE =,设AF =a ,2FE =b ,则△AEF 的面积S =ab ≤·=×=,所以三棱锥D AEF 的体积V ≤×1212a 2+b 2212221213×=(当且仅当a =b =1时等号成立).12226答案:269.(2018·昆明调研)在长方体ABCD A 1B 1C 1D 1中,AB =AD =4,AA 1=2.过点A 1作平面α与AB ,AD 分别交于M ,N 两点,若AA 1与平面α所成的角为45°,则截面A 1MN 面积的最小值是________.解析:如图,过点A 作AE ⊥MN ,连接A 1E ,因为A 1A ⊥平面ABCD ,所以A 1A ⊥MN ,所以MN ⊥平面A 1AE ,所以A 1E ⊥MN ,平面A 1AE ⊥平面A 1MN ,所以∠AA 1E 为AA 1与平面A 1MN 所成的角,所以∠AA 1E =45°,在Rt △A 1AE 中,因为AA 1=2,所以AE =2,A 1E =2,在Rt △MAN 中,由射影定理得ME ·EN =AE 2=4,由基本不等式得MN =2ME +EN ≥2=4,当且仅当ME =EN ,即E 为MN 的中点时等号成立,所以截面A 1MN ME ·EN 面积的最小值为×4×2=4.1222答案:4210.如图,在三棱锥A BCD 中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD 、BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ;(2)AD ⊥AC .证明:(1)在平面ABD 内,因为AB ⊥AD ,EF ⊥AD ,所以EF ∥AB .又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC .(2)因为平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,BC ⊂平面BCD 且BC ⊥BD ,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC ⊥AD .又因为AB ⊥AD ,BC ∩AB =B ,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC .又因为AC ⊂平面ABC ,所以AD ⊥AC .11.如图所示,已知AB ⊥平面ACD ,D E ⊥平面ACD ,△ACD 为等边三角形,A D =DE =2AB ,F 为CD 的中点.求证:(1)AF ∥平面BCE ;(2)平面BCE ⊥平面CDE .证明:(1)如图,取CE 的中点G ,连接FG ,BG .因为F 为CD 的中点,所以GF ∥DE 且GF =DE .12因为AB ⊥平面ACD ,DE ⊥平面ACD ,所以AB ∥DE ,所以GF ∥AB .又因为AB =DE ,所以GF =AB .12所以四边形GFAB 为平行四边形,则AF ∥BG .因为AF ⊄平面BCE ,BG ⊂平面BCE ,所以AF ∥平面BCE .(2)因为△ACD 为等边三角形,F 为CD 的中点,因为DE ⊥平面ACD ,AF ⊂平面ACD ,所以DE ⊥AF .又CD ∩DE =D ,所以AF ⊥平面CDE .因为BG ∥AF ,所以BG ⊥平面CDE .又因为BG ⊂平面BCE ,所以平面BCE ⊥平面CDE .12.如图1,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,BD ⊥DC ,点E 是BC 边的中点,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,连接AE ,AC ,DE ,得到如图2所示的几何体.(1)求证:AB ⊥平面ADC ;(2)若AD =1,AC 与其在平面ABD 内的正投影所成角的正切值为,求点B 到平面ADE 6的距离.解:(1)证明:因为平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,又DC ⊥BD ,DC ⊂平面BCD ,所以DC ⊥平面ABD .因为AB ⊂平面ABD ,所以DC ⊥AB .又因为折叠前后均有AD ⊥AB ,且DC ∩AD =D ,所以AB ⊥平面ADC .(2)由(1)知DC ⊥平面ABD ,所以AC 在平面ABD 内的正投影为AD ,即∠CAD 为AC 与其在平面ABD 内的正投影所成的角.依题意知tan ∠CAD ==,DC AD6因为AD =1,所以DC =.6设AB =x (x >0),则BD =,x 2+1易知△ABD ∽△DCB ,所以=,AB AD DC BD即=,解得x =,x 16x 2+12故AB =,BD =,BC =3.23由于AB ⊥平面ADC ,所以AB ⊥AC ,又E 为BC 的中点,所以由平面几何知识得AE ==,BC 232同理DE ==,BC 232所以S △ADE =×1× =.12(32)2 -(12)2 22因为DC ⊥平面ABD ,所以V A BCD =CD ·S △ABD =.1333设点B 到平面ADE 的距离为d ,则d ·S △ADE =V B ADE =V A BDE =V A BCD =,131236所以d =,即点B 到平面ADE 的距离为.6262。
高考语文一轮复习 第二部分古代诗文阅读专题四文言文阅读第二讲文言虚词教学案 新人教版
高考语文一轮复习第二部分古代诗文阅读专题四文言文阅读第二讲文言虚词教学案新人教版文言虚词的“意义和用法”,指的是一个文言虚词在不同语境中的不同意义或者作用。
近年高考对虚词的考查呈逐渐淡化的趋势,课标全国卷已经取消了专门的虚词考查题,但虚词在文言文阅读理解以及翻译句子中的作用不容小觑,有必要进行分类归纳、比较鉴别。
典题探究【典题】阅读下面的文言文,完成第1~4题。
赵岐字邠卿,京兆长陵人也。
岐少明经,有才艺。
仕州郡,以廉直疾恶见惮。
永兴二年,辟.司空掾,议二千石得去官为亲行服,朝廷从之。
会河东太守刘祐去郡,而中常侍左悺兄胜代之,岐耻疾宦官,即日西归。
京兆尹延笃复以为功曹。
先是中常侍唐衡兄玹为京兆虎牙都尉,郡人以玹进不由德,皆轻侮之。
岐及从兄袭又数为贬议,玹深毒恨。
延熹元年,玹为京兆尹,岐惧祸及,乃与从子戬逃避之。
玹果收岐家属宗亲,陷以重法,尽杀之。
岐遂逃难四方,江、淮、海、岱,靡所不历。
自匿姓名,卖饼北海市中。
时安丘孙嵩年二十余,游市见岐,察非常人,停车呼与共载。
岐惧失色,嵩乃下帷,令骑屏行人。
密问岐曰:“视子非卖饼者,又相问而色动,不有重怨,即亡命乎.?我北海孙宾石,阖门百口,势能相济.。
”岐素闻嵩名,即以实告之,遂以俱归。
嵩先入白母曰:“出行,乃.得死友。
”迎入上堂,飨.之极欢。
藏岐复壁中数年,岐作《厄屯歌》二十三章。
后诸唐死灭,因赦乃出。
三府闻之,同时并辟。
九年,乃应司徒胡广之命。
会南匈奴、乌桓、鲜卑反叛,公卿举岐,擢拜并州刺史。
岐欲奏守边之策,未及上,会坐党事免,因撰次以为《御寇论》。
灵帝初,复遭党锢十余岁。
中平元年,四方兵起,诏选故刺史、二千石有文武才用者,征岐拜议郎。
车骑将军张温西征关中,请补长史,别屯安定。
大将军何进举为敦煌太守,行至襄武,岐与新除诸郡太守数人俱为.贼边章等所执。
贼欲胁以为帅,岐诡辞得免,展转还长安。
及献帝西都,复拜议郎,稍迁太仆。
及李傕专政,使太傅马日磾抚慰天下,以岐为副。
选修三:专题四民主集中制:我国人民代表大会制度的组织和活动原则第二课按照民主集中制建立的新型政体.doc
专题四民主集中制:我国人民代表大会制度的组织和活动原则第二课按照民主集中制建立的新型政体一、体现人民当家作主的根本政治制度1.含义:广大人民通过____________的方式选出人大代表,由他们组成各级________机关,代表人民统一行使国家权力,按照____________的原则,决定全国和各级地方的一切重大事务,并由权力机关产生________和司法机关,各司其职,行使管理国家和社会的各项权力。
2.地位:人民代表大会制度是我国的根本政治制度。
3.原因。
(1)人民代表大会制度决定着国家的其他各种________。
(2)人民代表大会制度是中国人民当家作主的________和重要途径,也是中国社会主义________的重要制度载体。
答案:1.直接或间接国家权力民主集中制行政3.(1)具体制度(2)最高形式政治文明二、确保国家权力协调高效运行的民主集中制1.地位:是我国人民代表大会制度的组织和活动原则,是人民代表大会制度区别于任何资本主义国家________的鲜明特点。
2.含义:遵循________基础上的________和集中指导下的民主相结合的原则,就是民主集中制。
3.表现。
(1)从人民代表大会和人民的关系来看,各级人民代表大会都由________产生,对________负责,受________监督。
(2)从人民代表大会与其他国家机关的关系来看,人民代表大会是____________机关。
(3)从中央和地方的关系来看,中央和地方各级国家机构按____________的原则划分职权。
答案:1.政治制度2.民主集中3.(1)民主选举人民人民(2)国家权力(3)民主集中制三、民主与集中的统一1.民主与集中的关系:辩证统一。
(1)民主是集中的________和________。
只有尊重人民的民主权利,充分发扬民主,广泛听取各方面的意见、建议,集思广益,才能实现正确的集中。
(2)集中是民主得以实现的必要条件和________。
