七年级数学,直角坐标系的经典复习题
七年级平面直角坐标系动点问题专项练习
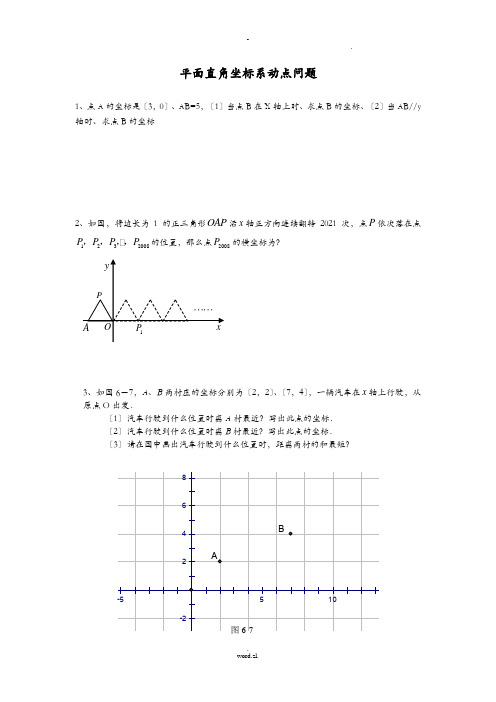
平面直角坐标系动点问题1、点A 的坐标是〔3,0〕、AB=5,〔1〕当点B 在X 轴上时、求点B 的坐标、〔2〕当AB//y 轴时、求点B 的坐标2、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2021次,点P 依次落在点1232008P P P P ,,,,的位置,那么点2008P 的横坐标为?3、如图6-7,A 、B 两村庄的坐标分别为〔2,2〕、〔7,4〕,一辆汽车在x 轴上行驶,从原点O 出发.〔1〕汽车行驶到什么位置时离A 村最近?写出此点的坐标. 〔2〕汽车行驶到什么位置时离B 村最近?写出此点的坐标. 〔3〕请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为〔-1,0〕,〔3,0〕,现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,假设存在这样一点,求出点P 的坐标,假设不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时〔不与B ,D 重合〕给出以下结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.(江岸)23.〔此题总分值12分〕如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)20b -=.(1) 那么A 点的坐标为___________,C 点的坐标为__________;(2) 坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之完毕.AC 的中点D 的坐标是(1,2),设运动时间为t (t >0)秒.问:是否存在这样的t ,使S △ODP =S △ODQ ,假设存在,请求出t 的值;假设不存在,请说明理由;(3) 点F 是线段AC 上一点,满足∠FOC =∠FCO ,点G 是第二象限中一点,连OG ,使得∠AOG =∠AOF .点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC∠+∠∠的值是否会发生变化,假设不变,请求出它的值;假设变化,请说明理由.〔江汉〕28.〔此题总分值12分〕如图,长方形AOCB 的顶点A 〔m ,n 〕和C 〔p ,q 〕在坐标轴上,⎩⎪⎨⎪⎧x =m ,y =n 和⎩⎪⎨⎪⎧x =p ,y =q都是方程x +2y =4的解,点B 在第一象限.〔1〕求点B 的坐标;图1 图2〔2〕假设P 点从A 点出发沿y 轴负半轴以1个单位每秒的速度运动,同时Q 点从C 点出发沿x 轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ 面积为长方形ABCO 面积的一半;〔3〕如图2,将线段AC 沿x 轴正方向平移,得到线段BD ,点E 〔a ,b 〕为线段BD 上任一点,试问式子a +2b 的值是否变化,假设变化,求其围;假设不变化,求其值.〔硚口〕24.〔12分〕如图1,在平面直角坐标系中,第一象限长方形ABCD , AB ∥y 轴,点A 〔1,1〕,点C 〔a , b 〕, 满足035=-+-b a .〔1〕求长方形ABCD 的面积.〔2〕如图2,长方形ABCD 以每秒1个单位长度的速度向右平移,同时点E 从原点O 出发沿x 轴以每秒2个单位长度的速度向右运动,设运动时间为t 秒. ①当t=4时,直接写出三角形OAC 的面积为 ; ② 假设AC ∥ED ,求t 的值;〔3〕在平面直角坐标系中,对于点()P x y ,,我们把点(11)P y x '-++,叫做点P 的伴随点,点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…,这样依次得到点1A ,2A ,3A ,…,n A .①假设点1A 的坐标为〔3,1〕,那么点3A 的坐标为,点2014A 的坐标为;②假设点1A 的坐标为〔a ,b 〕,对于任意的正整数n ,点n A 均在x 轴上方,那么a ,b 应满足的条件为.探究案【例1】如图,在平面直角坐标中,A(0,1),B(2,0),C〔2,1.5〕.〔1〕求△ABC的面积;〔2〕如果在第二象限有一点P〔a,0.5〕,试用a的式子表示四边形ABOP的面积;〔3〕在〔2〕的条件下,是否存在这样的点P,使四边形ABOP的面积与△ABC的面积相等?假设存在,求出点P的坐标,假设不存在,请说明理由.【例2】在平面直角坐标系中,A〔-3,0〕,B〔-2,-2〕,将线段AB平移至线段CD,连AC、BD.图2〔1〕如图1,直接写出图中相等的线段,平行的线段;〔2〕如图2,假设线段AB移动到CD,C、D两点恰好都在坐标轴上,求C、D的坐标;〔3〕假设点C在y轴的正半轴上,点D在第一象限,且S△ACD=5,求C、D的坐标;〔4〕在y轴上是否存在一点P,使线段AB平移至线段PQ时,由A、B、P、Q构成的四边形是平行四边形面积为10,假设存在,求出P 、Q 的坐标,假设不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A 〔1,0〕,B 〔-2,3〕,C 〔-3,0〕. 〔1〕求△ABC 的面积;〔2〕假设把△ABC 向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C ''';〔3〕假设点A 、C 的位置不变,当点P 在y 轴上什么位置时,使2ACPABCS S=;〔4〕假设点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQABCSS=.【例4】如图1,在平面直角坐标系中,A 〔a ,0〕,C 〔b ,2〕,且满足2(2)20a b ++-=,过C 作CB ⊥x 轴于B .〔1〕求三角形ABC 的面积;〔2〕假设过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,求∠AED 的度数;〔3〕在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,假设存在,求出P点坐标;假设不存在,请说明理由.训练案1、如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A〔0,0〕,B〔7,0〕,C〔9,5〕,D〔2,7〕〔1〕在坐标系中,画出此四边形;〔2〕求此四边形的面积;(3)在坐标轴上,你能否找一个点P,使S△PBC=50,假设能,求出P点坐标,假设不能,说明理由.2、如图,A点坐标为〔-2,0〕,B点坐标为〔0,-3〕.(1)作图,将△ABO沿x轴正方向平移4个单位,得到△DEF,延长ED交y轴于C点,过O点作OG⊥CE,垂足为G;(2) 在(1)的条件下,求证: ∠COG=∠EDF;〔3〕求运动过程中线段AB扫过的图形的面积.A(-2,0)B(0,-3)yx3、在平面直角坐标系中,点B 〔0,4〕,C 〔-5,4〕,点A 是x 轴负半轴上一点,S 四边形AOBC =24.图1yxHOFEDAC B〔1〕线段BC 的长为,点A 的坐标为;〔2〕如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF⊥AE 点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)假设点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.4、在平面直角坐标系中,OA =4,OC =8,四边形ABCO 是平行四边形.〔1〕求点B 的坐标及的面积ABCO S 四边形;〔2〕假设点P 从点C 以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQB 与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,假设存在,求出t的值,假设不存在,试说明理由;〔3〕在〔2〕的条件下,四边形QBPO 的面积是否发生变化,假设不变,求出并证明你的结论,假设变化,求出变化的围.5、如图,在平面直角坐标系中,点A ,B 的坐标分别为〔-1,0〕,〔3,0〕,现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D 连结AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;〔2〕在y 轴上是否存在一点P ,连结PA ,PB ,使S △PAB =S △PDB ,假设存在这样一点,求出点P 点坐标,假设不存在,试说明理由;〔3〕假设点Q 自O 点以0.5个单位/s 的速度在线段点就停顿,设移动的时间为t 秒,〔1〕是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?〔4〕是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?6、在直角坐标系中,△ABC 的顶点A 〔—2,0〕,B 〔2,4〕,C 〔5,0〕.〔1〕求△ABC 的面积〔2〕点D 为y 负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?假设存在,请求出点D 的坐标;假设不存在,请说明理由.〔3〕点F 〔5,n 〕是第一象限一点,,连BF ,CF ,G 是x 轴上一点,假设△ABG 的面积等于四边形ABDC 的面积,那么点G 的坐标为〔用含n 的式子表示〕2021年初中数学组卷一.选择题〔共8小题〕1.〔2021春•北流市校级期中〕点P〔0,a〕在y轴的负半轴上,那么点Q〔﹣a2﹣1,﹣a+1〕在〔〕A.第一象限 B.第二象限C.第三象限 D.第四象限2.〔2021春•县校级月考〕点P〔x,y〕的坐标满足|x|=3,=2,且xy<0,那么点P的坐标是〔〕A.〔3,﹣2〕B.〔﹣3,2〕C.〔3,﹣4〕D.〔﹣3,4〕3.〔2021 •〕在平面直角坐标系中,假设点P的坐标为〔﹣3,2〕,那么点P所在的象限是〔〕A.第一象限 B.第二象限C.第三象限 D.第四象限4.〔2021 •〕直线L的方程式为x=3,直线M的方程式为y=﹣2,判断以下何者为直线L、直线M画在坐标平面上的图形?〔〕A.B.C.D.5.〔2021 •〕点P〔﹣2,﹣3〕向左平移1个单位,再向上平移3个单位,那么所得到的点的坐标为〔〕A.〔﹣3,0〕B.〔﹣1,6〕C.〔﹣3,﹣6〕D.〔﹣1,0〕6.〔2021 •〕在平面直角坐标系中,将点A〔x,y〕向左平移5个单位长度,再向上平移3个单位长度后与点B〔﹣3,2〕重合,那么点A的坐标是〔〕A.〔2,5〕B.〔﹣8,5〕C.〔﹣8,﹣1〕D.〔2,﹣1〕7.〔2021 春•校级期中〕如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒,它从原点运动到〔0,1〕,接着它按图所示在x轴、y轴的平行方向来回运动,〔即〔0,0〕→〔0,1〕→〔1,1〕→〔1,0〕→〔2,0〕→…〕且每秒运动一个单位长度,那么2021秒时,这个粒子所处位置为〔〕A.〔14,44〕B.〔15,44〕C.〔44,14〕D.〔44,15〕8.〔2021 •宝应县校级模拟〕点P〔m+3,m﹣1〕在x轴上,那么点P的坐标为〔〕A.〔0,﹣2〕B.〔2,0〕C.〔4,0〕D.〔0,﹣4〕二.填空题〔共8小题〕9.〔2021 •〕如图,将平面直角坐标系中“鱼〞的每个“顶点〞的纵坐标保持不变,横坐标分别变为原来的,那么点A的对应点A′的坐标是.10.〔2021 •二模〕如下图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A1〔0,1〕、A2〔1,1〕、A3〔1,0〕、A4〔2,0〕,…,那么点A2021 的坐标为.11.〔2021春•洛龙区校级期中〕点O〔0,0〕,B〔1,2〕,点A在坐标轴上,且S△OAB=2,那么满足条件的点A的坐标为.12.〔2021春•信州区校级期中〕AB∥x轴,且AB=3,假设点A的坐标是〔﹣1,2〕,那么B 点的坐标是.13.〔2021春•区校级期中〕:点A〔0,5〕,B〔0,2〕,在坐标轴上找点C,使△ABC的面积为5,那么点C的坐标是.14.〔2021秋•靖江市校级期中〕在平面直角坐标系中,假设点M〔﹣2,6〕与点N〔x,6〕之间的距离是3,那么x的值是.15.〔2021春•江岸区期中〕在平面直角坐标系中,一个长方形的三个顶点坐标分别为〔﹣1,﹣1〕,〔﹣1,1〕,〔5,﹣1〕,那么第四个顶点的坐标是.16.〔2021春•鼓楼区校级期中〕A〔2,﹣6〕,B〔2,﹣4〕,那么线段AB=.三.解答题〔共14小题〕17.〔2021 •校级模拟〕在如下图的平面直角坐标系中描出下面各点:A〔0,3〕;B〔1,﹣3〕;C〔3,﹣5〕;D〔﹣3,﹣5〕;E〔3,5〕;F〔5,7〕;G〔5,0〕.〔1〕将点C向x轴的负方向平移6个单位,它与点重合.〔2〕连接CE,那么直线CE与y轴是什么关系?〔3〕顺次连接D、E、G、C、D得到四边形DEGC,求四边形DEGC的面积.18.〔2021 春•校级期末〕〔1〕在坐标平面画出点P〔2,3〕.〔2〕分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标.19.〔2021 秋•兴平市期末〕假设x,y为实数,且满足|x﹣3|+=0.〔1〕如果实数x,y对应为平面直角坐标系上的点A〔x,y〕,那么点A在第几象限?〔2〕求〔〕2021 的值?20.〔2021 春•平南县期末〕在平面直角坐标系中,点A〔a,3﹣2a〕在第一象限.〔1〕假设点A到x轴的距离与到y轴的距离相等,求a的值;〔2〕假设点A到x轴的距离小于到y轴的距离,求a的取值围.21.〔2021 秋•双柏县期末〕如图,A、B两点的坐标分别是〔2,﹣3〕、〔﹣4,﹣3〕.〔1〕请你确定P〔4,3〕的位置;〔2〕请你写出点Q的坐标.22.〔2021 秋•沭阳县校级期末〕如图,A〔﹣2,3〕、B〔4,3〕、C〔﹣1,﹣3〕〔1〕求点C到x轴的距离;〔2〕求△ABC的面积;〔3〕点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.23.〔2021 春•博兴县期末〕在平面直角坐标系中,四边形ABCD的顶点坐标分别为A〔1,0〕,B〔5,0〕,C〔3,3〕,D〔2,4〕.〔1〕求线段AB的长;〔2〕求四边形ABCD的面积.24.〔2021 春•丹江口市期末〕〔1〕两点A〔﹣3,m〕,B〔n,4〕,假设AB∥x轴,求m的值,并确定n的围;〔2〕假设点〔5﹣a,a﹣3〕在第一、三象限的角平分线上,求a的值.25.〔2021 秋•埇桥区期末〕点A〔m+2,3〕和点B〔m﹣1,2m﹣4〕,且AB∥x轴.〔1〕求m的值;〔2〕求AB的长.26.〔2021 春•建昌县期末〕:如图,在平面直角坐标系xOy中,A〔4,0〕,C〔0,6〕,点B 在第一象限,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周〔即:沿着O→A→B→C→O的路线移动〕.〔1〕写出B点的坐标〔〕;〔2〕当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;〔3〕在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.27.〔2021 春•文安县期末〕如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C 点坐标为〔1,2〕.〔1〕写出点A、B的坐标:A〔,〕、B〔,〕〔2〕将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,那么A′B′C′的三个顶点坐标分别是A′〔,〕、B′〔,〕、C′〔,〕.〔3〕△ABC的面积为.28.〔2021 春•校级期中〕我们规定以下三种变换:〔1〕f〔a,b〕=〔﹣a,b〕.如:f〔1,3〕=〔﹣1,3〕;〔2〕g〔a,b〕=〔b,a〕.如:g〔1,3〕=〔3,1〕;〔3〕h〔a,b〕=〔﹣a,﹣b〕.如:h〔1,3〕=〔﹣1,﹣3〕.按照以上变换有:f〔g〔2,﹣3〕〕=f〔﹣3,2〕=〔3,2〕,求f〔h〔5,﹣3〕〕的值.29.〔2021 春•繁昌县期中〕点A〔1+2a,4a﹣5〕,且点A到两坐标轴的距离相等,求点A 的坐标.30.〔2021 秋•务川县校级期中〕平面直角坐标系中,△ABC的三个顶点坐标分别为A〔0,4〕B〔2,4〕C〔3,﹣1〕.〔1〕试在平面直角坐标系中,标出A、B、C三点;〔2〕求△ABC的面积.〔3〕假设△DEF与△ABC关于x轴对称,写出D、E、F的坐标.2021年04月05日1148955744的初中数学组卷参考答案一.选择题〔共8小题〕1.B;2.D;3.B;4.B;5.A;6.D;7.A;8.C;二.填空题〔共8小题〕9.〔2,3〕;10.〔1007,0〕;11.〔2,0〕或〔-2,0〕或〔0,4〕或〔0,-4〕;12.〔-4,2〕或〔2,2〕;13.〔,0〕或〔-,0〕;14.1或-5;15.〔5,1〕;16.2;三.解答题〔共14小题〕17.D;〔-3,-5〕;18.;19.;20.;21.;22.;23.;24.;25.;26.〔4,6〕;27.2;-1; 4;3;0;0;2;4;-1; 3;5;28.;29.;30.;。
河北衡水中学七年级数学下册第七章【平面直角坐标系】经典复习题(培优专题)

一、选择题1.已知两点(,5)A a ,(1,)B b -且直线//AB x 轴,则( )A .a 可取任意实数,5b =B .1a =-,b 可取任意实数C .1a ≠-,5b =D .1a =-,5b ≠2.点A 到x 轴的距离是3,到y 轴的距离是6,且点A 在第二象限,则点A 的坐标是( ) A .(-3,6) B .(-6,3) C .(3,-6) D .(8,-3) 3.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,……按这样的运动规律,经过第2020次运动后,动点P 的坐标是( )A .()2020,0B .()2020,1C .()2021,1D .()2021,2 4.点()1,3P --向右平移3个单位,再向上平移5个单位,则所得到的点的坐标为( ) A .()4,2- B .()2,2 C .()4,8-- D .()2,8-5.若点(),A m n 到y 轴的距离是它到x 轴距离的两倍,则( ).A .2m n =B .2m n =C .2m n =D .2m n = 6.已知点M (9,﹣5)、N (﹣3,﹣5),则直线MN 与x 轴、y 轴的位置关系分别为( ) A .相交、相交B .平行、平行C .垂直相交、平行D .平行、垂直相交7.点()1,3M m m ++在x 轴上,则M 点坐标为( )A .()0,4-B .()4,0C .()2,0-D .()0,2-8.下列说法正确的是( )A .若0ab =,则点(,)P a b 表示原点B .点(1,)a 在第三象限C .已知点(3,3)A -与点(3,3)B ,则直线//AB x 轴D .若0ab >,则点(,)P a b 在第一或第三象限9.将点()1,2P 向左平移3个单位后的坐标是( )A .()2,2-B .()1,1-C .()1,5D .()1,1-- 10.如图是医院、公园和超市的平面示意图,超市B 在医院O 的南偏东25︒的方向上,且到医院的距离为300m ,公园A 到医院O 的距离为400m .若∠90AOB =︒,则公园A 在医院O 的( )A .北偏东75︒方向上B .北偏东65︒方向上C .北偏东55︒方向上D .北偏西65°方向上11.如图,△ABC 的顶点坐标分别为A(1,0),B(4,0),C(1,4),将△ABC 沿x 轴向右平移,当点C 落在直线y =2x -6上时,线段BC 扫过的面积为( )A .4B .8C .2D .16二、填空题12.已知点A(3,b)在第一象限,那么点B(-3,-b)在第________象限.13.定义:在平面直角坐标系xOy 中,把从点P 出发沿纵或横方向到达点(至多拐一次弯)的路径长称为P ,Q 的“实际距离”.如图,若(1,1)P -,(2,3)Q ,则P ,Q 的“实际距离”为5,即5PS SQ +=或5PT TQ +=.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A ,B ,C 三个小区的坐标分别为(2,2)A ,(4,2)B -,(2,4)C --,若点M 表示单车停放点,且满足M 到A ,B ,C 的“实际距离”相等,则点M 的坐标为______.14.已知点()3,2P -,//MP x 轴,6MP =,则点M 的坐标为______.15.直角坐标系内,一动点按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),……,按这样的运动规律,动点第2021次运动到的点的坐标为____________.16.如图点 A 、B 的坐标分别为(1,2)、(3,0),将△AOB 沿 x 轴向右平移,得到△CDE . 已知点 D 在的点 B 左侧,且 DB =1,则点 C 的坐标为 ____ .17.已知点A(3a ﹣6,a+4),B(﹣3,2),AB ∥y 轴,点P 为直线AB 上一点,且PA =2PB ,则点P 的坐标为_____.18.如图,在平面直角坐标系xOy 中,将四边形ABCD 先向下平移,再向右平移得到四边形A 1B 1C 1D 1,已知A (﹣3,5),B (﹣4,3),A 1(3,3),则B 1的坐标为_____.19.如图,在平面直角坐标系中,三角形ABC 经过平移后得到三角形A′B′C′,且平移前后三角形的顶点坐标都是整数.若点P (12,﹣15)为三角形ABC 内部一点,且与三角形A′B′C′内部的点P′对应,则对应点P′的坐标是_____.20.已知点 P(b+1,b-2)在x 轴上,则P 的横坐标值为____21.已知点P 在第四象限,且到x 轴的距离是1,到y 轴的距离是3,则P 的坐标是______.三、解答题22.在平面直角坐标系中,有A(﹣2,a +1),B(a ﹣1,4),C(b ﹣2,b )三点.(1)当点C 在y 轴上时,求点C 的坐标;(2)当AB ∥x 轴时,求A ,B 两点间的距离;(3)当CD ⊥x 轴于点D ,且CD =1时,求点C 的坐标.23.在平面直角坐标系中,有点(),1A a -,点()2,B b .(1)当A ,B 两点关于直线1x =-对称时,求AOB 的面积;(2)当线段//AB y 轴,且3AB =时,求-a b 的值.24.请在图中建立平面直角坐标系,使学校的坐标是()2,5,并写出儿童公园,医院,水果店,宠物店,汽车站的坐标.25.对于平面直角坐标系 xOy 中的点P (a ,b ),若点P ' 的坐标为,b a ka b k ⎛⎫++ ⎪⎝⎭(其中k 为常数,且0k ≠),则称点P '为点P 的“k 之雅礼点”.例如:P (1,4)的“2之雅礼点”为41,2142P ⎛⎫'+⨯+ ⎪⎝⎭,即P '(3,6). (1)①点P (-1,-3)的“3之雅礼点”P '的坐标为____________; ②若点P 的“k 之雅礼点”P '的坐标为(2,2),请写出一个符合条件的点P 的坐标____________; (2)若点P 在x 轴的正半轴上,点P 的“k 之雅礼点”为P '点,且OPP '△为等腰直角三角形,则k 的值为____________;(3)在(2)的条件下,若关于x 的方程2kx mx mn +=+有无数个解,求m n 、的值.一、选择题1.已知点A (0,-6),点B (0,3),则A ,B 两点间的距离是( )A .-9B .9C .-3D .32.如图,点A 的坐标是()3,1-将四边形ABCD 先向左平移3个单位,再向上平移2个单位,那么点A 的对应点A '的坐标是( )A .()0,1B .()6,1C .()0,3-D .()6,3-3.如图,一个粒子在第一象限内及x 轴,y 轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x 轴,y 轴平行的方向来回运动,且每分钟移动1个长度单位,那么,第2017分钟时,这个粒子所在位置的坐标是( )A .(7,44)B .(8,45)C .(45,8)D .(44,7)4.点A (n+2,1﹣n )不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限 5.在平面直角坐标系中,点P (−1,23)在( )A .第一象限B .第二象限C .第三象限D .第四象限 6.已知点A 坐标为()2,3-,点A 关于x 轴的对称点为A ',则A '关于y 轴对称点的坐标为( )A .()2,3--B .()2,3C .()2,3-D .以上都不对7.点()P 3,2-在平面直角坐标系中所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 8.如图是医院、公园和超市的平面示意图,超市B 在医院O 的南偏东25︒的方向上,且到医院的距离为300m ,公园A 到医院O 的距离为400m .若∠90AOB =︒,则公园A 在医院O 的( )A .北偏东75︒方向上B .北偏东65︒方向上C .北偏东55︒方向上D .北偏西65°方向上9.如图,在坐标平面内,依次作点()3,1P -关于直线y x =的对称点1P ,1P 关于x 轴对称点2P ,2P 关于y 轴对称点3P ,3P 关于直线y x =对称点4P ,4P 关于x 轴对称点5P ,5P 关于y 轴对称点6P ,…,按照上述变换规律继续作下去,则点2019P 的坐标为( )A .()1,3-B .()1,3C .()3,1-D .()1,3- 10.已知点P(a+5,a-1)在第四象限,且到x 轴的距离为2,则点P 的坐标为( ) A .(4,-2) B .(-4,2) C .(-2,4) D .(2,-4)11.在平面直角坐标中,点()1,2P 平移后的坐标是)3(3,-'P ,按照同样的规律平移其它点,则以下各点的平移变换中( )符合这种要求.A .()3,24(,2)→-B .()(104),5,--→-C .(1.2,5)→(-3.2,6)D .122.5, 1.5,33⎛⎫⎛⎫-→- ⎪ ⎪⎝⎭⎝⎭二、填空题12.在平面直角坐标系内,把点A (5,-2)向右平移3个单位,再向下平移2个单位,得到的点B 的坐标为______.13.小华在小明南偏西75°方向,则小明在小华______方向.(填写方位角)14.点(1,1)P -向左平移2个单位,向上平移3个单位得1P ,则点1P 的坐标是________. 15.已知点A (2m +,3-)和点B (4,1m -),若直线//AB x 轴,则m 的值为______. 16.若不在第一象限的点(),22A x x -+到两坐标轴距离相等,则A 点坐标为 _________. 17.下图是利用平面直角坐标系画出的老北京一些地点的示意图,这个坐标系分别以正东和正北方向为x 轴和y 轴的正方向,如果表示右安门的点的坐标为(-2,-3),表示朝阳门的点的坐标为(3,2),那么表示西便门的点的坐标为___________________.18.在平面直角坐标系中,点(,)A x y 的坐标满足方程34x y -=,(1)当点A 到两条坐标轴的距离相等时,点A 坐标为__________.(2)当点A 在x 轴上方时,点A 横坐标x 满足条件__________.19.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点2019A 的坐标是_________.20.若x ,y 为实数,且满足330x y -++=,则 A(x ,y)在第____象限21.点3(2,)A -到x 轴的距离是__________.三、解答题22.在平面直角坐标系中,有A(﹣2,a +1),B(a ﹣1,4),C(b ﹣2,b )三点.(1)当点C 在y 轴上时,求点C 的坐标;(2)当AB∥x轴时,求A,B两点间的距离;(3)当CD⊥x轴于点D,且CD=1时,求点C的坐标.23.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将ABC经过''',图中标出了点B的对应点B'.一次平移后得到A B C''';(1)在给定方格纸中画出平移后的A B C(2)画出AB边上的中线CD和BC边上的高线AE;''的面积是多少?(3)求A B C24.三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).(1)请你在方格中建立直角坐标系,并写出C点的坐标;(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是.(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.25.如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系;(2)写出点A、B、C、D的坐标;(3)求出四边形ABCD的面积.一、选择题1.已知两点(,5)A a ,(1,)B b -且直线//AB x 轴,则( )A .a 可取任意实数,5b =B .1a =-,b 可取任意实数C .1a ≠-,5b =D .1a =-,5b ≠2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A ()2,1-和B ()2,3--,那么第一架炸机C 的平面坐标是( )A .()2,1B .()3,1-C .()2,1-D .()3,13.在平面直角坐标系中,与点P 关于原点对称的点Q 为()1,3-,则点P 的坐标是( ) A .()1,3 B .()1,3-- C .()1,3- D .()1,3- 4.下列关于有序数对的说法正确的是( )A .(3,4)与(4,3)表示的位置相同B .(a ,b )与(b ,a )表示的位置肯定不同C .(3,5)与(5,3)是表示不同位置的两个有序数对D .有序数对(4,4)与(4,4)表示两个不同的位置5.如图,在ABC ∆中,90ACB ∠=︒,AC BC =,点C 的坐标为()2,0-,点B 的坐标为()1,4,则点A 的坐标为( )A .()6,3-B .()3,6-C .()4,3-D .()3,4- 6.若点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,则a 的值为( ) A .-1 B .79- C .1 D .27.点()1,3M m m ++在x 轴上,则M 点坐标为( )A .()0,4-B .()4,0C .()2,0-D .()0,2- 8.如图,在平面直角坐标系中,若干个半径为3个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P 从原点O 出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒3个单位长度,点在弧线上的速度为每秒π个单位长度,则2020秒时,点P 的坐标是( )A .(2020,0)B .(3030,0)C .( 3030,3)D .(3030,﹣3) 9.在下列点中,与点A(-2,-4)的连线平行于y 轴的是( )A .(2,-4)B .(4,-2)C .(-2,4)D .(-4,2) 10.如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)()()()()()1,01,11,22,13,0....→→→→→→,则2018分钟时粒子所在点的横坐标为( )A .900B .946C .990D .88611.若点P (﹣m ,﹣3)在第四象限,则m 满足( )A .m >3B .0<m≤3C .m <0D .m <0或m >3二、填空题12.对于平面直角坐标系xOy 中的点P (a ,b ),若点P 的坐标为(a +kb ,ka +b )(其中k 为常数,且k ≠0),则称点P 为点P 的“k 属派生点”,例如:P (1,4)的“2属派生点”为P (1+2×4,2×1+4),即P ′(9,6).若点P 在x 轴的正半轴上,点P 的“k 属派生点”为点P ′,且线段PP ′的长度为线段OP 长度的5倍,则k 的值为___.13.写一个第三象限的点坐标,这个点坐标是_______________.14.点P 先向左平移4个单位,再向上平移1个单位,得到点Q(2,-3),则点P 坐标为__ 15.直角坐标系内,一动点按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),……,按这样的运动规律,动点第2021次运动到的点的坐标为____________.16.如图,已知A 1(1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),…,则坐标为(﹣505,﹣505)的点是______.17.如图,一个机器人从0点出发,向正东方向走3米到达1A 点,记为()3,0;再向正北方向走6米到达2A 点,记为()3,6:再向正西方向走9米到达3A 点,记为()6,6-;再向正南方向走12米到达4A 点,再向正东方向走15米到达5A 点,按如此规律走下去,当机器人走到99A 点时,则99A 的坐标为________.18.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点2019A 的坐标是_________.19.已知点()24,1P m m +-.()1若点P 在x 轴上,则点P 的坐标为________;()2若点P 在第四象限,且到y 轴的距离是2,则点P 的坐标为________.20.已知点 P(b+1,b-2)在x 轴上,则P 的横坐标值为____21.已知线段AB 的长度为3,且AB 平行于y 轴,A 点坐标为()32,,则B 点坐标为______.三、解答题22.如图,在平面直角坐标系中,四边形OABC 各顶点的坐标分别是()0,0O ,()0,12A ,()10,8B -,()14,0C -,求四边形OABC 的面积.23.在平面直角坐标系中,已知点(),B a b ,线段BA x ⊥轴于A 点,线段BC y ⊥轴于C点,且2(2)a b -++ |22|0a b --=.(1)求A ,B ,C 三点的坐标.(2)若点D 是AB 的中点,点E 是OD 的中点,求AEC 的面积.(3)在(2)的条件下,若点()2,P a ,且AEP AEC S S =△△,求点P 的坐标. 24.在平面直角坐标系中,画出点(0,0)A ,(4,0)B ,(3,3)C ,(0,5)D ,并求出BCD 的面积.25.如图,已知三角形,ABC 把三角形ABC 先向上平移3个单位长度,再向右平移2个单位长度,得到三角形'''A B C .(1)在图中画出三角形'''A B C ,并写出',','A B C 的坐标;(2)连接,AO BO ,求三角形ABO 的面积;(3)在y 轴上是否存在一点P ,使得三角形BCP 与三角形ABC 面积相等?若存在请直接写出点P 的坐标;若不存在,请说明理由.。
《常考题》初中七年级数学下册第七单元《平面直角坐标系》习题(含答案解析)
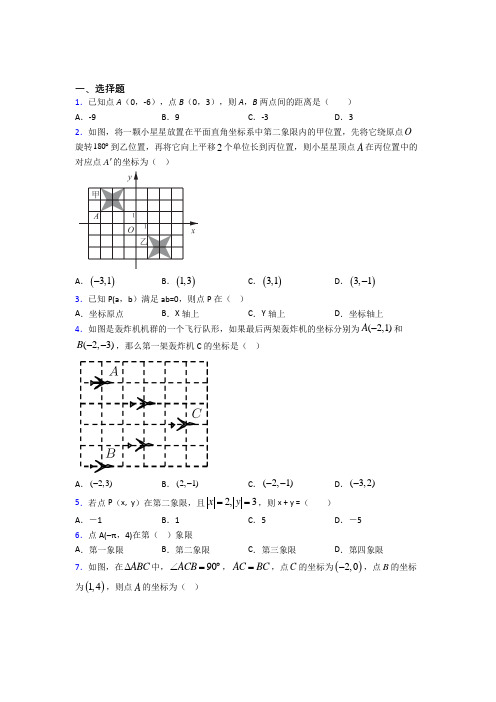
一、选择题1.已知点A (0,-6),点B (0,3),则A ,B 两点间的距离是( )A .-9B .9C .-3D .32.如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O 旋转180︒到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A 在丙位置中的对应点A '的坐标为( )A .()3,1-B .()1,3C .()3,1D .()3,1- 3.已知P(a ,b )满足ab=0,则点P 在( ) A .坐标原点 B .X 轴上 C .Y 轴上 D .坐标轴上 4.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的坐标分别为(2,1)A -和(2,3)B --,那么第一架轰炸机C 的坐标是( )A .(2,3)-B .(2,1)-C .(2,1)--D .(3,2)- 5.若点P (x, y )在第二象限,且2,3x y ==,则x + y =( )A .-1B .1C .5D .-5 6.点A(-π,4)在第( )象限 A .第一象限 B .第二象限 C .第三象限 D .第四象限 7.如图,在ABC ∆中,90ACB ∠=︒,AC BC =,点C 的坐标为()2,0-,点B 的坐标为()1,4,则点A 的坐标为( )A .()6,3-B .()3,6-C .()4,3-D .()3,4- 8.若某点A 位于x 轴上方,距x 轴5个单位长,且位于y 轴的左边,距y 轴10个单位长,则点A 的坐标是( )A .(510)-,B .(510)-,C .(105)-,D .(105)-,9.如图是医院、公园和超市的平面示意图,超市B 在医院O 的南偏东25︒的方向上,且到医院的距离为300m ,公园A 到医院O 的距离为400m .若∠90AOB =︒,则公园A 在医院O 的( )A .北偏东75︒方向上B .北偏东65︒方向上C .北偏东55︒方向上D .北偏西65°方向上10.课间操时,小华、小军和小刚的位置如图所示,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示为( )A .(5,4)B .(4,5)C .(3,4)D .(4,3)11.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2021次运动后,动点P 的坐标是( )A .(2021,0)B .(2020,1)C .(2021,1)D .(2021,2) 12.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m 其行走路线如图所示,第1次移动到1A ,第2次移动到2A ,…第n 次移动到n A .则32020OA A △的面积是( )A .2504.5mB .2505mC .2505.5mD .21010m 13.如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为(4,2),四号暗堡的坐标为(2,4)-,原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( )A .A 处B .B 处C .C 处D .D 处14.如图,线段OA ,OB 分别从与x 轴和y 轴重合的位置出发,绕着原点O 顺时针转动,已知OA 每秒转动45︒,OB 的转动速度是每秒转动30,则第2020秒时,OA 与OB 之间的夹角的度数为( )A .90︒B .145︒C .150︒D .165︒ 15.已知点M (12,﹣5)、N (﹣7,﹣5),则直线MN 与x 轴、y 轴的位置关系分别为( )A .相交、相交B .平行、平行C .垂直相交、平行D .平行、垂直相交 二、填空题16.如图,平面直角坐标系xOy 中,点A(4,3),点B(3,0),点C(5,3),OAB ∆沿AC 方向平移AC 长度的到ECF ∆,四边形ABFC 的面积为_________.17.如图,一只甲虫在55⨯的方格(每小格边长为1)上沿着网格线运动.它从A 处出发去看望B .C .D 处的其它甲虫,规定:向上向右走为正,向下向左走为负、如果从A 到B 记为:(1,4)A B →++,从B 到A 记为:(1,4)B A →--,其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A C →(______,______),B C →(______,______),C →______(1+,______);(2)若图中另有两个格点M .N ,且M A →(3,4)a b --,M N →(5,2)a b --,则N A →应记为______.18.在平面直角坐标系中,若点(1, 2)M m m -+与点(23, 2)N m m ++之间的距离是5,则m =______.19.若电影票上座位是12排5号可记为(12,5),则(5,6)表示_______________. 20.如图,有A ,B ,C 三点,如果A 点用()1,1表示,B 点用()2,3表示,则C 点的坐标为_______.21.如图,在平面直角坐标系中,已如点A (1,1),B (-1,1),C (-1,-2),D (1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A 处,并按A B C D A →→→→的规律紧绕在四边形ABCD 的边上,则细线的另一端所在位置的点的坐标是__________.22.已知点(1,0)A 、(0,2)B ,点P 在x 轴上,且PAB △的面积为5,则点P 的坐标为__________.23.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,-1),…,按照这样的运动规律,点P 第17次运动到的点的坐标为__________.24.已知P (a,b ),且ab <0,则点P 在第_________象限.25.若点A (-2,n )在x 轴上,则点B(n-2,n+1)在第_____象限 .26.如图,直线BC 经过原点O ,点A 在x 轴上,AD BC ⊥于D .若A (4,0),B (m ,3),C (n ,-5),则AD BC =______.三、解答题27.在平面直角坐标系中,已知点M 的坐标为()23,1m m +-.(1)若点M 在x 轴上,求m 的值;(2)已知点N 的坐标为(3,2)-,且直线MN x ⊥轴,求线段MN 的长.28.如图,在平面直角坐标系中,△ABC 的顶点C 的坐标为(1,3).(1)请直接写出点A 、B 的坐标.(2)若把△ABC 向上平移3个单位,再向右平移2个单位得△A′B′C′,画出△A′B′C′; (3)直接写出△A′B′C′各顶点的坐标;(4)求出△ABC 的面积29.如图,已知平面直角坐标系中,点A 在y 轴上,点B 、C 在x 轴上,S △ABO =8,OA =OB ,BC =10,点P 的坐标是(-6,a )(1)求△ABC 三个顶点A 、B 、C 的坐标;(2)连接PA 、PB ,并用含字母a 的式子表示△PAB 的面积(a ≠2);(3)在(2)问的条件下,是否存在点P ,使△PAB 的面积等于△ABC 的面积?如果存在,请求出点P 的坐标;若不存在,请说明理由.30.画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将ABC经过''',图中标出了点B的对应点B'.请利用网格点和直尺画图或计一次平移后得到A B C算:''';(1)在给定方格纸中画出平移后的A B C(2)画出AB边上的中线CD及高线CE;(3)在上述平移中,边AB所扫过的面积为.。
七年级数学平面直角坐标系典型例题及答题技巧

七年级数学平面直角坐标系典型例题及答题技巧单选题1、点A(−3,−5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为()A.(1,−8)B.(1,−2)C.(−6,−1)D.(0,−1)答案:C解析:利用平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减求解即可.解:点A的坐标为(−3,−5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是:−3−3=−6,纵坐标为:−5+4=−1,即(−6,−1).故选:C.小提示:本题考查图形的平移变换,关键是要懂得左右移动改变点的横坐标,左减、右加;上下移动改变点的纵坐标,下减、上加.2、若y轴负半轴上的点P到x轴的距离为2,则点P的坐标为()A.(0,2)B.(2,0)C.(﹣2,0)D.(0,﹣2)答案:D解析:点P在y轴上则该点横坐标为0,据此解答即可.∵y轴负半轴上的点P到x轴的距离为2,∴点P的坐标为(0,﹣2).本题考查了点的坐标,解决本题的关键是掌握好坐标轴上的点的坐标的特征,y轴上的点的横坐标为0.3、在平面直角坐标系中,将点(2,l)向右平移3个单位长度,则所得的点的坐标是()A.(0,5)B.(5,1)C.(2,4)D.(4,2)答案:B解析:在平面直角坐标系中,将点(2,l)向右平移时,横坐标增加,纵坐标不变.将点(2,l)向右平移3个单位长度,则所得的点的坐标是(5,1).故选B.小提示:本题运用了点平移的坐标变化规律,关键是把握好规律.4、下面四个点位于第四象限的是()A.(−1,2)B.(−2,−2)C.(2,5)D.(6,−2)答案:D解析:根据直角坐标系中,不同象限内点的坐标特点,依次对四个选项进行判断即可求解.A.(−1,2),因为-1<0,2>0,所以(−1,2)在第二象限,故A不符合题意B.(−2,−2),因为-2<0,所以(−2,−2)在第三象限,故B不符合题意C.(2,5),因为2>0,5>0,所以(2,5)在第一象限,故C不符合题意D.(6,−2),因为6>0,-2<0,所以(6,−2)在第四象限,故D符合题意本题考查了直角坐标系中不同象限内点的坐标特点,第四象限内的点,横坐标大于零,纵坐标小于零.5、以下能够准确表示宣城市政府地理位置的是()A.离上海市282千米B.在上海市南偏西80°C.在上海市南偏西282千米D.东经30.8°,北纬118°答案:D解析:根据点的坐标的定义,确定一个位置需要两个数据解答即可.解:能够准确表示宣城市政府地理位置的是:东经30.8°,北纬118°.故选:D.小提示:本题考查了坐标确定位置,是基础题,理解坐标的定义是解题的关键.6、在平面直角坐标系中.点P(1,﹣2)关于x轴的对称点的坐标是()A.(1,2)B.(﹣1,﹣2)C.(﹣1,2)D.(﹣2,1)答案:A解析:点P(1,-2)关于x轴的对称点的坐标是(1,2),故选A.7、某班级第3组第4排的位置可以用数对(3,4)表示,则数对(1,2)表示的位置是( )A.第2组第1排B.第1组第1排C.第1组第2排D.第2组第2排答案:C解析:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.故某班级第3组第4排位置可以用数对(3,4)表示,则数对(1,2)表示的位置是第1组第2排,故选C.8、观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是()A.(3,8)B.(4,7)C.(5,6)D.(6,5)答案:C解析:不难发现横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,根据此规律即可知第50个有序数对.观察发现,横坐标依次是:1、1、2、1、2、3、1、2、3、4、1、2、3、4、5…,纵坐标依次是:1、2、1、3、2、1、4、3、2、1、5、4、3、2、1…,∵1+2+3+4+5+6+7+8+9=45,∴第46、47、48、49、50个有序数对依次是(1,10)、(2,9)、(3,8)、(4,7)、(5,6).所以C选项是正确的.小提示:本题主要考查了点的坐标探索规律题,找出有序数对的横、纵坐标变化规律是解决问题的关键.填空题9、如图是中国象棋棋盘的一部分,如果我们把“馬”所在的位置记作(2,1),“卒”所在的位置就是(3,4),那么“相”所在的位置是____________.答案:(5, 3) .解析:马在第2列第1行,表示为(2,1),“卒”所在的位置就是(3,4),可知数对中前面的数表示的是列,后面的数表示的是行.据此进行解答.故答案为(5, 3)由已知可得:数对中前面的数表示的是列,后面的数表示的是行.所以,“相”所在的位置是(5, 3).小提示:本题主要考查了学生用数对表示位置的知识.10、点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为_____.答案:(2,1).解析:将点A的纵坐标加4,横坐标不变,即可得出点A′的坐标.解:将点A(2,﹣3)向上平移4个单位得到点A′,则点A′的坐标是(2,﹣3+4),即(2,1).故答案为(2,1).小提示:本题考查坐标与图形变化-平移,掌握平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.11、与点(2,−7)关于y轴对称的点的坐标为_______,关于y=−1对称的点的坐标为_______.答案:(−2,−7)(2,5)解析:关于y轴对称的点的坐标特征是:纵坐标不变,横坐标变为原数的相反数;关于y=−1对称的点的坐标特征是:横坐标不变,纵坐标关于y=−1对称,据此解题.解:点(2,−7)关于y轴对称的点的坐标为(−2,−7),关于y=−1对称的点的坐标为(2,5),所以答案是:(−2,−7);(2,5).小提示:本题考查直角坐标系、关于y轴对称的点的坐标等知识,是基础考点,掌握相关知识是解题关键.12、对于两个非零实数x,y,定义一种新的运算:x∗y=ax +by.若1∗(−1)=2,则(−2)∗2的值是__.答案:-1解析:根据新定义的运算法则即可求出答案.∵1*(-1)=2,∴a1+b−1=2,即a-b=2∴原式=a−2+b2=−12(a-b)=-1故答案为-1.小提示:本题考查代数式运算,解题的关键是熟练运用整体的思想.13、请写出一个在第三象限内的点的坐标:__________(只写一个).答案:(−1,−1)解析:根据第三象限内的点的横坐标和纵坐标都是负数直接写出即可.解:因为第三象限内的点的横坐标和纵坐标都是负数,故坐标可以是(−1,−1)(答案不唯一).小提示:本题考查了平面直角坐标系内点的坐标的特征,解题关键是熟知在不同象限的点的坐标的符号特征.解答题14、已知点P(2a−2,a+5),解答下列各题.(1)点P在x轴上,求出点P的坐标.(2)点Q的坐标为(4,5),直线PQ//y轴;求出点P的坐标.(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2020+2020的值.答案:(1)P(−12,0);(2)P(4,8);(3)2021解析:(1)根据x轴上点的坐标特征:纵坐标为0,列出方程即可求出结论;(2)根据与y轴平行的直线上两点坐标关系:横坐标相等、纵坐标不相等即可求出结论;(3)根据题意可得:点P的横纵坐标互为相反数,从而求出a的值,即可求出结论.解:(1)若点P在x轴上,∴a+5=0解得:a=-5∴P(−12,0);(2)∵点Q的坐标为(4,5),直线PQ//y轴∴2a−2=4解得:a=3∴P(4,8);(3)∵点P在第二象限,且它到x轴、y轴的距离相等∴2a−2+a+5=0解得:a=-1∴a2020+2020=(−1)2020+2020=2021小提示:此题考查的是根据题意,求点的坐标,掌握x轴上点的坐标特征、与y轴平行的直线上两点坐标关系和点到x 轴、y轴的距离与坐标关系是解题关键.15、适当建立直角坐标系,描出点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),并用线段顺次连接各点.(1)看图案像什么?(2)作如下变化:纵坐标不变,横坐标减2,并顺次连接各点,所得的图案与原来相比有什么变化?答案:(1)“鱼”;(2)向左平移2个单位.解析:(1)描点根据顺序连线即可.(2)根据平移前后图形的形状和大小没有变化可以知道,图案大小形状没有变化,位置向左平移两个单位.解:(1)像“鱼”.(2)纵坐标不变,横坐标减2,即向左平移两个单位,根据平移前后图形的形状和大小没有变化可以知道,图案大小形状没有变化,位置向左平移两个单位.小提示:本题考查直角坐标系中描点,平移作图,细心画图即可.。
人教版初中七年级数学平面直角坐标系经典大题例题

(每日一练)人教版初中七年级数学平面直角坐标系经典大题例题单选题1、若y轴负半轴上的点P到x轴的距离为2,则点P的坐标为()A.(0,2)B.(2,0)C.(﹣2,0)D.(0,﹣2)答案:D解析:点P在y轴上则该点横坐标为0,据此解答即可.∵y轴负半轴上的点P到x轴的距离为2,∴点P的坐标为(0,﹣2).故选:D.小提示:本题考查了点的坐标,解决本题的关键是掌握好坐标轴上的点的坐标的特征,y轴上的点的横坐标为0.2、小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是()A.B.C.D.答案:B解析:∵y轴表示当天爷爷离家的距离,X轴表示时间又∵爷爷从家里跑步到公园,在公园打了一会儿太极拳,然后沿原路慢步走到家,∴刚开始离家的距离越来越远,到公园打太极拳时离家的距离不变,然后回家时离家的距离越来越近又知去时是跑步,用时较短,回来是慢走,用时较多∴选项B中的图形满足条件.故选B.3、甲、乙、丙三人所处的位置不同,甲说:“以我为坐标原点,乙的位置是(2,3),”丙说:“以我为坐标原点,乙的位置是(−3,−2).”则以乙为坐标原点,甲、丙的坐标分别是(已知三人所建立的直角坐标系在同一平面内,且x轴、y轴的正方向相同)( )A.(−3,−2),(2,−3)B.(−3,2),(2,3)C.(−2,−3),(3,2)D.(−3,−2),(−2,−3)答案:C解析:由于已知三人建立坐标时,x轴y轴正方向相同,以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);同样,以乙为坐标原点,丙的位置是(3,2).∵以甲为坐标原点,乙的位置是(2,3),∴以乙为坐标原点,甲的位置是(−2,−3);∵以丙为坐标原点,乙的位置是(−3,−2),∴以乙为坐标原点,丙的位置是(3,2).故选C.小提示:本题考查了坐标确定位置:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应.填空题4、在平面直角坐标系中,将点P(−1,2)向下平移2个单位长度,再向左平移1个单位长度得到点Q,则点Q的坐标为________.答案:(−2,0)根据平移规律:横坐标右移加,左移减;纵坐标上移加,下移减即可得.解:平移后点Q的坐标为(-1-1,2-2),即(-2,0),所以答案是:(-2,0).小提示:此题主要考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.掌握点的坐标的变化规律是解题的关键.5、平面直角坐标系中,若点A(5,1−2m)在x轴上,则m的值为______.答案:12解析:根据x轴上的点坐标纵坐标等于0,即可求出结果.解:∵点A在x轴上,∴它的纵坐标等于0,即1−2m=0,解得m=1.2.故答案是:12小提示:本题考查平面直角坐标系中点坐标的特点,解题的关键是掌握坐标轴上点坐标的特点.6、已知A(3m,n+2)、B(2n−6,n)、C(2m+5,n−1),当B(2n−6,n)在y轴上,且△ABC的面积等于△AOC的面积时,求代数式|2m−5n|−(3m+2n)2的值.答案:-436解析:先根据B(2n−6,n)在y轴上,求得n的值,然后利用平行线之间距离相等得到AC∥BO,即可得到3m=2m+5,即可求出m,然后代值计算即可.解:∵B(2n−6,n)在y轴上,∴2n−6=0,∴n=3,∵△ABC的面积等于△AOC的面积,∴O、B到直线AC的距离相等,∵A点的纵坐标为n+2=5,C点的纵坐标为n-1=2,∴AC与x轴不平行,∴AC∥BO,∴3m=2m+5,∴m=5,∴|2m−5n|−(3m+2n)2=|2×5−5×3|−(3×5+2×3)2=5−212=−436.小提示:本题主要考查了y轴上点的坐标特征,平行线之间距离相等,坐标与图形等等,解题的关键在于能够熟练掌握相关知识进行求解.。
(必考题)初中七年级数学下册第七单元《平面直角坐标系》经典习题(提高培优)

一、选择题1.第24届冬季奥林匹克运动会将于2022年由北京市和张家口市联合举行.以下能够准确表示张家口市地理位置的是( )A .离北京市200千米B .在河北省C .在宁德市北方D .东经114.8°,北纬40.8°2.在平面直角坐标系中,点Q 的坐标是()35,1m m -+.若点Q 到x 轴的距离与到y 轴的距离相等,则m 的值为( )A .3B .1C .1或3D .2或3 3.点A(-π,4)在第( )象限 A .第一象限B .第二象限C .第三象限D .第四象限 4.在平面直角坐标系中,点A 的坐标为(21a +,3-),则点A 在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 5.如图,一个粒子在第一象限内及x 轴,y 轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x 轴,y 轴平行的方向来回运动,且每分钟移动1个长度单位,那么,第2017分钟时,这个粒子所在位置的坐标是( )A .(7,44)B .(8,45)C .(45,8)D .(44,7) 6.象棋在中国有三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图是一局象棋残局,已知棋子“马”和“车”表示的点的坐标分别为(4,1),(2,1)--,则在第三象限的棋子有( )A .1颗B .2颗C .3颗D .4颗 7.点A (n+2,1﹣n )不可能在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 8.在平面直角坐标系中,点P (−1,23)在( )A .第一象限B .第二象限C .第三象限D .第四象限 9.点()1,3M m m ++在x 轴上,则M 点坐标为( )A .()0,4-B .()4,0C .()2,0-D .()0,2- 10.一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )A .(4,0)B .(5,0)C .(0,5)D .(5,5) 11.某公交车上显示屏上显示的数据(),a b 表示该车经过某站点时先下后上的人数.若车上原有10个人,此公交车依次经过某三个站点时,显示器上的数据如下:()()()3,2,8,5,6,1,则此公交车经过第二个站点后车上的人数为( )A .9B .12C .6D .112.平面直角坐标系中,线段CD 是由线段AB 平移得到的,点A(-1,4)的对应点C(4,7),点B(-4,-1)的对应点D 的坐标为( )A .(-1,-4)B .(1,-4)C .(1,2)D .(-1,2) 13.在下列点中,与点A(-2,-4)的连线平行于y 轴的是( ) A .(2,-4) B .(4,-2) C .(-2,4) D .(-4,2) 14.如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)()()()()()1,01,11,22,13,0....→→→→→→,则2018分钟时粒子所在点的横坐标为( )A .900B .946C .990D .88615.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m .其行走路线如图所示,第1次移动到1A ,第2次移动到2A ,...,第n 次移动到n A .则22020OA A ∆的面积是( )A .210112mB .2505mC .220092mD .2504m二、填空题16.如图,平面直角坐标系xOy 中,点A(4,3),点B(3,0),点C(5,3),OAB ∆沿AC 方向平移AC 长度的到ECF ∆,四边形ABFC 的面积为_________.17.若点A (m +2,﹣3)与点B (﹣4,n +5)在二四象限角平分线上,则m +n =_____. 18.在x 轴上方的点P 到x 轴的距离为3,到y 轴距离为2,则点P 的坐标为________. 19.在平面直角坐标系中,点A ,B 的坐标分别为(1,0),(0,2),若将线段AB 平移到A 1B 1,点A 1,B 1的坐标分别为(2,a),(b ,3),则a 2-2b 的值为______.20.在平面直角坐标系中,点(,)A x y 的坐标满足方程34x y -=,(1)当点A 到两条坐标轴的距离相等时,点A 坐标为__________.(2)当点A 在x 轴上方时,点A 横坐标x 满足条件__________.21.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律经过第2021次运动后,动点P 的坐标是_____.22.点A (m ,﹣3),点B (2,n ),AB //x 轴,则n=_____.23.在平面直角坐标系中,点P (m ,1﹣m )在第一象限,则m 的取值范围是_____. 24.若x ,y 为实数,且满足330x y -++=,则 A(x ,y)在第____象限25.已知线段AB 的长度为3,且AB 平行于y 轴,A 点坐标为()32,,则B 点坐标为______.26.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,按这样的运动规律,经过第1000次运动后,动点P 的坐标是_______;经过第2019次运动后,动点P 的坐标是_______.三、解答题27.已知,在平面直角坐标系中,三角形ABC 三个顶点的坐标分别为()5,6A ,()2,3B -,()3,1C .请在所给的平面直角坐标系中按要求完成以下问题:(1)画出三角形ABC ;(2)将三角形ABC 先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形111A B C (点1A ,1B ,1C 分别是点A ,B ,C 移动后的对应点)请画出三角形111A B C ;并判断线段AC 与11A C 位置与数量关系.28.在平面直角坐标系中,已知点(),B a b ,线段BA x ⊥轴于A 点,线段BC y ⊥轴于C 点,且2(2)a b -++ |22|0a b --=. (1)求A ,B ,C 三点的坐标.(2)若点D 是AB 的中点,点E 是OD 的中点,求AEC 的面积.(3)在(2)的条件下,若点()2,P a ,且AEP AEC S S =△△,求点P 的坐标.29.平面直角坐标系中有点A(m+6n,-1),B(-2,2n-m),连接AB,将线段AB先向上平移,再向右平移,得到其对应线段A'B'(点A'和点A对应,点B'和点B对应),两个端点分别为A'(2m+5n,5),B'(2,m+2n).分别求出点A'、B'的坐标.30.三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).(1)请你在方格中建立直角坐标系,并写出C点的坐标;(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是.(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.。
【3套试题】人教版七年级数学下册第七章平面直角坐标系期中复习检测试题
人教版七年级数学下册第七章平面直角坐标系期中复习检测试题一、选择题(每题3分,共30分)1.在平面直角坐标系中,点P(-3,2)在( B )A.第一象限 B.第二象限 C.第三象限 D.第四象限2.经过两点A(2,3)、B(﹣4,3)作直线AB,则直线AB( B )A.经过原点 B.平行于x轴C.平行于y轴D.无法确定3.若y轴上的点P到x轴的距离为3,则点P的坐标是( D )A.(3,0)B.(0,3)C.(3,0)或(-3,0)D.(0,3)或(0,-3)4.已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( C )A.(7,1) B.B(1,7)C.(1,1) D.(2,1)5.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使三角形ABC的面积为3,则这样的点C共有( B )A.2个B.3个C.4个D.5个6.象棋在中国有三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.图7-2-1是一局象棋残局,已知棋子“马”和“车”所在位置用坐标表示分别为(4,3),(-2,1),则棋子“炮”所在位置用坐标表示为( D )A.(-3,3) B.(3,2) C.(0,3) D.(1,3)7.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在网格的格点上.若线段AB上有一个点P(a,b),则点P在线段A′B′上的对应点P′的坐标为( A )A.(a-2,b+3) B.(a-2,b-3) C.(a+2,b+3) D.(a+2,b-3)8.将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m 个数,如(4,2)表示9,则表示58的有序数对是(A)A.(11,3)B.(3,11)C.(11,9)D.(9,11)9.如图,点A,B的坐标分别为(2,0),(0,1).若将线段AB平移至A1B1的位置,则a+b 的值为( A )A.2 B.3 C.4 D.510.在平面直角坐标系xOy中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为(2,4),点的坐标为( D )A. (-3,3)B.(-2,-2)C.(3,-1)D.(2,4)二、填空题(每空3分,共18分)11.若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是(﹣3,4)。
(完整版)七年级数学下册平面直角坐标系练习题
(完整版)七年级数学下册平面直角坐标系
练习题
问题1
在平面直角坐标系中,已知点A(-2, 3),点B(4, -1)。
求线段AB的中点坐标。
问题2
在平面直角坐标系中,已知点C(3, 5),点D(-2, -4)。
求线段CD的长度。
问题3
在平面直角坐标系中,已知点E(-1, 2),点F(5, 6)。
求线段EF 的斜率。
问题4
在平面直角坐标系中,已知点G(2, -3),斜率为3/4的直线l经过点G。
求直线l的方程。
问题5
在平面直角坐标系中,已知点H(-4, 5),斜率为-2的直线m经过点H。
求直线m的方程。
问题6
在平面直角坐标系中,已知点I(1, 2),点J(3, 8)。
求线段IJ的中点坐标。
问题7
在平面直角坐标系中,已知点K(2, 1),点L(5, -3)。
求线段KL 的长度。
问题8
在平面直角坐标系中,已知点M(3, -2),点N(-1, 4)。
求线段MN的斜率。
问题9
在平面直角坐标系中,已知点P(6, -3),斜率为-1/2的直线r经过点P。
求直线r的方程。
问题10
在平面直角坐标系中,已知点Q(-5, 2),斜率为2的直线s经过点Q。
求直线s的方程。
以上是七年级数学下册平面直角坐标系练习题的完整版。
(必考题)初中七年级数学下册第七单元《平面直角坐标系》经典测试卷(含答案解析)
一、选择题1.如图是北京市地图简图的一部分,图中“故宫”、“颐和园”所在的区域分别是( )D E F6 颐和园奥运村7 故宫 日坛8天坛A .D7,E6B .D6,E7C .E7,D6D .E6,D72.已知点32,)6(M a a -+.若点M 到两坐标轴的距离相等,则a 的值为( ) A .4B .6-C .1-或4D .6-或233.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )A .(3,4)B .(5,4)C .(7,0)D .(8,1) 4.下列各点中,在第二象限的是( )A .()1,0B .()1,1C .()1,1-D .()1,1-5.太原植物园是山西省唯一集科学研究、科普教育、园艺观赏和文化旅游于一体的综合性植物园.其标志性建筑为热带植物馆、沙生植物馆、主题花卉馆三个展览温室,远远望去犹如镶嵌在湖边的3颗大小不一的“露珠”(图1).若利用网格(图2)建立适当的平面直角坐标系,表示东门的点的坐标为()3,2A ,表示热带植物馆入口的点的坐标为()3,3B -,那么儿童游乐园所在的位置C 的坐标应是( )A .()5,1-B .()2,4--C .()8,3--D .()5,1--6.点()1,3P --向右平移3个单位,再向上平移5个单位,则所得到的点的坐标为( ) A .()4,2- B .()2,2 C .()4,8-- D .()2,8- 7.点A(-π,4)在第( )象限A .第一象限B .第二象限C .第三象限D .第四象限8.如图,一个粒子在第一象限内及x 轴,y 轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x 轴,y 轴平行的方向来回运动,且每分钟移动1个长度单位,那么,第2017分钟时,这个粒子所在位置的坐标是( )A .(7,44)B .(8,45)C .(45,8)D .(44,7)9.在平面直角坐标系中,点P (−1,−2+3)在( ) A .第一象限B .第二象限C .第三象限D .第四象限10.点(,)M x y 在第二象限,且230,40x y -=-=,则点M 的坐标是( ) A .(3,2)-B .(3,2)-C .(2,3)-D .(2,3)-11.下列说法正确的是( ) A .若0ab =,则点(,)P a b 表示原点 B .点(1,)a 在第三象限C .已知点(3,3)A -与点(3,3)B ,则直线//AB x 轴D .若0ab >,则点(,)P a b 在第一或第三象限12.已知点(224)P m m +,﹣在x 轴上,则点P 的坐标是( ) A .(40),B .(0)4,C .40)(-,D .(0,4)- 13.过点A (﹣2,3)且垂直于y 轴的直线交y 轴于点B ,则点B 的坐标为( ) A .(0,﹣2)B .(3,0)C .(0,3)D .(﹣2,0)14.如图,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(0,1),将线段AB 平移,使其一个端点到C (3,2),则平移后另一端点的坐标为( )A .(1,3)B .(5,1)C .(1,3)或(3,5)D .(1,3)或(5,1)15.如图,数轴上的点A ,B ,O ,C ,D 分别表示数-2,-1,0,1,2,则表示数25-的点P 应落在( )A .线段AB 上B .线段BO 上C .线段OC 上D .线段CD 上二、填空题16.点(1,1)P -向左平移2个单位,向上平移3个单位得1P ,则点1P 的坐标是________. 17.在平面直角坐标系中,与点A (5,﹣1)关于y 轴对称的点的坐标是_____. 18.如图,已知A 1(1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),…,则坐标为(﹣505,﹣505)的点是______.19.已知点()1,2A ,//AC x 轴,5AC =,则点C 的坐标是______ .20.在平面直角坐标系中,有点A (a ﹣2,a ),过点A 作AB ⊥x 轴,交x 轴于点B ,且AB =2,则点A 的坐标是___.21.若P(2-a ,2a+3)到两坐标轴的距离相等,则点P 的坐标是____________________. 22.点A (m ,﹣3),点B (2,n ),AB //x 轴,则n=_____.23.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点2019A 的坐标是_________.24.如图,已知点A 的坐标为(−2,2),点C 的坐标为(2,1),则点B 的坐标是____.25.若点M(a-2,a+3)在y 轴上,则点N(a+2,a-3)在第________象限.26.点3(2,)A -到x 轴的距离是__________.三、解答题27.在平面直角坐标系中,ABC 的位置如图所示,把ABC 先向左平移2个单位,再向下平移4个单位可以得到A B C '''.(1)画出三角形A B C ''',并写出,,A B C '''三点的坐标; (2)求A B C '''的面积.28.如图,△ABC 在直角坐标系中, (1)请写出△ABC 各点的坐标.(2)若把△ABC 向上平移2个单位,再向左平移1个单位得到△A ′B ′C ′,写出A ′、B ′、C ′的坐标.(3)求出三角形ABC 的面积.29.(1)请在网格中建立平面直角坐标系,使得A ,B 两点的坐标分别为()4,1,()1,2-;(2)在(1)的条件下,过点B 作x 轴的垂线,垂足为点M ,在BM 的延长线上取一点C ,使MC BM =. ①写出点C 的坐标;②平移线段AB 使点A 移动到点C ,画出平移后的线段CD ,并写出点D 的坐标.30.已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.(1)点P在y轴上;(2)点P到x轴、y轴的距离相等,且点P在第二象限;(3)点P在过点A(2,﹣4)且与y轴平行的直线上.。
人教版七年级数学下册期末复习三平面直角坐标系测试题
期末复习(三) 平面直角坐标系各个击破命题点1 确定字母的取值范围【例1】 (上城区校级模拟)若点A(m -3,1-3m)在第三象限,则m 的取值范围是(D )A .m >13B .m <3C .m >3D .13<m <3【方法归纳】 解答此类题的关键是根据平面直角坐标系内点的特征,列出一次不等式(组)或者方程(组),解所列出的不等式(组)或者方程(组),得到问题的解.1.(淄博中考)如果m 是任意实数,那么点P(m -4,m +1)一定不在(D )A .第一象限B .第二象限C .第三象限D .第四象限2.点P(2a ,1-3a)是第二象限内的一个点,且点P 到两坐标轴的距离之和为4,则点P 的坐标是(-65,145).命题点2 用坐标表示地理位置【例2】 (北京中考)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x 轴、y 轴的正方向,表示太和门的点坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是(B )A .景仁宫(4,2)B .养心殿(-2,3)C .保和殿(1,0)D .武英殿(-3.5,-4)【思路点拨】 因为表示太和门的点坐标为(0,-1),所以太和门在y 轴上,在x 轴下方一个单位;因为表示九龙壁的点的坐标为(4,1),所以九龙壁在y 轴右侧,距离y 轴四个单位,所以可以得到每个小方格内的边长是1,由此确定坐标原点的位置,进而求出各个宫殿的所在点的坐标.【方法归纳】 在平面内,如果已知两点的坐标求第三个点的坐标时,通常根据已知两点的横坐标和纵坐标分别确定y 轴和x 轴的位置,从而建立平面直角坐标系,然后求出第三个点的坐标.3.小明同学向大家介绍自己家的位置,其表达正确的是(D )A .距学校300米处B .在学校的西边C .在西北方向300米处D .在学校西北方向300米处4.(延庆县期末)如图是天安门周围的景点分布示意图.若以正东、正北方向为x 轴、y 轴的正方向建立坐标系,表示电报大楼的点的坐标为(-4,0),表示王府井的点的坐标为(3,2),则表示博物馆的点的坐标是(D )A.(1,0) B.(2,0)C.(1,-2) D.(1,-1)5.中国象棋的走棋规则中,有“象飞田字”的说法,如图,象在点P处,走一步可到达的点的坐标记作(0,2)或(4,2).命题点3 图形的平移与坐标变换【例3】已知三角形ABC在平面直角坐标系中的位置如图所示,将三角形ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是(B)A.(5,-2)B.(1,-2)C.(2,-1)D.(2,-2)【思路点拨】由三角形ABC在平面直角坐标系中的位置可知点C的坐标为(3,3),将三角形ABC向下平移5个单位,再向左平移2个单位后,点C的横坐标减2,纵坐标减5,即可求出C点坐标.【方法归纳】在平面直角坐标系中,点P(x,y)向右(或左)平移a个单位后的坐标为P(x+a,y)[或P(x-a,y)];点P(x,y)向上(或下)平移b个单位后的坐标为P(x,y+b)[或P(x,y-b)].6.(来宾中考)如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为(A) A.(2,-1)B.(2,3)C.(0,1)D.(4,1)7.在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A′的坐标是(-2,2),现将三角形ABC平移,使点A变换为点A′,点B′,C′分别是B,C的对应点.(1)请画出平移后的三角形A′B′C′(不写画法),并直接写出点B′,C′的坐标;(2)若三角形ABC内部一点P的坐标(a,b),求点P的对应点P′的坐标.解:(1)画图如图,点B′(-4,1),C′(-1,-1).(2)P′(a-5,b-2).命题点4 平面直角坐标系内图形的面积【例4】(罗定月考)如图,已知四边形ABCD.(1)写出点A,B,C,D的坐标;(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)【思路点拨】过点D作DE⊥BC,AF⊥BC,垂足分别为E,F,则S四边形ABCD=S三角形ABF+S四边形AFED+S三角形DEC.【解答】(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).(2)过点D作DE⊥BC,AF⊥BC,垂足分别为E,F.S四边形ABCD=S三角形ABF+S四边形AFED+S三角形DEC=12×1×3+12×(3+4)×3+12×2×4=16.【方法归纳】求平面直角坐标系中平面图形的面积时,常常利用平行于坐标轴的线段当底,点的横坐标或者纵坐标的绝对值当高.不规则图形的面积常常通过割补法转化为几个规则图形的面积求解.8.在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则三角形ABO的面积为(D) A.15 B.7.5C.6 D.39.已知点A,点B在平面直角坐标系中的位置如图所示,则:(1)写出这两点坐标:A(-1,2),B(3,-2); (2)求三角形AOB 的面积.解:S 三角形AOB =12×1×1+12×1×3=2.命题点5 规律探索型【例5】 如图,已知A 1(1,0),A 2(1,1),A 3(-1,1),A 4(-1,-1),A 5(2,-1),…,则点A 2 017的坐标为(505,-504).【思路点拨】 要求A 2 017的坐标,可先从简单的点的坐标开始探究,发现其中的规律.从各点的位置可以发现:A 1(1,0),A 2(1,1),A 3(-1,1),A 4(-1,-1);A 5(2,-1),A 6(2,2),A 7(-2,2),A 8(-2,-2);A 9(3,-2),A 10(3,3),A 11(-3,3),A 12(-3,-3);….因为2 017÷4=504……1,所以可判断A 2 017所在象限及坐标.【方法归纳】 规律探究题往往是从个例、特殊情况入手,发现其中的规律,从而推广到一般情况,用适当的式子表示出来即可,这是近几年来考试的一个热点.10.(河南中考改编)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3,…组成一条平滑的曲线.点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2 017秒时,点P 的坐标是(C )A .(2 017,0)B .(2 017,-1)C .(2 017,1)D .(2 018,0)11.(甘孜中考)如图,正方形A 1A 2A 3A 4,A 5A 6A 7A 8,A 9A 10A 11A 12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A 1,A 2,A 3,A 4;A 5,A 6,A 7,A 8;A 9,A 10,A 11,A 12;…)的中心均在坐标原点O ,各边均与x 轴或y 轴平行,若它们的边长依次是2,4,6…,则顶点A 20的坐标为(5,-5).整合集训一、选择题(每小题3分,共30分)1.(广东中考)在平面直角坐标系中,点P(-2,-3)所在的象限是(C)A.第一象限B.第二象限C.第三象限D.第四象限2.(柳州中考)如图,在平面直角坐标系中,点P的坐标为(A)A.(3,-2) B.(-2,3)C.(-3,2) D.(2,-3)3.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到点B,点B的坐标是(B) A.(-5,3) B.(1,3)C.(1,-3) D.(-5,-1)4.(株洲中考)如图是株洲市的行政区域平面地图,下列关于方位的说法明显错误的是(C) A.炎陵位于株洲市区南偏东约35°的方向上B.醴陵位于攸县的北偏东约16°的方向上C.株洲县位于茶陵的南偏东约40°的方向上D.株洲市区位于攸县的北偏西约21°的方向上5.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比(D) A.向右平移了3个单位B.向左平移了3个单位C.向上平移了3个单位D.向下平移了3个单位6.在平面直角坐标系中,点(-1,m2+1)一定在(B)A.第一象限B.第二象限C.第三象限D.第四象限7.如图是中国象棋的一盘残局,如果用(4,0)表示“帅”的位置,用(3,9)表示“将”的位置,那么“炮”的位置应表示为(A)A.(8,7) B.(7,8)C.(8,9) D.(8,8)8.在平面直角坐标系内有一点P,已知P点到x轴的距离为2,到y轴的距离为4,则P点的坐标不可能是(A) A.(-2,-4) B.(4,2)C.(-4,2) D.(4,-2)9.已知A(-4,3),B(0,0),C(-2,-1),则三角形ABC的面积为(C)A.3 B.4C.5 D.610.如图,点A1,A2,A3,A4是某市正方形道路网的部分交汇点.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有(B)A.4种B.6种C.8种D.10种提示:共有如图所示的6种情况:二、填空题(每小题4分,共20分)11.(铜山县校级月考)教室里的座位摆放整齐,如果1排2号用(1,2)表示,那么(4,5)表示的意思是4排5号.12.若点P(x,y)的坐标满足x+y=xy,则称点P为“和谐点”.请写出一个“和谐点”的坐标为答案不唯一,如:(2,2)或(0,0).x+2=0,则点A在第二象限.13.若点A(x,y)的坐标满足(y-1)2+||14.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-4,-1)、N(0,1),将线段MN平移后得到线段M′N′(点M、N分别平移到点M′、N′的位置),若点M′的坐标为(-2,2),则点N′的坐标为(2,4).15.(建瓯校级月考)如图,货轮与灯塔相距30海里,如何用方向和距离描述货轮相对于灯塔的位置北偏东60°,30海里.三、解答题(共50分)16.(8分)如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.(1)写出A,B,C,D,E的坐标;(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?解:(1)A(2,3),B(5,2),C(3,9),D(7,5),E(6,11).(2)在原点北偏东45°的点是点F,其坐标为(12,12).17.(8分)如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),如果以O为原点建立平面直角坐标系,用(2,2.5)表示金凤广场的位置,用(11,7)表示动物园的位置.根据此规定:(1)湖心岛、光岳楼、山陕会馆的位置如何表示?(2)(11,7)和(7,11)是同一个位置吗?为什么?解:(1)湖心岛(2.5,5)、光岳楼(4,4)、山陕会馆(7,3).(2)不是,因为根据题目中点的位置确定可知水平数轴上的点对应的数在前,竖直数轴上的点对应的数在后,是有序数对.18.(8分)如图,已知单位长度为1的方格中有个△AB C.(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′;(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B、点B′的坐标:B(1,2);B′(3,5).19.(12分)如图,在所给的坐标系中描出下列各点的位置:A(-4,4),B(-2,2),C(3,-3),D(1,-1),E(-3,3),F(0,0).你发现这些点有什么关系?你能再找出一些类似的点吗?(至少3个)解:因为A(-4,4),B(-2,2),C(3,-3),D(1,-1),E(-3,3),F(0,0), 所以各点的横坐标与纵坐标互为相反数.答案不唯一,类似的点有(4,-4)、(-1,1)、(10,-10)等.20.(14分)如图,四边形ABCD 各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0).(1)确定这个四边形的面积,你是怎么做的?(2)如果把原来四边形ABCD 各个顶点的纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?解:(1)将四边形分割成如图所示的长方形、直角三角形,分别为①、②、③、④,共4个部分,可求出各自的面积:S 长方形①=9×6=54,S 直角三角形②=12×2×8=8,S 直角三角形③=12×2×9=9,S 直角三角形④=12×3×6=9.∴四边形的面积为54+8+9+9=80.(2)如果把原来四边形ABCD 各个顶点的纵坐标保持不变,横坐标增加2,所得的四边形就是将原来的四边形向右平移两个单位长度得到的,所以其面积不变,还是80.人教版七年级上册期末测试卷一、选择题(每题3分,共30分)1.某天的最高气温是8℃,最低气温是-3℃,那么这天的温差是( ) A .-3℃ B .8℃ C .-8℃D .11℃2.下列立体图形中,从上面看能得到正方形的是( )3.下列方程是一元一次方程的是( ) A .x -y =6 B .x -2=x C .x 2+3x =1D .1+x =34.今年某市约有108 000名应届初中毕业生参加中考,108 000用科学记数法表示为( )A .0.108×106B .10.8×104C .1.08×106D .1.08×1055.下列计算正确的是( ) A .3x 2-x 2=3 B .3a 2+2a 3=5a 5 C .3+x =3xD .-0.25ab +14ba =06.已知ax =ay ,下列各式中一定成立的是( ) A .x =yB .ax +1=ay -1C .ax =-ayD .3-ax =3-ay7.某商品每件标价为150元,若按标价打8折后,再降价10元销售,仍获利10%,则该商品每件的进价为( ) A .100元 B .105元 C .110元D .120元8.如果一个角的余角是50°,那么这个角的补角的度数是( ) A .130° B .40° C .90°D .140°9.如图,C ,D 是线段AB 上的两点,点E 是AC 的中点,点F 是BD 的中点,EF =m ,CD =n ,则AB 的长是( )A .m -nB .m +nC .2m -nD .2m +n10.下列结论:①若a +b +c =0,且abc ≠0,则a +c 2b =-12;②若a +b +c =0,且a ≠0,则x =1一定是方程ax +b +c =0的解; ③若a +b +c =0,且abc ≠0,则abc >0; ④若|a |>|b |,则a -ba +b>0. 其中正确的结论是( ) A .①②③ B .①②④ C .②③④D .①②③④二、填空题(每题3分,共24分)11.-⎪⎪⎪⎪⎪⎪-23的相反数是________,-15的倒数的绝对值是________.12.若-13xy3与2x m-2y n+5是同类项,则n m=________.13.若关于x的方程2x+a=1与方程3x-1=2x+2的解相同,则a的值为________.14.一个角的余角为70°28′47″,那么这个角等于____________.15.下列说法:①两点确定一条直线;②两点之间,线段最短;③若∠AOC=12∠AOB,则射线OC是∠AOB的平分线;④连接两点之间的线段叫做这两点间的距离;⑤学校在小明家南偏东25°方向上,则小明家在学校北偏西25°方向上,其中正确的有________个.16.在某月的月历上,用一个正方形圈出2×2个数,若所圈4个数的和为44,则这4个日期中左上角的日期数值为________.17.规定一种新运算:a△b=a·b-2a-b+1,如3△4=3×4-2×3-4+1=3.请比较大小:(-3)△4________4△(-3)(填“>”“=”或“<”).18.如图是小明用火柴棒搭的1条“金鱼”、2条“金鱼”、3条“金鱼”……则搭n条“金鱼”需要火柴棒__________根.三、解答题(19,20题每题8分,21~23题每题6分,26题12分,其余每题10分,共66分) 19.计算:(1)-4+2×|-3|-(-5);(2)-3×(-4)+(-2)3÷(-2)2-(-1)2 018.20.解方程:(1)4-3(2-x)=5x;(2)x-22-1=x+13-x+86.21.先化简,再求值:2(x2y+xy)-3(x2y-xy)-4x2y,其中x=1,y=-1.22.有理数b在数轴上对应点的位置如图所示,试化简|1-3b|+2|2+b|-|3b-2|.23.如图①是一些小正方体所搭立体图形从上面看得到的图形,方格中的数字表示该位置的小正方体的个数.请在如图②所示的方格纸中分别画出这个立体图形从正面看和从左面看得到的图形.24.已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.25.为鼓励居民节约用电,某市电力公司规定了电费分段计算的方法:每月用电不超过100度,按每度电0.50元计算;每月用电超过100度,超出部分按每度电0.65元计算.设每月用电x度.(1)当0≤x≤100时,电费为________元;当x>100时,电费为____________元.(用含x的整式表示)(2)某用户为了解日用电量,记录了9月前几天的电表读数.该用户9月的电费约为多少元?(3)该用户采取了节电措施后,10月平均每度电费0.55元,那么该用户10月用电多少度?26.如图,O为数轴的原点,A,B为数轴上的两点,点A表示的数为-30,点B表示的数为100.(1)A,B两点间的距离是________.(2)若点C也是数轴上的点,点C到点B的距离是点C到原点O的距离的3倍,求点C表示的数.(3)若电子蚂蚁P从点B出发,以6个单位长度/s的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向左运动,设两只电子蚂蚁同时运动到了数轴上的点D,那么点D表示的数是多少?(4)若电子蚂蚁P从点B出发,以8个单位长度/s的速度向右运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/s的速度向右运动.设数轴上的点N到原点O的距离等于点P到原点O 的距离的一半(点N在原点右侧),有下面两个结论:①ON+AQ的值不变;②ON-AQ的值不变,请判断哪个结论正确,并求出正确结论的值.(第26题)答案一、1.D 2.A 3.D 4.D 5.D 6.D7.A8.D9.C10.B二、11.23;512.-813.-514.19°31′13″15.316.717.>18.(6n+2)三、19.解:(1)原式=-4+2×3+5=-4+6+5=7;(2)原式=12+(-8)÷4-1=12-2-1=9.20.解:(1)去括号,得4-6+3x=5x.移项、合并同类项,得-2x=2.系数化为1,得x=-1.(2)去分母,得3(x-2)-6=2(x+1)-(x+8).去括号,得3x-6-6=2x+2-x-8.移项、合并同类项,得2x=6.系数化为1,得x=3.21.解:原式=2x2y+2xy-3x2y+3xy-4x2y=(2x2y-3x2y-4x2y)+(2xy+3xy)=-5x2y+5xy.当x=1,y=-1时,原式=-5x2y+5xy=-5×12×(-1)+5×1×(-1)=5-5=0.22.解:由题图可知-3<b<-2.所以1-3b>0,2+b<0,3b-2<0.所以原式=1-3b-2(2+b)+(3b-2)=1-3b-4-2b+3b-2=-2b-5.23.解:如图所示.24.解:(1)设∠COF=α,则∠EOF=90°-α.因为OF是∠AOE的平分线,所以∠AOE=2∠EOF=2(90°-α)=180°-2α.所以∠BOE=180°-∠AOE=180°-(180°-2α)=2α.所以∠BOE =2∠COF .(2)∠BOE =2∠COF 仍成立.理由:设∠AOC =β,则∠AOE =90°-β,又因为OF 是∠AOE 的平分线,所以∠AOF =90°-β2.所以∠BOE =180°-∠AOE =180°-(90°-β)=90°+β,∠COF =∠AOF +∠AOC =90°-β2+β=12(90°+β).所以∠BOE =2∠COF .25.解:(1)0.5x ;(0.65x -15)(2)(165-123)÷6×30=210(度),210×0.65-15=121.5(元).答:该用户9月的电费约为121.5元.(3)设10月的用电量为a 度.根据题意,得0.65a -15=0.55a ,解得a =150.答:该用户10月用电150度.26.解:(1)130(2)若点C 在原点右边,则点C 表示的数为100÷(3+1)=25;若点C 在原点左边,则点C 表示的数为-[100÷(3-1)]=-50.故点C 表示的数为-50或25.(3)设从出发到同时运动到点D 经过的时间为t s ,则6t -4t =130,解得t =65.65×4=260,260+30=290,所以点D 表示的数为-290.(4)ON -AQ 的值不变.设运动时间为m s ,则PO =100+8m ,AQ =4m .由题意知N 为PO 的中点,得ON =12PO =50+4m ,所以ON +AQ =50+4m +4m =50+8m ,ON -AQ =50+4m -4m =50.故ON-AQ的值不变,这个值为50.。
