变位齿轮的计算方法
机械设计基础变位齿轮

si
sri r
2ri (invi
inv )
k inv(k )
θ
二、变位齿轮传动
1、正确啮合条件与连续传动条件同 标准齿轮传动。
即:m1 m2 m,1 2 ;
[ ].
2、中心距和啮合角
1).无侧隙传动
中心距要求:
2).满足标准顶隙
节 圆 与 分 度 圆 不 重 合a, a 中心距与啮合角的关系仍为:
4) 渐开线圆柱齿轮任意圆上的齿厚
C ssi
B i A i
C
B ra
A ri r
o rb
4) 渐开线圆柱齿轮任意圆上的齿厚
C ssi
B i A i
o
C
B ra
A ri r
rb
如图所示:
si CC rii
i BOB 2BOC s r 2(i ) s r 2(invi inv )
1)正传动: x1 x2 0
a a,
齿数条件:不受任何限制。
优点:可配凑中心距;结构尺寸小,改善 磨损情况;强度提高,承载能力大。
缺点: 下降,互换性差。
2)负传动: x1 x2 0
a a,
齿数条件: z1 z2 2zmin
优点:可配凑中心距; 略有增大。
缺点:强度下降,承载能力下降,互换 性差。
x
ha*
z sin 2
2
ha* (1
z )
z m in
因此,用标准齿条刀切 制少于最小齿数齿轮不出 现根切的最小变为系数要 进行讨论
r rb
xmin m
O
B刀 N
P
Q ham
最小变位系数
(h*a x)m NQ
变位齿轮中心距计算公式【终于整全了】

目前手册上的跨齿数计算公式大都是近似的,有误差的,并非精确的计算公式,因而有时影响跨齿数的合理性。
就是那些精确的公式,它们在角度变位中也是有不足之处的。
而且至今在手册上似乎还未见到有斜齿精确的跨齿数计算公式。
有人说:“手册上的5.01800+'=n z k α不就是标准斜齿轮跨齿数精确的计算公式吗?”不,它算出的也是近似值(文章后面进行验证)。
笔者已退休多年,精力尚可,因而对此进行了研究、探讨,于是给出一个高度、角度变位都是情况良好的公式。
公式为:5.01)cos sin 2(+--'=παααzinv m xm W k k (用于直齿) (1)5.01)cos sin 2(+'--'=παααn n n n n n n inv z m m x W k (用于斜齿) (1)公式中的'k W 和'n W 当为高度变位直齿时, bKd xm d W 22)2(-+='; 斜齿时, b bn n n d m x d W βcos )2(22-+='。
当为角度变位直齿时, b k d xm d W 22)9.1(-+=';斜齿时, 。
cos )9.1(22b bn n n d m x d W β-+='上列公式中:d ——分度圆直径; b d ——基圆直径;m ——模数,斜齿时为n m ;z —— 齿数;___z '斜齿轮的假想齿数,ntinv inv zz αα=' ; ___α压力角,斜齿轮法面压力角为n αx —— 变位系数,斜齿时法面变位系数为n x ; ___bβ斜齿轮基圆螺旋角;k W '——直齿轮的公法线长度原始计算值 ; n W '——斜齿轮的公法线长度原始计算值 。
2、公式(1)的由来公式(1)是怎么来的?其实它的来历很简单,就是由公法线长度计算公式变换而来的。
公法线长度计算公式为 :[] sin 2)5.0( cos ααπαm x zinv k m W k ++-= (直齿) (2)[] sin 2)5.0cos n n n n n n n m x inv z k m W ααπα+'+-=((斜齿) (2) 将公式(2)中的k 移到等号左边,将k W 和n W 移到等号右边(且变为k W '和n W ')即为公式(1)。
变位斜齿轮设计计算,重合度计算

0.39743474
1.7449207
端面重合度 ε
α
纵向重合度ε
β
总重合度ε
γ
b sin db 1 arccos z tan tan z tan tan at1 t 2 at 2 t m d a 2 1 n
端面模数mt
mt
mn cos
11
2
20
9.986
0.4
1
16
2.03
54
2
20
9.986
-0.4
1
16
2.03
于外啮合齿轮
分度圆直径 d 齿顶高 ha 齿顶圆直径da 中心距 a
d m t z1
m n z1 * dm h ( h x) a n a an cos
d 2ha
斜齿轮重合度计算,本算例只适合于外啮合齿轮
齿数 Z 模数 m 压力角 α 螺旋角 β 变为系数 齿顶高系 齿宽 b * χ 数 h an 端面模数mt
mt
mn cos
9
2.5
20
11.25
0.5
1
16
2.55
42
2.5
20
11.25
-0.5
1
16
2.55
齿数 Z
模数 m
压力角 α
螺旋角 β
变为系数 齿顶高系 齿宽 b χ 数 h* an
22.34
27.94 66.00
109.66
1.2
112.06
端面压力角 α
t
基圆直径 db
齿顶圆压力角α
at
mn d b ) d cos ( z1 z2 ) t arctan(tan n / cos cos
标准齿轮变位系数

标准齿轮变位系数
标准齿轮变位系数,又称修形系数,是齿轮行业中一个重要的参数。
它是指齿轮齿形弧线在设计时所加入的修正量,以弥补理论齿形与实际齿形误差之间的差异,达到减小齿轮工作时的噪声和振动,提高齿轮传动的精度和使用寿命。
标准齿轮变位系数的计算方法是根据齿轮设计所需副调量和齿数、模数等参数来确定。
修型系数的计算公式为:
*X = (a0 + a1(m-2.5) + a2(m-2.5)^2) / cosαm
其中,a0、a1、a2是常数,αm是压力角,m是模数。
标准齿轮变位系数还受到其他因素的影响,如齿顶高度、弧齿间隙等。
因此,在齿轮设计中,要根据实际情况适当调整修型系数的大小,以达到最佳的使用效果。
在齿轮加工中,标准齿轮变位系数的控制非常重要。
一般来说,修型系数过大或过小都会对齿轮的传动性能产生不良影响。
修型系数过大会导致齿形过修,使齿轮噪声和振动等问题更加严重;修型系数过小则会使齿轮实际齿形与理论齿形之间的误差增大,影响齿轮传动的精度和寿命。
总之,标准齿轮变位系数是齿轮设计与加工中一个非常关键的参数。
它对于提高齿轮传动效率、降低噪声和振动、延长使用寿命等方面都有着重要作用。
因此,
在齿轮设计和制造的过程中,要严格按照标准齿轮变位系数要求进行控制,以确保齿轮传动的质量和可靠性。
变位圆柱齿轮跨测齿数的简便计算

变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工周万峰摘要:本文给出一个简便的跨齿数计算的经验公式,并验证了该公式确定的跨齿数是合理的。
关键词:变位齿轮,跨齿数,公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样,五花八门:有教科书上公式,有各种手册上公式,有参考书上的公式,还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式序号用于直齿用于斜齿1234[]+0.5 []+0.5注:早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出,表1中的几个公式大都比较复杂:平方、开放、三角函数等等项目很多,计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此,笔者通过分析研究,并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角时,经验公式为:——齿数,斜齿时代入(,可查手册)。
——变位系数,斜齿时。
——与变位系数正负有关的系数。
当变位系数为正(时p=1.4,当变位系数为负(时p=1.9。
通过大量的算例验证后得知,当变位系数为负时,由经验公式确定的跨齿数与表1中的公式(4)确定的跨齿数是完全一样的(见表2)。
当变位系数为正时,经验公式与表1中的(2)、(3)、(4)确定的跨齿数绝大多数是相同的,只在极少数情况下两者的跨齿数不同。
但在不同的情况下,经验公式的情况比理论公式的情况还好些(见表3)。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表()齿数z 变位系数x跨齿式计算值确定的跨齿数齿数z变位系数x跨齿数计算值确定的跨齿数经验公式理论公式经验公式理论公式经验公式理论公式经验公式理论公式14 0.40 2.61 2.63 3 3 56 -0.4 5.96 5.97 6 6 19 0.60 3.45 3.47 3 3 67 -0.52 6.95 6.96 7 7 24 0.70 4.14 4.18 4 4 80 -0.63 8.19 8.19 8 8 28 0.72 4.61 4.67 5 5 96 -0.7 9.83 9.85 10 10 52 1.0 7.67 7.80 8 8 124 -0.8 12.75 12.79 13 13 100 1.50 13.71 13.96 14 14 150 -1.20 14.89 14.90 15 15注:表2中的“理论公式”为表1中的公式(4)。
齿轮变位系数计算公式
齿顶高ha=
0.664884418
齿根高hf=
0.76
齿顶圆直径da=
6.129768836
齿根圆直径df=
3.28
基圆直径db=
4.51052458
齿距p=
基圆齿距pb=
齿厚s=
1.431342774
基圆齿厚sb=
1.412247101
齿顶圆压力角αa= 42.62181966
顶圆齿厚sa=
端面重合度εa=
#NUM!
校验干涉
应满足
渐开线干涉
1
≧
小齿轮过渡曲线干涉
≧
由表2-11查 #NUM!
外啮合标准斜齿(人字齿)圆柱齿轮传动
大轮齿数z2=
9
小轮齿数z1=
9
法向模数mn=
1.5
法向压力角αn=
30
螺旋角β=
25
端面模数mt=
1.655066878
端面压力角αt=
32.49858487
法向齿顶高系数han*= 1 法向顶隙系数cn*= 0.25
1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮 斜齿外齿轮
跨测齿数 公法线长度 跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度 跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
变位齿轮公式

变位齿轮公式变位齿轮传动的设计步骤设计变位齿轮时,根据不同的已知条件,可采用不同的设计步骤。
(1)已知z1、z2、m、α、ha*和c*时,其设计步骤为:1)选择传动类型,若z1+z2 < 2zmin,必须采用正传动,否则可考虑其它传动类型;2)选择两齿轮的变位系数;3)计算两齿轮的几何尺寸;4)验算重合度及轮齿强度。
(2)已知z1、z2、m、a'、α、ha*和c*时,其设计步骤为:1)计算啮合角α'cosα'=(a/a')cosα2)选择两齿轮的变位系数invα'=2tgα(x1+x2)/(z1+z2) + invαx1+x2=(z1+z2)(invα'-invα)/2tgαx1≥ha*(zmin-z)/zmin,x2≥ha*(zmin-z)/zmin3)计算两齿轮的几何尺寸4)验算重合度及轮齿强度(3)已知i、m、a'、α、ha*和c*时,其设计步骤为:1)确定两齿轮的齿数因a'=acosα/cosα'=[m(z1+z2)/2]cosα/cosα'=[mz1(1+i)/2]cosα/cosα' 故z1≈2a'/(i+1)m 取整数,z2=iz1 取整数。
思考题:1)某机器中的一对外啮合标准圆柱直齿轮,小齿轮轮齿严重磨损,拟报废,大齿轮轮齿磨损较轻,拟修复。
试问采用什么方法可使传动能恢复使用?2)图示为一单联滑移齿轮机构,已知基本参数为m=3mm,z1=18,z2=30,z3=27。
试问有几种设计方案?哪种方案较好?3)吊车行走机构中有一对标准直齿轮传动,已知z1=13,z2=47,m=3mm,齿轮1因根切经常断齿。
试问采用什么方案来解决这个问题?例用齿条插刀加工一个直齿圆柱齿轮。
已知被加工齿轮轮坯的角速度ω1=5 rad/s,刀具的移动速度为0.375m/s,刀具的模数m=10mm,压力角α=200。
变位齿轮参数及计算
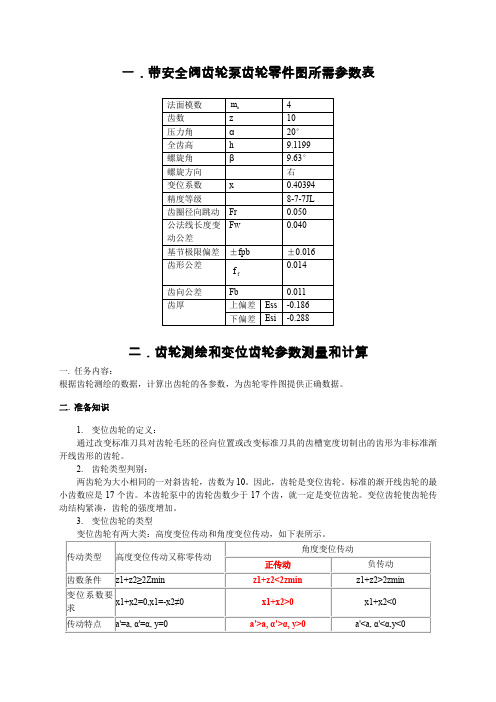
一.带安全阀齿轮泵齿轮零件图所需参数表法面模数nm 4齿数z 10压力角α20°全齿高h 9.1199螺旋角β9.63°螺旋方向右变位系数x 0.40394精度等级8-7-7JL齿圈径向跳动Fr 0.050公法线长度变动公差Fw 0.040基节极限偏差±fpb ±0.016齿形公差ff0.014齿向公差Fb 0.011齿厚上偏差Ess -0.186下偏差Esi -0.288二.齿轮测绘和变位齿轮参数测量和计算一.任务内容:根据齿轮测绘的数据,计算出齿轮的各参数,为齿轮零件图提供正确数据。
二.准备知识1.变位齿轮的定义:通过改变标准刀具对齿轮毛坯的径向位置或改变标准刀具的齿槽宽度切制出的齿形为非标准渐开线齿形的齿轮。
2.齿轮类型判别:两齿轮为大小相同的一对斜齿轮,齿数为10。
因此,齿轮是变位齿轮。
标准的渐开线齿轮的最小齿数应是17个齿。
本齿轮泵中的齿轮齿数少于17个齿,就一定是变位齿轮。
变位齿轮使齿轮传动结构紧凑,齿轮的强度增加。
3.变位齿轮的类型变位齿轮有两大类:高度变位传动和角度变位传动,如下表所示。
传动类型高度变位传动又称零传动角度变位传动正传动负传动齿数条件z1+z2≥2Zmin z1+z2<2zmin z1+z2>2zmin 变位系数要求x1+x2=0,x1=-x2≠0x1+x2>0 x1+x2<0 传动特点a'=a, α'=α, y=0 a'>a, α'>α, y>0 a'<a, α'<α,y<0主要优点小齿轮取正变位,允许z1<zmin ,减小传动尺寸。
提高了小齿轮齿根强度,减小了小齿轮齿面磨损,可成对替换标准齿轮。
传动机构更加紧凑,提高了抗弯强度和接触强度,提高了耐磨性能,可满足a'>a 的中心距要求。
重合度略有提高,满足a'<a 的中心距要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变位齿轮的计算方法1 变位齿轮的功用及变位系数变位齿轮具有以下功用:(1)避免根切;(2)提高齿面的接触强度和弯曲强度;(3)提高齿面的抗胶合和耐磨损能力;(4)修复旧齿轮;(5)配凑中心距。
对于齿数z=8~20的直齿圆柱齿轮,当顶圆直径d a=mz+2m+2xm时,不产生根切的最小变位系数x min,以及齿顶厚S a=0。
4m和S a=0时的变位系数x sa=0.4m和x sa=0如表1所列。
2 变位齿轮的简易计算将变位齿轮无侧隙啮合方程式作如下变换:总变位系数中心距变动系数齿顶高变动系数表 1 齿数z=8~20圆柱齿轮的变位系数z x min x sa=0.4m x sa=08 910111213141516171819 200。
53 0.47 0。
42 0.36 0。
30 0.24 0.18 0。
12 0.06 0-0。
05 -0.11 -0。
170.180.220。
270.310.350。
390。
430.460.500。
530.560.590。
620.560.630。
700。
760.820。
880。
930.981。
031。
081.131。
181.23或Δy=xΣ-y式中:α-—压力角,α=20°;α′--啮合角;z2、z1——大、小齿轮的齿数。
将上述三式分别除以,则得:由上述公式可以看出,当齿形角α一定时,x z、y z和Δy z均只为啮合角α′的函数。
在设计计算时,只要已知x z、y z、Δy z和α′四个参数中的任一参数,即可由变位齿轮的x z、y z、Δy z和啮合角α′的数值表(表2)中,查出其他三个参数,再进行下列计算。
一般齿轮手册上均列有此数值表。
式中正号用于外啮合,负号用于内啮合。
3 计算实例例1:已知一对外啮合变位直齿轮,齿数z1=18,z2=32,压力角α=20°,啮合角α′=22°18′,试确定总变位系数xΣ、中心距变动系数y及齿顶高变动系数Δy。
解:根据α′=22°18′查表2,得:x z=0.01653,y z=0.01565,Δy z=0.00088由此得:例2:已知一直齿内啮合变位齿轮副,齿数z1=19,z2=64,α=20°,啮合角α′=21°18′。
求xΣ、y 及Δy。
解:根据α′=21°18′查表2,得:x z=0。
00886,y z=0。
00859,Δy z=0。
00027。
由此得:其他几何尺寸计算按常规计算进行.此外,变位齿轮的公法线长度的变动量ΔW=2sinαxm,当α=20°时,公法线长度变动量ΔW=0.684xm,式中x为变位系数,应计及正、负号。
因此,变位齿轮的公法线长度为:W k=W k*m+0。
684xm式中:W k*——某齿数齿轮跨测k齿时,模数m=1的公法线长度。
表 2 变位齿轮的y z、x z、Δy z和啮合角α′(α=20°)α′(分)19°20°21°y z x zΔy z y z x zΔy z y z x zΔy z0 1 2 3 4 5 6 7 8 9-0。
00616606596586576566556546536526-0。
006015925825735635545445355255150.000150140140130130120120110110110.000000110210320420530640750850960.000000110210320430530640750860960。
000000000000000000000000000000000。
006556666776897007117227347457560。
006716836947067187307427547667780.00016017017017018019020020021022101112131415161718 19-0.00516506496486476466456445435425-0。
005064964864774674574484384284180.000100100100090090090080070070070.001061171281391491601711821922030。
001071181291391501611721831942050.000010010010010010010010010020020.007687797908028138258368478598700。
007898018148258378508628748868980.00022023023024024025026027027028202122232425262728 29-0。
00415405395384374364354344333323-0.004083983893793693593493393293190.000070070060050050050050050040040。
002142252362462572682792903013120。
002162272382492602712822933043150。
000020020020030030030030030030030。
008828939059169289399519629749850。
009109239359479599729849960。
010090210。
00029030030031032033033034035036303132333435363738 0。
00313303292282272261251241-0。
003092992892792692592492380.000040040040030030020020020020.003233343443553663773883994100。
003263383493603713833944050030040050050050060060060070。
009970.010090200320430550670870.010330460580700830951081211330.00036037038039040040041042043。
