变位齿轮几何参数计算
变位齿轮参数及计算
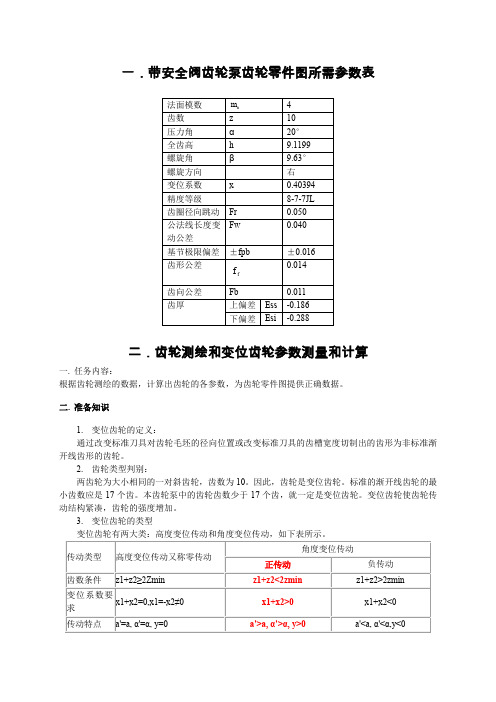
x 0.40394
3.计算其他参数的公式 端面模数 mt mn / cos 啮合角 cos '
a cos a'
总变位系数: xt
z1 z2 (invt' invt ) 2 tan t
12t2tantttzzxinvinv???????分度圆直径d齿顶圆直径mz?2aaddh??齿根圆直径2ffddh??基圆直径cosbtdd??齿顶高ananntthmhxym????齿根高nfnannhmhcx???标准中心距1212add??中心距变动系数ttaaym??齿顶高变动系数tttyxy????固定弦齿厚2cos2tan2cnnnnnsmx?????五计算软件界面
* a
② 然后按全齿高计算模数:
m
③从而从标准模数系列中选择 m 4 ,进行下面的试算,然后校核。
2.验算压力角和计算变位系数 依据公法线长度公式可选择压力角,然后计算变位系数。 ① 通过基圆齿距 Pb Wk1 Wk m cos 公式计算模数 m。 ② 将公法线值和压力角值 20°和 15°分别代入上式验算模数 m, 其中压力角为 20°时算得结果接 近模数 4,故取 n 20 。 ③ 求变位系数
ห้องสมุดไป่ตู้
主要缺点
由于我们的齿轮副的两个齿轮的齿数之和小于 17 齿的两倍,所以这对齿轮是采用角度变位中的 正变位加工而成的。 三. 齿轮参数测量结果: 齿数 z : 10 齿顶圆直径 Da : 49.94 齿根圆直径 D f
31.81
端面公法线长度 Wk 18.876mm 端面公法线长度 Wk 1 30.055mm 斜齿螺旋角 9.63° 啮合中心距离 a 42mm 其他已知参数: 压力角 n 20°or15° 齿顶高系数 径向间隙系数
变位齿轮几何尺寸计算

变位齿轮几何尺寸计算
变位齿轮是齿轮传动系统中常用的一种齿轮,主要用于传递旋转运动和扭矩。
其特点是在齿轮齿条的侧面具有斜面,能够实现平滑传动和减小齿轮传动时的冲击和噪声。
在设计变位齿轮时,需要进行几何尺寸的计算来保证齿轮的运转性能。
变位齿轮的几何尺寸计算主要包括齿轮的模数、齿数、齿顶高和齿根深等参数。
下面将详细介绍每个参数的计算方法。
1.模数(m)的计算:
模数是齿轮齿条的基本尺寸,它表示齿轮齿条的大小。
模数的计算根据传动所需的扭矩和功率来确定,通常使用公式:
m=K∛(T/P)
其中,m为模数,K为系数(一般取20),T为传动所需扭矩,P为传动功率。
2.齿数(z)的计算:
齿数表示齿轮上的齿的数量。
齿数的计算根据传动比和模数来确定,一般使用公式:
z=m×i
其中,i为传动比。
3.齿顶高(h_a)和齿根深(h_f)的计算:
齿顶高表示齿轮齿条的最高点到齿顶的距离,齿根深表示齿轮齿条的最低点到齿底的距离。
它们的计算可以使用公式:
h_a=1.25×m
h_f=1.35×m
上述是变位齿轮几何尺寸计算的基本方法,但实际设计中还需要考虑齿轮的齿向角、齿轮间的啮合角、齿轮侧隙等因素。
此外,变位齿轮的几何尺寸还需要满足一些额外的要求,如齿轮的强度和刚度等。
关于变位齿轮几何尺寸计算的更详细内容可以参考相关的齿轮设计手册和专业参考书籍。
(完整版)变位齿轮的计算方法

Wk=Wk*m+0.684xm
式中:Wk*——某齿数齿轮跨测k齿时,模数m=1的公法线长度。
表 2 变位齿轮的yz、xz、Δyz和啮合角α′(α=2ห้องสมุดไป่ตู้°)
α′
(分)
19°
20°
21°
yz
xz
Δyz
yz
xz
Δyz
yz
xz
Δyz
0
1
2
3
4
5
6
7
8
9
-0.00616
606
596
0.00107
118
129
139
150
161
172
183
194
205
0.00001
001
001
001
001
001
001
001
002
002
0.00768
779
790
802
813
825
836
847
859
870
0.00789
801
814
825
837
850
862
874
886
898
0.00022
023
023
024
236
246
257
268
279
290
301
312
0.00216
227
238
249
260
271
282
293
304
315
0.00002
002
002
003
003
变位齿轮几何参数计算

(invα '−invα )
invα '及invα 可根据 a' 、 a 由
表查得
χ ∑ = x1 + x2
χn∑
=
z1 + z2 2 tanα n
(invα 't −invαt )
invα '及invα 可根据 α 't 、α t 查得
χ n ∑ = xn1 + xn2
Δy 或 Δyn
Δy = χ ∑ − y
Δyn = χ n ∑ − yn
按线 图计
算
齿高变动系数 中心距变动系数
Δy 或 Δyn y 或 yn
根据 z∑ 及 χ ∑ 查得 y = χ ∑ − Δy
中心距
α'
α ' = a + ym
注:1.表内公式中的x、xn(xt)本身应带正负号代入;Δy、Δyt永为正号。 2.计算高度变位圆柱齿轮几何尺寸时,公式中的y或yt,Δy或Δyt均为零。
y = z1 + z2 ( cosα −1) 2 cosα '
α ' = a + ym
invat
'=
2(xn1 + xn2 ) z1 + z2
tanα n
+
invα t
yn
=
z1 + z2 2 cos β
( cosαt cosα 't
− 1)
α ' = a + ynmn
Δy 或 Δyn
Δy = χ ∑ − y
名称
代号
已知条件及要求项目
直齿轮
斜齿(人字齿)轮
已 知 z1、z2、m、a' 求 χ ∑ 及 已知 z1、z2、mn (mt )、β、a` 求 χ n ∑
变位齿轮齿顶圆齿厚计算公式

变位齿轮齿顶圆齿厚计算公式
在机械工程中,变位齿轮是一种常见的齿轮类型,它具有非常重要的应用价值。
在变位齿轮的设计过程中,其中一个重要参数就是齿顶圆齿厚。
齿顶圆齿厚是指变位齿轮齿顶圆上的齿廓厚度,它需要根据一定的计算公式来确定。
变位齿轮齿顶圆齿厚的计算公式可以通过以下步骤来求解:
1. 首先,根据变位齿轮的模数(m)、齿数(Z)、压力角(α)、齿侧间隙系
数(x)和齿顶高(h_a),计算出分度圆齿厚(s_t)。
分度圆齿厚的计算公式为:s_t = m * π / 2 * (Z + 2 * x) * cos(α)
2. 然后,根据变位齿轮的模数(m)、压力角(α)和齿顶高(h_a),计算出
齿顶圆半径(r_a)。
齿顶圆半径的计算公式为:r_a = m * (Z + 2) / 2 * cos(α) - h_a
3. 最后,根据变位齿轮的模数(m),计算出齿面高度(h_f)。
齿面高度的计算公式为:h_f = 2 * m * cos(α)
综上所述,变位齿轮齿顶圆齿厚的计算公式可以表示为:s_t = m * π / 2 * (Z +
2 * x) * cos(α)
值得注意的是,上述计算公式仅适用于一些特定的变位齿轮设计,实际设计中
可能需要结合具体要求进行修改和优化。
因此,在进行齿顶圆齿厚计算时,建议根据实际情况进行验证和调整。
变位齿轮的计算方法

变位齿轮的计算方法变位齿轮是一种齿轮传动装置,它由两个或多个具有不同齿数的齿轮组成,通过啮合来传递动力和运动。
变位齿轮广泛应用于各种机械设备中,如汽车变速器、工程机械、纺织机械等。
在设计和计算变位齿轮时,需要考虑齿轮的齿数、模数、齿宽、啮合角等参数。
下面将介绍变位齿轮的计算方法。
一、齿轮齿数的选择:在变位齿轮传动设计中,首先要确定齿轮的齿数。
齿数的选择需要考虑传动比、装置的重量、运动平稳性等因素。
一般来说,齿数越多,传动比越大,装置越重,运动平稳性越差。
因此,需要在齿数和传动比之间进行权衡。
二、模数的确定:模数是变位齿轮设计中的一个重要参数,它决定了齿轮的尺寸和齿面强度。
模数的选择需要根据变位齿轮的工作条件和要求来确定。
通常情况下,模数应该使齿轮在满足强度要求的前提下,尽可能小,以减小齿轮的体积和重量。
三、齿宽的计算:齿宽是指齿轮齿面的有效工作宽度,它决定了变位齿轮传动的承载能力和寿命。
齿宽的计算需要考虑齿轮的载荷、齿数和模数等因素。
一般来说,齿宽应该使齿轮在满足强度要求的前提下,尽可能小,以减小齿轮的尺寸和重量。
四、啮合角的计算:啮合角是指变位齿轮齿面的啮合角度,它决定了齿轮传动的配合性能和工作平稳性。
啮合角的计算需要考虑齿轮的齿数、齿宽和模数等因素。
一般来说,啮合角应该使齿轮在满足配合性能要求的前提下,尽可能小,以减小齿轮的摩擦和磨损。
以上是变位齿轮的基本计算方法。
在实际设计和计算中,还需要考虑齿面的修形、齿轮的加工精度、齿轮的轴向力和径向力等因素。
设计变位齿轮需要综合考虑齿轮传动的强度、齿轮的尺寸和重量、齿轮的运动平稳性和配合性能等因素,以满足机械设备的要求。
变位齿轮的计算方法

变位齿轮的计算方法
变位齿轮的计算方法包括以下几个步骤:
1. 确定传动比:根据所需的输出速比确定传动比。
例如,如果需要将输入齿轮的速度增加一倍,则传动比为2。
2. 计算总齿数:根据传动比和输入齿轮的齿数确定输出齿轮的齿数。
总齿数等于输入齿轮的齿数乘以传动比。
例如,如果输入齿轮有20齿,传动比为2,则输出齿轮应有40齿。
3. 确定齿轮模数:根据总齿数和齿轮的模数确定齿轮的模数。
模数是一个标准参数,可以在齿轮手册或标准表中查找得到。
4. 计算节圆直径:根据齿轮的模数和齿数计算节圆直径。
节圆直径等于模数乘以齿数。
5. 计算齿轮高度:根据齿轮模数,齿数和节圆直径计算齿轮高度。
齿轮高度可以根据标准表或公式计算得到。
6. 设计齿轮齿型:根据齿轮的模数,齿数和齿轮高度,选择合适的齿轮齿型。
常见的齿型有直齿、斜齿、渐开线齿等。
变位齿轮几何参数计算

变位齿轮几何参数计算变位齿轮是一种能够实现传动的机械装置,其特点是能够传递转矩和变速的功能。
变位齿轮几何参数计算是设计变位齿轮传动的重要步骤之一,本文将对变位齿轮几何参数计算进行详细介绍。
主要内容涵盖变位齿轮的基本概念、几何参数的计算方法以及相关的应用举例。
一、变位齿轮的基本概念变位齿轮是由一对轴平行并且具有相同模数的齿轮组成的,其中一只齿轮的齿数是固定不变的,称为定齿轮;另一只齿轮的齿数是可变的,称为动齿轮。
变位齿轮传动通过改变动齿轮的齿数来实现变速。
二、几何参数的计算方法1.变位齿轮的齿数计算变位齿轮的齿数计算需要确定定齿轮的模数和动齿轮的模数变化量。
固定的定齿轮齿数N1可根据传动比和任意选定的动齿轮齿数N2计算得到。
变位齿轮的齿轮传动比等于定齿轮的齿数除以动齿轮的齿数,即传动比i=N1/N22.变位齿轮的齿廓计算变位齿轮的齿廓计算需要根据变位齿轮的齿数、螺旋角和压力角来确定。
变位齿轮的齿形是沿齿轮直齿廓方向逐渐变化的。
在变位齿轮的齿廓计算中,首先需要确定变位齿轮的基圆半径和齿顶高,然后根据基圆半径和齿顶高计算齿根高和齿根圆半径。
最后,根据齿根高、齿根圆半径和变位齿轮的螺旋角、压力角来计算出齿廓。
三、相关应用举例1.变位齿轮传动装置的设计根据给定的传动比和传动功率,可以利用变位齿轮几何参数计算的结果设计出适合的变位齿轮传动装置,以实现所需的变速和传动效果。
2.变位齿轮传动的优化通过调整变位齿轮的几何参数,如齿数、齿廓等,可以优化传动装置的性能,比如降低传动中的噪音和振动,提高传动效率等。
3.变位齿轮的制造利用变位齿轮几何参数计算的结果可以指导齿轮的加工制造,保证制造出的变位齿轮符合设计要求。
总结:变位齿轮几何参数计算是设计变位齿轮传动的基本步骤之一,通过计算齿数和齿廓等参数可以实现变位齿轮传动的设计、优化和制造。
变位齿轮传动在机械装置中具有重要的应用和发展前景,对于提高传动效果和性能具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(invα '−invα )
invα '及invα 可根据 a' 、 a 由
表查得
χ ∑ = x1 + x2
χn∑
=
z1 + z2 2 tanα n
(invα 't −invαt )
invα '及invα 可根据 α 't 、α t 查得
χ n ∑ = xn1 + xn2
Δy 或 Δyn
Δy = χ ∑ − y
Δyn = χ n ∑ − yn
按线 图计
算
齿高变动系数 中心距变动系数
Δy 或 Δyn y 或 yn
根据 z∑ 及 χ ∑ 查得 y = χ ∑ − Δy
中心距
α'
α ' = a + ym
注:1.表内公式中的x、xn(xt)本身应带正负号代入;Δy、Δyt永为正号。 2.计算高度变位圆柱齿轮几何尺寸时,公式中的y或yt,Δy或Δyt均为零。
y 或 yn α或α t
y = a'−a m
α = 20°
yn
=
a'−a mn
α n = 20° ; tanα t = tanα n / cos β
按公 式计
算
பைடு நூலகம்
啮合角
α '或α t '
cosα
'
=
α α'
cosα
t
cosα
t
'
=
α α'
cosα
t
总变位系数 齿高变动系数
χ∑或 χn∑
χ∑
=
z1 + z2 2 tanα
Δyn = χ n ∑ − yn
中心距变动系数
按线 图计
算
齿高变动系数
总变位系数
y 或 yn Δy 或 Δyn χ∑或 χn∑
y = a'−a ,其中 m
a
=
1 2
m( z1
+
z2 )
根据 z∑ 及 χ ∑ 查得
yn
=
a'−a mn
,
yt
=
a'−a mt
,其中
a
=
mn 2 cos
β
( z1
+
z2 )
Δyn = (Δyt − ω × z∑ ) / cos β Δyt 根据 z∑ 及 yt 查得, ω 根据 1000 yt / z∑ 及 β 查得
χ ∑ = y + Δy ; χ ∑ = x1 + x2
χ n ∑ = yn + Δyn ; χ n ∑ = xn1 + xn2
已知条件及要求项目
已知 z1、z2、m、a' 求 χ ∑ 及 Δy
y = z1 + z2 ( cosα −1) 2 cosα '
α ' = a + ym
invat
'=
2(xn1 + xn2 ) z1 + z2
tanα n
+
invα t
yn
=
z1 + z2 2 cos β
( cosαt cosα 't
− 1)
α ' = a + ynmn
Δy 或 Δyn
Δy = χ ∑ − y
已 知 z1、z2、mn (mt )、β 、 χ n ∑ ( χ t ∑ )求 a' 及 Δyn
压力角
α 或αt
α = 20°
α n = 20° ; tanαt = tanα n / cos β
啮合角
按公 式计
算
中心距变动系数
中心距
齿高变动系数
α ' 或α't y 或 yn α'
inva' = 2(x1 + x2 ) tanα + invα z1 + z2
名称
代号
已知条件及要求项目
直齿轮
斜齿(人字齿)轮
已 知 z1、z2、m、a' 求 χ ∑ 及 已知 z1、z2、mn (mt )、β、a` 求 χ n ∑
Δy
及 Δyn
未变位时的中心距
a
a
=
1 2
m( z1
+
z2
)
a
=
1 2
mt
( z1
+
z2 )
=
mn 2 cos
β
( z1
+
z2 )
中心距变动系数 压力角
Δyn = (Δyt − μz∑ ) / cos β Δyt 根据 z∑ 及 χ t ∑ 查得
μ 根据1000 χ t ∑ / z∑ 及 β 查得 yn = χ n ∑ − Δyn
α ' = a + ynmn
